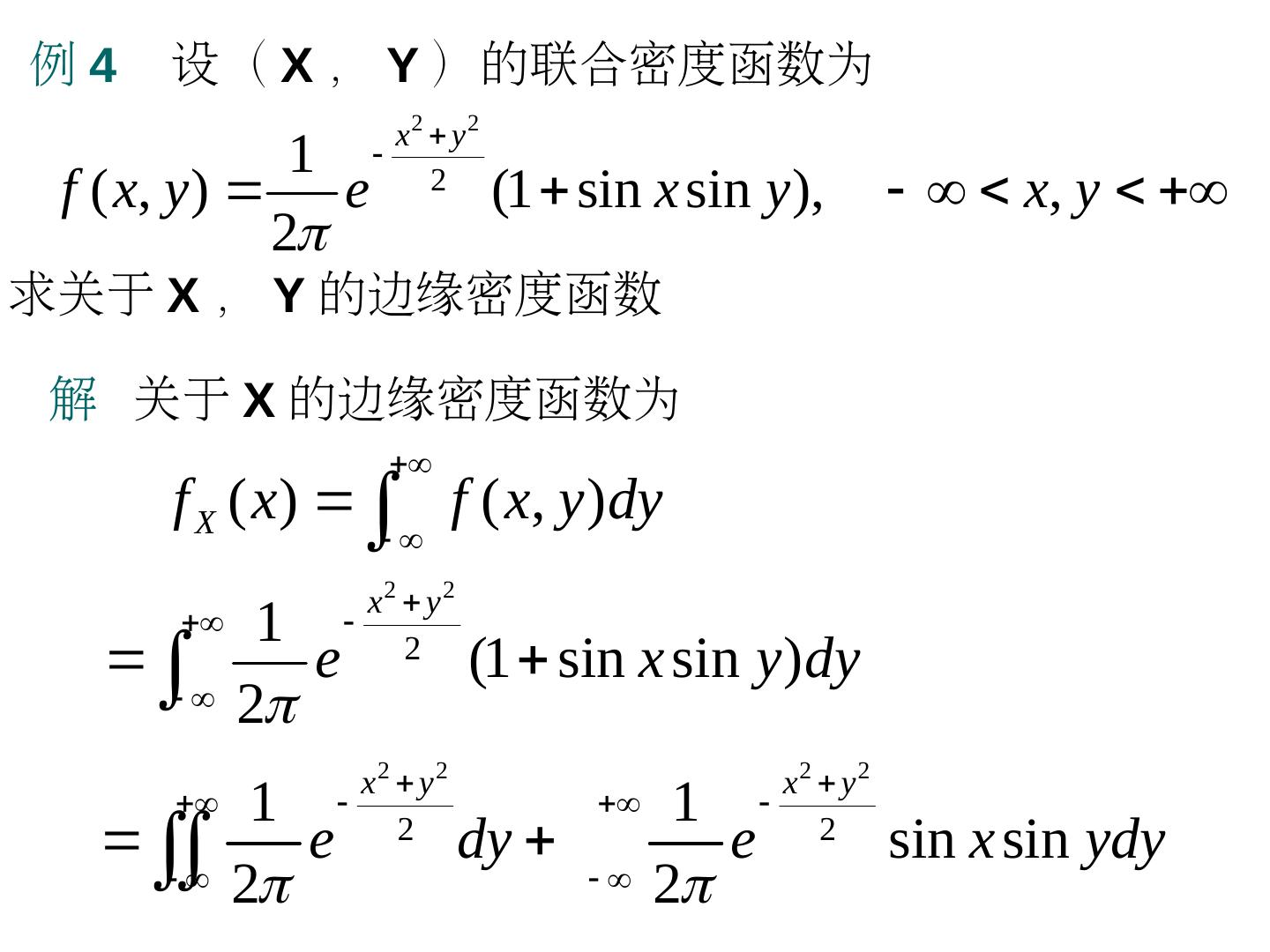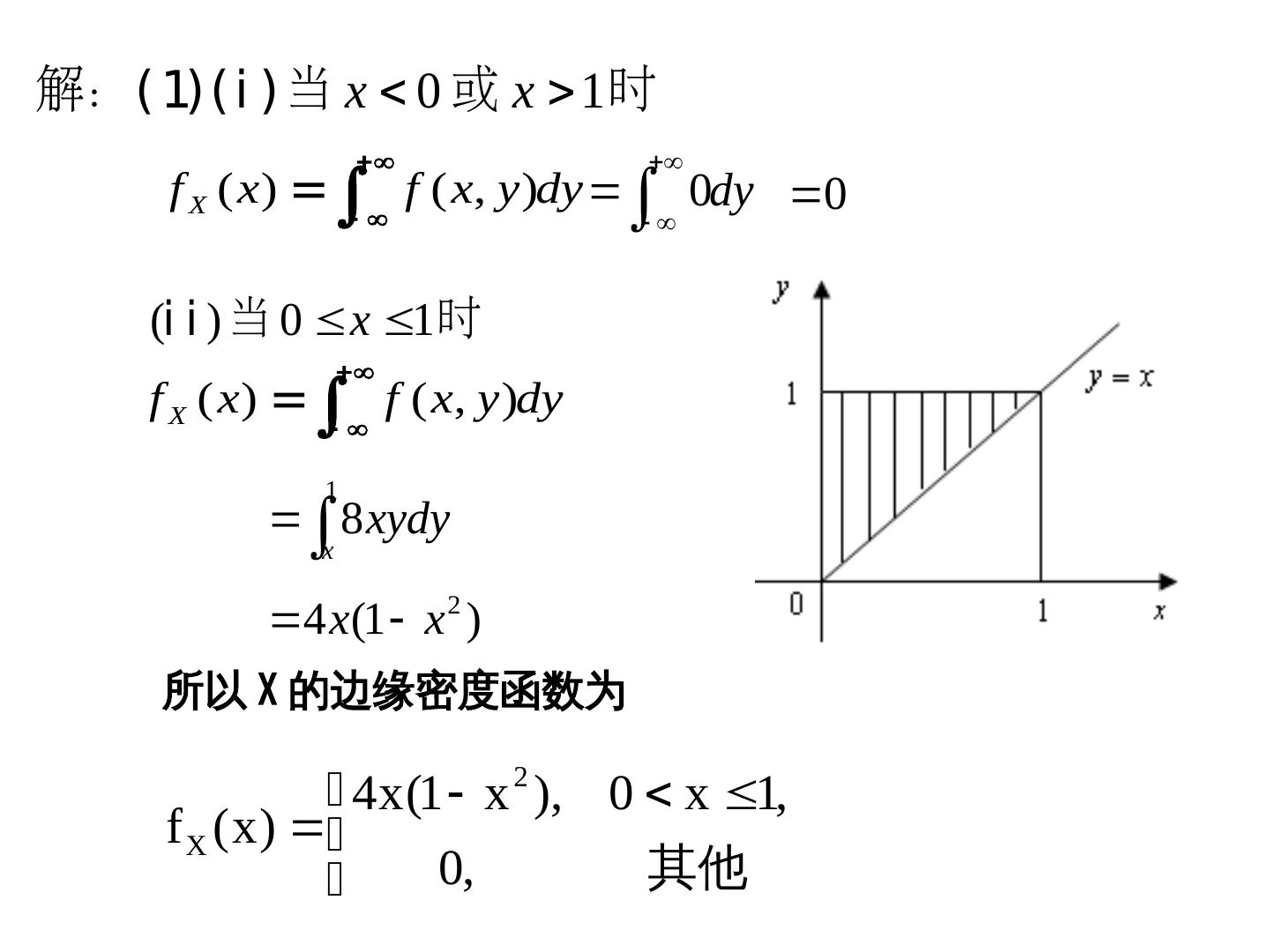
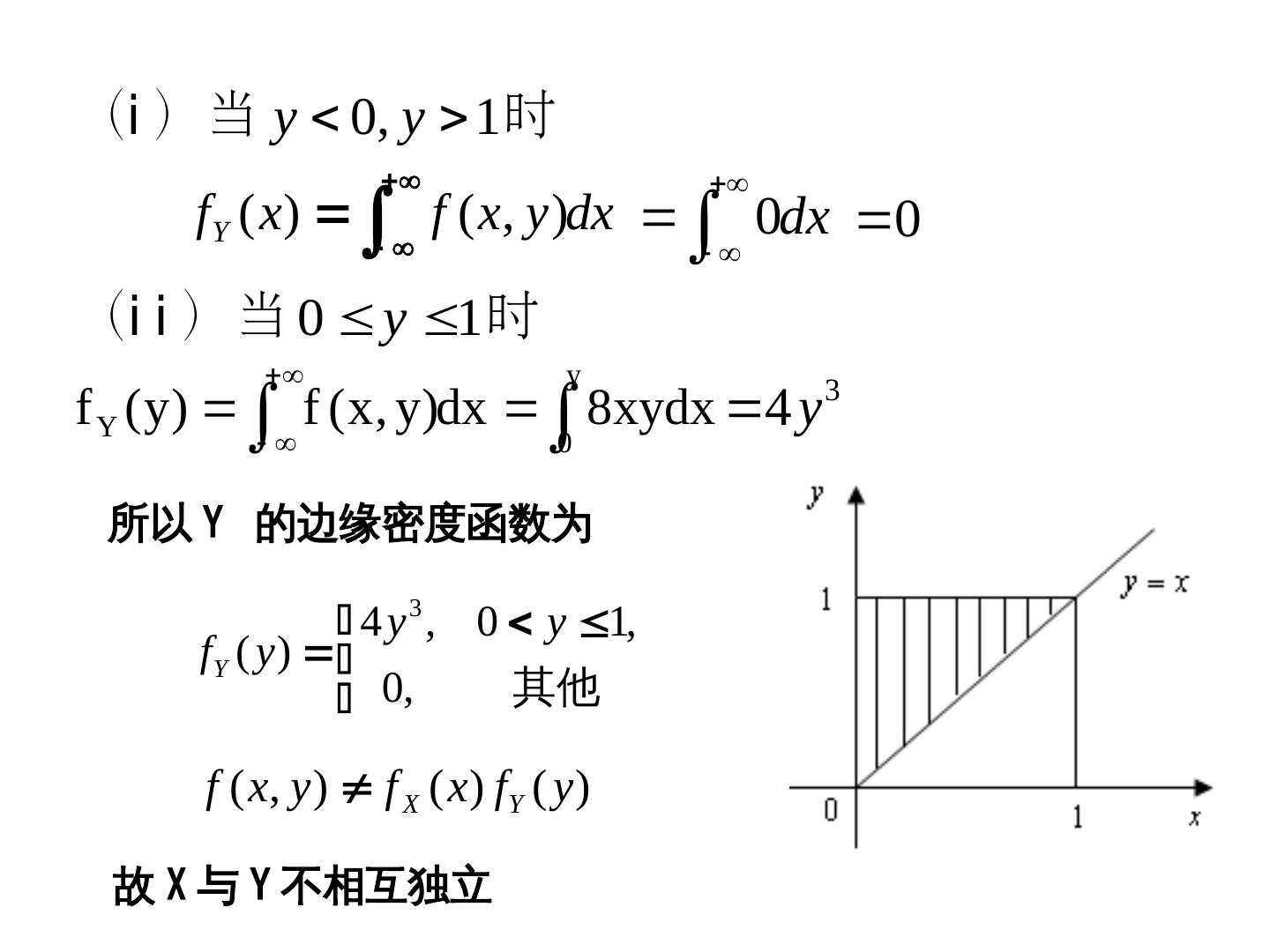
概率论与数理统计第五章--二维随机变量及其分布

1 .第五章 二维随机变量及其分布  二维随机变量及分布函数  二维离散型随机变量  二维连续型随机变量  边缘分布  随机变量的独立性  条件分布 

2 .§1.1 二维随机变量及分布函数 一、 二维随机变量 一般地，如果两个变量所组成的有序数组即 二维变量（ X ， Y ），它的取值是随着实验结 果而确定的，那么称这个二维变量（ X ， Y ） 为二维随机变量，相应地，称（ X ， Y ）的取 值规律为二维分布 

3 .§5.1 二维随机变量及分布函数 二、联合分布函数 定义： 设 (X,Y)X,Y) 是二维随机变量， 则称 F(X,Y)x,y)=P{Xx,Yy} 为 (X,Y)X,Y) 的分布函数，或 X 与 Y 的联合分布函数 , 其 中 x,y 是任意实数 . 注：联合分布函数是事件 {X≤x} 与 {Y≤y} 同时发 生 (X,Y) 交 ) 的概率 

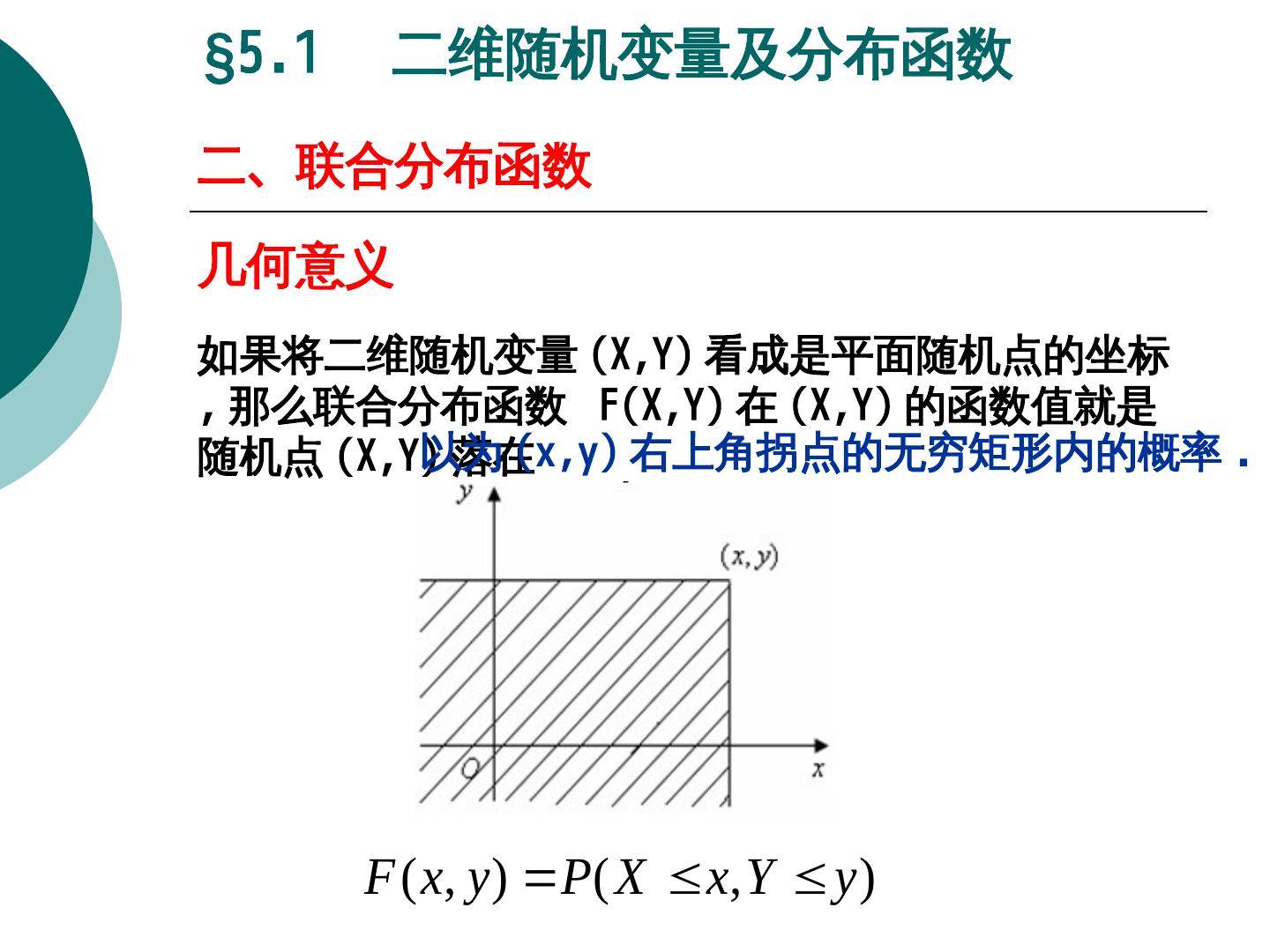
4 .§5.1 二维随机变量及分布函数 二、联合分布函数 几何意义 如果将二维随机变量 (X,Y)X,Y) 看成是平面随机点的坐标 , 那么联合分布函数 F(X,Y)X,Y) 在 (X,Y)X,Y) 的函数值就是 以为 随机点 (X,Y)X,Y) (X,Y)x,y) 右上角拐点的无穷矩形内的概率 . 落在 F ( x , y )  P ( X  x, Y  y ) 

5 .§5.1 二维随机变量及分布函数 二、联合分布函数 性质 ① 对任意的 x,y, 有 0≤F(X,Y)x,y)≤1; ② F(X,Y)x,y) 关于 x 、关于 y 单调不减； 当 x1  x2 时，有 F ( x1 , y ) P( X  x1 , Y  y ) P ( X  x2 , Y  y ) F ( x2 , y ) 当 y1  y2 时，有 F ( x, y1 ) P( X x, Y  y1 ) P ( X  x, Y  y2 )  F ( x, y2 ) 

6 .§5.1 二维随机变量及分布函数 二、联合分布函数 性质 ③ F(X,Y)x,y) 关于 x 、关于 y 右连续 F ( x0  0, y )  lim F ( x, y ) F ( x0 , y ) x  x0 0 F ( x, y0  0)  lim F ( x, y ) F ( x, y0 ) y  y0 0 

7 . §5.1 二维随机变量及分布函数 二、联合分布函数 性质 ④ F (  , )  lim F ( x, y ) 0 x   y   F (, )  lim F ( x, y ) 1 x   y   F ( x, )  lim F ( x, y ) 0 y   F (  , y )  lim F ( x, y ) 0 x   

8 .§5.1 二维随机变量及分布函数 二、联合分布函数 性质 ⑤ 随机点 (X,Y)X,Y) 落在矩形区域 {( x, y ) | x1  X x2 , y1  Y  y2 } y 的概率 y2 y1 0 x1 x2 x P( x1  X x2 , y1  Y  y2 ) F ( x2 , y2 )  F ( x2 , y1 )  F ( x1 , y2 )  F ( x1 , y1 ) 

9 .§5.1 二维随机变量及分布函数 二、联合分布函数 性质 注：任何一个二维联合分布函数 F(X,Y)x,y) 必具有以 上五条基本性质，还可证明具有以上五条性质的 二元函数 F(X,Y)x,y) 一定是某个二维随机变量的分布 函数 . 即这五条性质是判定一个二元函数是否为 某个随机变量的分布函数的充要条件 

10 .例 1. 已知二维随机变量 (X,Y)X,Y) 的分布函数为 F ( x, y )  A[ B  arctan x][C  arctan y ] 求常数 A ， B ， C.   解 : F ( , )  A[ B  ][C  ] 1 2 2  F (  , y )  A[ B  ][C  arctan y ] 0 2  F ( x, )  A[ B  arctan x ][C  ] 0 2  1  B C  A 2 2  

11 . §5.2 二维离散型随机变量 一、二维离散型随机变量及联合分布律 1. 二维离散型随机变量定义 若二维随机变量 (X,Y)X,Y). 如果它可能取的值是有限个或 可数多个数组对 (X,Y)xi,yj),(X,Y)i,j ＝ 1,2,… ) ，则称 (X,Y)X,Y) 为二维离散型随机变量。 2. 联合分布律 若二维离散型随机变量 (X,Y)X,Y) 取 (X,Y)xi,yj) 的概率为 pij , 则称 P{X ＝ xi,Y ＝ yj} ＝ pij ， (X,Y)i,j ＝ 1, 2,…) ， 为二维离散型随机变量 (X,Y)X,Y) 的分布律，或随机变量 X 与 Y 的联合分布律 . 可记为 (X,Y)X,Y) ～ P{X ＝ xi, Y ＝ yj,} ＝ pij ,(X,Y)i,j ＝ 1,2,…) ， 

12 .§5.2 二维离散型随机变量 一、二维离散型随机变量及联合分布律 二维离散型随机变量的分布律也可列表表示如下 : Y y1 y2 … yj … X x1 p11 p12 … p1j … x2 p21 p22 … p2j … … … … … … … xi pi1 pi2 … pij … … … … … … … 联合分布律的性质 (X,Y)1) 0≤pij≤1, i, j ＝ 1, 2, … (X,Y)2)  i 1 j 1 pij＝1 

13 .§5.2 二维离散型随机变量 一、二维离散型随机变量及联合分布律 例 2一口袋中有三个球，它们依次标有数字 1,2,2. 从这 袋中任取一球后 , 不放回袋中 , 再从袋中任取一球 . 设每 次取球时 , 袋中各个球被取到的可能性相同 . 以 X,Y 分别 记第一次、第二次取得的球上标有的数字 . 求 : (X,Y)1) X,Y 的分布律 ;(2) P(X≥Y). 解 : P(X=1,Y=2)=(1/3)×1=1/3 P(X=2,Y=1)=(2/3)×(1/2)=1 /3 P(X=2,Y=2)=(2/3)×(1/2)=1/ 3 Y 1 2 X 1 0 1/3 2 1/3 1/3 

14 . §5.2 二维离散型随机变量 一、二维离散型随机变量及联合分布律 (2) 由于事件 {X≥Y}={X=1,Y=1}∪{X=2,Y=1}∪{X=2,Y=2} 且三个事件互不相容 , 因此 P(X≥Y)=P(X=1,Y=1)+P(X=2,Y=1)+P(X=2,Y=2) =0+(1/3)+(1/3)=2/3 有放回抽取方式 P(X=1,Y=1)=1/9 Y 1 2 P(X=1,Y=2)=2/ X 9 P(X=2,Y=1)=2/9 1 1/9 2/9 P(X=2,Y=2)=4/ 2 2/9 4/9 9 

15 .§5.2 二维离散型随机变量 一、二维离散型随机变量及联合分布律 分布律与分布函数的关系 若 (X,Y)X,Y) 的分布律为 P{X=xi,Y=yj}=pij, i,j=1,2,… 则 (X,Y)X,Y) 的分布函数为 F(x,y)  p xi x,yj y ij 其中和式是对一切满足 xi≤x , yj≤y 求和。 

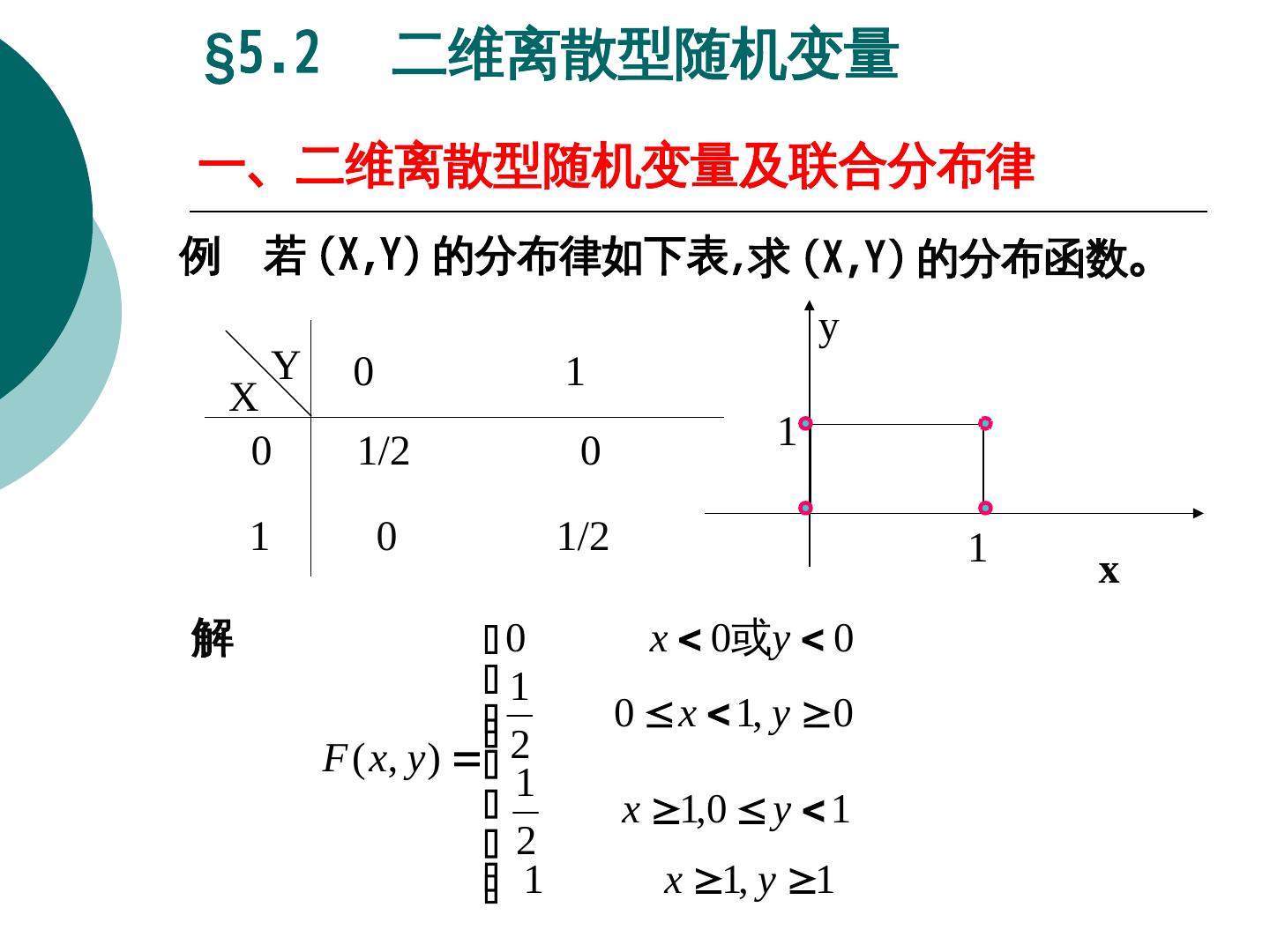
16 .§5.2 二维离散型随机变量 一、二维离散型随机变量及联合分布律 例 若 (X,Y)X,Y) 的分布律如下表， 求 (X,Y)X,Y) 的分布函数。 y Y 0 1 X 0 1/2 0 1 1 0 1/2 1 x 解 0 x  0或y  0 1  0  x  1, y 0 F ( x, y )   2 1  x 1,0  y  1  2  1 x 1, y 1 

17 . §5.3 二维连续型随机变量 一、二维连续型随机变量及联合密度函数 1. 定义：设 (X,Y)X,Y) 的分布函数为 F(X,Y)x,y), 若存在一非负 函数 f(X,Y)x,y), 使得对于任意的实数 x,y 有 y x F ( x, y )    f ( x, y )dydx   则称 (X,Y)X,Y) 是连续型二维随机变量 , 函数 f(X,Y)x,y) 称 为二维随机变量 (X,Y)X,Y) 的 (X,Y) 联合 ) 概率密度函数 . 2 ．概率密度 f(X,Y)x,y) 的性质 （1）非负性 f ( x, y ) 0.   （2）规范性   f ( x, y )dxdy  F (,) 1.   

18 . §5.3 二维连续型随机变量 一、二维连续型随机变量及联合密度函数 (X,Y)3). 若 f(X,Y)x,y) 在点 (X,Y)x,y) 连续，则有 F2 ( x, y) f ( x , y)  xy y x 因为 F( x, y)   f (u, v)dudv.   (X,Y)4). 设 G 是 xy 平面上的一个区域 , 点 (X,Y)X,Y) 落在f ( x, y ) G 内的概率为 : P{( X , Y )  G }  f ( x , y )dxdy G 在几何上 z= f(X,Y)x,y) 表示空间的一个曲面。 P{(X,Y)X,Y)∈G} 的值等于以 G 为底 , 以曲面 z= f(X,Y)x,y) 为顶面的柱体体积。 y D x 

19 . §5.3 二维连续型随机变量 一、二维连续型随机变量及联合密度函数 例 3: 设二维随机变量 (X,Y)X,Y) 具有概率密度  ce  ( 2 x  4 y ) , x  0, y  0, f ( x, y )    0 其他 求： (X,Y)1) 常数 c ； (2)P(X≥Y).   解 : (X,Y)1) 由性质     f ( x, y )dxdy 1 得到    0 0 ce  ( 2 x  4 y ) dxdy 1     1 1  dxdy c  e dx  e  (2 x4 y )  2x  4y ce dy c   0 0 0 0 2 4 因此解得 c=8 

20 .§5.3 二维连续型随机变量 一、二维连续型随机变量及联合密度函数 (2)P(X≥Y)= f ( x, y)dxdy x y  x   dx 8e dy  2e  2 x ( e  4 y ) |0x dx  (2 x4 y ) = 0 0 0     )dx  2e   2x  4y  2x = 2e (1  e dx  2e  6 x dx 0 0 0 = 1 1  6 x  e |0 3 1 2 = 1  3 3 

21 .§5.3 二维连续型随机变量 二、两个常见二维连续型随机变量的联合密度函数 (X,Y) 一 ) 均匀分布 定义 : 设 G 是平面上的有限区域 , 面积为 A, 若二维 随机向量 (X,Y)X,Y) 具有概率密度 . 1  ( x, y)  G f ( x , y )  A  0 其他 则称 (X,Y)X,Y) 在 G 上服从均匀分布。 

22 . §5.3 二维连续型随机变量 二、两个常见二维连续型随机变量的联合密度函数 例：设二维随机变量 (X,Y)X,Y) 服从区域 G 上的均匀分布 , 其中 G={0<x<1,|y|<x}, 求 (X,Y)X,Y) 的联合密度函数 . y 解： (1,1) y=x o x y=-x (1,-1)  1 0  x  1, | y | x; f ( x, y )    0 其他 

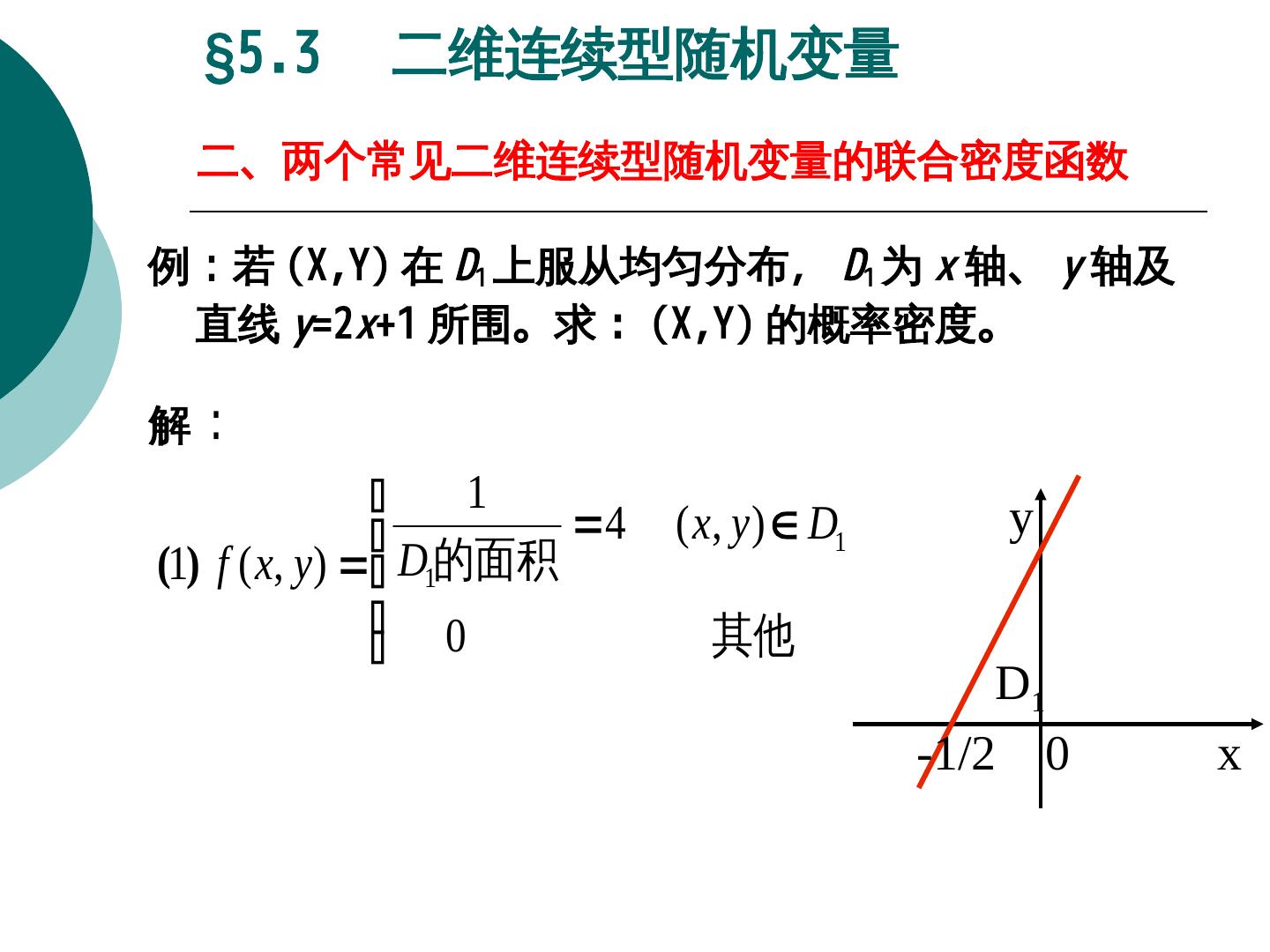
23 . §5.3 二维连续型随机变量 二、两个常见二维连续型随机变量的联合密度函数 例：若 (X,Y)X,Y) 在 D1 上服从均匀分布， D1 为 x 轴、 y 轴及 直线 y=2x+1 所围。求 : (X,Y)X,Y) 的概率密度。 解：  1  4 ( x, y )  D1 y (1) f ( x, y )  D1的面积  0 其他  D1 -1/2 0 x 

24 . §5.3 二维连续型随机变量 二、两个常见二维连续型随机变量的联合密度函数 (X,Y) 二 ) 二维正态分布 定义 : 若 (X,Y)X,Y) 具有概率密度 1 ( x  1 ) 2 ( x  1 )( y   2 ) ( y   2 ) 1  2 2 (1  ) [  12  2  2   22 ] f ( x , y)  e 2 1 2 1   2    x  ,  y   其中 -∞<μ1<+∞, -∞<μ2<+∞,σ1>0,σ2>0 ,|ρ|<1, 则称 (X,Y)X,Y) 服从参数为 μ1,μ2,σ21,σ22,ρ 的二维正态分布 ， 记为 :(X,Y)X,Y)N(X,Y)μ1,μ2, σ21,σ22,ρ). 

25 . 1. 随机变量（ X ， Y ）的概率密度为  e y 0 x y f ( x , y )   0 others 求：（ 1 ） P{X0},(X,Y)2)P{X1},(X,Y)3)P{Y  y0} 答 : P{X0}=0 y 1  P { X 1}  dx e  y dy 1  e  1 D 0 x  y0 y0  dx  e  y dy y0  0 P {Y  y0 }  x  0 x  0 y 0 0 

26 .2. 已知二维随机变量（ X ， Y ）的分布密度为 的分布密度为 1  (6  x  y ), 0  x  2, 2  y  4 f ( x, y )  8  0, 其他 求概率 (1) P  X  1, Y  3 ; (2) P  X  Y  3 解 P  X  1, Y  3  4 f ( x, y )dxdy D 1 1 3 2 dx (6  x  y )dy 0 2 8 1 2 11 1 2 3 3  (6 y  xy  y ) 2 dx  08 2 8 

27 .续解 ……… . P  X  Y  3 f ( x, y )dxdy D 1 3 x 1 dx (6  x  y )dy 0 2 8 1 1 1 2 x+y=3  (6 y  xy  y ) 3 x 2 dx 08 2 5  24 

28 . §5.4 边缘分布 一、边缘分布函数 1 ．边缘分布 设 F(X,Y)x,y) 为二维随机变量 (X,Y)X,Y) 的联合分布函数，称 P(X,Y)X≤x)=P(X,Y)X≤x,Y<+∞) (X,Y)-∞<x<+∞) 为 X 的边缘分布函数 , 并记为 Fx(X,Y)x). 2. 公式 . 由于 Fx(X,Y)x)=P(X,Y){X≤x}∩{Y<+∞})=P{X≤x,Y<+∞} =F(X,Y)x,+∞) 同理有 FY(X,Y)y)=F(X,Y)+∞,y). 

29 . §5.4 边缘分布 一、边缘分布函数 例 试从联合分布函数 F(X,Y)x,y) ，求关于 X, 关于 Y 的边 : 缘分布函数 FX(X,Y)x),FY(X,Y)y). 1   F ( x, y )  2 [  arctan x][  arctan y ]  2 2 解 由边缘分布函数的定义我们有 : 1   FX ( x)  lim F ( x, y )  lim 2 [  arctan x][  arctan y ] y   y    2 2 1   [  arctan x] (  x  )  2 1   FY ( x)  lim F ( x, y )  lim 2 [  arctan x][  arctan y ] x   x    2 2 1   [  arctan y ] (  y  )  2