- 快召唤伙伴们来围观吧
- 微博 QQ QQ空间 贴吧
- 文档嵌入链接
- 复制
- 微信扫一扫分享
- 已成功复制到剪贴板
概率论与数理统计第四章--随机变量及其分布
展开查看详情
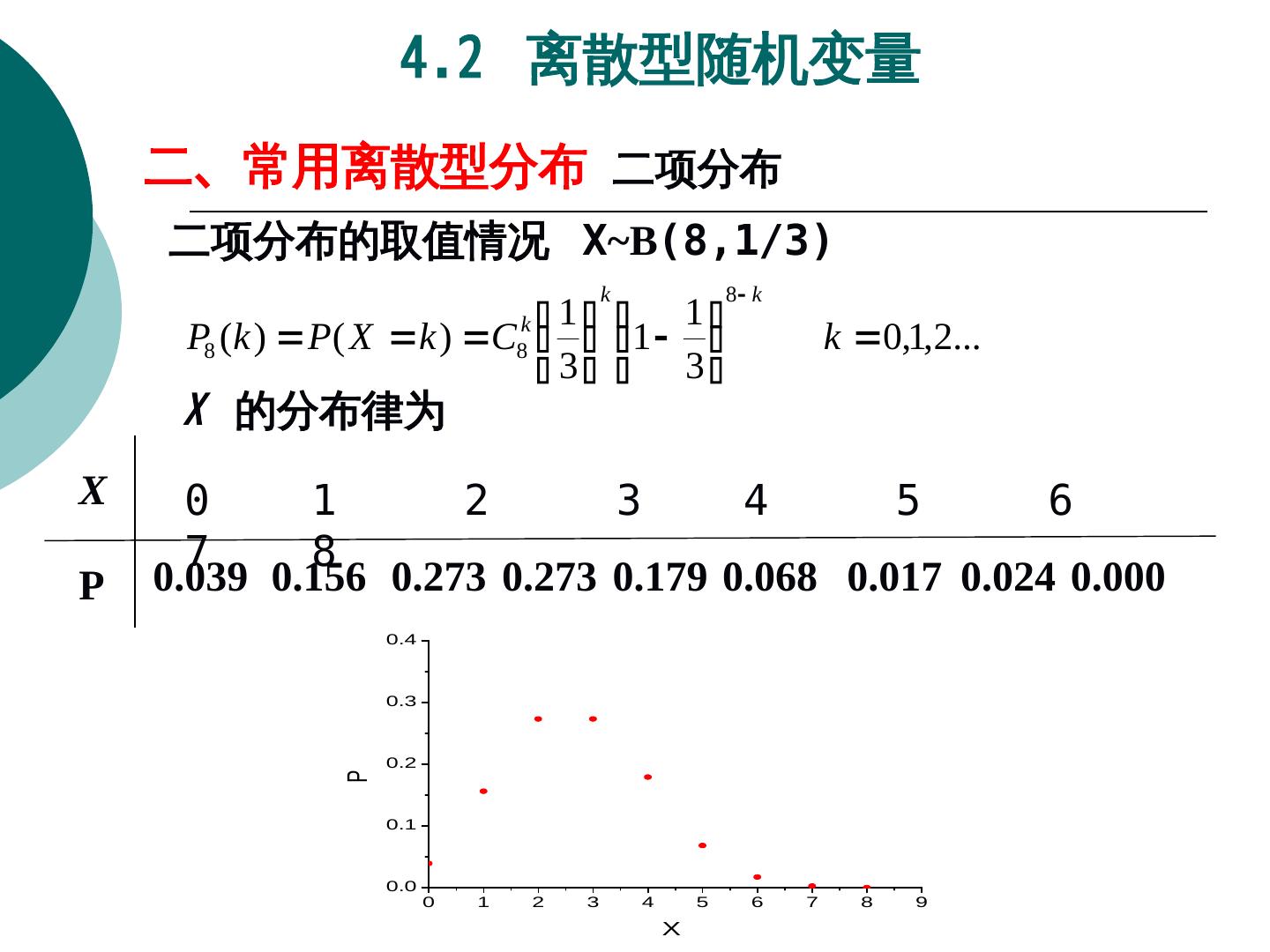
1 .第四章 随机变量及其分布 随机变量及分布函数 离散型随机变量 连续型随机变量
2 . 4.1 随机变量及分布函数 随机变量 概率论与数理统计是从数量的侧面来研 究随机现象的统计规律性的一门学科 , 为了 全面地研究随机试验的结果 , 揭示客观存在 着的统计规律性 , 我们将随机试验的结果与 实数对应起来 , 将随机试验的结果数量化 , 引入随机变量的概念 .
3 . 随机变量 Random Variable 基本思想 将样本空间数量化 , 即用数值来表示试验的结果 有些随机试验的结果可直接用数值来表示 . 例如 : 在掷骰子试验中 , 结果可用 1,2,3,4,5,6 来表 示 有些随机试验的结果不是用数量来表示, 但可数量化 例如 : 掷硬币试验 , 其结果是用汉字“正面”和“反面”来表示“正面”和“反面”来表示”和“反面”来表示“反面”和“反面”来表示”来表示 的 可规定 : 用 1 表示 “正面”和“反面”来表示朝上” 用 ” 用 0 表示“反面”和“反面”来表示朝 上” 用 ”
4 . 试验结果的数量化 例 设箱中有 10 个球,其中有 2 个红球, 8 个 白 球;从中任意抽取 球;从中任意抽取 2 个 , 观察抽球结果。 取球结果为 : 两个白球 ; 两个红球 ; 一红一白 如果用 X 表示取得的红球数,则 X 的取值可为 0 , 1 , 2 。 此时, “两只红球” = “X 取到值 2”, 可记为 {XX=2} “ 一红一白”记为 一红一白” {XX=1}, “ 两只白球”记为 两只白球” {XX=0} 特点:试验结果数量化了,试验结果与数建立了 对应关系
5 . 随机变量的定义 随机变量 设随机试验的样本空间为 Ω ,如果对于每一 个样本点 ,均有唯一的实数 与 ,均有唯一的实数 与 X与( ) 之对应,称 为样本空间 ) X X (为样本空间 Ω 上” 用 的随机 变量。 随机变量的特征 : 1) 它是一个变量; 2) 它的取值随试验结果而改变; 3) 随机变量在某一范围内取值,表示一个随机 事件。
6 .注:随机变量 X() 与高等数学中的实函数的区别: 1. X() 的定义域是样本空间 ,而 不一定 是实数集; 2. X() 的取值是随机的,它的每一个可能取值 都有一定的概率; 3 . 随机变量是随机事件的数量化 . 即对于任意 实数 x, {XX()≤x } 是随机事件 . 4 . 对于随机变量 , 我们常常关心它的取值 .
7 . 4.1 随机变量及分布函数 随机变量 特点: 1. X 的全部可能取值是互斥且完备的 2. X 的部分可能取值描述随机事件 分类: 离散型随机变量 随机变量 连续型 非离散型 奇异型(混合型)
8 . 4.1 随机变量及分布函数 随机变量 例 : 考察掷两次硬币这一试验,样本空间为 S= { HH , HT , TH , TT },令 X 表示正面出现的次数, X 是一随机 变量,且有{ X = 1 ={ HT , TH },值域 Rx= { 0 , 1,2} 例 : 假设我们关心某地区居民的身高情况,可引入 随机变量 X : ( 单位 cm) X =随机抽出一个人其身高 则 X 就是随机变量,事件“随机抽出一个人的身高不超 过 170cm” 可表示为{ X≤170 }。
9 . 4.1 随机变量及分布函数 随机变量 例 从一批量为 N 、次品率为次品率为 p 的产品中,不放回抽 取 n ( n≤Np )个,观察此样品中的次品数个,观察此样品中的次品数 . 此时观察对象为样品的次品数,我们记之为 Y , 那么 Y 的可能的取值为 0 , 1 , 2,…,n. 引入随机变量后,就可以用随机变量表示随机 试验下的各种形式的随机事件 , 比如本例中: A={X 没有次品 } A={Xω|Y(Y(ω)=0} A={Y=0} B={X 至少有 2 个次品 } B={Xω|Y(Y(ω)≥2} B={XY≥2} C={X 不多于 k 个次品 } C={Xω|Y(Y(ω)≤k} C={XY≤k}
10 . 4.1 随机变量及分布函数 随机变量 例 : 某射手向一目标射击,其弹着点的横坐标 X 是一随 机变量,其纵坐标 Y 也是随机变量。 例 : 一批产品共 100 件,其中 95 件合格, 5 件不合格。 从中有放回地一件一件地取产品,直到取出一件合格 品为止时所取出的产品件数 X 是一随机变量。 例 : 一个月某交通路口的事故数 X, 是随机变量。 例 : 用天平称量某物体的重量的误差 X ,是随机变量。
11 . 4.1 随机变量及分布函数 随机变量的分布函数 如果我们对随机事件 {XX()≤x } 求概率 , 就引出 了随机变量分布函数的概念 . 1. 分布函数的定义 设 X 是一个随机变量,称定义域为 (-∞,+∞), 函数值在区间 [0,1] 上的实值函数 F(x)=P(X≤x) (-∞<x<+∞) 为随机变量 X 的分布函数 .
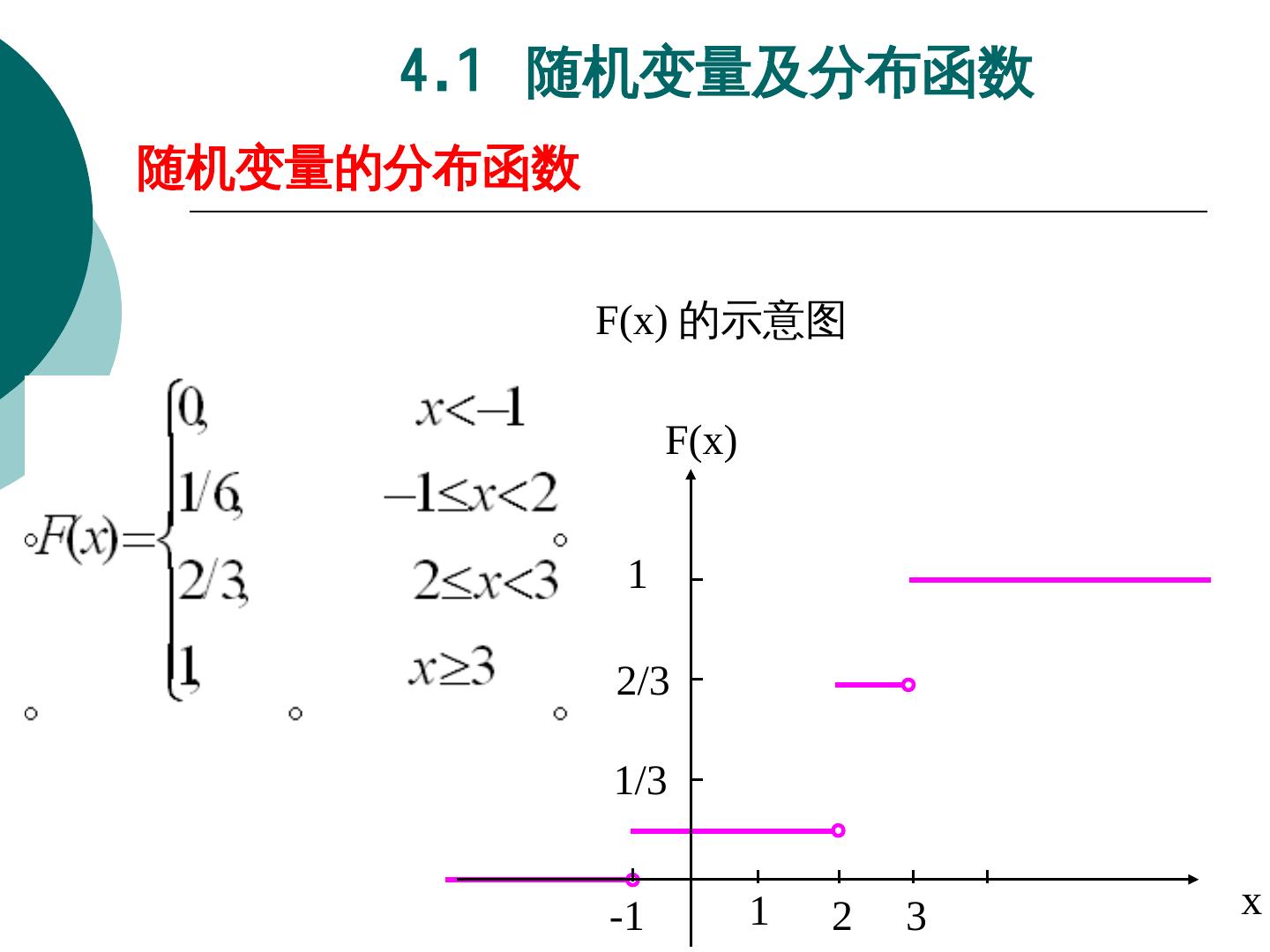
12 . 4.1 随机变量及分布函数 随机变量的分布函数 例 设一口袋中依次标有 -1,2,2,2,3,3 数字的六个 球,从中任取 1 个球,记 X 为取得的球上标有的数字, 求 X 的分布函数 . 解: X 的可能取值为 -1 , 2 , 3 ,取这些值的概率分 别为 1/6 , 1/2 , 1/3 {XX≤x} 是不可能事件, F(x)=0; 当 x 〈 -1 时, {XX≤x} 等同于 {XX=-1} , F(x)=1/6; 当 -1≤x 〈 2 时, 当 2≤x 〈 3 时, F(x)=2/3; {XX≤x} 等同于 {XX=-1 或 X=2} , 当 x≥3 时,{XX≤x} 是必然事件, F(x)=1;
13 . 4.1 随机变量及分布函数 随机变量的分布函数 F(x) 的示意图 F(x) 1 2/3 1/3 -1 1 2 3 x
14 . 4.1 随机变量及分布函数 随机变量的分布函数 由此题可以看出 一般地,若 X 为离散型随机变量,其概率 分布 P(X=xk)=Pk(k=1,2,3…) 则 X 的分布函数 为 F ( x) P{ X x} P( X xk ) pk xk x xk x
15 . 4.1 随机变量及分布函数 随机变量的分布函数 注1: ( 1 )个,观察此样品中的次品数由分布函数的定义知,分布函数 F(x) 在 x 处的函数值 是事件 F(x)=P{XX≤x}=P({Xe|Y(X(e)≤x} 的概率。 若把 X 看成数轴上的随机点的坐标,那么分布函数 F(x) 在 x 处的函数值,就是表示 X 落在区间 [-∞,x] 上的概率。 ( 2 )个,观察此样品中的次品数若已知 x 的分布函数 F(x) ,我们就知道了 X 落在任 一区间的概率,从这个意义上讲,分布函数完整地描述了 随机变量的统计规律。 ( 3 )个,观察此样品中的次品数分布函数是在 (-∞,+∞) 上值域为 [0 , 1] 的普通函 数,它具有良好的分析性质,许多概率论的问题归结为函 数的运算从而利用数字分析出许多结果,这是引入分布函 数的好处之一,再加上分布函数对任意随机变量都有定义 ,因此分布函数在理论上有极重要的地位。
16 . 4.1 随机变量及分布函数 随机变量的分布函数 注2: ( 1 )个,观察此样品中的次品数随机变量 X 是一个从样本空间到实数空间的函数,它 的定义域为样本空间 Ω。它的值域 Rx 为全体实数集或它 的一个子集。 ( 2 )个,观察此样品中的次品数从随机变量的定义来看,它与通常的函数概念没有什 么不同,把握这个概念的关键之点在于试验前后之分:在 试验前,我们不能预知它取何值,这要凭机会,“随机”的 意思就在这里,一旦试验完成后,它的取值就确定了。
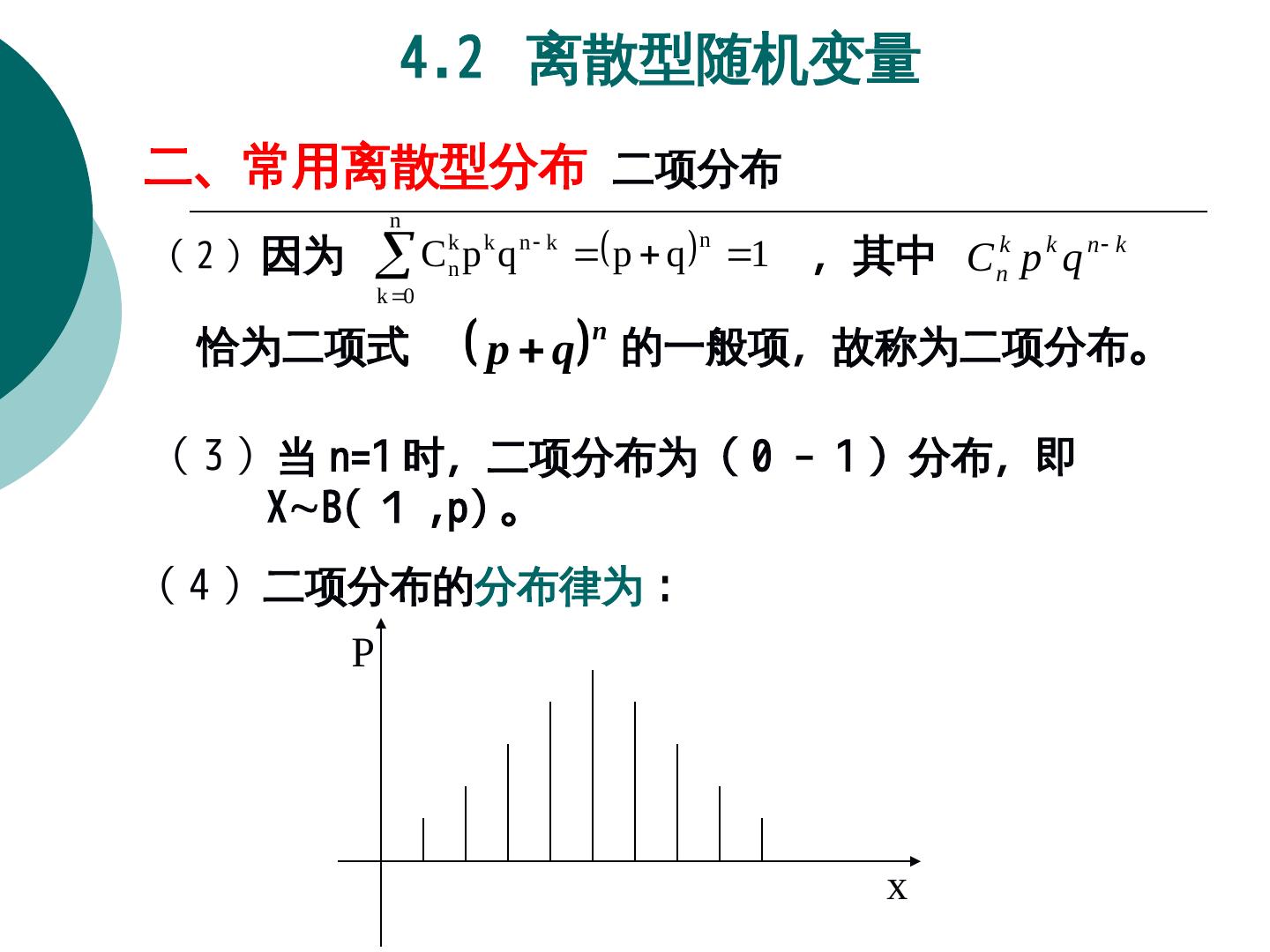
17 . 4.1 随机变量及分布函数 随机变量的分布函数 2. 分布函数的性质 (1) 0 F ( x ) 1, x R; ( 2) F ( x )是单调不减的; ( 3) F ( ) lim F ( x ) 0 ; x F ( ) lim F ( x ) 1; x (4) F ( x )为右连续,即 lim F ( x ) F ( x0 ), x0 R. x x0 0
18 . 4.1 随机变量及分布函数 随机变量的分布函数 证 (1) 由于对于任意 x R, F ( x ) 的 为一概率 , 根据概率公理化定义 , 有 0 F ( x ) 1 (2)对于 b a (a,b R), 由于 F (b ) F (a ) P ( X b ) P ( X a ) P (a X b ) 0 所以F(x)单调不减F(x)单调不减.
19 . 4.1 随机变量及分布函数 二、次品率为随机变量的分布函数 ( 3) P ( X ) P (n X n 1) n F (n 1) F (n) n lim F ( n) lim F ( m ) 1 n m 又F ( x )单调不减, 0 F ( x ) 1, 对于任意实数 与x , 有n x n 1 ( n Z ), 所以 F ( n) F ( x ) F ( n 1),0 F ( n) 1.
20 . 4.1 随机变量及分布函数 二、次品率为随机变量的分布函数
21 . 4.1 随机变量及分布函数 随机变量的分布函数 重要公式 (1) P { X b} F ( b ); ( 2) P{a X b} F (b) F (a ); ( 3) P{ X a } 1 F (a ); (4) P{ X b} F (b 0); (5) P ( X b ) F (b) F (b 0), b R.
22 . 4.1 随机变量及分布函数 二、次品率为随机变量的分布函数 重要公式 (6) P{a X b} F (b) F (a 0) (7) P{a X b} F (b 0) F (a ) (8) P{a X b} F (b 0) F (a 0)
23 . 1 F ( x) 2 是不是某一随机变量的分布函数 与? 1 x 不是 因为 lim F ( x) 0 x 1 ( x 0) 函数 与 G ( x) 1 x 2 可作为分布函数 与 1 ( x 0)
24 .例 1: 设随机变量 X 的分布函数为 0, x 1 0.2, 1 x 2 F ( x ) 0.7,2 x 4 , 1, x 4 1 求 P( X 3) ,P( 2 X 3) 及 P ( X 2) . 解: P ( X 3) F (3) 0.7 1 1 P ( X 3) F (3) F ( ) 0.7 0.2 0.5 2 2 P ( X 2) 1 P ( X 2) 1 P ( X 2) P ( X 2) 1 F ( 2) F ( 2 0) F ( 2 0) 1 0.7 0.5 0.8
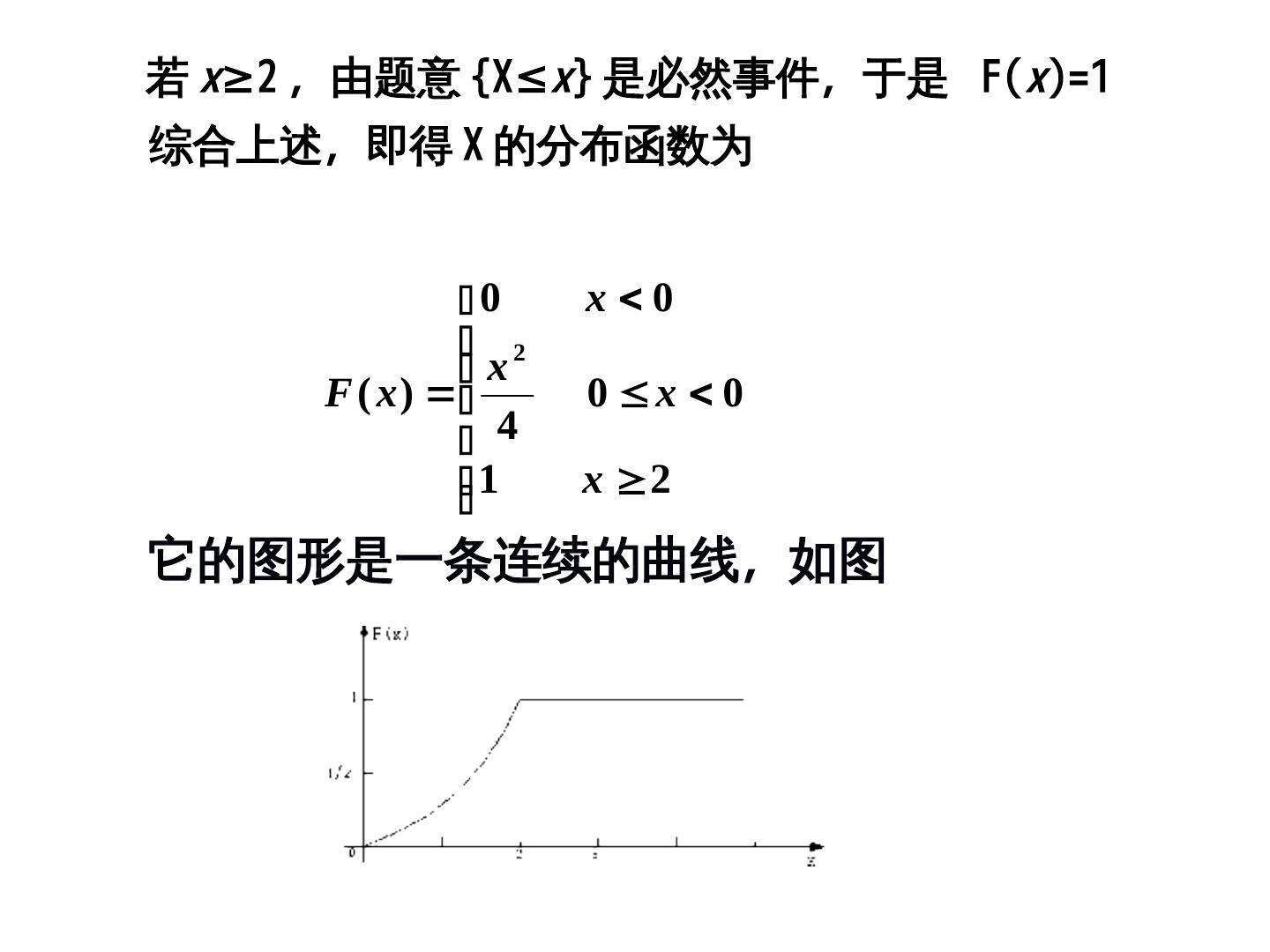
25 .例 一个靶子是半径为 2 米的圆盘,设击中靶上任一 同心圆盘上的点的概率与该圆盘的面积成正比,并设 击中都能中靶,以 X 表示弹着点与圆心的距离。试求 随机变量 X 的分布函数。 解 : 若 x<0, 则 {XX≤x} 是不可能事件,于是 F(x)=P{XX≤x}=0 若 0≤x≤2 ,由题意, P{X0≤X≤x}=kx2, k 是某一 常数,为了确定 k 的值,取 x=2 ,有 P{X0≤X≤2}=22k ,但已知 P{X0≤X≤2}=1 ,故得 k=1/4 ,即 P{X0≤X≤x}=x2/4 ,于是 F(x)=P{XX≤x}=P{Xx <0}+P{X0≤X≤x}=x2/4
26 .若 x≥2 ,由题意 {XX≤x} 是必然事件,于是 F(x)=1 综合上述,即得 X 的分布函数为 0 x0 2 x F ( x ) 0 x 0 4 1 x 2 它的图形是一条连续的曲线,如图
27 .练习 1 设连续型随机变量 X 的分布函数为 : F ( x ) A B arctan x x 求 : (1) 常系数 A 及 B ; (2) 随机变量 X 落在 (-1,1) 内的概 率. 解 (1) 根据分布函数的性质可知 F ( ) 1, F ( ) 0 依题意可得
28 . π F ( ) A B 1 2 π F ( ) A B 0 2 联立上面两个方程可以解得 1 1 A ,B 2 π (2) 随机变量 X 落在 (-1,1) 内的概率可以表示为 P { 1 X 1} F (1 0) F ( 1) 1 1 π 1 1 π 1 ( ) ( ) 2 π 4 2 π 4 2
29 .练习 2 抛掷均匀硬币 1, 正面 , X 0, 反面 . 求随机变量 X 的分布函数 . 1 解 P { X 0} P { X 1} 2 当X 0时 F ( x ) P { X x 0} 0,