概率论与数理统计第三章---条件概率与事件的独立性

1 .

2 .第三章 条件概率与 事件的独立性 • 条件概率 • 全概率公式 • 贝叶斯公式 • 事件的独立性 • 伯努力试验和二项概率 • 主观概率 

3 . 第一节条件概率 Conditional Probability  抛掷一颗骰子 , 观察出现的点数 A={ 出现的点数是奇数 } ＝｛１，３， ５｝ B={ 出现的点数不超过 3}} ＝｛１，２， ３｝ 若已知出现的点数不超过 3} ，求出现的点数是 奇数的概率 即事件 B 已发生，求事件 AB A 的概率　Ｐ（Ａ｜Ｂ）Ｐ（Ａ｜Ｂ） A (  AB ) B ( A ) (B ) 　Ｐ（Ａ｜Ｂ）　Ｐ（Ａ｜Ｂ） A B 都发生，但样本空间 缩小到只包含Ｂ的样本点Ｂ的样本点   AB 2 ( n) P( A | B)   B 3 

4 . 条件概率 Conditional Probabilit y  定义 设Ａ，Ｂ为同一个随机试验中的两个随机事Ａ，Ｂ为同一个随机试验中的两个随机事 件 , 且Ｐ（Ｂ）＞０， 则称Ｐ（Ｂ）＞０， 则称 P ( AB ) P( A B)  P( B) 为在事件 Ｂ发生的条件 下，事件 Ａ发生的条件 概率． 

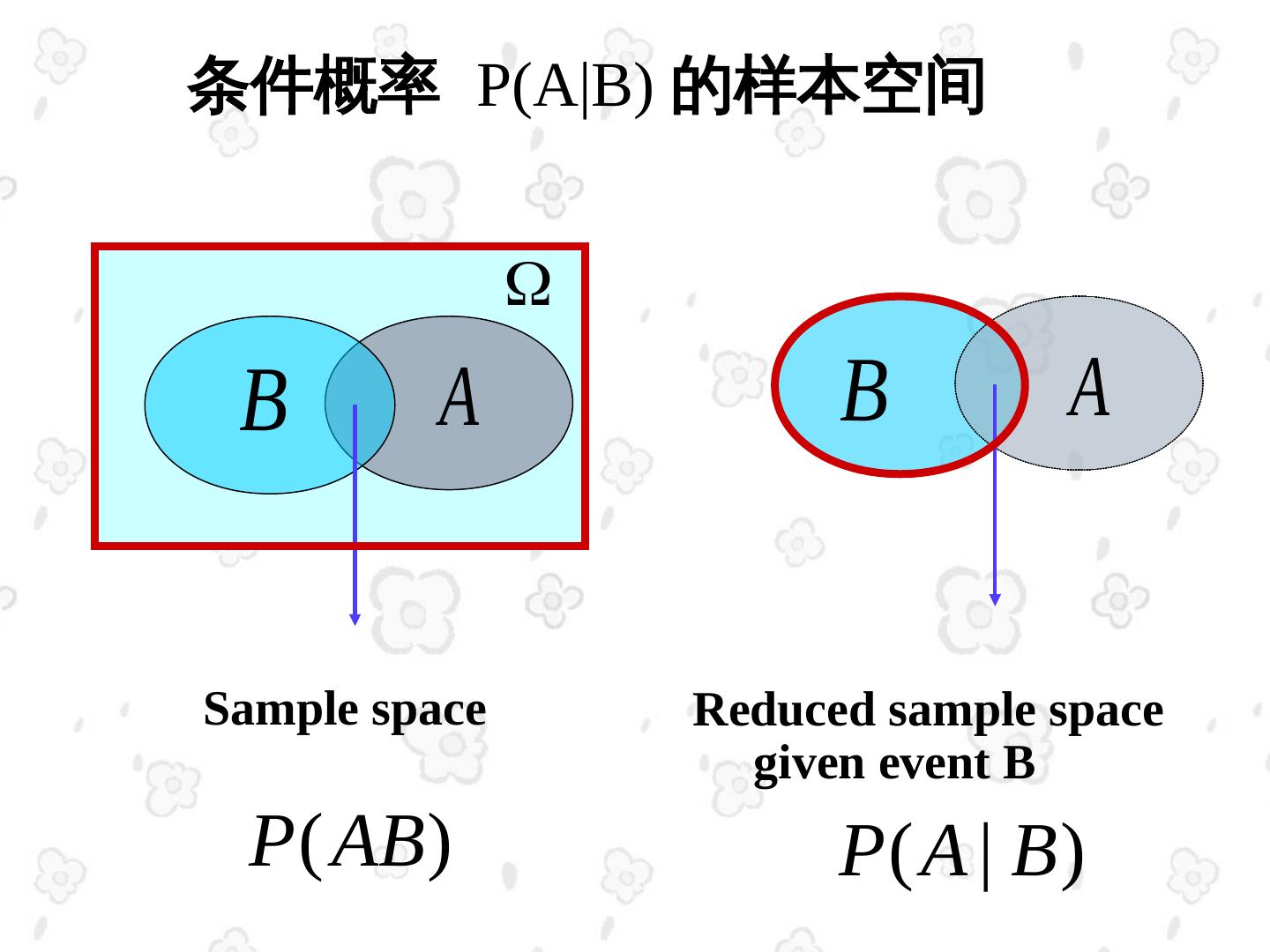
5 .条件概率 P(A|B) 的样本空间  B A B A Sample space Reduced sample space given event B P ( AB ) P( A | B) 

6 . 概率 P(A|B) 与 P(AB) 的区别与联 系 联系：事件 A ， B 都发生了 区别： （ 1 ）在 P(A|B) 中，事件 A ， B 发生有时间上的差异， B 先 A 后；在 P （ AB ）中，事件 A ， B 同时发生。 （ 2 ）样本空间不同，在 P(A|B) 中，事件 B 成为样本 空间；在 P （ AB ）中，样本空间仍为  。 因而有 P ( A B ) P ( AB ) 

7 .例 设袋中有 3 个白球， 2 个红球，现从袋中任意抽取两次 ，每次取一个，取后不放回， （ 1 ）已知第一次取到红球，求第二次也取到红球的概率 ; （ 2 ）求第一次取到红球的概率 （ 3 ）求两次均取到红球的概率 设 A—— 第一次取到红球 ,B——B—— 第二次取到红 球 (1) P ( B | A)  1 2 4 (2) P ( A)  5 2 1 1 (3) P ( AB)   5 4 10 

8 .例 设有两个口袋，第一个口袋装有 3 个黑球， 2 个 白球；第二个口袋装有 2 个黑球和 4 个白球 . 今 从第一个口袋任取一球放到第二个口袋，再从第 二个口袋任取一球，求已知从第一个口袋取出的 是白球的条件下从第二个口袋取出白球的概率 . 解 : 记 A={ 从第一个口袋取出白球 } B={ 从第二个口袋取出白球 } P(B|A)=5/7 P(A)=2/5, P(AB)=(2×5)/(5×7)=2/7 P(B|A)= P(AB)/ P(A)= 5/7 

9 .例 设Ａ，Ｂ为同一个随机试验中的两个随机事 100 件 产品中有 70 件 一等品， 25 件 二等 品，规定一、二等品为合格品．从中任取 1 件 ，求 (1) 取得一等品的概率； (2) 已知取得的是合格品，求 它是一等品的概率． 解 设Ａ，Ｂ为同一个随机试验中的两个随机事Ａ表示取得一等品，Ｂ表示取得合格品，则 （ 1 ）因为 100 件 产品中有 70 件 一等品，所以 70 P ( A)  0.7 100 （ 2 ）方法 1 因为 95 件 合格品中有 70 件 一等品，所以 ： 70 P ( A B )  0.7368 95 P( AB ) 70 100 方法 2 ： P ( A B )   0.7368 P( B) 95 100 

10 . 条件概率的另一种定义 设 A, B 是两个事件 , 且 P(A)>0, 则称 P(AB) P(B | A) = P(A) 为事件 A 发生的条件下事件 B 的条件概率 。设 A, B 是两个事件 , 且 P(B)>0, 则称 P(AB) P(A | B) = P(B) 为事件 B 发生的条件下事件 A 的条件概率 。 

11 .条件概率的性质 1. 非负性 0 ≤P(B|A) ≤1P(B|A) ≤P(B|A) ≤11 2. 规范性 P(Ω|A)=1 3. 完全可加性 对任意一两两互斥事件 B1,B2 ,…, 有   P (Bi | A)  P ( Bi | A) i 1 i 1 4. P(Ā|B)=1-P(A|B) 5. P(B1∪B2|A)=P(B1|A)+P(B2|A)-P(B1B2|A ） 

12 .条件概率 P(B|A) 的两中计算方法 1. 直接在缩减了的样本空间中计算 B 发生的 概率得到 P(B|A); 2. 在样本空间 Ω中 , 先计算 P(AB), 再得到 P(AB) P(B | A) = P(A) B A Ω 

13 .例 . 一盒中混有 100 只新 , 旧乒乓球，各有红、白 两色，分 类如下表。从盒中随机取出一球，若取得 的是一只红球，试求该红球是新球的概率。 设 A-- 从盒中随机取到一只红 球. B-- 从盒中随机取到一只新球 红 白 P ( A) 60 / 100 3 / 5 新 40 30 . 旧 20 10 P( AB ) 40 / 100 2 / 5 P ( AB ) 2 P ( B | A)   P ( A) 3 

14 . 乘法定律 P( AB) P ( AB ) P ( A) P ( B A) P( B A)  P( A) P ( B ) P ( A B ) P( AB) P( A B)  P( B)  推广 P( ABC ) P ( A) P( B A) P(C | AB) P ( A1 A2  An ) P( A1 ) P ( A2 A1 ) P ( A3 ( A1 A2 ))  P ( An ( A1 A2  An  1 )) 

15 .　Ｐ（Ａ｜Ｂ）　Ｐ（Ａ｜Ｂ）一批产品中有 4% 的次品，而合格品中一等品占 45% . 从这批产品中任取一件 ，求该产品是一等品的概 率． 解 设Ａ，Ｂ为同一个随机试验中的两个随机事Ａ表示取到的产品是一等品，Ｂ表示取 出的产品是合格品， 则 P ( A | B ) 45% P ( B ) 4% 于是 P ( B ) 1  P ( B ) 96% 所以 P( A) P( AB) P ( B ) P ( A | B ) 96% 45% 43.2% 

16 .　Ｐ（Ａ｜Ｂ）　Ｐ（Ａ｜Ｂ） 一个盒子中有６只白球、４只黑球，从中不放回地 每次任取１只，连取２次，求 (1) 第一次取得白球的 概率； (2) 第一、第二次都取得白球的概率； (3) 第一 次取得黑球而第二次取得白球的概率． 解 设Ａ，Ｂ为同一个随机试验中的两个随机事Ａ表示第一次取得白球 , Ｂ表示第二次取得白球 , 则 6 （ 1 ） P ( A)  0.6 10 6 5 （ 2 ）P ( AB ) P ( A) P ( B A)   0.33 10 9 4 6 （ 3 ）P ( AB ) P ( A) P ( B A)   0.27 10 9 

17 . 例 考虑恰有两个小孩的家庭 . 若已知某一家有男孩 ，求这家有两个男孩的概率；若已知某家第一个是男孩 ，求这家有两个男孩（相当于第二个也是男孩）的概率 . （假定生男生女为等可能） 解 Ω={ ( 男 , 男 ) , ( 男 , 女 ) , ( 女 , 男 ) , ( 女 , 女)} 则 Ｂ ={( 男 , 男 ) , ( 男 , 女 ) , 设Ａ，Ｂ为同一个随机试验中的两个随机事 Ｂ = “ 有男孩” ， (女 , 男)} Ａ = “ 有两个男孩” ， Ａ ={( 男 , 男 ) } ， B1 =“ 第一个是男孩” B1 ={( 男 , 男 ) , ( 男 , 女)} 于是得 3 1 P B   P BA  P A  4 4 1 1 P  B1   P  B1 A  P  A  2 4 

18 . 全年级 100 名学生中，有男生（以 事件 A 表 示） 80 人，女生 20 人； 来自北京的（以 事件 B 表示）有 20 人，其中男生 12 人，女生 8 人 ；免修英语的（以 事件 C 表示） 40 人中，有 3 2 名男生， 8 名女生。求 P( A), P( B), P( A B), P( B A), P ( AB ), 80 20 12 12 12 100 100 20 80 100 P (C ), P (C A), P ( A B ), P ( AC ) 40 32 12 32 100 80 80 100 

19 . 某种动物出生之后活到 20 岁的概率为 0.7 ， 活到 25 岁的概率为 0.56 ，求现年为 20 岁的 这种动物活到 25 岁的概率。 解 设Ａ，Ｂ为同一个随机试验中的两个随机事 A 表示“活到 20 岁”， B 表示“活到 25 岁” 则 P ( A) 0.7, P ( B ) 0.56 P ( AB ) P ( B ) 所求概率为 P ( B A)   0.8 P ( A) P ( A) 

20 . 甲，乙，丙 3 人参加面试抽签，每人的试题 通过不放回抽签的方式确定。假设Ａ，Ｂ为同一个随机试验中的两个随机事被抽的 10 个试题签中 有 4 个是难题签，按甲先，乙次，丙最后的次序抽签。 试求 1 ）甲抽到难题签， 2 ）甲和乙都抽到难题签， 3 ）甲没抽到难题签而乙抽到难题签， 4 ）甲，乙，丙 都抽到难题签的概率。 解 设Ａ，Ｂ为同一个随机试验中的两个随机事 A ， B ， C 分别表示“甲、乙、丙抽到难签” 4 4 3 则 P(1) P ( A)  P(2) P( AB)   10 10 9 6 4 4 3 2 P(3) P ( AB)   P (4) P( ABC )    10 9 10 9 8 

21 .例 1 有甲乙两个袋子，甲袋中有两个白球， 1 个红球 ，乙袋中有两个红球，一个白球．今从甲袋中任取一球 放入乙袋，再从乙袋中任取一球，问此球是红球的概率 ？ 解：设 A1—— 从甲袋放入乙袋的是白球； A2—— 从甲袋放入乙袋的是红球； B—— 从乙袋中任取一球是红球； B=A1B∪A2B ， P(B)=P(A1B)+ P(A2B) 2 2 3 1 1 P ( B ) P ( B | A1 ) P ( A1 )  P ( B | A2 ) P ( A2 )      4 3 4 3 12  甲 乙 甲 乙 

22 . 第二节 全概率公式 全概率公式 定义 事件组 A1 ， A2 ，…， An (n 可为 ) 两两 互斥 , 且 P(Ai)>0,(1≤P(B|A) ≤1i ≤P(B|A) ≤1n). 又事件 B 满足： n B BA i i 1 则有 n P ( B )  P ( Ai )P ( B | Ai ) i 1 注 : 这里只要求 B 发生当且仅当 B 与 A1 ， A2 ，…， An 之一同时发生 . 并不要求 A1 ， A2 n，…， An 为样本空 间 Ω 的一个划分，只要求 B  Ai i 1 

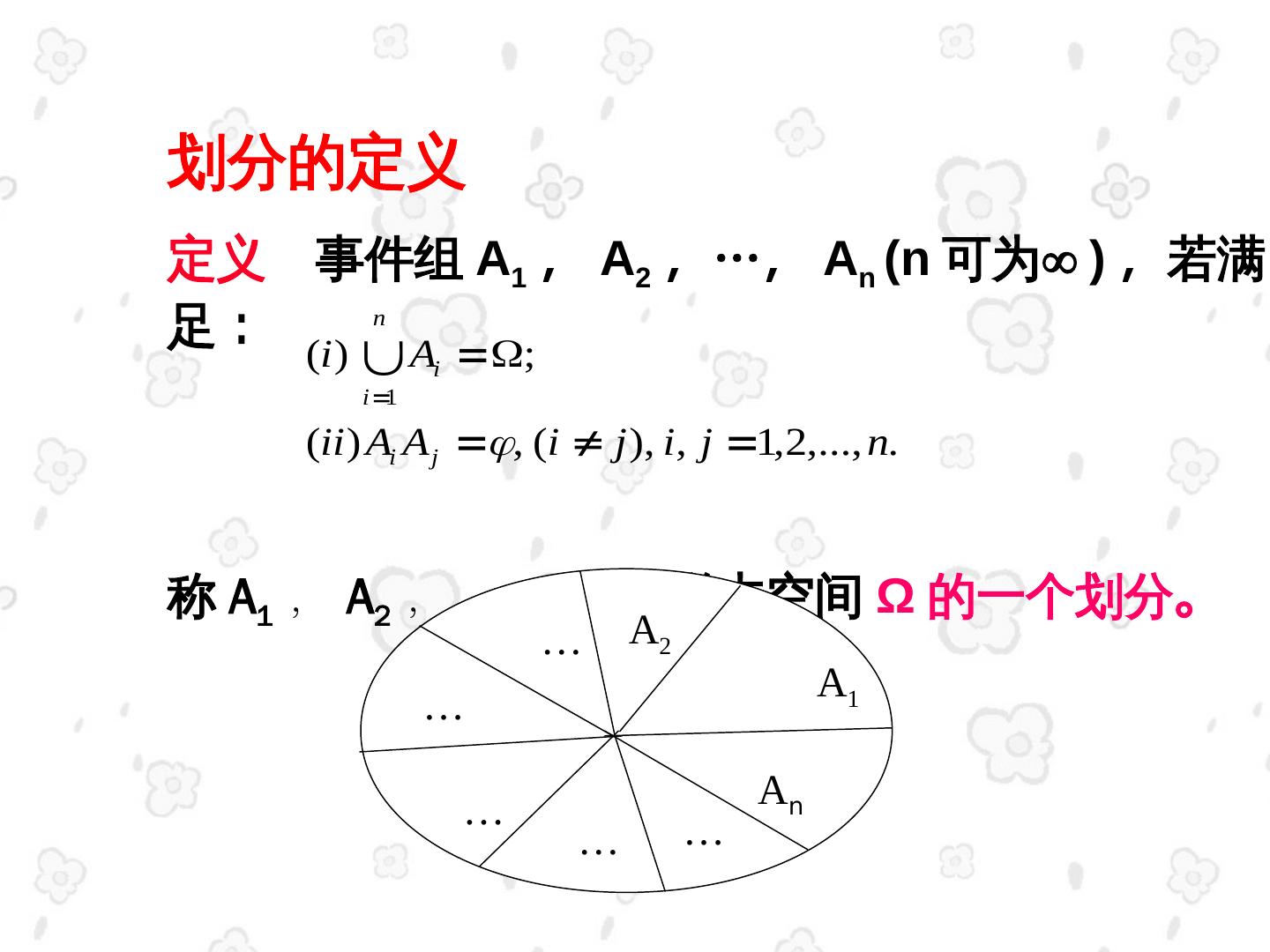
23 .划分的定义 定义 事件组 A1 ， A2 ，…， An (n 可为 ) ，若满 足： n (i ) Ai ; i 1 (ii ) Ai A j , (i  j ), i, j 1,2,..., n. 称 A1 ， A2 ，…， An 为样本空间 Ω 的一个划分。 … A2 A1 … … An … … 

24 .例如：设实验 E 为“掷一颗骰子观察其点数” . 它 的样本空间为： Ω={1,2,3,4,5,6} E 的一组事件： A1={1,3,5}, A2={2,4}, A3={6} 是 Ω的一个划分。 B1={1,2,3}, B2={3,4},B3={5,6} 不是 Ω的一个划分。 

25 .例 1. 市场上供应的灯泡中 , 甲厂的产品占有 70% , 乙厂占有 30%, 甲厂产品合格率是 95%, 乙厂产 品合格率是 80% 。求从市场上买到一个灯泡是合 格品的概率。 解：用 A 表示甲厂的产品 , 用 B 表示合格品 , B  AB  A B P(B) P(AB)  P(AB) P(A)P(B | A) + P(A)P(B | A) 0.70 0.95  0.30 0.80 0.905. 

26 .例 2: 有三个形状相同的箱子 , 在第一个箱中有两个正品 , 一个次品 ; 在第二个箱中有三个正品 , 一个次品 ; 在第 三个箱中有两个正品 , 两个次品 . 现从任何一个箱子 中任取一件产品 , 求取得的是正品的概率 . 解 : 设 Bi={ 从第 i 个箱子中取到产品 }(i=1,2,3), A={ 取得正品 }. 由题意知 Ω=B1+B2+B3 且 B1,B2,B3 是两两互不相容的事件 . P(B1)=P(B2)=P(B3)=1/3 P(A|B1)=2/3,P(A|B2)=3/4,P(A|B3)=2/4=1/2 由全概率公式得 P(A)=P(B1)P(A|B1)+P(B2)P(A|B2)+P(B3)P(A|B3) =0.64 

27 . 例 3: 有十个袋子，各袋中装球的情况如下：（ 1 ）两个袋 子中各装有 2 个白球与 4 个黑球；（ 2 ）三个袋子中各装有 3 个白球与 3 个黑球；（ 3 ）五个袋子中各装有 4 个白球与 2 个黑球 . 任选一个袋子，并从其中任取 2 个球，求取出 的 2 个球都是白球的概率 . 解 设 事件 B 表示取出的 2 个球都是白球， 事件 Ai 表示所选袋子中装球的情况属于第 i 种 （ i=1 、 2 、 3 ） 2 3 5 易知 P(A 1 )  P(A 2 )  P(A 3 )  10 10 10 2 C2 1 C 2 3 2 P(B | A 1 )  2  P(B | A 2 )  3  P(B | A )  4  6 C C6 15 C62 15 3 C62 15 于是按全概率公式所求的概率 3 P(B)  P(A i )P(B | A i ) i 1 2 1 3 3 5 6       0.273 10 15 10 15 10 15 

28 .例 4. 有三个箱子，分别编号为 1 、 2 、 3 ， 1 号箱装有 1 个红球、 4 个白球， 2 号箱装有 2 个红球、 3 个白球， 3 号箱装有 3 个红球 . 某人从三箱中任取一箱，从中任意摸出一球 . 求取得红球的概率 . 解： Ai—— 球取自 i 号箱， i=1 、 2 、 3 B —— 取得红球 P B  P A1 B   P A2 B   P A3 B  P A1  P B / A1   P A2  P B / A2   P A3  P B / A3  若问题为：发现是红球，求取自 1 号箱的概率 P( A1 B ) P A1  P B / A1  P A1 / B    P( B) P A1  P B / A1   P A2  P B / A2   P A3  P B / A3  

29 . 第三节 贝叶斯公式  问题？ 在全概率公式中我们知道 , 引起事件 B 发生的原因有 A1,A2,…,An 等多种 . 在实际 问题中 , 常遇到已知事件 B 已经发生 , 如 何求出事件 B 发生是由某种原因 Ak 引起的 概率 P(Ak|B).