概率论与数理统计第二章--随机事件的概率

1 .

2 .• 概率的概念 • 古典概型 • 几何概型 • 概率的公理化定义 

3 . 第一节 概率的概念 尽管随机事件有随机性，但在一次试验 中发生的可能性大小是客观存在的，而且是可以 度量的。 

4 . 随机事件的频率 Frequency 随机试验 抛掷一枚均匀的硬币 试验总次数 n 将硬币抛掷 n 次 随机事件A出现的次数 A=“ 出现正面”” 事件A出现的次数 A 出现次数 m 出现正面” m 次 m 随机事件A出现的次数的频率 f n ( A) n 事件A出现的次数A出现的次数出现的次数m f n ( A)  试验总次数n 

5 . 抛掷硬币的试验 Experiment of tossing coin 历史纪录 试 验 者 抛 掷 次 数 n 出现正面”的次数 m出现正面”的频率 m/n 德 . 摩 根 根 2048 1061 0.518 蒲 丰 丰 4040 2048 0.5069 皮尔逊 12000 6019 0.5016 皮尔逊 24000 12012 0.5005 维 尼 尼 30000 14994 0.4998 

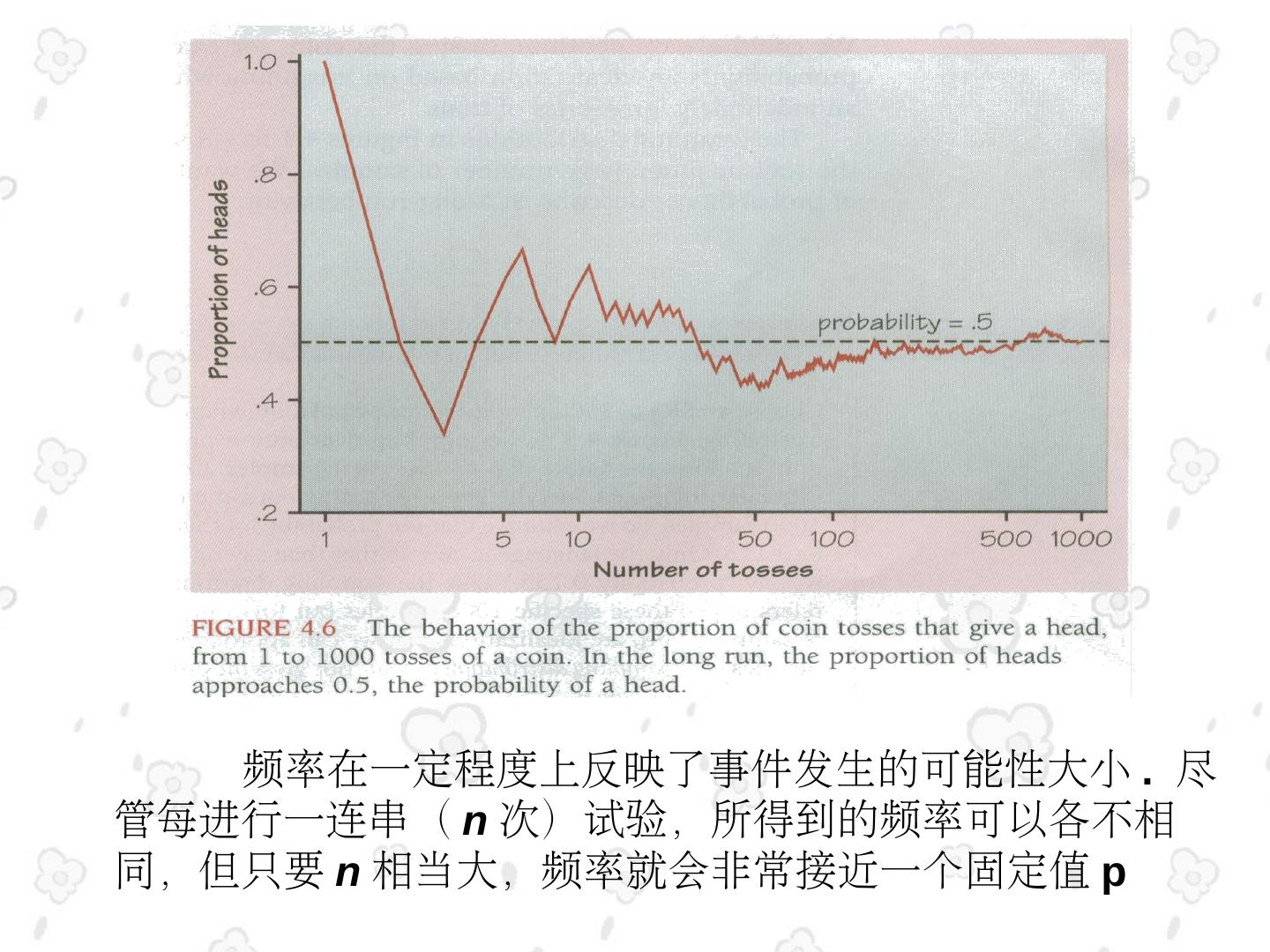
6 . 频率在一定程度上反映了事件A出现的次数发生的可能性大小 . 尽 管每进行一连串（ n 次）试验，所得到的频率可以各不相 同，但只要 n 相当大，频率就会非常接近一个固定值 p 

7 . 频率和概率  频率的稳定性 随机事件A出现的次数 A 在相同条件A出现的次数下重复多次时，事件A出现的次数 A 发生的频率在一个固定的数值 p 附近摆动，随试验次 数的增加更加明显  事件A出现的次数的概率 事件A出现的次数 A 的频率稳定在数值 p ，说明了数值 p 可以用来“测量”事件Ａ发生可能性大小，可以规定“测量”事件Ａ发生可能性大小，可以规定”事件A出现的次数Ａ发生可能性大小，可以规定发生可能性大小，可以规定 为事件A出现的次数 A 的概率 

8 . 概率的统计定义 对任意事件A出现的次数Ａ发生可能性大小，可以规定，在相同的条件A出现的次数下重复进行 n 次试验，事件A出现的次数Ａ发生可能性大小，可以规定发 生的频率 m/n ，随着试验 次数 n 的增大而稳定地在某个常数 附近摆动那 么称 p 为事件A出现的次数Ａ发生可能性大小，可以规定的概率 P ( A)  p 当试验次数足够大时，可以用事件A出现的次数 A 发生 的频率近似的代替事件A出现的次数 A 的概率 

9 . 再分析一个例子，为检查某种小麦的发芽情况 ，从一大批种子中抽取 10 批种子做发芽试验，其结 果如表 1-2 ： 种子粒数 2 5 10 70 130 310 700 1500 2000 3000 2 4 9 60 116 282 639 1339 1806 2715 发芽粒数 1 0.8 0.9 0.857 0.892 0.910 0.913 0.893 0.903 发芽率 0.905 从表 1-2 可看出，发芽率在 0.9 附近摆动，随着 n 的增大，将逐渐稳定在 0.9 这个数值上 . 

10 . 概率的统计定义 m 频率 f n ( A)  稳定于概率 p P ( A) n 性质： （ 1 ） 0  p 1 （ 2 ） P () 1, P ( ) 0 （3） 若 A ， B 互斥，则 P ( A  B ) P ( A)  P ( B ) 若 A1 ， A2 ， A3… ， An 互斥，则 n n P(A k )  P(A k ) k 1 k 1 

11 . 第二节 古典概率模型 若随机试验有如下特征： 有限性：每次试验中，所有可能发生的结果只有有 限个，即样本空间 Ω 是个有限集   1 , 2 , , n   等可能性 每次试验中，每一种可能结果的发生的可能性 相同，即 1 P ( A1 ) P ( A2 )  P ( An )  n 其中 , i 1, 2, , n Ai   i  . 

12 . 古典概型的概率计算  确定试验的基本事件A出现的次数总数 设试验结果共有 n 个基本事件A出现的次数 ω1 ， ω2 ， ... ， ωn ，而且这些事件A出现的次数的发生具有相同的可能性  确定事件A出现的次数 A 包含的基本事件A出现的次数数 事件A出现的次数Ａ发生可能性大小，可以规定由其中的 m 个基本事件A出现的次数组成 事件A出现的次数A包含的基本事件A出现的次数数 m P ( A)   试验的基本事件A出现的次数总数 n 

13 . 古典概率的计算：抛掷骰子 抛掷一颗匀质骰子 , 观察出现的点数 , 求“出现“出现 的点数是不小于 3 的偶数”的概率． 试验 抛掷一颗匀质骰子 , 观察出现的点数 样本空间 Ω ={1 ， 2 ， 3 ， 4 ， 5 ， 6} n=6 事件A出现的次数 A Ａ发生可能性大小，可以规定 =“ 出现的点数是不小于 3 的偶数”={4 ， 6} m=2 事件A出现的次数 A 的概 率 m 2 1 P( A)    n 6 3 

14 .古典概率的计算：正品率和次品率 设在 100 件A出现的次数产品中，有 4 件A出现的次数次品，其余均 为正品． 这批产品的次品率 4 n ＝ 100 mA ＝ 4 P ( A)  0.04 100 任取 3 件A出现的次数，全是正品的概率 3 3 C n C3 mB C 96 P( B)  3 96 100 C100 任取 3 件A出现的次数，刚好两件A出现的次数正品的概率 2 n C3 2 1 C96 C41 100 mC C C 96 4 P (C )  3 C100 

15 . 古典概率的计算： 有放回抽样和无放回抽样 例 设在 10 件A出现的次数产品中，有 2 件A出现的次数次品， 8 件A出现的次数正品． A=“ 第一次抽取正品，第二次抽取次品”  第一次抽取后，产品放回去 8 2 n 10 10 mA 8 2 P( A)  0.16 10 10  第一次抽取后，产品不放回去 8 2 n 10 9 mA 8 2 P( A)  0.1778 10 9 

16 .古典概率的计算：投球入盒 例 将 n 只球随机的放入 N (N  n) 个盒子中去 ，求每个盒子至多有一只球的概率 ( 设盒子的容量不 限）。 解： 将 n 只球放入 N 个盒子中去 , 共有 N N  N  N n 种放法, 而每个盒子中至多放一只球 , 共有 N ( N  1)  [ N  ( n  1)]  PNn 种放法 , N ( N  1)  [ N  ( n  1)] PNn 故 p n  n . N N 思考：某指定的 n 个盒子中各有一球的概率。 

17 . 古典概率的计算：投球入盒 把 3 个小球随机地投入 5 个盒内。设球与 盒都是可识别的。  A=“ 指定的三个盒内各有一球 3! n 53 mA 3! P ( A)  3 5  B =“ 存入三个盒，其中各有一球 3 mB C 3! C53 3! n 53 5 P( B)  3 5 a b c d e 1 2 3 

18 . 古典概率的计算：生日问题 某班有 50 个学生，求“出现他们的生日各不相同的概率 （设一年 365 天） 分析 此问题可以用投球入盒模型来“测量”事件Ａ发生可能性大小，可以规定模拟 50 个学生 50 个小球 365 天 365 个盒子 50 C 50! P ( A)  365 50 0.03 365 相似地有分房问题 人 小球 房子 盒子 

19 . 生日问题模型 某班有 n 个学生，设一年 N 天 , 则 他们的生日各 n C n ! P ( A)  不相同的概率为 n N N 至少有两人 生日相同的概率为 n 没问题 可能吗 可能吗 没问题 C n ! P( A) 1  n N ？ ！ ？ ！ N N 10 20 23 30 40 50 P( A) 0.12 0.41 0.51 0.71 0.89 0.97 

20 . 古典概率的计算：抽签 10 个学生，以抽签的方式分配 3 张音乐会入场券 ，抽取 10 张外观相同的纸签，其中 3 张代表入场券 . 求“出现 A={ 第五个抽签的学生抽到入场券 } 的概率。 基本事件A出现的次数总数 n 10! 基本事件A出现的次数总数 mA C31 9! 第五个学生抽 另外 9 个学生 1 到入场券 抽取剩下 9 张 mA C 9! 3 P( A)   3  n 10! 10 

21 . 古典概率的计算：数字排列 用 1 ， 2 ， 3 ， 4 ， 5 这五个数字构成三位 数  没有相同数字的三位数的概率 3 P53 3 n 5 m A P5 P ( A)  3 0.48 5  没有相同数字的三位偶数的概率 3 2 1 P42 P21 n 5 mB P P 4 2 P( B)  3 ＝ 0.192 5 百位十位 个位 

22 . 匹 配 问 题 某人 写了 4 封信和 4 个信封，现随机地将信装入信封中， 求“出现全部装对的概率。 解 设“全部装对”为事件 设“全部装对”为事件A出现的次数 A 总的基本事件A出现的次数数为 4 ！  A 所包含的基本事件A出现的次数数为 1 1 1 所以 P ( A)   4! 24 

23 .古典概型的概率计算步骤： (1) 判断试验为古典试验 , 即基本事件总数为有 限个 , 且各基本事件出现的可能性相同； (2) 计算样本空间中样本点的个数 n ; (3) 计算事件 A 包含样本点的个数 m ; (4) 由 P(A)=m/n 计算事件 A 的概率。 

24 . 概率的古典定义 事件A出现的次数A包含的基本事件A出现的次数数 m P ( A)   试验的基本事件A出现的次数总数 n 性质 （ 1 ） 0 P ( A) 1 （ 2 ） P () 1, P ( ) 0 （3） 若 A ， B 互斥，则 P ( A  B ) P ( A)  P ( B ) 

25 . 第三节 几何概型 Geometric Probability  将古典概型中的有限性推广到无限性，而保留等 可能性，就得到几何概型。  特点  有一个可度量”事件Ａ发生可能性大小，可以规定的几何图形 S 试验 E 看成在 S 中随机地投掷一点 事件A出现的次数 A 就是所投掷的点落在 S 中的可度量”事件Ａ发生可能性大小，可以规定图形 A 中 A 的几何度量”事件Ａ发生可能性大小，可以规定 L ( A) P ( A)   S的几何度量”事件Ａ发生可能性大小，可以规定 L( S )  几何度量”事件Ａ发生可能性大小，可以规定 -------- 指长度、面”积或体积 

26 . 几何概型的计算 一个质地均匀的陀螺的圆周上均匀地刻有 [0 , 5) 上诸数字，在桌面”上旋转它，求“出现当它停下来“测量”事件Ａ发生可能性大小，可以规定时，圆 周与桌面”接触处的刻度位于区间 [2 , 3] 上的概率。 S [0, 5) A = [2 , 3] L( S ) = 5- 0 = 5 L ( A) = 3-2 = 1 1 2 L ( A) 1 0 P ( A)   4 3 L( S ) 5 

27 .例 . 某公共汽车站从上午 7 时起，每隔 15minmin 来一趟 车，一乘客在 7 ： 00 到 7 ： 30 之间随机到达该车 站，求 （ 1 ）该乘客等候不到 5minmin 乘上车的概率 ；（ 2 ）该乘客等候时间超过 10min 才乘上车的概 率. 解： Ω={7 ： 00 ＜ T ＜ 7:30}, SA={7:10 ＜ T ＜ 7:15min 或 7 ： 25min ＜ T ＜ 7:30} ， SB={7:00 ＜ T ＜ 7:05min 或 7 ： 15min ＜ T ＜ 7:20}. 如将 T 的单位化为分钟，则有 |Ω|=30,|SA|=10, |S`B|=10, 因此 P(A)= P(B)=1/3≈0.333 

28 . 几何概型的计算：会面问题 甲乙二人 相约定 6 ： 00-6 ： 30 在预定地点 会面”，先到的人 要等候另一人 10 分钟后，方可离 开。求“出现甲乙二人 能会面”的概率，假定他们在 6 ： 0 0-6 ： 30 内的任意时刻到达预定地点的机会是等可 能的。 解 设“全部装对”为事件 设甲乙二人 到达预定地点 y 的时刻分别为 x 及 y （分钟） 30 , 则 0  x 30 0  y 30 二人 会面”  x  y  10 10 2 30  (30  10) 2 5 x p 2  10 30 30 9 

29 . 几 何 概 型 A 的几何度量”事件Ａ发生可能性大小，可以规定 L ( A) P ( A)   S的几何度量”事件Ａ发生可能性大小，可以规定 L( S ) 性质 （ 1 ） 0 P ( A) 1 （ 2 ） P () 1, P ( ) 0 （3） 若 A ， B 互斥，则 P ( A  B ) P ( A)  P ( B )