展开查看详情
1 .教师 : 边海琴
e-mail: bianhaiqin @ nwnu.edu.cn
2 . 教材及参考书目
教材： 《概率统计简明教程》
同济大学应用数学系编
高等教育出版社
参考书： 1. 《概率论与数理统计》
浙江大学 盛骤 等 编
高等教育出版社 2001
2. 《数理统计》
赵选民 等 编
科学出版社 2003
3 .第一章 随机事件 随机事件
样本空间和随机事件
事件关系和运算
4 . 什么是概率论
必然现象 Certainty phenomena
在 101325 Ｐ a 的大气压下，将纯净水加热到
100℃ 时必然沸腾
垂直上抛一重物，该重物会垂直下落
必然现象 ：在一定的条件下必然会发生的现象 。
5 .随机现象 Random phenomena
掷一颗骰子，可能出现 1 ， 2 ， 3 ， 4 ， 5 ， 6 点
抛掷一枚均匀的硬币，会出现正面向上、反面向上
两种不同的结果
随机现象 ：在一定的条件下可能发生也可能不发生的
现象 。
6 .随机现象 的特点：
在一定条件下对某一现象 观察时，观察
到的结果是多个可能结果中的某一个，且在
每次观察前都无法预知观察结果到底是哪一
个，既结果出现呈现偶然性，或者说：出现
哪个结果凭机会而定。
7 . 明天的最高气温；
投一个骰子，观察其向上的点数；
新生婴儿的体重；
在闹市区的某个街口，在给定的时间段内
观察交通堵塞现象 。
8 .随机现象 是不是没有规律可言？
否；在一定条件下对随机现象 进行大量重
复观察后就会发现：随机现象 的发生有一定的
规律性。
例如：测量一物体的长度，由于仪器及观察受
到环境的影响，每次测量的结果可能有差异，
但多次测量结果的平均值随着测量次数的增加
而逐渐稳定于一固定的常数，并且诸测量值大
多落在此常数附近，离常数越远的测量值出现
的可能性越小。
9 .“ 天有不测风云”和“天气可以预报”有矛盾吗”和“天气可以预报”有矛盾吗”有矛盾吗
？
没有； “天有不测风云”指的是对随机现
象进行一次观测，其观测结果具有偶然性；
“天气可以预报”指的是研究者从大量的气象资
料来观察这些观测结果的规律性。
10 . 总结：随机现象 具有偶然性一面，也有必然性
一面。偶然性一面表现在“对随机现象 做一次观
测时，观测结果具有偶然性”；必然性一面表现
在“对随机现象 进行大量重复观测，观测结果有
一定的规律性” 。亦即“统计规律。”“统计规律。”
概率论就是研究随机现象的统计规律性的数学学科
11 . 第一节 样本空间和随机事件 样本空间和随机事件
一、随机试验 random E)xperiments
随机试验 (E)E)) ：把对某种随机现象 的一次观察、观测
或测量等称为一个试验。
E)1 ：抛一枚硬币，观察正面，反面出现的情况；
E)2 ：将一枚硬币连抛掷三次，观察正面 H ，反面 T
出现的情况；
E)3 ：抛一颗骰子，观察出现的点数；
E)4 ：记录某电话在一天内 接到呼唤的次数；
E)5 ：记录一昼夜的最高温度和最低温度；
12 .随机试验特点
试验在相同的条件下可重复进行，
每次试验的结果具有多种可能性，而且在试验之前可
以确定试验的所有可能结果，
每次试验前不能准确预言试验后会出现哪一种结果．
13 .二、随机事件 random E)vents
在随机试验中，可能出现也可能不出现，而在大量重
复试验中具有某种规律性的事件叫做随机事件 (E)rando
m E)vents ) ，简称事件（ E)vents) ．
随机事件通常用大写英文字母Ａ、Ｂ、Ｃ等表示．Ａ、Ｂ、Ｃ等表示．等表示．
例如：在抛掷一枚均匀硬币的试验中，“正面向上”是
一 个随机事件，可用Ａ＝｛正面向上｝表示．
掷骰子，“出现偶数点”是一个随机事件，
试验结果为 2 ， 4 或 6 点，都导致“出现偶数点”发生。
可用 B ＝｛出现偶数点｝表示．
14 . 三、基本事件与样本空间
样本点 Sample Point
随机试验中的每一个可能出现的试验结果称为
i
这个试验的一个 样本点 ，记作 ．
样本空间 Sample Space
全体样本点组成的集合称为这个试验的样本空间
1 , 2 , , n ,
，记作 Ω ． 即“统计规律。”
基本事件
仅含一个样本点的随机事件称为基本事件．
含有多个样本点的随机事件称为复合事件．
15 . 写出下列试验的样本空间
E)1: 掷一颗匀质骰子，观察骰子出现的点数
Ω={1 ， 2 ， 3 ， 4 ， 5
点数：一维离散型随机变量
， 6}
E)2: 射手向一目标射击，直到击中目标为止
Ω={1,2,…} 射击次数：一维离散型随机变量
E)3: 从四张扑克牌 J,Q,K,A 任意抽取两张。
Ω={(E)J,Q),…(E)Q,A)} 二维离散型随机变量
E)4: 在一批灯泡中任意抽取一只，测试它的寿命
Ω={ ｔ | 0≤ ｔ≤ T} 寿命：一维连续型随机变量
16 . 随机事件（ Random Events)
在随机试验中，随机事件一般是由若干个基本事
件组成的．
例如，抛掷一颗骰子，观察出现的点数，那么
“出现 1 点”、“出现 2 点”、 ... 、“出现 6 点”为该试
验的基本事件．
A = ｛出现奇数点｝是由三个基本事件 “出现出现奇数点｝是由三个基本事件 “出现 1
点”、“出现 3 点” 、 “出现 5 点” 组合而成的随机
事件．
样本空间 Ω的任一子集 A 称为随机事件
A
属于事件 A 的样本点出现，则称事件 A 发生。
17 . 特例—必然事件 Certainty Events
必然事件 —— 记作 Ω
•样本空间 Ω 也是其自身的一个子集
•Ω 也是一个“随机”事件
•每次试验中必定有 Ω 中的一个样本点出现
•必然发生
例
• “ 抛掷一颗骰子，出现的点数不超过 6”
为
18 . 特例—不可能事件 Impossible E)vent
不可能事件 —— 记作 Φ
•空集 Φ 也是样本空间的一个子集
•Φ 也是一个特殊的“随机”事件
•不包含任何样本点
•不可能发生
例
• “ 抛掷一颗骰子，出现的点数大于 6”
是
19 . 随机试验：抛掷硬币
Tossing a coin
随机试验
掷一枚均匀的硬币，观察它出现正面或反面的情况
试验的样本点和基本事件
• H ：“正面向上”
• T ：“反面向上”
样本空间
Ω={H ， T} ．
20 . 随机事件
试验：掷一枚硬币三次，观察它出现正面或反面的情况
Ω={HHH,HHT,HTH,THH,HTT,THT,TTH,TTT}
A=“ 正面出现两次” ={HHT,HTH,THH}
B=“ 反面出现三次” ={TTT}
C=“ 正反次数相等” = Φ
D=“ 正反次数不等” =Ω
21 . 随机试验：抛掷两颗骰子
Rolling two die
随机试验
抛掷两颗骰子，观察出现的点数
样本空间
Ω ＝｛出现奇数点｝是由三个基本事件 “出现（ 1 ， 1 ），（ 1 ， 2 ） , （ 1 ， 3 ），
（ 1 ， 4 ），（ 1 ， 5 ），（ 1 ， 6 ）， ... ，（ 6
， 1 ），（ 6 ， 2 ）， ... ，（ 6 ， 6 ）｝．
22 . 随机事件
试验：抛掷两颗骰子，观察出现的点数
A=“ 点数之和等于 3” ={ （ 1 ， 2 ），（ 2 ，
1）}
B=“ 点数之和大于 11”={6 ， 6}
C=“ 点数之和不小于 =Ω
2”
D=“ 点数之和大于 1 = Φ
2”
23 . 第二节 事件的关系与运算
事件 事件之间的关系与事件的运算
集合 集合之间的关系与集合的运算
给定一个随机试验，设 Ω 为其样本空间，事
件Ａ，Ｂ， Ak ( k =1 , 2 , 3 , ... ) 都是 Ω 的
子集．
24 . 子事件 (E) 事件的包含 Contain
）
事件Ａ是事件Ｂ的子事件
事件Ａ发生必然导致事件Ｂ发生
事件Ａ的样本点都是事件Ｂ的样本点
记作
A B
B
A BA
例如 抛掷两颗骰子，观察出现的点数
A={ 出现 1 点 }B={ 出现奇数 A B
25 . 相等事件（ E)qual ）
B A且 A B A=B
B
A
事件 A 与事件 B 含有相同的样本点
例如：在投掷一颗骰子的试验中，事件“出现偶数点”
与事件“出现 2 ， 4 或 6 点”是相等事件。
26 . 和事件 Union
和事件 A∪B 发生 A 发生或 B 发生
事件 A 与事件 B 至少有一个发
生
由事件 A 与事件 B 所有样本点组成
B
A B
A
n
多个事件的和 A1 A2 An =Ai
i 1
A1 A2 An = A
i 1
i
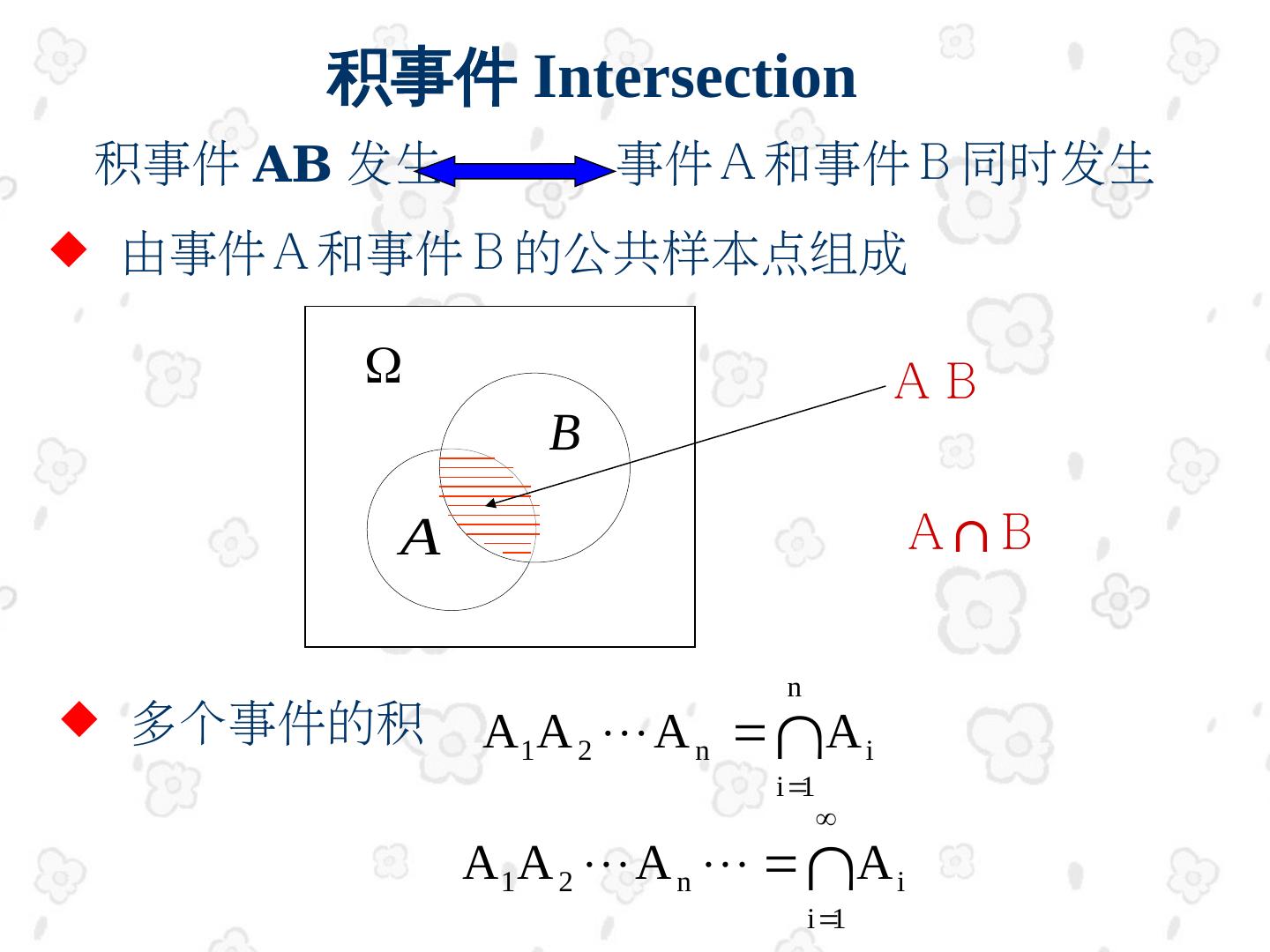
27 . 积事件 Intersection
积事件 AB 发生 事件Ａ和事件Ｂ同时发生
由事件Ａ和事件Ｂ的公共样本点组成
ＡＢ
B
A Ａ∩Ｂ
n
多个事件的积 A 1 A 2 A n A i
i 1
A 1 A 2 A n A i
i 1
28 . 互斥事件 (E) 互不相容事件 ) E)xclusive
事件 A 与事件 B 互斥 AB=Φ
事件 A 与事件 B 不能同时发生
事件 A 与事件 B 没有公共的样本点
A
B
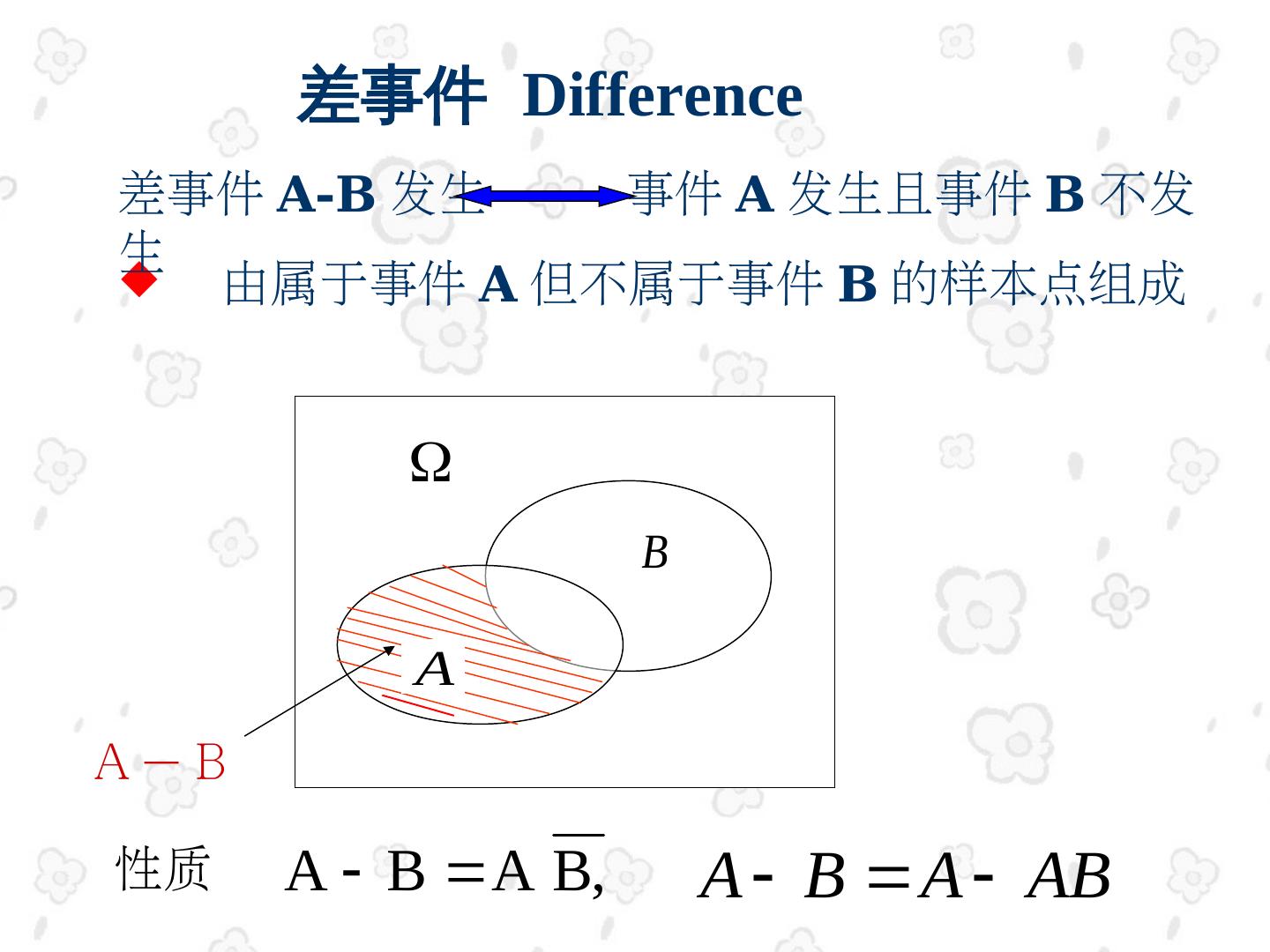
29 . 对立事件 Contrary
事件 A 不发生
是由所有不属于 A 的样本点组成
记作 A A
A
性 AA A A ( A) A
质
热门城市
