09现代密码学理论与实践--公钥密码学与RSA

1 .现代密码学理论与实践 第 9 章 公钥密码学与 RSA 苗 付友 mfy@ustc.edu.cn 2017 年 11 月

2 .本章要点 Diffie -Hellman 秘钥交换 非对称 密码是一种密码体制，其加密算法和解密算法使用不同的密钥，一个是公钥，一个是私钥。非对称密码也称为公钥密码。 非对称密码用两个密钥中的一个以及加密算法将明文转换为密文，用另一个密钥以及解密算法从密文恢复出明文。 非对称密码可以用来保密、认证或者两者兼而有之。 应用最广泛的公钥密码体制是 RSA ，破解 RSA 的困难，是基于分解大合数的素因子的困难。

3 .本章目录 9.1 Diffie -Hellman 密钥交换 9.2 公开密钥密码体制的基本原理 9.2.1 基本概念 9.2.2 应用方法 9.2.3 功能 9.2.4 对公开密钥密码编码系统的 要求 9.3 RSA 公钥系统 9.3.1 RSA 密码体制基本原理 9.3.2 RSA 的安全性

4 .Whitfield Diffie and Martin Hellman Whitfield Diffie Martin Hellman Born in 1944/ fascinated in Math/ Graduated from MIT 1965/ freethinking independent cryptographer in 1970s/ insightful in the significance of Key Distribution in then rising ARPAnet / visit to IBM lab in Setp.1974  Martin Hellman Prof. of Stanford Univ./Born in 1945/ to be different->cipher with The Coderbreakers /1974,9 Diffie

5 .Finding a one-way function --Martin Hellman

6 .2018/5/3 现代密码学理论与实践-10 6 /57 9 .1 Diffie -Hellman 密钥交换 Diffie 和 Hellman 在 1976 年首次提出了公钥算法，给出了公钥密码学的定义，该算法通常被称为 Diffie -Hellman 密钥交换算法 Diffie -Hellman 密钥交换算法是一种公钥分发机制 它不是用来加密消息的 所生成的是通信双方共享的会话密钥，必须保密，其值取决于通信双方的私钥和公钥信息 Diffie -Hellman 密钥交换算法是基于有限域 GF 中的指数运算的 ( 模一素数或多项式 ) Diffie -Hellman 密钥交换算法的安全性依赖于求解离散对数问题 DLP

7 .9.1.1 离散对数问题回顾 如果 a 是素数 p 的一个原根 ( 本原元素 ) ，则 a mod p, a 2 mod p, ......, a p-1 mod p ，生成模 p 的完全剩余集 {1, 2, ......, p-1} 对于所有素数，其原根必定存在，即 对于一个整数 b 和素数 p 的一个原根，可以找到唯一的指数 i , 使得 b = a i mod p, 其中 0<= i <= p-1 指数 i 称为 b 的以 a 为基数的模 p 的离散对数或者指数。 离散对数密码体制的安全性基于 DLP 问题 , 在下式中已知 C 和 P 的情况下 , 由 d 求 M 很容易 , 由 M 求 d 很困难 , d = log C M in GF(P), 最快的算法需要 T=exp(( ln (P) lnln (P) 1/2 ) 次运算。当 P 是 200 位时 , T = 2.7x10 11 , 如果 1 μ s 解一次 , 需要 2~3 天；如果 P = 664 位 , 则 T = 1.2x10 23 , 约 10 12 天或 2.739x10 9 年 , 约 2.7 亿年 . 只要 P 足够大 , 可以达到足够安全。

8 .9.1.2 Diffie -Hellman Key Exchange 通信双方约定一个大素数 ( 或多项式 )p, 和模 p 的一个素根 α 各方产生公开密钥 选择一个秘密钥 ( 数值 ) ，如 x A < p ， x B < p 计算公钥 , 如 y A = α x A mod p, y B = α x B mod p, 并相互交换 双方共享的会话密钥 K AB 可以如下算出 K AB = α x A· x B mod p = y A x B mod p (which B can compute) = y B x A mod p (which A can compute) K AB 是双方用对称密码通信时共享的密钥 如果双方继续通信，可以继续使用这个密钥，除非他们要选择新的密钥 攻击者如果想要获得 x= x A ·x B , 则必须解决 DLP 问题

9 .Diffie-Hellman Example Users Alice & Bob who wish to swap keys Agree on prime p=353 and α =3 Select random secret keys: A chooses x A =97, B chooses x B =233 Compute public keys: y A = 3 97 mod 353 = 40 (Alice) y B = 3 233 mod 353 = 248 (Bob) Compute shared session key as: K AB = y B x A mod 353 = 248 97 mod 353 = 160 (Alice) K AB = y A x B mod 353 = 40 233 mod 353 = 160 (Bob)

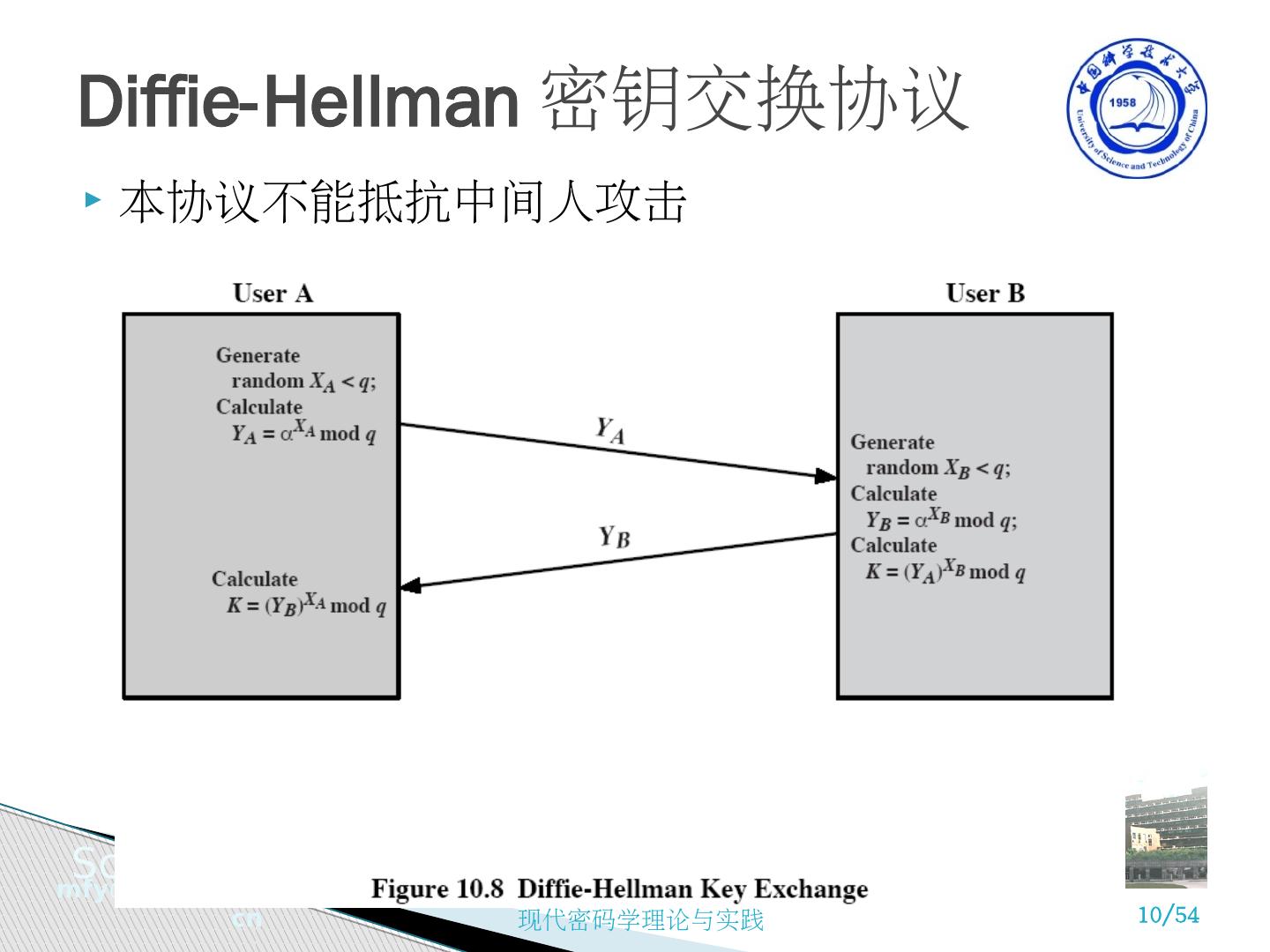
10 .Diffie-Hellman 密钥交换协议 本协议不能抵抗中间人攻击

11 .1976 年， Whitfield Diffie 和 Martin Hellman 提出这样的设想：每个用户 A 有一加密密钥 k a ，不同于解密密钥 k a ’ ，可将加密密钥 k a 公开， k a ’ 保密，要求 k a 的公开不影响 k a ’ 的安全。若 B 要向 A 秘密发送明文 m ，可查 A 的公开密钥 k a ，加密得密文 C= E ka (m) A 收到 C 后用只有 A 才拥有的解密密钥 k a ’ 对 C 进行解密得 m= D ka ’(C). 实用方案的发展依赖于单向陷井函数 Diffie 的公钥密码体制概念

12 .9.2 公开密钥密码体制的基本原理 对称密码体制的问题 加密能力与解密能力是捆绑在一起的 密钥更换、传递和交换需要可靠信道，密钥分发困难 如有 N 用户，则需要 C=N(N-1)/2 个密钥， n=1000 时， C(1000, 2)≈500000, 密钥管理困难 无法满足不相识的人之间通信的保密要求 不能实现数字签名 非对称密码体制的基本特点 加密能力与解密能力是分开的 密钥分发简单 需要保存的密钥量大大减少， N 个用户只需要 N 个密钥 可满足不相识的人之间保密通信 可以实现数字签名

13 .9.2.1 公开密钥密码体制 公钥算法依赖于一个加密密钥和一个与之相关的不同的解密密钥，算法有如下特点： 仅根据密码算法和加密密钥来确定解密密钥在计算上是不可行的 两个密钥的任何一个都可用来加密，另一个用来解密 公钥密码体制的组成 明文：算法的输入，可读信息或数据 加密算法：对明文进行各种转换 公钥和私钥：算法的输入，分别用于加密和解密 密文：算法的输出，依赖于明文和密钥 解密算法：根据密文和密钥，还原明文

14 .9.2.2 公钥算法的主要步骤 Encryption: 每个 用户产生密钥，用来加密和解密消息 每个用户将其中一个密钥 ( 公钥 ) 存于公开的寄存器或其他可访问的文件中，另一密钥私有，每个用户可以拥有若干其他用户的公钥 若 Bob 要发消息给 Alice ，则要用 Alice 的公钥对消息加密 Alice 收到消息后，用其私钥对消息解密，由于只有 Alice 知道其自身的私钥，所以其他的接收者均不能解密 消息 Authentication ： 需要 认证时示证方用自己的私钥加密消息 ( 签名 ) 验证方用示证方的公钥解密消息 ( 验证 ) ，如果结果证实公钥与示证方的私钥相吻合，则可以确认示证方确为合法的用户 ( 认证 ) 加密和认证可以结合起来，同时实现保密性和认证

15 .常规和公开密钥加密的重要特征

16 .9.2.3 公钥算法的主要应用 1 ）公开密钥加密 2 ）公开密钥认证 3 ）密钥交换

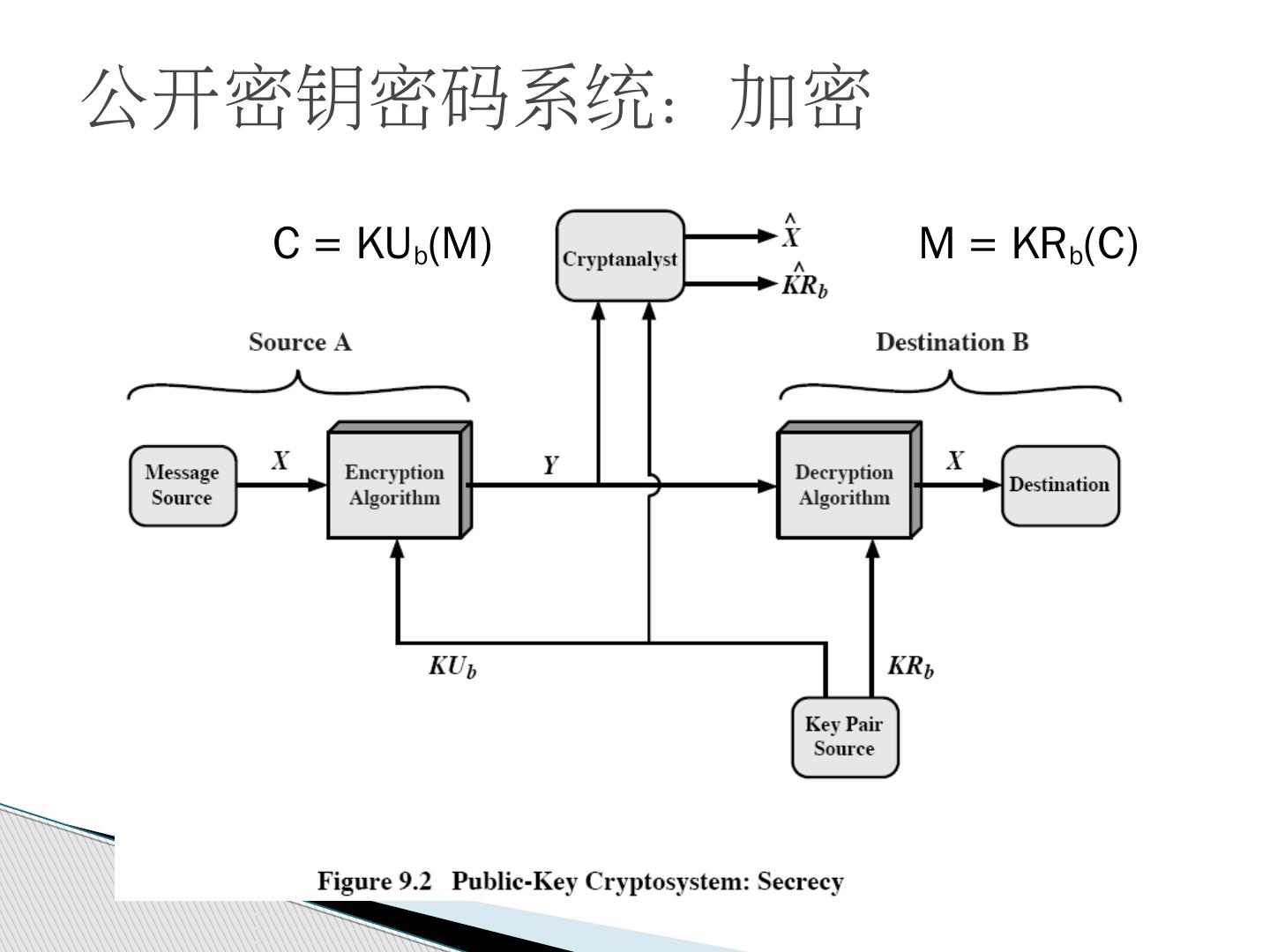
17 .公开密钥密码系统 ：加密 C = KU b (M) M = KR b (C)

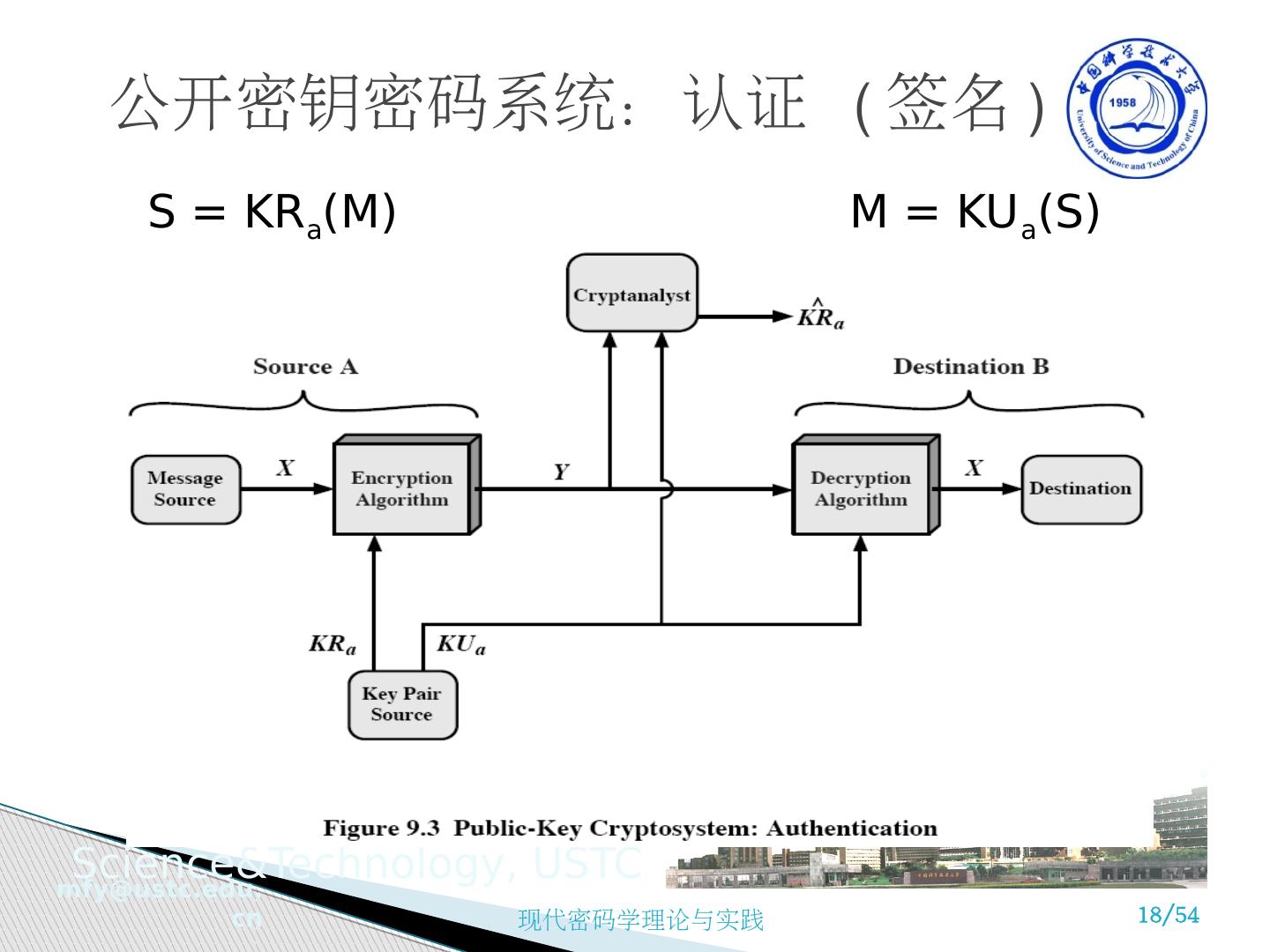
18 .公开密钥密码系统： 认证 ( 签名 ) S = KR a (M) M = KU a (S)

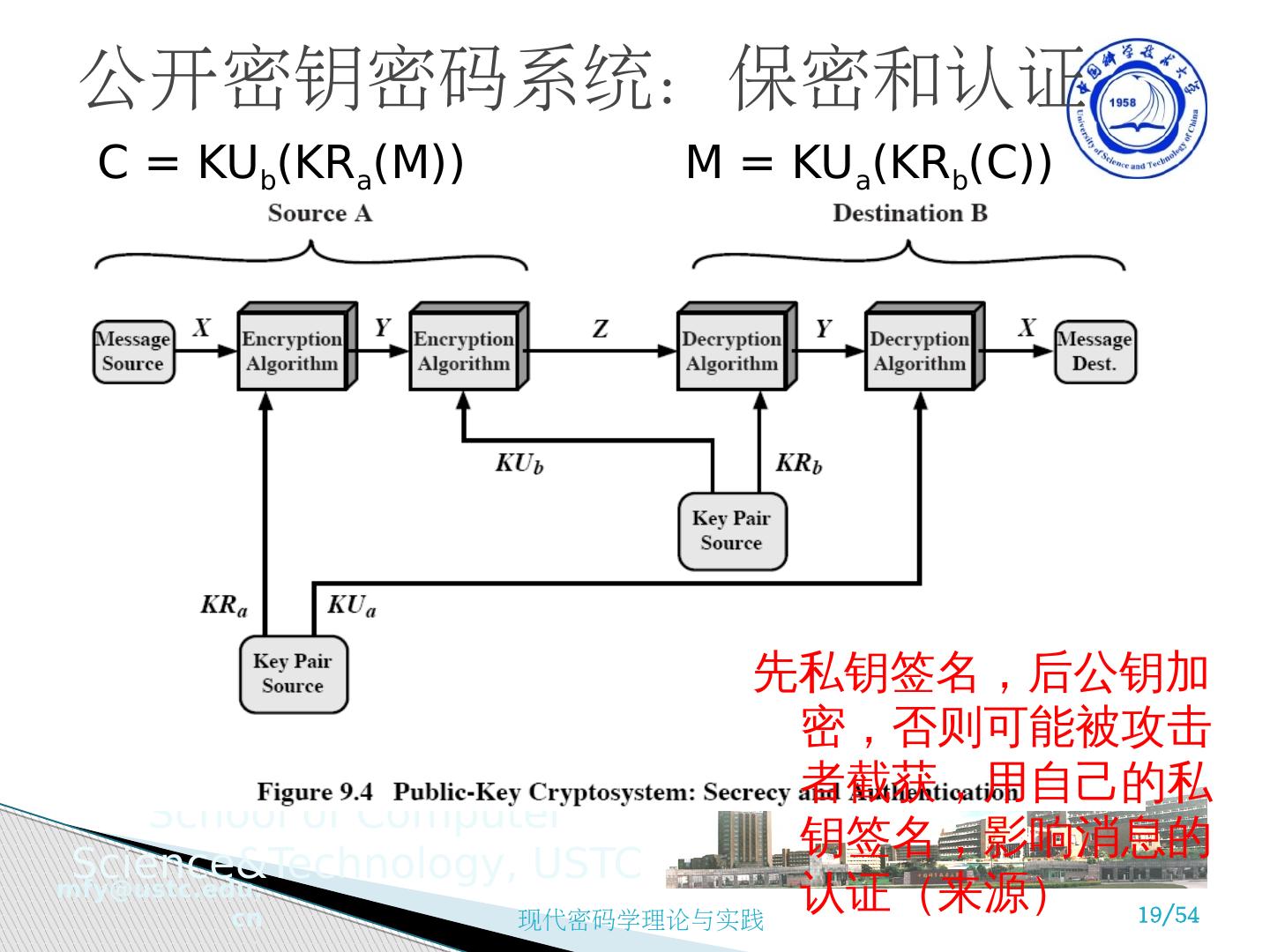
19 .公开密钥密码系统：保密和认证 C = KU b ( KR a (M )) M = KU a ( KR b (C )) 先私钥签名，后公钥加密，否则可能被攻击者截获，用自己的私钥签名，影响消息的认证（来源）

20 .公钥密码体制的应用 加密 / 解密：发送方用接收方的公钥对消息加密 数字签名：发送方用其私钥对消息签名，可以对整体消息签名或对消息的摘要签名 密钥交换：通信双方交换会话密钥

21 .产生一对密钥 ( 公钥 k e 和私钥 k d ) 在计算上是容易的 不难计算 C=E( k e , m) 和 m=D( k d , C) 知道 k e , 计算 k d 不可行 不知道 k d ，即使知道 k e , E, D 及 C ，计算 m 也不可行 对明文 m, E( k e , m) 有定义，且 D( k d , E( k e , m))=m 对密文 C, D( k d , C) 有定义，且 E( k e , D( k d , C))=C 加密变换和解密变换可以互换顺序 , 即 D(E(m))=E(D(m )) 9.2.4 对公开密钥密码编码系统的要求

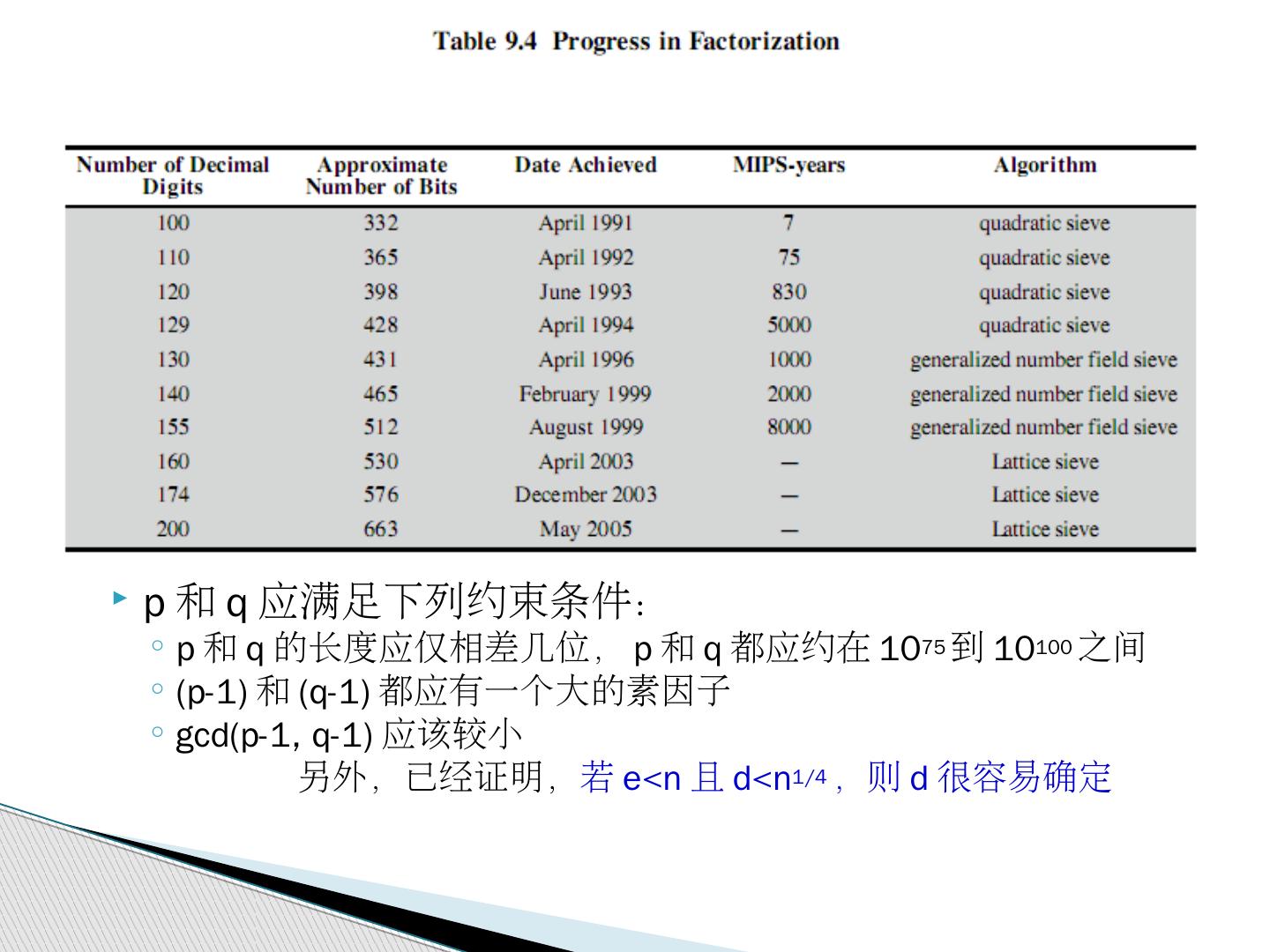
22 .9.3 RSA 算法 概述 1977 年， Rivest 、 Shamir 、 Adleman 提出的非对称密码体制，是基于大合数的素因子分解问题的困难性。 1994 年 4 月一个小组通过 Internet 合作， 8 个月时间成功分解 129 位的数，大约 428 比特； 1999 年分解 155 位合数，最新的记录是 2005 年 5 月分解 200 位十进制数。 RSA 专利于 2000 年 9 月 20 日到期。

23 .R-S-A Ron Rivest , Adi Shamir, Len Adleman (Left to Right: Ron Rivest, Adi Shamir, Len Adleman)

24 .算法流程 随机选择两个秘密大素数 p 和 q ； 计算公开模数 n=p*q ； 计算秘密的欧拉函数 φ (n)=(p-1)(q-1) ； 选择一个与 φ (n) 互素的数，作为 e 或 d ； 用 Euclid 算法计算模 φ (n) 的乘法逆元素，即根据 ed mod φ (n)=1, 求 d 或 e ； 加密： C = M e mod n 解密： M= C d mod n = (M e mod n) d mod n = M 这里， φ (n) 为 Euler Totient Function, 欧拉商数 , 即集合 (1, 2, ..., n-1) 中与 n 互素的数的个数。 9.3.1 RSA 密码体制基本原理

25 .

26 .

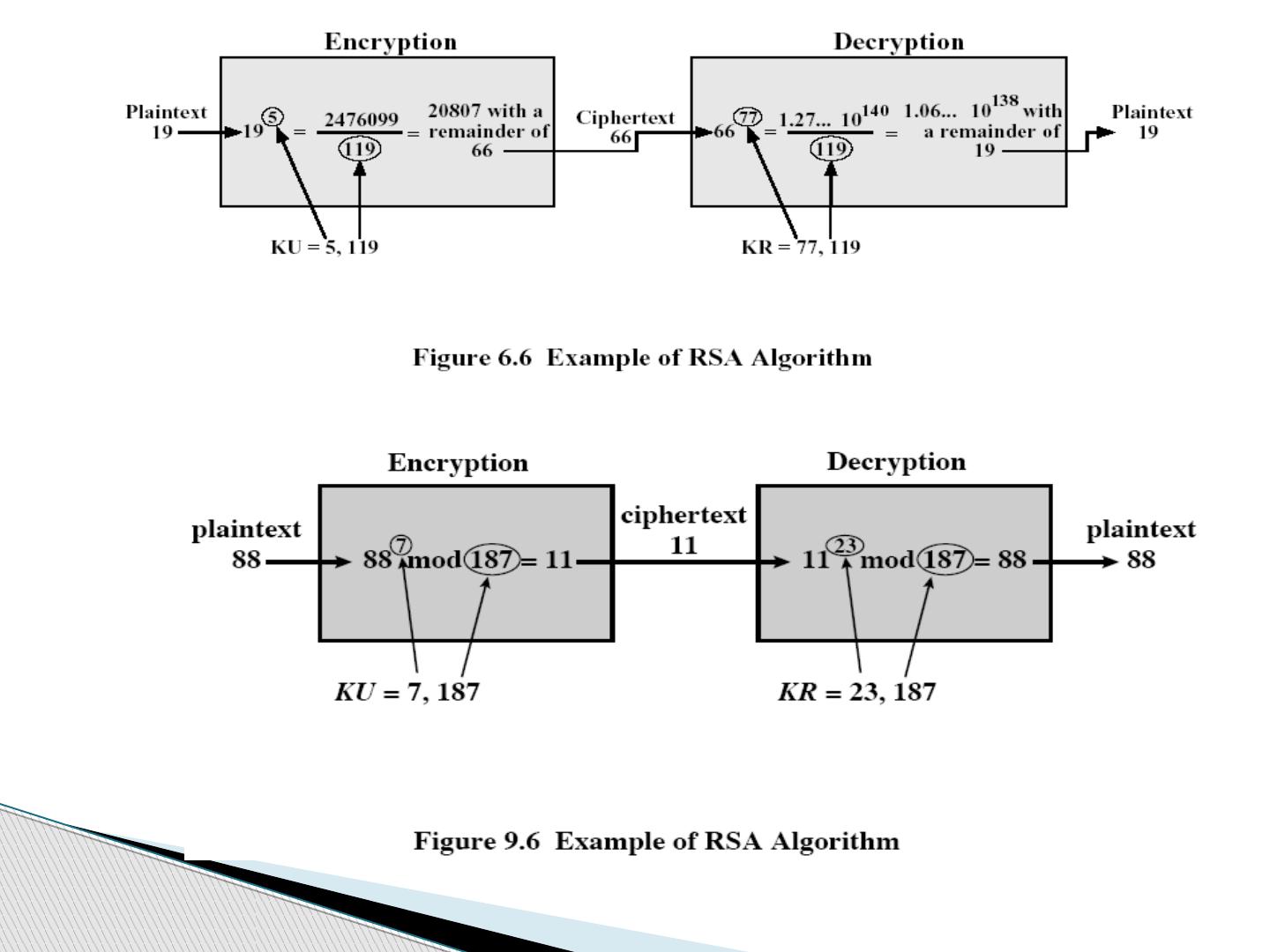
27 .一个例子 p=17,q=11,n= pq =17x11=187, φ (n)=(p-1)(q-1) =16x10=160 选择 e=7, gcd (7,160)=1, 23x7=161, 所以 d=23 公钥 KU={7,187}, 私钥 KR={23,187}, M=88 加密计算 C=88 7 mod 187 88 7 mod 187 =[(88 4 mod187)x88 2 mod187)x88 1 mod187)]mod187 88 1 mod187=88 88 2 mod187=7744mod187=77 88 4 mod187=59969536mod187=132 88 7 mod187=(88x77x132)mod187=894432mod187=11 解密计算 M=11 23 mod 187 = 88

28 .RSA 密码体制基本原理 RSA 算法满足公开密钥加密的要求 , 必须符合下列条件： 有可能找到 e, d, n 的值 , 使得对所有 M<n 有 M ed mod n = M 对于所有 M<n 的值 , 要计算 M e 和 C d 是相对容易的 在给定 e 和 n 时 , 计算 d 是不可行的 几个关系 φ (n) = φ ( pq )= φ (p) φ (q)=(p-1)(q-1), p,q are prime ed mod φ (n)=1, ed = k φ (n)+1, 即 ed≡1 mod φ (n), d≡e -1 mod φ (n)

29 .定理：给定 ed mod φ (n) =1, m∈[0, n-1], gcd (m, n)=1, 则： (m e mod n ) d mod n = m ed mod n = m 证明： ∵ ed mod φ (n) = 1 ∴ ed = k φ (n)+1 ，对 某整数 k ∴ m ed mod n = m kφ (n)+1 mod n = m( m kφ (n) mod n) mod n ∵ m kφ (n) mod n = ( m φ (n) mod n) k mod n = 1 k mod n = 1 ∴m ed mod n = (m* 1) mod n = m RSA 密码体制基本原理 如果 m= px 与 n 不互素 , gcd ( x,n )=1 ，则 m ed =( px ) ed mod n ={ p ed mod n ） ( x ed mod n)}mod n={( pp k φ (n) – lpq ) (x mod n)}mod n={p( p k φ (p) φ (q) – lq ) (x mod n)}mod n= px mod n