08现代密码学理论与实践--数论入门

1 .现代密码学理论与实践 第 8 章 数论入门 Fifth Edition by William Stallings 苗付友 mfy@ustc.edu.cn 2017 年 11 月

2 .第二部分 公钥密码和散列函数 第 8 章：数论入门 第 9 章：公钥密码与 RSA 第 10 章：密钥管理和其他公钥密码体制 第 11 章：消息认证和散列函数 第 12 章：散列和 MAC 算法 第 13 章：数字签名和认证协议

3 .本章要点 素数 是一种整数，在整除意义下，它只能被自身 ( 正负 ) 和 1 整除。素数在数论和密码学里扮演重要角色。 在公钥密码里起重要作用的两个定理是 费马定理 和 欧拉定理 。 许多密码算法的一个重要前提是能够选择一个大的 素数 。开发有效算法 判定 一个随机整数是否为素数是密码研究的重要课题。 离散对数 是许多公钥算法的基础。离散对数和普通对数类似，但是在模算术上进行运算。

4 .本章目录 8.1 素数 8.2 单向函数 8.3 费马定理和欧拉定理 8.4 素性测试 8.5 计算乘法逆元素 8.6 求解 ax mod n =b 的问题 8.7 中国余数定理 8.8 离散对数问题 8.9 二次剩余问题 8.10 不经意传输

5 .8.1 素数 Prime Numbers 整数 p>1 是素数当且仅当它只有因子 ± 1 和 ± p ，如 2,3,5,7 是素数，而 4,6,8,9,10 不是素数 素数不能写作其他数的乘积形式 1 是素数，但是通常没有什么用 素数是数论的核心 小于 200 的素数如下 2 3 5 7 11 13 17 19 23 29 31 37 41 43 47 53 59 61 67 71 73 79 83 89 97 101 103 107 109 113 127 131 137 139 149 151 157 163 167 173 179 181 191 193 197 199 素数  合数  最大公因数

6 .小于 2000 的素数如下

7 .2018/4/26 现代密码学理论与实践-08 7 /69 合数的素因子分解 分解一个数 n 就是把它写成其他数的乘积形式，如 n= a×b×c 比起用乘的方法把几个因子乘起来生成合数，分解合数通常要困难得多。 任何整数 a>1, 都可以唯一地分解为 a= p 1 a 1 p 2 a 2 … p t a t , 其中 , p 1 <p 2 <…<p t 是素数，所有的 a i 都是正整数。如 91=7x13; 3600=2 4 x3 2 x5 2 ; 11011=7x11 2 x13 素因子分解就是把一个合数写成若干素数的乘积形式，如 3600=2 4 x3 2 x5 2 ， 其中每个 a p ≥ 0, 对于某一整数 a ， 其大多数指数 a p 为 0 .

8 .合数的素因子分解 任一给定的正整数 , 可通过简单列出所有后面公式中非零指数分量来说明 . Ex ： 12 可以表示为 { a 2 =2, a 3 =1}, 18 可以表示为 { a 2 =1, a 3 =2}, 91 可以表示为 { a 7 =1, a 13 =1} 两个数的乘法等同于对应指数分量的加法 k= mn → k p = m p + n p 对所有 p Ex ： k =12x18=(2 2 x3)x(2x3 2 )=216, k 2 =2+1=3, k 3 =1+2=3, ∴ 216=2 3 x3 3 任何以 p k 形式表示的整数仅能被对应素数分量小于或等于它的另一个整数 p j 整除 , 其中 j ≤ k ， 即有 a | b → a p ≤ b p ，对所有素数 p 成立 。 Ex ： a =12, b =36, 12 | 36, 12=2 2 x3 1 , 36=2 2 x3 2 a 2 =2= b 2 , a 3 =1≤2= b 3

9 .互素和最大公约数 GCD gcd (a, b)=c, 即 c 是 a 和 b 的最大公约数 , 当 c 是 a 和 b 的因子 任何 a 和 b 的因子也是 c 的因子 两 个整数 a, b, 如果除了 1 以外没有公共因子 , 则称它们 互素 (Relatively Prime) 8 和 15 互素 , 因为 8 的因子是 1,2,4,8, 而 15 的因子是 1,3,5,15, 1 是它们唯一的公共因子。 如果将整数表示为素数之积 , 则容易确定两个正整数的最大公 因子 下列关系总是成立的 如果 k= gcd ( a, b ), 则 k p = min( a p , b p ), 对于任意的 p ∊ P 例子： 300=2 2 x3 1 x5 2 , 18=2 1 x3 2 , gcd (18, 300)=2 1 x3 1 x5 0 =6

10 .8.2 单向函数 One-way Function 单向陷井门函数 One-way Trapdoor Function 定义 8.1 单向函数 (One-way Function) 一函数 f 若满足下列条件 , 则称 f 为单向函数： (1) 对于所有属于 f 之域的任一 x , 容易计算 y = f ( x ) (2) 对于几乎所有属于 f 之域的任一 y , 求得 x , 使 y = f ( x ), 在计算上不可行。 定义 8.2 单向陷井门函数 (One-way Trapdoor Function) 一“可逆”函数 F 若满足下列两条件 , 则称 F 为单向陷井门函数： (1) 对于所有属于 F 之域的任一 x , 容易计算 F ( x )= y ； (2) 对于几乎所有属于 F 之域的任一 y , 除非获得暗门信息 (trapdoor), 否则求出 x , 使得 x = F -1 ( y ) 在计算上不可行 , F -1 为 F 之逆函数 ; 如有额外信息 ( 暗门 ), 则容易求出 x = F -1 ( y ) ，如 旅馆房间门 。

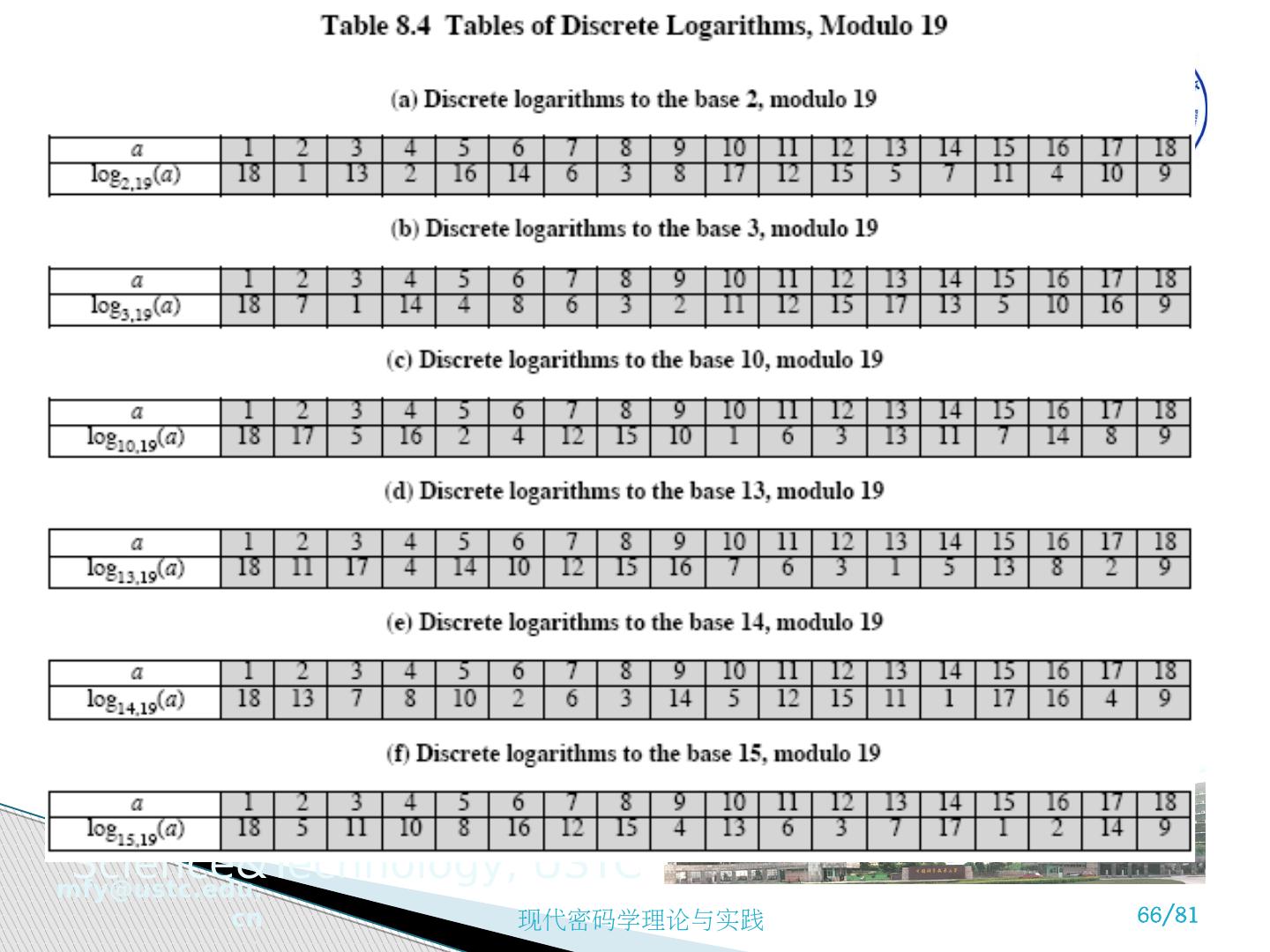
11 .1. 离散对数问题 Discrete Logarithm Problem (DLP) 令素数 p 满足 p-1 含有另一大素数 q (q 整除 p-1) 及一整数 g, 1<g< p-1 。 若给定整数 x, 求 y = g x mod p, 最多需要 L log 2 x ｣ +w(x)-1 次乘法 , w(x) 为 x 中所有 1 的个数。如 x =15, 即 x =(1111) 2 , w(x)=4, 则 g 15 =((g 2 )g) 2 ·g) 2 ·g mod p, 只需要 3 + 4 -1=6 次乘法。 但是若给定 p, g 及 y, 求 x, 则为 DLP 问题 , 最快方法需要 L(p)=exp{( lnp ) 1/3 ( ln ( lnp )) 2/3 } 次运算。 当 p=512 位时 , L(p) 约为 2 256 ≈10 77 , 计算上不可行 , 因为 2 100 ≈10 30 , 计算要 10 16 年 。 单向函数举例

12 .2. 因数分解问题 Factorization Problem 给定大素数 p 和 q, 求 n = p×q , 只要一次乘法 给定 n, 求 p 和 q, 即为因数分解问题 (FAC), 最快方法需要 T(n) = exp {c( ln n ln ( ln n)) ½ } 次运算 , 其中 c 为大于 1 的正整数。 3. 背包问题 Knapsack Problem 给定有限个自然数序列集合 B=(b 1 ,b 2 ,… b n ) 及二进制序列 x=(x 1 ,x 2 ,… x n ), x i ∈(0,1), 求 S=∑ x i b i 最多只需 n-1 次加法；但若给定 B 和 S, 求 x 则非常困难。 穷举时有 2 n 种可能 , 当 n 很大时为计算上不可行。 Garey 和 Johnson 证明 , 背包问题是 NP 问题 (Non-Polynomial) 单向函数举例 ( 续 )

13 .单向函数的交换性 (commutative property) 单向函数本身对近代密码学领域用处不大，但若具有交换性，则作用大。 定义 8.3 交换性 令 Z 为一集合， F 为将 Z 映射到 Z 本身的函数集合。 令 z∈Z , F x (z) 表示此函数集合之第 x 函数 , 若 F x ( F y (z))= F y ( F x (z)) ，则称此函数集合具有交换性。例： D(E(m))=E(D(m)) 单向函数及其交换性

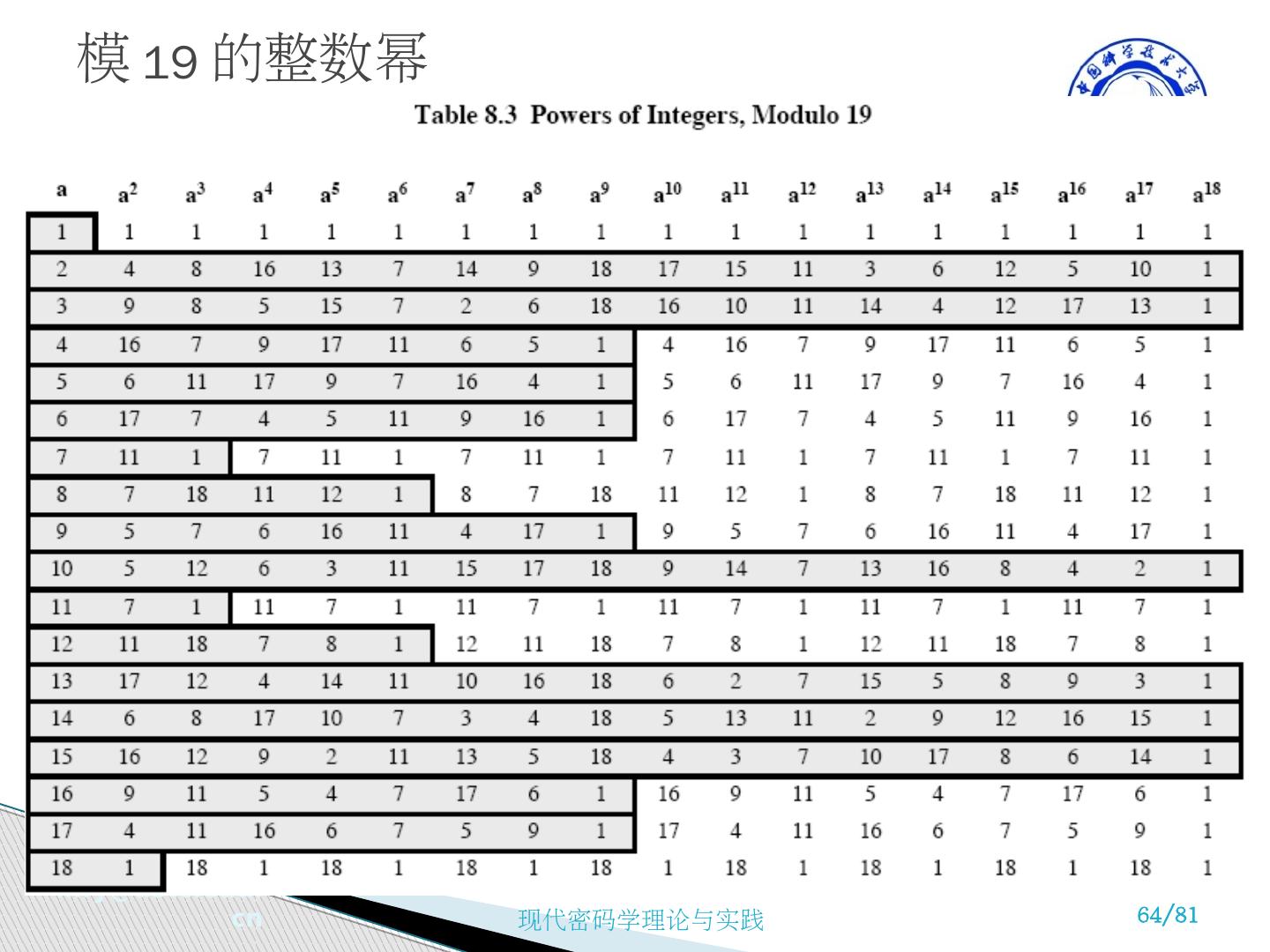
14 .指数函数 (Exponentiation Function) 定义 8.4 指数函数 令 G 为有限乘法群 , g∈G , 则对于所有整数 x, E x (g)= g x mod p ∈G, 是为指数函数。 通常 , 令 G={1,2,…,p-1}, p 为素数 , 则 E x (g)= g x mod p 为指数函数。 指数函数之特性 1. 周期性 (Periodicity) 令序列 <E x (g)>={g 0 ,g 1 ,g 2 ,…} 为 g 所产生之序列。因为 G 是有限群 , E x (g) 不可能不重复 , 故 E x (g) 产生之序列为周期序列。

15 . 当存在 最小正整数 T , 使得 E T (g)= g T =1=g 0 时 , 称 T 为 g 在 G 中的阶或序 (order) 。根据 Fermat’s Theorem, 对于所有 g, T 必定整除 p-1. 例： p=11, g=2, <E x (g)>={2 0 ,2 1 ,2 2 ,…,2 10 }={1,2,4,8,5,10,9,7,3,6,1} 即： 2 0 =1 mod 11 2 6 =9 mod 11 2 1 =2 mod 11 2 7 =7 mod 11 2 2 =4 mod 11 2 8 =3 mod 11 2 3 =8 mod 11 2 9 =6 mod 11 2 4 =5 mod 11 2 10 =1 mod 11 2 5 =10 mod 11 所以 T=10=11-1=p-1 指数函数之特性 ( 续 )

16 .2. 本原元素 ( 素根、原根 )Primitive Element (Root) 本原元：若 g∈G 的阶为 T=p-1, 则称 g 为模 p 的本原元。 (1) 当 g 为 mod p 的本原元时 , 由 g 产生的序列 <E x (g)> 具有最大周期 ( 安全性较高 ) 。 (2) 对于所有素数 p, 其本原元必定存在。 (3) 当 g 为模 p 的本原元且 a 与 p-1 互素时 , 即 gcd (a, p-1)=1, 则 g a mod p 亦必为模 p 之本原元素。 (4) 模 p 的本原元素个数为 φ (p-1), 称为尤拉商数 (Euler Totient Function), 表示不大于 p-1, 且与 p-1 互素的正整数之个数 , 即 φ (p-1) 。 指数函数之特性 ( 续 )

17 .求一个大素数 p 很容易，用现成的素性验证算法就可以了。不过已知一个素数 p ，求其本原根则很困难，因为需要将 p - 1 的素因子 q 1 ， q 2 ， ……q k-1 ， q k 都找出来，然后分别验证 g q 1 mod p ， g q 2 mod p ， ……g q k-1 mod p ， g q k mod p ，如果都不等于 1 ，则 g 是 p 的一个本原根。而然，如果 p 是一个很大的素数，例如 128 个 2 进制位的素数，要分解出 p - 1 的所有素因子来则是一件很困难的事情。 附：求 本原元

18 .指数函数之特性 ( 续 ) 本原元素举例： p=11, g=2, φ (p-1)= φ (10)=4, 即 1, 3, 7, 9 与 p-1 互素。若 g=2 为模 p 之本原元素 , 则 2 1 =2, 2 3 =8, 2 7 =7, 2 9 mod 11=6 均为模 11 之本原元素。找到一个本原元素后可以容易找到所有本原元素 , 问题是如何找到第一个本原元素 。 算法如下： P1. 利用素性验证算法，生成一个大素数 q ； P2. 令 p = q * 2 + 1 ； P3. 利用素性验证算法，验证 p 是否是素数，如果否，则跳转到 P1 ； P4. 生成一个随机数 g ， 1 < g < p - 1 ； P5. 验证 g 2 mod p 和 g q mod p 都不等于 1 ，否则跳转到 P4 ； P6. g 是大素数 p 的本原根。

19 .3. 交换性 指数函数满足交换性 , 因为 : E x ( E y (g))=E x ( g y )=( g y ) x = g yx E y (E x (g))= E y ( g x )=( g x ) y = g xy ∴ E x ( E y (g))= E y (E x (g)) 指数函数之特性 ( 续 )

20 .4. 非对称性 (Asymmetric Property) ∵E x (-g)=(-g) x =(-1) x g x =(-1) x E x (g) ∴ 若 x 为偶，则 E x (-g)= E x (g) 若 x 为奇，则 E x (-g)= -E x (g) 5. 乘法性 (Multiplicative Property) E x (g 1 )E x (g 2 )=g 1 x g 2 x =(g 1 g 2 ) x =E x (g 1 g 2 ) 指数函数之特性 ( 续 )

21 .6. 乘法逆元 素 Multiplicative Inverse 若 T 为 g 之序 , 则对于所有 x, 0≤x<T, E x (g -1 )=E T-X (g) g -1 为 g 的乘法逆元素 . 因为： E x (g -1 )=g -x =1•g -x = g T •g -x = g T -x = E T-x (g) 这是一种求乘法逆元素的方法 , 欲求 g -1 时 , 由于 g T-1 =g -1 ( 这里 x=1) ∵T 整除 p-1, ∴g -1 =g T-1 =g p-1-1 = g p-2 (mod p) g•g -1 mod p=1, 这是因为 g x g T -x mod p= g T mod p=1 7. 安全性 给定 g∈G 及 y∈<E x (g)>, 求 x 使得 y=E x (g)= g x mod p 为 DLP 问题。 指数函数之特性 ( 续 )

22 .8. 可逆性 若 T 为 g∈G 之序 , x ­ 1 为 x 在模 T 时的乘法逆元素 , 即 xx -1 =1 mod T, 则 E x (E x -1 (g)) = E x -1 (E x (g))=g xx -1 mod p = g mod p 这是因为 E x (g) 满足交换性 , 所以 E x (E x -1 (g))=E x -1 (E x (g)) 。 另一种证明方法： ∵ x -1 x = 1 mod T = kT+1 ∴E x (E x -1 (g))=g xx -1 =g kT+1 =( g T ) k •g =1 k g=g mod p 这实际上是利用费马定理对 RSA 算法正确性的证明 指数函数之特性 ( 续 )

23 .快速指数运算法 — 平方再乘法 快速指数运算法 — 平方再乘法 (Square and multiply) 当 x 为 n 位时即 x=(x n-1 , x n-2 ,…,x 1 , x 0 ) E x (g)= g x =(…(1•g x n-1 ) 2 •g x n-2 ) 2 •g x n-3 …) 2 •g x 0 此算法共需要 n-1 次平方及 w(x)-1 次乘法 , 平均而言 w(x)=n/2, x 在二进制表示时有 n/2 个 ”0” 及 n/2 个 ”1” 。因此，当 x 为 n 位时 , 平均需要 1.5n-2 个乘法 ( 平方算一次乘 ) 。

24 .Algorithm fastexp (a, z, n) begin “return x= a z mod n” a 1 := a; z 1 :=z; x:=1 while z 1 ≠0 do “x(a 1 z 1 mod n)= a z mod n” begin while z 1 mod 2 = 0 do begin “square a 1 while z 1 is even” z 1 :=z 1 div 2 a 1 :=(a 1 *a 1 ) mod n end; z 1 :=z 1 -1 x:= (x*a 1 ) mod n “multiply” end; fastexp :=x end 快速指数运算法 — 平方再乘法

25 .8.3 费马定理和欧拉定理 定理 8.1 费马定理 Fermat’s Theorem 若 p 是素数 , a 是正整数且不能被 p 整除 , 则 a p-1 mod p=1 证明： 因为 {a mod p, 2a mod p, ..., (p-1)a mod p} 是 {1, 2, ..., (p-1)} 的置换形 , 所以 , (a ｘ 2a ｘ ... ｘ (p-1)a) ≡ (1 ｘ 2 ｘ ... ｘ (p-1)) (mod p) ≡ (p-1)! mod p. 但是 , a ｘ 2a ｘ ... ｘ (p-1)a=(p-1)!a p-1 , 因此 (p-1)!a p-1 ≡ (p-1)! mod p, 两边去掉 (p-1)!, 即得 a p-1 mod p = 1 证毕 例如： a=7, p=19, a p-1 mod p=7 18 mod 19=? 7 2 =49 ≡ 11 mod 19 7 4 =121 ≡ 7 mod 19 7 8 =49 ≡ 11 mod 19 7 16 =121 ≡ 7 mod 19 a p-1 =7 18 =7 16 x7 2 ≡ 7x11 ≡ 1 mod 19

26 .费马定理的 等价形式 费马定理等价形式 a p ≡ a mod p, p 是素数， a 是任意正整数 例如： p=5, a=3, 3 5 =243 ≡ 3 mod 5 p=5, a=10, 10 5 =100000 ≡ 10 mod 5 ≡ 0 mod 5

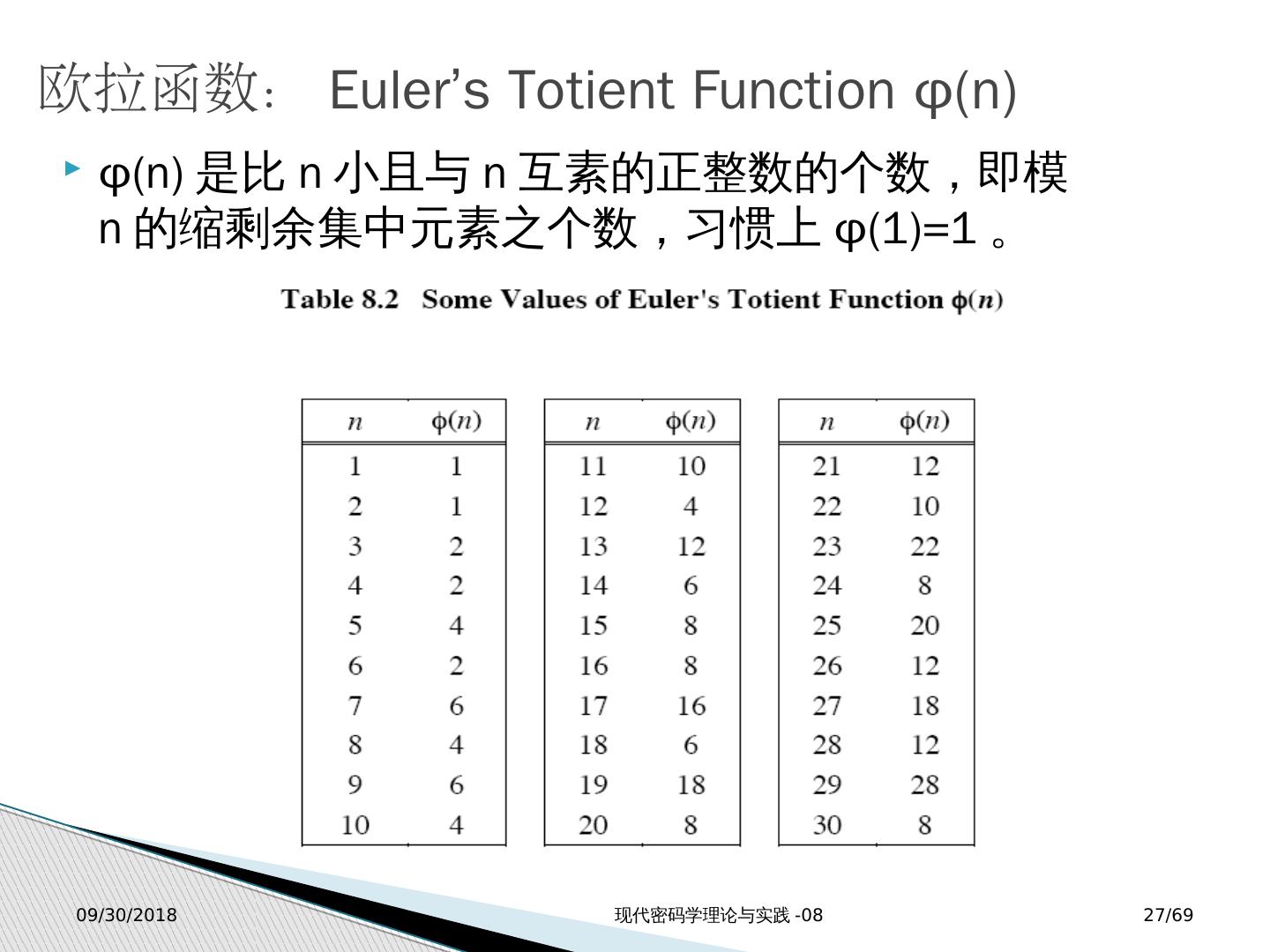
27 .2018/4/26 现代密码学理论与实践-08 27 /69 欧拉函数： Euler’s Totient Function φ (n) φ (n) 是比 n 小且与 n 互素的正整数的个数，即模 n 的缩剩余集中元素之个数，习惯上 φ (1)=1 。

28 .欧拉函数 φ (n) 的证明 定理 8.2 p 和 q 是素数 , n=p*q, φ (n)= φ (p) φ (q)=(p-1)(q-1) 证明 ： 考虑余数集合 {0, 1, …, (pq-1)} 中不与 n 互素的余数集合是 {p, 2p, …, (q-1)p}, {q, 2q, …, (p-1)q} 和 0, 所以 φ (n)= pq -[(q-1)+(p-1)+1]= pq -( p+q )+1= (p-1)(q-1)= φ (p) φ (q) 一般说来 , 对任意 n, φ (n) 由下式给出： φ (n)= ( p i -1), n= ... P i 均为素数。 或 φ (n)= n(1-1/p 1 )(1-1/p 2 )…(1-1/ p t )

29 .例： φ (35)=24= φ (5) φ (7)=4x6=24 n=24=2 3 x3 1 , φ (n)= φ (24)=2 2 (2-1)3 0 (3-1 )= 8 φ (MN)= φ (M) φ (N) gcd (M,N)=1