- 快召唤伙伴们来围观吧
- 微博 QQ QQ空间 贴吧
- 文档嵌入链接
- 复制
- 微信扫一扫分享
- 已成功复制到剪贴板
07现代密码学理论与实践--利用对称密钥实现保密
展开查看详情
1 .现代密码学理论与实践 第 7 章 利用对称密钥实现保密 Fifth Edition by William Stallings 苗付友 mfy@ustc.edu.cn 2016 年 10 月
2 .链路加密中每个结点都需要一套加密设备,端到端加密只需在系统的两个终端执行加密和解密操作 即使通信数据都被加密,攻击者仍能通过流量分析来获取信息。有效的对付手段是对传输数据进行填充。 密钥分配为需要传输加密数据的通信双方提供传递密钥的功能,需要机制和协议保障密钥传输的安全性 主密钥不经常使用并长期存在,临时生成会话密钥并分发给通信双方 随机或伪随机数发生器数许多密码函数在实际应用中必备的能力,其原则是产生的比特串不能够被猜测。 本章要点
3 .7.1 密码功能的位置 7.1.1 安全隐患 7.1.2 链路加密与端到端加密 7.2 传输保密性 7.2.1 链路加密方式 7.2.2 端到端加密的方法 7.3 密钥分配 7.3.1 一个密钥分配方案 7.3.2 层次化密钥控制和会话密钥的使用寿 7.3.3 一种透明的密钥控制方案命 7.3.4 分散式密钥的控制 7.3.5 控制密钥的使用方式 7.4 随机数的产生 7.4.1 随机数的来源 7.4.2 伪随机数产生器 7.4.3 线性拟合发生器 7.4.4 用密码学方法生成随机数 7.4.5 Blum Blum Shub (BBS) Generator 7.4.6 真随机数发生器和偏差 本章提纲
4 .第 7 章 用对称密码实现保密性 本章讨论加密逻辑功能所处的位置,使用加密防止通信量分析攻击的方法,密钥分配问题及随机数的产生。 7.1 密码功能的位置 7.1.1 安全隐患 从同一网上其他工作站发起的窃听 使用拨号进入局域网或服务器进行窃听 使用外部路由链接进入网络和窃听 在外部链路上对通信业务的监听和修改
5 .基本方法:链路加密与端到端加密 链路加密 加密是在每一条链路上独立发生的 意味着链路之间每次分组交换都必须被解密 要求的设备多,且需要成对的密钥 端到端加密 加密解密的过程在两端系统中进行 在两端需要加密装置,源主机与目的主机共享密钥 依然存在弱点: 不能对整个数据包加密,否则不能实现包的路由 如果只对数据加密,信息头保持明文,则传输过程又不安全了,因为可以有通信量分析攻击 7.1.2 链路加密与端到端加密
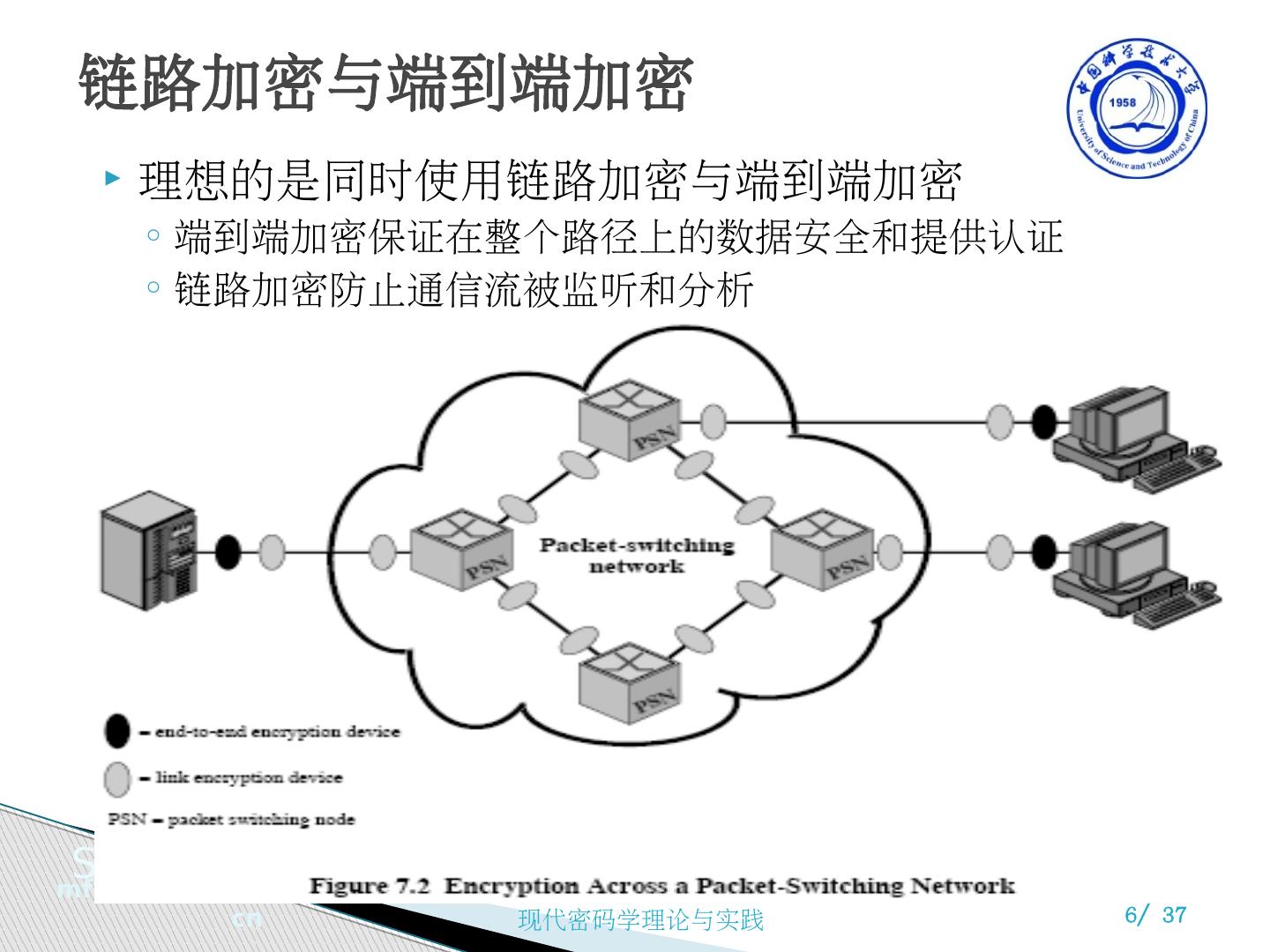
6 .理想的是同时使用链路加密与端到端加密 端到端加密保证在整个路径上的数据安全和提供认证 链路加密防止通信流被监听和分析 链路加密与端到端加密
7 .两种加密策略的特点
8 .可以在 OSI 参考模型的各个层次上设置加密功能 链路加密可以在物理层和数据链路层 端到端加密可以在网络层、传输层、表示层和应用层 越往高层移,需要加密的信息量越少,参与的实体和密钥越多,加密越复杂,但是会更安全 采用前端处理器 FEP 实现加密功能 端系统用户进程和应用使用同一个密钥采用同一个加密方案 加密函数的逻辑位置
9 .通信量分析是监控通信双方的通信流 军事和商业环境下都有用 也可用于产生隐蔽信道 链路加密掩盖了头部细节 但是在网络中和端节点的额外通信量仍然是可见可读的 通信量填充可以进一步掩盖通信流信息 但是会带来连续的通信量 通信量分析 Traffic Analysis
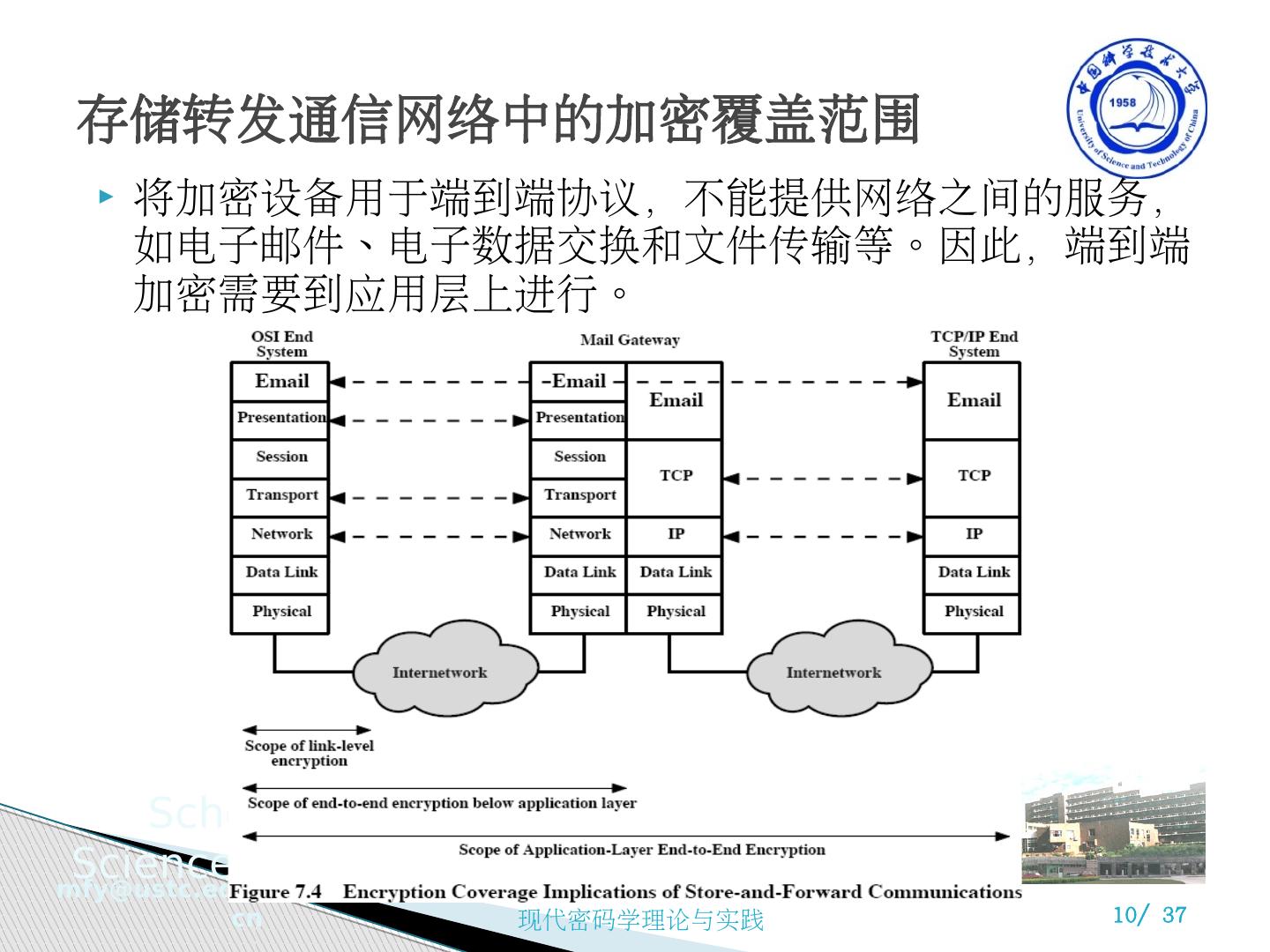
10 .将加密设备用于端到端协议,不能提供网络之间的服务,如电子邮件、电子数据交换和文件传输等。因此,端到端加密需要到应用层上进行。 存储转发通信网络中的加密覆盖范围
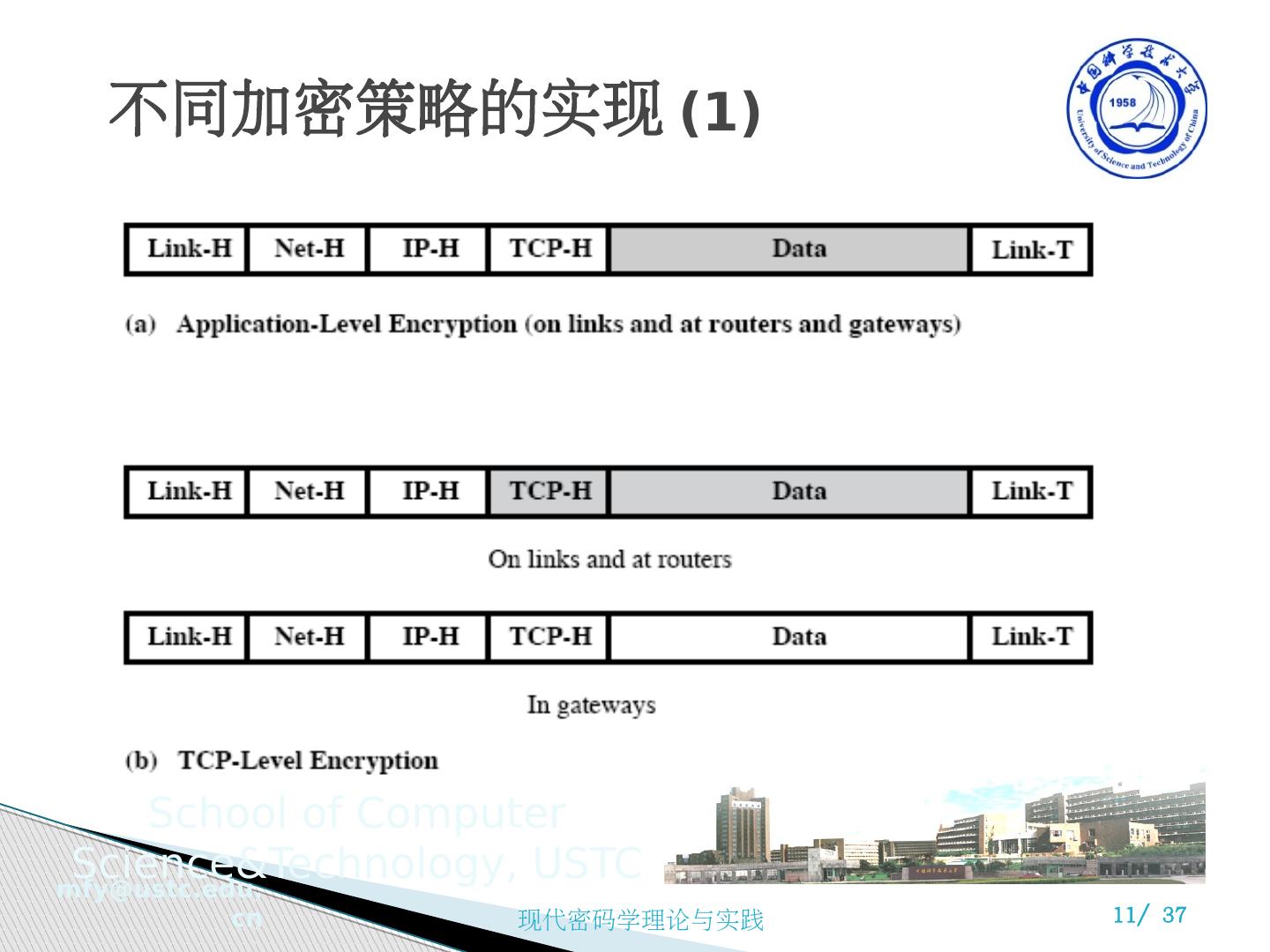
11 .不同加密策略的实现 (1)
12 .不同加密策略的实现 (2)
13 .可以从通信量分析攻击得到的信息类型 传输双方的标识 传输双方的联系频率 消息格式、消息长度,或者消息交换频繁程度可以暗示出消息的重要性 与传输双方的某些谈话相关的事件 7.2 传输保密性
14 .使用链路加密时分组首部要加密,因此可以减少通信量分析的机会,但攻击者仍有可能估算出网络上的通信量并观察到进入和离开每个端系统的通信量的大小。有效防范措施是通信量填充 (traffic padding) 7.2.1 链路加密方式
15 .端到端加密方式 端到端加密方式使信息防护者可以采用的措施更有限,例如应用层加密可以使攻击者确定哪些通信实体参与了通信过程;传输层加密仍会透露网络层地址和通信量模式。 解决办法是在传输层或应用层把所有数据单元都填充到一个统一的长度,以防止攻击者获得端用户之间交换的数据量信息,掩盖通信量模式。 7.2.2 端到端加密的方法
16 .密钥分发问题 对称的加密机制要求双方一个秘密密钥 问题是如何安全保密地传递这个密钥 许多密码系统出问题多在密钥分发上 密钥分发可以采用的多种方法 密钥由 A 选择,并亲自交给 B 第三方 C 选择密钥后亲自交给 A 和 B 如果 A 和 B 以前或最近使用过某密钥,其中一方可以用它加密一个新密钥后再发送给另一方 A 和 B 与第三方 C 均有秘密渠道,则 C 可以将密钥分别秘密发送给 A 和 B 7.3 密钥分配
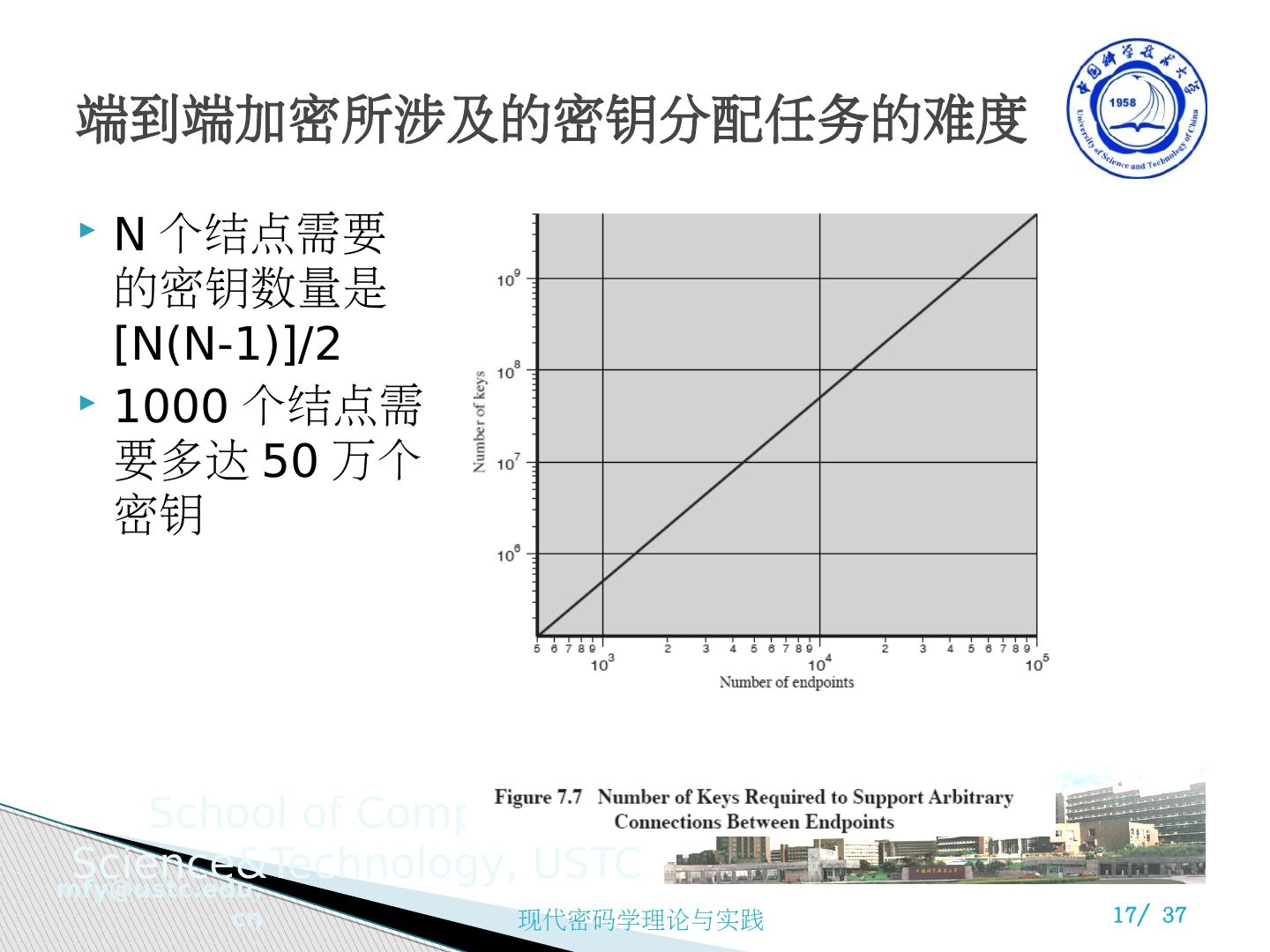
17 .端到端加密所涉及的密钥分配任务的难度 N 个结点需要的密钥数量是 [N(N-1)]/2 1000 个结点需要多达 50 万个密钥
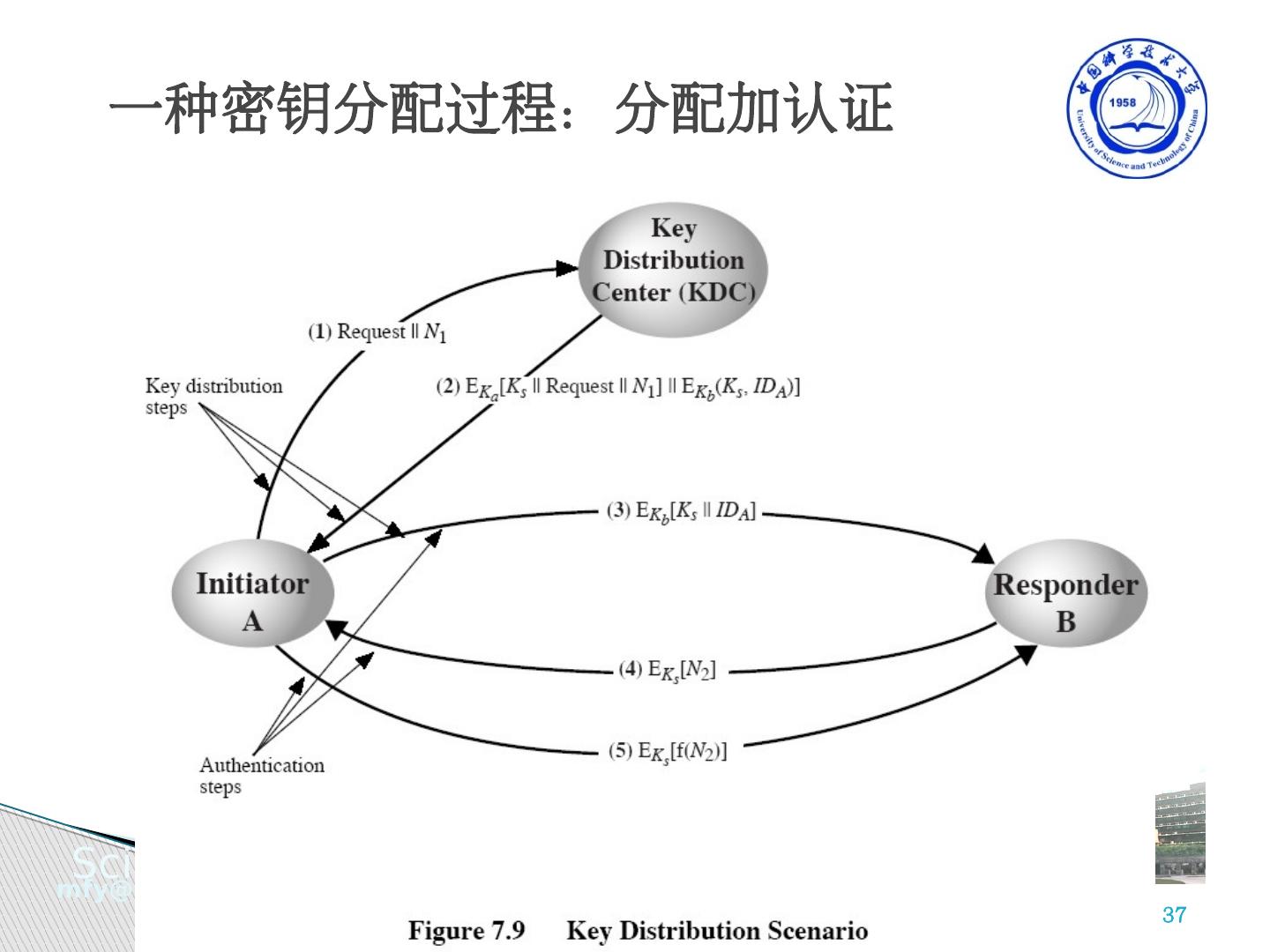
18 .密钥层次结构的使用
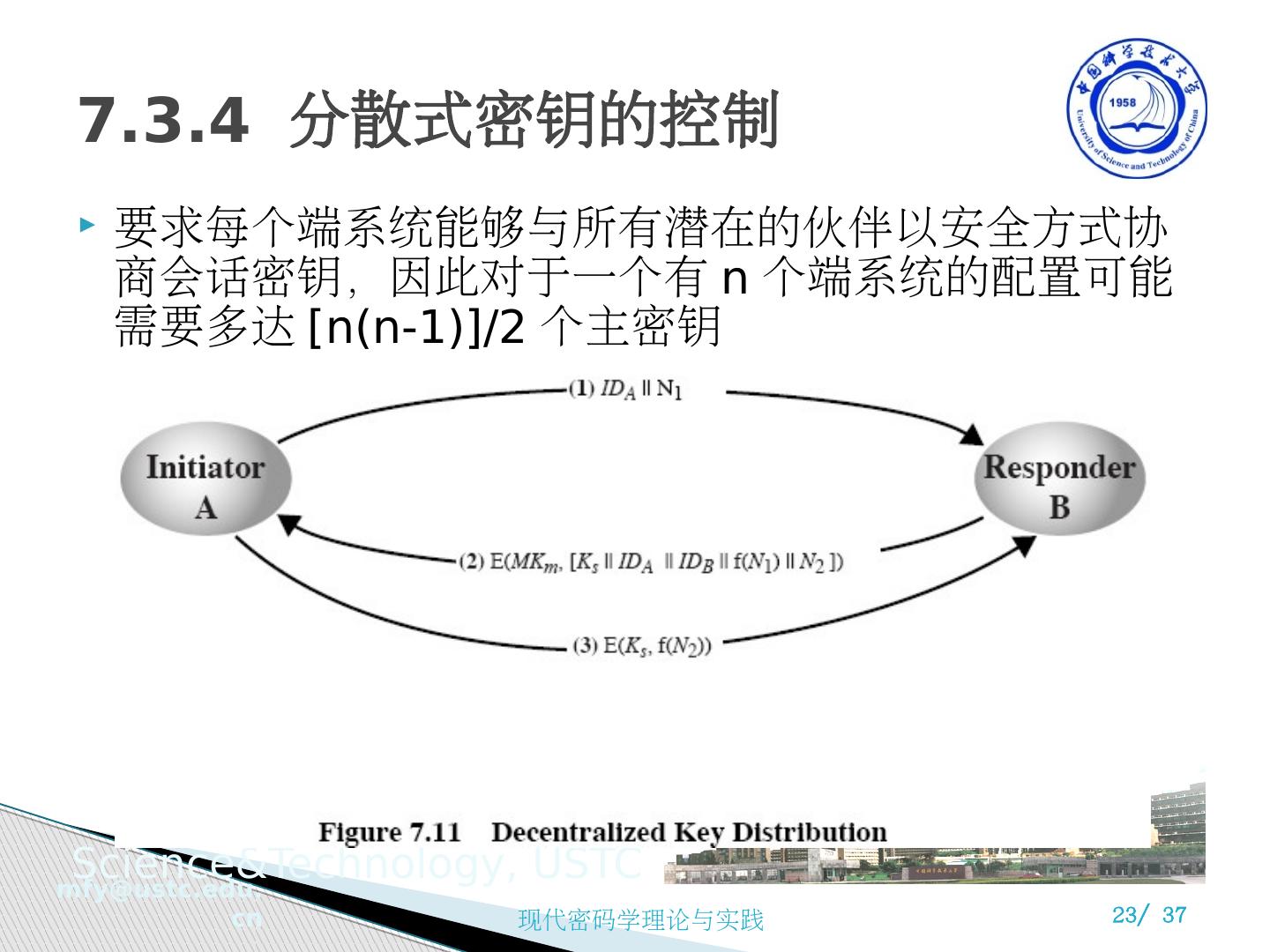
19 .A 和 B 各自拥有与 KDC 共享的主密钥 K A 和 K B : A 向 KDC 发出请求,要求得到与 B 通信的会话密钥 KDC 用 K A 加密传送给 A 如下内容: 一次性会话密钥 K S 原始请求报文 用 K B 加密的要发给 B 的会话密钥 K S 和 A 的标识符 ID A A 得到会话密钥 K S 并将有关信息发给 B A 和 B 之间进行认证,并正式秘密通信 Nonces( 临时交互号,或现时,可以是时间戳、计数器或随机数 ) ,主要用在认证协议中防范重放攻击 7.3.1 一个密钥分配方案
20 .一种密钥分配过程:分配加认证
21 .分层式密钥的控制 建立一系列 KDC ,各个 KDC 之间存在层次关系,使得主密钥分配所涉及的工作量减至最小,因为大部分的主密钥都是由一个本地的 KDC 和它的本地实体共享的,并将出错或受到破坏的 KDC 的危害限制在它的本地区域 会话密钥的生命期 会话密钥更换越频繁就越安全 对于面向连接的协议,每次会话使用新的密钥 对于无连接的协议,每次交互使用新的密钥,或者每个固定时间或对于一定数量的交互使用一个给定的会话密钥 7.3.2 层次化密钥控制和会话密钥的使用寿命
22 .7.3.3 一种透明的密钥控制方案
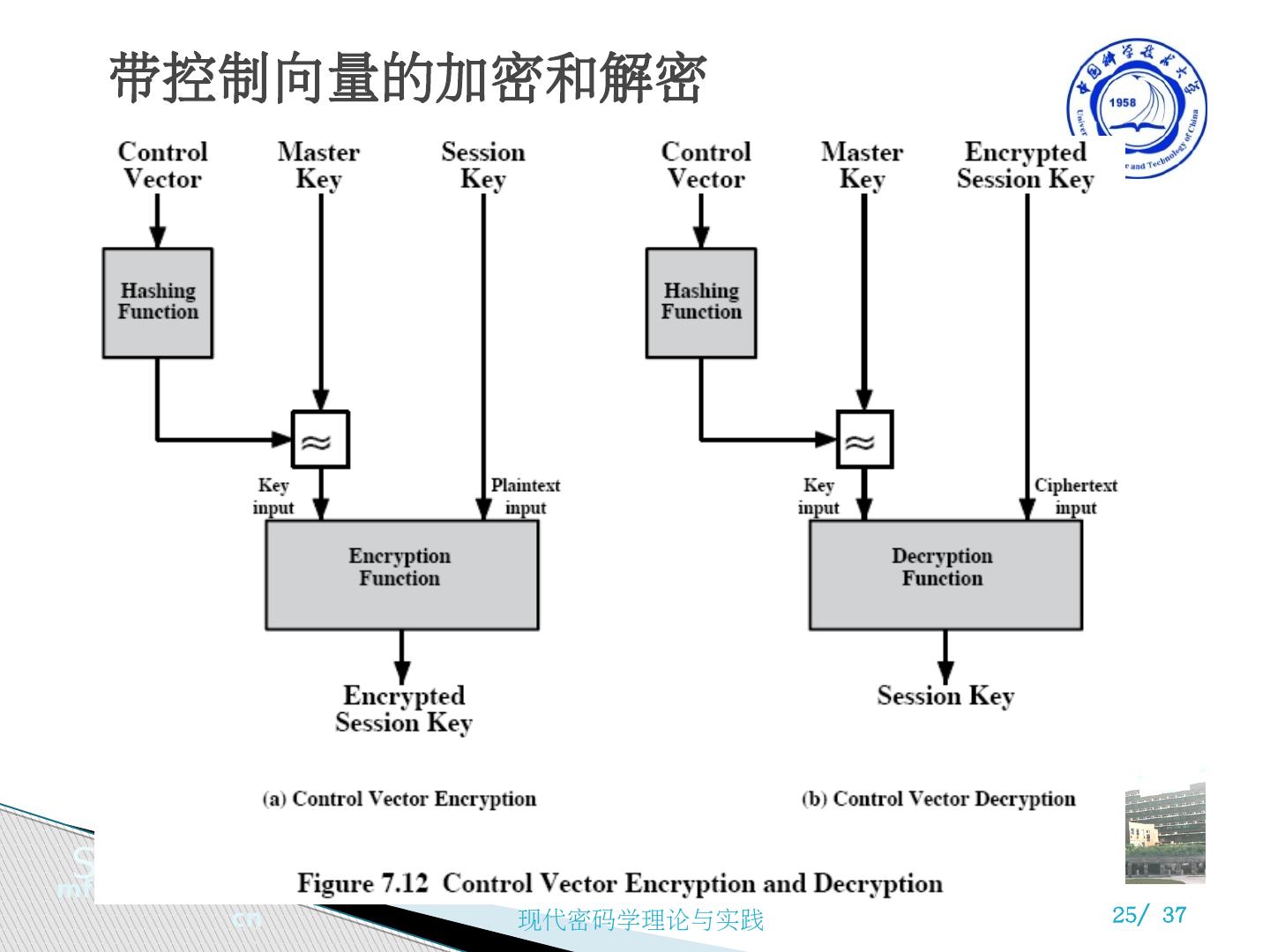
23 .要求每个端系统能够与所有潜在的伙伴以安全方式协商会话密钥,因此对于一个有 n 个端系统的配置可能需要多达 [n(n-1)]/2 个主密钥 7.3.4 分散式密钥的控制
24 .因用途不同而定义的不同类型密钥 数据加密密钥 PIN 加密密钥 文件加密密钥 依据密钥特征限制密钥的使用方式 给予每个密钥一个关联标记,如 DES64 位密钥中留作做奇偶校验的 8 位非密钥比特 1 比特指示此密钥是主密钥还是会话密钥 1 比特指示此密钥是否可以用于加密 1 比特指示此密钥是否可以用于解密 其余比特留待将来使用 控制向量的方案 7.3.5 控制密钥的使用方式
25 .带控制向量的加密和解密
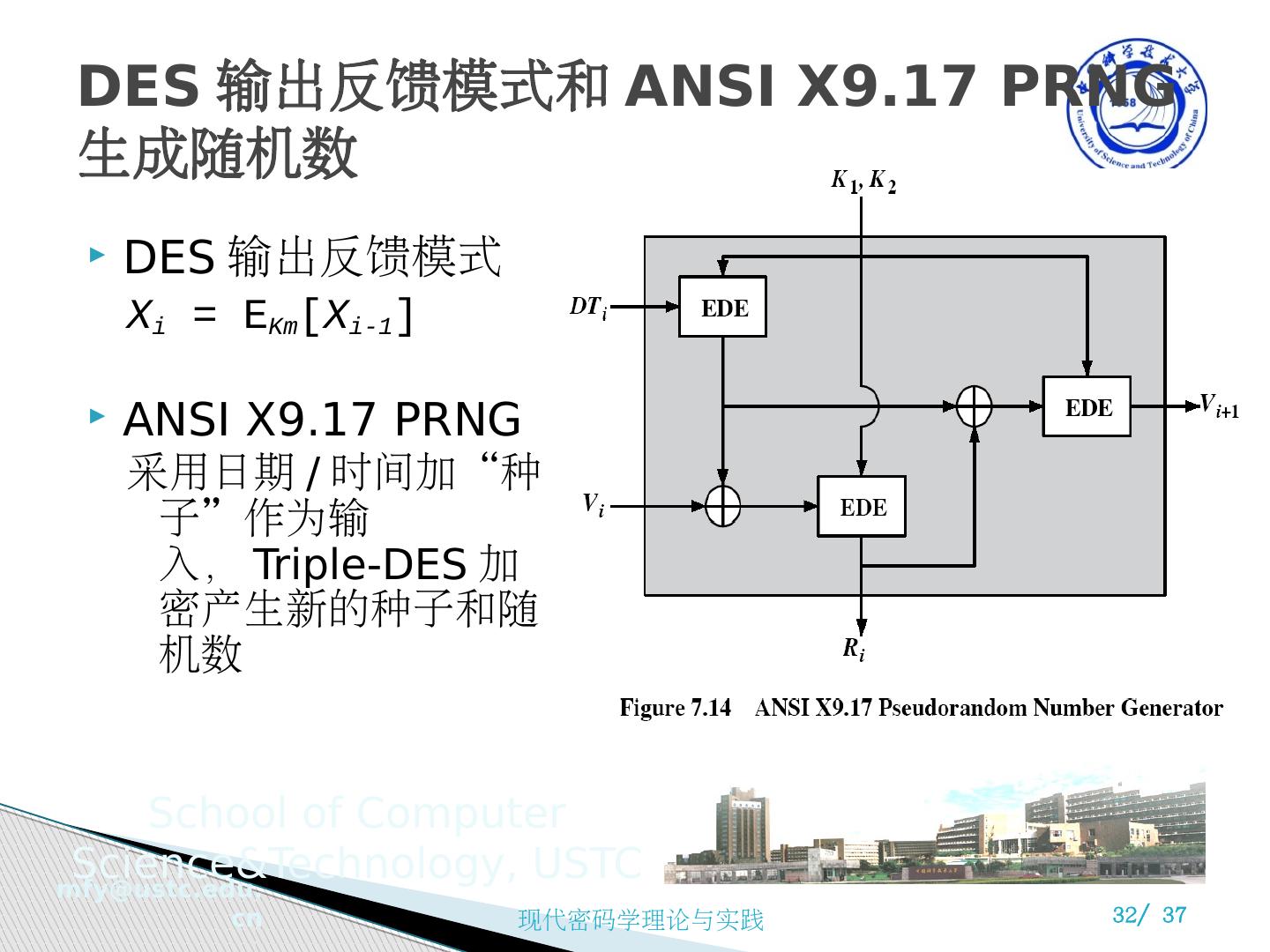
26 .随机数 random numbers 的用途 用于相互鉴别 authentication ,以防重放攻击 会话密钥 session keys 的产生 产生公开密钥,如在 RSA 算法中产生密钥 一次一密密码中的密钥流 Nonces( 临时交互号或现时,可以是时间戳、计数器或随机数 ) Statistically random( 随机程度 ) uniform distribution, 均匀分布,每个数出现的频率应该近似相等 Independent ,独立性,系列中的任意一个数都无法从其他数推测得到 Unpredictable ( 不可预测程度 ) ,基于前值不能推导出未来的 随机数序列 7.4 随机数的产生
27 .最好的来源是真实世界中的自然随机事件 可以找一个一般的但是随机的事件进行监控 一般需要特殊的硬件来实现,如衰变计数器,无线电噪声,声音噪声,二极管热噪声,漏电电容, 闸流 管等。 这些随机数源的问题是信号偏离或者信号的不均匀分布 所以在采样和使用时需要加以补偿 最好是只使用每个采样中最具噪声的位 还可以来自随机数出版物的内容,但是随机数有限,有些知名随机数用得太多太滥了 7.4.1 随机数的来源
28 .Pseudorandom Number Generators (PRNGs) 产生随机数的算法与技术 尽管不是完全随机,但是产生的伪随机数仍然可以通过某些随机性测试 7.4.2 伪随机数产生器 (PRNG)
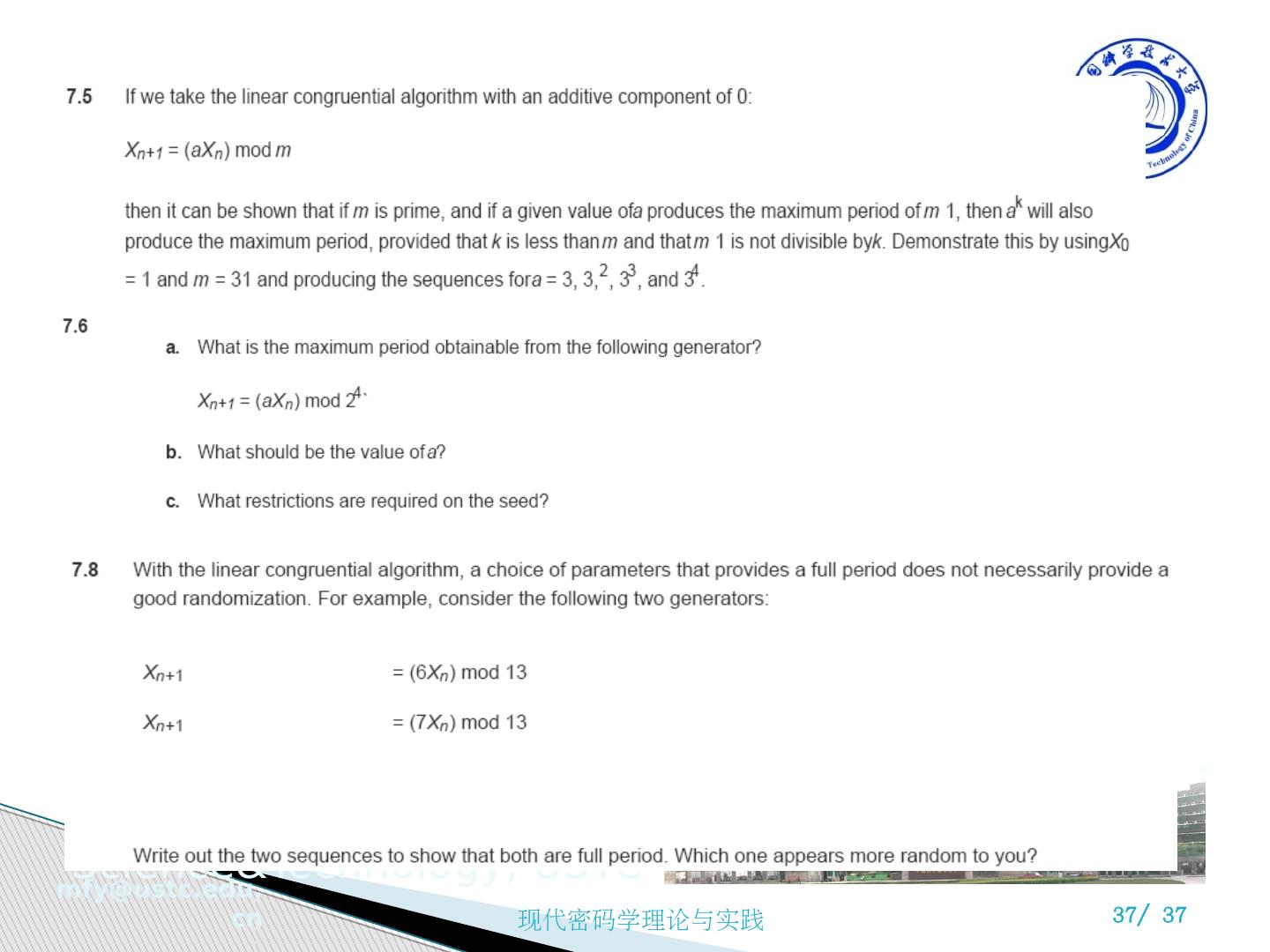
29 .Linear Congruential Generator ( 线性同余 ) m ,模数, m>0 a ,乘数, 0<=a<=m c ,增量, 0<=c<=m X 0 ,初始值或种子, 0<= X 0 <=m 通用迭代技术采用 X n+1 = ( aX n + c) mod m 给定恰当的参数,能够产生长的类随机序列 e.g. a=7, c=0, m=32, X 0 =1, 产生 {7, 17, 23, 1, 7, ...}, 不满足随机性,因为周期是 4 e.g. a=5, c=0, m=32, X 0 =1, 产生 {1, 5, 25, 29, 17, 21, 9, 13, 1, ...}, 周期为 8 (上例中,如果 a 是 Z m 的生成元,则可以实现全周期长的随机数) 7.4.3 线性拟合发生器