04现代密码学理论与实践--有限域

1 .现代密码学理论与实践 第 4 章 有限域 苗付友 mfy@ustc.edu.cn staff.ustc.edu.cn/~ mfy 2016 年 10 月

2 .本章要点 域是一些元素的集合，其上定义了两个算术运算 ( 加法和乘法 ) ，具有常规算术性质，如封闭性、结合律、交换律、分配律、加法逆和乘法逆等。 模算术是一种整数算术，它将所有整数约减为一个固定的集合 [0,1,…, n -1] ， n 为某个整数。任何这个集合外的整数通过除以 n 取余的方式约减到这个范围内。 两个整数的最大公因子是可以整除这两个整数的最大正整数。 一个有限域就是有有限个元素的域。可以证明有限域的阶 ( 元素个数 ) 一定可以写作素数的幂形式 p n ， n 为一个整数， p 为素数。 阶为 p 的有限域可以由模 p 的算术来定义。 阶为 p n ， n >1 的有限域可由多项式算术来定义。

3 .本章目录 4.1 群 , 环和域 4.2 模算术 4.3 欧几里得算法 4.4 有限域 GF(p) 4.5 多项式运算 4.6 有限域 GF(2 n )

4 .4.1 群 , 环和域 Groups, Rings, and Fields 群 G, 记作 {G, • }, 定义一个二元运算 • 的集合， G 中每一个序偶 (a, b) 通过运算生成 G 中元素 ( a • b ) ，满足下列公理： (A1) 封闭性 Closure: 如果 a 和 b 都属于 G, 则 a • b 也属于 G. (A2) 结合律 Associative: 对于 G 中任意元素 a, b, c ，都有 a • ( b • c )=( a • b ) • c 成立 (A3) 单位元 Identity element: G 中存在一个元素 e ，对于 G 中任意元素 a ，都有 a • e = e • a =a 成立 (A4) 逆元 Inverse element: 对于 G 中任意元素 a, G 中都存在一个元素 a’ ，使得 a • a ’= a’ • a =e 成立

5 .群、有限群和无限群 用 N n 表示 n 个不同符号的集合， {1,2,…,n}. n 个不同符号的一个置换是一个 N n 到 N n 的一一映射。定义 S n 为 n 个不同符号的所有置换组成的集合。 S n 中的每一个元素都代表集合 {1,2,…,n} 的一个置换，容易验证 S n 是一个群： A1 ：如果 π , ρ∈ S n ，则合成映射 π • ρ 根据置换 π 来改变 ρ 中元素的次序而形成，如， {3,2,1} • {1,3,2}={2,3,1}, 显然 π • ρ ∈ S n A2 ：映射的合成显而易见满足结合律 A3 ：恒等映射就是不改变 n 个元素位置的置换，对于 S n ，单位元是 {1,2,…,n} A4 ：对于任意 π ∈ S n ，抵消由 π 定义置换的映射就是 π 的逆元，这个逆元总是存在，例如： {2,3,1} • {3,1,2}={1,2,3}, 有限群 Finite Group 和无限群 Infinite Group ：如果一个群的元素是有限的，则该群称为有限群，且群的阶等于群中元素的个数；否则称为无限群

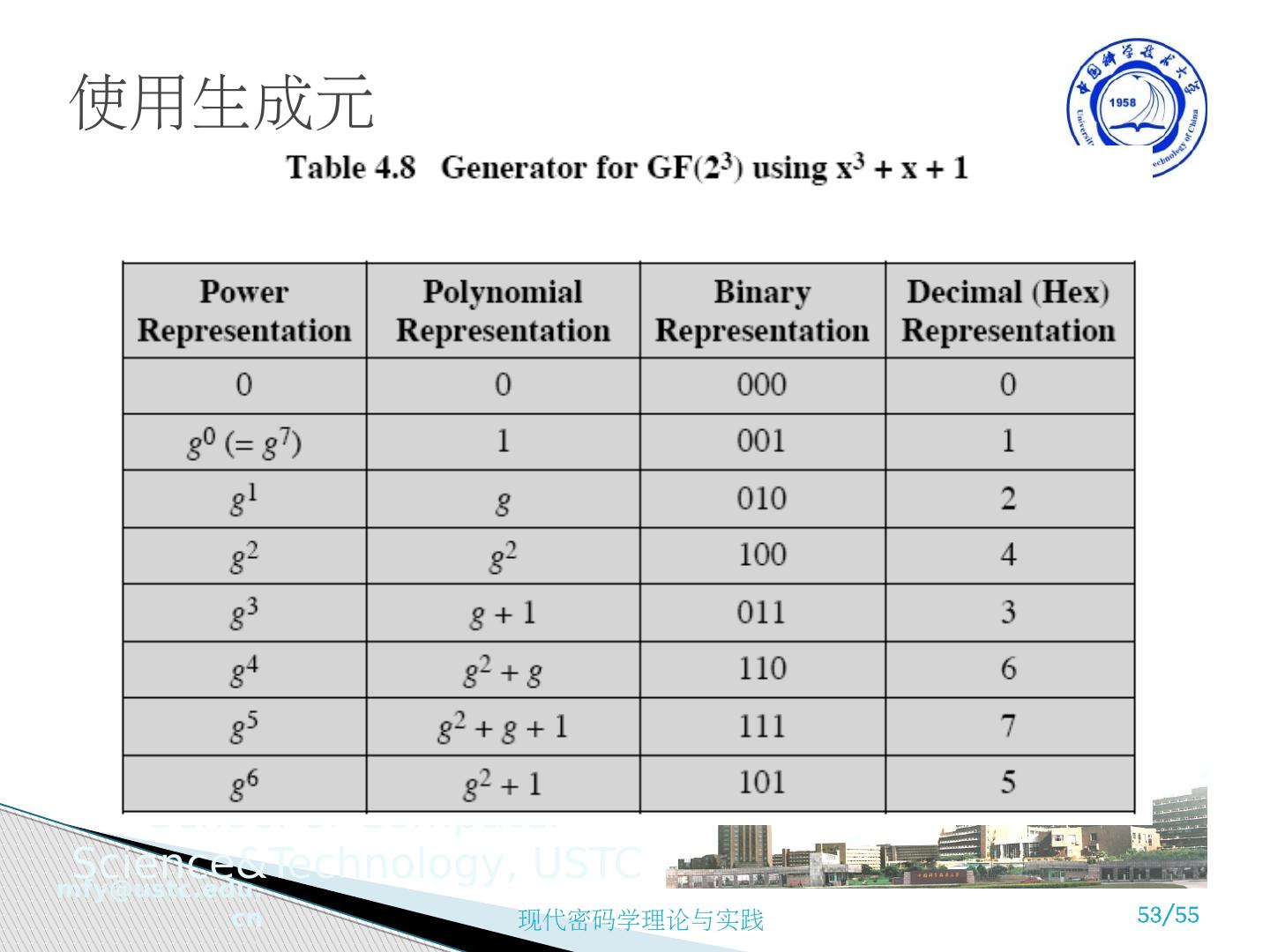
6 .交换群和循环群 交换群 Abelian Group ：还满足以下条件的群称为交换群 ( 又称阿贝尔群 ) (A5) 交换律 Commutative ：对于 G 中任意的元素 a, b ，都有 a • b=b • a 成立 当群中的运算符是加法时，其单位元是 0 ； a 的逆元是 -a, 并且减法用以下的规则定义： a – b = a + (-b) 循环群 Cyclic Group 如果群中的每一个元素都是一个固定的元素 a (a ∈G) 的幂 a k (k 为整数 ) ，则称群 G 为循环群。元素 a 生成了群 G ，或者说 a 是群 G 的生成元。

7 .环 (Rings) 环 R, 由 {R, +, x} 表示 , 是具有加法和乘法两个二元运算的元素的集合，对于环中的所有 a, b, c, 都服从以下公理： (A1-A5), 单位元是 0 ， a 的逆是 -a. (M1), 乘法封闭性 , 如果 a 和 b 属于 R, 则 ab 也属于 R (M2), 乘法结合律 , 对于 R 中任意 a, b, c 有 a(bc)=(ab)c. (M3), 乘法分配律 , a(b+c)=ab+ac or (a+b)c=ac+bc (M4), 乘法交换律 , ab=ba ，交换环 (M5), 乘法单位元 , R 中存在元素 1 使得所有 a 有 a1=1a. (M6), 无零因子 , 如果 R 中有 a, b 且 ab=0, 则 a=0 or b=0. 满足 M4 的是交换环；满足 M5 和 M6 的交换环是整环

8 .域 (Fields) 域 F, 可以记为 {F, +, x}, 是有加法和乘法的两个二元运算的元素的集合，对于 F 中的任意元素 a, b, c, 满足以下公理： (A1-M6), F 是一个整环 (M7), 乘法逆元 , 对于 F 中的任意元素 a( 除 0 以外 ), F 中都存在一个元素 a -1 , 使得 aa -1 =(a -1 )a=1. 域就是一个集合，在其上进行加减乘除而不脱离该集合 , 除法按以下规则定义 : a/b=a(b -1 ). 有理数集合 , 实数集合和复数集合都是域；整数集合不是域，因为除了 1 和 -1 有乘法逆元，其他元素都无乘法逆元

9 .群、环和域的关系

10 .4.2 Modular Arithmetic 给定任意正整数 n 和 a ，如果用 a 除以 n ，得到的商 q 和余数 r 满足如下关系 : a= qn + r 0≤r <n; q = ⌊ a/n 」 ⌊ x 」表示小于等于 x 的最大整数。 给定 a 和 n 时， q 和 r 即唯一确定。 （证明） Eg : 11=1x7 + 4, r=4; -11=(-2)x7 + 3, r=3

11 .因子 (Divisors) 如果 a= mb , 其中 a, b, m 为整数，则当 b ≠0 时，即 b 能整除 a, 或 a 除以 b 余数为 0, b|a . b 是 a 的一个因子。 24 的正因子有 1, 2, 3, 4, 6, 8, 12 和 24 。 以下关系成立 如果 a| 1, 则 a=±1 如果 a|b ，且 b|a , 则 a=±b 任何 b ≠0 能整除 0 如果 b|g ，且 b|h , 则对任何整数 m 和 n 有 b|( mg+nh ) 例 : b=7, g=14, h=63, m=3, n=2, 7| 14 and 7| 63 求证： 7|(3x14 + 2x63) 证明： (3x14 + 2x63)=7(3x2 + 2x9) 显然 , 7|(7(3x2 + 2x9)) 如果 a ≡ 0 mod n ，则 n|a

12 .同余 ( congruence) 给定整数 a, b 及 n≠0, 当且仅当 a-b= kn 时， a 与 b 在模 n 时同余，记为 a≡b mod n 或 a≡ n b 例 : 17≡ 5 7 ∵17-7=2*5; 53≡ 7 11 ∵53-11=6*7 a≡ n b 当且仅当 a mod n = b mod n 如果 a 是整数， n 是正整数，定义 a 除以 n 所得之余数为 a 模 n 。对于任意整数 a ，我们总可写出： a = ⌊ a/n 」 × n + (a mod n) 11 mod 7 = 4; -11 mod 7 = 3 如果 (a mod n)=(b mod n), 则称整数 a 和 b 是模 n 同余，表示为 a≡b mod n 或 a≡ n b 73 ≡ 4 mod 23 ； 21 ≡ -9 mod 10

13 .同余的性质 如果 n|(a-b), 则 a≡b mod n 证明 : 如果 n|(a-b), 则有 (a-b)= kn , k 为某些整数， 所以 a= b+kn 。 故 a mod n = (b + kn ) 除以 n 的余数 = b 除以 n 的余数 = b mod n a≡b mod n  b≡a mod n a≡b mod n 和 b≡c mod n  a≡c mod n Ex: 23≡8(mod 5) ，因为 23-8=15=5x3 -11≡5(mod 8) ，因为 -11-5=-16=8x(-2) 81≡0(mod 27) ，因为 81-0=81=27x3

14 . (a 1 op a 2 ) mod n =[(a 1 mod n )] op (a 2 mod n)] mod n ① 反身性 (reflexive) ： a=a mod n ② 对称性 (symmetric) ：若 a=b mod n ，则 b=a mod n ③ 传递性 (transitive): 若 a=b mod n 且 b=c mod n ，则 a=c mod n ④ a=b mod n  c=d mod n ，则 a+c =( b+d ) mod n a-c=(b-d) mod n a•c =( b•d ) mod n ⑤ ( a+b ) mod n = (a mod n + b mod n) mod n (a-b) mod n = (a mod n - b mod n) mod n ( a•b ) mod n = (a mod n • b mod n) mod n ⑥ 如果 ac= bd mod n 且 c=d mod n, gcd ( c,n )=1, 则 a=b mod n 证明：留给学生 例： 3*2=1*2 mod 4 且 2=2 mod 4, 但 3≠1 mod 4 ， ∵ gcd (2,4)≠1 同余的性质

15 .

16 .加法逆元和乘法逆元 加法逆元 (-w) 对每一个 w ∈ Z n ，存在一个 z ，使得 w+z ≡ 0 mod n ，则 z 即为加法逆元 -w 乘法逆元 (w -1 ) 对每一个 w ∈ Z p ，存在一个 z ，使得 w × z ≡ 1 mod p ， p 为素数， w 与 p 互素，则 z 即为乘法逆元 w -1 因为 w 与 p 互素， 如果用 w 乘以 Z p 中的所有数模 p ，得到的余数将以不同次序涵盖 Z p 中的所有数 ，那么至少有一个余数的值为 1 。因此，在 Z p 中的某个数与 w 相乘模 p 的余数为 1, 这个数就是 w 的乘法逆元 , w -1 在模数不是素数时，某些但非全部整数存在一个乘法逆元（如上页的模 8 运算）。如果 gcd (a, n)=1, 则能在 Z n 中找到 b ，使得 axb ≡ 1 mod n ，则 b 即为乘法逆元 a -1 , 因为 a 与 n 互素。

17 .剩余集 (Set of Residues) 定义比 n 小的非负整数集合为 Z n ： Z n ={0,1,…,(n-1)} b 是 a mod n 的剩余，如果 a=b mod n 或 a 是 b mod n 的剩余，如果 b=a mod n (1) 模 n 的完全剩余集 Complete Set of Residues mod n 如果对每个整数 a ，在集合 {r 1 ,r 2 ,…, r n } 中恰有一个余数 r i , 使得 a= r i mod n , 则称 {r 1 ,r 2 ,…, r n } 为模 n 的完全剩余集， {0,1,…,n-1} 形成模 n 的完全剩余集。 与同余不同之处： a≡ n b , 当且仅当 a mod n=b mod n a≡ n r ，即 a=r mod n, 不是说 a mod n = r 比如 20≡ 3 14 ，得 20=14 mod 3, r=2 ，但 20 mod 3 ≠14 ，而是 20 mod 3=14 mod 3 剩余集

18 .剩余集 (2) 模 n 的缩剩余集 (Reduced set of Residues mod n) 完全剩余集的一个子集，包含其中所有与 n 互素的元素。（小于 n 且与 n 互素的所有非负整数构成的集合） 例 :n=10 ，模 n 的完全剩余集是 {0, 1, 2,…,9} ，缩剩余集是 {1, 3, 7, 9}

19 . 数论的一个最基本的技巧是 Euclid 算法，求两个正整数的最大公约数 gcd (a, n), greatest common divisor 对于任何非负的整数 a 和 n ， gcd (a, n)= gcd (n mod a, a) 原理是计算 g i+1 =g i-1 mod g i 直到 g i =0 为止。 { 若 b= gcd ( a,n ), 则 b|a 且 b|n , b|(n- ⌊n/a 」 a ) 且 b|a  b|(n mod a ) 且 b|a } 4.3 欧几里得算法 Euclid Algorithm Algorithm gcd (a, n) begin g 0 :=n, g 1 :=a, i :=1 while g i ≠0 do begin g i+1 =g i-1 mod g i i := i ++ end n gcd := g i-1 end 例如： gcd (22, 55)= gcd (55 mod 22, 22)= gcd (11, 22)=11

20 .Euclids GCD Algorithm Euclids Algorithm to compute GCD( a,b ): A ￩ a, B ￩ b 若 B=0 ，则返回 A= gcd (a, b) R = A mod B A ￩ B, B ￩ R 转到 2 Int gcd ( int x,int y){          Return (!y) ? x: gcd ( y,x%y ); } 如果 a 和 b 只有唯一的正公因子 1 ，则称整数 a 和 b 是互素的，即 gcd (a, b)=1

21 .Euclids GCD Algorithm Euclids Algorithm to compute GCD( a,b ): A ￩ a, B ￩ b 若 B=0 ，则返回 A= gcd (a, b) R = A mod B A ￩ B, B ￩ R 转到 2 Int gcd ( int x,int y){          Return (!y) ? x: gcd ( y,x%y ); } 如果 a 和 b 只有唯一的正公因子 1 ，则称整数 a 和 b 是互素的，即 gcd (a, b)=1

22 .Example: 求 gcd (1970, 1066) 1970 = 1 x 1066 + 904 gcd (1066, 904) 1066 = 1 x 904 + 162 gcd (904, 162) 904 = 5 x 162 + 94 gcd (162, 94) 162 = 1 x 94 + 68 gcd (94, 68) 94 = 1 x 68 + 26 gcd (68, 26) 68 = 2 x 26 + 16 gcd (26, 16) 26 = 1 x 16 + 10 gcd (16, 10) 16 = 1 x 10 + 6 gcd (10, 6) 10 = 1 x 6 + 4 gcd (6, 4) 6 = 1 x 4 + 2 gcd (4, 2) 4 = 2 x 2 + 0 gcd (2, 0) GCD(1970,1066)=2

23 .Theorem 4 ( Bezout’s Identity). If the greatest common divisor of a and b is d, then d = ar+bs for some integers r and s. Bezout’s Identity

24 .Theorem 4 ( Bezout’s Identity). If the greatest common divisor of a and b is d, then d = ar+bs for some integers r and s. Replace in the inverse direction Bezout’s Identity

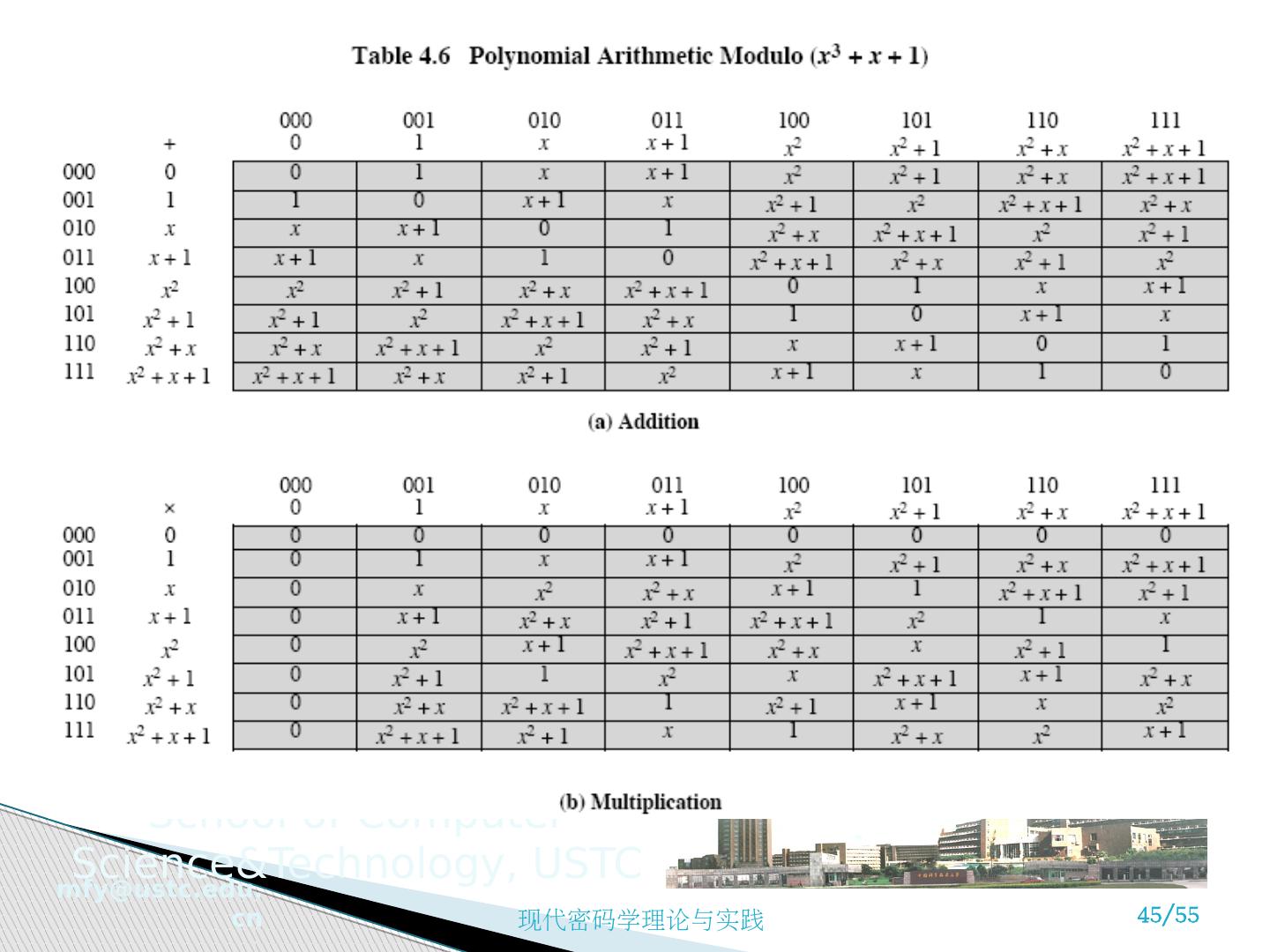
25 .4.4 有限域 GF(p) Galois Fields 有限域在密码学中扮演重要角色 有限域的阶 ( 元素个数 ) 必须是一个素数的幂 p n , n 为正整数。元素个数是 p n 的有限域一般记为 GF( p n ) ，即 Galois fields, 模 p n . 关注两种特殊情形， n=1 时的有限域和 p 为 2 时的有限域，即 GF(p) 和 GF(2 n ) 最简单的有限域是 GF(2) ，它的代数运算简述如下： + 0 1 x 0 1 w -w w -1 0 0 1 0 0 0 0 0 1 1 0 1 0 1 1 1 1 加 乘 求逆

26 .Galois Fields GF(p) 阶为 p 的有限域 GF(p) 给定一个素数 p ，元素个数为 p 的有限域 GF(p) 被定义为整数 {0,1, … , p-1} 的集合 Z p ，其运算为模 p 的算术运算 Z n 中的任一整数有乘法逆元当且仅当该整数与 n 互素，若 n 为 素数 ， Z n 中的所有 非零整数 都与 n 互素，因此 Z n 中所有非零整数都有乘法逆元 对每一个 w ∈ Z p ，存在一个 z ，使得 w×z ≡ 1 mod p ，则 z 即为乘法逆元 w -1 因为 w 与 p 互素，如果用 w 乘以 Z p 中的所有数模 p ，得到的余数将以不同次序涵盖 Z p 中的所有数，即余数集合是 {0,1, … , p-1} 的置换形，那么至少有一个余数的值为 1 。因此，在 Z p 中的某个数与 w 相乘模 p 的余数为 1, 这个数就是 w 的乘法逆元， w -1 。 所以， Z p 是一个有限域。 gcd ( w,p )=1  rw+sp =1 w -1 =r mod p

27 .Galois Fields GF(p) 阶为 p 的有限域 GF(p) 给定一个素数 p ，元素个数为 p 的有限域 GF(p) 被定义为整数 {0,1, … , p-1} 的集合 Z p ，其运算为模 p 的算术运算 Z n 中的任一整数有乘法逆元当且仅当该整数与 n 互素，若 n 为 素数 ， Z n 中的所有 非零整数 都与 n 互素，因此 Z n 中所有非零整数都有乘法逆元 对每一个 w ∈ Z p ，存在一个 z ，使得 w×z ≡ 1 mod p ，则 z 即为乘法逆元 w -1 因为 w 与 p 互素，如果用 w 乘以 Z p 中的所有数模 p ，得到的余数将以不同次序涵盖 Z p 中的所有数，即余数集合是 {0,1, … , p-1} 的置换形，那么至少有一个余数的值为 1 。因此，在 Z p 中的某个数与 w 相乘模 p 的余数为 1, 这个数就是 w 的乘法逆元， w -1 。 所以， Z p 是一个有限域。 gcd ( w,p )=1  rw+sp =1 w -1 =r mod p

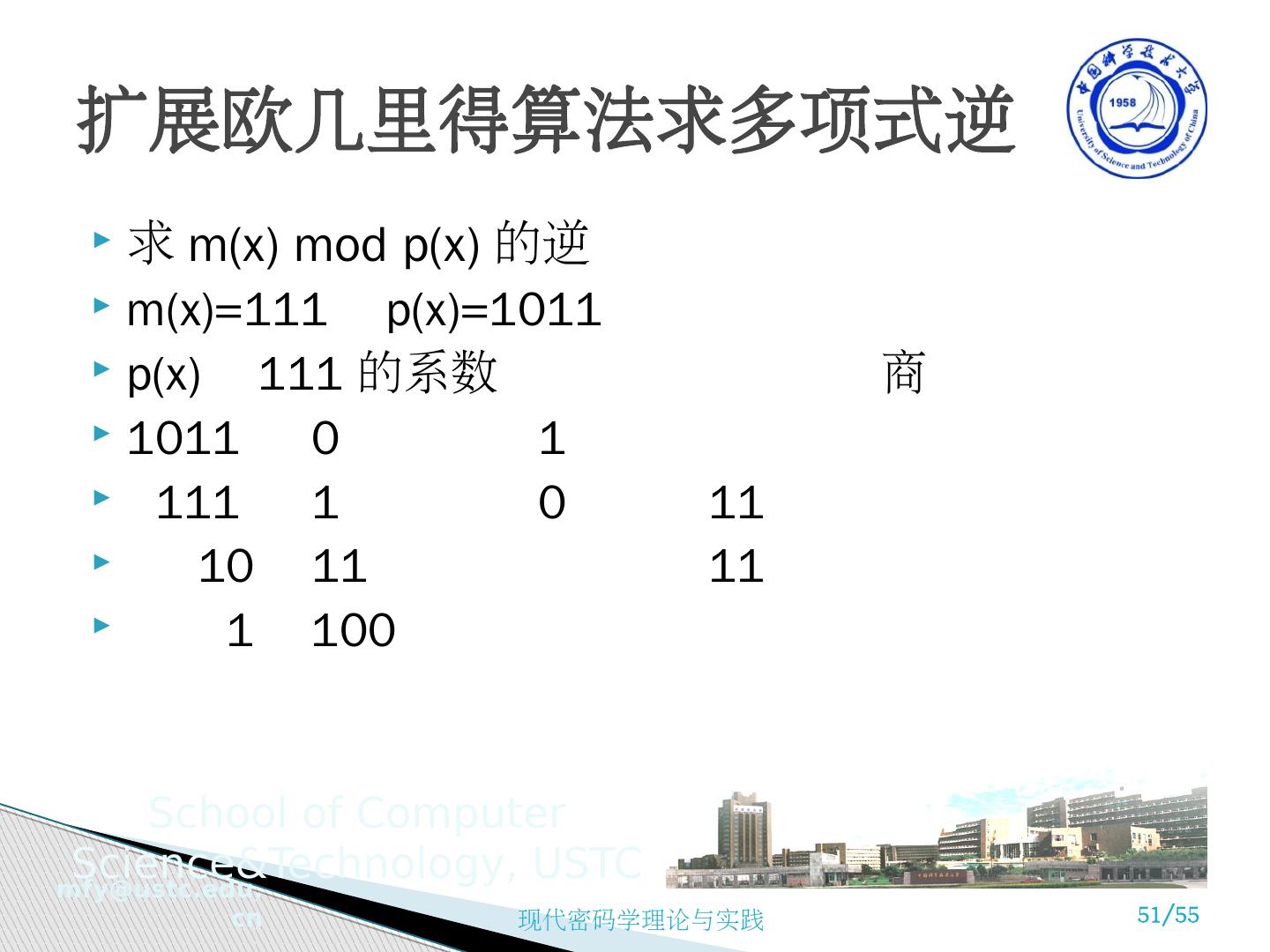
28 .Computing multiplicative inverses ax mod n = 1, x=a -1 =? 给定 a∈[0, n-1], gcd (a, n)=1 ，若能找到唯一整数 x∈[0,n-1] ，满足： ax mod n=1, 则称 a 和 x 互逆 如 n=10, a=3, x=7, ax mod n=1 =3x7 mod 10 n=17, a=5, x=7, ax mod n=1 =5x7 mod 17 引理 4.1: 如果 gcd (a, n)=1, 则对于每个 i , j, 0≤i<j<n, ai mod n≠aj mod n 证明： ( 略 ) 可以用反证法证明 此性质意味着每一个 ai mod n ( i =0,…,n-1) 都是不同的模 n 剩余，而 { ai mod n } ， i =0,1,…,n-1 是完全剩余集 {0,1,…,n-1} 的置换形式 计算乘法逆元素

29 .例如 : n=5, a=3, gcd (3,5)=1, {0,1,…,n-1}={0,1,2,3,4} 3*0 mod 5=0 3*1 mod 5=3 3*2 mod 5=1 3*3 mod 5=4 3*4 mod 5=2 { ai mod n} i =0,1, … ,n-1 ={0,3,1,4,2} 引理 4.1 说明，当 gcd (a, n)=1 时， a 一定有唯一的逆元素。 定理 4.1 如果 gcd (a, n)=1, 一定存在整数 x, 0<x<n ， 满足 ax mod n=1 可以用 Euclid’s 计算最大公约数算法的扩展来求逆。 计算乘法逆元素