展开查看详情
1 .现代密码学理论与实践 第 3 章 分组密码和数据加密标准 苗 付友 mfy@ustc.edu.cn http ://staff.ustc.edu.cn/~mfy 2018 年 9 月
2 .本章重点 分组密码是一种加密解密算法，将输入明文分组当做一个整体处理，输出一个等长的密文分组。 许多分组密码都采用 Feistel 结构，这样的结构由许多相同的轮函数组成。每一轮里，对输入数据的一半进行代换，接着用一个置换来交换数据的两个部分，扩展初始的密钥使得每一轮使用不同的子密钥。 DES 是应用最为广泛的分组密码，它扩展了经典的 Feistel 结构。 DES 的分组和密钥分别是 64 位和 56 位的。 差分分析和线性分析是两种重要的密码分析方法。 DES 对这两种攻击有一定的免疫性。
3 .本章内容 3.1 分组密码的原理 3.1.2 Feistel 密码结构的设计动机 3.1.3 Feistel 密码结构 3.2 数据加密标准 DES 1 ）初始置换 IP (Initial Permutation) 和逆置换 IP-1 2 ） Feistel Cipher 分组加密 循环细节 3 ） S 盒 4 ）子密钥的产生 3.3 DES 的安全强度 3.4 差分分析和线性分析 3.5 分组密码的设计原理
4 .3.1 分组密码的原理 流密码 (Stream Cipher) 和分组密码 (Block Cipher) 如果密文不仅与最初给定的算法和密钥有关，同时也与明文 位置 有关 ( 是所处位置的函数 ) ，则称为流密码体制。加密以明文 比特 为单位，以伪随机序列与明文序列模 2 加后，作为密文序列，一次一比特 / 字节。 如果经过加密所得到的密文仅与给定的密码算法和密钥有关，与被处理的明文数据在整个明文中的位置无关，则称为分组密码体制。通常以大于等于 64 位的数据块为单位，加密得相同长度的密文。
5 .乘积密码的设计思想 1949 年， Claude Shannon 引进了 Substitution-Permutation (S-P) Networks 的思想，即现代的乘积加密器，形成了现代分组加密的基础。 S-P Networks 是基于替代和置换这两个基本操作的。 乘积加密 提供了对明文信息处理所做的 confusion ( 扰乱 ) 和 diffusion ( 扩散 ) Shannon 认为，为了对付基于统计分析的密码破译，必须对明文作 confusion( 扰乱 ) 和 diffusion( 扩散 ) 处理，以减少密文的统计特性，为统计分析制造障碍 。 diffusion – 扩散，明文统计结构扩散消失到大批密文统计特性中，使明文和密文之间统计关系尽量复杂； confusion – 扰乱，使密文和加密密钥之间的关系尽量复杂 。
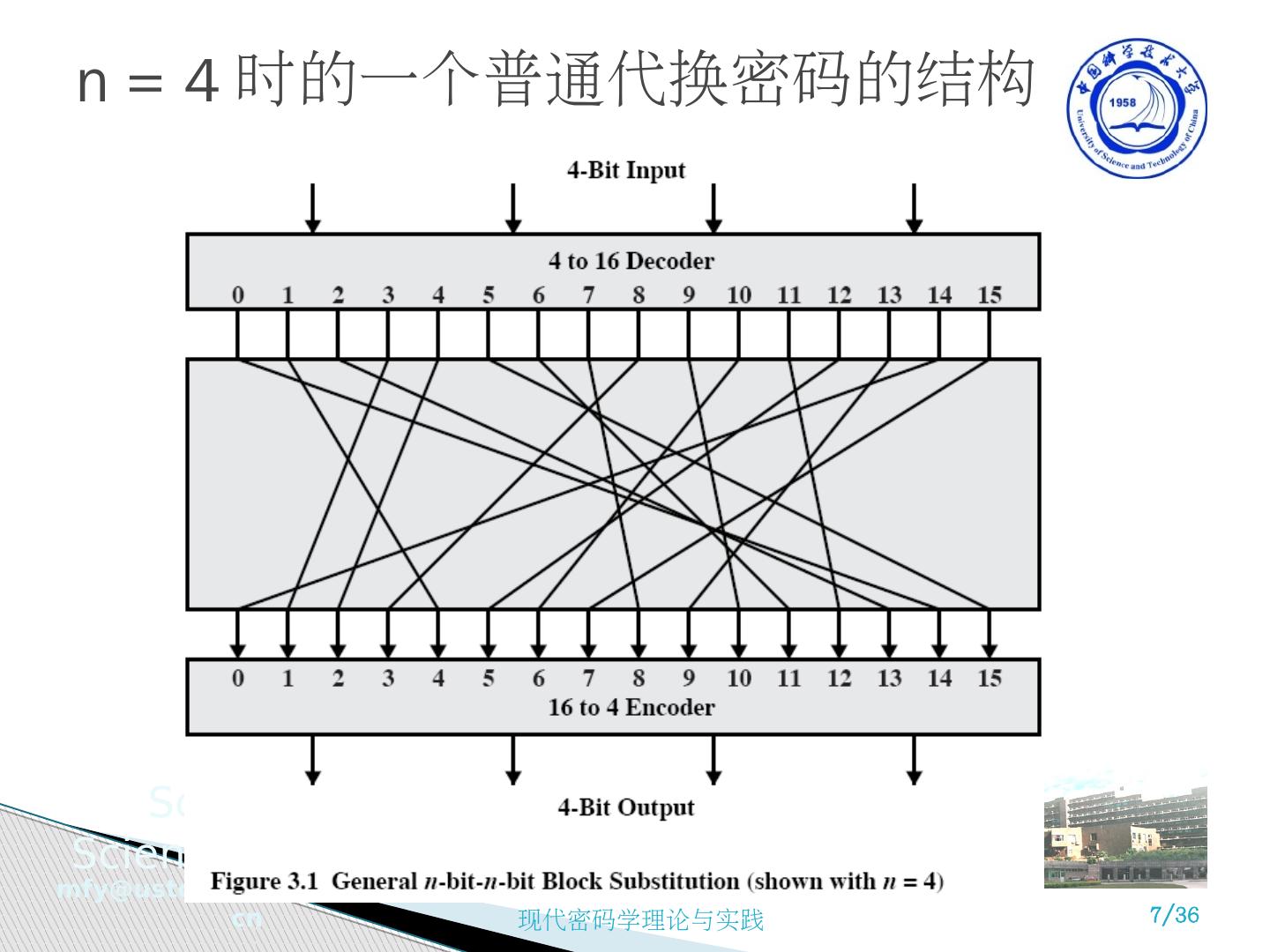
6 .3.1.2 Feistel 密码结构的设计动机 分组密码 大多数分组密码基于 Feistel Cipher Structure 分组加密器本质上就是一个巨大的替换器 64 位的分组就有 2 64 种输入 采用了乘积加密器的思想，即轮流使用替代和置换 Feistel 密码结构的设计动机 分组密码对 n 比特的明文分组进行操作，产生一个 n 比特的密文分组，共有 2 n 个不同的明文分组， 每一种都必须产生一个唯一的密文分组 ，这种变换称为可逆的或非奇异的。 可逆映射 不可逆映射 00 11 00 11 01 10 01 10 10 00 10 01 11 01 11 01
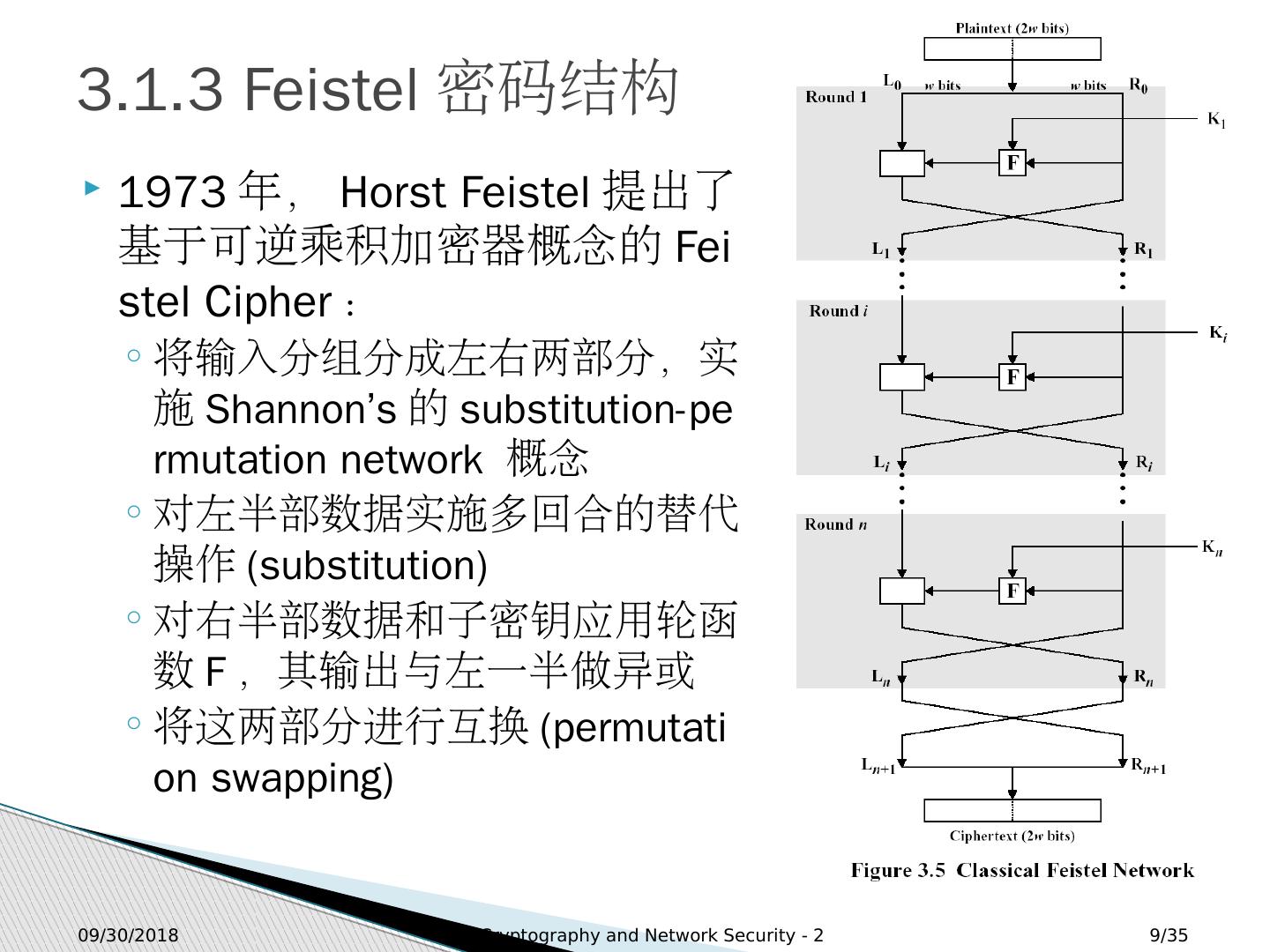
9 .2018/9/13 Cryptography and Network Security - 2 9 /35 3.1.3 Feistel 密码结构 1973 年， Horst Feistel 提出了基于可逆乘积加密器概念的 Feistel Cipher ： 将输入分组分成左右两部分，实施 Shannon’s 的 substitution-permutation network 概念 对左半部数据实施多回合的替代操作 (substitution) 对右半部数据和子密钥应用轮函数 F ，其输出与左一半做异或 将这两部分进行互换 ( permutation swapping )
10 .分组长度：分组越长则安全性越高，但加 / 解密速度越低，分组长度为 64 位是一个合理的折衷 密钥长度：密钥越长越安全，但加 / 解密速度越低， 64 位长的密钥已被证明是不安全的， 128 位是常用的长度 迭代次数：迭代越多越安全，通常为 16 次迭代 子密钥产生算法：越复杂则密码分析越困难 轮循环函数：越复杂则抗密码分析的能力越强 快速的软件加密 / 解密：算法的执行速度很重要 简化分析难度：算法简洁清楚，易于分析弱点，发现问题 Feistel 解密算法：以密文作为算法的输入，以相反的次序使用密钥 K i ， K n 、 K n － 1 、 ... 、 K 0 . Feistel 加密器设计原则
11 .Feistel Cipher Encryption and Decryption
12 .历史的回顾 IBM 公司在 1971 年由 Horst Feistel 领导开发了 Lucifer Cipher ，使用 128 位密钥加密 64 位的分组 Tuchman-Mayer 在此基础上开发了一个商用密码，使用 56 位密钥加密 64 位分组，容易在单个芯片上硬件实现 1973 美国国家标准局 NBS 全面征集加密方案，作为国家密码标准 IBM 提交了经过修改的 Lucifer 加密器，并最终在 1976 年被接受，公布为数据加密标准 DES DES 加密 3.2 数据加密标准 DES
14 .1 ） 初始置换 IP (Initial Permutation) 和逆置换 IP -1
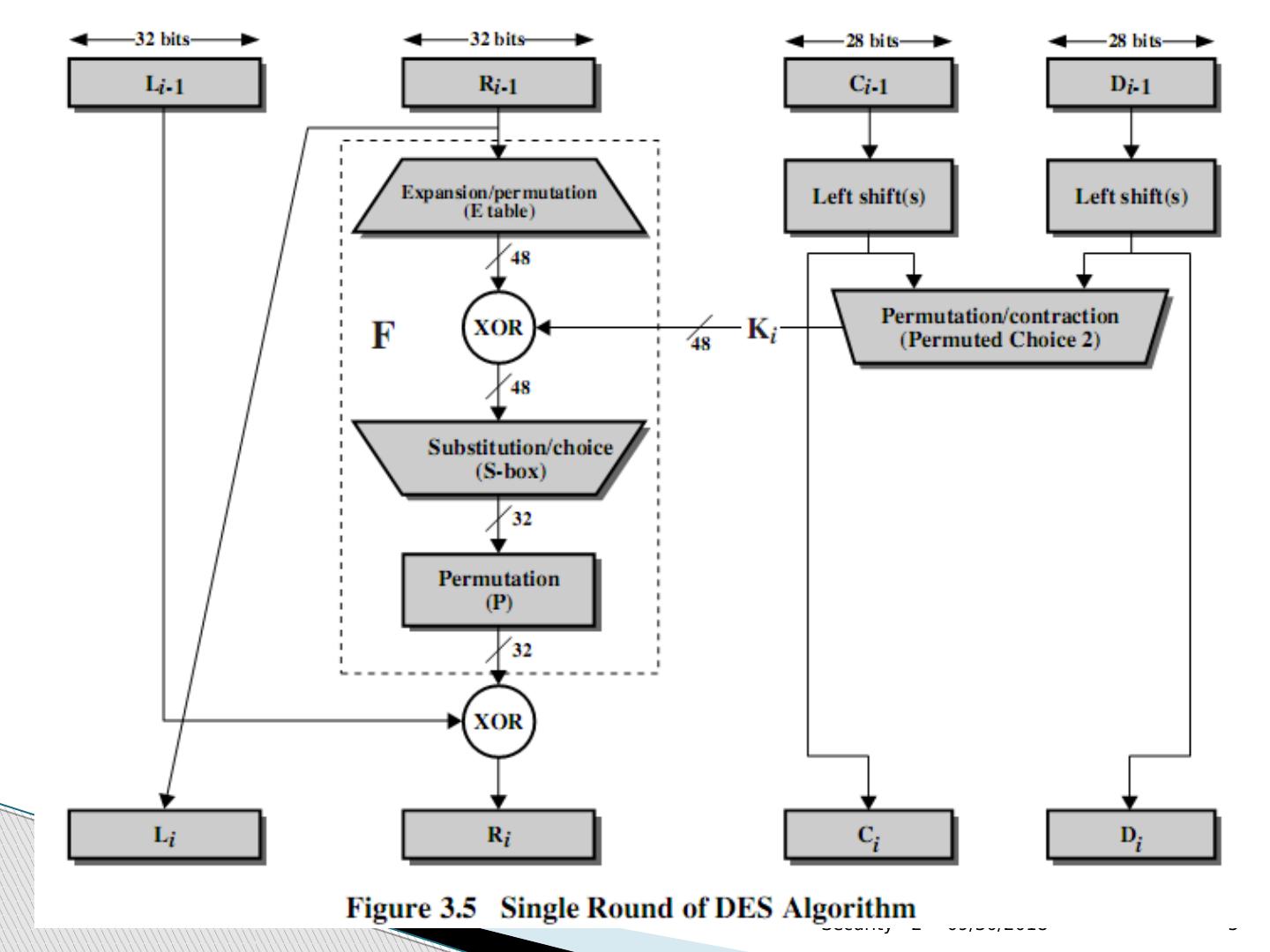
15 .将明文分成左右两部分 L i = R i –1 R i = L i –1 xor F( R i –1 , K i ) 2 ） Feistel Cipher 分组加密 循环细节
16 .2018/9/13 Cryptography and Network Security - 2 16 /35
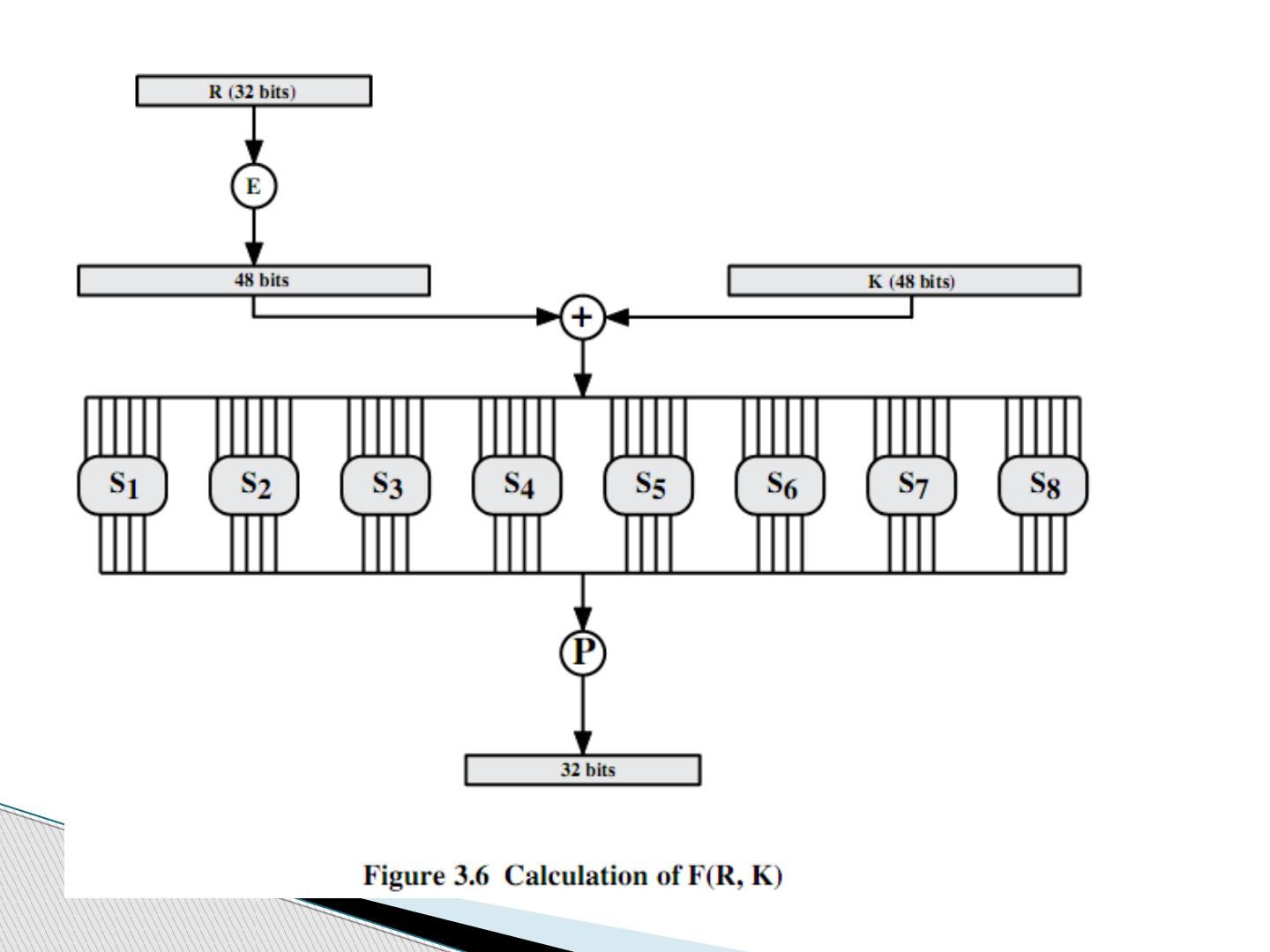
17 .将 32-bit 右半部和 48-bit 子密钥做以下动作 使用置换表 E ，将 32 位右半部 R 扩展成 48 位 与 48 位子密钥做异或 48 位结果送给 8 个替换盒 S-boxes ，得到 32 位结果 最后使用 32 位置换表 P ，把 32 位结果再进行一次置换处理 Feistel Cipher 分组加密 循环细节
19 .3 ） S 盒 (Substitution Boxes) 有 8 个将 6 位数据映射成 4 位数据的 S 盒 6 到 4 的映射规则是 外侧的第 1 位和第 6 位用作行选择 其余 4 位 (2-5bit) 用作列选择 这样每盒就有 4 行 16 列，输出 4 位， 8 个 S 盒输出 32 位 行的选择依赖于数据和密钥 例如 S(18 09 12 3d 11 17 38 39) = 5fd25e03
20 .3 ） S 盒 (Substitution Boxes) 有 8 个将 6 位数据映射成 4 位数据的 S 盒 6 到 4 的映射规则是 外侧的第 1 位和第 6 位用作行选择 其余 4 位 (2-5bit) 用作列选择 这样每盒就有 4 行 16 列，输出 4 位， 8 个 S 盒输出 32 位 行的选择依赖于数据和密钥 例如 S(18 09 12 3d 11 17 38 39) = 5fd25e03
21 .3 ） S 盒 (Substitution Boxes) 有 8 个将 6 位数据映射成 4 位数据的 S 盒 6 到 4 的映射规则是 外侧的第 1 位和第 6 位用作行选择 其余 4 位 (2-5bit) 用作列选择 这样每盒就有 4 行 16 列，输出 4 位， 8 个 S 盒输出 32 位 行的选择依赖于数据和密钥 例如 S(18 09 12 3d 11 17 38 39) = 5fd25e03
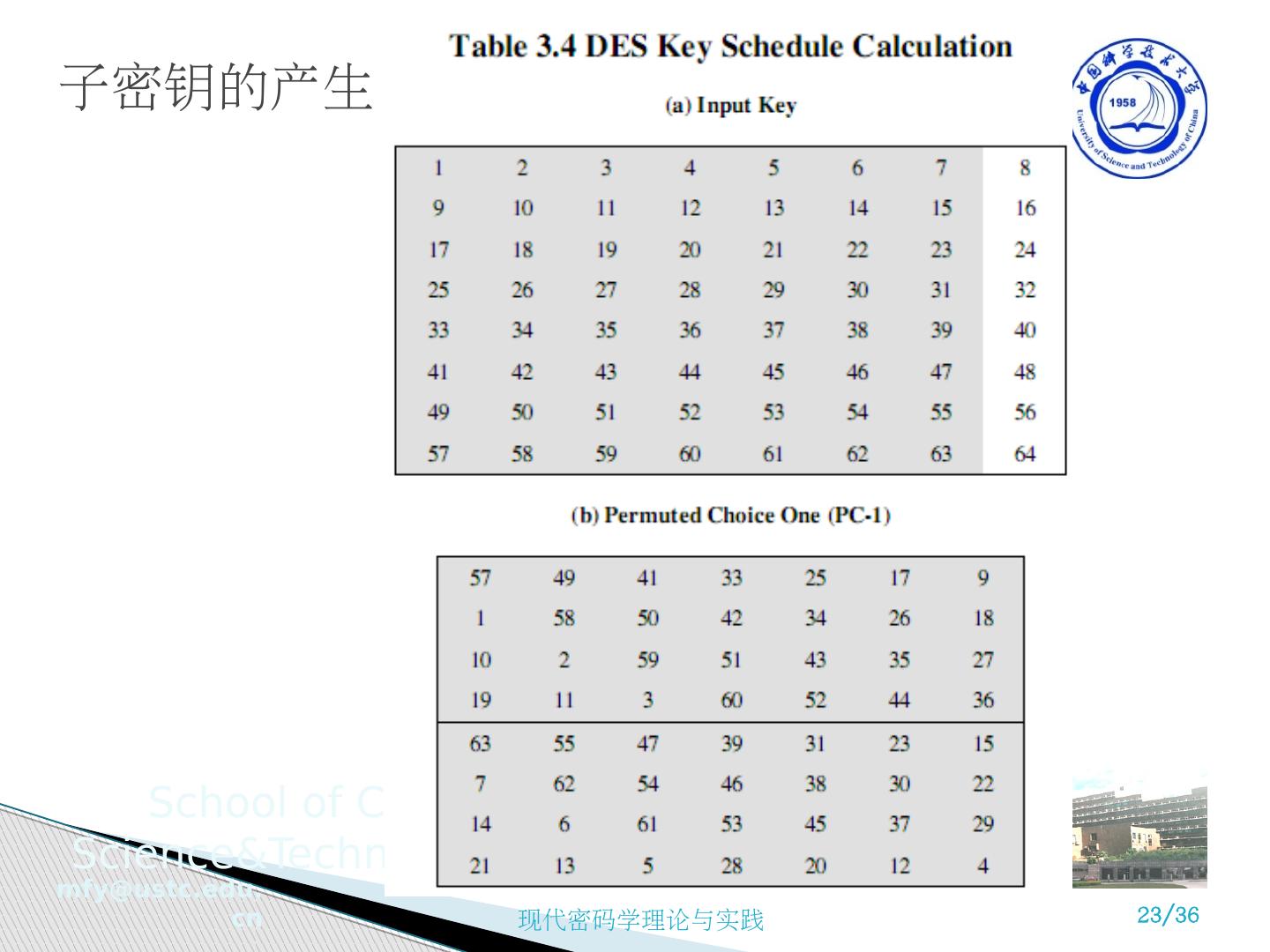
22 .4 ）子密钥的产生 每一轮都要生成一个子密钥以供加密使用 子密钥生成过程包括 使用密钥置换选择 1(PC-1) ，将 56 位密钥分成两半，每一部分 28 位 使用置换选择 2(PC-2) ，形成 48 位子密钥用在某一轮的 F 函数中 根据密钥左移表 K 将这两 半 (28bit) 分别 左移 1 位或 2 位 重复置换选择 2(PC-2) ，形成新的 48 位子密钥用在下一轮的 F 函数中
24 .DES 的解密 DES 的解密是加密的逆过程，采用相同算法，但是子密钥使用的次序正好相反。 子密钥的产生
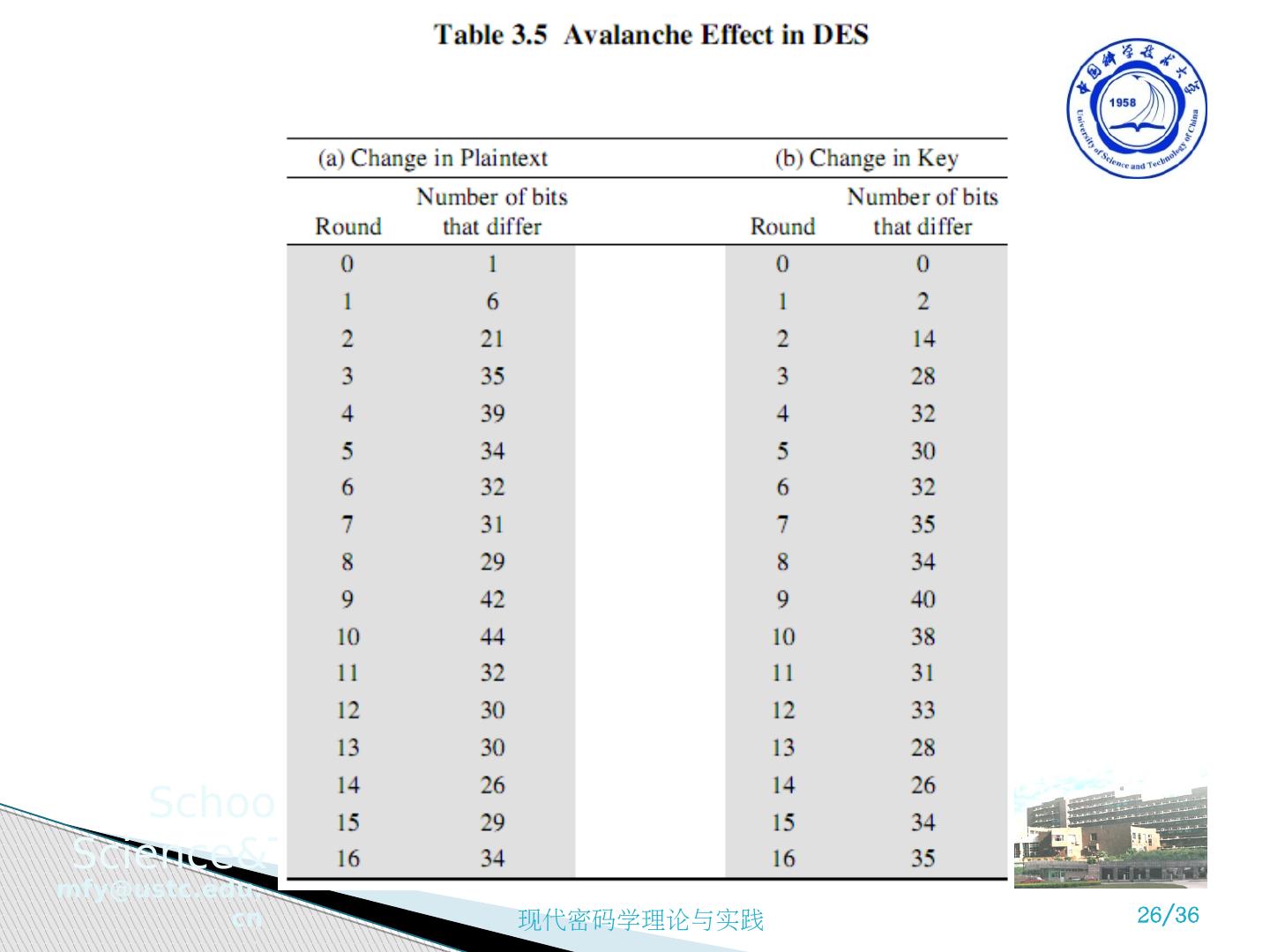
25 .DES 加密的雪崩效应 雪崩 效应 Avalanche Effect 明文或密钥的一比特的变化，引起密文许多比特的改变。如果变化太小，就可能找到一种方法减小有待搜索的明文和密文空间的大小。 如果用 同样密钥 加密只 差一比特的两个明文 ： 0000000000000000......00000000 1000000000000000......00000000 3 次循环以后密文有 21 个比特不同， 16 次循环后有 34 个比特不同 如果用只 差一比特的两个密钥 加密同样明文： 3 次循环以后密文有 14 个比特不同， 16 次循环后有 35 个比特不同 3.3 DES 的安全强度
26 .DES 加密的雪崩效应 雪崩 效应 Avalanche Effect 明文或密钥的一比特的变化，引起密文许多比特的改变。如果变化太小，就可能找到一种方法减小有待搜索的明文和密文空间的大小。 如果用 同样密钥 加密只 差一比特的两个明文 ： 0000000000000000......00000000 1000000000000000......00000000 3 次循环以后密文有 21 个比特不同， 16 次循环后有 34 个比特不同 如果用只 差一比特的两个密钥 加密同样明文： 3 次循环以后密文有 14 个比特不同， 16 次循环后有 35 个比特不同 3.3 DES 的安全强度
27 .密钥的长度问题 56-bit 密钥有 2 56 = 72,057,584,037,927,936 ≈ 7.2 亿亿之多 强力搜索 ( brute force search ) 似乎很困难， 20 世纪 70 年代估计要 1000 － 2000 年 技术进步使穷举搜索成为可能 1997 年 1 月 29 日， RSA 公司发起破译 RC4 、 RC5 、 MD2 、 MD5 ，以及 DES 的活动，破译 DES 奖励 10000 美金。明文是： Strong cryptography makes the world a safer place. 结果仅搜索了 24.6% 的密钥空间便得到结果，耗时 96 天。 1998 年在一台专用机上 (EFF) 只要三天时间即可 1999 年在超级计算机上只要 22 小时 ! 现在只需 要 ? 小时 ！ 3.3 DES 的安全强度
28 .S-box 问题 其设计标准没有公开，但是迄今没有发现 S 盒存在致命弱点 计时攻击 计时攻击利用的事实是加密或解密算法对于不同的输入所花的时间有细微的差别 DES 能够很好地抵抗计时攻击 差分密码分析攻击问题 DES 对差分分析攻击有较好的免疫力 针对 DES 的密码分析攻击主要利用了加密器的深层结构 搜集加密信息 最终设法恢复部分或全部子密钥的位 如果必要的话对其余部分再辅以穷举搜索 这些攻击实际上是统计分析，包括 差分分析、线性分析、相关密钥攻击 DES 的安全强度
29 .3.4 差分分析和线性分析 差分密码分析 Differential Cryptanalysis 1990 年， Murphy 、 Biham 和 Shamir 首次提出用差分密码分析攻击分组密码和散列函数，是第一种可以以少于 2 55 的复杂性对 DES 进行破译的方法。若有 2 47 个选择明文，用差分分析就可以在 2 47 次加密运算内成功攻击 DES 。尽管 2 47 比 2 55 小得多，但是要拥有 2 47 个选择明文的条件使得这种方法只具有理论上的意义。对 DES 并不奏效。 差分密码分析攻击方法 关注一对明文在加密过程中通过轮函数的演变情况，而不是观测单个明文分组的演变。 两个报文的异或 Δ m= m ⊕ m ’ ，中间过程有 Δ m i = m i ⊕ m i ’ ，则
热门城市
