13现代密码学理论与实践--数字签名/认证协议秘密共享

1 .现代密码学理论与实践 第 13 章 数字签名 / 认证协议秘密共享 苗 付友 mfy@ustc.edu.cn http://202.38.64.11/~mfy

2 .13.1 数字签名 Digital Signature 直接数字签名 仲裁数字签名 13.2 认证协议 Authentication 双向认证 （对称密码，公开密码） 单向认证 （对称密码，公开密码 ） 13.3 数字签名标准 (DSS) 主要内容

3 .13.4 其他数字签名与加密算法 RSA 方法 Elgamal 方法 13.5 密钥管理 13.6 秘密共享 13.6.1 对称多项式方法 13.6.2 离散对数的方法 13.6.3 ( t , w ) Threshold Scheme 1) 拉格朗日插值多项式法 2) 中国剩余定理方法 2.1 ） Mignotte’s SS 2.2 ） Asmuth-Bloom‘s SS 主要内容

4 .数字签名是一种认证机制，它使得消息的产生者可以添加一个起签名作用的码字。通过计算消息的散列值并用产生者的私钥加密散列值来生成签名。签名保证了消息的来源和完整性。 相互认证协议使得通信的各方对相互的身份感到放心，并交换会话密钥。 单向认证时，接收方想确信消息确实来自声称的发送方。 数字签名标准 (DSS) 是 NIST 标准，它使用安全散列算法 (SHA) 。 门限秘密共享方案使得足够多的成员合作可以恢复一个共享的秘密 本章要点

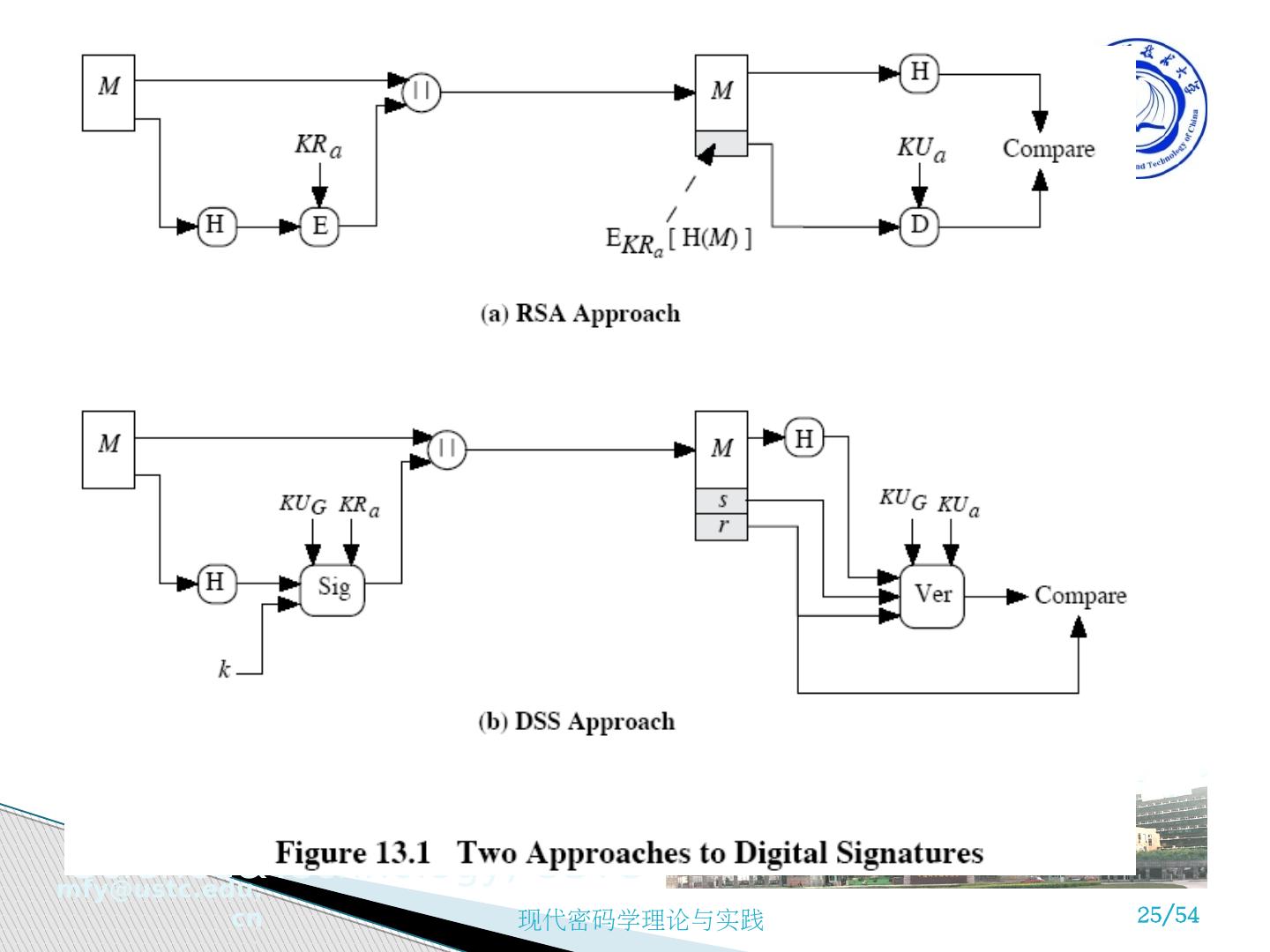
5 .数字签名的简单定义 数字签名是使以数字形式存储的明文信息经过特定密码变换生成密文，作为相应明文的签名，使明文信息的 接收者能够验证信息确实来自合法用户，以及确认信息发送者身份 。 对数字签名的基本要求 在收发双方不能完全信任的情况下，需要除认证之外的其他方法来解决假冒和否认的问题，数字签名则是解决办法； 签名接收者能容易地验证签字者对消息所做的数字签名，包括日期和时间； 任何人，包括签名接收者，都不能伪造签名者的签字； 发生争议时，可由第三方解决。 13.1 数字签名 Digital Signature

6 .数字签名与消息认证的区别 消息认证是使消息接收方验证消息发送者发送的内容有无被修改过，对防止第三者破坏足够，但收发双方有利害冲突时就无法解决纷争，需要更严格的手段，即数字签名。 数字签名的基本形式 对消息签名的两种方法 对消息整体的签字，将被签消息整体经过密码变换得到签字； 对消息摘要的签字，附在被签消息之后，或嵌在某一特定位置上作一段签字图样。 两类数字签名 确定性数字签名，明文与签名一一对应； 概率性数字签名，一个明文可以有多个合法签名，每次都不一样。 特殊数字签名：盲签名，代理签名，群签名，环签名 …… 数字签名的基本形式

7 .直接数字签名仅涉及通信方 ( 信源、信宿 ) 假定信宿知道信源的公开密钥 数字签名通过信源对整个报文用私有密钥加密，或对报文的摘要加密来实现 通常先签名，然后对消息和签名一起加密 安全性依赖于信源私有密钥的安全性 13.1.2 直接数字签名

8 .涉及到一个仲裁方 (arbitrator A) 签名方的签名报文首先送给仲裁者 仲裁者对报文和签名进行测试以检验出处和内容，然后注上日期和仲裁说明后发给接收方 要求仲裁方在一定程度上是可以信任的 可以用对称密码或公开密钥密码实现 仲裁方可以知道消息，也可以不知道消息 13.1.3 仲裁数字签名

9 .需要仲裁的数字签名技术

10 .认证服务和功能 认证是证实信息交换过程有效性和合法性的一种手段，包括对通信对象的认证 ( 身份认证 ) 和报文内容的认证 ( 报文认证 ) ，起到数据完整性的保护。这里有 信息的真实性 存储数据的真实性 接收方提供回执 发送方不可否认 时效性和公证可能性 认证的目的 防窃听、防假冒或拦截、防窃取等 13.2 认证协议

11 .单向认证 使用对称加密方法，即一次一密方法的变形 使用公开密钥方法： A 向 B 声称是 A ， B 则向 A 送一随机数 R ， A 用其私有密钥加密送 B ， B 用 A 的公开密钥验证。 使用改进的口令方式 双向认证 对称密钥方式 ( 三次握手 ) 公开密钥方式， A 、 B 双向使用不同的 R 值 时标方式 可信中继 使用 KDC 密钥分发中心 通过 DASS (Distributed Authentication Security Service) 群认证 (Group Authentication) 基本认证方法

12 .双向认证协议可以使通信双方达成一致并交换会话密钥 重放攻击：合法的签名消息被拷贝后重新送出 简单重放 可检测的重放 不可检测的重放 不加修改的逆向重放 重放攻击的解决方法 使用序列号 使用时间戳 ( 需要同步时钟 ) 挑战 / 应答 ( 使用单独的 nonce) 13.2.1 双向认证

13 .使用两层传统加密密钥结构来保证分布环境中通信的保密性 通常需要可信密钥分发中心 Key Distribution Center (KDC) 每一方与 KDC 共享主密钥 KDC 产生双方通信要用的会话密钥 用主密钥来分发会话密钥 对称加密方法

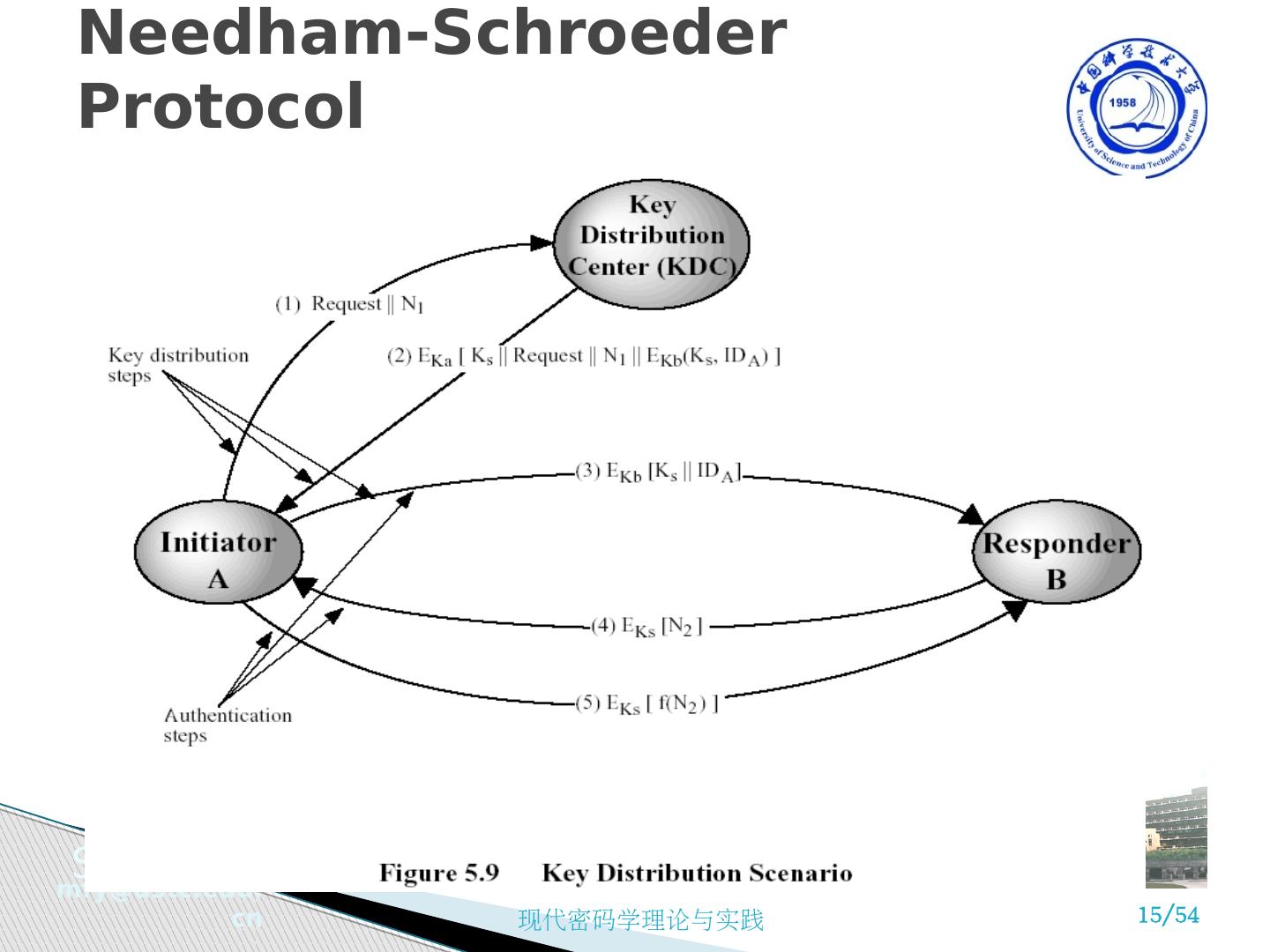
14 .最初期的第三方密钥分发协议之一 KDC 负责为用户 A 和 B 之间的通信产生会话密钥 协议如下 : 1. A → KDC: ID A || ID B || N 1 2. KDC→A: E Ka [Ks || ID B || N 1 || E Kb [ Ks || ID A ] ] 3. A→B: E Kb [ Ks || ID A ] 4. B→A: E Ks [ N 2 ] 5. A→B: E Ks [f( N 2 )] Needham-Schroeder Protocol

15 .Needham-Schroeder Protocol

16 .用于安全地分发 A 和 B 通信的新会话密钥 对于重放攻击是脆弱的，如果老会话密钥被破了的话 ( 攻击者 A 已知旧 Ks ，重放消息（ 3 ） ) 因此需要第三个消息来使得 B 相信是和 A 通信 有几种改进方法 增加时间戳 (Denning 81) 使用一个额外的 nonce ( Neuman 93) Needham-Schroeder Protocol

17 .Denning 81 1. A → KDC: ID A || ID B 2. KDC→A: E Ka [Ks || ID B ||T|| E Kb [ Ks || ID A ||T] ] 3. A→B: E Kb [ Ks || ID A ||T] 4. B→A: E Ks [ N 1 ] 5. A→B: E Ks [f( N 1 )] A and B verify timeliness by |Clock – T| < Δ t 1 + Δ t 2 Δ t 1 : time difference between KDC and local ones, Δ t 2 : network delay Denning 方法

18 .Neuman 93 1. A → B: ID A || N A 2. B→KDC: ID B || N B || E Kb [ ID A || N A ||T b ] 3. KDC→A: E Ka [ ID B || N A ||Ks||T b ]||E Kb [ ID A || Ks ||T b ]|| N B 4. A→B: E Kb [ ID A || Ks ||T b ] ||E Ks [ N B ] 在有效时限内， A 与 B 建立新的会话： 1. A→B: E Kb [ ID A || Ks ||T b ], N’ a 2. B→A: N’ b , E Ks [N’ a ] 3. A→B: E Ks [N’ b ] Neuman 方法

19 .有很多使用公开密钥密码的双向认证方法 需要确保其他各方都拥有正确的公开密钥 使用一个集中式的认证服务器 (AS) 现有很多不同的使用时间戳或 nonce 的方法 使用公开密钥密码

20 .Denning 81 presented the following: 1. A → AS: ID A || ID B 2. AS→A: E KRas [ ID A || KU a ||T] || E KRas [ ID B || KU b ||T] 3. A→B: E KRas [ ID A || KU a ||T] || E KRas [ ID B || KU b ||T] || E KUb [ E KRa [K s ||T]] 会话密钥由 A 选择的 , 因此 AS 滥用会话密钥 时间戳可以防范重放攻击 , 但是需要同步时钟 Denning AS Protocol

21 .当通信双方不同时在线时需要用到单向认证，比如发送电子邮件 消息头部必须是可读的以便在系统中传输 也可能希望消息的主体保密，发送者认证 13.2.2 单向认证

22 .可以把 KDC 使用方法应用于此，不需要最终交换 nonce 1. A → KDC: ID A || ID B || N 1 2. KDC→A: E Ka [Ks || ID B || N 1 || E Kb [ Ks || ID A ] ] 3. A→B: E Kb [ Ks || ID A ] || E Ks [M] 不能抗重放攻击 可以在消息中加入时间戳，由于电子邮件处理可能存在大量时延，加入时间戳的作用是有限的 使用对称密码

23 .已有一些适用的公钥方法 如果保密是主要关心的问题，可以使用 A → B: E KUb [Ks] || E Ks [M] 消息和会话密钥都加密了 如果需要认证，则可基于数字证书使用数字签名的方法 A→B: M || E KRa [H(M)] || E KRas [T||ID A ||KU a ] 这里有消息 , 签名 , 证书 公钥加密方法

24 .DSS 是美国政府作为标准 FIPS 186 发布的 DSS 使用 SHA 作为散列算法 由 NIST 和 NSA 在 90 年代早期设计 DSS 是标准 , DSA 是其算法 DSS 是 ElGamal 和 Schnorr 算法的变形 DSS 产生 320 位数字签名 , 但是具有 512-1024 位的安全性 DSS 的安全依赖于 DLP 问题 13.3 数字签名标准 (DSS)

25 .

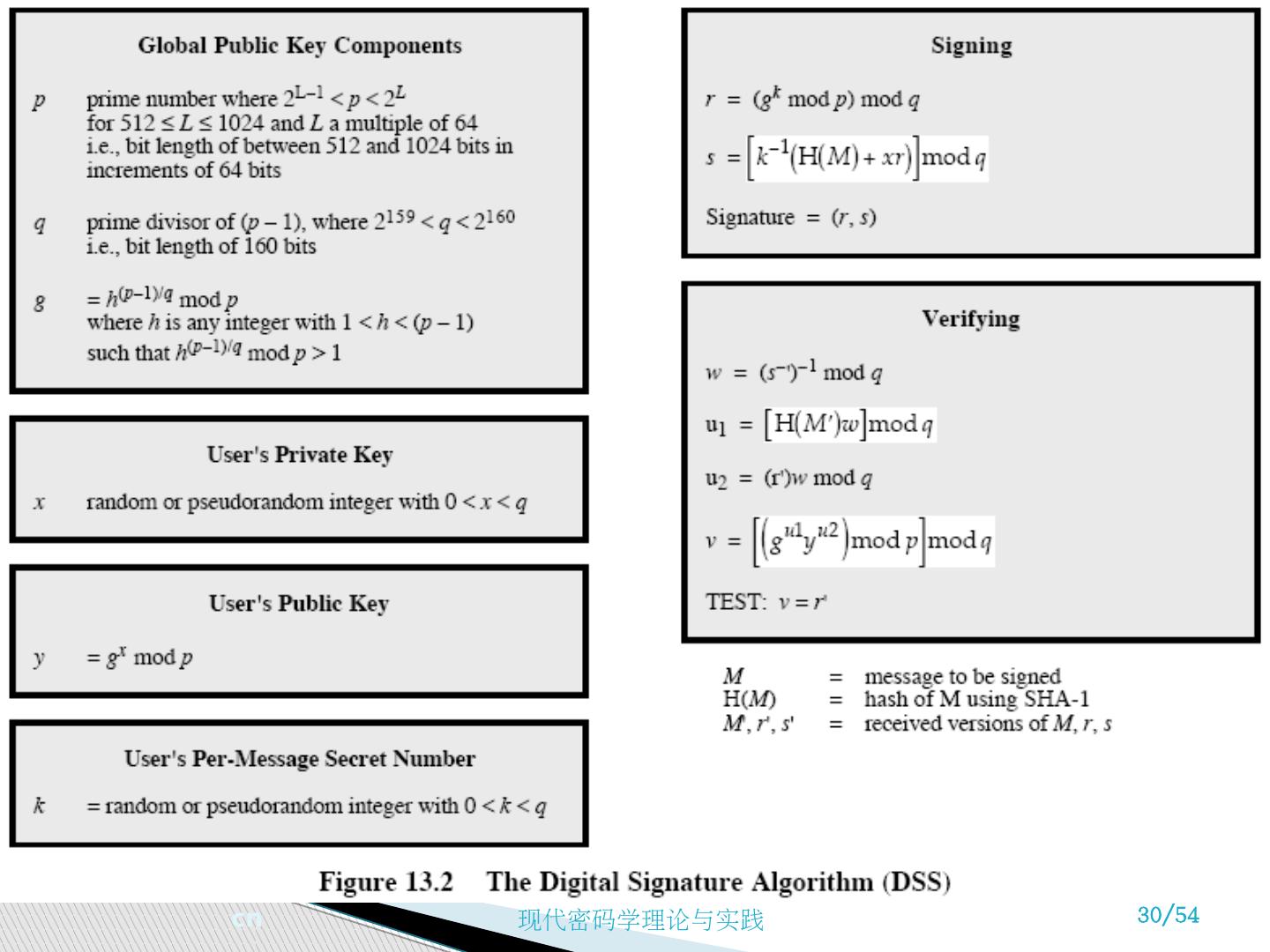
26 .全局共享的公开密钥值为 (p, q, g) p 是大素数 p = 2 L L 为 512 到 1024 位并且是 64 的倍数 选择 q, 是 p-1 的 160 位的素因子 选择 g, 使得 g = h (p-1)/q （ g 的阶为 q ） where h<p-1, h (p-1)/q (mod p) > 1 用户选择私钥，并计算其公开密钥 选择 x<q 计算 y = g x (mod p) DSA 密钥产生

27 .若要签名消息 M , 签名方则 产生一个随机的签名密钥 k, k<q k 必须是随机的，并且不能重复使用 计算签名 r = (g k (mod p))(mod q) s = k -1 ((SHA(M)+ x.r)(mod q) 把签名 (r,s) 和消息 M 一起发送给接收方 DSA 签名的产生

28 .接收方收到消息 M 和签名 (r,s) 接收方计算 w = s -1 (mod q) u1= (SHA(M).w)(mod q) u2= (r.w)(mod q) v = (g u1 .y u2 (mod p)) (mod q) 如果 v=r, 则签名通过验证 更多的证明细节可以参考有关资料 DSA 签名的验证

29 .DSS Signing and Verifying