- 快召唤伙伴们来围观吧
- 微博 QQ QQ空间 贴吧
- 文档嵌入链接
- 复制
- 微信扫一扫分享
- 已成功复制到剪贴板
12现代密码学理论与实践 --RSA安全性,二次剩余平方根,大数分解,离散对数与生成元
展开查看详情
1 . 苗付友 mfy@ustc.edu.cn 2018年12月
2 . 1. 泄露旧私钥情况下RSA安全性 2. 二次剩余平方根与大数分解的关系 3. 生成元构造 mfy@ustc.edu.cn 现代密码学理论与实践 2/89
3 . 问题9.7:在RSA算法中, Bob公钥为(e, n), n为两个 大素数p和q的乘积。如果Bob泄露了其私钥(d, n)后, 重新生成新的公钥(e`, n)以及私钥(d`, n), 是否安全? 答案:不安全, 因为一旦Bob泄露了他的私钥,攻 击者就可以借此分解模数n, 进而可以破解Bob发送 的任何消息。 mfy@ustc.edu.cn 现代密码学理论与实践 3/89
4 . 1)让 k=ed-1, 那么 ɸ(n)| k ,在Zn乘法群中选择 随机数x ,那么根据欧拉定理:xk=1 mod N, xk/2 是xk mod N 的平方根。 2)如果xk/2=1 mod N,则计算xk/4, xk/8, xk/16 … 直到 k / 2i k / 2i x 1 而且 x 1 如果不满足上式,需要重新选择x. (以上步骤可以在多项式时间内完成) 3)则 gcd( x k / 2i 1, n) p or q; 或者 k / 2i gcd( x 1, n) q or p mfy@ustc.edu.cn 现代密码学理论与实践 4/89
5 . k / 2i1 n=p*q , x k / 2i 1是 x 1 的平方根; i 1 即 b是a mod n的平方根; i 令 ax k / 2 , bx k / 2 很显然,x2=a mod n 有4个平方根 x2=a mod n =1 a mod p=1, a mod q=1. ◦ 对于a mod p=1, a的两个二次方根: 1) b1=1 mod p , 2) p-b1=p-1; ◦ 对于a mod q=1, a的两个二次方根,1) b2=1 mod q , 2) q-b2=q-1. mfy@ustc.edu.cn 现代密码学理论与实践 5/89
6 . 利用中国剩余定理,我们就可以得出a 在 Zn 的4个二 次方根表示形式: ◦ B1 = CRT(n,p,q, b1, b2 ) ◦ = (b1qq-1 mod p + b2pp-1modq ) mod n ◦ = (q q-1 mod p + pp-1modq ) mod n ◦ B2 = CRT(n,p,q, b1,q-b2 ) ◦ = (b1qq-1 mod p + (q-b2)pp-1modq ) mod n ◦ = (qq-1 mod p + (q-1)pp-1modq ) mod n ◦ B3 = CRT(n,p,q,p-b1, b2) ◦ = ((p-b1)qq-1 mod p +b2pp-1modq ) mod n ◦ = ((p-1)qq-1 mod p +pp-1modq ) mod n ◦ B4 = CRT(n,p,q,p-b1,q- b2) ◦ = ((p-b1)qq-1 mod p +(q-b2)pp-1modq ) mod n ◦ =((p-1)qq-1 mod p +(q-1)pp-1modq ) mod n mfy@ustc.edu.cn 现代密码学理论与实践 6/89
7 . 在上述4个平方根{B1,B2,B3,B4}中,必有一个为 1,另一个为n-1, 假设B1=1 mod n,则 B4=(pqq-1 mod p + qpp-1modq -qq-1 mod p -pp-1modq) mod n =-1 mod n. 那么 B2,B3 必 然即不等于1也不等于-1, 即必有上述 b {B2 , B3 }. mfy@ustc.edu.cn 现代密码学理论与实践 7/89
8 . B2=(qq-1 mod p + (q-1)pp-1modq ) mod n =(qq-1 mod p + qpp-1modq-pp-1modq ) mod n ={q(q-1modp+pp-1mod q)-(kq+1) } mod n 注意: -pp-1modq=-(kq+1), k为某个整数。因此 q|(B2+1)mod n , 且 (B2+1)mod n ≠0 因为B2≠-1mod n. 类似地: B3= ((p-1)qq-1 mod p +pp-1modq ) mod n = (p qq-1 mod p+ pp-1modq- qq-1 mod p) mod n = {p(qq-1 mod p+p-1modq)-(kp+1)} mod n 因此 p|(B3+1) mod n,且(B3+1)mod n ≠0 因为B3 ≠-1mod n. p, b B3 ; 所以 gcd(b 1, n) q, b B2 ; mfy@ustc.edu.cn 现代密码学理论与实践 8/89
9 . 再次分析 B2=(qq-1 mod p + (q-1)pp-1modq ) mod n: 因为我们已经假设:B1=1 mod n, 即(q q-1 mod p + pp-1modq ) mod n=1;所以 B2=(qq-1 mod p + (q-1)pp-1modq ) mod n =(qq-1 mod p + qpp-1modq-pp-1modq ) mod n ={(qq-1 mod p + pp-1modq)+ qpp-1modq- 2pp-1modq} mod n ={1+p(qp-1modq-2p-1modq)} mod n 因此 p|(B2-1) mod n 且 (B2-1) mod n ≠0 因为B2 mod n ≠1 类似地,q|(B3-1) mod n且 (B3-1) mod N ≠0 p, b B2 ; 因此,我们有 gcd(b 1, n) q, b B3 ; mfy@ustc.edu.cn 现代密码学理论与实践 9/89
10 . 在RSA中如果泄露了私钥d,那么模数n就可以在多 项式时间内被分解,n 就不可以再次使用了。 mfy@ustc.edu.cn 现代密码学理论与实践 10/89
11 . 由上一节,我们可以在不知道私钥d情况下,针对 RSA算法做如下尝试: 设模数n=p*q, 公钥为(e, n): 在Zn的乘法群上任选c0,连续做如下运算: c0e mod N c1 , c12 mod N c2 ,..., ci2 mod N ci 1 ,... 存储 c1 , c2 ,..., ci , ci 1 ,..., ct , ct 1,令 a ci1 , 如果 a 在整数集合 Z上是一个整数 的平方, 即b2=a,且 ci b, ci n b 则 gcd( c b, N )为n的一个因子, 对 i 应的私有秘钥(d, n)即可获得。 mfy@ustc.edu.cn 现代密码学理论与实践 11/89
12 . n=p*q , ci 是 ci+1 的平方根; 令 a ci 1 ci , b ci 即 b是a mod n的平方根; 2 a mod n= b2 a mod p= b2且a mod q= b2: ◦ 对于a mod p= b2,有a的两个二次方根, 1) b1=b mod p , 2) p-b1=p-b mod p; ◦ 对于a mod q= b2, 有a的两个二次方根, 1) b2=b mod q , 2) q-b2=q-b mod q. mfy@ustc.edu.cn 现代密码学理论与实践 12/89
13 . 利用中国剩余定理,我们就可以得出a 在Zn 上的4个二 次方根表示形式: ◦ B1=CRT(n,p,q, b1, b2 ) ◦ = (b1qq-1 mod p + b2pp-1modq ) mod n ◦ = (bq q-1 mod p + bpp-1modq ) mod n ◦ B2=CRT(n,p,q, b1,q-b2 ) ◦ = (b1qq-1 mod p + (q-b2)pp-1modq ) mod n ◦ = (bqq-1 mod p + (q-b)pp-1modq ) mod n ◦ B3=CRT(n,p,q,p-b1, b2) ◦ = ((p-b1)qq-1 mod p +b2pp-1modq ) mod n ◦ = ((p-b)qq-1 mod p +bpp-1modq ) mod n ◦ B4=CRT(n,p,q,p-b1,q- b2) ◦ = ((p-b1)qq-1 mod p +(q-b2)pp-1modq ) mod n ◦ =((p-b)qq-1 mod p +(q-b)pp-1modq ) mod n mfy@ustc.edu.cn 现代密码学理论与实践 13/89
14 . 在上述4个平方根{B1,B2,B3,B4}中,必有一个为b,另一个为 n-b 假设B1=b mod n,则 B4=(pqq-1 mod p + qpp-1modq -bqq-1 mod p - bpp- 1modq) mod n =(n-b) mod n. 那么 B2,B3 必然即不等于b也不等于n-b. B2=(bqq-1 mod p + (q-b)pp-1modq ) mod n =(bqq-1 mod p + qpp-1modq-bpp-1modq ) mod n ={q(bq-1modp+pp-1mod q)-b(kq+1) } mod n 注意 -pp-1modq=-(kq+1), k为某个整数。因此 q|(B2+b)mod n , 且(B2+b)mod n ≠0 因为B2 ≠n-b mod n 所以: q, ci B gcd( ci b, N ) 2 p, ci B3 mfy@ustc.edu.cn 现代密码学理论与实践 14/89
15 . 再次分析 B2=(bqq-1 mod p + (q-b)pp-1modq ) mod n: 因为我们已经假设:B1=b mod n, 即(bq q-1 mod p + bpp-1modq ) mod n=b;所以 B2=(bqq-1 mod p + (q-b)pp-1modq ) mod n =(bqq-1 mod p + qpp-1modq-bpp-1modq ) mod n ={(bqq-1 mod p + bpp-1modq)+ qpp-1modq- 2bpp-1modq} mod n ={b+p(qp-1modq-2bp-1modq)} mod n 因此 p|(B2-b) mod n 且 (B2-b) mod n因为B2 mod N 类似地,q|(B3-b) mod n且 (B3-b) mod n ≠0因为B3 mod n ≠b p, ci B2 所以得: gcd( ci b, N ) q, ci B3 mfy@ustc.edu.cn 现代密码学理论与实践 15/89
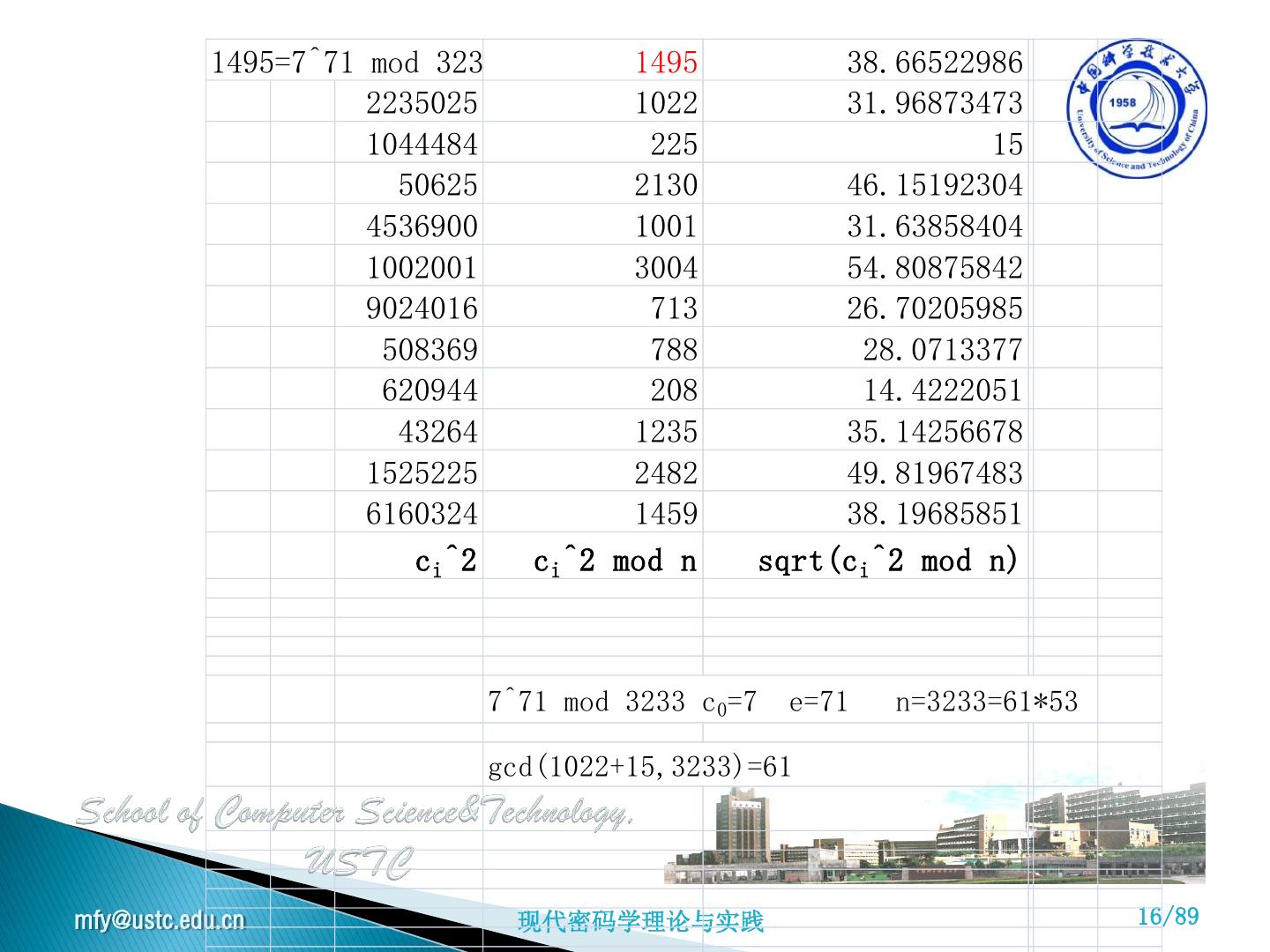
16 . 1495=7^71 mod 3233 1495 38.66522986 2235025 1022 31.96873473 1044484 225 15 50625 2130 46.15192304 4536900 1001 31.63858404 1002001 3004 54.80875842 9024016 713 26.70205985 508369 788 28.0713377 620944 208 14.4222051 43264 1235 35.14256678 1525225 2482 49.81967483 6160324 1459 38.19685851 ci ^2 ci ^2 mod n sqrt(ci ^2 mod n) 7^71 mod 3233 c0=7 e=71 n=3233=61*53 gcd(1022+15,3233)=61 mfy@ustc.edu.cn 现代密码学理论与实践 16/89
17 . 给定公钥(e,n)就可以分解 np,qɸ(n)d 破解RSA? 事实上,上述过程与公钥e无关,可以自己任意选 择e. mfy@ustc.edu.cn 现代密码学理论与实践 17/89
18 . 必须能够在存储的 c1 , c2 ,...,ci ,...,ct , ct 1 序列中找到 整数群Z上某个值的平方根。比如,找到了 ct 1 的平 方根r,而且 ct r, ct n r. mfy@ustc.edu.cn 现代密码学理论与实践 18/89
19 . 上述条件存在的概率是? 约为1/n1/2, 如果x2 mod n在Zn上均匀分布。 mfy@ustc.edu.cn 现代密码学理论与实践 19/89
20 . 即:找到a mod n 的平方根,就可以分解n, 但是分解n是困难的,也就意味着找到a mod n 的平方根也应该是困难 的。 在Zn上求平方根的问题可以规约为大数分解问题,同样,大数分解问题也 可以规约为求Zn上的某个数的平方根的问题。 mfy@ustc.edu.cn 现代密码学理论与实践 20/89
21 . n=p*q; 任选元素a,r,s,使得a,r均与n互素。若不互素,则可以 直接分解n。 对于r∊Zn ,必存在s, 使得r×s=1 mod n, 如果可以快速求出r和s的离散对数,即i=logar mod n, j=logas mod n 则r×s=ai+j =1 mod n 若(i+j)为偶数且a(i+j)/2ǂ1或-1modn, 则 gcd(a(i+j)/2+1,n)=p或q 因此,大数分解不会比离散对数问题更困难。 mfy@ustc.edu.cn 现代密码学理论与实践 21/89
22 . 是否容易? mfy@ustc.edu.cn 现代密码学理论与实践 22/89
23 . n=p*q; 有限循环群中寻找非1的元素a的阶;若a的阶k>2, (k为偶 数)。 计算a, a2, a3, …,ai,…, aj, …., an mod n 如果 ak+2 =a2 mod n ( k为偶数) 若a(k+2)/2 ǂa或-a mod n, 则 gcd(a(k+2)/2∓a,n)=p或q 分解n的问题可以归结为求有限循环群元素的阶。 E.g.,36=1 mod 14, 36+2=38=32 mod p, thus, 38/2 =34 =11 mod 14, gcd(11-3,14)=2, a factor of 14. 1712=1 mod 351712+2=172 mod 35,due to177=3 ,thus gcd(3+17,35)=5 or gcd (3-17,35)=7 mfy@ustc.edu.cn 现代密码学理论与实践 23/89
24 . n=p*q; 有限循环群中寻找非1的元素a的阶;若a的阶k>2, (k为奇数?)。To be solved 计算a, a2, a3, …,ai,…, aj, …., an mod n 如果 ak+2 =a2 mod n ( k为偶数) 若a(k+2)/2 ǂa或-a mod n, 则 gcd(a(k+2)/2∓a,n)=p或q 分解n的问题可以归结为求有限循环群元素的阶。 mfy@ustc.edu.cn 现代密码学理论与实践 24/89
25 . n=p*q; 有限循环群中寻找非1的元素a的阶;若a的阶k>2, (k为奇数)。 计算a, a2, a3, …,ai,…, aj, …., an mod n 如果 ak+1 =a mod n 且 ak ǂ1 mod n 则 gcd(a,n)=p或q 分解n的问题可以归结为求有限循环群元素的阶。 Due to 57mod 35=5 and 56mod 35=15, thus Gcd(5,35)=7 一个因子 mfy@ustc.edu.cn 现代密码学理论与实践 25/89
26 . For prime p, given a with the order t, i.e., at=1 mod p, how to find the discrete logarithm ax=b mod p (Pollard’s ρ 方法?如何跟踪a,b指数?) For composite n=pq for prime p and q, given a with the order t, i.e., at=1 mod p, how to find the discrete logarithm ax=b mod n and factorize n. mfy@ustc.edu.cn 现代密码学理论与实践 26/89
27 . For the reduced set mod N, {a1,a2,…a φ(N) } 1) For N=pq, select g with gcd(g,N)=1,g≠1, compute the sequence, g, g2, g3,…, gi ,… mod N 2) if gi=1and gi/2 ≠1,then gcd((gi mod N)+1, N)=p or q. In RSA, note that aφ(N)/gcd(p-1,q-1) =1 mod N, if p-1 and q-1 have large greatest common divisor, we can formulate the sequence in 1) such that gi=1, gi/2 ≠1 to factor N. However, φ(N)/gcd(p-1,q-1) is always larger than p-1 or q-1. mfy@ustc.edu.cn 现代密码学理论与实践 27/89
28 . 求一个大素数 p 很容易,用现成的素性验证算法就可以了。不过已知一 个素数 p,求其本原根则很困难,因为需要将 p - 1 的素因子 q1,q2, ……qk-1,qk都找出来,然后分别验证 gq1 mod p, gq2 mod p, ……gqk-1 mod p, gqk mod p,如果都不等于 1,则 g 是 p 的一个本 原根。而然,如果 p 是一个很大的素数,例如 128 个 2 进制位的素数, 要分解出 p - 1 的所有素因子来则是一件很困难的事情。 算法如下: ◦ P1. 利用素性验证算法,生成一个大素数q; P2. 令 p = q * 2 + 1; P3. 利用素性验证算法,验证 p 是否是素数,如果否,则跳转到P1; P4. 生成一个随机数 g,1 < g < p - 1; P5. 验证 g2 mod p 和 gq mod p 都不等于 1,否则跳转到 P4; P6. g 是大素数 p 的本原根。 mfy@ustc.edu.cn 现代密码学理论与实践 28/89