11现代密码学理论与实践--消息认证与哈希函数

1 .Cryptography and Network Security 第 11 章 消息认证与哈希函数 苗付友 mfy@ustc.edu.cn http://202.38.64.11/~mfy 2017 年 12 月

2 .消息认证 是用来验证消息完整性的一种机制或服务。消息认证确保收到的数据确实就发送时的一样 ( 即没有修改、插入、删除或重放 ) ，且发送方声称的身份是真实有效的。 对称密码在那些相互共享密钥的用户间提供认证。用消息发送方的私钥加密消息也可提供一种形式的认证。 用于消息认证的最常见的密码技术是 消息认证码 和 安全散列 (hash) 函数 。 MAC 是一种需要使用 秘密密钥 的算法，以可变长的消息和秘密密钥作为输入，产生一个认证码。拥有秘密密钥的接收方产生一个认证码来验证消息的完整性。 散列函数 将可变长度的消息映射为固定长度的散列值，或叫消息摘要。对于消息认证码，安全散列函数必须以某种方式和秘密密钥捆绑起来。 本章要点

3 .11.1 消息认证 Message Authentication 对认证的要求 11.2 认证函数 11.2.1 消息加密 1) 对称密钥加密 2 ）公开密钥加密 11.2.2 消息认证码 MAC 11.2.3 散列函数 Hash Function 11.3 消息认证码 MAC 11.4 散列函数 11.4.1 对散列函数的要求 11.4.2 强哈希函数 11.4.3 对哈希函数的攻击法 1) Rabin 的对哈希函数的攻击法 2) Yuval 对哈希函数的生日悖论攻击法 本章提纲

4 .消息认证 ( 报文认证 ) 关心的问题是 保护消息的完整性 验证发起方身份 消息源的不可否认 ( 解决分歧 ) 消息认证要考虑安全需求 三种消息认证的方法 消息加密 消息认证码 (MAC) 哈希函数 11.1 Message Authentication

5 .泄密 Disclosure ，将消息透露给没有合法身份的第三方 传输分析 Traffic analysis ，分析双方通信模式 伪装 Masquerade ，欺诈源向网络中插入一条消息 内容篡改 Content modification ，对消息内容的修改 顺序篡改 Sequence modification ，对消息顺序的修改 计时篡改 Timing modification ，对消息的延时和重放 信源抵赖 Source repudiation, 发送方否认发送过某消息 信宿抵赖 Destination repudiation ，接收方否认接收过某消息 对认证的要求

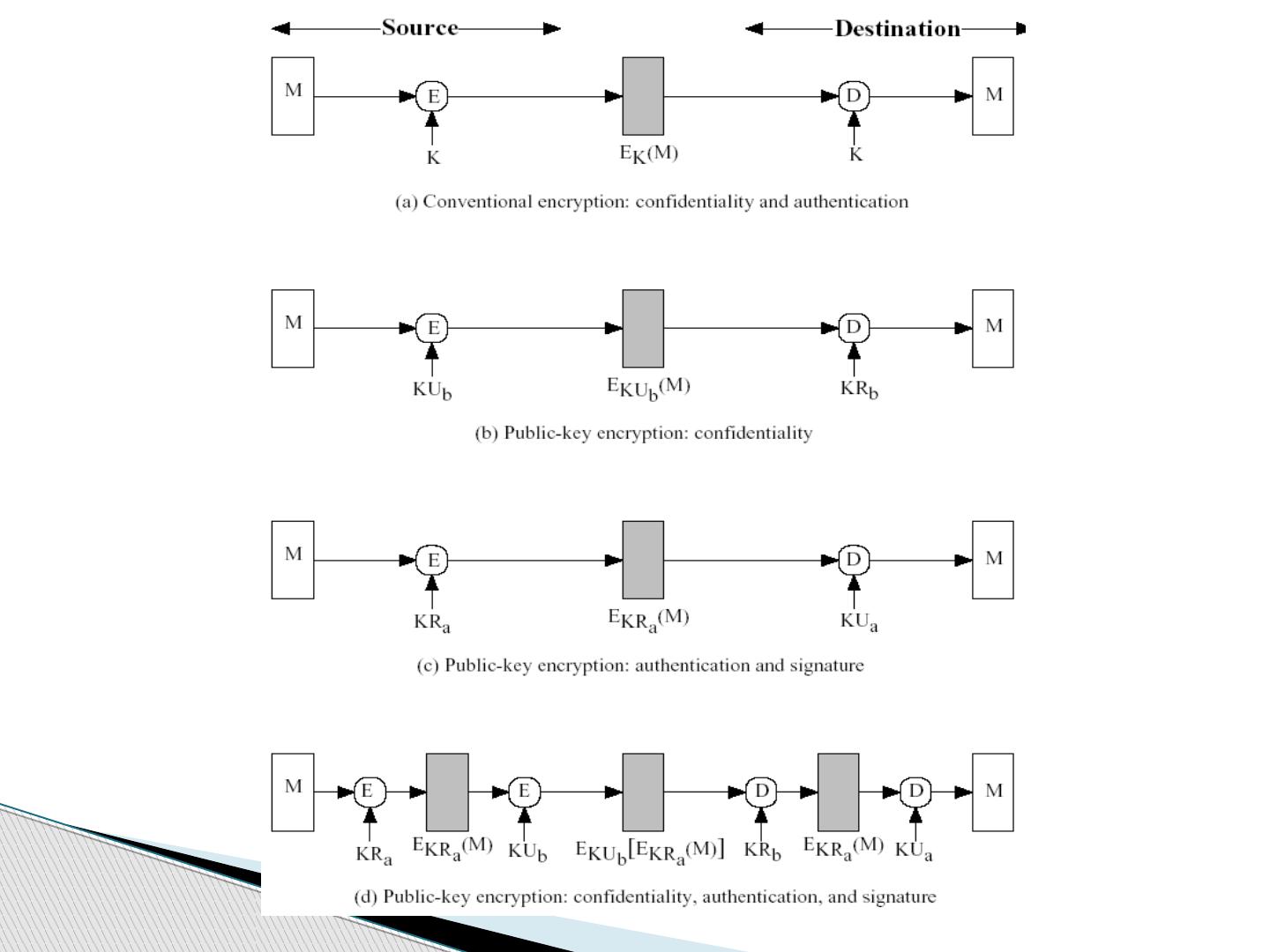
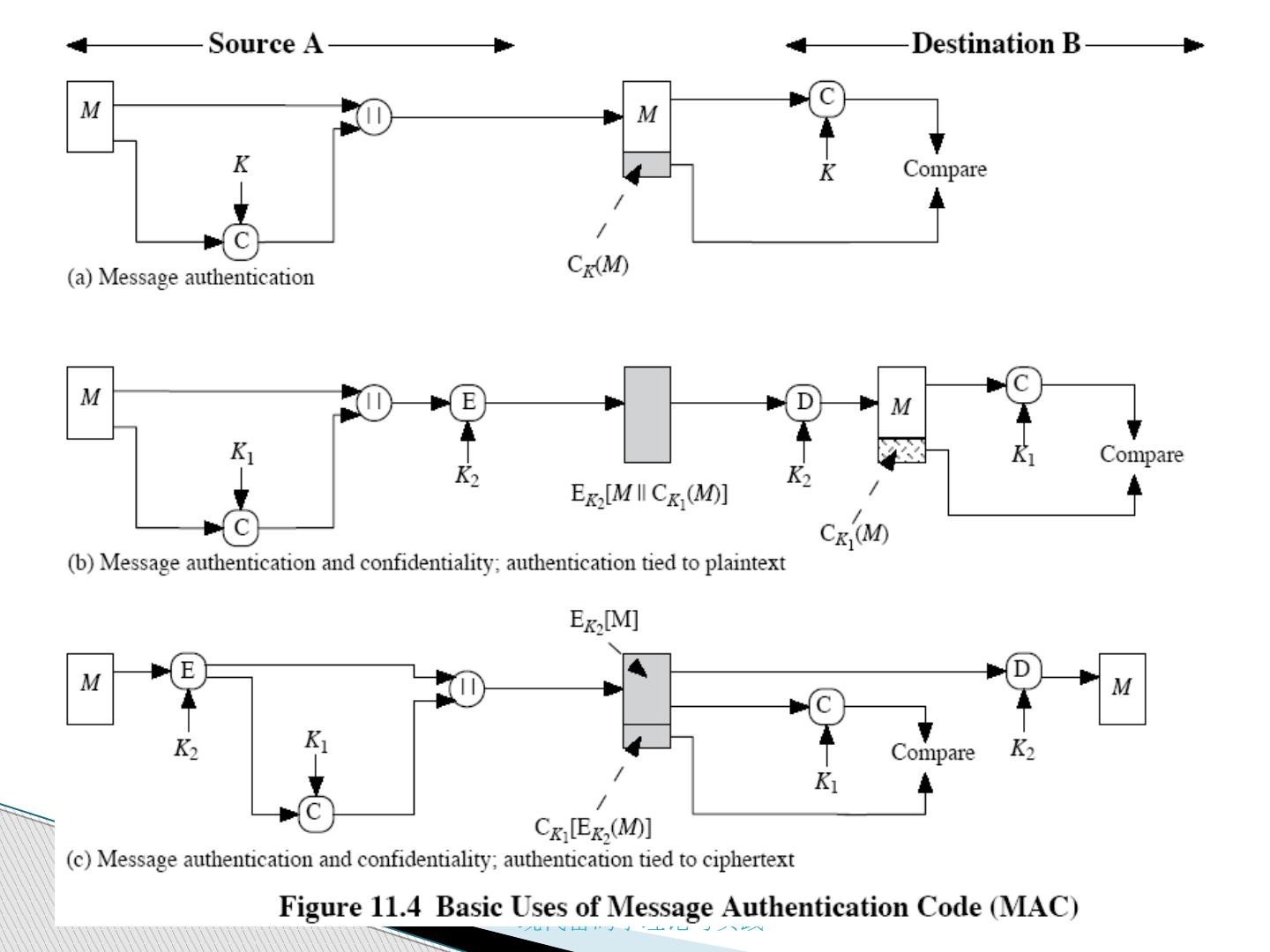
6 .11.2.1 消息加密 消息加密本身提供了一种认证手段 1) 对称加密 接收方可以确信消息是由发送方产生的，因为除了接收方以外只有发送方拥有加密密钥，产生出用此密钥可以解密的密文 如果消息可以是任意的位模式，接收方无法确定收到的消息是合法明文的密文。因此，通常不管密文的值是什么，如果解密后得到的明文有合法明文的位模式，接收方都会作为真实的密文接收。 11.2 认证函数 对称加密情况下，选取明文消息（比如二进制的密钥等）使得其用另外一种编码方式时具有合法明文结构，从而可以利用不同编码节省验证码？

7 .

8 .

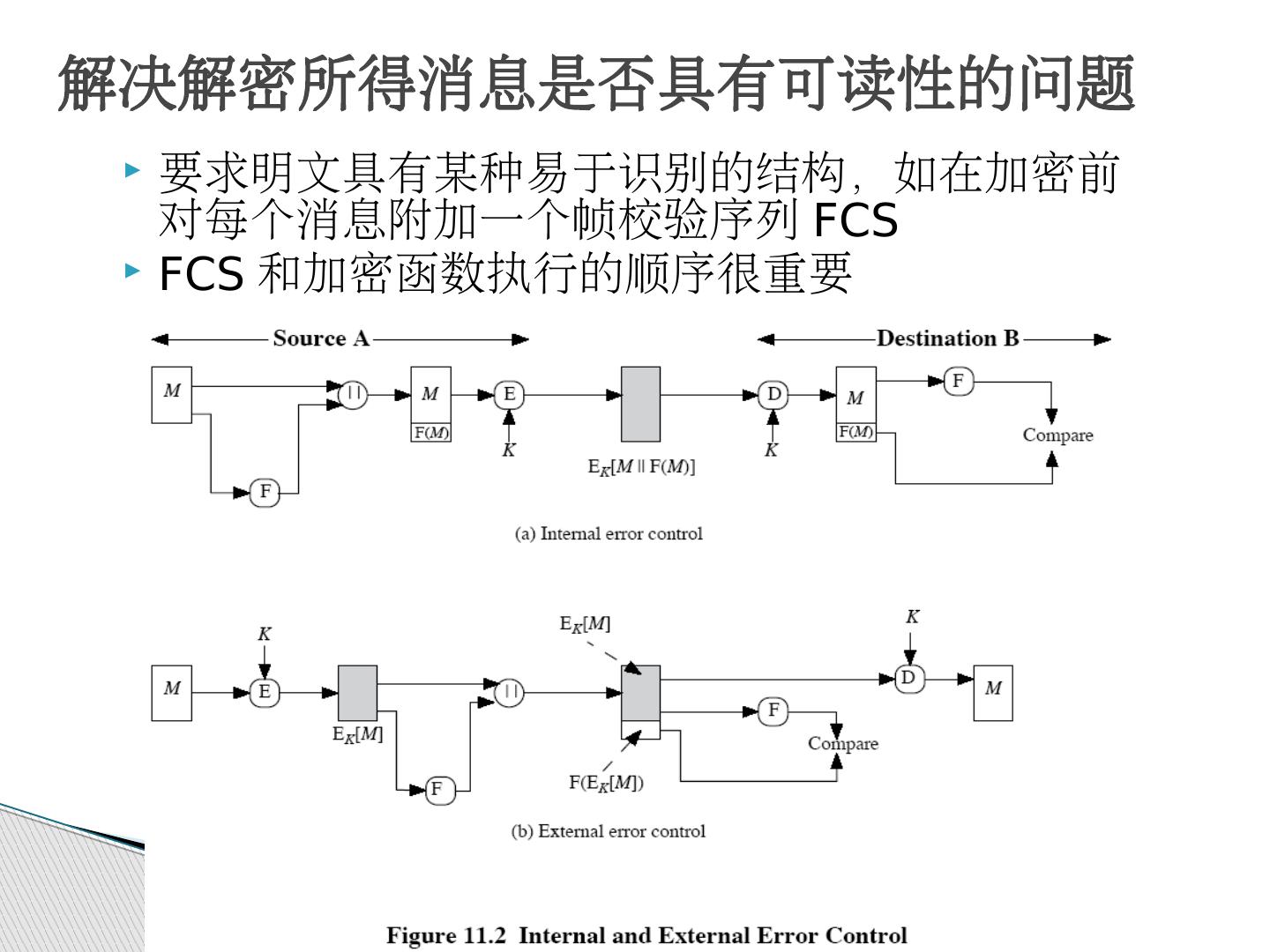
9 .解决解密所得消息是否具有可读性的问题 要求明文具有某种易于识别的结构，如在加密前对每个消息附加一个帧校验序列 FCS FCS 和加密函数执行的顺序很重要

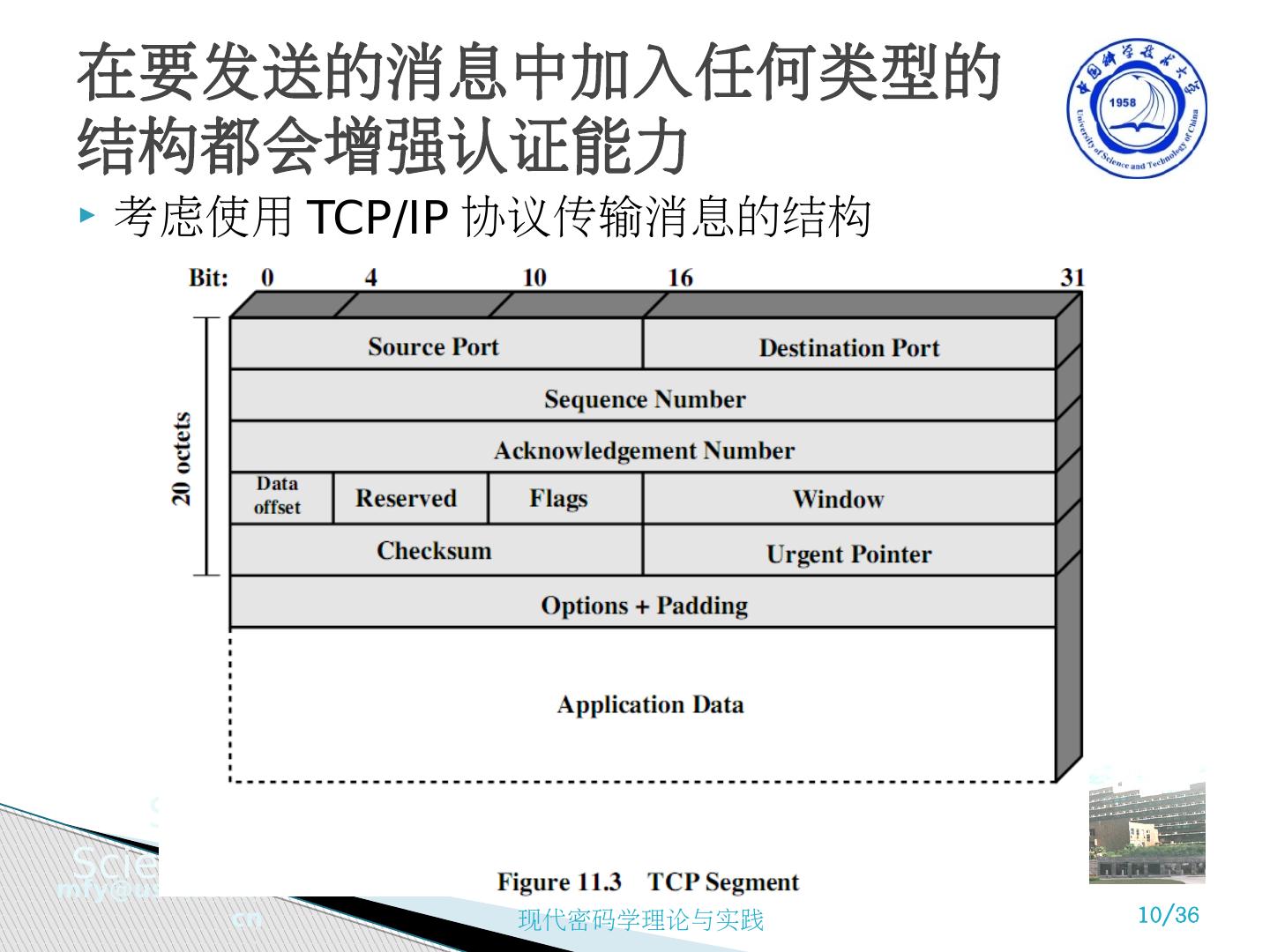
10 .考虑使用 TCP/IP 协议传输消息的结构 在要发送的消息中加入任何类型的结构都会增强认证能力

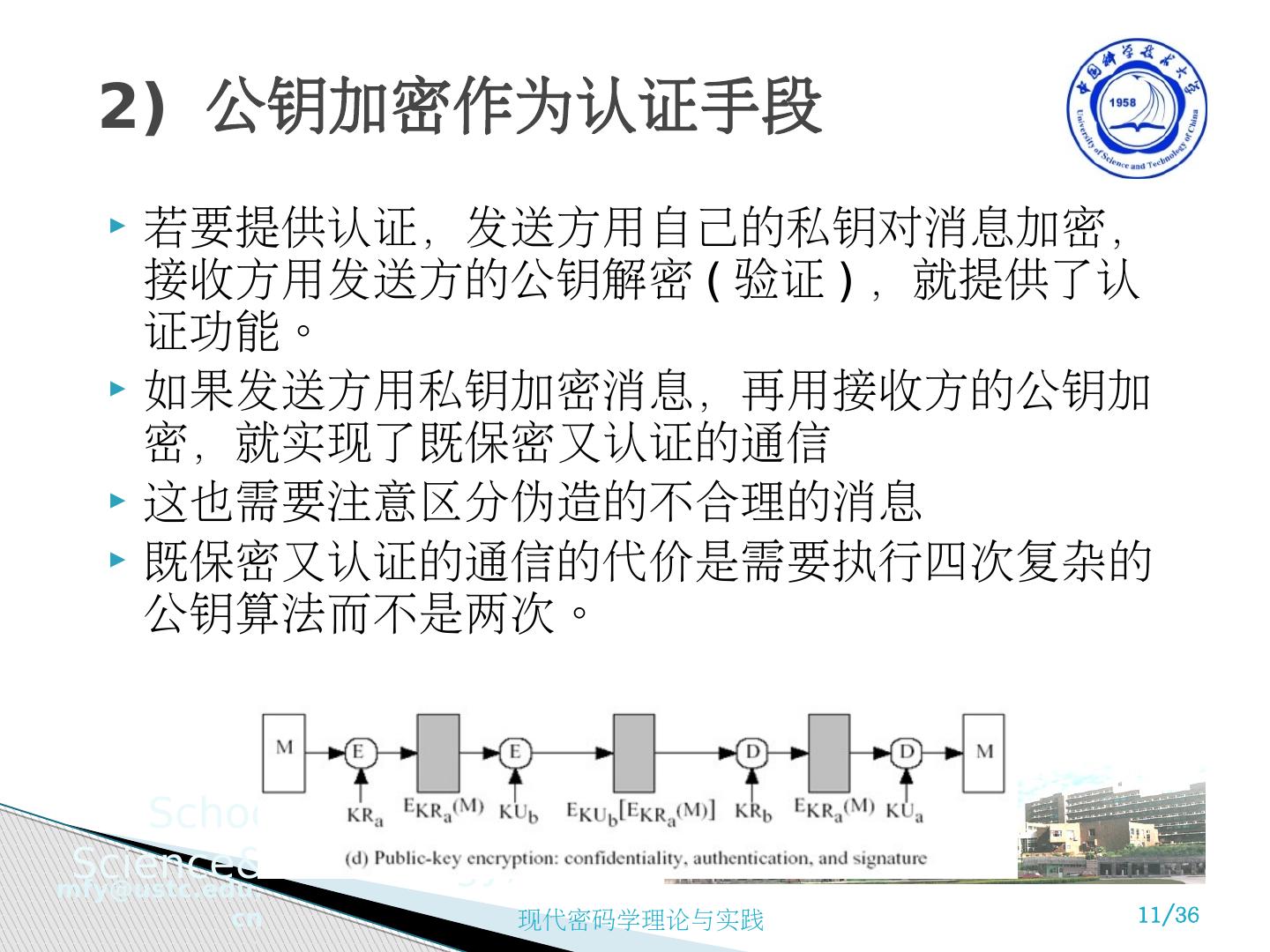
11 .若要提供认证，发送方用自己的私钥对消息加密，接收方用发送方的公钥解密 ( 验证 ) ，就提供了认证功能。 如果发送方用私钥加密消息，再用接收方的公钥加密，就实现了既保密又认证的通信 这也需要注意区分伪造的不合理的消息 既保密又认证的通信的代价是需要执行四次复杂的公钥算法而不是两次。 2) 公钥加密作为认证手段

12 .只有特定接受者可验证 使用密钥产生短小的定长数据分组，即所谓的密码检验 MAC ，将它附加在报文中。通信双方 A 和 B 共享密钥 K ，报文从 A 发往 B ， A 计算 MAC=C K (M), 附在报文后发给 B 。 B 对接收到的报文重新计算 MAC ，并与接收到的 MAC 比较。如果只有收发双方知道密钥且两个 MAC 匹配，则： 接收方可以确信报文未被更改； 接收方可以确信报文来自声称的发送者； 接收方可以确信报文序号正确，如果有的话。 Message Authentication( 报文认证 ) 不提供保密 MAC 函数类似加密，但非数字签名，也无需可逆 将 MAC 直接与明文并置，然后加密传输比较常用 11.2.2 消息认证码 MAC

13 .MAC 加密所得的消息校验和 MAC = C K (M) 使用一个秘密密钥 K ，浓缩一个变长的消息 M ，产生一个固定长度的认证子 MAC 是一种多对一的函数 定义域由任意长的消息组成，值域由所有可能的 MAC 和密钥组成。若使用 n 位长的 MAC, 则有 2 n 个可能的 MAC; 有 N 条可能的消息 , N>>2 n . 若密钥长度为 k, 则有 2 k 种可能的密钥。 如 N 为 100 位 , n 为 10 位 , 共有 2 100 不同的消息 , 2 10 种不同的 MAC, 平均而言同一 MAC 可由 2 100 / 2 10 =2 90 条不同的消息产生。若密钥长度为 5 ，则从消息集合到 MAC 值的集合有 2 5 =32 不同映射。 可以证明，由于认证函数的数学性质，与加密相比，认证函数更不易被攻破 MAC: 消息认证码的特点

14 .MAC 加密所得的消息校验和 MAC = C K (M) 使用一个秘密密钥 K ，浓缩一个变长的消息 M ，产生一个固定长度的认证子 MAC 是一种多对一的函数 定义域由任意长的消息组成，值域由所有可能的 MAC 和密钥组成。若使用 n 位长的 MAC, 则有 2 n 个可能的 MAC; 有 N 条可能的消息 , N>>2 n . 若密钥长度为 k, 则有 2 k 种可能的密钥。 如 N 为 100 位 , n 为 10 位 , 共有 2 100 不同的消息 , 2 10 种不同的 MAC, 平均而言同一 MAC 可由 2 100 / 2 10 =2 90 条不同的消息产生。若密钥长度为 5 ，则从消息集合到 MAC 值的集合有 2 5 =32 不同映射。 可以证明，由于认证函数的数学性质，与加密相比，认证函数更不易被攻破 MAC: 消息认证码的特点

15 .MAC 加密所得的消息校验和 MAC = C K (M) 使用一个秘密密钥 K ，浓缩一个变长的消息 M ，产生一个固定长度的认证子 MAC 是一种多对一的函数 定义域由任意长的消息组成，值域由所有可能的 MAC 和密钥组成。若使用 n 位长的 MAC, 则有 2 n 个可能的 MAC; 有 N 条可能的消息 , N>>2 n . 若密钥长度为 k, 则有 2 k 种可能的密钥。 如 N 为 100 位 , n 为 10 位 , 共有 2 100 不同的消息 , 2 10 种不同的 MAC, 平均而言同一 MAC 可由 2 100 / 2 10 =2 90 条不同的消息产生。若密钥长度为 5 ，则从消息集合到 MAC 值的集合有 2 5 =32 不同映射。 可以证明，由于认证函数的数学性质，与加密相比，认证函数更不易被攻破 MAC: 消息认证码的特点

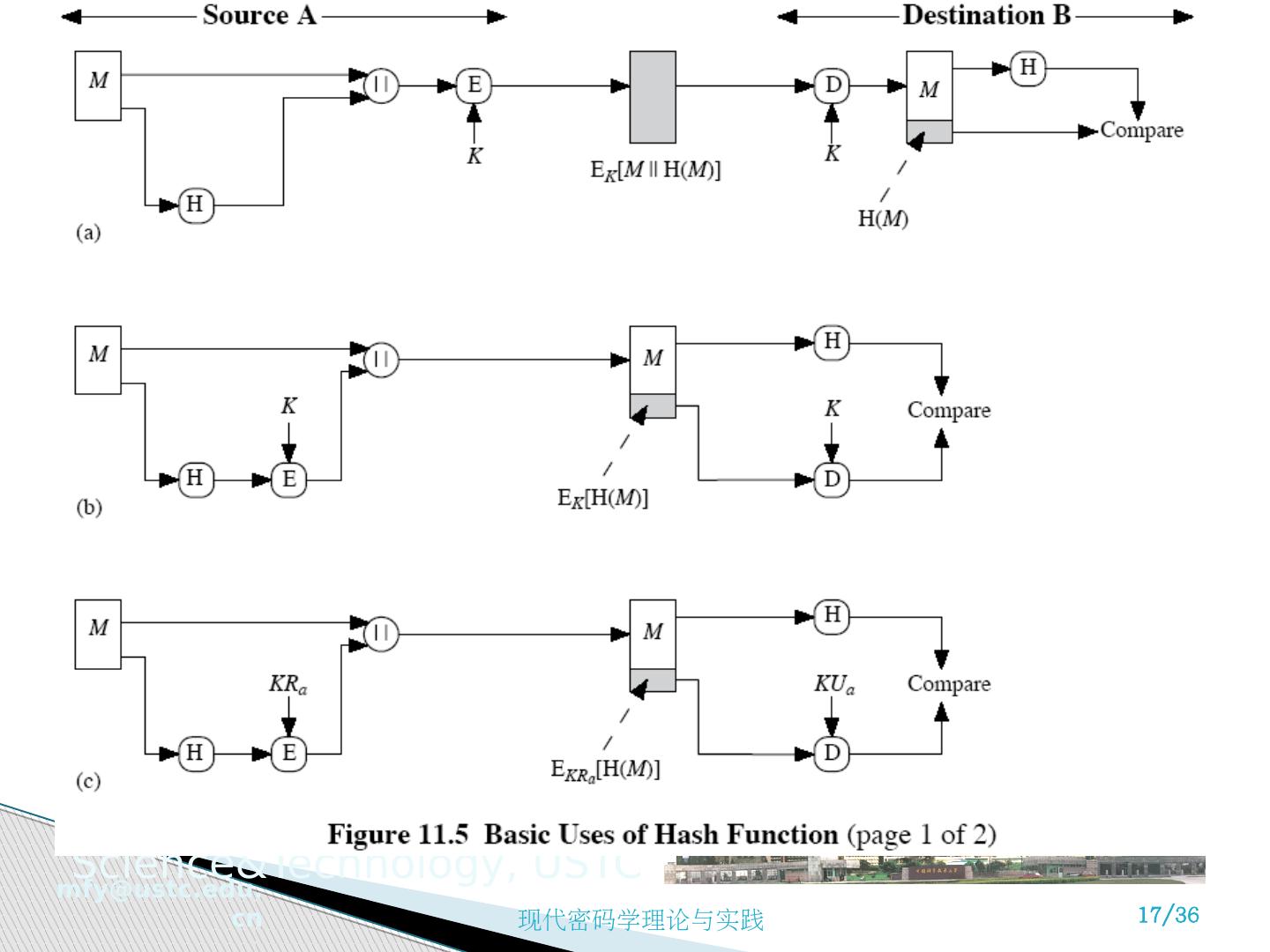
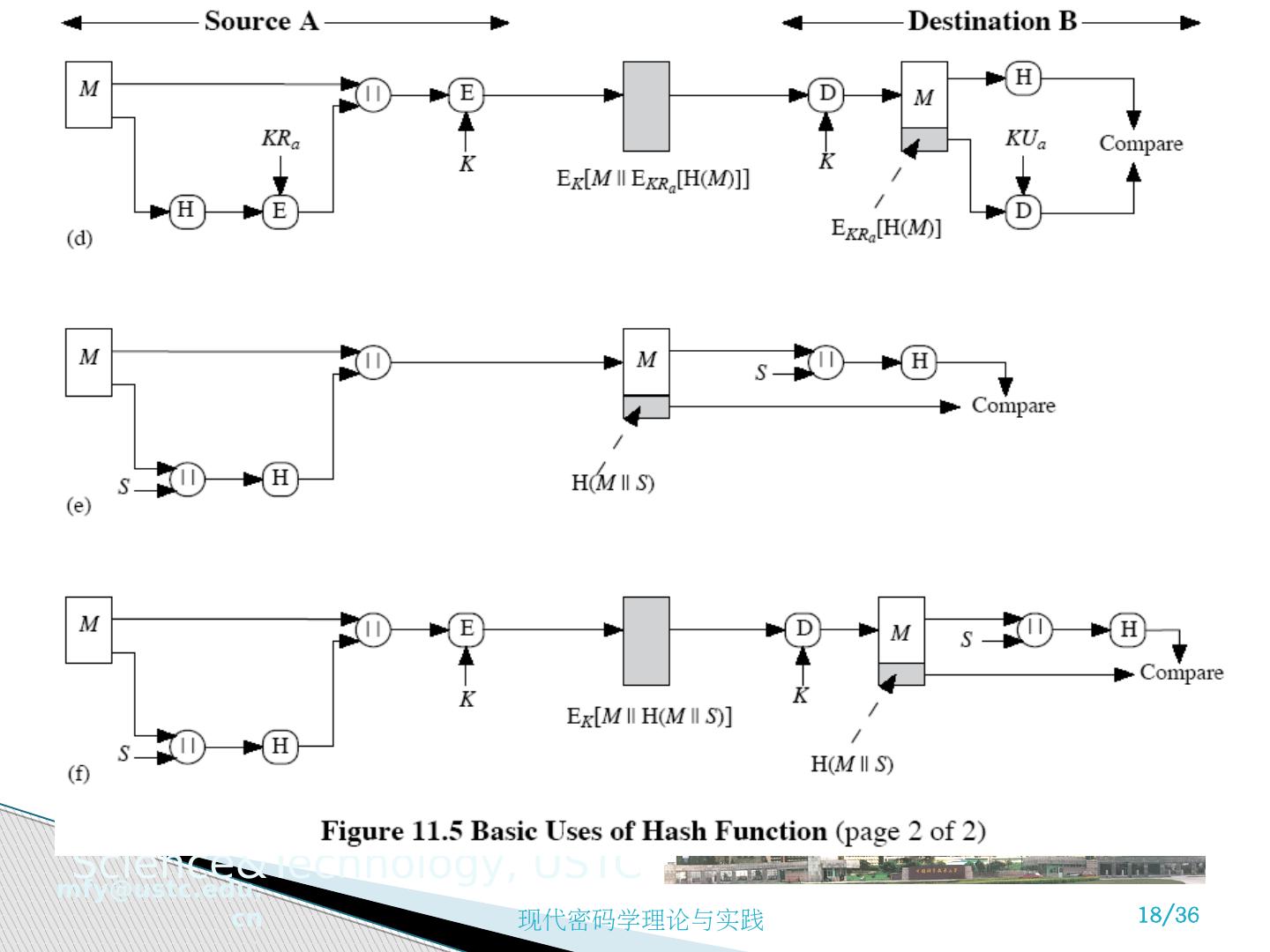
16 .一个散列函数以变长的报文 M 作为输入，产生定长的散列码 H(M) ，作为输出，亦称作报文摘要 Message Digest. 散列码是报文所有比特的函数值，具有差错检测能力，报文任意一比特的改变都将引起散列码的改变 不同的散列码使用方式 对附加了散列码的报文进行加密 使用常规加密方法仅对散列码加密 使用公开密钥方法仅对散列码加密，提供数字签名 同时提供保密和签名，可以分别使用常规方法加密报文及使用公开密钥方法加密散列码 其他 对避免加密的方法重视的原因 加密过程很慢，硬件开销大，初始化的开销，专利问题，出口限制 11.2.3 散列函数 Hash Function

17 .一个散列函数以变长的报文 M 作为输入，产生定长的散列码 H(M) ，作为输出，亦称作报文摘要 Message Digest. 散列码是报文所有比特的函数值，具有差错检测能力，报文任意一比特的改变都将引起散列码的改变 不同的散列码使用方式 对附加了散列码的报文进行加密 使用常规加密方法仅对散列码加密 使用公开密钥方法仅对散列码加密，提供数字签名 同时提供保密和签名，可以分别使用常规方法加密报文及使用公开密钥方法加密散列码 其他 对避免加密的方法重视的原因 加密过程很慢，硬件开销大，初始化的开销，专利问题，出口限制 11.2.3 散列函数 Hash Function

18 .一个散列函数以变长的报文 M 作为输入，产生定长的散列码 H(M) ，作为输出，亦称作报文摘要 Message Digest. 散列码是报文所有比特的函数值，具有差错检测能力，报文任意一比特的改变都将引起散列码的改变 不同的散列码使用方式 对附加了散列码的报文进行加密 使用常规加密方法仅对散列码加密 使用公开密钥方法仅对散列码加密，提供数字签名 同时提供保密和签名，可以分别使用常规方法加密报文及使用公开密钥方法加密散列码 其他 对避免加密的方法重视的原因 加密过程很慢，硬件开销大，初始化的开销，专利问题，出口限制 11.2.3 散列函数 Hash Function

19 .一个散列函数以变长的报文 M 作为输入，产生定长的散列码 H(M) ，作为输出，亦称作报文摘要 Message Digest. 散列码是报文所有比特的函数值，具有差错检测能力，报文任意一比特的改变都将引起散列码的改变 不同的散列码使用方式 对附加了散列码的报文进行加密 使用常规加密方法仅对散列码加密 使用公开密钥方法仅对散列码加密，提供数字签名 同时提供保密和签名，可以分别使用常规方法加密报文及使用公开密钥方法加密散列码 其他 对避免加密的方法重视的原因 加密过程很慢，硬件开销大，初始化的开销，专利问题，出口限制 11.2.3 散列函数 Hash Function

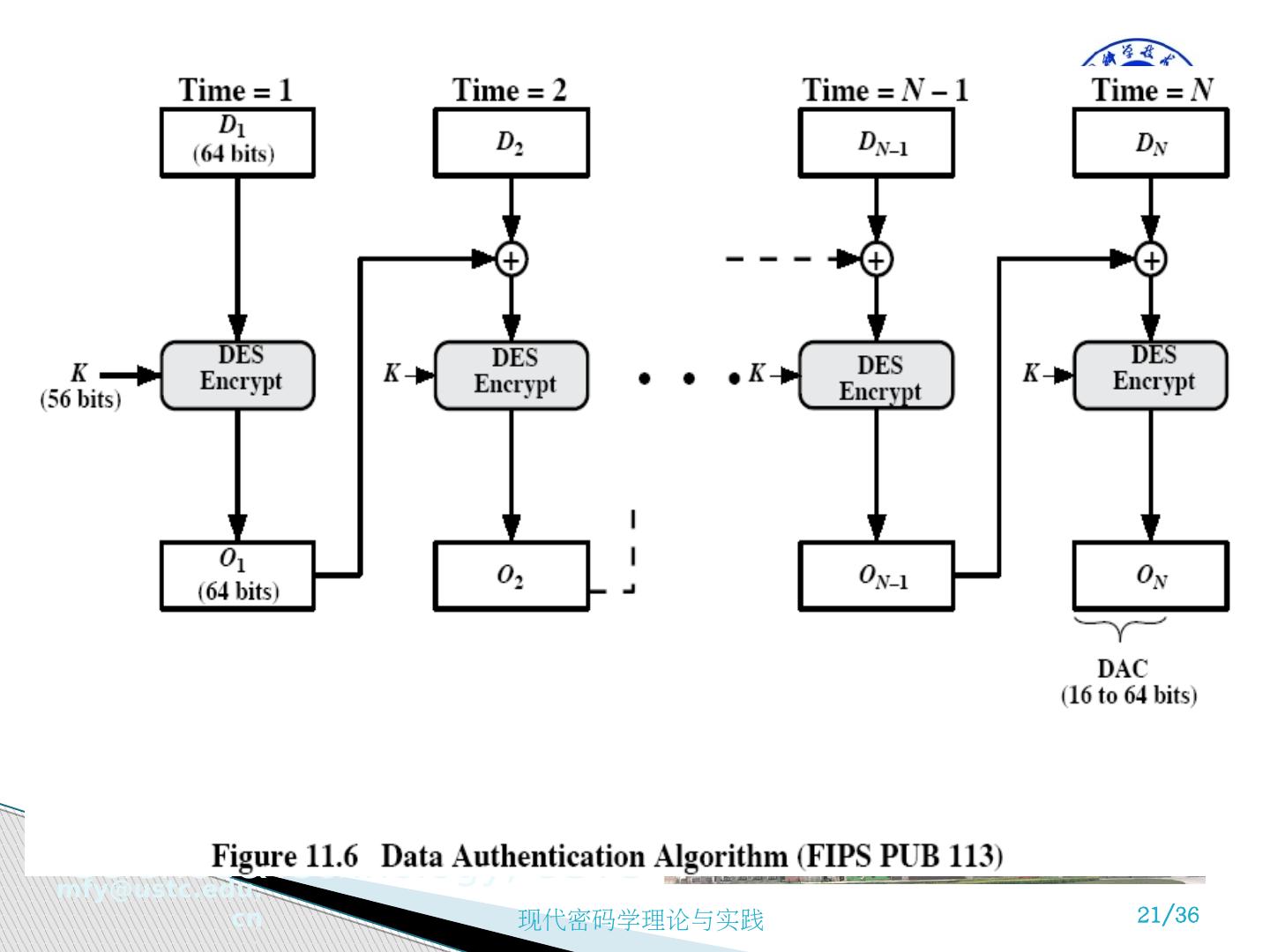
20 .对 MAC 的要求 若攻击者已知 M 和 MAC 码 C(K,M ) ，则构造满足 C(K,M’)=C(K,M) 的消息 M’ 在计算上是不可行的 C(K,M) 应该是 均匀分布 的，即对任何随机选择的消息 M 和 M’ ， C(K,M’)=C(K,M) 的概率是 2 -n ，其中 n 是 MAC 的位数 设 M’ 是 M 的某个已知的变换，即 M’=f(M) ，如 f 可能表示逆转 M 的一位或多位，那么 Pr[C(K,M)=C(K,M’)] 的概率是 2 -n . （ Malleability ） 基于 DES 的消息认证码 FIPS PUB 113 该算法定义为以密码分组链接 (CBC) 为操作方式的用 0 作为初始化向量的 DES 11.3 消息认证码 MAC

21 .对 MAC 的要求 若攻击者已知 M 和 MAC 码 C(K,M ) ，则构造满足 C(K,M’)=C(K,M) 的消息 M’ 在计算上是不可行的 C(K,M) 应该是 均匀分布 的，即对任何随机选择的消息 M 和 M’ ， C(K,M’)=C(K,M) 的概率是 2 -n ，其中 n 是 MAC 的位数 设 M’ 是 M 的某个已知的变换，即 M’=f(M) ，如 f 可能表示逆转 M 的一位或多位，那么 Pr[C(K,M)=C(K,M’)] 的概率是 2 -n . （ Malleability ） 基于 DES 的消息认证码 FIPS PUB 113 该算法定义为以密码分组链接 (CBC) 为操作方式的用 0 作为初始化向量的 DES 11.3 消息认证码 MAC

22 .相同报文进行多点广播，以明文加对应 MAC 的形式进行广播，接收者负责鉴别，不正确时发出告警 接收方无法对所有收到的报文进行解密工作，则可以进行有选择地鉴别，对报文作随机检查 对明文计算机程序进行鉴别，检查完整性 某些应用不关注报文的保密而更重视鉴别报文的真实性，如 SNMPv3 ，将保密与鉴别分开 保密函数与鉴别函数的分离能提供结构上的灵活性，如在应用层完成鉴别而在较低层加密 在超过接收时间后继续延长保护期限，同时允许处理报文内容 MAC 不提供数字签名，因为双方共享密钥。 使用消息认证码的几种情形

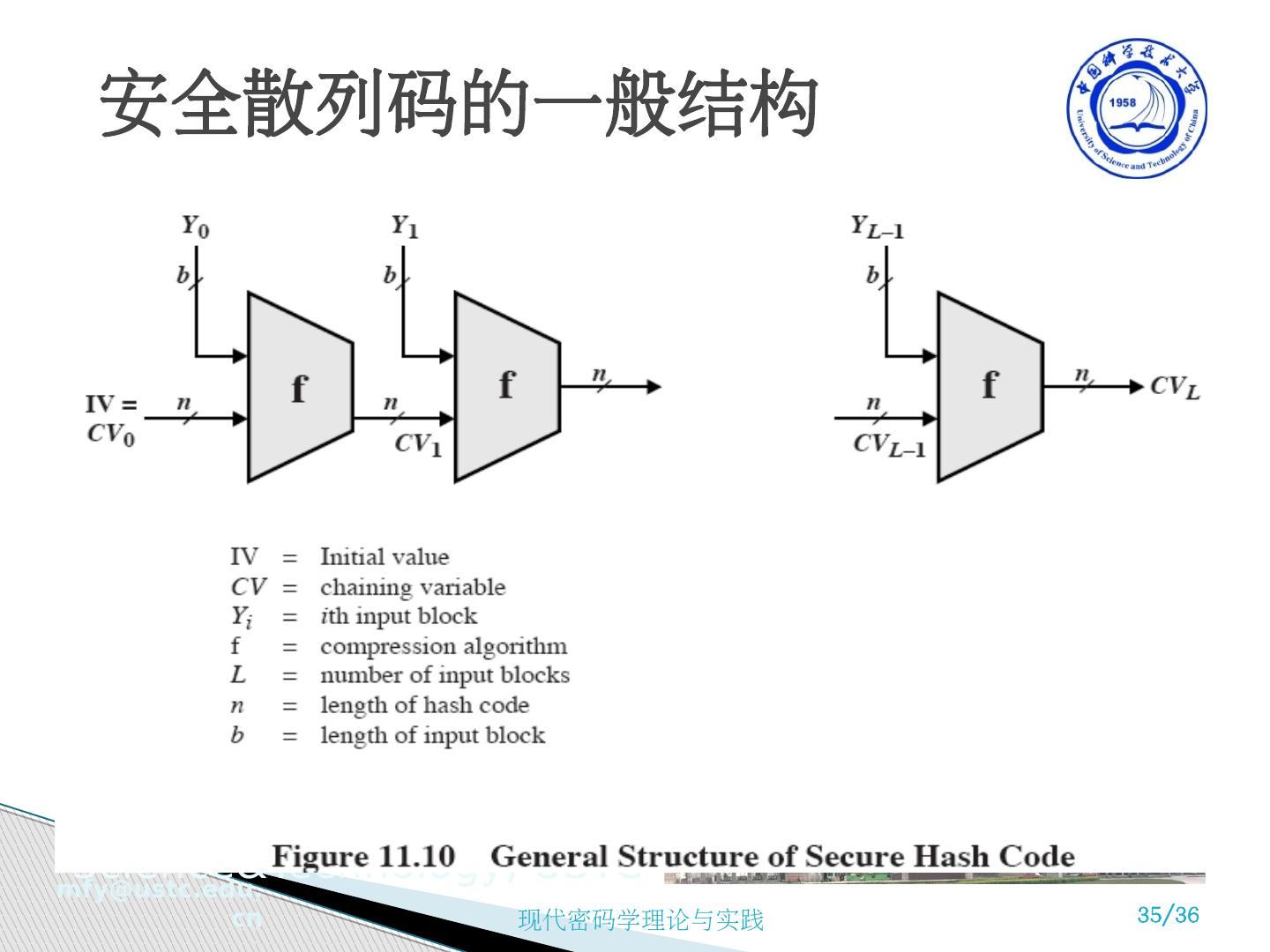
23 .散列函数 一个散列函数以变长的报文 M 作为输入，产生定长的散列码 H(M) ，作为输出，亦称作报文摘要 Message Digest. 散列码是报文所有比特的函数值，具有差错检测能力，报文任意一比特的改变都将引起散列码的改变。 h=H(M) 报文摘要的基本原理 对任意长度的明文 m ，经由哈希函数 ( 杂凑函数 ) h 产生固定长度的哈希值 h ( m ) ，用来对明文作鉴别 (authentication) 或数字签名 (digital signature) 。哈希函数值是对明文的一种“指纹” (finger print) 或是摘要 (digest) 。对哈希函数值的数字签名，就是对此明文的数字签名，可以用来提高数字签名的效率。 11.4 散列函数

24 .散列函数 一个散列函数以变长的报文 M 作为输入，产生定长的散列码 H(M) ，作为输出，亦称作报文摘要 Message Digest. 散列码是报文所有比特的函数值，具有差错检测能力，报文任意一比特的改变都将引起散列码的改变。 h=H(M) 报文摘要的基本原理 对任意长度的明文 m ，经由哈希函数 ( 杂凑函数 ) h 产生固定长度的哈希值 h ( m ) ，用来对明文作鉴别 (authentication) 或数字签名 (digital signature) 。哈希函数值是对明文的一种“指纹” (finger print) 或是摘要 (digest) 。对哈希函数值的数字签名，就是对此明文的数字签名，可以用来提高数字签名的效率。 11.4 散列函数

25 .1. H 可以应用于任意大小的数据块 2. H 产生固定长度的输出 3. 对任意给定的明文 x ，计算 H(x) 容易，可由硬件或软件实现 4. 对任意给定的散列码 h ，找到满足 H(x)=h 的 x ，在计算上不可行， 单向性 5. 对于给定的分组 x ，找到满足 y ≠x 且 H(x)=H(y) 的 y ，在计算上不可行， 抗弱碰撞性 6. 找到任何满足 H(x)=H(y) 的偶对 (x, y) ， 在计算上不可行， 抗强碰撞性 11.4.1 对散列函数的要求 h=H(M)

26 .条件 1, 2, 3 ， 4 是所谓单向性问题 (One-way) 条件 5 是对使用的哈希值的数字签名方法所做的安全保障，否则攻击者可由已知的明文及相关的数字签名任意伪造对其他明文的签名 条件 6 主要用于防范所谓的生日攻击法 能满足条件 1-5 的，称为弱哈希函数 (Weak Hash Function) 能同时满足条件 6 的，称为强哈希函数 (Strong Hash Function) 应用在数字签名上的哈希函数必须是强哈希函数 11.4.2 强哈希函数

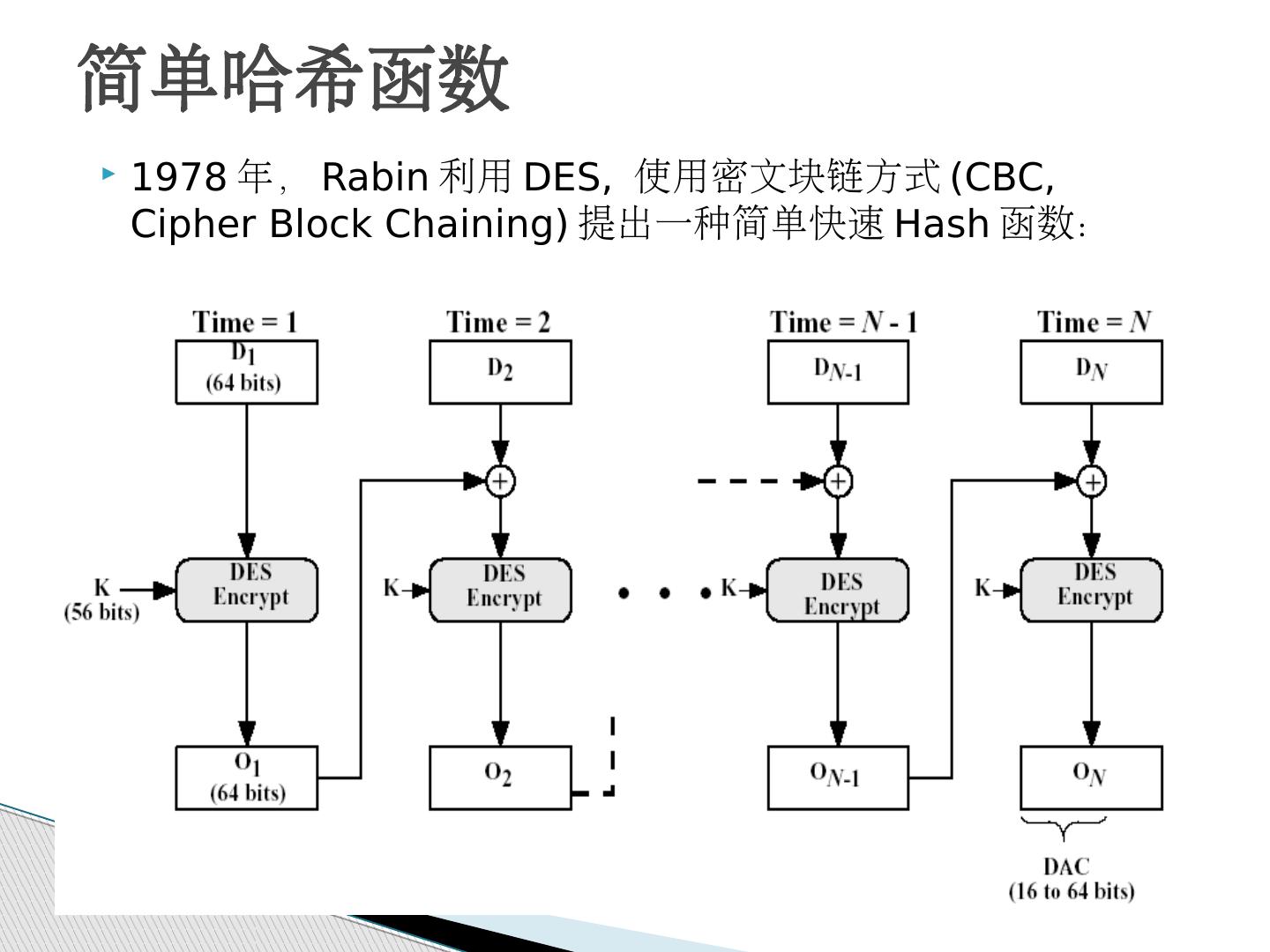
27 .简单哈希函数 1978 年， Rabin 利用 DES, 使用密文块链方式 (CBC, Cipher Block Chaining) 提出一种简单快速 Hash 函数：

28 .简单哈希函数 将明文 M 分成固定长度 64 位的明文块 (block)m 1 , m 2 , …, m n ，使用 DES 的 CBC 操作方法，对每一明文块陆续加密 令 h 0 = 初始值， h i = E mi [h i-1 ] 以及 G = h n 。 这种方法不使用密钥 , G 就是 64 位的哈希函数值 , 不安全。

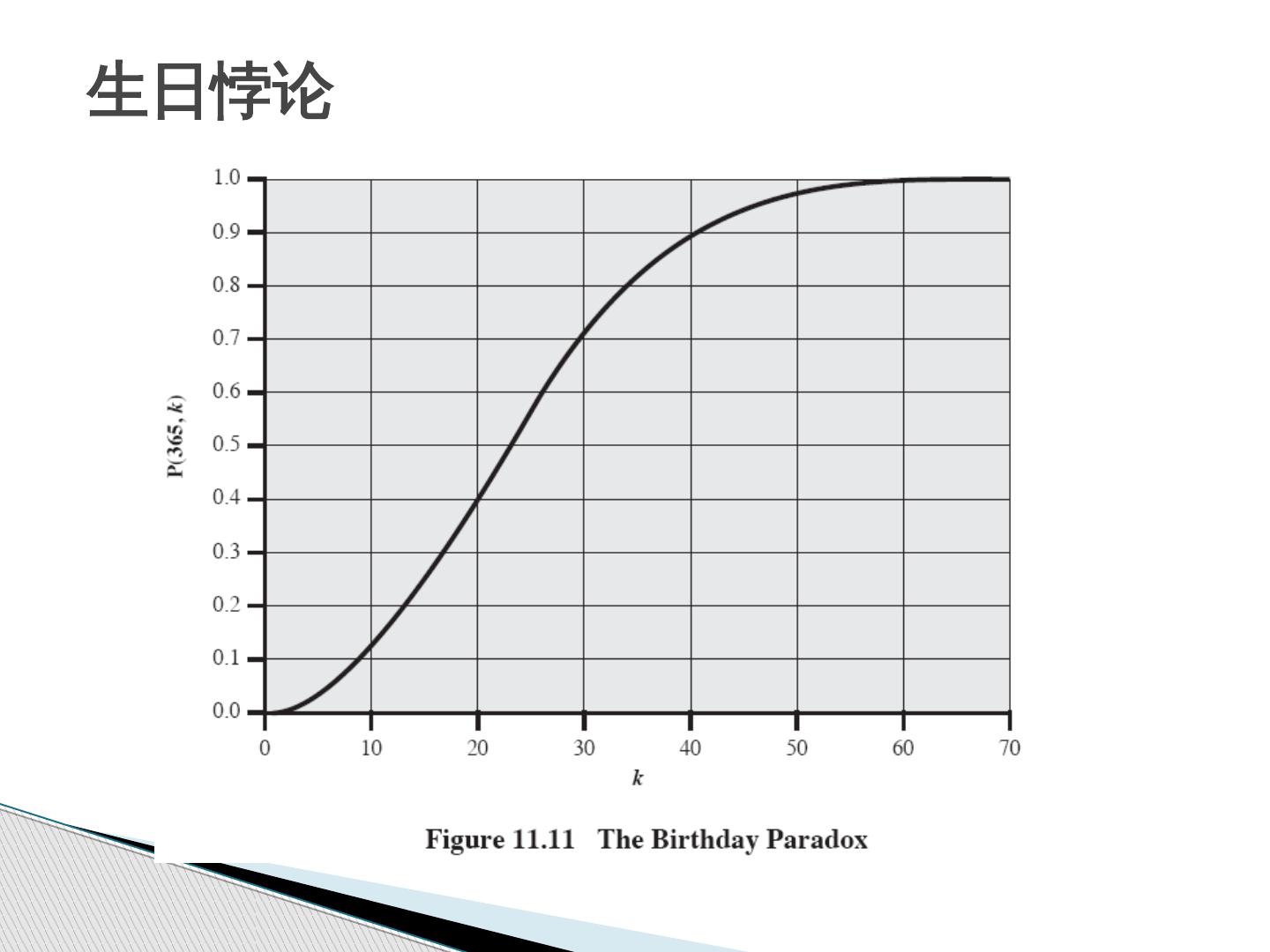
29 .生日悖论攻击法 (Birthday Paradox) 若试图伪造明文 M 的签名，要求签字人签名 M’ ，即要找到满足 H(M’)=H(M) 的 M’ ，到底需要找多少明文才能找到这个对应的 M’ ？ Rabin 的方法 若一个函数可能有 n 个函数值，且 已知一个函数值 h(x) ，任选 k 个任意数作为函数输入值，问： k 必须多大才能保证至少找到一个输入值 y ，且 h(x) = h(y) 的概率大于 1/2 ？ 当 k>n/2 时，这个概率将超过 1/2 。 11.4.3 对哈希函数的攻击法