10现代密码学理论与实践--密钥管理与其他公钥体制

1 .现代密码学理论与实践 第 10 章 密钥管理与其他公钥体制 苗付友 mfy@ustc.edu.cn http://202.38.64.11/~mfy

2 .公钥密码方案是安全的，仅当公钥的真实性能够得到保证。 公钥证书 方案提供了必要的安全性。 一个简单的公钥算法是 Diffie -Hellman 密钥交换协议 。这个协议使得通信双方利用基于离散对数问题的公钥算法建立秘密密钥。这个协议是安全的，仅当通信双方的真实性能够得到保证。 椭圆曲线 (ECC) 算术可以用来开发许多 椭圆曲线密码 方案，包括密钥交换，加密和数字签名。 椭圆曲线算术是指使用定义在有限域上的椭圆曲线方程。方程里的系数和变量都是域里的元素。已经开发了很多使用 Z p 和 GF(2 m ) 的方案。 本章要点

3 .10.1 密钥分配 10.1.1 密钥管理之 公钥的分配 10.1.2 公钥证书 10.1.3 利用公钥密码分配传统密码体制的密钥 10.2 基于离散对数的公钥体制 10.2.1 离散对数问题回顾 10.2.2 Diffie-Hellman Key Exchange 10.2.3 Pohlig-Hellman 离散对数密码 10.2.4 基于 DLP 的概率密码系统 ElGamal Cryptosystem 10.3 椭圆曲线算术 10.3.1 实数域上的椭圆曲线 10.3.2 有限域上的椭圆曲线 10.3.3 椭圆曲线点加运算 10.4 椭圆曲线密码学 10.4.1 椭圆曲线上的离散对数问题 10.4.2 椭圆曲线密码 10.4.3 椭圆曲线密码应用 10.4.4 椭圆曲线加 / 解密 本章目录

4 .公开密码的主要作用之一就是解决密钥分配问题， 公钥密码实际上可以用于以下两个不同的方面 公钥的分配 公钥密码用于传统密码体制的密钥分配 几种公钥分配方法 公开发布、公开可访问的目录 公钥授权、公钥证书 公钥的公开发布 用户将他的公钥发送给另一通信方，或者广播给通信各方，比如在电子邮件后附上 PGP 密钥，或者发布到邮件列表上 最大问题在于任何人都可以伪造这种公钥的发布 10.1.1 密钥管理之 公钥的分配 10.1.1 密钥 分配

5 .自由的公钥发布

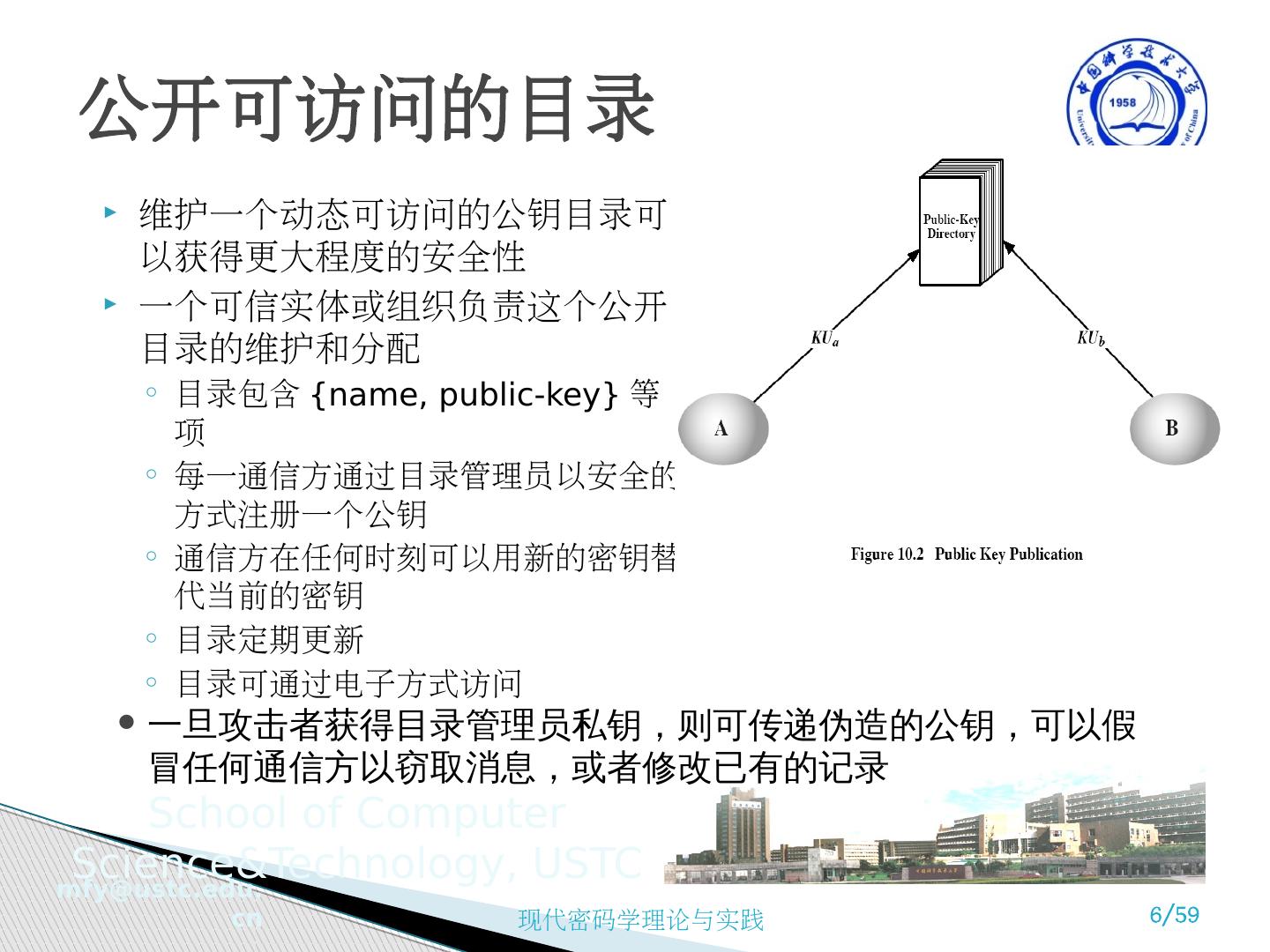
6 .维护一个动态可访问的公钥目录可以获得更大程度的安全性 一个可信实体或组织负责这个公开目录的维护和分配 目录包含 {name, public-key} 等项 每一通信方通过目录管理员以安全的方式注册一个公钥 通信方在任何时刻可以用新的密钥替代当前的密钥 目录定期更新 目录可通过电子方式访问 公开可访问的目录 一旦攻击者获得目录管理员私钥，则可传递伪造的公钥，可以假冒任何通信方以窃取消息，或者修改已有的记录

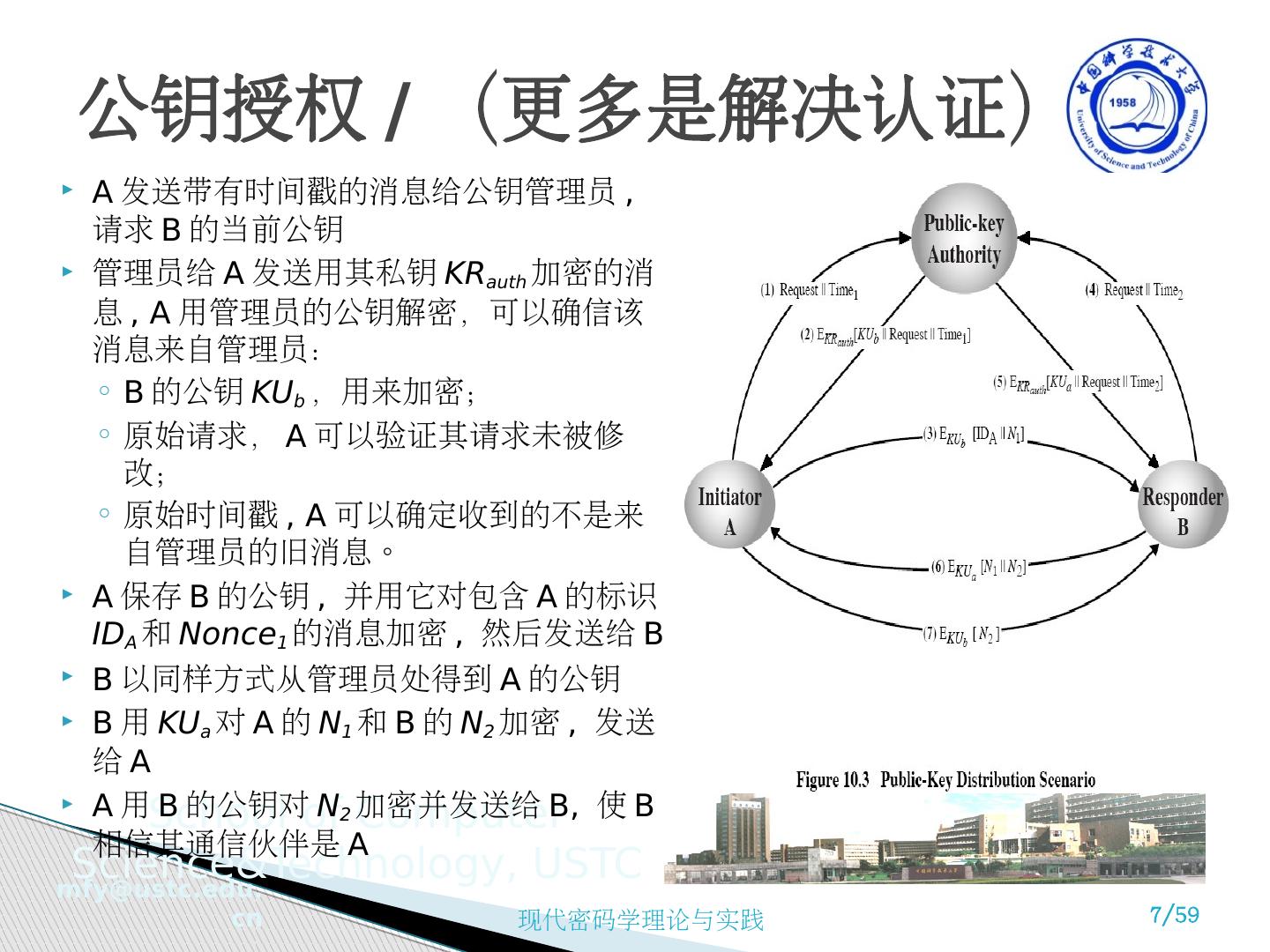
7 .A 发送带有时间戳的消息给公钥管理员 , 请求 B 的当前公钥 管理员给 A 发送用其私钥 KR auth 加密的消息 , A 用管理员的公钥解密，可以确信该消息来自管理员： B 的公钥 KU b ，用来加密； 原始请求， A 可以验证其请求未被修改； 原始时间戳 , A 可以确定收到的不是来自管理员的旧消息。 A 保存 B 的公钥 , 并用它对包含 A 的标识 ID A 和 Nonce 1 的消息加密 , 然后发送给 B B 以同样方式从管理员处得到 A 的公钥 B 用 KU a 对 A 的 N 1 和 B 的 N 2 加密 , 发送给 A A 用 B 的公钥对 N 2 加密并发送给 B, 使 B 相信其通信伙伴是 A 公钥授权 / （更多是解决认证）

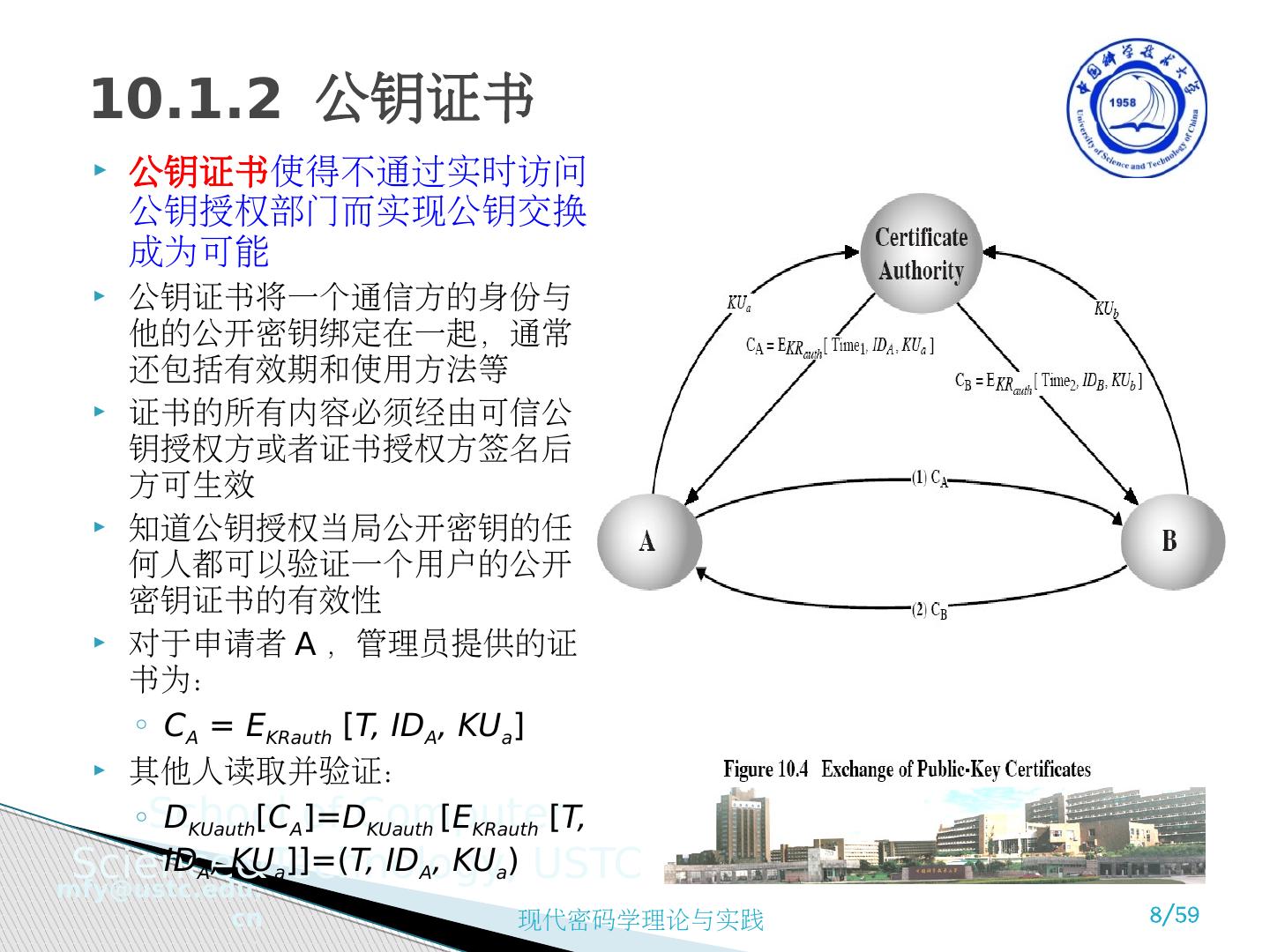
8 .公钥证书 使得不通过实时访问公钥授权部门而实现公钥交换成为可能 公钥证书将一个通信方的身份与他的公开密钥绑定在一起 ， 通常还包括有效期和使用方法等 证书的所有内容必须经由可信公钥授权方或者证书授权方签名后方可生效 知道公钥授权当局公开密钥的任何人都可以验证一个用户的公开密钥证书的有效性 对于申请者 A ，管理员提供的证书为： C A = E KRauth [ T, ID A , KU a ] 其他人读取并验证： D KUauth [ C A ]= D KUauth [ E KRauth [ T, ID A , KU a ]]=( T, ID A , KU a ) 10.1.2 公钥证书

9 .采用前述方法获得的公开密钥可以用于保密和认证之需 公钥密码算法速度较慢，因此更适合作为传统密码中实现秘密密钥分配的一种手段 因此，需要产生会话密钥来加密 已经有一些方法用来协商适当的会话密钥 10.1.3 利用公钥密码分配传统密码体制的密钥

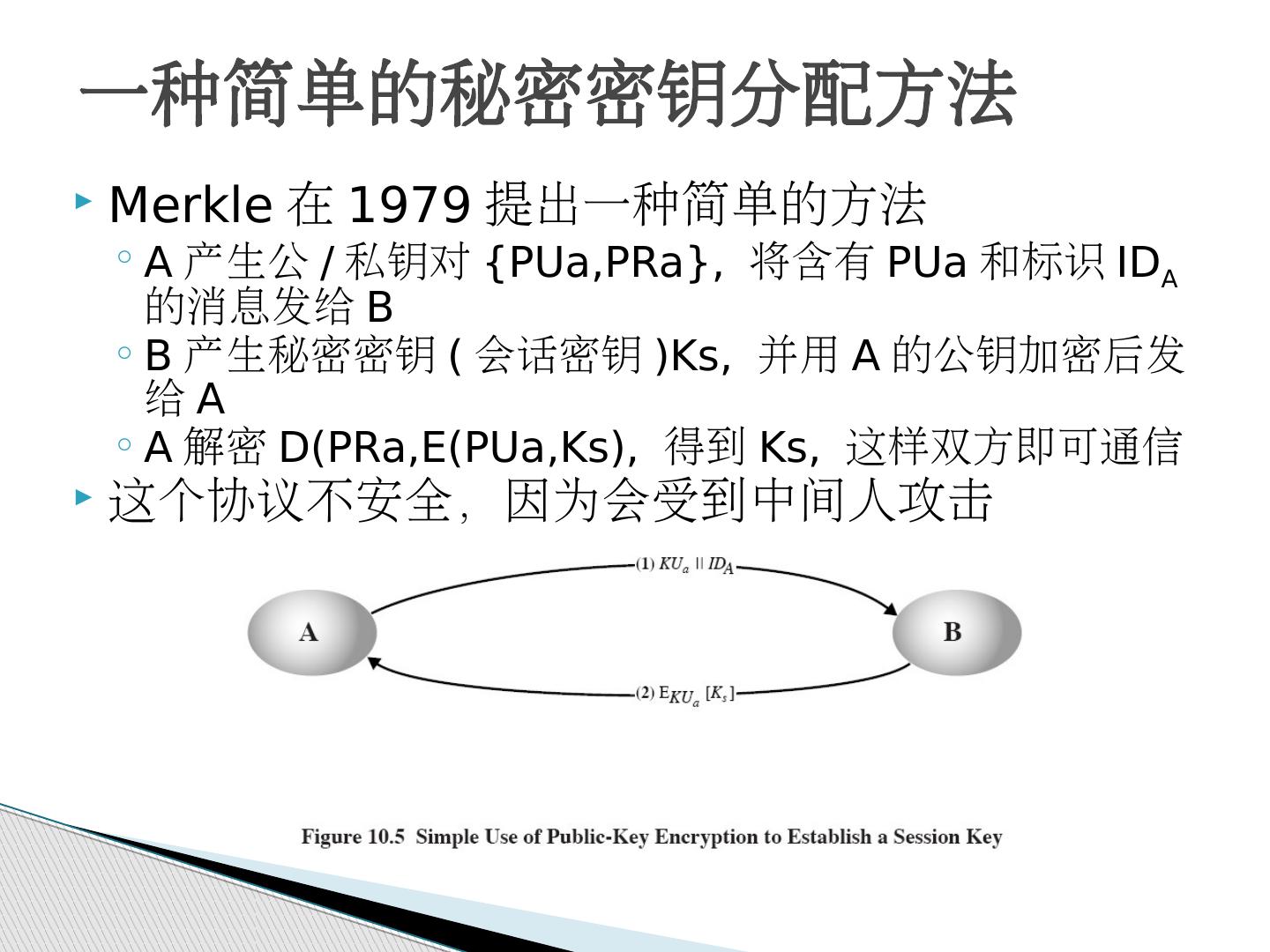
10 .一种简单的秘密密钥分配方法 Merkle 在 1979 提出一种简单的方法 A 产生公 / 私钥对 {PUa,PRa}, 将含有 PUa 和标识 ID A 的消息发给 B B 产生秘密密钥 ( 会话密钥 )Ks, 并用 A 的公钥加密后发给 A A 解密 D(PRa,E(PUa,Ks), 得到 Ks, 这样双方即可通信 这个协议不安全，因为会受到中间人攻击

11 .具有保密性和真实性的密钥分配

12 .Diffie 和 Hellman 在 1976 年首次提出了公钥算法，给出了公钥密码学的定义，该算法通常被称为 Diffie -Hellman 密钥交换算法 Diffie -Hellman 密钥交换算法是一种公钥分发机制 它不是用来加密消息的 所生成的是通信双方共享的会话密钥，必须保密，其值取决于通信双方的私钥和公钥信息 Diffie -Hellman 密钥交换算法是基于有限域 GF 中的指数运算的 ( 模一素数或多项式 ) Diffie -Hellman 密钥交换算法的安全性依赖于求解 DHP 问题 10.2 基于离散对数的公钥体制

13 .如果 a 是素数 p 的一个原根 ( 本原元素 ) ，则 a mod p, a 2 mod p, ......, a p-1 mod p ，生成模 p 的完全剩余集 {1, 2, ......, p-1} 对于所有素数，其原根必定存在，即 对于一个整数 b 和素数 p 的一个原根，可以找到唯一的指数 i, 使得 b = a i mod p, 其中 0<= i <= p-1 指数 i 称为 b 的以 a 为基数的模 p 的离散对数或者指数。 离散对数密码体制的安全性基于 DLP 问题 , 在已知 C 和 P 的情况下 , 由 d 求 M 很容易 , 由 M 求 d 很困难 , d = log C M in GF(P), 最快的算法需要 T=exp((ln(P)lnln(P) 1/2 ) 次运算。当 P 是 200 位时 , T = 2.7x10 11 , 如果 1 μ s 解一次 , 需要 2~3 天；如果 P = 664 位 , 则 T = 1.2x10 23 , 约 10 12 天或 2.739x10 9 年 , 约 2.7 亿年 . 只要 P 足够大 , 可以达到足够安全。 10.2.1 离散对数问题回顾

14 .DLP Given p, a and b , find x such that b=a x mod p . DHP g is the generator of F p , given g x mod p and g y mod p, find g xy mod p. DLP DHP, DLP=?DHP DLP 与 DHP

15 .通信双方约定一个大素数 ( 或多项式 )p, 和模 p 的一个素根 α 各方产生公开密钥 选择一个秘密钥 ( 数值 ) ，如 x A < p ， x B < p 计算公钥 , 如 y A = α x A mod p, y B = α x B mod p, 并相互交换 双方共享的会话密钥 K AB 可以如下算出 K AB = α x A. x B mod p = y A x B mod p (which B can compute) = y B x A mod p (which A can compute) K AB 是双方用对称密码通信时共享的密钥 如果双方继续通信，可以继续使用这个密钥，除非他们要选择新的密钥 攻击者如果想要获得 x, 则必须解决 DLP 问题 10.2.2 Diffie -Hellman Key Exchange

16 .Users Alice & Bob who wish to swap keys Agree on prime p=353 and α =3 Select random secret keys: A chooses x A =97, B chooses x B =233 Compute public keys: y A = 3 97 mod 353 = 40 (Alice) y B = 3 233 mod 353 = 248 (Bob) Compute shared session key as: K AB = y B x A mod 353 = 248 97 mod 353 = 160 (Alice) K AB = y A x B mod 353 = 40 233 mod 353 = 160 (Bob) Diffie -Hellman Example

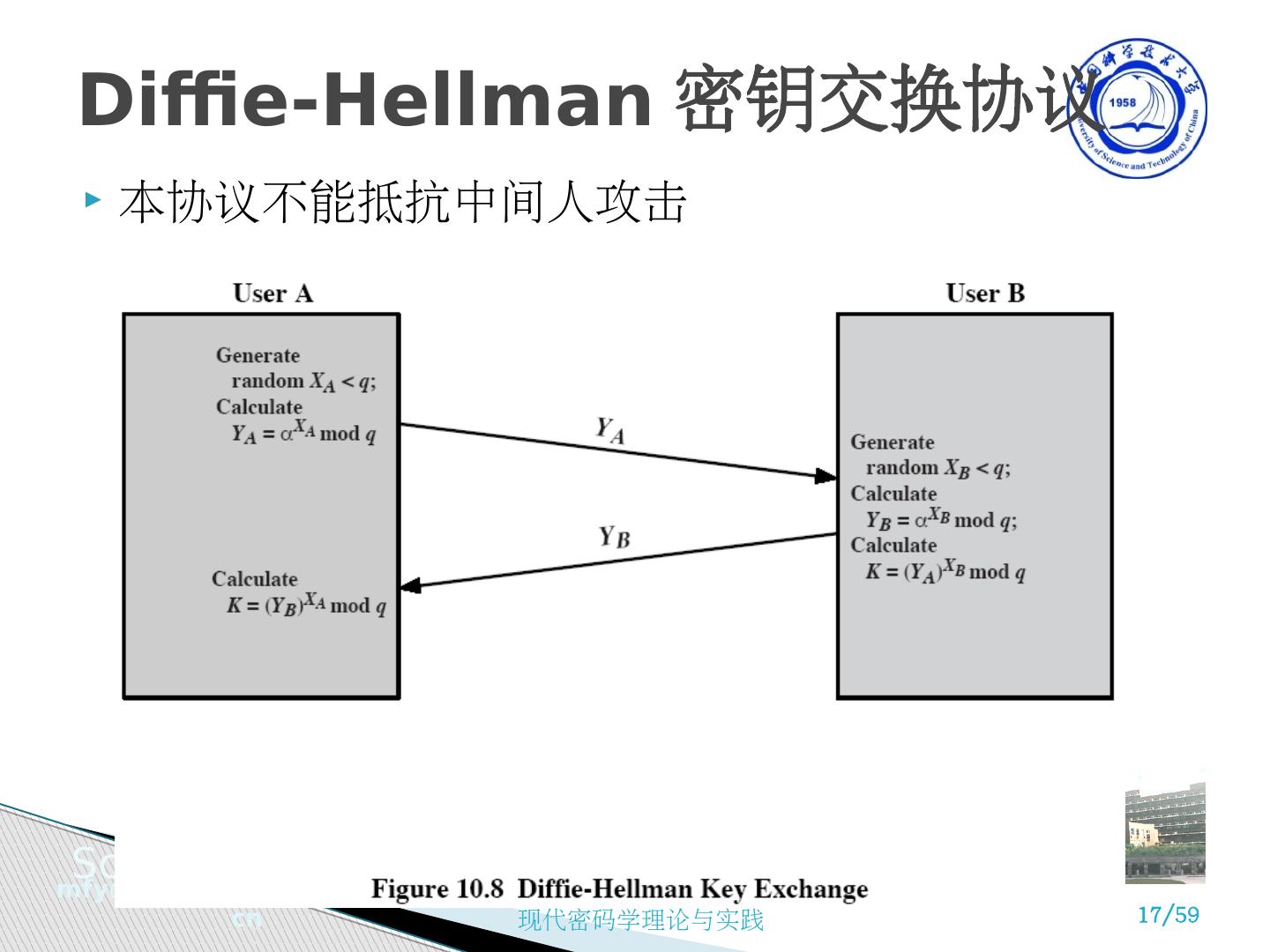
17 .本协议不能抵抗中间人攻击 Diffie -Hellman 密钥交换协议

18 .Pohlig -Hellman Scheme ，其安全性基于 DHP 问题 加密： C = M e mod P 解密： M = C d = (M e ) d mod P 这里， ed mod φ (P) = 1 ， φ (P) 为模 P 的欧拉商数，即在 (1, 2, ..., P-1) 中所有与 P 互素的数的个数 。 P 为大素数，显然， φ (P)=P-1 。 因为 P 是素数， φ (P) 容易获得，因此 e 和 d 都需要保密。 P = 11 ， φ (P) = 10 ， d = 7 ， 则 e = d -1 = inv (7, 10) = 3 。 假定 M = 5 ，则 C = M e mod P = 5 3 mod 11 = 4 M = C d mod P = 4 7 mod 11 = 5 10.2.3 Pohlig -Hellman 离散对数密码

19 .假设 A 和 B 互相通信，共享大素数 p ，本原元素 α ， 0 ≤ m ≤ p-1 加密： A 选择 k∈[0, p-1], k 的作用其实即为 A 的临时密钥（ Ephemeral Key ） , A 访问公共区域找到 B 的公开密钥 Y B = α xB mod p, 计算： K = (Y B ) k mod p, 即 K = ( α xB ) k mod p c 1 = α k mod p （ α k 实质上就是 A 的临时公钥 ） c 2 = mK mod p （ A,B 共享 K ，与 diffie-Helman 密钥交换协议本质上相同 ） 密文即为 (c 1 , c 2 ) 解密： B 首先恢复 K ： K = c 1 xB mod P = α kxB mod p 然后恢复 m ： m = c 2 /K mod P = c 2 K -1 mod p 10.2.4 基于 DHP 的概率密码系统 ElGamal Cryptosystem

20 .这里特别注意， k 不能重复使用，如果 (1) c 1,1 = α k mod p c 2,1 = m 1 K mod p (2) c 1,2 = α k mod p c 2,2 = m 2 K mod p 得： m 1 /m 2 = c 2,1 /c 2,2 mod p. 如果 m 1 已知， m 2 即可算出。 ElGamal 密码体制是概率密码体制，同样的明文每次加密得到不同的密文 , 因为每次随机选择 k 。 ElGamal 密码体制加密效率是 50% ，因为密文大小是明文的两倍。 ElGamal 密码体制的破译难度同 Diffie-Hellman 的方法 , 即基于 DLP ，离散对数问题，最快的算法需要 T=exp((ln(p)lnln(p) 1/2 ) 次运算。 ElGamal Cryptosystem

21 .例： P = 17, α= 3, x A = 2, x B = 5, m = 11, m 从 A 发送到 B, A 选择 k = 7. 求：密文 (c 1 , c 2 ) 并解密 加密： Y A = α xA mod P = 3 2 mod 17 = 9 Y B = α xB mod P = 3 5 mod 17 = 5 K = (Y B ) k mod P = 5 7 mod 17 = 10 c 1 = α k mod P = 3 7 mod 17 = 11 c 2 = mK mod P = 10x11 mod 17 = 8 所以，密文 C = (c 1 , c 2 ) = (11, 8) 解密： K = c 1 xB mod P = 11 5 mod 17 = 10 c 2 = mK mod P = 10m mod 17 = 8 m = c 2 /K mod P = c 2 K -1 mod P K K -1 mod P = 1 ，即 10 K -1 mod 17 = 1 ，得 K -1 = 12 所以，明文 m = c 2 K -1 mod P = 8x12 mod 17 = 11 ElGamal Cryptosystem

22 .椭圆曲线密码编码学 ECC 大多数公开密钥密码系统如 RSA, D-H 都使用具有非常大数目的整数或多项式 , 计算量大 , 密钥和报文存储量也极大。因此 , 可以使用椭圆曲线密码系统 ECC, 达到同样安全但位数要小得多。 椭圆曲线 椭圆曲线并非椭圆 , 它指的是由 Weierstrass 方程所确定的平面曲线： y 2 + axy + by = x 3 + cx 2 + dx + e 满足上述方程的数偶 (x, y) 称为椭圆曲线 E 上的点。 同时定义无穷点 (point at infinity) 或零点 (zero point) 的 O 。 10.3 椭圆曲线算术

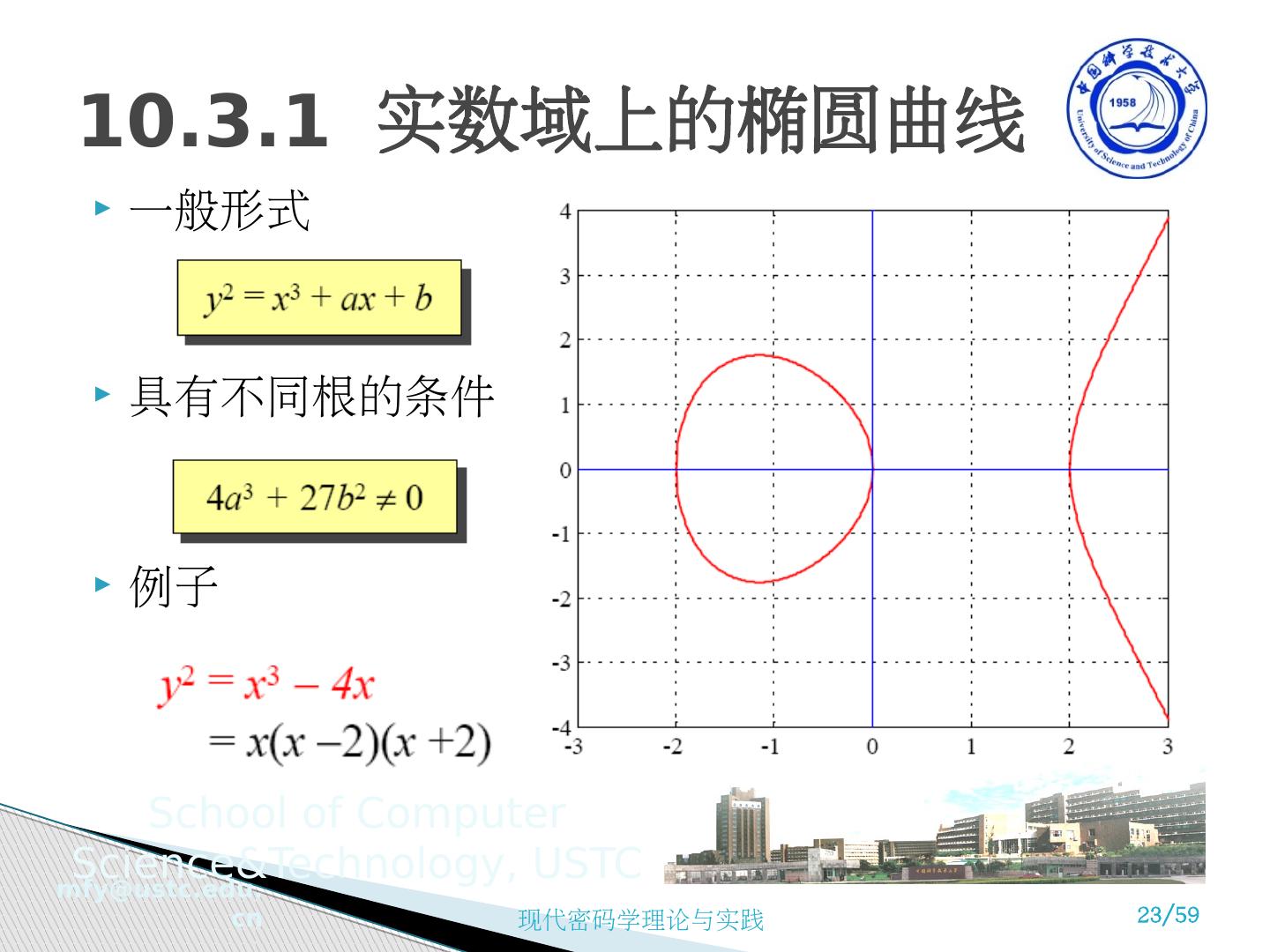
23 .一般形式 具有不同根的条件 例子 10.3.1 实数域上的椭圆曲线

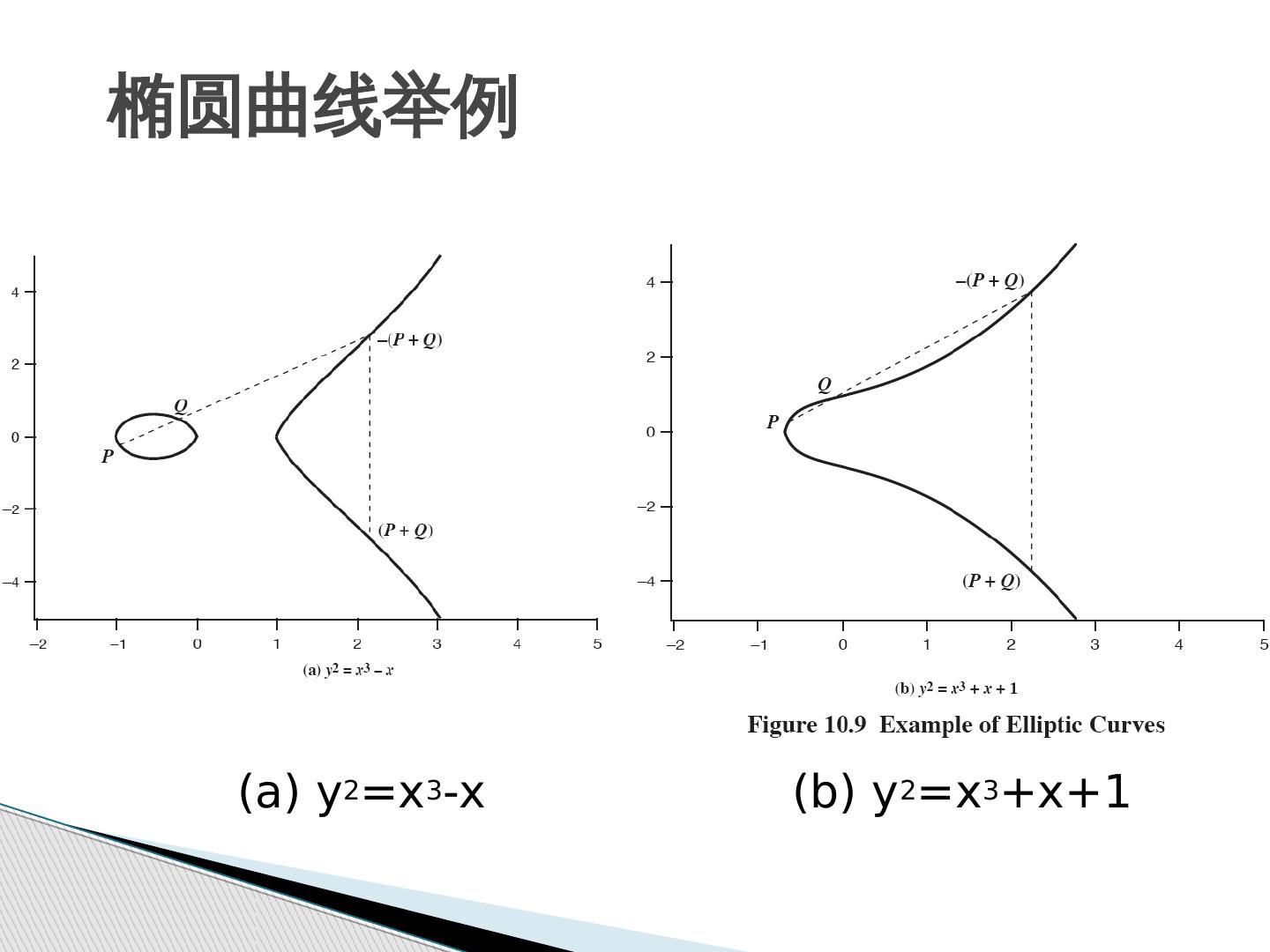
24 . (a) y 2 =x 3 -x (b) y 2 =x 3 +x+1 椭圆曲线举例

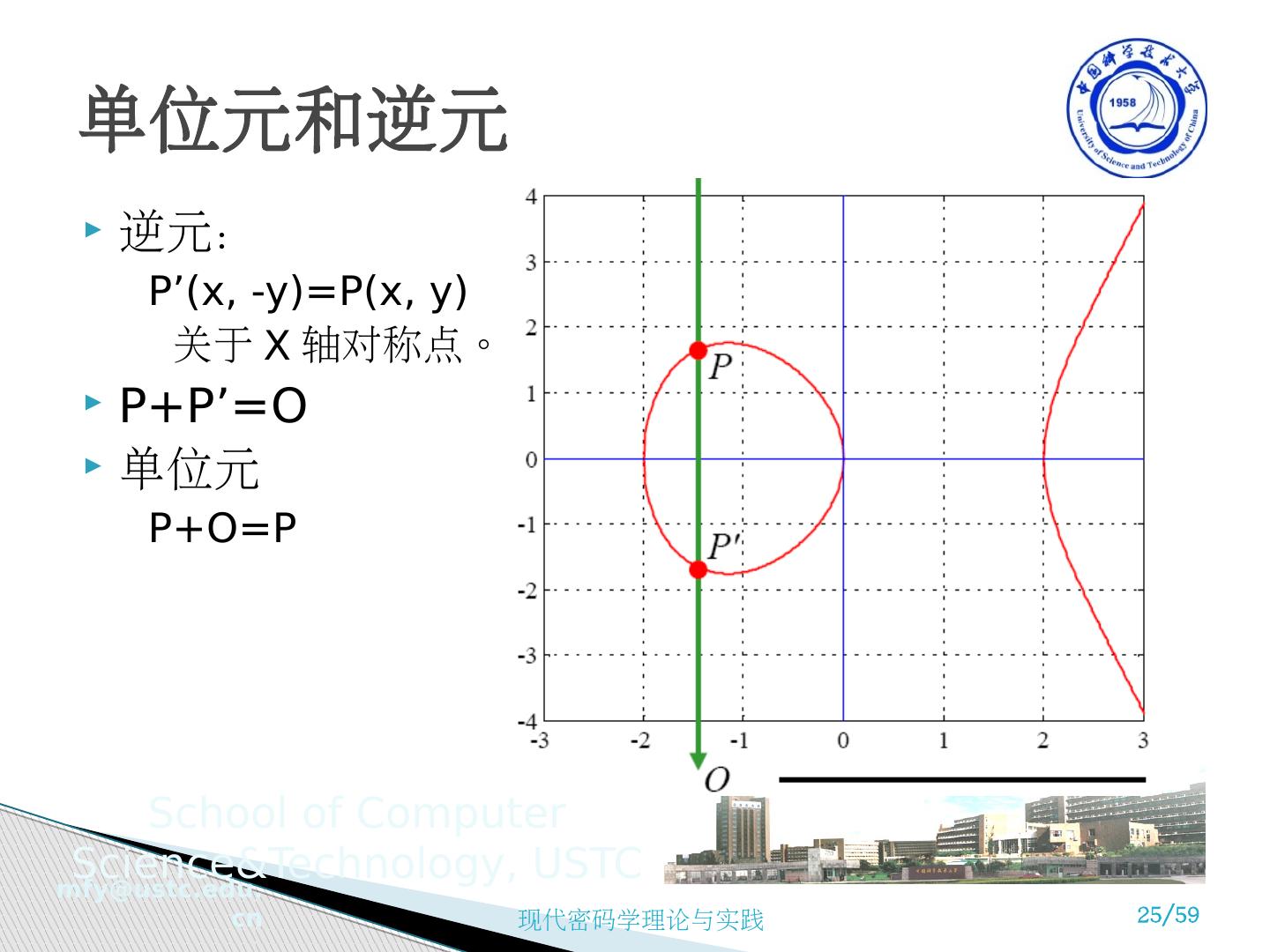
25 .逆元： P’(x, -y)=P(x, y) 关于 X 轴对称点。 P+P’=O 单位元 P+O=P 单位元和逆元

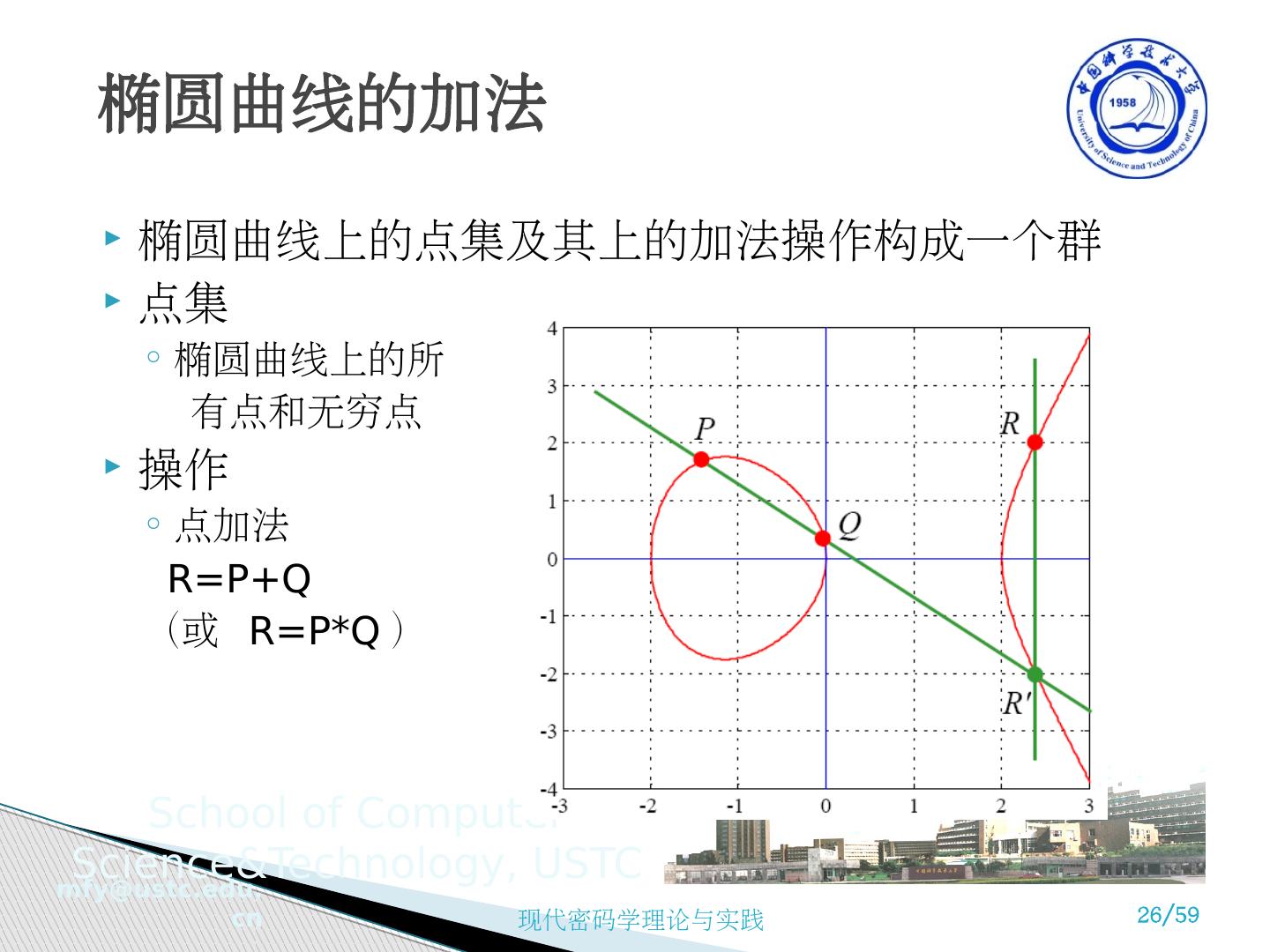
26 .椭圆曲线上的点集及其上的加法操作构成一个群 点集 椭圆曲线上的所 有点和无穷点 操作 点加法 R=P+Q （ 或 R=P*Q） 椭圆曲线的加法

27 .如果椭圆曲线上的三个点处于一条直线上 , 那么它们的和为 O 。加法规则： O 是加法的单位元 (additive identity), O = － O ；对于椭圆曲线上的任一点 P, 有 P + O = P 。 一条垂直线与曲线相交于 P 1 =(x, y) 和 P 2 =(x, － y), 也相交于无穷点 O, 有 P 1 +P 2 +O = O 和 P 1 = － P 2 。 对具有不同的 x 坐标的 Q 和 R 相加 , 在它们之间画一条直线求出第三个交点 P 1 , 这种交点是唯一的。因为 Q+R+P 1 =O, 因此 Q+R= － P 1 对点 Q 加倍 , 画一切线求出另一交点 S, 则 Q+Q=2Q= － S 一条椭圆曲线上的一点 P 被一个正整数 k 相乘的乘法被定义为 k 个 P 的相加 椭圆曲线上的形式加法

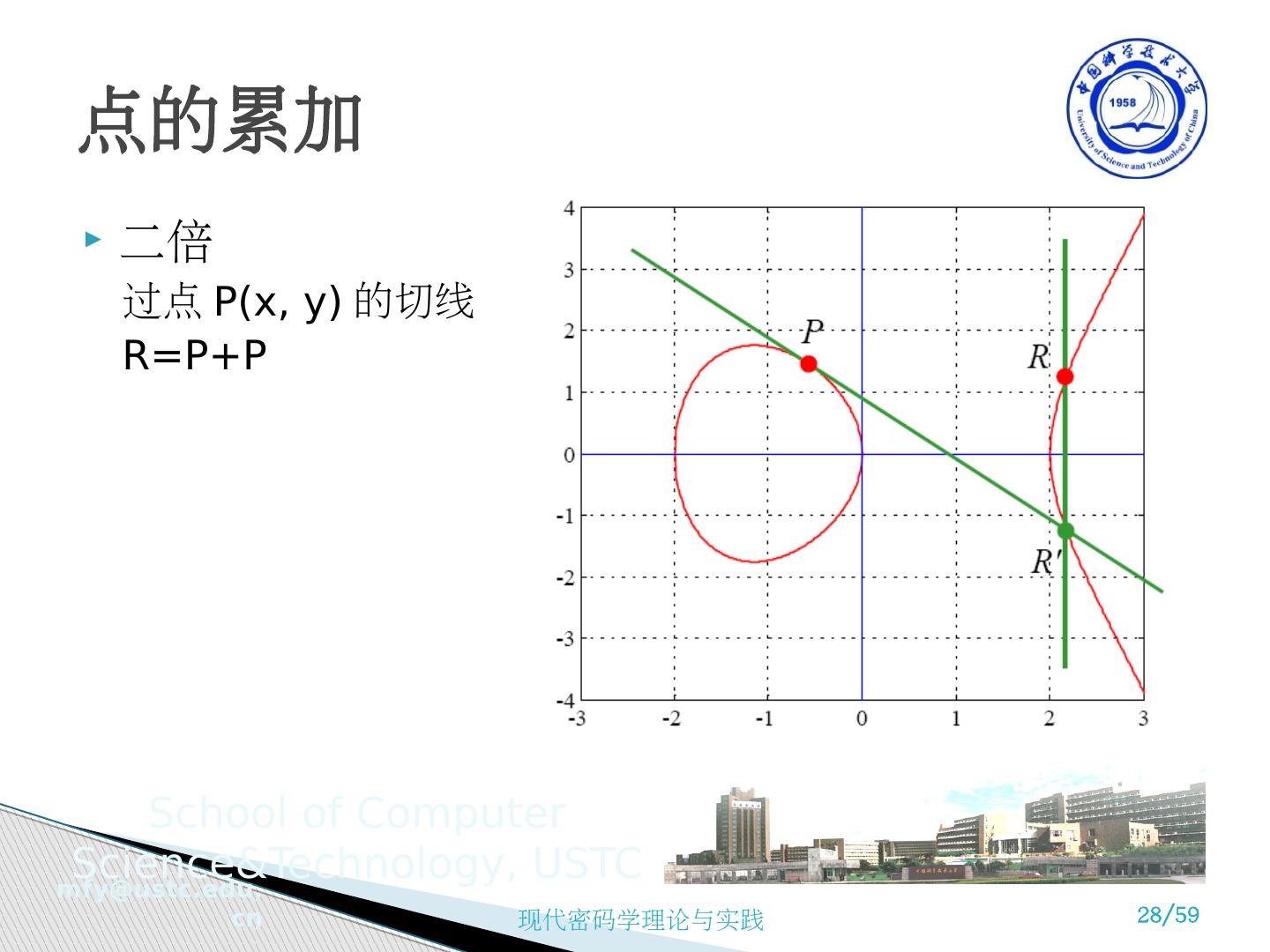
28 .二倍 过点 P(x, y) 的切线 R=P+P 点的累加

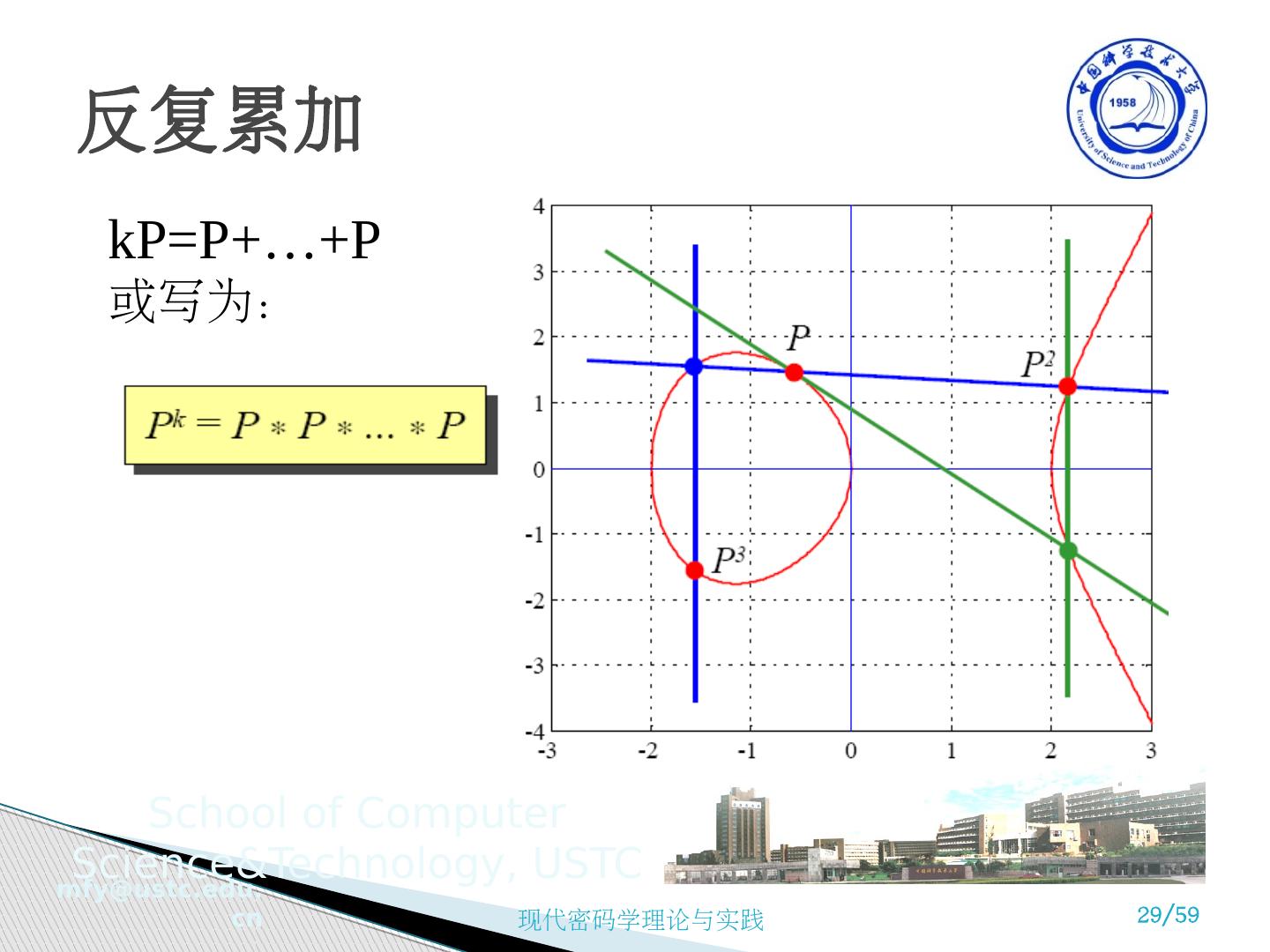
29 .反复累加 kP=P+…+P 或写为：