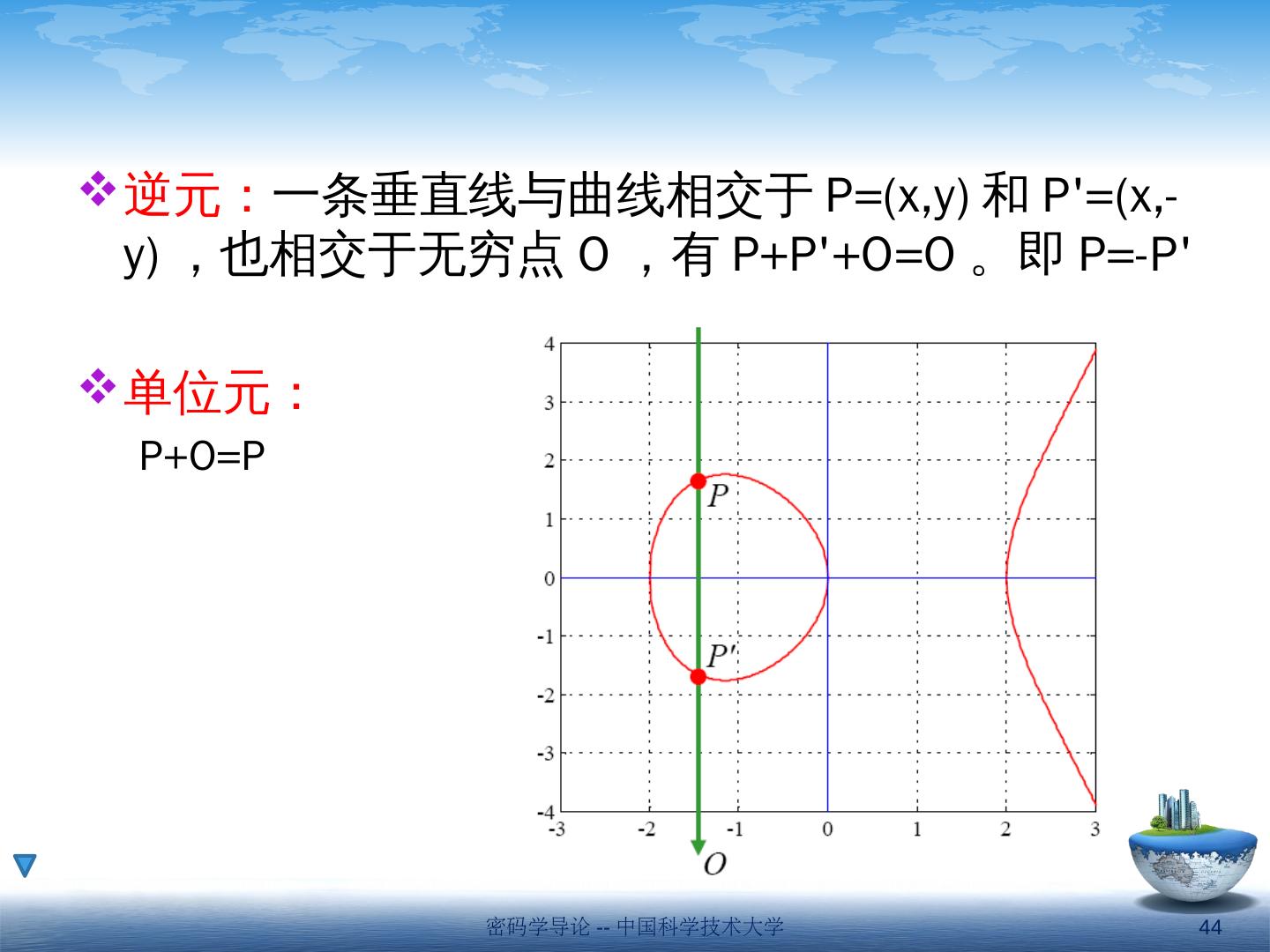
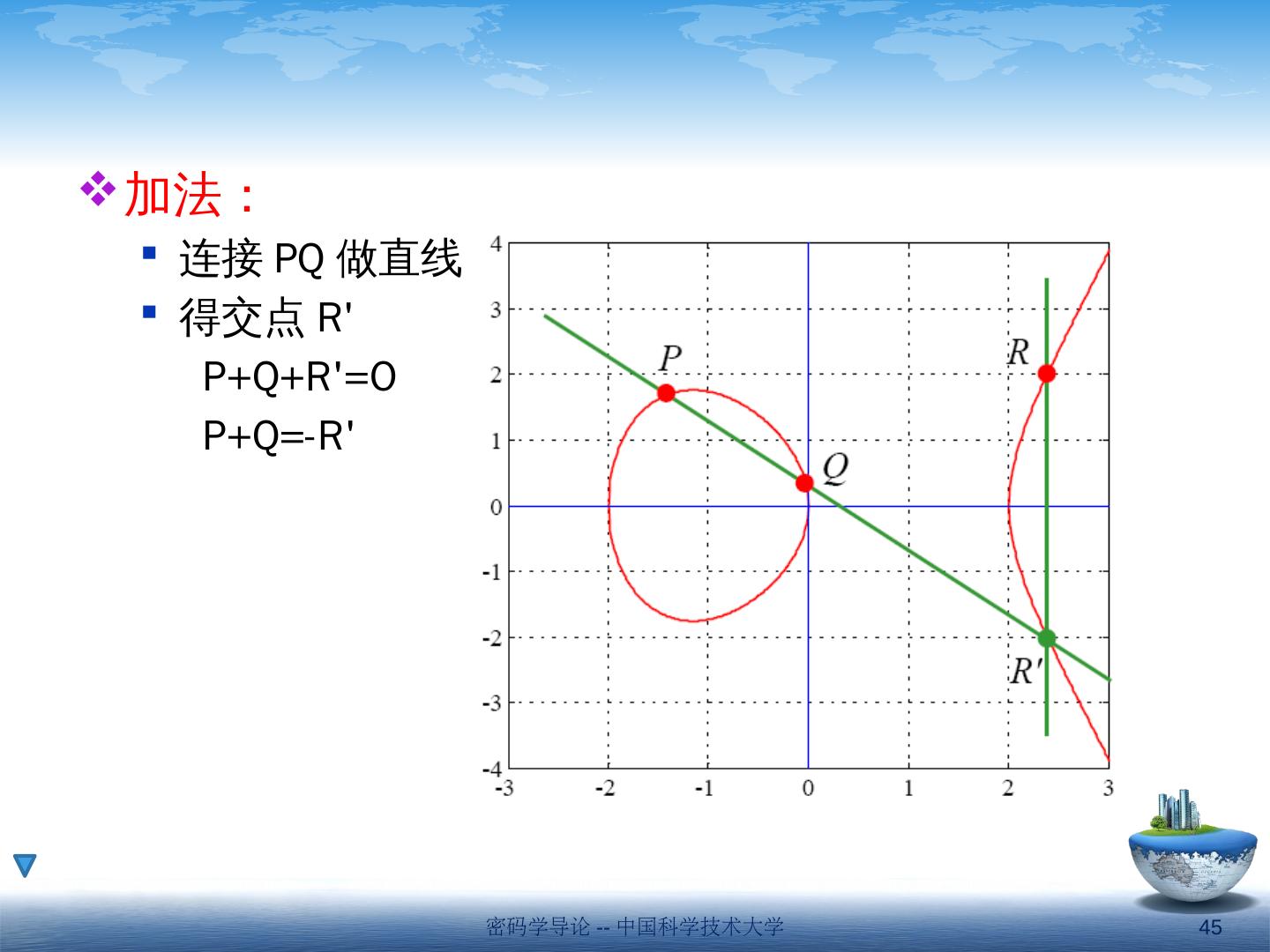
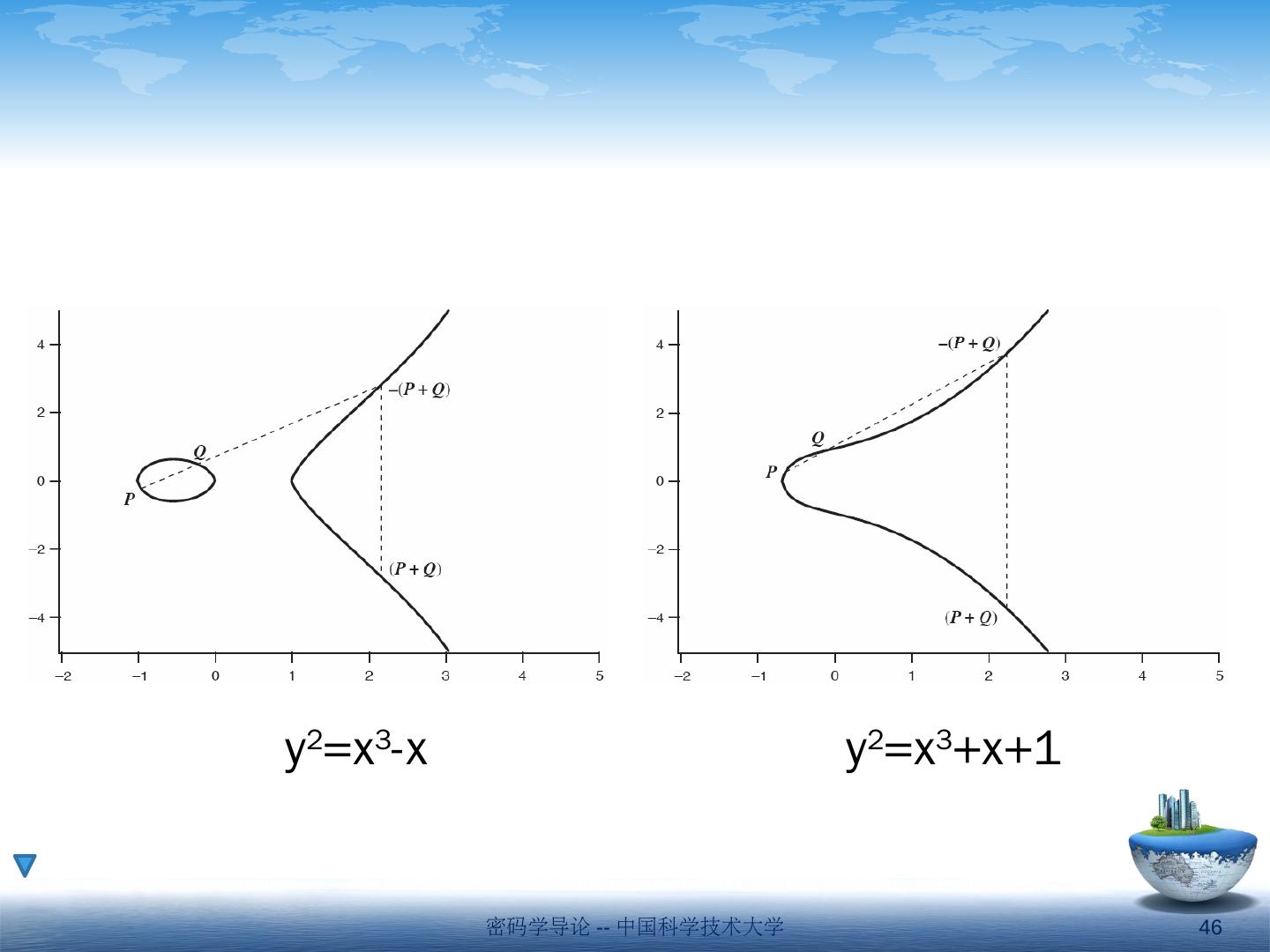
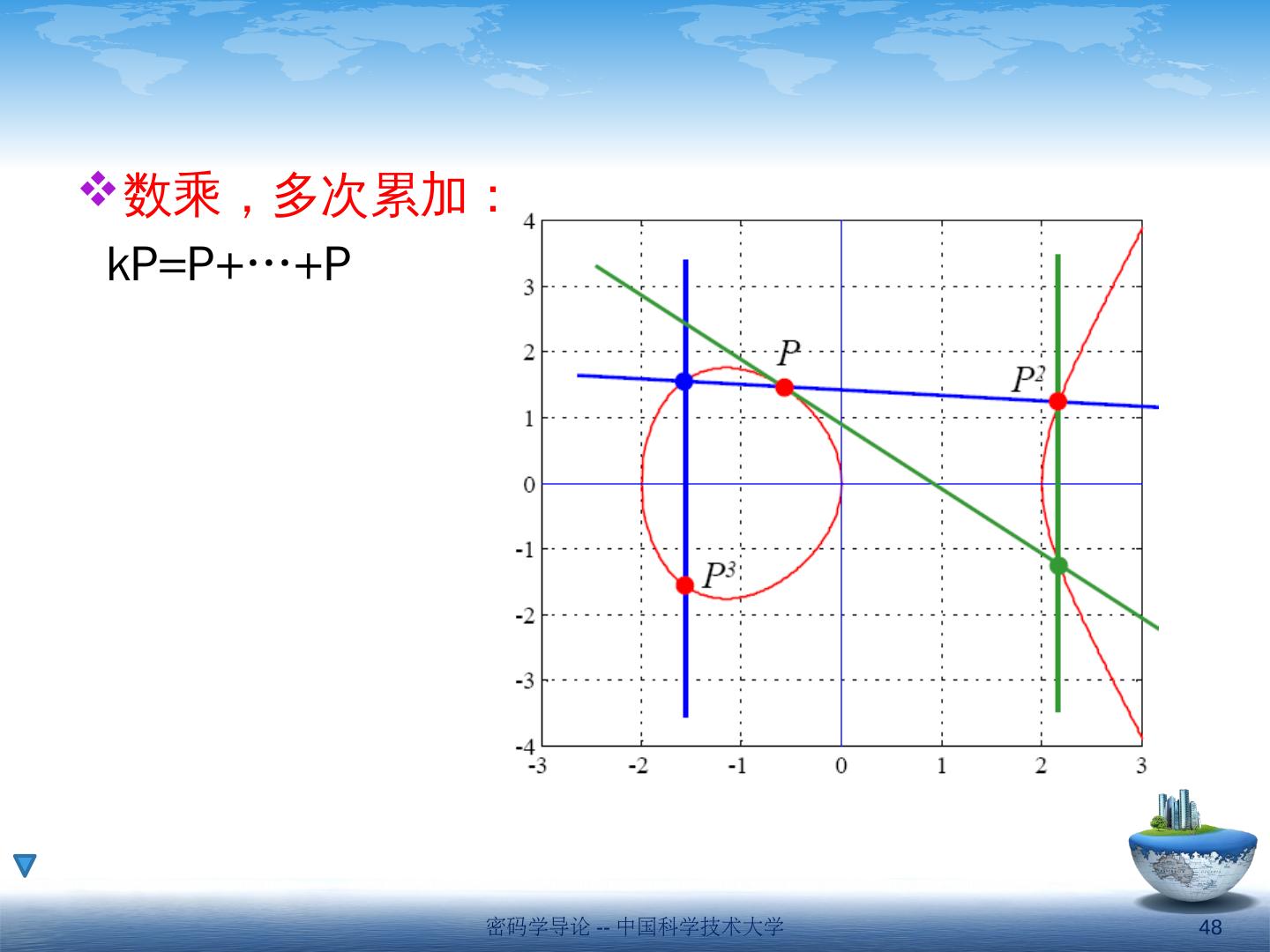
- 快召唤伙伴们来围观吧
- 微博 QQ QQ空间 贴吧
- 文档嵌入链接
- 复制
- 微信扫一扫分享
- 已成功复制到剪贴板
07密码学--公开密钥密码
展开查看详情
1 .密码学 导论˙第 7 章 公开密钥密码 李卫海
2 .本章 内容 密码学导论 -- 中国科学技术大学 2
3 .第一节 公开密钥密码的概念 密码学导论 -- 中国科学技术大学 3
4 .对称密码体制的问题 加密能力与解密能力是捆绑在一起的 能加密即能解密,能解密也能加密 不能 实现数字签名 密钥更换、传递和交换需要可靠信道,密钥分发困难 密钥管理困难 如有 N 用户,则需要 C=N(N-1)/2 个密钥, N=1000 时, C(1000,2)≈500000 无法满足不相识的人之间通信的保密要求 密码学导论 -- 中国科学技术大学 4
5 .对称密码体制的问题 加密能力与解密能力是捆绑在一起的 能加密即能解密,能解密也能加密 不能 实现数字签名 密钥更换、传递和交换需要可靠信道,密钥分发困难 密钥管理困难 如有 N 用户,则需要 C=N(N-1)/2 个密钥, N=1000 时, C(1000,2)≈500000 无法满足不相识的人之间通信的保密要求 密码学导论 -- 中国科学技术大学 4
6 .对称和非对称密钥加密的主要区别 密码学导论 -- 中国科学技术大学 6
7 .非对称密码体制的基本特点 加密能力与解密能力是分开的 从密码算法和加密密钥来确定解密密钥在计算上是不可行的 两个密钥的任何一个都可用来加密,另一个用来 解密。如何使用,取决于需求 密钥分发简单 需要保存的密钥量大大减少, N 个用户只需要 N 个密钥 可满足不相识的人之间保密通信 可以实现数字签名 密码学导论 -- 中国科学技术大学 7
8 .公开密钥密码体制 公钥密码体制的组成 明文:算法的输入,可读信息或数据 加密算法:对明文进行各种转换 公钥和私钥:算法的输入,分别用于加密和解密 每一用户产生一对密钥,用来加密和解密消息 其中 一个密钥(公钥)存于公开的寄存器或其他可访问的文件中;另一密钥(私钥)秘密 保存 密文:算法的输出,依赖于明文和密钥 解密算法:根据密文和密钥,还原明文 密码学导论 -- 中国科学技术大学 8
9 .公钥密码体制的主要应用 保密: Alice 要发消息给 Bob Alice 用 Bob 的公钥对消息加密 C=E( PU b ,m ) Bob 收到消息后,用其私钥对消息解密 M=D( PR b ,C ) 只有 Bob 知道自身的私钥,其他接收者均不能解密消息 密码学导论 -- 中国科学技术大学 9
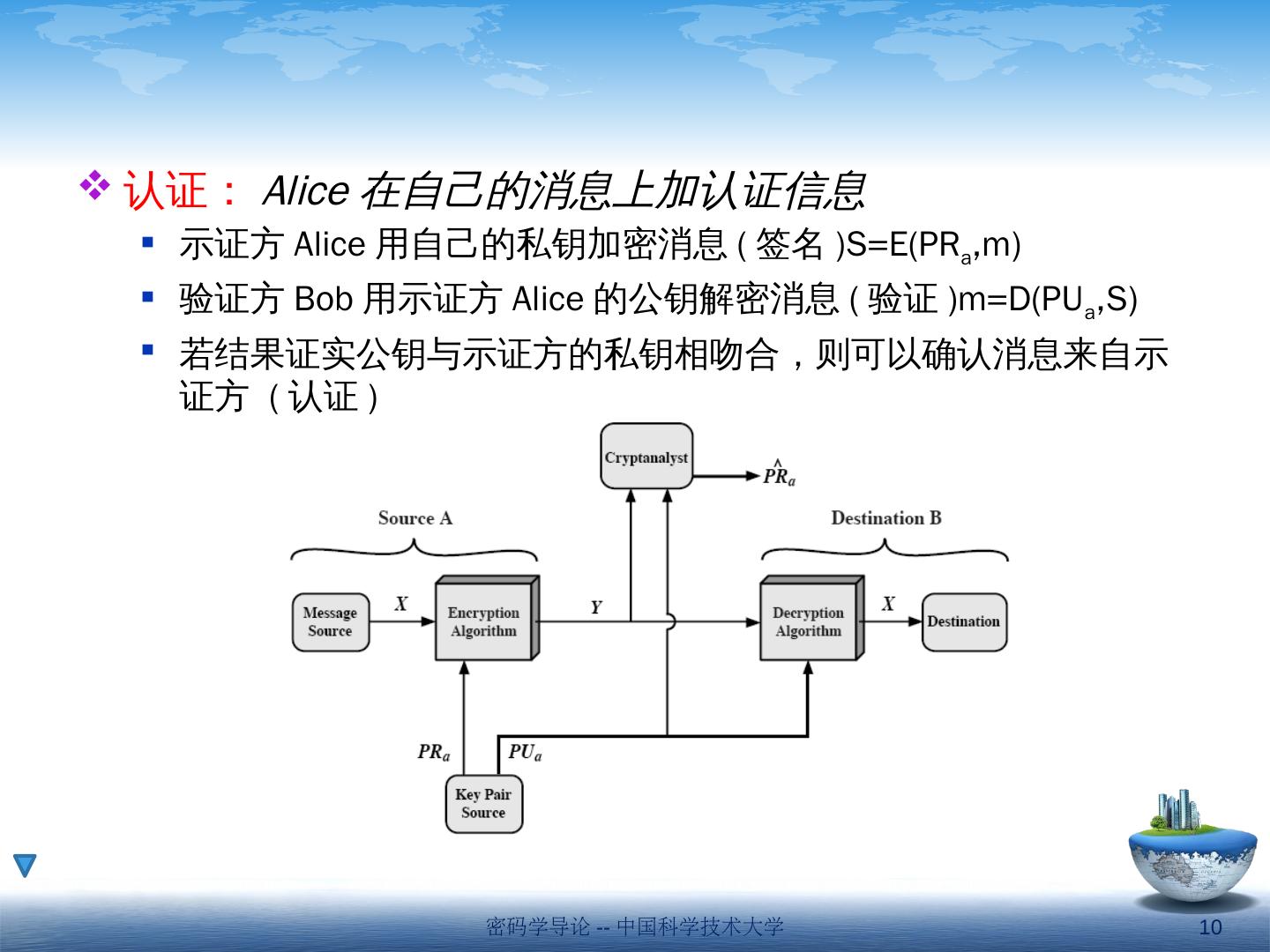
10 .认证 : Alice 在 自己的消息上加认证信息 示证 方 Alice 用 自己的私钥加密消息 ( 签名 )S=E( PR a ,m ) 验证 方 Bob 用 示证 方 Alice 的 公钥解密消息 ( 验证 )m=D( PU a ,S ) 若结果证实公钥与示证方的私钥相吻合,则可以确认消息来自示证方 ( 认证 ) 密码学导论 -- 中国科学技术大学 10
11 .即保密又认证: 把保密 和 认证过程结合起来 密钥交换 : 例如 Diffie -Hellman C = E( PU b , D( PR a , m)) m = E( PU a , D( PR b , C)) 密码学导论 -- 中国科学技术大学 11
12 .对公开密钥密码编码系统的要求 计算是容易的 产生一对密钥 ( 公钥 k e 和私钥 k d ) 在计算上是容易的 不难计算 C=E( k e ,m ) 和 m=D( k d ,C ) 分析是不可行的 知道 k e , 计算 k d 不可行 不知道 k d ,即使知道 k e , E, D 及 C ,计算 m 不可行 加密变换和解密变换可以互换顺序 即 D(E(m))=E(D(m)) 密码学导论 -- 中国科学技术大学 12
13 .公钥密码的 常规 分析 公钥密码易受 穷举密钥 攻击 解决方法是使用长密钥 同时为了便于实现加密和解密,又希望密钥足够短 目前仅限于密钥管理和签名 从给定的公钥 计算 出私钥是第二种攻击方法 多数公钥算法尚未在数学上证明可以抵抗这种攻击 穷举消息 攻击是第三种攻击形式 攻击者用公钥对所有可能的消息加密,并与传送的密文匹配,从而解密任何消息 抵抗的方法是在要发送的消息后附加随机数。 密码学导论 -- 中国科学技术大学 13
14 .第二节 RSA 公开密钥标准 密码学导论 -- 中国科学技术大学 14
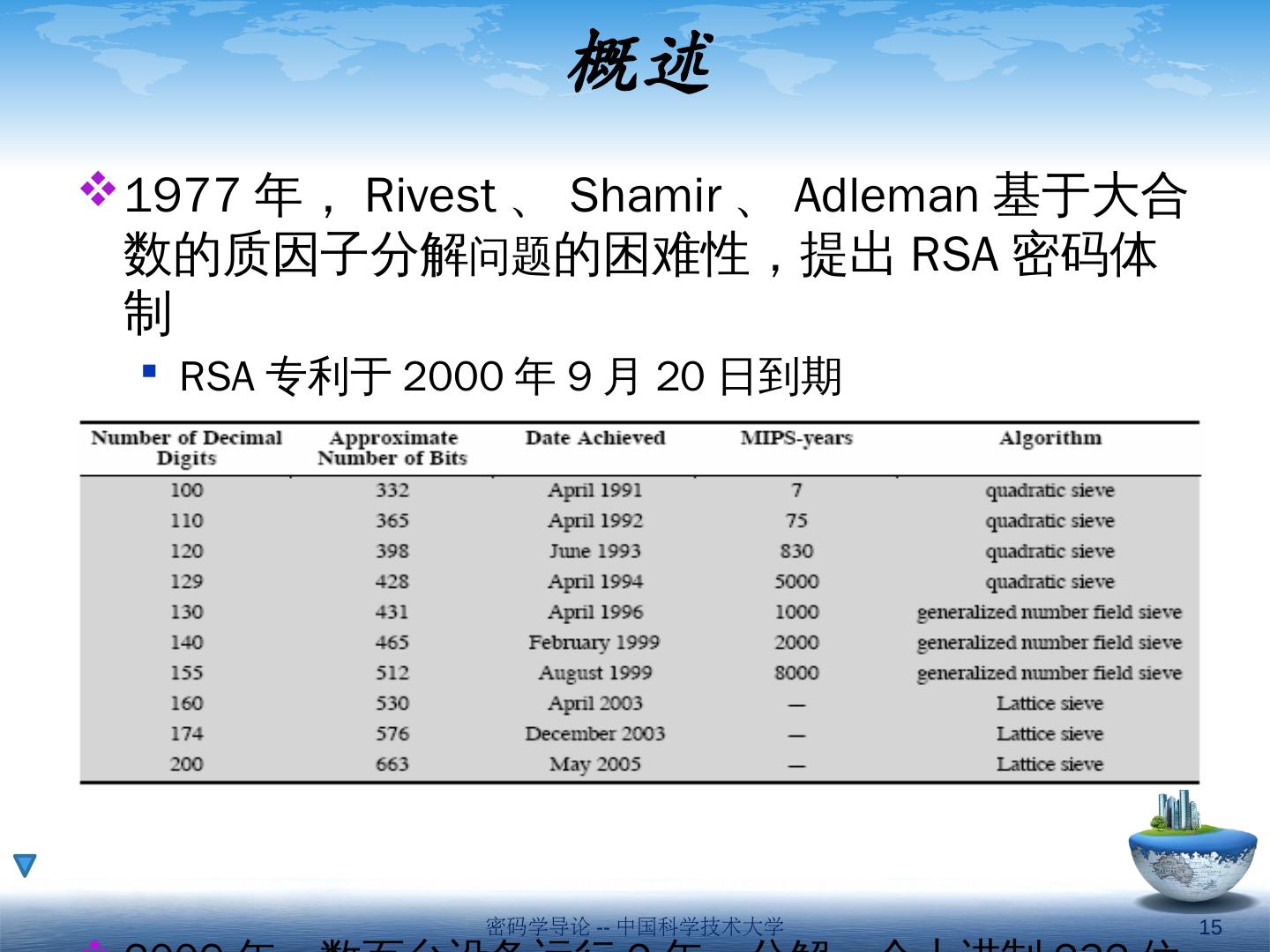
15 .概述 1977 年, Rivest 、 Shamir 、 Adleman 基于大合数的质因子分解 问题 的困难 性,提出 RSA 密码体制 RSA 专利于 2000 年 9 月 20 日到期 2005 年已能分解十进制 200 位的大合数 2009 年,数百台设备运行 2 年,分解一个十进制 232 位大数 密码学导论 -- 中国科学技术大学 15
16 .RSA 算法满足公开密钥加密的要求,基本思路: 找到适当的 e,d,n ,使得对所有 m<n 有 m ed mod n=m 对于所有 m<n 的值,要计算 m e 和 C d 是相对容易的 在给定 e 和 n 时,计算出 d 是不可行的 几个关系 m p-1 mod p=1 , m k (p-1)+1 mod p=m ed =k(p-1)+1 ? ed =1 mod (p-1) p 必须公开, p-1 也是公开的。由 e 计算 d 是容易的 m Φ (n) mod n=1 , m k Φ (n )+1 mod n=m ed = k Φ (n)+ 1 ? ed =1 mod Φ (n) n 是公开的,但由 n 计算 Φ (n ) 是困难的 密码学导论 -- 中国科学技术大学 16
17 .RSA 算法流程 随机选择两个秘密大质数 p 和 q 计算公开模数 n=p*q 计算秘密的欧拉指数函数 Φ (n)=(p-1)(q-1) 选择一个与 Φ (n) 互素的数,作为 e 计算 e 模 Φ (n) 的乘法逆元素,作为 d 公开密钥 PU={ e,n } ;私有密钥 PR={ d,n } 加密: C = m e mod n 解密: m = C d mod n = m ed mod n = m 密码学导论 -- 中国科学技术大学 17
18 .18 例: p=17,q=11,e=7 n= pq =17×11=187, Φ (n)=(p-1)(q-1)=16×10=160 选择 e=7, gcd (7,160)=1, 23×7=161 , 所以 d=23 公钥 PU={7,187} , 私钥 PR={23,187} 消息 m =88 加密计算 C=88 7 mod 187=11 解密计算 m =11 23 mod 187=88
19 .注意: 在欧拉定理中, m Φ (n) =1 mod n 要求 gcd ( m,n )=1 ,即要求 m 不能被 p 或 q 整除。那么 p 或 q 的倍数能否不能出现在明文中? 从解密角度考虑 由费马定理, q p-1 mod p =1 ,即 q Φ (n) mod p =1 则 q Φ (n) -1 = kp 两边同乘 q ,有 q Φ (n )+1 - q = kpq ,即 q Φ (n )+1 mod n =q 考虑任意 m= bq , gcd ( b,n )=1, 有 ( bq ) Φ (n)+1 mod n = bq 当明文是 p 或 q 的 倍数时,仍可以正确解密 m 不能是 0 、 ±1 ,否则密文就是明文( e 必为奇数) 密码学导论 -- 中国科学技术大学 19
20 .实现方面的考虑 加密与解密 模指数运算,可通过下面两个手段减少运算量 模运算特性 [(a mod n) op (b mod n)] mod n = (a op b) mod n 快速指数算法 公钥的有效 运算 e 常选 65537( 即 2 16 +1) :仅有两个比特为 1 ,乘法 次数最小 若先选择 e ,再选择 p,q ,则为 保证 gcd (e, Φ (n))= 1 , 选择 p,q 时 应保证 gcd (e,p-1 )= gcd (e,q-1)= 1 密码学导论 -- 中国科学技术大学 20
21 .e 有时也选 3 或 17 。但过小的 e 容易受到攻击 例如:假设有三个用户的 e 都选择 3 ,但模数分别为 n 1 ,n 2 ,n 3 若要向他们发送 m ,密文分别为 C 1 =m 3 mod n 1 , C 2 =m 3 mod n 2 , C 3 =m 3 mod n 3 各用户的素数是随机生成的,因此模数 n 1 ,n 2 ,n 3 两两互素的可能很大 由中国剩余定理可以计算 C=CRT(n 1 ,n 2 ,n 3 ,C 1 ,C 2 ,C 3 ) 显然有 C=m 3 mod n 1 n 2 n 3 由 RSA 算法规则, m< n i , 因此 m 3 < n 1 n 2 n 3 因而可以直接计算 m=C 1/3 密码学导论 -- 中国科学技术大学 21
22 .私钥的有效运算 运用中国剩余定理简化运算:求 m=C d mod n 计算: X p =q×(q -1 mod p), X q =p×(p -1 mod q) 定义: V p = C d mod p= C d mod (p-1) mod p V q =C d mod q=C d mod (q-1) mod q 则 m=( V p X p +V q X q ) mod n 比直接运算 m=C d mod n 快 4 倍 密码学导论 -- 中国科学技术大学 22
23 .RSA 的安全性 有四种可能的对 RSA 的攻击方法 穷举攻击: 尝试所有可能的密钥 数学攻击: 对两个素数乘积的因子分解 (FAC 问题 ) 计时攻击: 依赖于解密算法的运行时间 选择密文攻击: 利用了 RSA 算法的性质 密码学导论 -- 中国科学技术大学 23
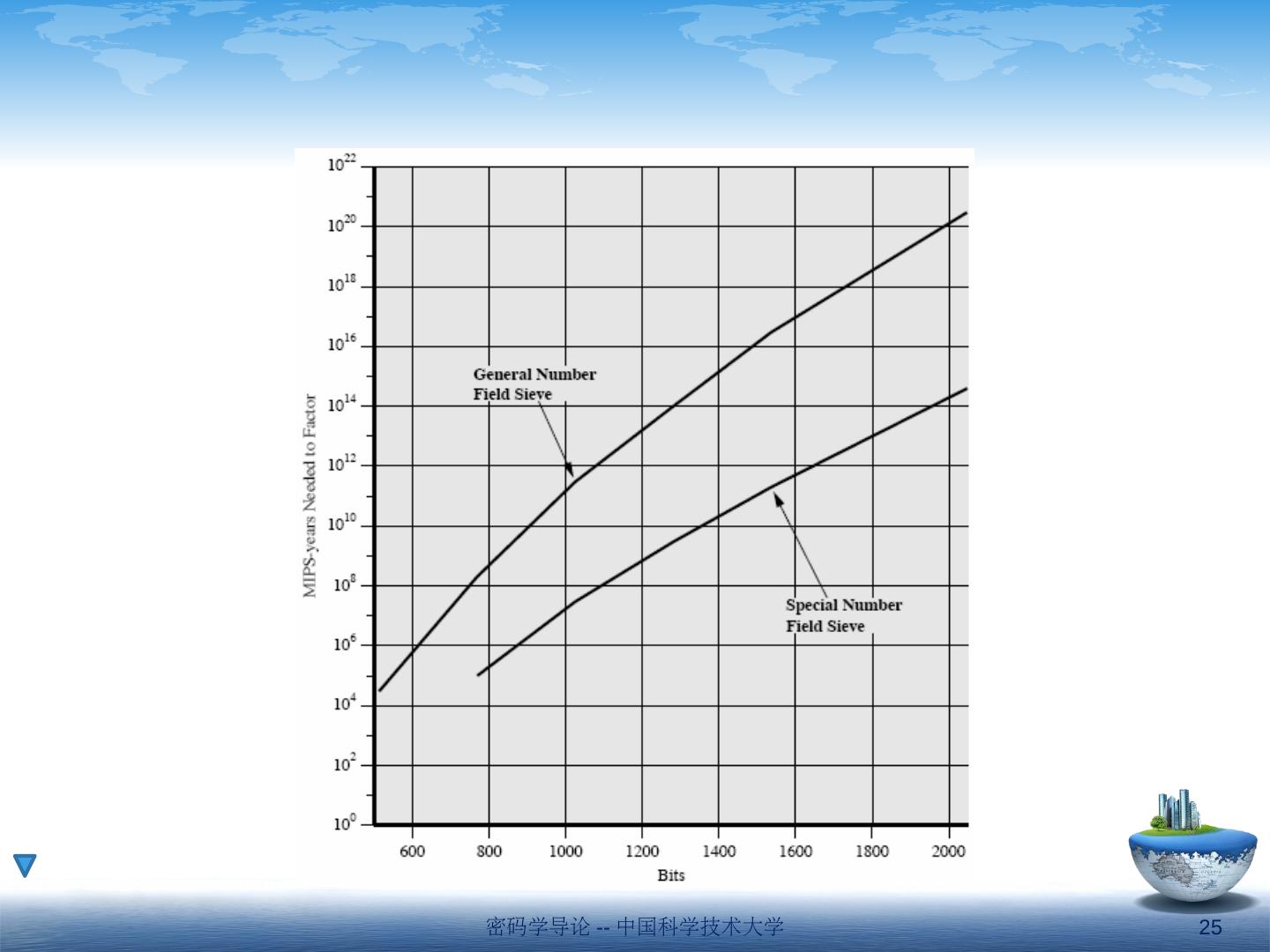
24 .数学攻击 数学攻击: 分解 n 为两个素数 p,q ,并进而求出 d 直接找出 Φ (n) ,并进而求出 d 直接找出 d RSA 的安全性问题依赖于大合数的素因子分解,即 factorization problem (FAC) 2005 年分解了 200 位十进制(约 664 bits )大合数 2009 年分解了 232 位十进制( 768 bits )大合数 当前,密钥应选取 1024 或 2048 位 密码学导论 -- 中国科学技术大学 24
25 .密码学导论 -- 中国科学技术大学 25
26 .p 和 q 的选取约束 p 和 q 应该是随机的,且不包含在素数表中 总可以查表或遍历特殊形式的素数 强 素数 p : p-1 有一个大的素因子 r p+1 有一个大的素因子 r-1 有一个大的素因子 p 和 q 大小不能太接近 否则 p 和 q 接近 n 1/2 ,容易被穷举攻击 选择 p 和 q 在长度上有几个比特差异是可行的 密码学导论 -- 中国科学技术大学 26
27 .(p-1) 和 (q-1) 都应有一个不相等的大素因子 可能存在基于重复加密的攻击: c e ,( c e ) e ,… 若 c e t ≡ c (mod n) ,则 c e t-1 ≡ m (mod n) ,即 m e t -1 =m (mod n) 当 (p-1) 和 (q-1) 都有一个不相等的大素因子时,这种攻击可以忽略 GCD(p-1 , q-1) 应该较小 d>n 1/4 若 d<n 1/4 ,则可以用 Wiener 攻击在多项式时间内分解 n “Cryptanalysis of short RSA secret exponents”, 1990. 密码学导论 -- 中国科学技术大学 27
28 .先 找出 Φ (n) , 再分解 n p 和 q 是方程 x 2 -( p+q ) x+pq =0 的根 pq =n 若找到 Φ (n) , Φ (n )=(p-1)(q-1)=n-( p+q )+1 则方程为 x 2 -[ n- Φ (n)+1] x+n =0 密码学导论 -- 中国科学技术大学 28
29 .先 找出 Φ (n) , 再分解 n p 和 q 是方程 x 2 -( p+q ) x+pq =0 的根 pq =n 若找到 Φ (n) , Φ (n )=(p-1)(q-1)=n-( p+q )+1 则方程为 x 2 -[ n- Φ (n)+1] x+n =0 密码学导论 -- 中国科学技术大学 28