06密码学--序列密码

1 .密码学 导论˙第 6 章 序列 密码 李卫海

2 .本章内容 密码学导论 -- 中国科学技术大学 2

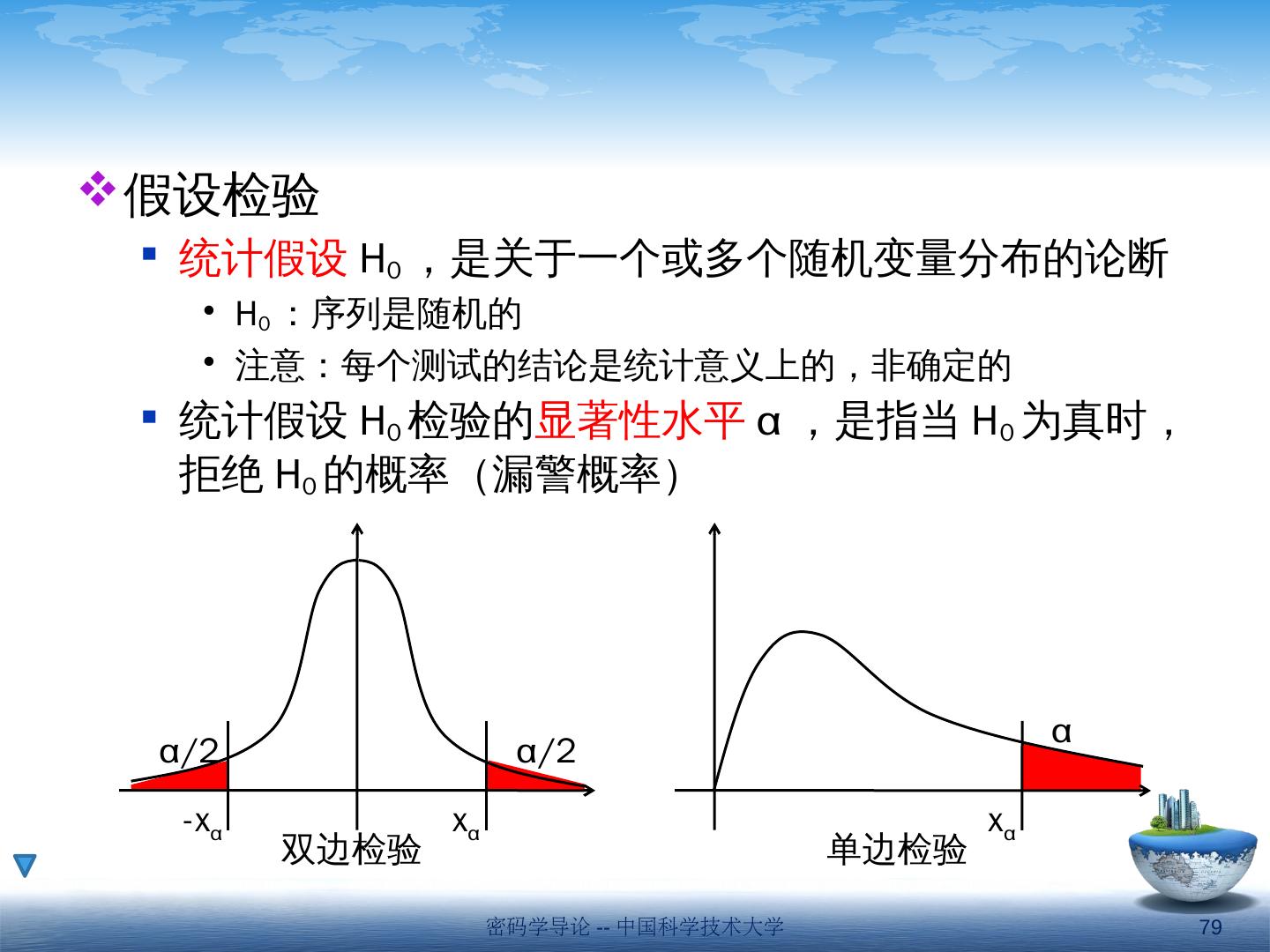
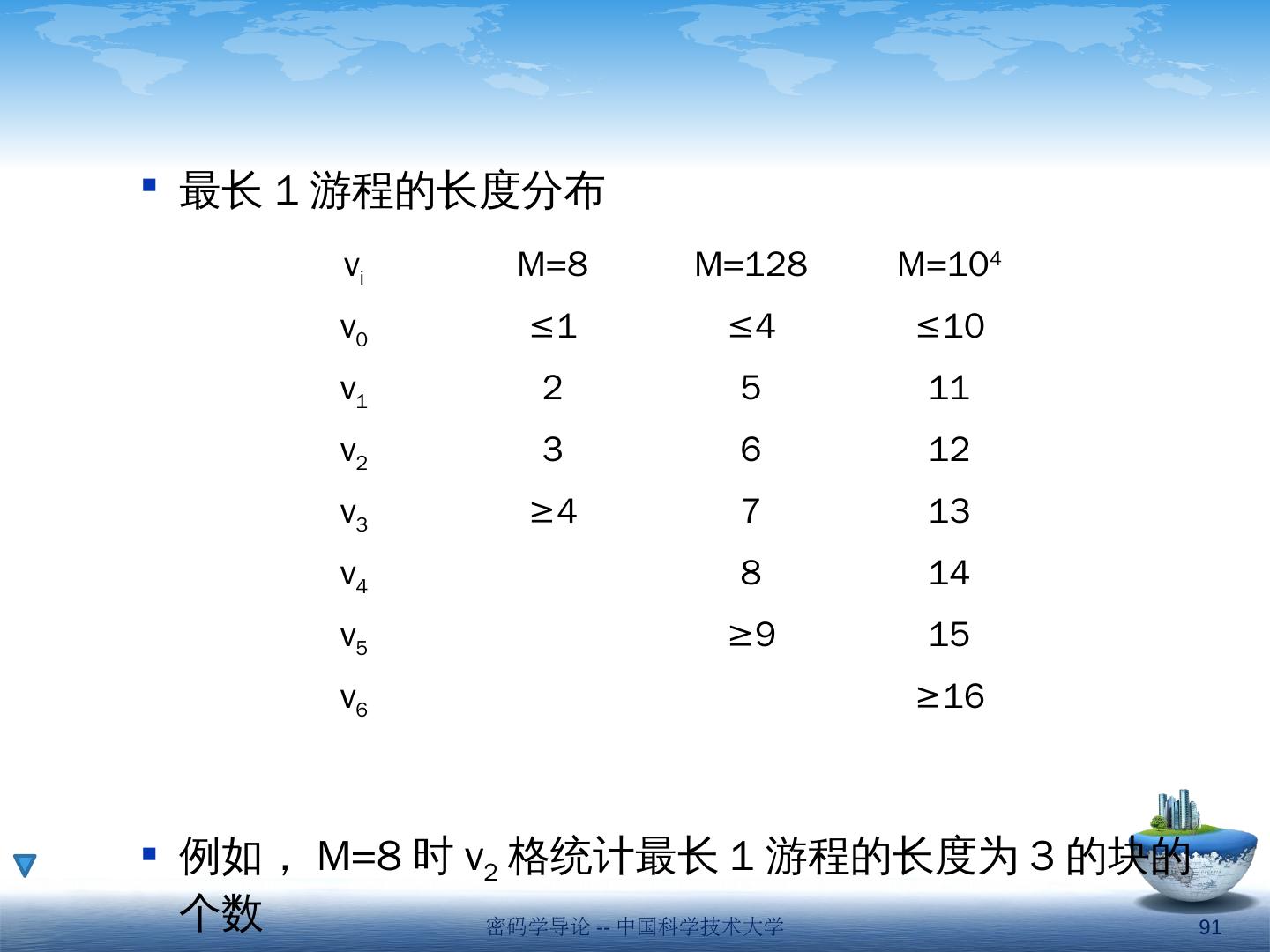
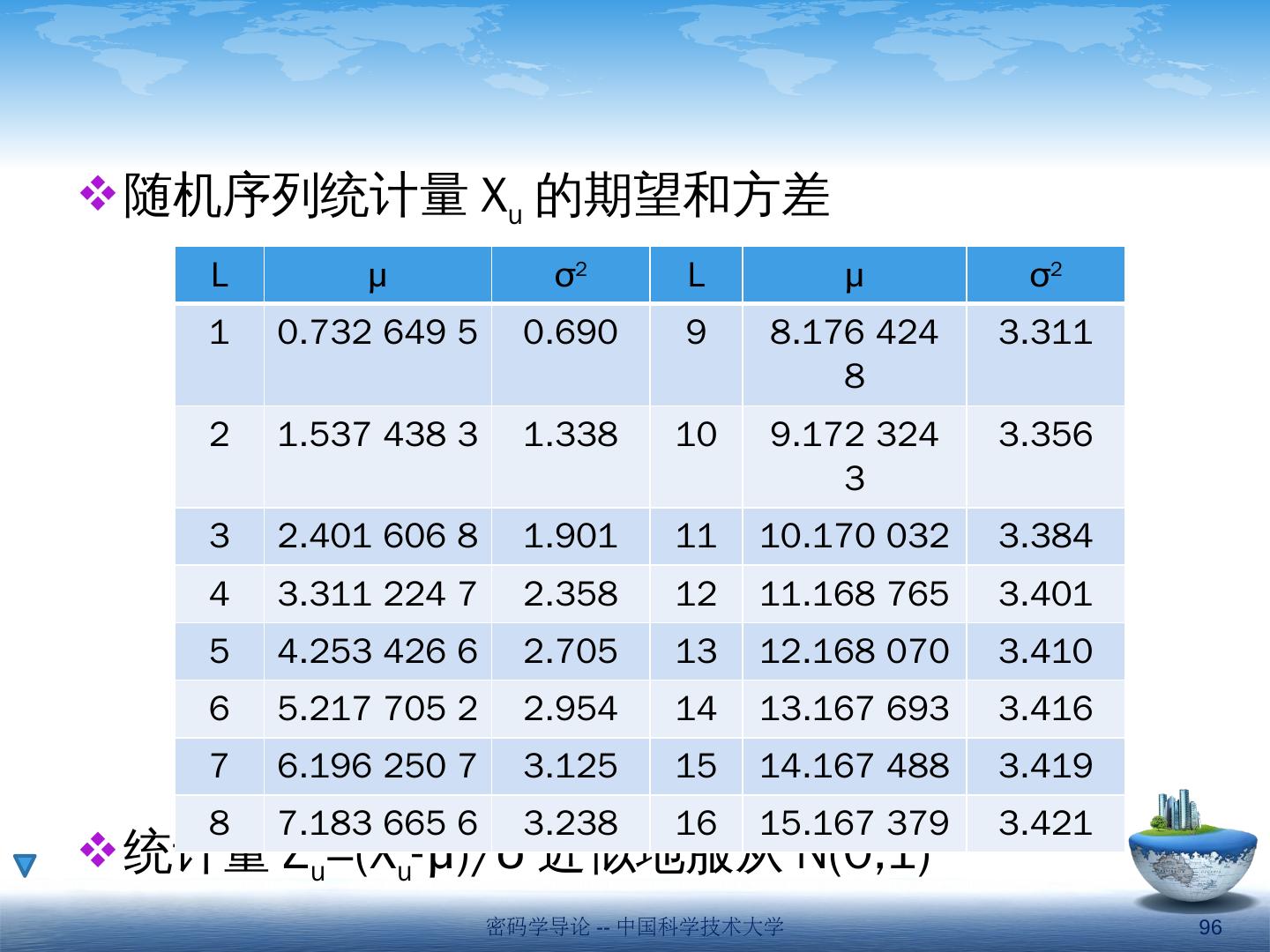
3 .第一节 序列密码的概念 密码学导论 -- 中国科学技术大学 3

4 .序列密码 ， 又 称流密码 ，它逐个比特处理信息 典型流密码体制 使用 （伪）随机数序列 做加密密钥流 加密、解密算法 加密密钥流与明文流按比特异或 C i = M i  StreamKey i 密钥 K 密钥 K 伪随机数发生器 k 加密 伪随机数发生器 k 解密 明文码流 M 明文码流 M 密文码流 C 密码学导论 -- 中国科学技术大学 4

5 .明文信息中的统计特征被流密钥的随机性所掩盖 加密算法极为简单！！ 加解密简单，速率极快 密钥流严格不可重复使用 已知明文攻击可以轻易获得密钥流 关键在设计一个好的伪随机数发生器 设计优良的流密码可以具有与分组密码相当的安全性 密码学导论 -- 中国科学技术大学 5

6 .流密码的一些设计准则 密码学导论 -- 中国科学技术大学 6

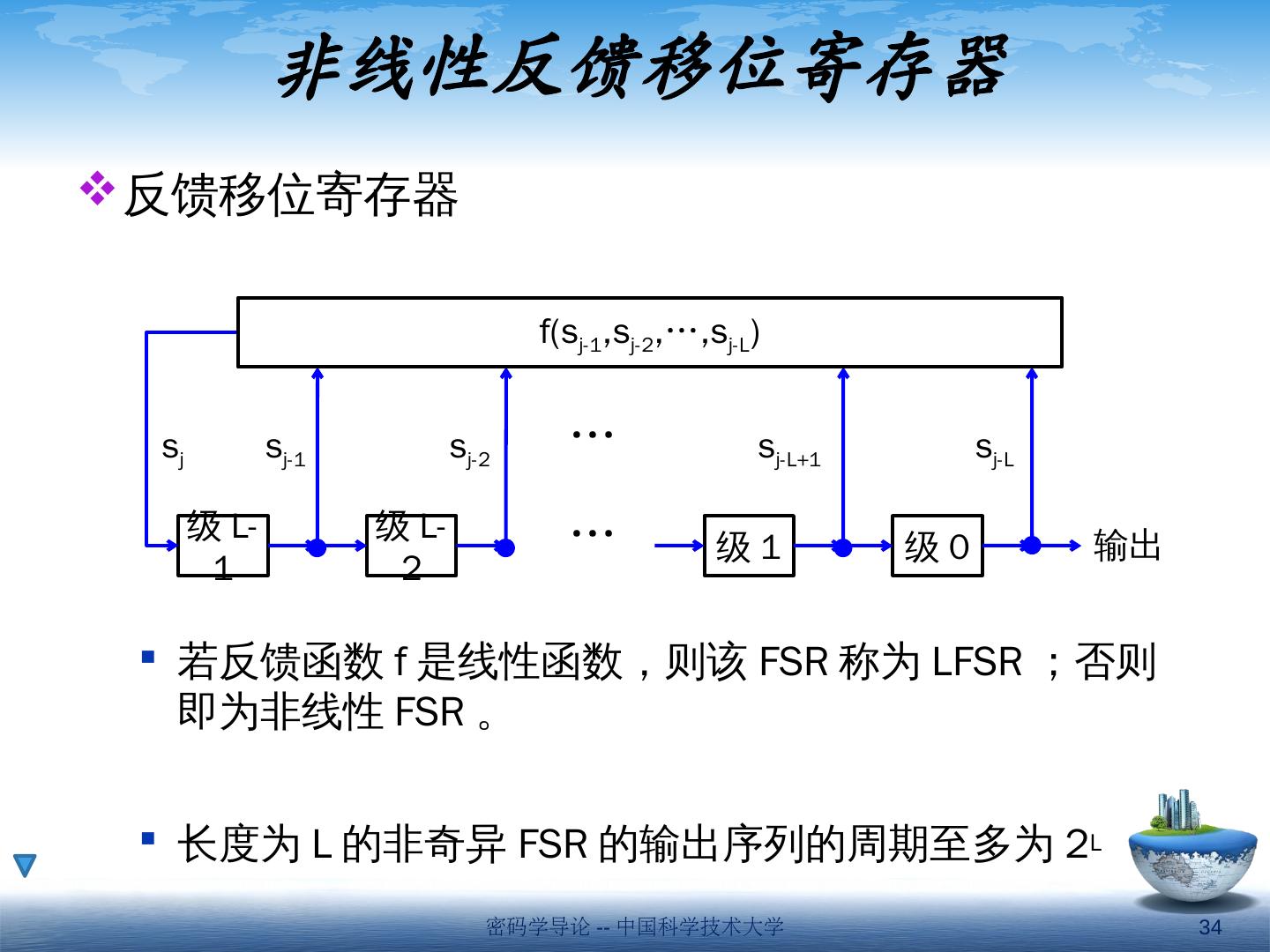
7 .多数流密码的基本构造模块为 反馈移位寄存器 FSR 特别是 线性反馈移位寄存器 LFSR 寄存器存储当前状态，流密码有时也称为状态密码 流密码通常可分为同步和自同步两类 同步流密钥 ： 通信双方需要密钥严格同步 同步被破坏时，密文无法解密 自同步流密钥 ： 同步被破坏时，可以自动重建，正确解密 密码学导论 -- 中国科学技术大学 7

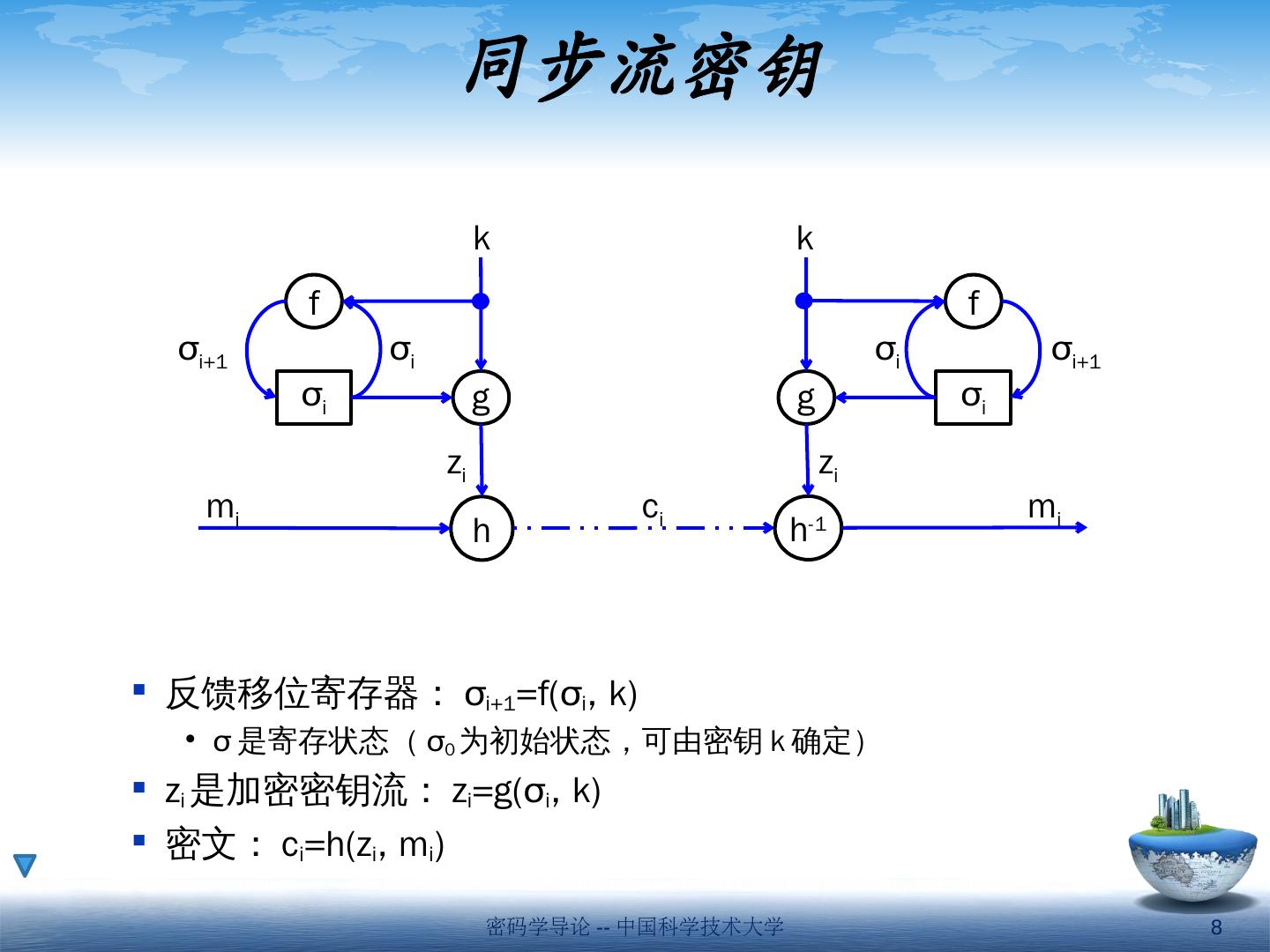
8 .同步流密钥 反馈移位寄存器： σ i+1 =f( σ i , k) σ 是寄存状态（ σ 0 为初始状态，可由密钥 k 确定） z i 是加密密钥流： z i =g( σ i , k) 密文： c i =h( z i , m i ) f g σ i h σ i+1 z i k m i σ i h -1 g z i σ i f σ i σ i+1 k m i c i 密码学导论 -- 中国科学技术大学 8

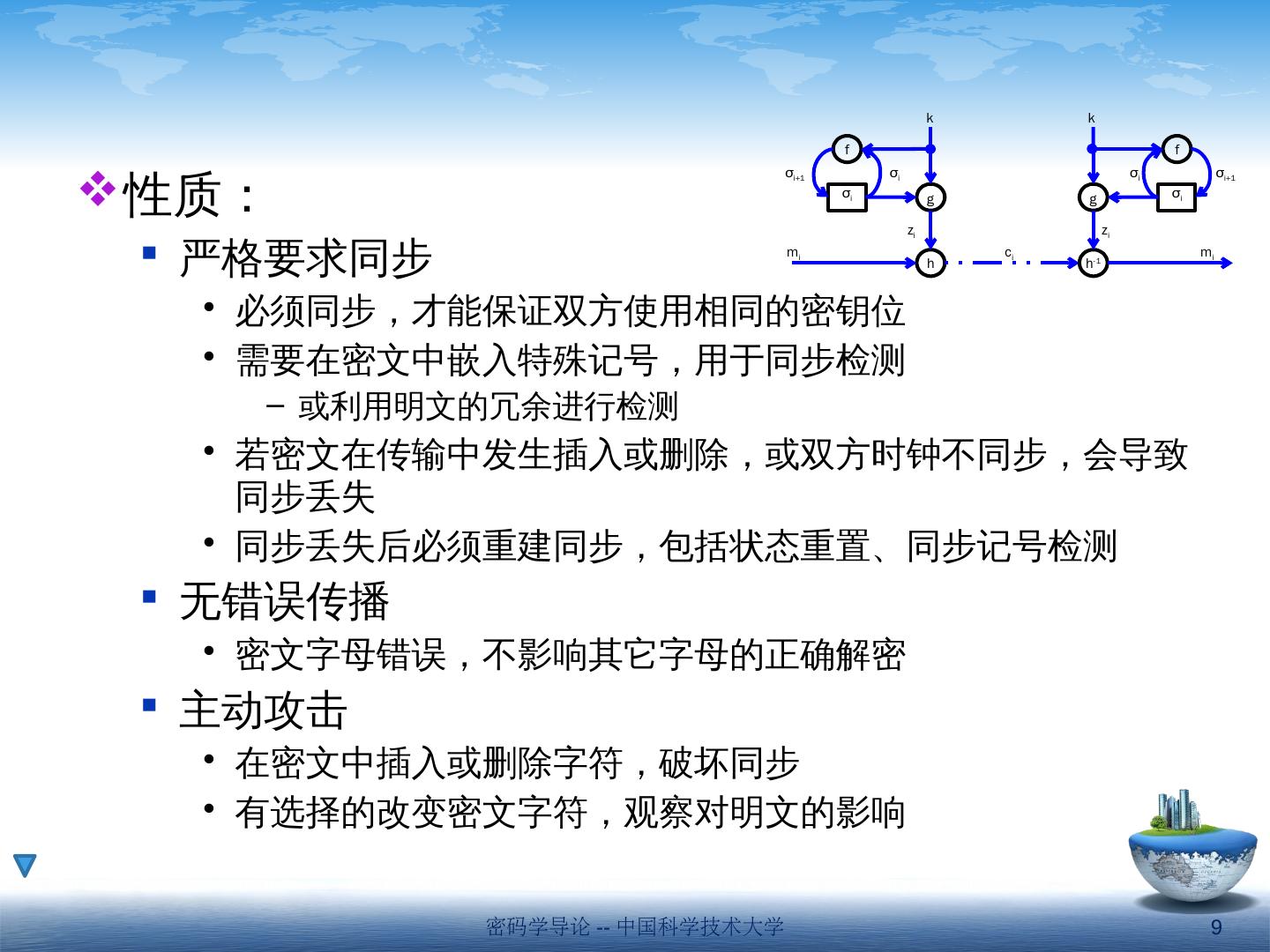
9 .性质： 严格要求同步 必须同步，才能保证双方使用相同的密钥位 需要在密文中嵌入特殊记号，用于同步检测 或利用明文的冗余进行检测 若密文在传输中发生插入或删除，或双方时钟不同步，会导致同步丢失 同步丢失后必须重建同步，包括状态重置、同步记号检测 无错误传播 密文字母错误，不影响其它字母的正确解密 主动攻击 在密文中插入或删除字符，破坏同步 有选择的改变密文字符，观察对明文的影响 f g σ i h σ i+1 z i k m i σ i h -1 g z i σ i f σ i σ i+1 k m i c i 密码学导论 -- 中国科学技术大学 9

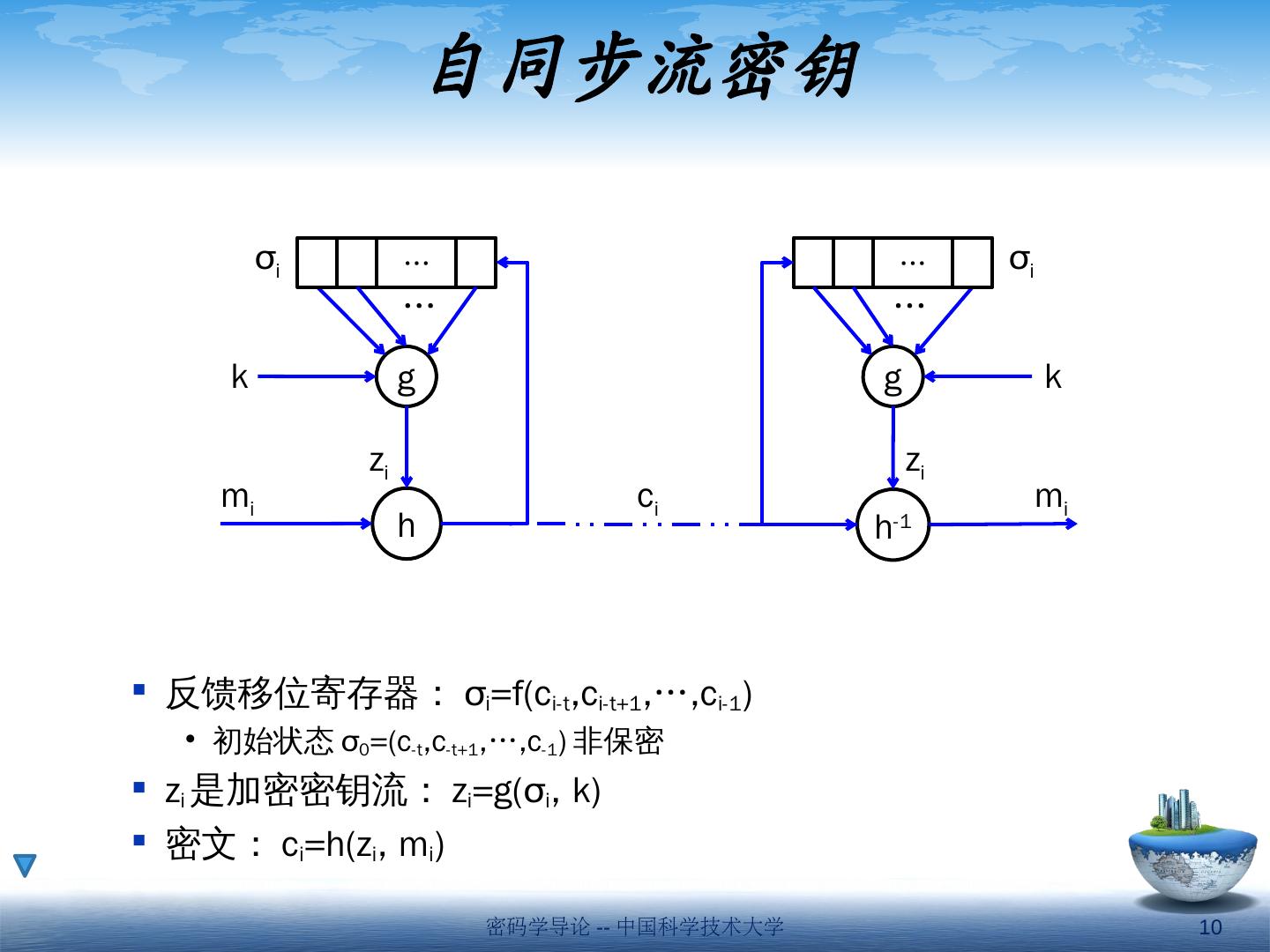
10 .自同步流密钥 反馈移位寄存器： σ i =f(c i-t ,c i-t+1 ,…,c i-1 ) 初始状态 σ 0 =( c -t ,c -t+1 ,…,c -1 ) 非保密 z i 是加密密钥流： z i =g( σ i , k) 密文： c i =h( z i , m i ) g h z i k m i h -1 g z i k m i c i … … … … σ i σ i 密码学导论 -- 中国科学技术大学 10

11 .性质： 自同步 状态仅依赖以前的 t 个密文。同步丢失时，再接收 t 个密文即可自动恢复同步 有限的错误传播 当单个密文出错（或插入、删除）时，除当前明文字符错误外，之后最多会有 t 个解密明文错误 主动攻击 对密文的修改，会引发后面一些字符解密错误，增加了被解密器发现的可能性 自同步特性使得解密器发现主动攻击的可能性降低，因而需要附加技术来保证数据完整性 明文统计扩散 每个明文字符会影响其后的整个密文 g h z i k m i h -1 g z i k m i c i … … … … σ i σ i 密码学导论 -- 中国科学技术大学 11

12 .第二节 反馈移位寄存器 密码学导论 -- 中国科学技术大学 12

13 .一、线性反馈移位寄存器 LFSR 优点： 非常适合于硬件实现 可以产生大周期序列 可以产生具有良好统计性质的序列 易于利用代数方法对其进行分析 密码学导论 -- 中国科学技术大学 13

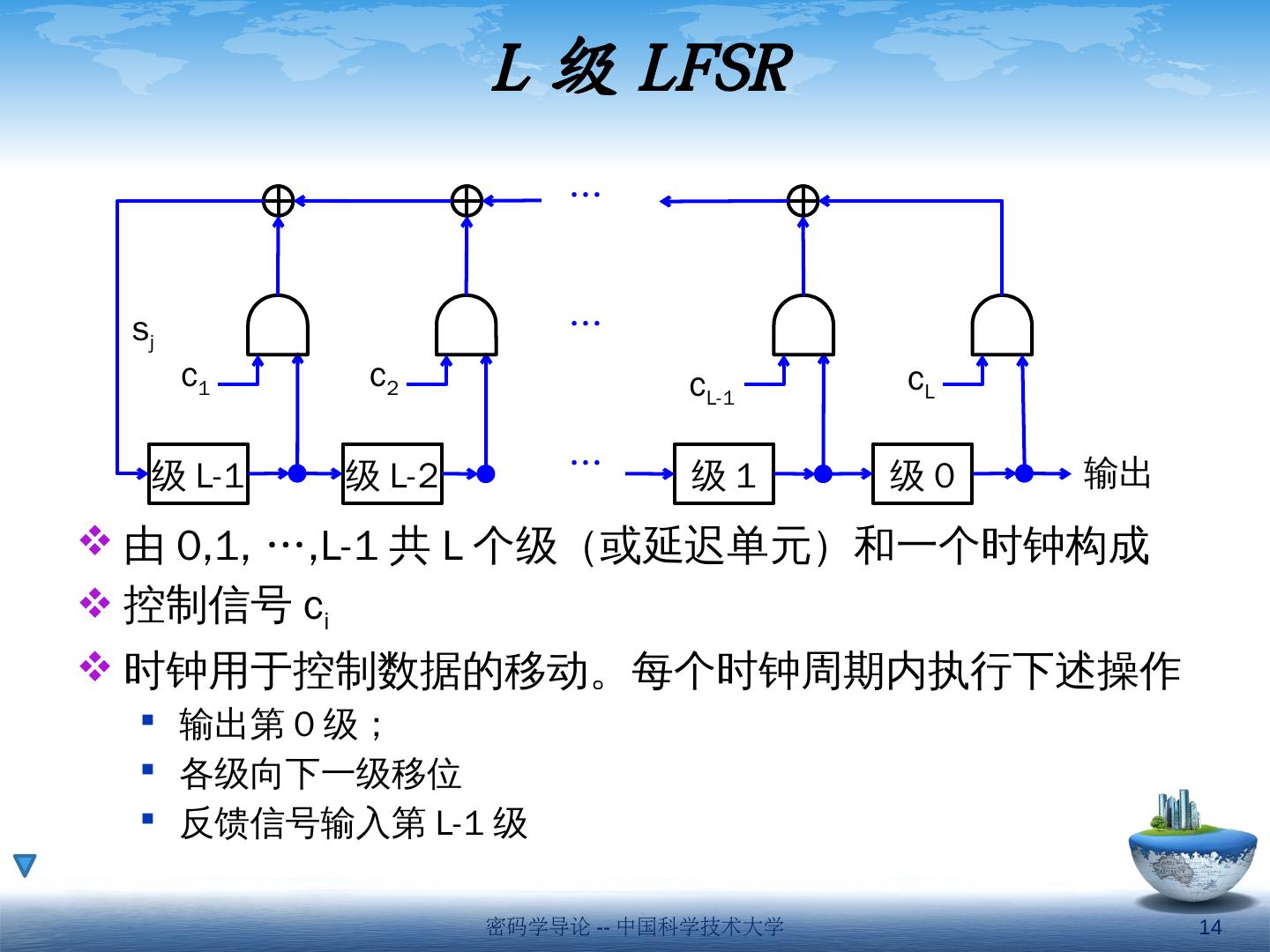
14 .L 级 LFSR 由 0,1, …,L-1 共 L 个级（或延迟单元）和一个时钟构成 控制信号 c i 时钟用于控制数据的移动。每个时钟周期内执行下述操作 输出 第 0 级； 各级向下一级移位 反馈信号输入第 L-1 级 级 0 级 1 级 L-2 级 L-1 … … … c L c L-1 c 2 c 1 s j 输出 密码学导论 -- 中国科学技术大学 14

15 .定义 ：如前图的长为 L 的 LFSR 可记为 (L,C(D)) ，其中 C(D)=1+c 1 D+c 2 D 2 +…+ c L D L ∈GF (2 D ) 为 联结多项式 若 C(D) 的次数为 L （即 c L =1) ，则称此 LFSR 为 非奇异 的 各级的初始值 [s L-1 ,…,s 1 ,s 0 ] 称为该 LFSR 的 初始状态 初始状态为 [s L-1 ,…,s 1 ,s 0 ] 的 LFSR ，输出序列 s=s 0 ,s 1 ,… 为 s j =(c 1 s j-1 +c 2 s j-2 +…+ c L s j -L ) mod 2, j≥L 密码学导论 -- 中国科学技术大学 15

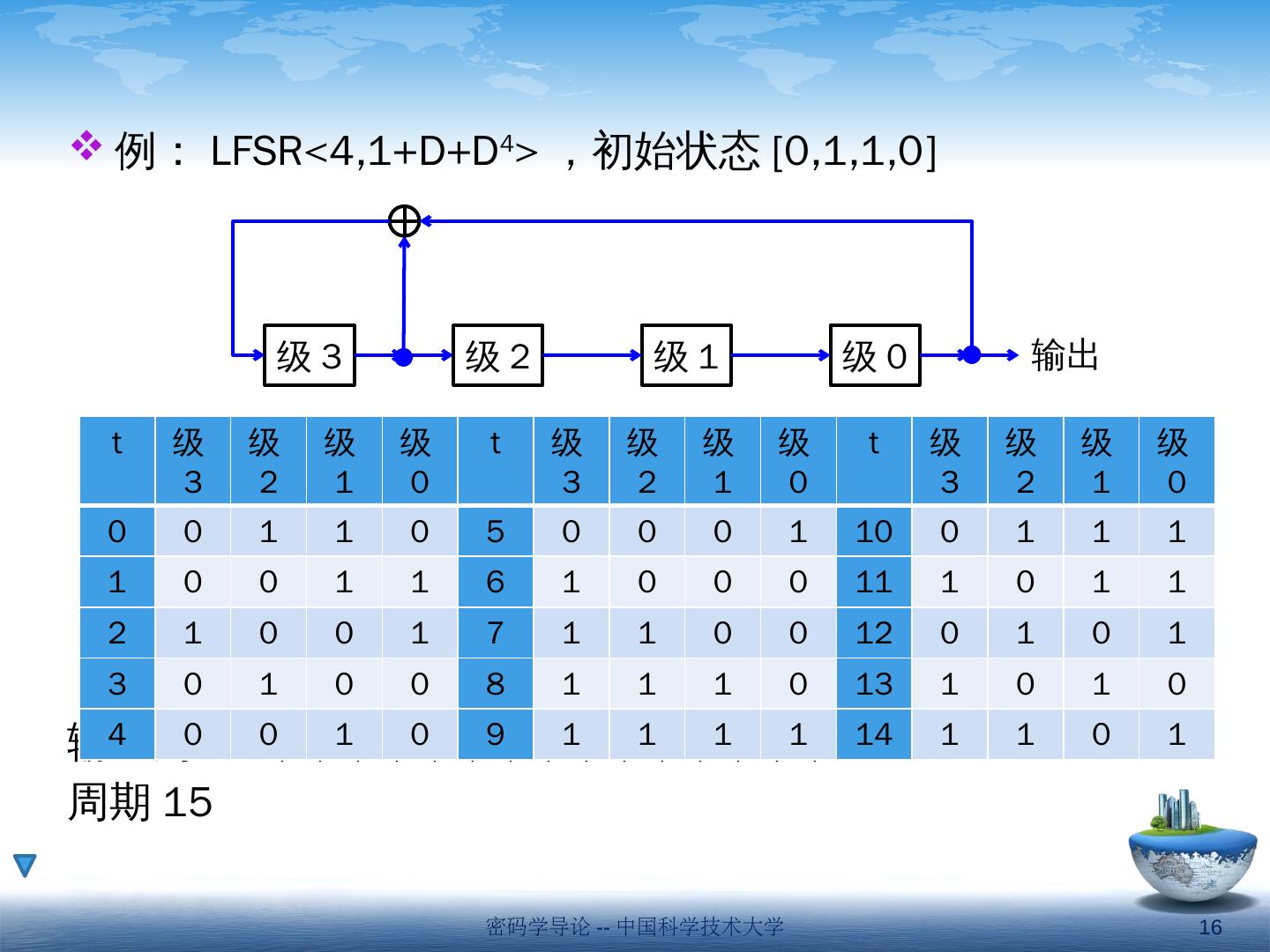
16 .例： LFSR<4,1+D+D 4 > ，初始状态 [0,1,1,0] 输出为 s=0,1,1,0,0,1,0,0,0,1,1,1,1,0,1,… 周期 15 级 0 级 1 级 2 级 3 输出 t 级 3 级 2 级 1 级 0 t 级 3 级 2 级 1 级 0 t 级 3 级 2 级 1 级 0 0 0 1 1 0 5 0 0 0 1 10 0 1 1 1 1 0 0 1 1 6 1 0 0 0 11 1 0 1 1 2 1 0 0 1 7 1 1 0 0 12 0 1 0 1 3 0 1 0 0 8 1 1 1 0 13 1 0 1 0 4 0 0 1 0 9 1 1 1 1 14 1 1 0 1 密码学导论 -- 中国科学技术大学 16

17 .矩阵表示 广义线性序列发生器： s j + c 1 s j-1 +c 2 s j-2 +…+ c L s j -L =0, j≥ L c i 为任意数 字 联结 矩阵 密码学导论 -- 中国科学技术大学 17

18 .LFSR<L,C(D)) 的每一个输出序列（任何非零初始状态）是 周期的 ，当且仅当联结多项式 C(D) 的次数为 L 。 对奇异 LFSR ，除去开始的固定有限项后，是周期的 例： LFSR<4,1+D+D 2 > ，初始状态 [1,0,0,0] 输出为 s= 0,0 ,0,1,1,0,1,1 后面仅讨论非奇异 LFSR 级 0 级 1 级 2 级 3 输出 密码学导论 -- 中国科学技术大学 18

19 .LFSR 输出序列的周期 若 C(D) 在 GF(2 L ) 上是不可约的，则每一个非零初始状态都可以产生一个 周期为 N 的输出序列。其中 N 是满足下述性质的最小正整数： C(D) 能够整除 1+D N （注意， N 总是的 2 L -1 因子） 若 C(D) 是本原多项式（即生成元），则每一 个非零初始状态都 可以产生具有 最大周期为 2 L -1 的输出序列。此 LFSR 称为 最大长度 LFSR ，输出序列称为 m 序列 。 密码学导论 -- 中国科学技术大学 19

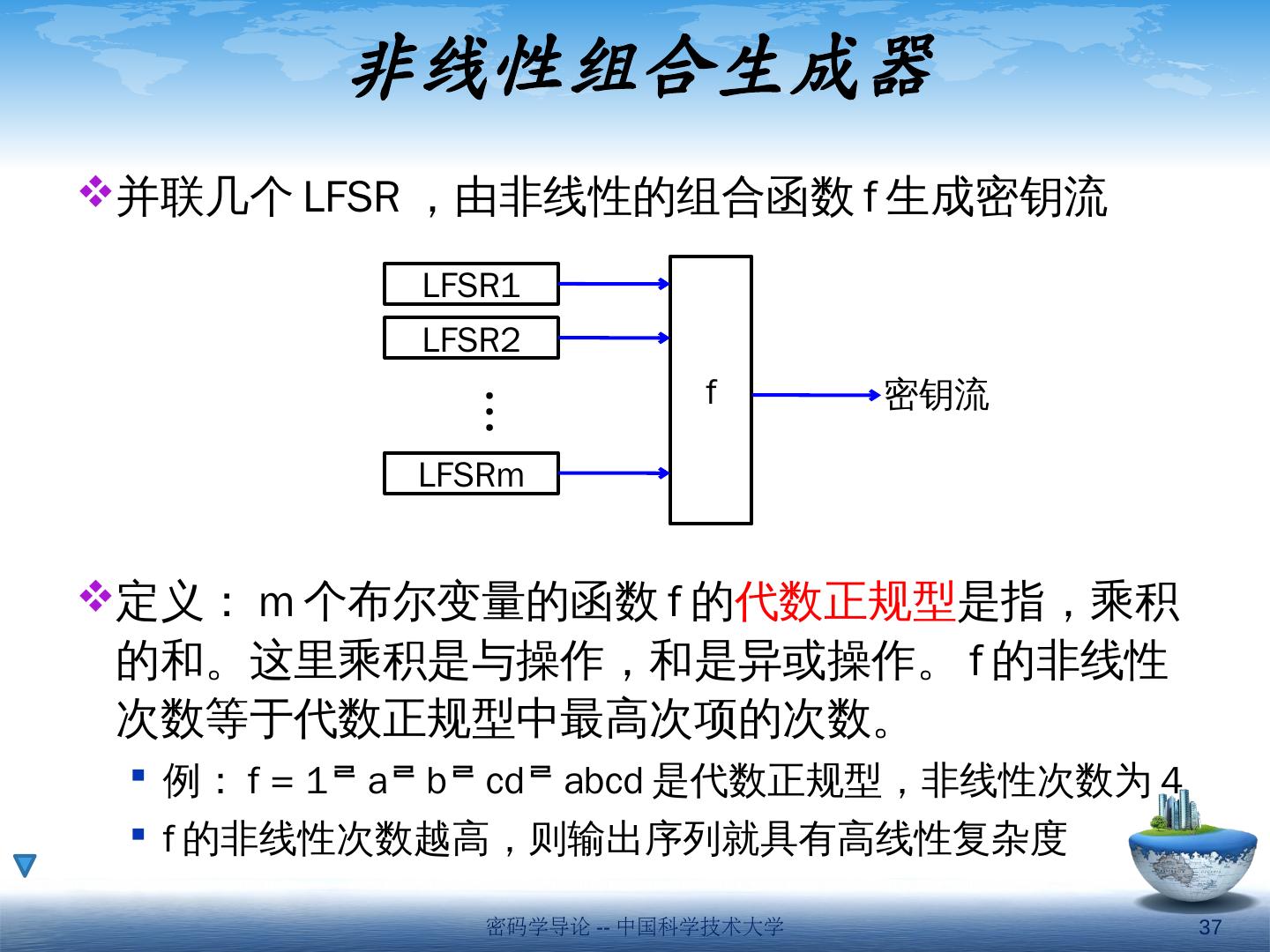
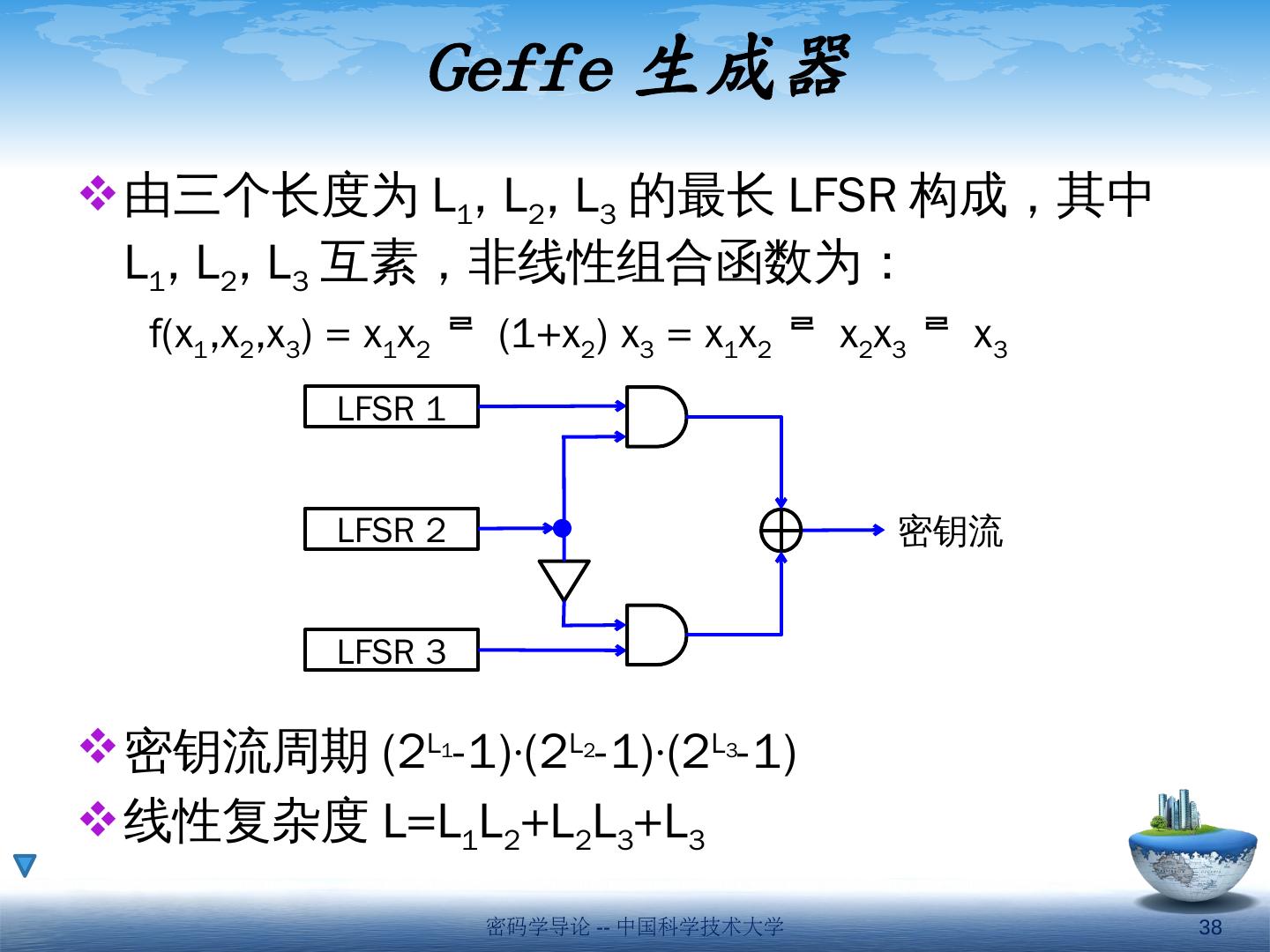
20 .常用移位寄存器序列 m 序列： 最长线性移位寄存器序列 Gold 序列： 两个级数相同（码长相同）的 m 序列的输出的异或 M 序列： 最长非线性移位寄存器序列。周期 2 L 密码学导论 -- 中国科学技术大学 20

21 .m 序列 的 长度为 k( k≤L ) 的模型分布几乎是均匀的。即若 s 是长为 L 的 LFSR 生成的 m 序列，设 k(1≤k≤L) 为整数， s 是 s 的长为 2 L +k-2 的任意子序列，则： s 的每个长度为 k 的非零子序列恰好出现 2 L-k 次 长度为 k 的零子序列恰好出现 2 L-k -1 次。 密码学导论 -- 中国科学技术大学 21 k L-k

22 .线性复杂度 无穷序列 s=s 0 ,s 1 ,,s 2 ,… 有限序列 s n =s 0 ,s 1 ,,s 2 ,…,s n-1 若某 LFSR 在某初始状态下输出序列的前 n 项为 s n 的话，则称该 LFSR 生成有限序列 s n 可以设想用 LFSR 来描述序列的复杂程度 LFSR 是线性的，因此它描述的是线性的复杂程度 密码学导论 -- 中国科学技术大学 22

23 .无穷二元序列 s 的 线性复杂度 L(s) 定义为 ： 若 s 为零序列，即 s=0,0,0,… ，则 L(s)= 0 若 没有 LFSR 能够生成 s ，则 L(s)= ∞ 否则 ， L(s) 就为生成 s 的最短 LFSR 的 长度 有限二元序列 s n 的 线性复杂度 L( s n ) 定义为： 生成以 s n 为开始的二元序列的最短 LFSR 的长度 设 L N 表示子序列 s N =s 0 ,s 1 ,,s 2 ,…,s N-1 的线性复杂度，则序列 L 1 ,L 2 ,… 称为 s 的 线性复杂度轮廓 密码学导论 -- 中国科学技术大学 23

24 .线性复杂度的性质 ：令 s 和 t 都为二元序列 对任意 n≥1 ，子序列 s n 的线性复杂度满足 0≤L( s n )≤n 若 s 的周期为 N ，则 L(s)≤N L( s n )=0 ，当且仅当 s n 是长度为 n 的零序列 L( s n )=n ，当且仅当 s n =0,0,0,…,0,1 L( s  t )≤L(s)+L(t) 线性复杂度轮廓的性质 ： 若 j> i ，则 L j ≥L i 若 L N+1 >L N ，则 L N ≤N/2 若 L N+1 >L N ，则 L N+1 +L N =N+1 密码学导论 -- 中国科学技术大学 24

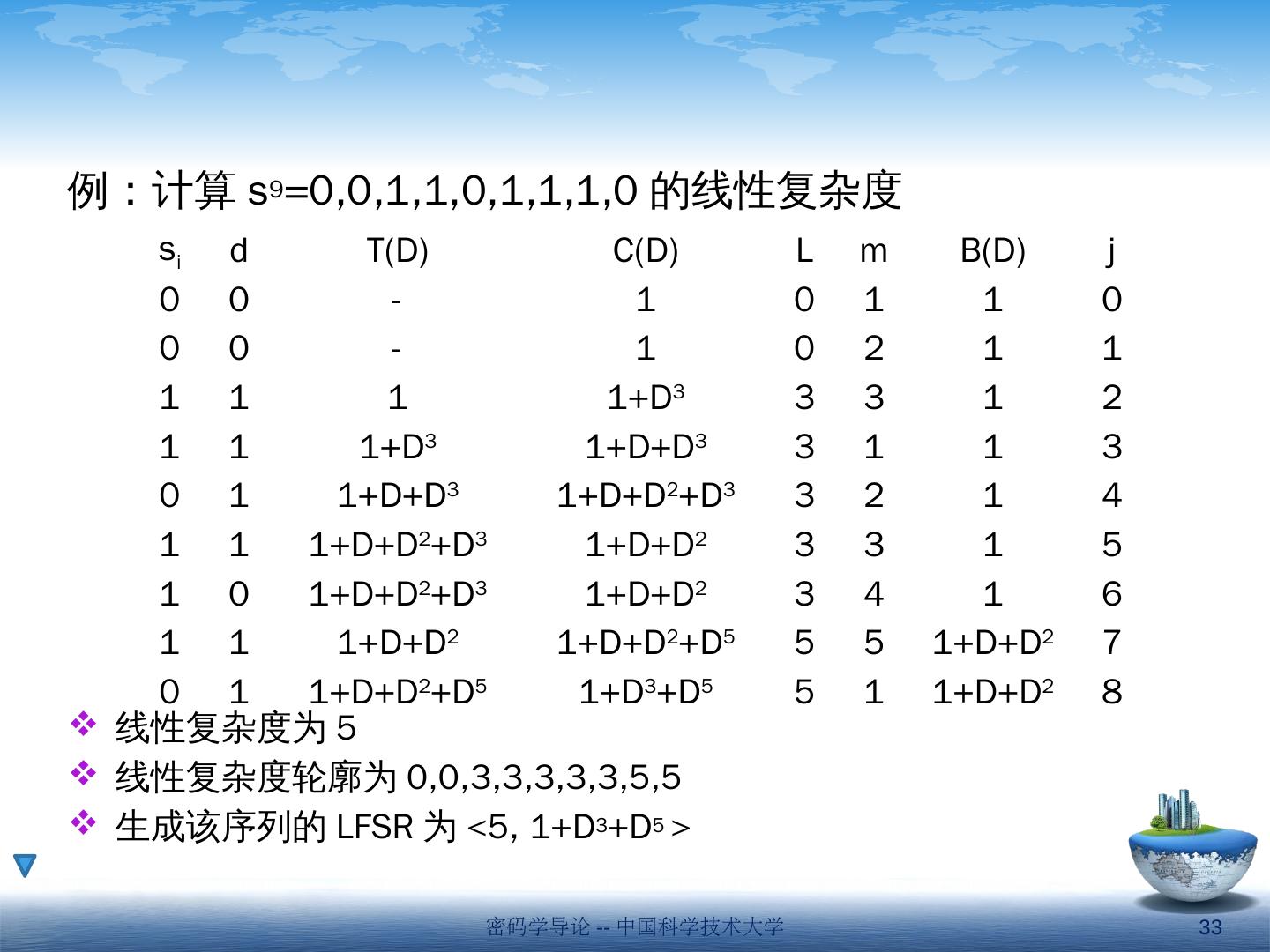
25 .Berlekamp -Massey 算法 求解最小阶数 L 及相应的 C(x) ，使之满足 s j + c 1 s j-1 +c 2 s j-2 +… c L s j -L =0, j=L,L+1,…,N-1 序列 s 1 ,s 2 ,…, s N 多项式 C(x)=1+c 1 x+c 2 s 2 +…+ c L s L 若以上算法定义在模 2 多项式运算中，即为求解线性复杂度及联结多项式的算法。 定义 d=s k +c 1 s k-1 +c 2 s k-2 +…+ c L s k -L 为迭代到第 k 轮时的下一步离差。即第 k-1 轮迭代结果对 s k 的预测与实际 s k 的差。 密码学导论 -- 中国科学技术大学 25

26 .B-M 算法： j 表示 当前已迭代轮数， B(x) 和 b 分别表示当 L 最后一次更新前的 C(x) 和 d ， m 表示当 L 更新后的轮数 密码学导论 -- 中国科学技术大学 26

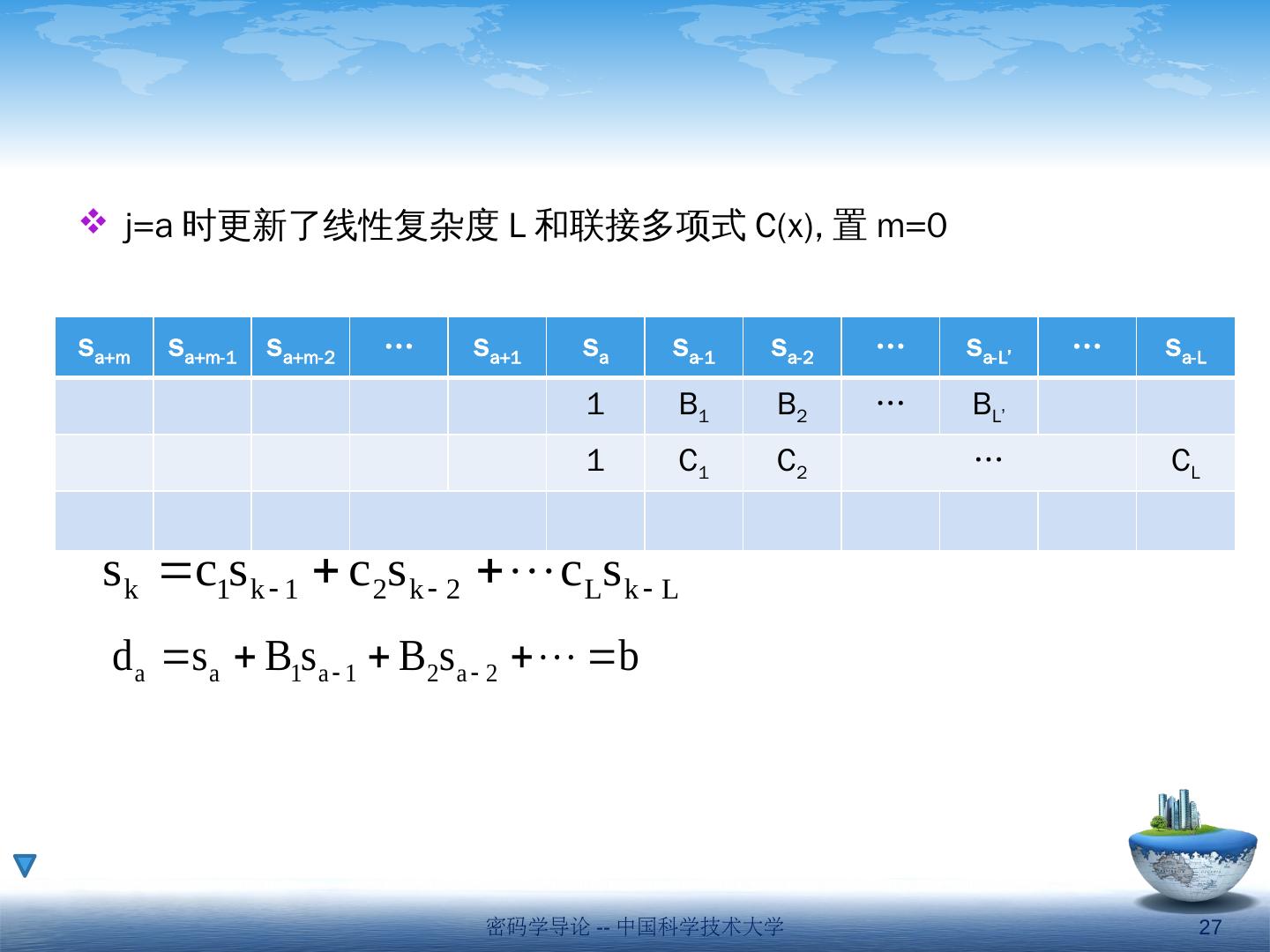
27 .密码学导论 -- 中国科学技术大学 27 s a+m s a+m-1 s a+m-2 … s a+1 s a s a-1 s a-2 … s a -L’ … s a -L 1 B 1 B 2 … B L’ 1 C 1 C 2 … C L j=a 时更新了线性复杂度 L 和联接多项式 C(x), 置 m=0

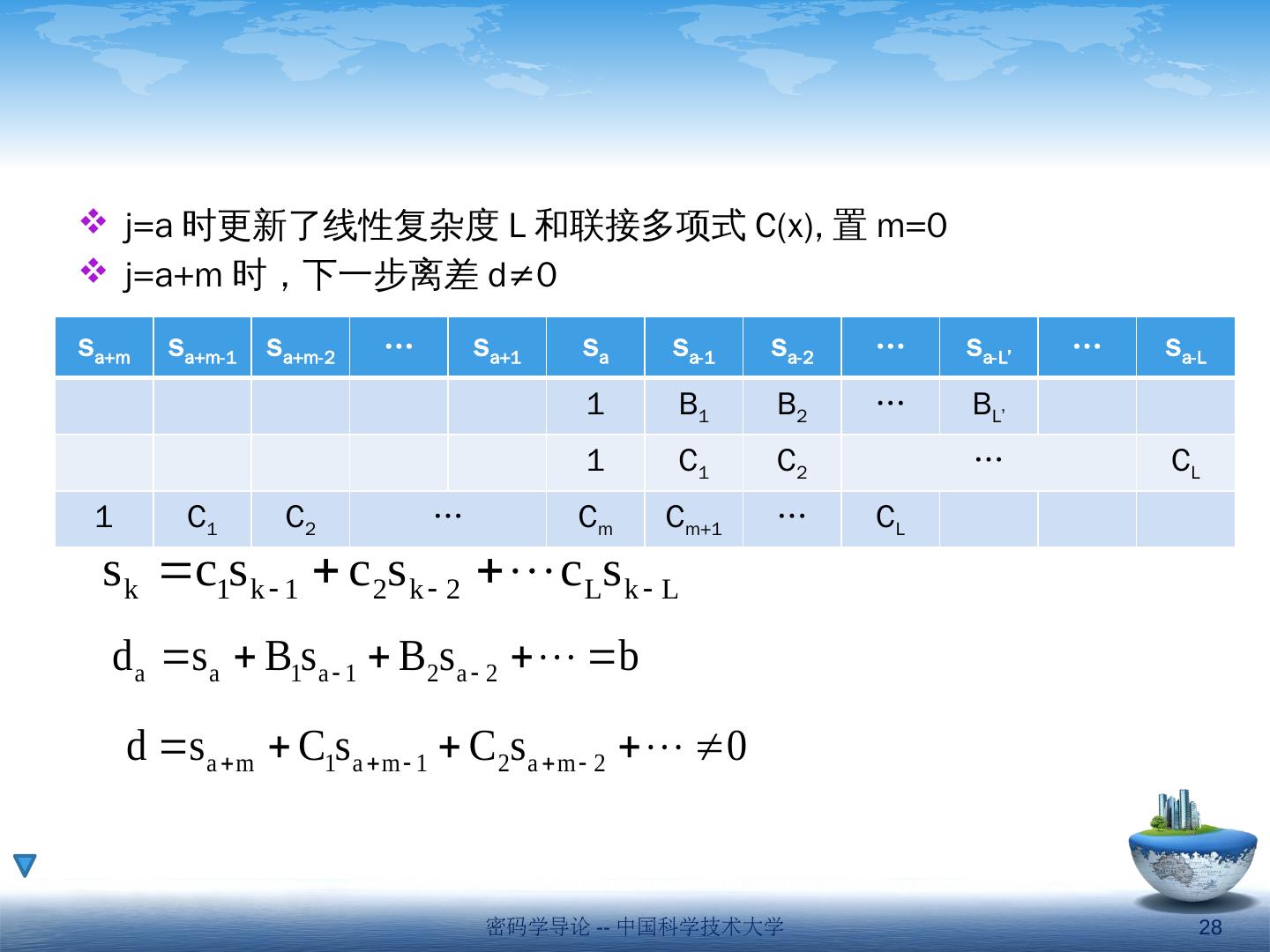
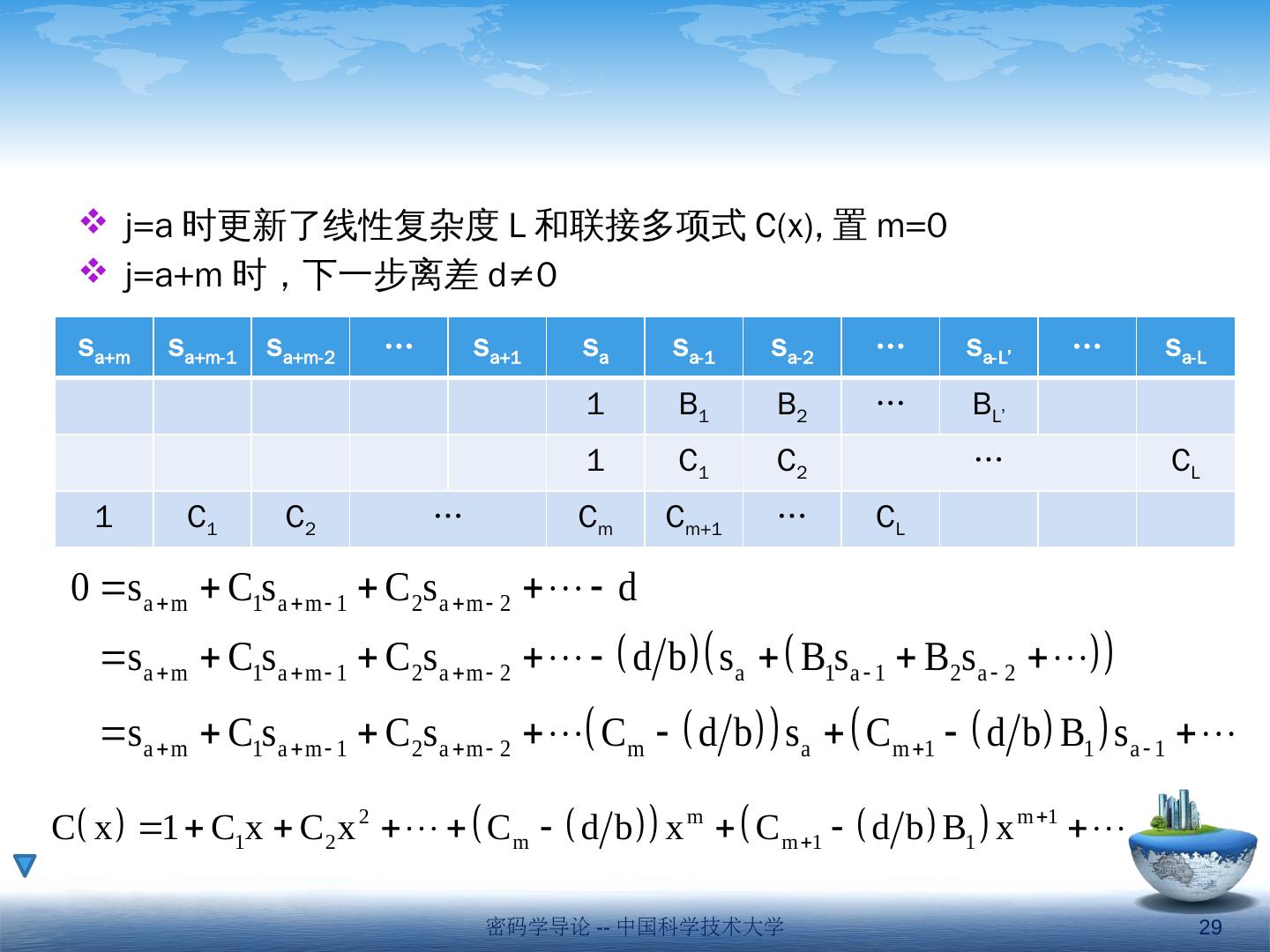
28 .密码学导论 -- 中国科学技术大学 28 s a+m s a+m-1 s a+m-2 … s a+1 s a s a-1 s a-2 … s a -L’ … s a -L 1 B 1 B 2 … B L’ 1 C 1 C 2 … C L 1 C 1 C 2 … C m C m+1 … C L j=a 时更新了线性复杂度 L 和联接多项式 C(x), 置 m=0 j= a+m 时，下一步离差 d≠0

29 .密码学导论 -- 中国科学技术大学 29 s a+m s a+m-1 s a+m-2 … s a+1 s a s a-1 s a-2 … s a -L’ … s a -L 1 B 1 B 2 … B L’ 1 C 1 C 2 … C L 1 C 1 C 2 … C m C m+1 … C L j=a 时更新了线性复杂度 L 和联接多项式 C(x), 置 m=0 j= a+m 时，下一步离差 d≠0