04密码学---数论基础

1 .密码学 导论˙第 4 章 数论基础 李卫海

2 .本章目录 密码学导论 -- 中国科学技术大学 2

3 .第一节 有限域计算 密码学导论 -- 中国科学技术大学 3

4 .一、群、环和域 群 Group ： 群 G ，记作 {G, •}, 定义一个二元运算“ • ”的集合， G 中每一个序偶 ( a,b ) 通过运算生成 G 中元素 ( a•b ) ，满足下列公理： (A1) 封闭性 Closure ：如果 a 和 b 都属于 G ，则 a•b 也属于 G (A2) 结合律 Associative ：对 G 中的任意元素 a ， b ， c ，都有 a•( b•c )=( a•b )•c 成立 (A3) 单位元 Identity element ： G 中存在一个元素 e ，对于 G 中任意元素 a ，都有 a•e = e•a =a 成立 (A4) 逆元 Inverse element ：对于 G 中任意元素 a, G 中都存在一个元素 a -1 ，使得 a•a -1 =a -1 •a=e 成立 密码学导论 -- 中国科学技术大学 4

5 .有限群 Finite Group 和 无限群 Infinite Group ： 如果一个群的元素是有限的，则该群称为有限群，且 群的阶 等于群中元素的个数；否则称为无限群 交换群（阿贝尔群） Abelian Group ： 满足交换律的群 (A5) 交换律 Commutative ：对于 G 中任意的元素 a, b ，都有 a•b = b•a 成立 循环群 Cyclic Group: 如果群中的每一个元素都是一个固定的元素 a( a∈G ) 的幂 a k (k 为整数 ) ，则称群 G 为循环群。 元素 a 生成了群 G ，或者说 a 是群 G 的 生成元 。 密码学导论 -- 中国科学技术大学 5

6 .减法 ： 当群中的运算符是加法时，其单位元是 0 a 的逆元是 -a 减法定义为： a–b=a+(-b) 密码学导论 -- 中国科学技术大学 6

7 .环 Ring ： 环 R ，记作 { R,+,x } ，定义二元运算加法“ + ”和乘法“ × ”的集合， R 中任意元素 a,b,c 满足下列公理： (A1-A5), R 关于 加法是交换群 ，单位元是 0 ， a 的逆元是 -a (M1) 乘法封闭性 ：如果 a 和 b 都属于 R ，则 ab 也属于 R (M2) 乘法结合律 ：如果 a,b,c 都属于 R ，则 a( bc )=( ab )c (M3) 分配律 ：如果 a,b,c 都属于 R ，则 a( b+c )= ab+ac 或 ( a+b )c = ac+bc 密码学导论 -- 中国科学技术大学 7

8 .交换环 C ommutative R ing ：满足下列条件的环 (M4) 乘法交换律 ：对 R 中任意元素 a,b ，都有 ab = ba 成立 整环 Integral D omain ：满足下列条件的交换环 (M5) 乘法单位元 ：在 R 中存在元素 1 ，使得对于 R 中任意元素 a ，都有 a1=1a 成立 (M6) 无零因子 ：若元素 a,b 满足 ab =0 ，则必有 a=0 或 b=0 密码学导论 -- 中国科学技术大学 8

9 .域 Field ： 域 F ，记作 {F,+,×} ，定义为满足下列关系的整环： (M7) 乘法逆元 Multiplicative inverse: 对 F 中每个元素 a （除 0 以外），存在元素 a -1 满足 aa -1 =(a -1 )a=1 除法 ： 对 F 中任意元素 a 和任意非零元素 b ，定义为 a/b=a(b -1 ) 密码学导论 -- 中国科学技术大学 9

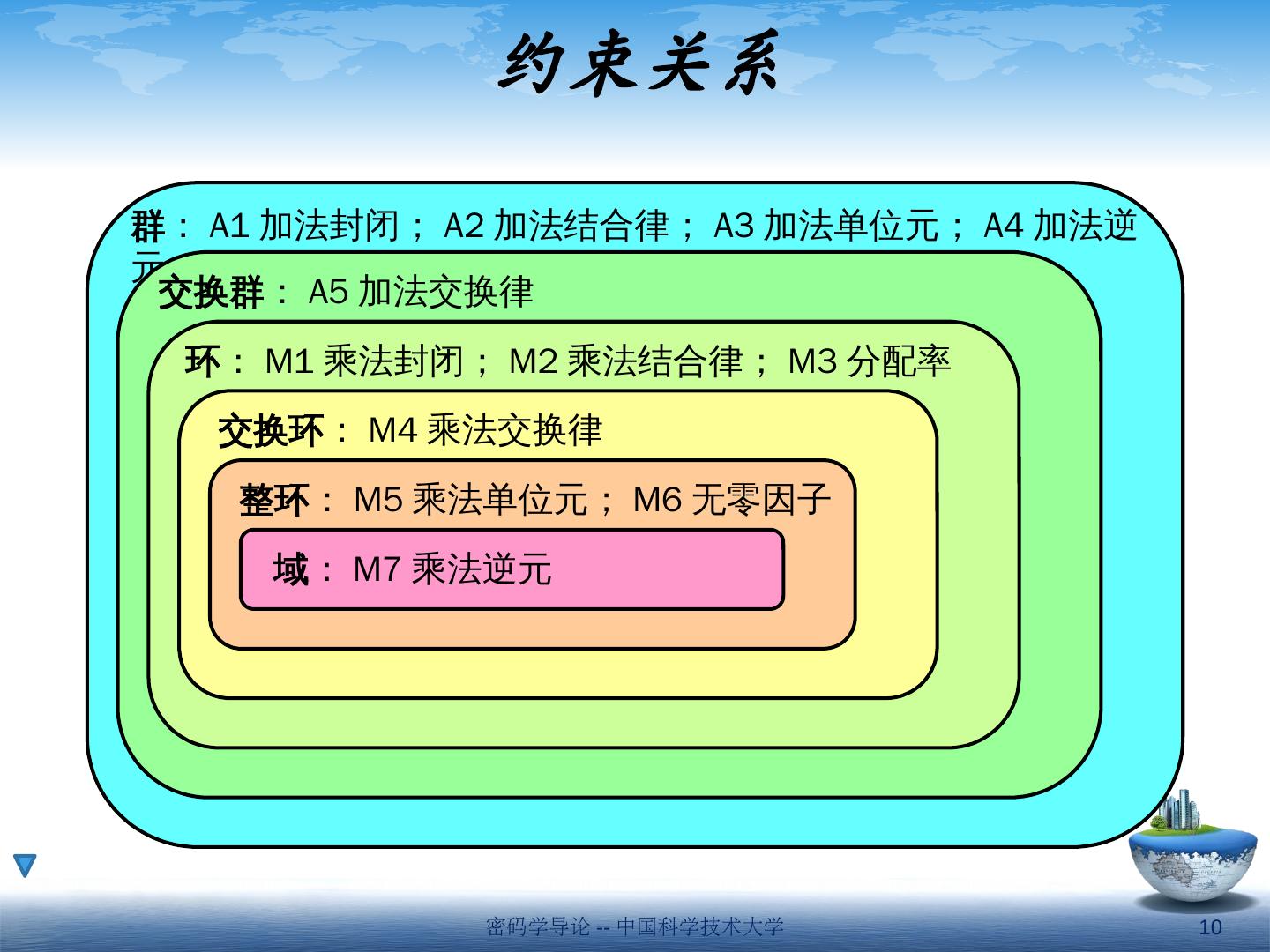
10 .约束关系 群 ： A1 加法封闭； A2 加法结合律； A3 加法单位元； A4 加法逆元 交换群 ： A5 加法交换律 环 ： M1 乘法封闭； M2 乘法结合律； M3 分配率 交换环 ： M4 乘法交换律 整环 ： M5 乘法单位元； M6 无零因子 域 ： M7 乘法逆元 密码学导论 -- 中国科学技术大学 10

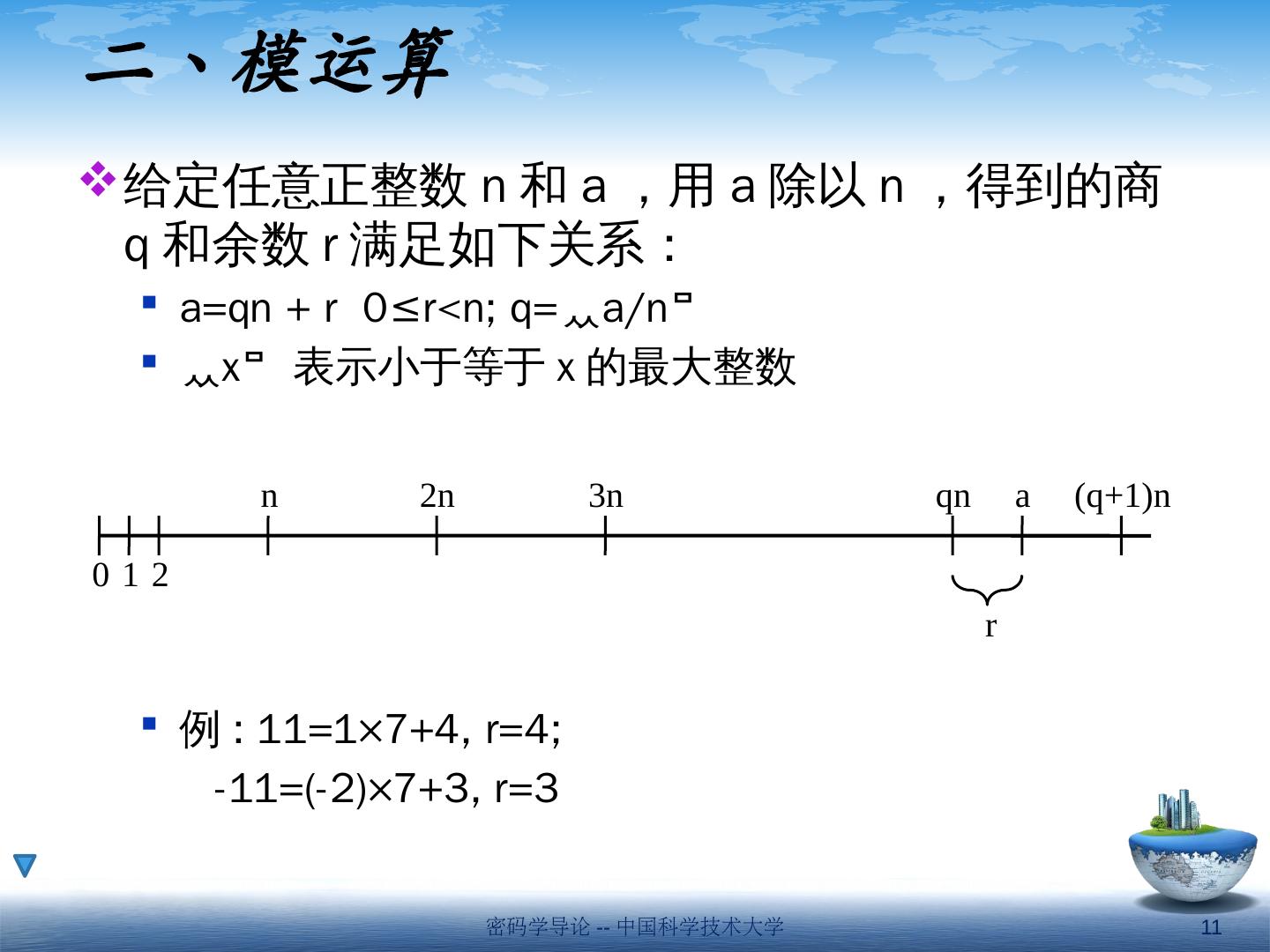
11 .二、模运算 给定任意正整数 n 和 a ，用 a 除以 n ，得到的商 q 和余数 r 满足如下关系： a= qn + r 0≤r<n; q=  a/n   x  表示小于等于 x 的最大整数 例 : 11=1×7+4, r=4; -11=(-2)×7+3, r=3 n 2n 3n qn (q+1)n 0 1 2 a r 密码学导论 -- 中国科学技术大学 11

12 .同余 ( congruence) 给定整数 a, b 及 n≠0, 当且仅当 a-b= kn 时， a 与 b 是模 n 同余 ，记为 a≡b mod n 例： 17≡7 mod 5 53≡11 mod 7 a≡b mod n 当且仅当 a mod n = b mod n 若 a 是整数， n 是正整数，定义 a 除以 n 的 余数为 a 模 n 对于任意整数 a ，总可写出： a=  a/n  ×n+(a mod n) 例： 11 mod 7 = 4 -11 mod 7 = 3 密码学导论 -- 中国科学技术大学 12

13 .因子 Divisors 如果 a= mb , 其中 a,b,m 为整数，则当 b≠0 时，称 b 能 整除 a, b 是 a 的一个 因子， 或 a 除以 b 余数为 0 ，记为 b|a 例： 24 的正因子有 1, 2, 3, 4, 6, 8, 12 和 24 。 以下关系成立 如果 a|1, 则 a=±1 如果 a|b ，且 b|a , 则 a=±b 任何 b≠0 能整除 0 如果 b|g ，且 b|h ，则对任何整数 m 和 n ，有 b|( mg+nh ) 例： 7|14 and 7|63 ，则 7|(3×14 + 2×63) 如果 a≡0 mod n ，则 n|a 密码学导论 -- 中国科学技术大学 13

14 .同余的性质 如果 n|(a-b), 则 a≡b mod n 证明：如果 n|(a-b), 则有 (a-b)= kn , k 为某些整数， 所以 a= b+kn 。 故 a mod n = (b + kn ) mod n = b mod n 反身性 ： a≡a mod n 对称性 ： a≡b mod n ，则 b≡a mod n 传递性 ： a≡b mod n 且 b≡c mod n ，则 a≡c mod n 密码学导论 -- 中国科学技术大学 14

15 .逆元 加法逆元 (-w) 对每一个 w∈Z n ，存在一个 z ，使得 w+z≡0 mod n ，则 z 即为加法逆元 -w 乘法逆元 (w -1 ) 若 p 为素数，对每一个 w∈Z p ， w 与 p 互素，存在一个 z ，使得 w × z≡1 mod p 。 z 即为乘法逆元 w -1 用 w 乘以 Z p 中的所有数模 p ，余数将以不同次序涵盖 Z p 中的所有数，其中必有一个为 1 。这个数就是 w 的乘法逆元， w -1 模数不是素数时，某些但非全部整数存在一个乘法逆元。如果 gcd (a, n)=1, 则能在 Z n 中找到 b ，使得 a × b≡1 mod n 。 b 即为乘法逆元 a -1 密码学导论 -- 中国科学技术大学 15

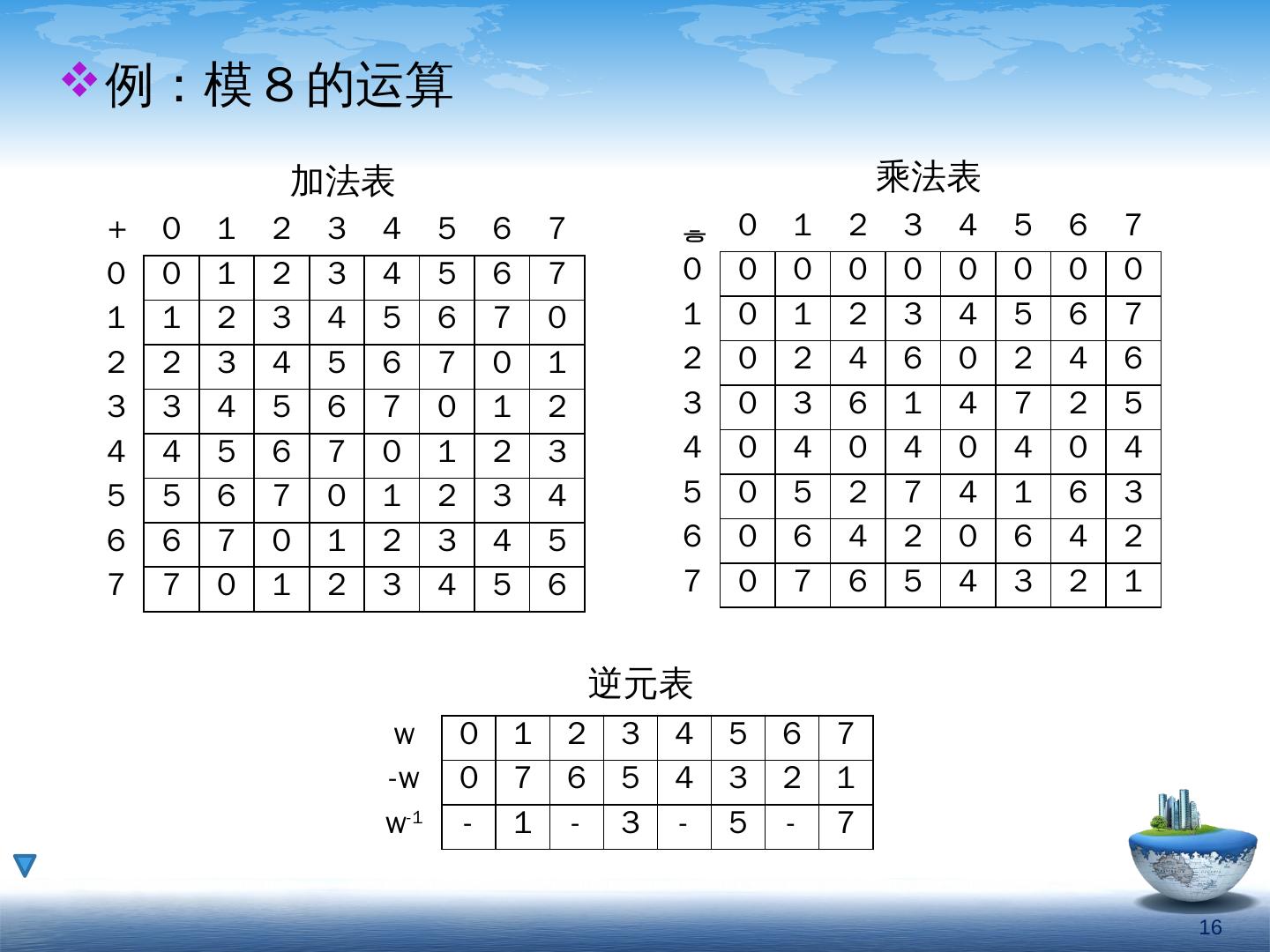
16 .16 例：模 8 的运算 加法表 乘法表 逆元表 ＋ 0 1 2 3 4 5 6 7 0 0 1 2 3 4 5 6 7 1 1 2 3 4 5 6 7 0 2 2 3 4 5 6 7 0 1 3 3 4 5 6 7 0 1 2 4 4 5 6 7 0 1 2 3 5 5 6 7 0 1 2 3 4 6 6 7 0 1 2 3 4 5 7 7 0 1 2 3 4 5 6  0 1 2 3 4 5 6 7 0 0 0 0 0 0 0 0 0 1 0 1 2 3 4 5 6 7 2 0 2 4 6 0 2 4 6 3 0 3 6 1 4 7 2 5 4 0 4 0 4 0 4 0 4 5 0 5 2 7 4 1 6 3 6 0 6 4 2 0 6 4 2 7 0 7 6 5 4 3 2 1 w 0 1 2 3 4 5 6 7 -w 0 7 6 5 4 3 2 1 w -1 - 1 - 3 - 5 - 7

17 .模算术运算 (a 1 op a 2 ) mod n =[(a 1 mod n )] op (a 2 mod n)] mod n ( a+b ) mod n = (a mod n + b mod n) mod n (a-b) mod n = (a mod n - b mod n) mod n ( a•b ) mod n = (a mod n • b mod n) mod n 如果 a=b mod n 且 c=d mod n ，则 a+c =( b+d ) mod n a-c=(b-d) mod n a•c =( b•d ) mod n 如果 ac= bd mod n 且 c=d mod n ， gcd ( c,n )=1 ，则 a=b mod n 例： 3*2=1*2 mod 4 且 2=2 mod 4, 但 3≠1 mod 4 密码学导论 -- 中国科学技术大学 17

18 .模运算的性质 剩余类集 (Residues) 定义比 n 小的非负整数集合为 Z n ： Z n ={0,1,…,(n-1)} 模 n 的完全剩余类集 (Complete Set of Residues mod n) ：如果对每个整数 a ，在集合 {r 1 ,r 2 ,…, r n } 中恰有一个余数 r i ，使得 a mod n= r i ，则称 {r 1 ,r 2 ,…, r n } 为模 n 的完全剩余类集， {0,1,…,n-1} 形成模 n 的完全剩余类集。 模 n 的缩剩余类集 (Reduced set of Residues mod n) ：完全剩余集的子集，其中的元素都和 n 互素（包括 1 ） 例： n=10 ， 模 n 的完全剩余集是 {0, 1, 2,…,9} 模 n 的缩剩余集是 {1, 3, 7, 9} 密码学导论 -- 中国科学技术大学 18

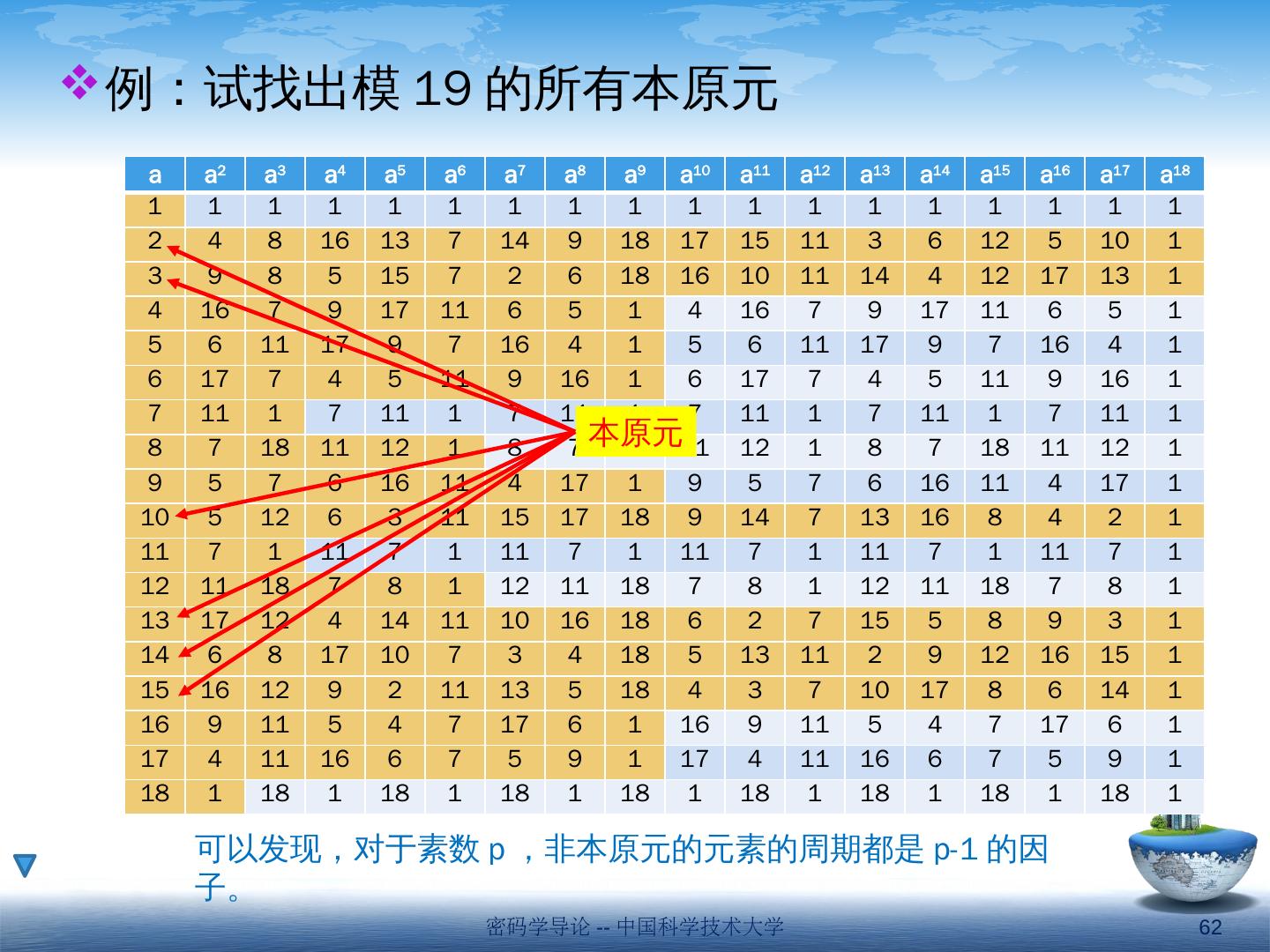
19 .三、有限域 GF(p) Galois Fields 有限域在密码学中扮演重要角色 有限域的元素个数是一个素数的幂 p n , n 为正整数，一般记为 GF( p n ) ，即 Galois fields, 模 p n . 关注两种特殊情形 n=1 时的有限域，即 GF(p) p 为 2 时的有限域，即 GF(2 n ) 最简单的有限域是 GF(2) ，代数运算简述如下： + 0 1  0 1 w -w w -1 0 0 1 0 0 0 0 0 1 1 0 1 0 1 1 1 1 加 乘 求逆 密码学导论 -- 中国科学技术大学 19

20 .（ 1 ） 伽罗瓦域 GF(p) 当模数是素数 p ，每个整数 a∈[1,p-1] 与 p 互素，因而都有唯一的模 p 的乘法逆。这一组模 p 的整数，加上算术运算，被称为有限域 — 伽罗瓦域 GF(p) 的空间是模 p 的完全剩余类 Z p ： {0,1, … , p-1} 例， GF(7) 上的运算 密码学导论 -- 中国科学技术大学 20 加法表 乘法表 逆元表 ＋ 0 1 2 3 4 5 6 0 0 1 2 3 4 5 6 1 1 2 3 4 5 6 0 2 2 3 4 5 6 0 1 3 3 4 5 6 0 1 2 4 4 5 6 0 1 2 3 5 5 6 0 1 2 3 4 6 6 0 1 2 3 4 5  0 1 2 3 4 5 6 0 0 0 0 0 0 0 0 1 0 1 2 3 4 5 6 2 0 2 4 6 1 3 5 3 0 3 6 2 5 1 4 4 0 4 1 5 2 6 3 5 0 5 3 1 6 4 2 6 0 6 5 4 3 2 1 w 0 1 2 3 4 5 6 -w 0 6 5 4 3 2 1 w -1 - 1 4 5 2 3 6

21 .（ 2 ） 伽罗瓦域 GF(2 n ) 系数是二进制 0 和 1 的多项式，最高不超过 n-1 次项 一个元素 a 可被表示成一个位矢量，长度为 n ， (a n-1 ,…,a 1 , a 0 ) ，每一个长度为 n 的矢量都对应着 GF(2 n ) 中的不同元素 例如二进制数 11001 2 在 GF(2 5 ) 中可以记作 x 4 +x 3 +1 如何计算？ 密码学导论 -- 中国科学技术大学 21

22 .四 、多项式计算 多项式 三种多项式运算： 使用代数基本规则的普通多项式运算； 系数在 Z p 中的多项式运算； 系数在 GF(2) 中，且多项式被定义为模一个 n 次多项式 m(x) ：有限域 GF(2 n ) 上的计算 密码学导论 -- 中国科学技术大学 22

23 .普通多项式运算 加法和减法规则：对应项系数的加或减 乘法规则：各项相乘 例：令 f(x) = x 3 + x 2 + 2 和 g(x) = x 2 - x + 1 f(x) + g(x) = x 3 + 2x 2 - x + 3 f(x) - g(x) = x 3 + x + 1 f(x) ×g(x) = x 5 + 3x 2 - 2x + 2 f(x) / g(x) = x + 2 ……x 密码学导论 -- 中国科学技术大学 23

24 .24

25 .系数在 Z p 中的多项式运算 系数进行模 p 运算 模可以是任意素数，一般取 2 ，此时 所有系数为 0 或 1 例：令 f(x) = x 3 + x 2 + 1 和 g(x) = x 2 + x + 1 f(x) + g(x) = x 3 + x f(x) × g(x) = x 5 + x + 1 密码学导论 -- 中国科学技术大学 25

26 .26

27 .有限域 GF(2 n ) 上的多项式计算 有助于二进制计算机实现 有限域 GF(2 n ) 系数对 2 取模运算 最高次数小于 n 多项式对 n 次素多项式取模运算 非零元素有逆 可以用扩展 Euclidean 算法求逆 密码学导论 -- 中国科学技术大学 27

28 .素多项式 任何多项式可以写为： f(x)=q(x)g(x)+r(x) r(x) 称为 余式 r(x)=f(x) mod g(x) 若不存在余式，则称 g(x) 整除 f(x) ， g(x)|f(x) 若 f(x) 除了它本身和 1 外，不存在其它因式，则称 f(x) 是 不可约多项式 ，或 既约多项式 、 素多项式 系数在 GF(p) 中，以素多项式取模的多项式构成一个域 密码学导论 -- 中国科学技术大学 28

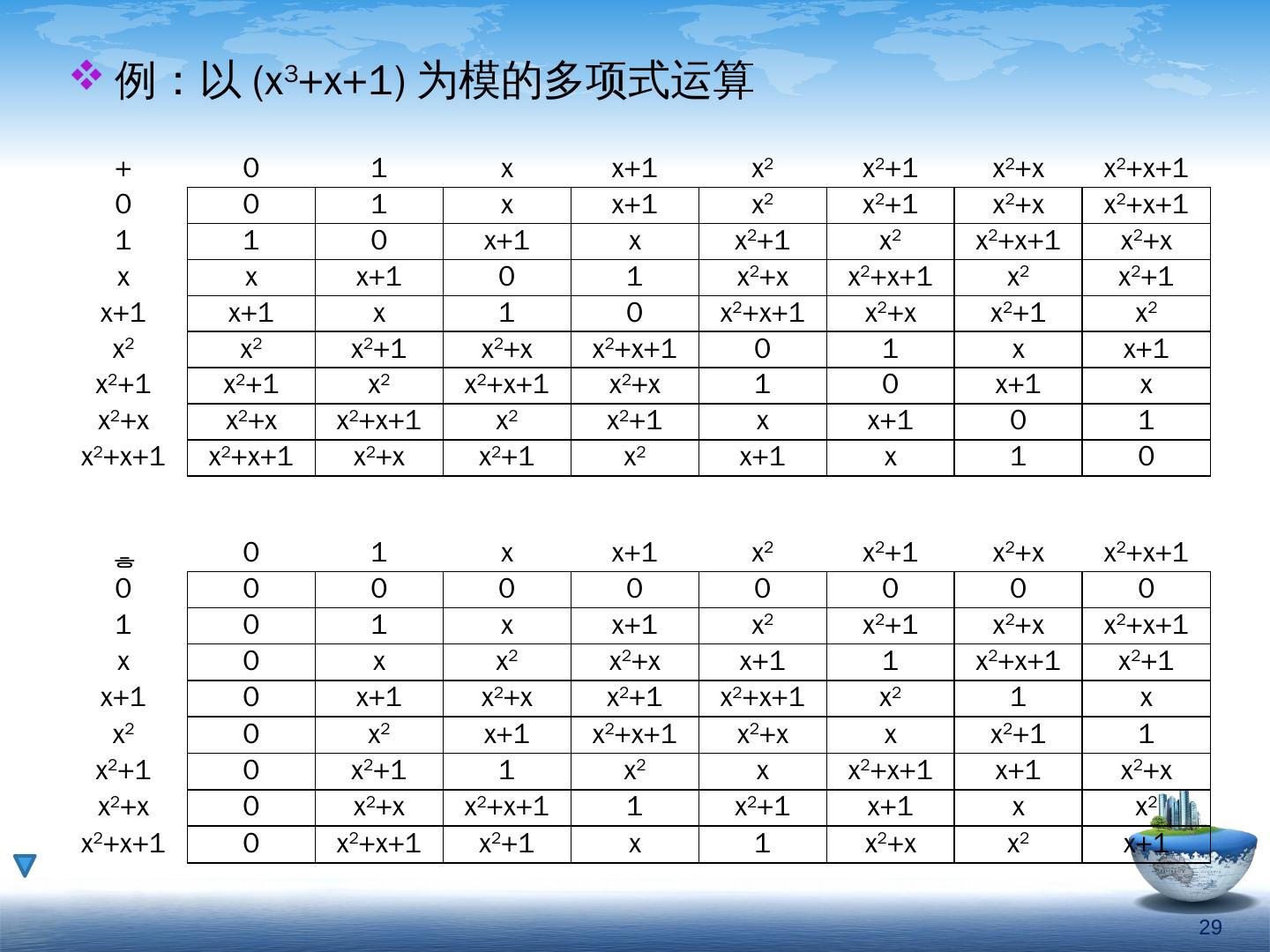
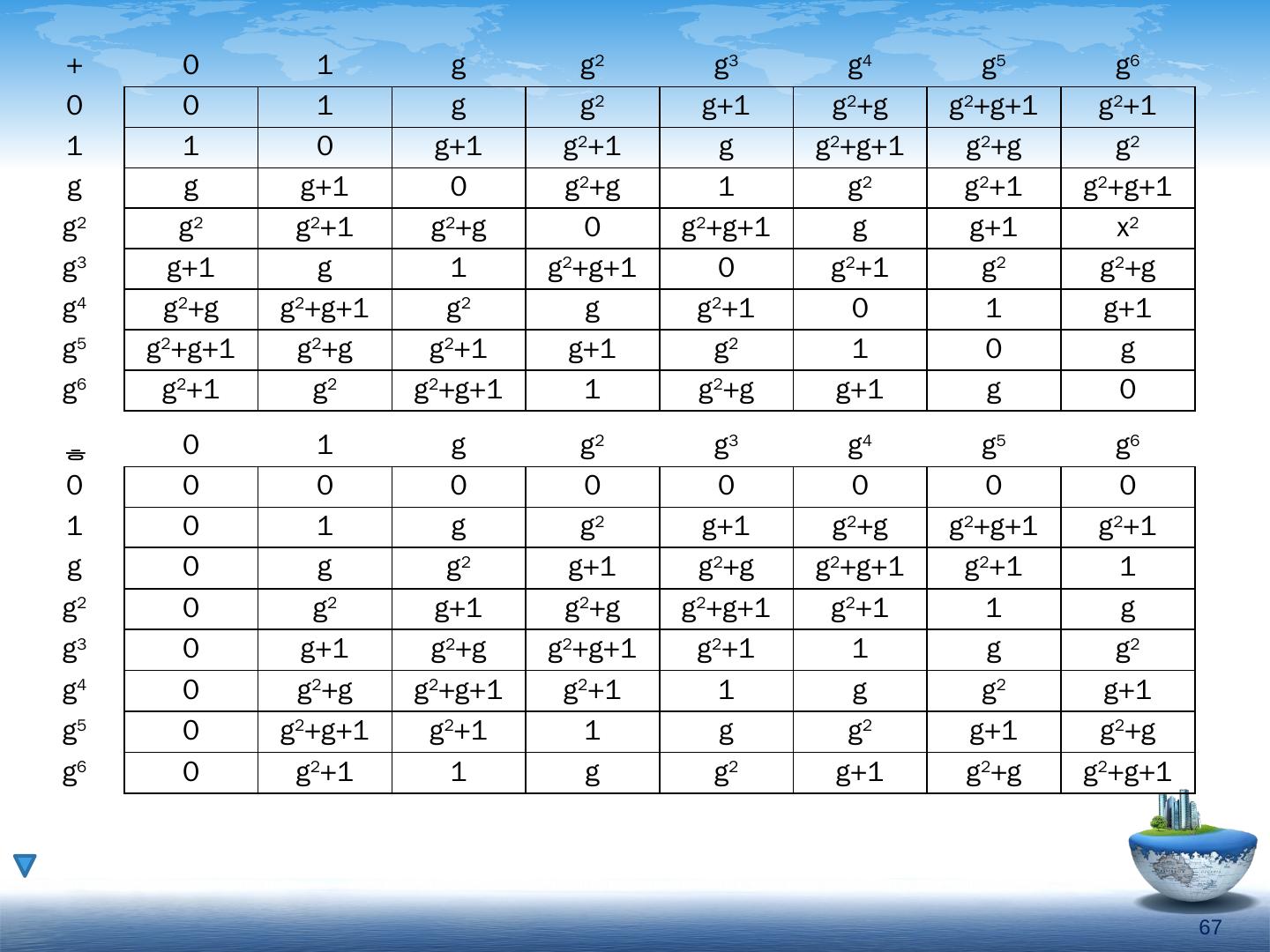
29 .29 例：以 (x 3 +x+1) 为模的多项式运算 + 0 1 x x+1 x 2 x 2 +1 x 2 +x x 2 +x+1 0 0 1 x x+1 x 2 x 2 +1 x 2 +x x 2 +x+1 1 1 0 x+1 x x 2 +1 x 2 x 2 +x+1 x 2 +x x x x+1 0 1 x 2 +x x 2 +x+1 x 2 x 2 +1 x+1 x+1 x 1 0 x 2 +x+1 x 2 +x x 2 +1 x 2 x 2 x 2 x 2 +1 x 2 +x x 2 +x+1 0 1 x x+1 x 2 +1 x 2 +1 x 2 x 2 +x+1 x 2 +x 1 0 x+1 x x 2 +x x 2 +x x 2 +x+1 x 2 x 2 +1 x x+1 0 1 x 2 +x+1 x 2 +x+1 x 2 +x x 2 +1 x 2 x+1 x 1 0  0 1 x x+1 x 2 x 2 +1 x 2 +x x 2 +x+1 0 0 0 0 0 0 0 0 0 1 0 1 x x+1 x 2 x 2 +1 x 2 +x x 2 +x+1 x 0 x x 2 x 2 +x x+1 1 x 2 +x+1 x 2 +1 x+1 0 x+1 x 2 +x x 2 +1 x 2 +x+1 x 2 1 x x 2 0 x 2 x+1 x 2 +x+1 x 2 +x x x 2 +1 1 x 2 +1 0 x 2 +1 1 x 2 x x 2 +x+1 x+1 x 2 +x x 2 +x 0 x 2 +x x 2 +x+1 1 x 2 +1 x+1 x x 2 x 2 +x+1 0 x 2 +x+1 x 2 +1 x 1 x 2 +x x 2 x+1