03密码学--密码学基本理论

1 .密码学 导论 ˙第 3 章 密码学 基础理论 李卫海

2 .本章目录 密码学导论 -- 中国科学技术大学 2

3 .Claude Elwood Shannon 1948 年，“ A Mathematical Theory of Communication ”在数学上奠定了信息论基础； 1949 年，“ Communication Theory of Secrecy Systems ”从信息论角度奠定了密码学的理论基础。 密码学导论 -- 中国科学技术大学 3

4 .第一节 密码系统的概率模型 密码学导论 -- 中国科学技术大学 4

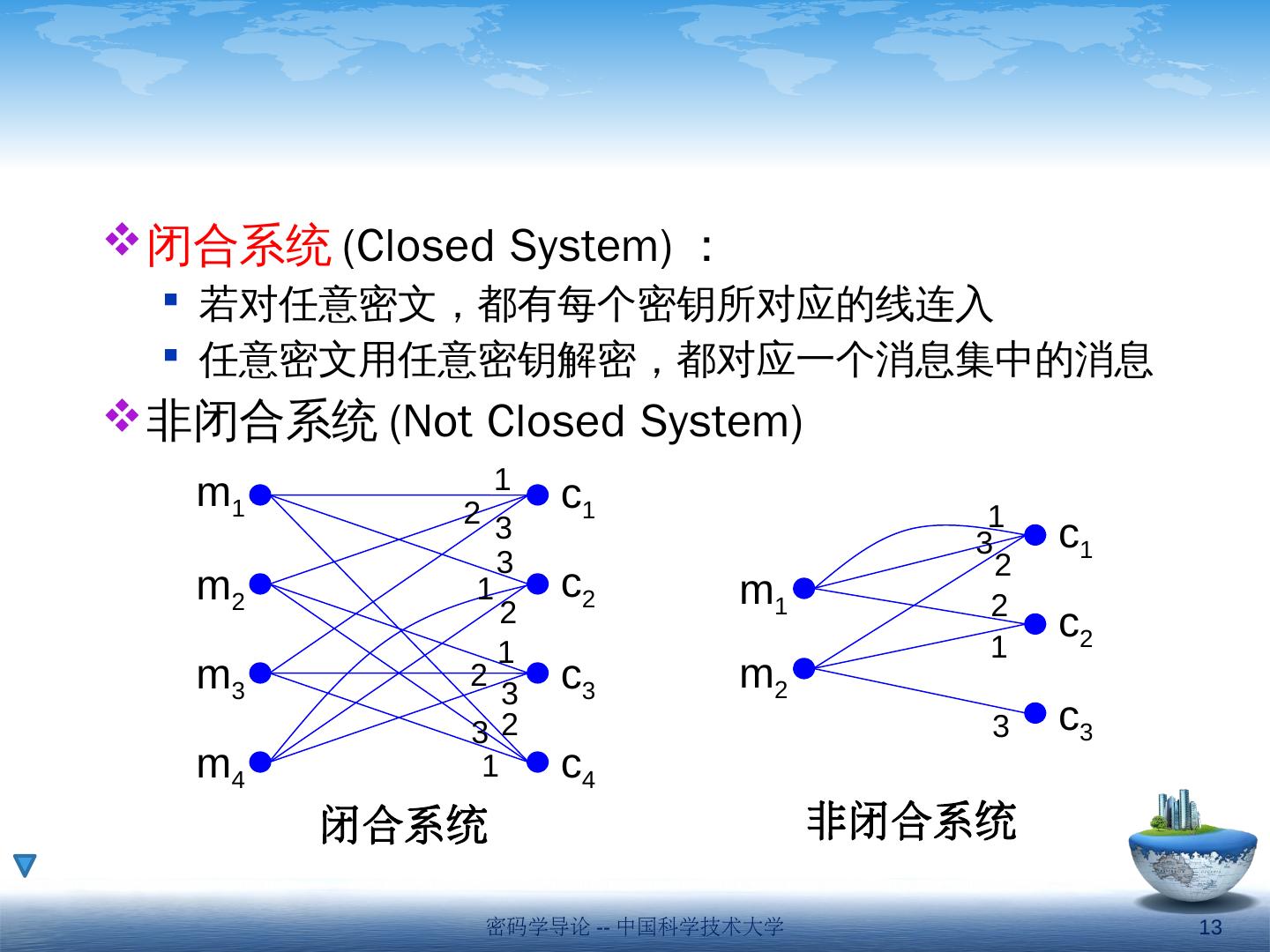
5 .一、概率映射模型 对称密码系统的数学模型 加密算法： c = f( m,k ) = E i (m) 解密算法： m = D i (c) E i D i = I 信源 密钥源 加密器 E i 解密器 D i 消息 m 密钥 k 密钥 k 密文 c 消息 m 密码分析员 密码学导论 -- 中国科学技术大学 5

6 .概率模型 消息空间： 有限消息集合 M 信源 以 先验概率 q 1 ,q 2 ,…, q r 产生消息 m 1 ,m 2 ,…, m r 无意义消息的概率为 0 密钥集空间： 有限密钥空间 K 密钥源以先验概率 p 1 ,p 2 ,…, p s 产生密钥 k 1 ,k 2 ,…, k s 密文空间： 有限密文集合 C 密文 c 1 ,c 2 ,…, c t 的先验概率由消息和密钥的先验概率共同决定 密码学导论 -- 中国科学技术大学 6

7 .概率模型 密码系统： 是一族可逆映射，从 消息空间映射到密文 空间。其中各映射具有一定的使用概率，由实际密钥 确定具体的 映射 可逆映射 E 1 ,E 2 ,…, E s 的使用概率为 p 1 ,p 2 ,…, p s 解密映射 D 1 ,D 2 ,…,D s 分别与加密映射 E 1 ,E 2 ,…, E s 互逆 密码系统相同： 是指映射集、消息空间、密文空间、密钥空间相同，且相应的先验概率相同 密码学导论 -- 中国科学技术大学 7

8 .基本原则 柯克霍夫原则： 公开加密映射族、解密映射族； 公开明文的先验概率 q i 和密钥的先验概率 p i ； 公开密文 仅保密实际消息和实际密钥 密码分析员利用密文和消息、密钥的先验概率，计算消息和密钥的后验概率 当某个消息或密钥的后验概率接近为 1 ，其它的接近 0 时，则该密文被破译，否则密文安全。 密码学导论 -- 中国科学技术大学 8

9 .若干问题的说明 将消息视为一个整体，不考虑消息内部文字间的关系 消息可视为一个马尔克夫链随机过程，不同消息的概率由马尔克夫链决定 这里将消息简化，用一个 符号 m i 代替，并赋予一个 概率 不考虑在明文中插入的无效内容，基本密码系统中不考虑多次加密 只增加了系统的复杂性，没有从根本上改变基本性质 复杂密码系统可以由多个基本密码系统构成 密码学导论 -- 中国科学技术大学 9

10 .可能的密钥与实际的密钥同等重要 策略 游戏（如象棋）中，可能的威胁与实际威胁同等 重要 存在可能的密钥，将密文映射为与明文不同的有意义消息。正是 这些可能的密钥提供了密码系统的 安全性 合法 解密者知道实际的密钥，可以确认明文；窃听者只知道可能密钥的先验概率，无法确认真实明文 密码学导论 -- 中国科学技术大学 10

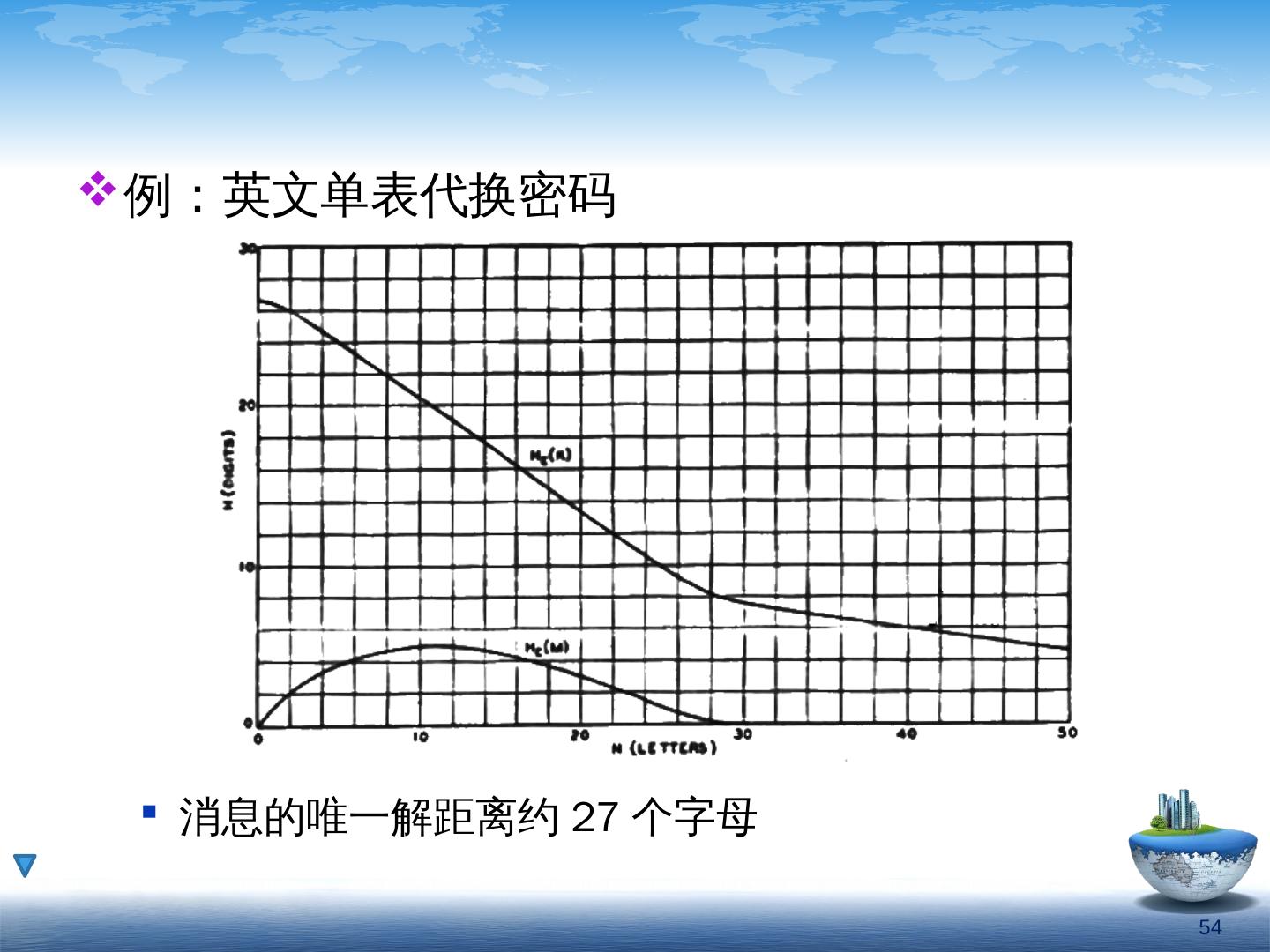
11 .例：英文单表替换加密系统 消息集 若以单字母为消息，则消息的先验概率即普通字母的统计概率 若以单词为消息，则消息的先验概率为词汇的统计概率 若以有意义的句子为消息，则先验概率与具体环境有关 密钥集 有 26! 个可能的等概率密钥 密钥的实际先验概率略高（存在部分不可用密钥） 密文集 与消息和密钥相关 对单字母的模型，当密文长度 N 大于 30 时，平均会有一组消息和密钥的后验概率接近于 1 ，其它的近似为 0 密码学导论 -- 中国科学技术大学 11

12 .密码系统的映射图 左侧是消息集合，右侧是密文集合 某消息在密钥作用下映射用连线表示 对每个消息，每个密钥引出各自的连线 m 1 m 2 m 3 m 4 c 1 c 2 c 3 c 4 1 2 3 1 2 3 1 2 3 1 2 3 密码学导论 -- 中国科学技术大学 12

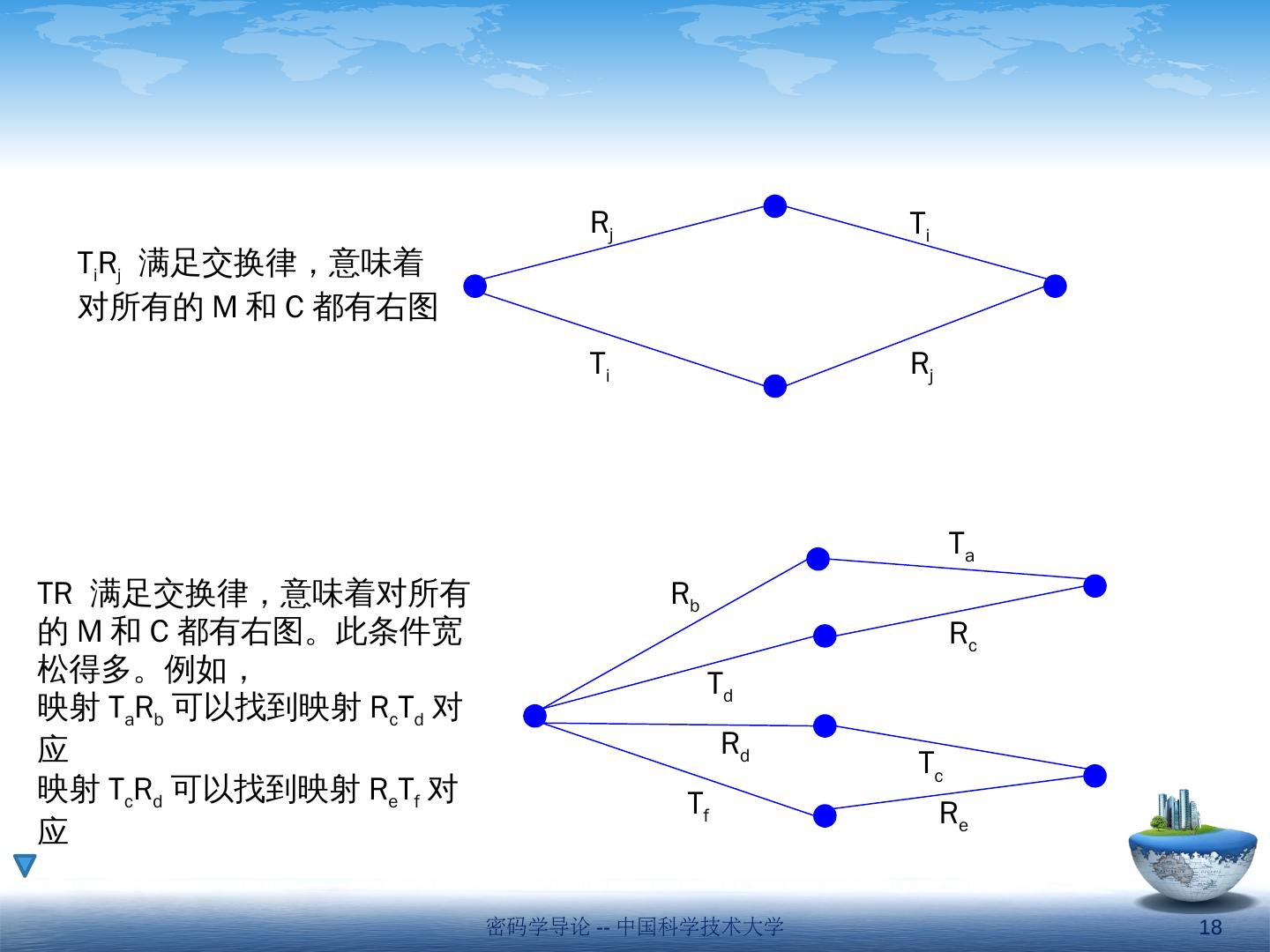
13 .闭合系统 (Closed System) ： 若对任意密文，都有每个密钥所对应的线连入 任意密文用任意密钥解密，都对应一个消息集中的消息 非闭合系统 (Not Closed System) c 1 c 2 c 3 m 1 m 2 1 3 2 2 1 3 闭合系统 非闭合系统 m 1 m 2 m 3 m 4 c 1 c 2 c 3 c 4 1 2 3 1 2 3 1 2 3 1 2 3 密码学导论 -- 中国科学技术大学 13

14 .二、密码系统的运算 1 、密码系统的加权和 若密码系统 T 和 R 的消息空间相同，则加权和系统 S ： 系统 S 先根据部分密钥以概率 p 和 q 选择密码系统 T 或 R ，再用剩余的密钥和选定的系统来加密明文 设系统 T 有映射 T 1 ,T 2 ,…,T m ，概率分别为 p 1 ,p 2 ,…,p m 设 系统 R 有映射 R 1 ,R 2 ,…, R n ， 概率分别为 q 1 ,q 2 ,…, q n 则系统 S 有映射 T 1 ,T 2 ,…,T m ,R 1 ,R 2 ,…, R n ，对应概率为 pp 1 ,pp 2 ,…,pp m , qq 1 ,qq 2 ,…, qq n 密码学导论 -- 中国科学技术大学 14

15 .一般地，若密码系统 T i 的消息空间相同，则加权和系统 S 为： 注意到，密码系统 T i 可以写为映射的叠加 则有 密码学导论 -- 中国科学技术大学 15

16 .2 、密码系统的乘积 若密码系统 R 的消息空间和密码系统 T 的密文空间相同，则存在乘积系统 S ： 系统 S 首先用密码系统 T 加密明文，再将得到的密文用密码系统 R 加密。 设系统 T 有映射 T 1 ,T 2 ,…,T m ，概率分别为 p 1 ,p 2 ,…,p m 设系统 R 有映射 R 1 ,R 2 ,…, R n ， 概率分别为 q 1 ,q 2 ,…, q k 则系统 S 有映射 R 1 T 1 ,R 2 T 1 ,…,R n T 1 ,…,R 1 T m ,R 2 T m ,…, R n T m ，对应概率为 q 1 p 1 ,q 1 p 2 ,…,q 1 p m ,…,q n p 1 ,q n p 2 ,…, q n p m 密码学导论 -- 中国科学技术大学 16

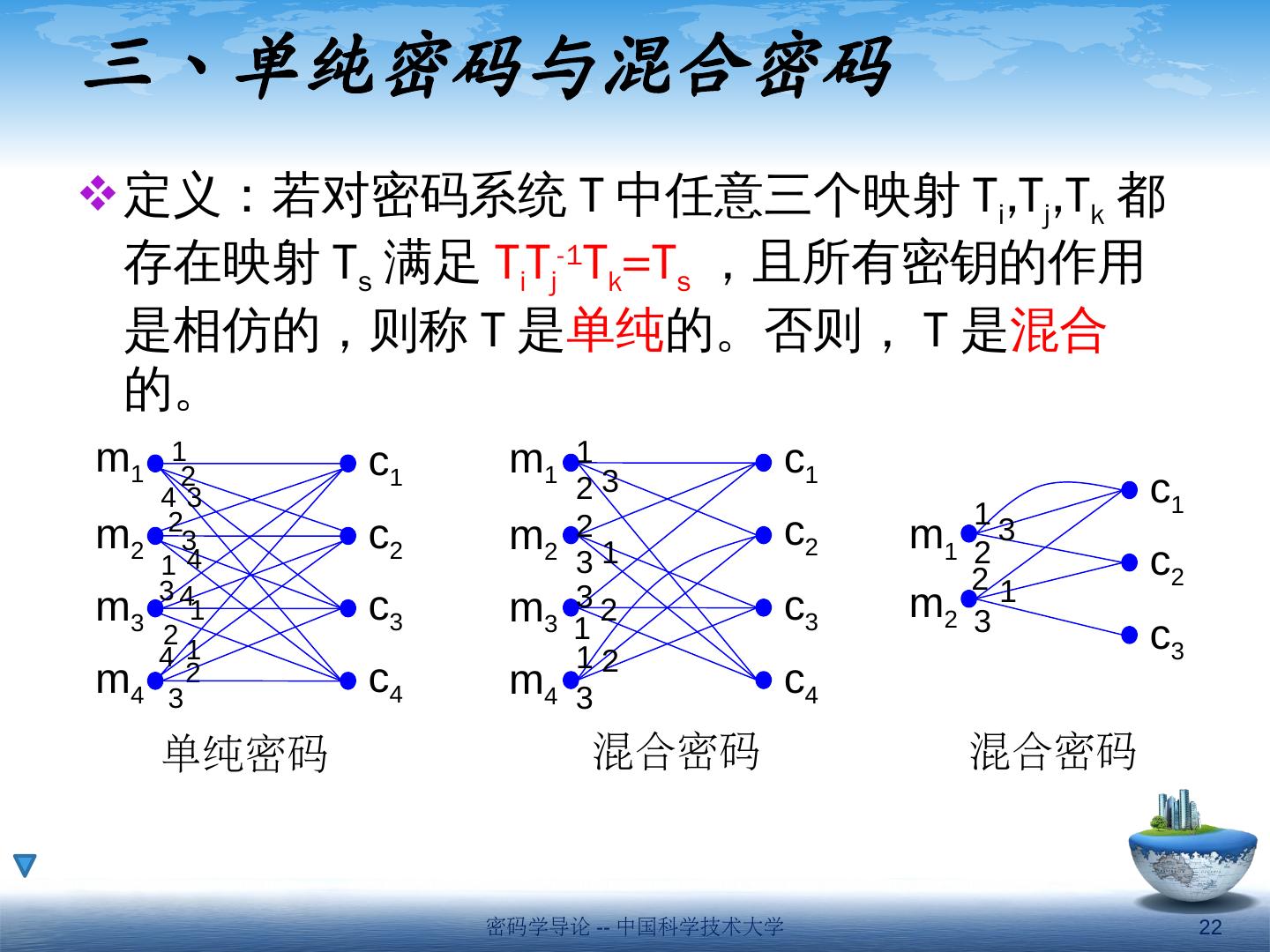
17 .运算律 乘积密码满足结合律 乘积密码一般不满足交换律 特殊情况下可交换，例如单表代换和置换。 若 T i R j 满足交换律，则 TR 满足交换律； 若 TR 满足交换律， T i R j 不一定满足交换律 例如 T a R b = R c T d ， T c R d = R a T b 密码学导论 -- 中国科学技术大学 17

18 .18 密码学导论 -- 中国科学技术大学 T i R j R j T i T i R j 满足交换律，意味着对所有的 M 和 C 都有右图 TR 满足交换律，意味着对所有的 M 和 C 都有右图。此条件宽松得多。例如， 映射 T a R b 可以找到映射 R c T d 对应 映射 T c R d 可以找到映射 R e T f 对应 T a R b R c T d R d T c T f R e

19 .运算律 加权和密码满足结合律 分配律 密码学导论 -- 中国科学技术大学 19

20 .自同构与幂等 定义：若密码系统 T 的消息空间与密文空间相同，则称它是 自同构 的。 若密码系统 T 是自同构的，则可定义指数运算： 定义：若密码系统 T 满足 TT=T ，则称它是 幂等 的。 维吉尼亚密码是幂等的 某确定消息空间上的所有自同构密码系统构成了定义在加权加法和乘法上的代数簇。 密码学导论 -- 中国科学技术大学 20

21 .密码系统运算可用于： 构建新的复杂密码；分析合成密码系统 若密码分析员不知道密码系统，则他将面临解决系统 其中 A,B,…,S 是各种已知可能使用的系统， X 是未知的新系统 密码学导论 -- 中国科学技术大学 21

22 .三、单纯密码与混合密码 定义：若对密码系统 T 中任意三个映射 T i ,T j ,T k 都存在映射 T s 满足 T i T j -1 T k =T s ，且所有密钥的作用是相仿 的 ，则称 T 是 单纯 的。否则， T 是 混合 的。 c 1 c 2 c 3 m 1 m 2 1 3 2 2 1 3 m 1 m 2 m 3 m 4 c 1 c 2 c 3 c 4 1 2 3 1 2 3 1 2 3 1 2 3 m 1 m 2 m 3 m 4 c 1 c 2 c 3 c 4 1 2 3 4 1 2 3 4 2 3 4 1 3 4 2 1 单纯密码 混合密码 混合密码 密码学导论 -- 中国科学技术大学 22

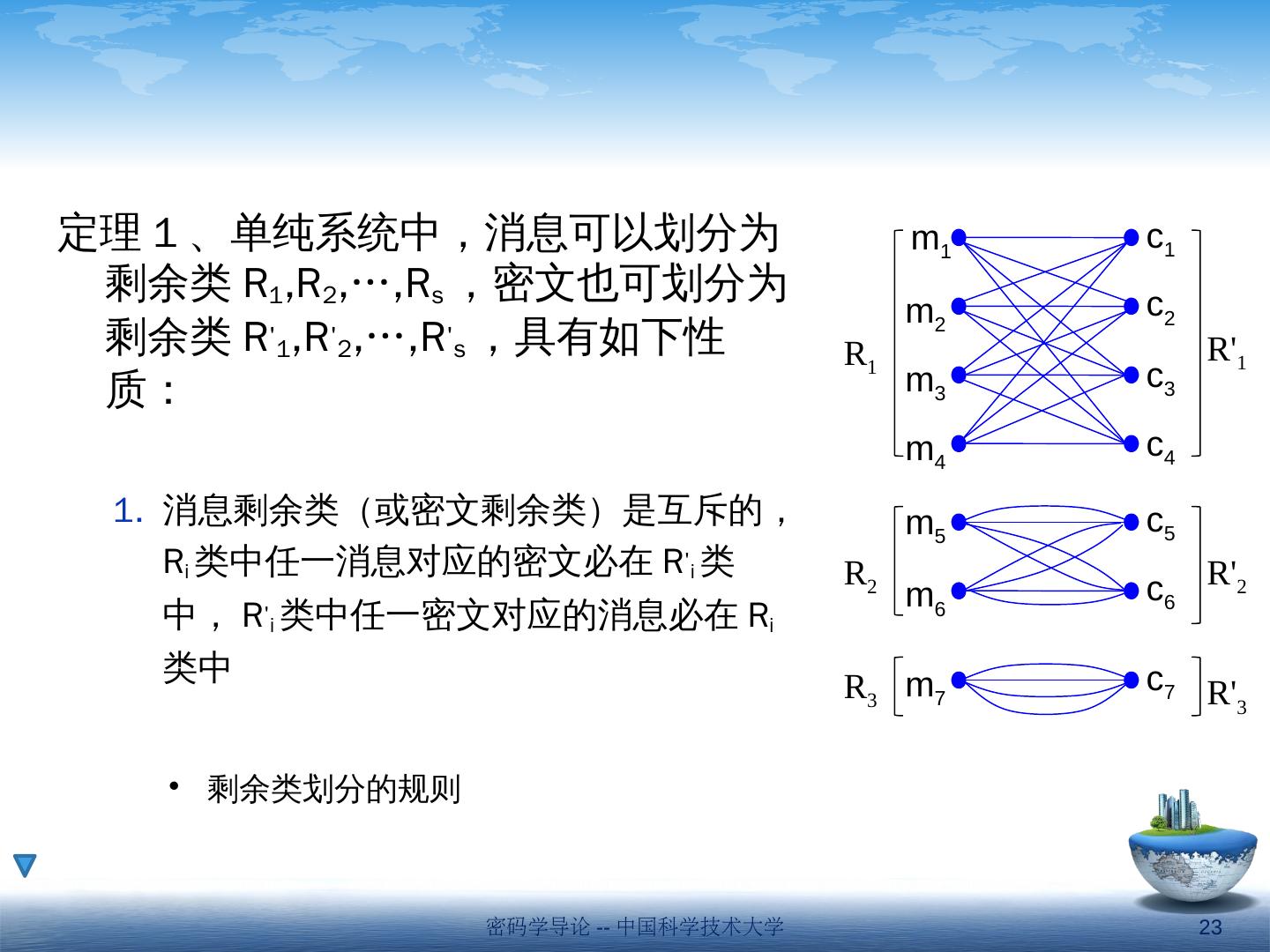
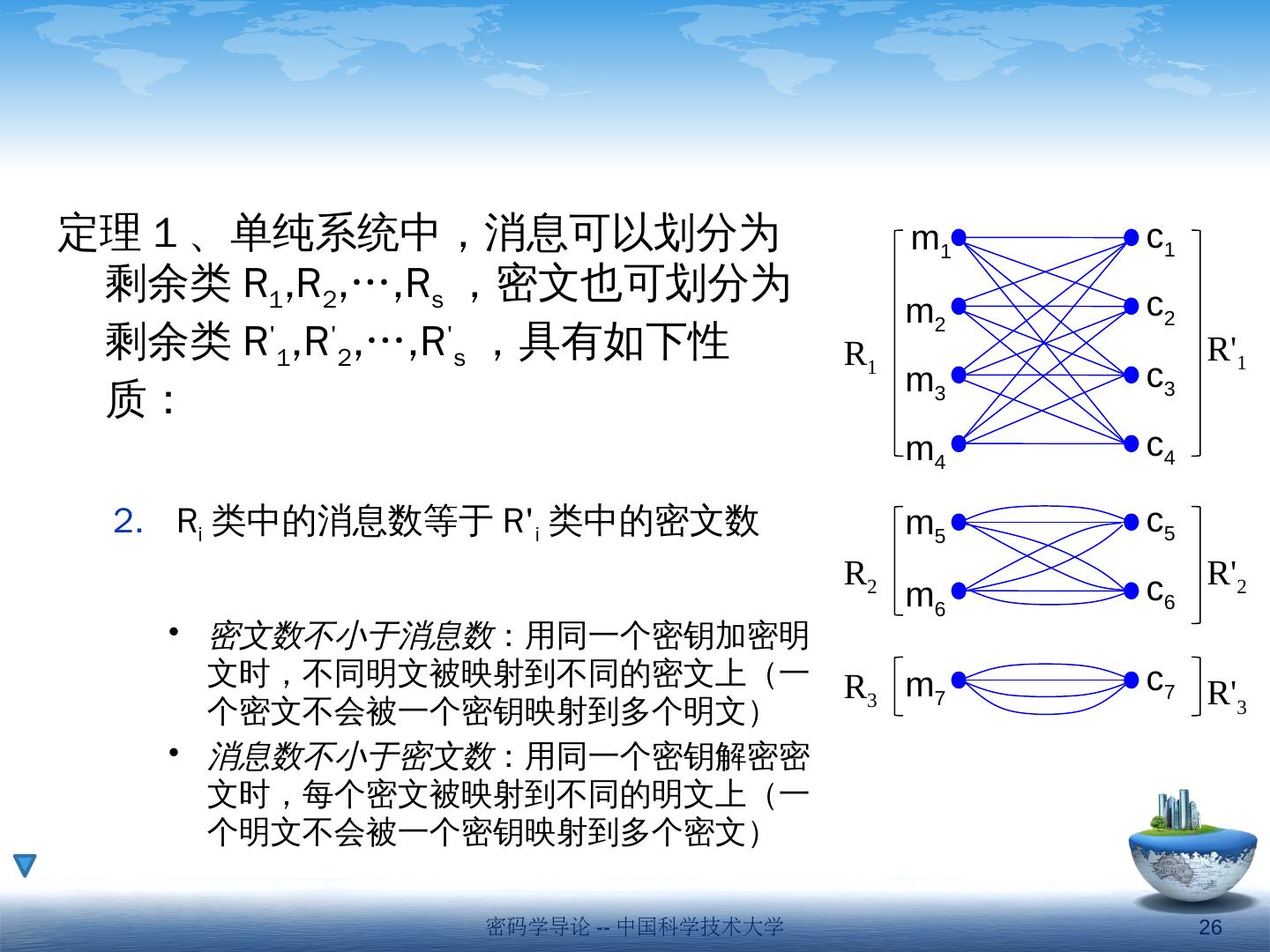
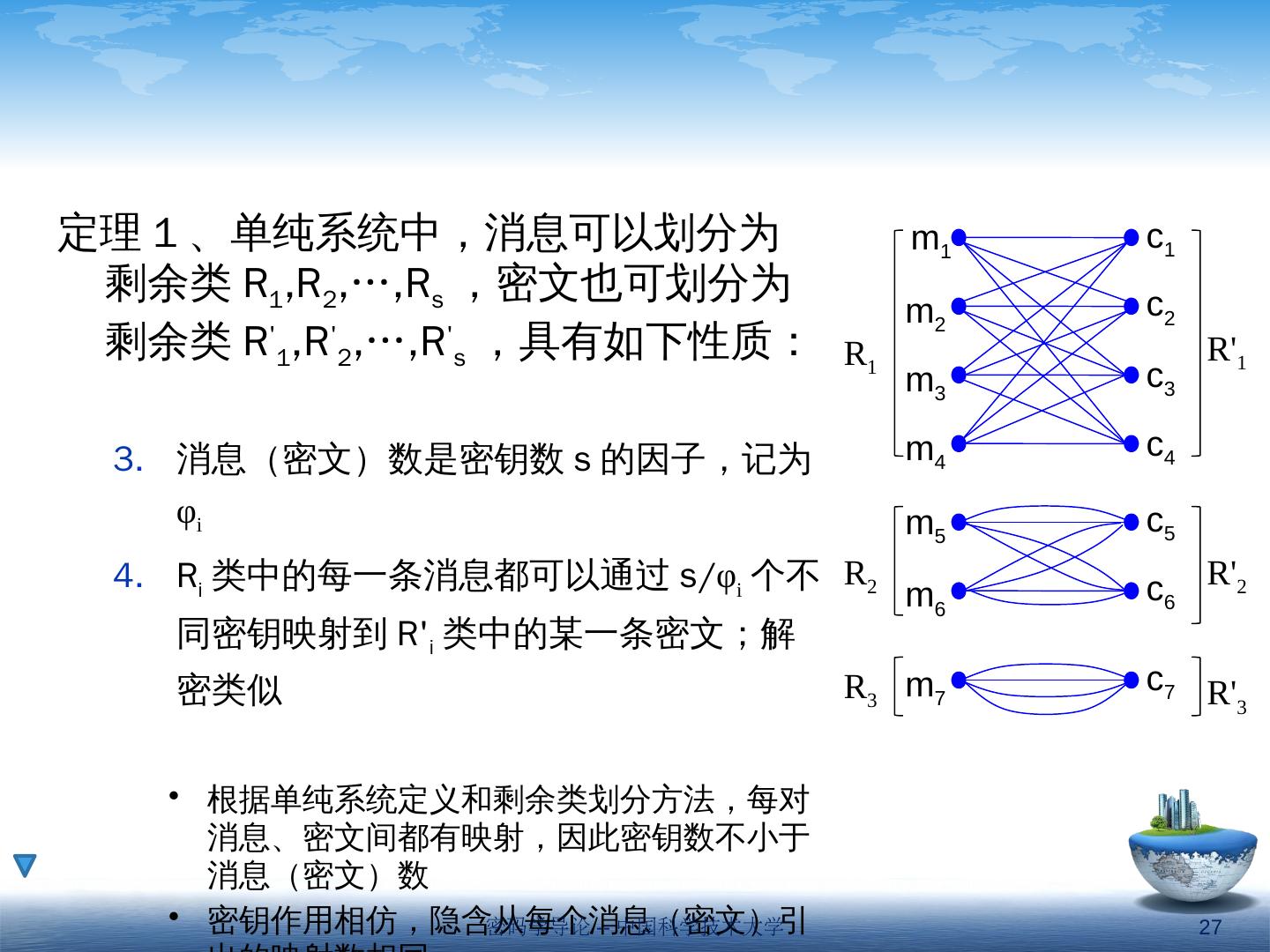
23 .定理 1 、单纯系统中，消息可以划分为剩余类 R 1 ,R 2 ,…,R s ，密文也可划分为剩余类 R 1 ,R 2 ,…,R s ，具有如下性质： 消息剩余类（或密文剩余类）是互斥的， R i 类中任一消息对应的密文必在 R i 类中， R i 类中任一密文对应的消息必在 R i 类 中 剩余类划分的规则 m 1 m 2 m 3 m 4 c 1 c 2 c 3 c 4 m 5 m 6 m 7 c 5 c 6 c 7 R 1 R 2 R 3 R 1 R 2 R 3 密码学导论 -- 中国科学技术大学 23

24 .剩余类集的例子： 单表代换是单纯密码系统。密文 c 与 T i T k -1 c 属于同一剩余类。 例如， c=XCPPGCFQ ， c 1 =RDHHGDSN ， c 2 =ABCCDBEF 等等属于同一剩余类。可以看到，它们有相同的字母重复模式。 凯撒密码中，字母差距恒定的密文属于同一剩余类。 c,c+1,c+2,…,c+25 属于同一剩余类。 破译时，只须列出该剩余类中的其余 25 个消息，挑出有意义的一个。 24

25 .剩余类集的例子： 周期为 d 的维吉尼亚密码是单纯密码系统。消息 c 与跟 c 周期性等差的明文属于同一剩余类。 假设 d=3 ，即指 m 1 -m 4 =c 1 -c 4 , m 2 -m 5 =c 2 -c 5 , m 3 -m 6 =c 3 -c 6 , m 4 -m 7 =c 4 -c 7 , … 周期 为 d 的置换密码是单纯密码系统。剩余类中元素的特征为：字符的移位不跨越长度为 d 的块；两个距离为 d 的字符在置换后距离仍为 d 。 25

26 .剩余类集的例子： 周期为 d 的维吉尼亚密码是单纯密码系统。消息 c 与跟 c 周期性等差的明文属于同一剩余类。 假设 d=3 ，即指 m 1 -m 4 =c 1 -c 4 , m 2 -m 5 =c 2 -c 5 , m 3 -m 6 =c 3 -c 6 , m 4 -m 7 =c 4 -c 7 , … 周期 为 d 的置换密码是单纯密码系统。剩余类中元素的特征为：字符的移位不跨越长度为 d 的块；两个距离为 d 的字符在置换后距离仍为 d 。 25

27 .剩余类集的例子： 周期为 d 的维吉尼亚密码是单纯密码系统。消息 c 与跟 c 周期性等差的明文属于同一剩余类。 假设 d=3 ，即指 m 1 -m 4 =c 1 -c 4 , m 2 -m 5 =c 2 -c 5 , m 3 -m 6 =c 3 -c 6 , m 4 -m 7 =c 4 -c 7 , … 周期 为 d 的置换密码是单纯密码系统。剩余类中元素的特征为：字符的移位不跨越长度为 d 的块；两个距离为 d 的字符在置换后距离仍为 d 。 25

28 .定理 2 、单纯系统中， 同一剩余类中的密文概率相等，与消息的先验概率无关 证明 ：在剩余类 R i 中 消息 的先验分布概率，被密钥的均匀性所 掩盖 密码学导论 -- 中国科学技术大学 28

29 .续定理 2 消息的后验概率与所属剩余类有关，与具体密文无关 证明： 当 时， 当 时， 截获密文无助于分析消息的后验概率   密码学导论 -- 中国科学技术大学 29