- 快召唤伙伴们来围观吧
- 微博 QQ QQ空间 贴吧
- 文档嵌入链接
- 复制
- 微信扫一扫分享
- 已成功复制到剪贴板
08算法设计与分析---NP完全问题
展开查看详情
1 .东南大学计算机学院 方效林 NP 完 全问题
2 .本章内容 NP 问题 NP 完全问题 NP 完全问题证明方法 2
3 .NP 问题 P 问题 (Polynomial) 多项式时间可解的问题 多项式时间: O(n), O( logn ), O( n c ) 非多项式时间: O(2 n ), O(n!) NP 问题 (Non-Deterministic Polynomial) 多项式时间可验证一个解的问题 3 所有 NP 问题都是判定问题,回答 yes 或 no
4 .NP 问题 3CNF-SAT 问题 给定 n 个布尔变 元 , 子句 是 3 个文字 ( 变元或变元的非 ) 的 析取操作 给定 m 个子句的合取操作 问该合取范式的值可否为真? 给定 n 个变元的一个取值 x 1 ,x 2 , …, x n , x i =1 或 0 ,判断能否使合取范式为真,时间复杂度 O(n) ,即多项式时间可判定 C1 C2 C3 x 1 =0 , x 2 =1 , x 3 =0 , 则 c 1 ∧ c 2 ∧ c 3 =1
5 .NP 问题 K 团问题 给定一个图 G 和常数 k , G 有没有 k 团 ? 一 个图 G 的 k 团是 G 的 k 个 顶点的集合,使得这个集合中每对顶点之间都有 边 任取 k 个顶点,判断是否两两之间有边,时间复杂度为 O(n 2 ) ,即多项式时间可判定这 k 个点是否是一个团 5
6 .NP 问题 Hamilton 路径问题 给定无向图 G ,问 是否存在一条路径经过 G 中所有顶点一次且 只经过一 次? 给定 n 个顶点的一个排列 v i1 ,v i2 , …, v in ,依次判断 v ik 和 v i(k+1) 之间是否存在边,时间复杂度 O(n) ,即多项式时间可判定这个排列是否是一条路径 6
7 .NP 问题 最优化问题可与一个判定问题对应 最优化问题: 给定一个图 G ,寻找 最大团 判定问题: 给定一个图 G 和常数 k , G 有没有 k 团? 如何对应 ? 若判定问题多项式时间可解,则可采用二分搜索策略找到最优的 k 反之,若已求解最优化问题,就已求解判定问题 7
8 .NP 完全问题 问题 A 是一个 NP 完全问题,则有 A ∈ NP 问题 ( 多项式时间可 验证 解是否正确 ) 且 B ∈ NP,B ≤ p A 任意 NP 问题 B 都 可多项式时间归约到 A 构造一个多项式时间对应关系 8 NP 问题 P 问题 N P 完全 问题 P ≠ NP 否还不知道, 现在普遍认为 P≠NP
9 .NP 完全问题 引入 NP 完全性的意义 若 某个 NP 完全 问题多项式时间 可 解,则 所有 NP 问题均 可多项式时间求解 ,从而有 P=NP 若 能证明 某个 NP 问题不存在 多项式时间求解算法 ( 即 P ≠ NP), 则 所有 NP 完全 问题 都不存在 多项式时间求解 算法,即有 NP 完全 ∩ P= 。 ∴ NP 完全 问题 是 NP 问题 中 ”” 最难的” 9 NP 问题 P 问题 N P 完全 问题 P ≠ NP 否还不知道, 现在普遍认为 P≠NP
10 .NP 完全问题证明 证明问题 A 是 NP 完全问题分两步: A 是 一个 NP 问题 ( 多项式时间可 验证 解是否正确 ) 从一个已知的 NP 完全问题 A’ ,多项式时间规约到 A 的一个实例 A’’ ,证明 A’ 有解当且仅当 A’’ 有解 10
11 .第一个 NP 完全问题 CNF-SAT 问题 ( 可满足问题 ) 给定 n 个 布尔变量 ,和 m 个 子句, 子句 是 1 个或多个个 文字 ( 变量或变量的 非 ) 的析取操作 如: , 给定这 m 个子句的 合取范式 问该合取范式的值可否为真? 11
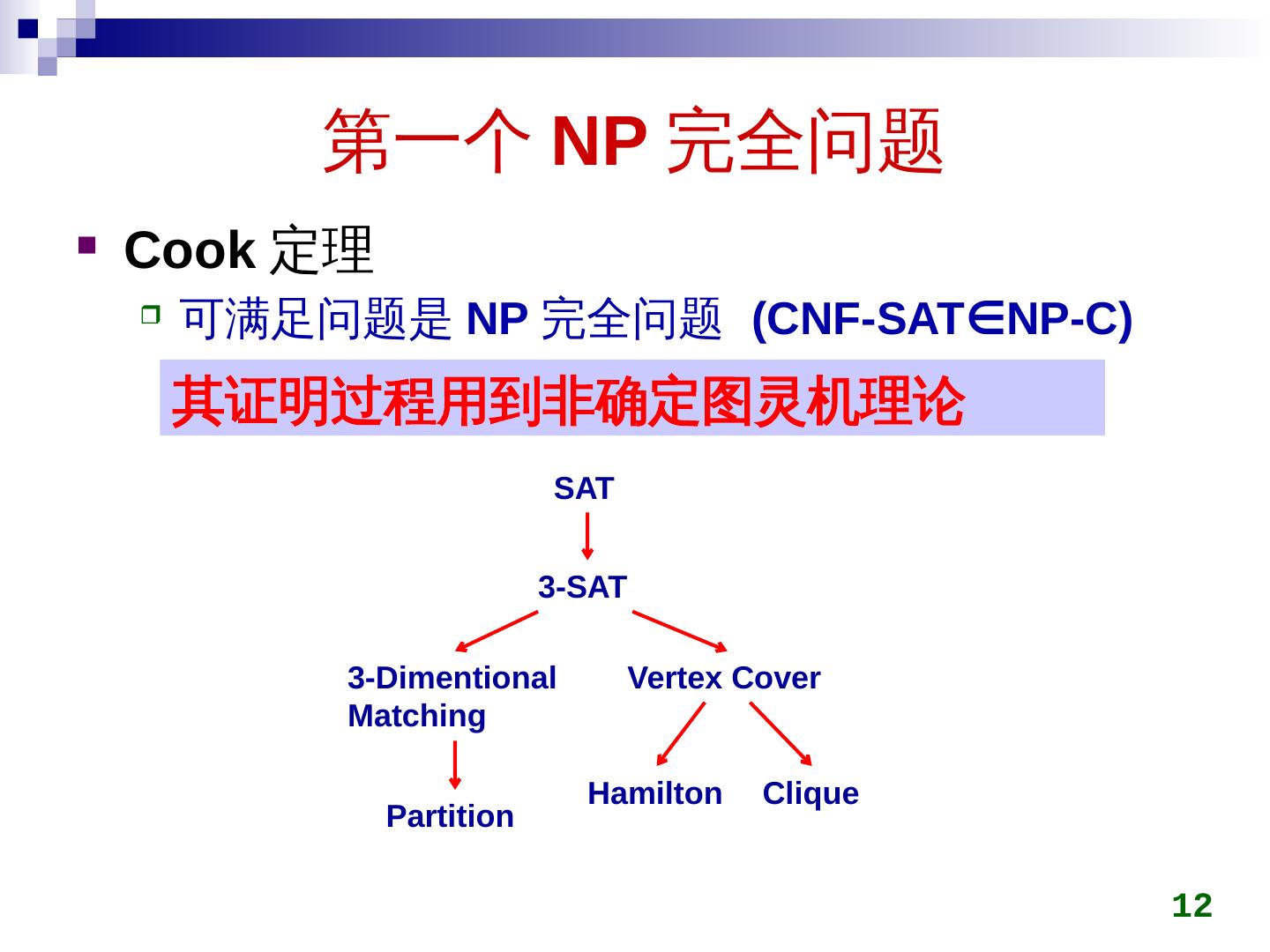
12 .第一个 NP 完全问题 Cook 定理 可满足问题是 NP 完全问题 (CNF-SAT ∈ NP-C) 12 其证明过程用到非确定图灵机 理论 SAT 3-SAT 3-Dimentional Matching Partition Vertex Cover Hamilton Clique
13 .3CNF-SAT 问题是 NP 完全问题 3CNF-SAT 问题 给定 n 个布尔变元和 m 个子句,子句是 3 个文字 ( 变元或变元的非 ) 的析取操作 问这 m 个子句的合取范式的值可否为真? 13 C1 C2 Cm
14 .3CNF-SAT 问题是 NP 完全问题 证明 显然 3CNF-SAT 是 NP 问题 ( 多项式时间可判定 ) 将 CNF-SAT 归约 ( 多项式时间转换 ) 到 3CNF-SAT CNF-SAT 中各子句中文字个数可能为 1 , 2 , 3 或≥ 3 个 时 , 设 。增加两个布尔变量 子句变换为 时 , 设 。增加一个布尔变量 ,子句变换为 时 , 设 。 时 , 设 。增加 个布尔变量 ,子句变换为
15 .3CNF-SAT 问题是 NP 完全问题 证明 显然 3CNF-SAT 是 NP 问题 ( 多项式时间可判定 ) 将 CNF-SAT 归约 ( 多项式时间转换 ) 到某 3CNF-SAT 实例 证明 CNF-SAT 可满足当且仅当构造的 3CNF-SAT 可满足 必要性: CNF-SAT 可 满足 ( 每个 子句都可 满足 ) , 则 3CNF-SAT 可满足 。 时可满足 , 即 ,得 时可满足 , 即 ,得 时可满足 , 即 ,得 时可满足 , 即 ,得
16 .3CNF-SAT 问题是 NP 完全问题 证明 显然 3CNF-SAT 是 NP 问题 ( 多项式时间可判定 ) 将 CNF-SAT 归约 ( 多项式时间转换 ) 到某 3CNF-SAT 实例 证明 CNF-SAT 可满足当且仅当构造的 3CNF-SAT 可满足 充分性 : 3CNF-SAT 可 满足, 则 CNF-SAT 可满足 。 ,得 , 得 , 得
17 .NP 完全问题证明 假设已知 3CNF-SAT 问题是 NP 完全问题 现在要证 k 团问题 顶点覆盖问题 子集和问题 17
18 .k 团问题是 NP 完全问题 k 团问题 给定一个图 G 和常数 k , G 有没有 k 团? 3CNF-SAT 问题 给定 n 个布尔变元和 m 个子句,子句是 3 个文字 ( 变元或变元的非 ) 的析取操作 问这 m 个子句的合取范式 的值可否为真 ? 18
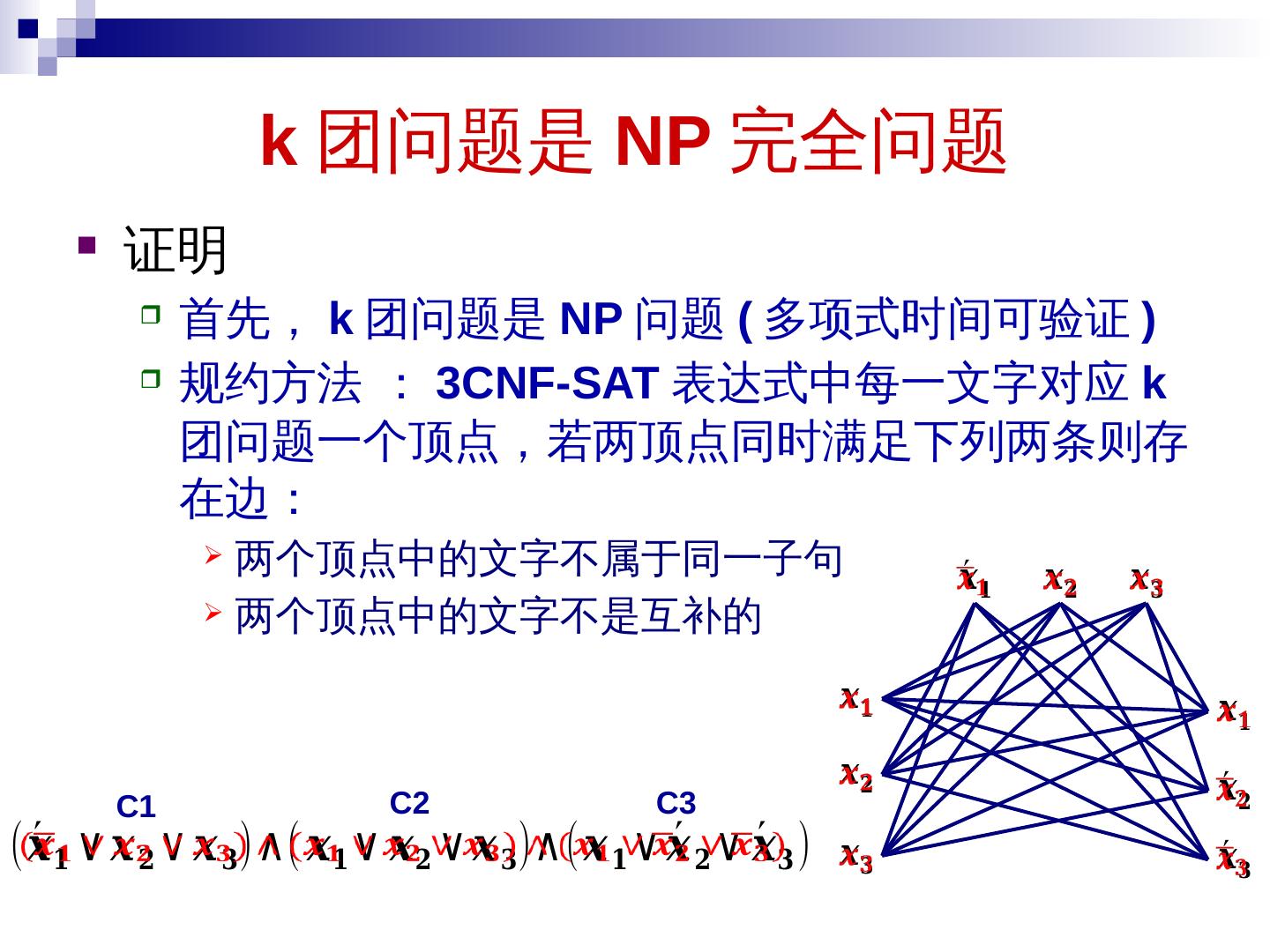
19 .k 团问题是 NP 完全问题 证明 首先, k 团问题是 NP 问题 ( 多项式时间可验证 ) 规约方法 : 3CNF-SAT 表达式中每一文字对应 k 团问题一个顶点, 若两顶点 同时满足下列两 条 则存在 边 : 两个顶点中的文字不属于同一 子句 两 个顶点 中的文字不是互补的 C1 C2 C3
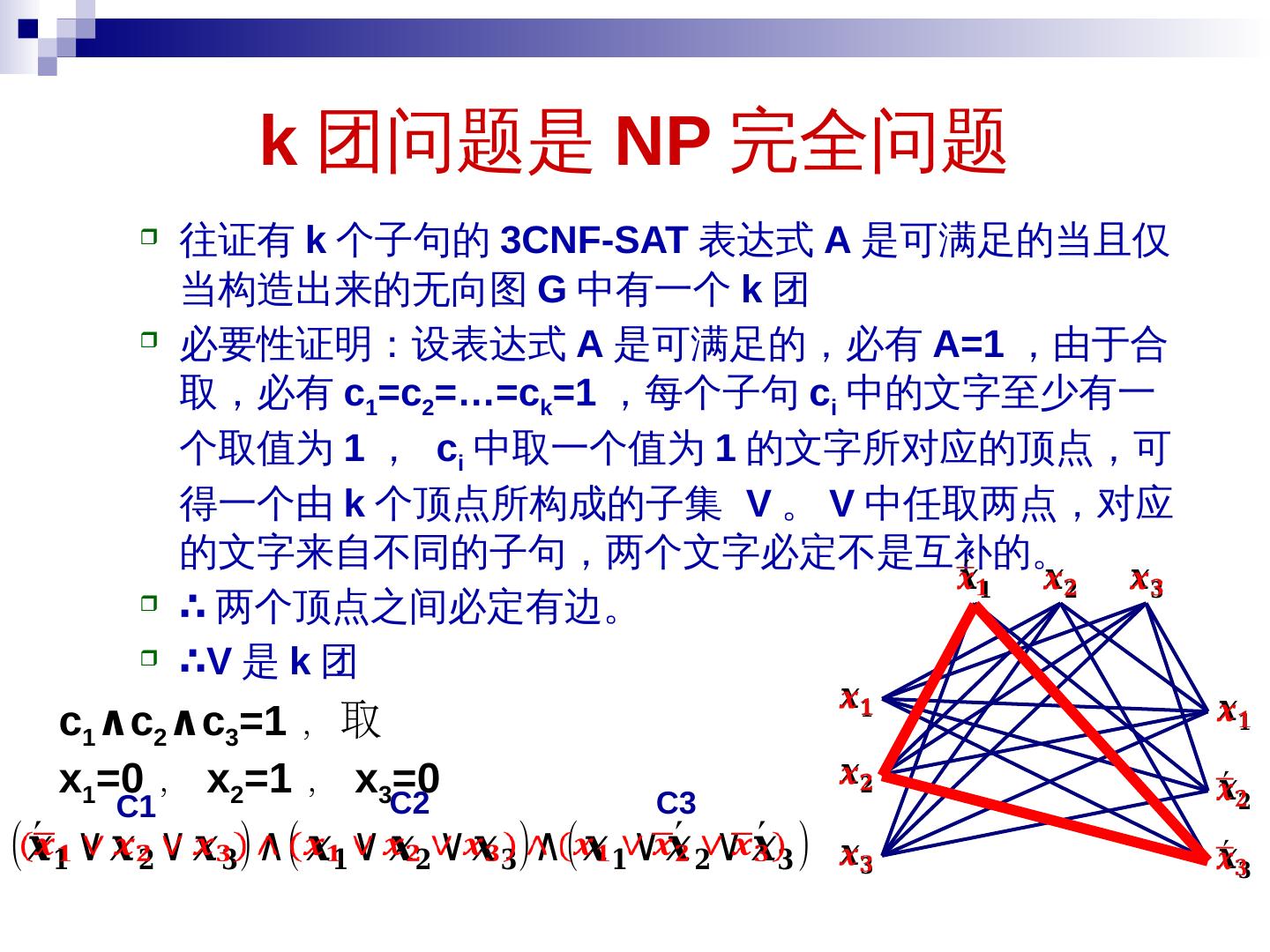
20 .k 团问题是 NP 完全问题 往证 有 k 个子句的 3CNF-SAT 表达 式 A 是 可满足 的 当且仅当 构造 出来的无向图 G 中有一个 k 团 必要性证明 :设表达式 A 是 可满足的 , 必有 A =1 ,由于合取, 必 有 c 1 =c 2 = … = c k =1 , 每个 子句 c i 中的 文字至少 有一个取值为 1 , c i 中 取 一 个 值为 1 的 文字 所对应的顶点 ,可 得一个由 k 个顶点所构成的 子集 V 。 V 中 任取两 点 , 对应 的文字来自不同的子句 ,两 个文字必定不是互补的 。 ∴ 两个顶点之间必定 有边。 ∴ V 是 k 团 C1 C2 C3 c 1 ∧ c 2 ∧ c 3 =1 ,取 x 1 =0 , x 2 =1 , x 3 =0
21 .k 团问题是 NP 完全问题 充分 性证明 : 设 V 是构造出来的无向图中的 k 团, 则 V 中任意两点 间 有边 。 由于同一子句中的顶点无边相连,故 k 个点恰好来自 k 个不同的子句。 现 对这 k 个顶点文字进行 赋值: 若 顶点 文字为 , 则 赋值 1 , 其 所在 子 句 的值为 1 ; 若 顶点 文字 为 , 则 赋值 0 , 其 所在 子 句 的值为 1 由于 与 无边相连 ,这 k 个顶点文字不会同时出现 与 , ∴ 上述的赋值 方法 可使表达式为 1 C1 C2 C3 x 1 =0 , x 2 =1 , x 3 =0 , 则 c 1 ∧ c 2 ∧ c 3 =1
22 .顶点覆盖 问题是 NP 完全问题 顶点覆盖问题 无向图 G 中是否存在顶点数为 k 的顶点覆盖? G 中大小为 k 的顶点集合,使得 G 中 任一条边的两个顶点至少有一个在此集合中 3CNF-SAT 问题 给定 n 个布尔变元和 m 个子句,子句是 3 个文字 ( 变元或变元的非 ) 的析取操作 问这 m 个子句的合取范式的值可否为真? 22
23 .顶点覆盖 问题是 NP 完全问题 证明 首先 , 顶点覆盖问题是 NP 问题 ( 多项式时间可验证 ) 规约方法 : n 个变元对应 2n 个顶点 ( 和 , 共 2n 个 ) , 和 间有边 m 个子句对应 3m 个顶点 (3m 文字 ), 子句内文字两两有边 子句内的文字与变元对应的顶点间有边 令 k=n+2m C1 C2 k=n+2m=3+2 * 2=7
24 .顶点覆盖 问题是 NP 完全问题 往证 3CNF-SAT 表达 式是 可满足 的 当且仅当 构造出来的无向图 G 中有一 个 大小为 k 覆盖集合,其中 k=n+2m 必要性证明: 若表达式可满足 , 则有一种变元 的赋值方式 , 使得表达式为真。 变元对应的 2n 个顶点选择方式:若变元 =1 ,则将 加入集合;若变元 = 0 ,则将 加入 集合。共选择了 n 个 子句对应的 3m 个顶点选择方式: 表达式 可 满足 ,每个子句至少 有一个 文字 值 为 1 ,该文字对应 的 顶点 与变元对应顶点之间的边 已被覆盖 。选择剩下的两个顶点即可,共 2m 个 ∴ G 中有大小为 k=n+2m 的覆盖集合 C1 C2 k=n+2m=3+2 * 2=7 x 1 =0 , x 2 =0 , x 3 =1 , 则 c 1 ∧ c 2 =1
25 .顶点覆盖 问题是 NP 完全问题 充分性证明: 若 G 中有大小为 k=n+2m 的覆盖集合 。 变元对应的 2n 个顶点有 n 条边 , 要覆盖这 n 条边 , 每条边至少得选 1 个顶点,至少共 n 个顶点。 子句对应的 3m 个 顶点是 m 个大小为 3 的团,要覆盖每个大小为 3 的团至少得选 2 个顶点,至少共 2m 个顶点。 必然在 变 元对应 的 2n 个 顶点选 n 个 ( 每条边选一个 ) ; 子句 对应的 3m 个 顶点选 2m 个 ( 每个子句选 2 个 ) 剩哪一个不选?剩 和变元对应的顶点相连的不选 如何对变元赋值使表达式为真? 若选择的变元 对应的顶点为 ,则 赋 1 ; 若 顶点为 ,则 赋 0 C1 C2 k=n+2m=3+2 * 2=7 x 1 =0 , x 2 =0 , x 3 =1
26 .子集和问题是 NP 完全问题 子集和问题 有一个数 集 A ={ a 1 ,a 2 , … ,a n } 及一 个目标数 B , 问 A 中是否能 找出子集 , 使得 ? 3CNF-SAT 问题 给定 n 个布尔变元和 m 个子句,子句是 3 个文字 ( 变元或变元的非 ) 的析取操作 问这 m 个子句的合取范式的值可否为真? 26 A ={2, 5, 3, 6, 8, 9, 11}, B=13 A’={2, 3, 8} ⊆ A , 2+3+8=13
27 .子集和问题是 NP 完全问题 证明 首先 , 子集和问题 是 NP 问题 ( 多项式时间可验证 ) 规约方法 : 3CNF-SAT 有 n 个变元, m 个子句, 构造 2( n+m )+1 个十进制数 ( 每个数 n+m 位 ) : 前 2n 个数: 与 第 i 位 为 1 ,出现在 第 j 个子句, n+j 位 为 1 ,其他位为 0 中间 2m 个数: 与 第 n+j 位为 1 最后一个数: 1……13……3( n 个 1 , m 个 3 ) 1 0 0 0 1 1 0 0 1 0 0 1 0 1 0 0 1 0 0 1 0 0 1 1 0 0 0 1 0 1 0 0 0 1 0 0 0 0 1 0 0 0 0 0 1 0 0 0 0 1 B 1 1 1 3 3 与 在 子集 和 问题中 表示十进制数 C1 C2
28 . 1 0 0 0 1 1 0 0 1 0 0 1 0 1 0 0 1 0 0 1 0 0 1 1 0 0 0 1 0 1 0 0 0 1 0 0 0 0 1 0 0 0 0 0 1 0 0 0 0 1 B 1 1 1 3 3 子集和问题是 NP 完全问题 往证 3CNF-SAT 表达 式是可满足的 当且仅当 构造 出 的前 2( n+m ) 个十进制数中 的 若干个数之和等于 B 必要性证明: 若 3CNF-SAT 表达式 可满足,则有一种变元的赋值方式 , 使得表达式为真 。 若 变元 赋值为 真 , 就 把十进制数 放入 子集 若 变元 赋值 为 假 , 就 把十进制数 放入 子集 此时,选择 的数的和前 n 位中每位均 为 1 , 后 m 位:第 n+i 位可能 为 1 ,可能为 2 ,可能为 3 。 为 1 则 和 均选择加入子集;为 2 则 和 任选 一个加入子集;为 3 则均不选择 此时选择数的和的后 m 位每位均为 3 C1 C2 x 1 =0 , x 2 =0 , x 3 =1
29 . 1 0 0 0 1 1 0 0 1 0 0 1 0 1 0 0 1 0 0 1 0 0 1 1 0 0 0 1 0 1 0 0 0 1 0 0 0 0 1 0 0 0 0 0 1 0 0 0 0 1 B 1 1 1 3 3 子集和问题是 NP 完全问题 充分性证明: 设 2( n+m ) 个数中有若干个加起来恰好为 1 …… 13 …… 3 即使是所有数加和每位最多为 5 ,不会产生进位 和中 前 n 位 中 每位均为 1 ,说明 与 恰好 只 取 了一个。 若 十进制 数 在 子集中,则令 变 元 为 1( 真 ) 若 十进制数 在 子集中,则 令 变元 为 0( 假 ) 和中后 m 位中每位均为 3 即使所有 和 ( 中间 2m 个数 ) 均在子集中, 后 m 位中每位 的 和也不过为 2 ,必然还要加上 前面某个已在子集中的 或 ,和才为 3 C1 C2 x 1 =0 , x 2 =0 , x 3 =1