- 快召唤伙伴们来围观吧
- 微博 QQ QQ空间 贴吧
- 文档嵌入链接
- 复制
- 微信扫一扫分享
- 已成功复制到剪贴板
07算法设计与分析---随机算法
展开查看详情
1 .东南大学计算机学院 方效林 随机 算法
2 .本章内容 随机算法的基本概念 随机采样 问题 第 k 小元素问题的随机算法 Sherwood 随机化方法 判断 字符串是否相等问题 子 串匹配问题 求 最近点对的随机算法 素数 测试 2
3 .随机 算法的基本概念 例子 判断 函数 f(x 1 ,x 2 , … x n ) 在区域 D 中 是否恒为 0 , f 很复杂, 不能 数学 化简 , 如何 判断就很 麻烦 若 随机产生 一个 n 维坐标 (r 1 ,r 2 , … r n ) D , 代入得 f( r 1 ,r 2 , … r n ) ≠ 0 ,则可 判 定区域 D 内 f 不恒为 0 若 对很多个 随机产生的坐标进行测试 ,结果 次次均为 0 , 则 可说 f ≠ 0 的概率是 非常小 有不少问题,目前只有效率很差的确定性求解算法, 但 用随机算法去求解 ,可以很快地获得 相当可信的结果 3
4 .随机 算法的基本概念 随机算法 随机算法是一种使用概率和统计方法在其执行过程中对于下一计算步骤作出随机选择的算法 随机 算法的优越性 对于有些 问题:算法 简单 对于有些 问题:时间复杂性 低 对于有些 问题:同时 兼有简单和时间复杂性 低 4
5 .随机 算法的基本概念 随机算法分类 随机 数值算法 Monte Carlo 算法 Las Vegas 算法 Sherwood 算法 随机数值算法 主要 用于数值问题求解 算法的输出往往是近似解 近似解的精确度与算法执行时间 成正比 5
6 .随机 算法的基本概念 随机算法分类 随机 数值算法 Monte Carlo 算法 Las Vegas 算法 Sherwood 算法 Monte Carlo 算法 主要 用于求解需要准确解的问题 算法可能给出错误解 获得精确解概率与算法执行时间 成正比 6
7 .随机 算法的基本概念 随机算法分类 随机 数值算法 Monte Carlo 算法 Las Vegas 算法 Sherwood 算法 Las Vegas 算法 一旦 找到一个解 , 该解一定是正确 的 找到 解的概率与算法执行时间 成正比 增加 对问题反复求解次数 , 可是求解无效的概率任意 小 7
8 .随机 算法的基本概念 随机算法分类 随机 数值算法 Monte Carlo 算法 Las Vegas 算法 Sherwood 算法 Sherwood 算法 一定 能够求得一个正确 解 确定 算法的最坏与平均复杂性差别大时 , 加入随机性 , 即得到 Sherwood 算法 消除 最坏行为与特定实例的联系 8
9 .随机算法的基本概念 随机算法分析的 目标 平均时间复杂性:时间复杂性 随机变量的均值 获得正确解的概率 获得优化解的概率 解的精确度估计 9
10 .随机数值算法 计算 值 设有 一个半径 为 r 的圆及其 外切 四边形 向 正方形随机地投掷 n 个点 , 设 k 个点 落入圆内 投掷 点 落入圆内 的概率为 ( r 2 )/(4r 2 )= /4 . 用 k/n 逼近 /4, 即 k/n/4, 于是 ( 4k)/n . 10 r
11 .随机数值算法 计算 值 k=0 ; for i=1 to n do 随机地产生四边形中的一点 (x, y); if x 2 +y 2 1 then k=k+1; return (4k)/n ; 时间复杂性 =O(n ) , n 是随机样本 的大小 解的 精确度随着 随机样本大小 n 增加而增加 11
12 .随机数值算法 计算积分 强大数定律 假定 {s(x)} 是相互独立同分布的随机变量序列,如果它们有有限的 数学期望 E(s(x ) )=a , 则 计算积分 令 f(x)=1/(b-a) 为概率密度函数 , a x b { s(x)} 为离散随机变量 , 期望 {s(x)} 若 为连续型的,期望 令 g(x)=s(x)f(x) ,则期望 12 独立同分布
13 .随机数值算法 计算积分 强大数定律 计算积分 令 g(x)=s(x)f(x) ,则期望 13
14 .随机数值算法 计算积分 R=0 ; for i=1 to n do 随机产生 [a, b] 中点 x; R= R+g (x) ; return (b-a )*R/n 时间复杂性 =O(n) , n 是随机样本的大小 解的精确度随着随机样本大小 n 增加而增加 14
15 .第 k 小元素 ( Las Vegas ) 输入: S ={x 1 , x 2 , …, x n } , 整数 k , 1 k n . 输出: S 中第 k 小 元素 . 15
16 .第 k 小元素 (Las Vegas) 随机算法 在 n 个数中随机的找一个数 A[i]=x, 然后 将其余 n-1 个数与 x 比较,分别放入三个数组中 : S 1 ( 元素均 < x ) , S 2 ( 元素 均 = x ) , S 3 ( 元素均 > x) 若 |S 1 | ≥ k 则调用 Select(S 1 ,k) ; 若 |S 1 |<k 但 ( | S 1 |+|S 2 | ) ≥ k ,则第 k 小元素就是 x ; 否则有 (| S 1 |+|S 2 | ) < k ,调用 Select(S 3 ,k-|S 1 |-|S 2 | ) 。 16
17 .第 k 小 元素 (Las Vegas) 定理 若以等概率方法在 n 个数中随机取数 ,则 该算法用到的比较次数的期望值不超过 4n 证明: 设 C(n) 是输入规模为 n 时 ,算法比较次数的期望值 , 并 设取到任一个数的概率 相同 。 假定取到第 j 小的 数 若 j > k ,则需要调用 Select(S 1 ,k ) 。 ∵ |S 1 |= j-1 ( 因为 x 是第 j 小的 数 ) ,∴ 调用 Select(k,S 1 ) 的比较次数的期望值为 C(j-1) 。 若 j = k ,则直接返回第 j 个元素,无需继续进行比较。 若 j < k ,则需要调用 Select(S 3 ,k-j) ( j =|S 1 |+|S 2 | ) 。 ∵ |S 3 | = n-j ,∴ 本 次调用的比较 次数的期望值是 C(n-j)
18 .第 k 小 元素 (Las Vegas) 18 由于 C(i) 是非减 函数 ,即 i < j 时,总有 C(i) ≤ C(j ) , C(n) 在 k= n/2 时取得最大 值 归纳法 证明 C(n)≤4n
19 .第 k 小 元素 (Las Vegas) 归纳法证明 当 n=1 时, C(1) ≤ 4 显然成立 假设当 n<m 时, C(n) ≤ 4n 成立 证明当 n=m 时, 19
20 .Sherwood 随机化 方法 一般过程 若 问题 已经 有 平均 性质较好的确定性算法, 但是该算法在最坏情况下效率不高, 引入 一个随机数 发生器 ( 通常服从均匀分布 ) 将 一个确定性算法改成一个随机 算法 例如: 快速 排序,每次选择一个基准数,比它小的放左边,大的放右边 ,如此递归 平均效率很好,但是最坏情况下,每次选择的基准若都是最小的,或是最大的,算法效率不高 可随机预处理 ( 洗牌 ) ,使输入均匀分布,再运行算法 20
21 .判断字符串是否相等 (Monte Carlo) 设 A 处有一个长字符串 x ( e.g. 长度为 10 6 ), B 处也有一个长字符串 y , A 将 x 发给 B ,由 B 判断是否有 x=y 首先由 A 发一个 x 的长度给 B ,若长度不等 ,则 x ≠ y 若 长度相等,则采用“取指纹”的方法: A 对 x 进行处理,取出 x 的“指纹” ,将指纹发给 B 由 B 检查 x 的指纹是否 等于 y 的指纹 若取 k 次指纹 ( 每次 指纹 不同 ) , 每次两者结果均相同 ,则 认为 x 与 y 是相等的 。 随着 k 的增大,误判率可趋于 0 21
22 .判断字符串是否相等 (Monte Carlo) 字符串 X 的指纹取法 令字符串 x 的 二进制 编码 ,长度为 n ,则 x < 2 n 取 f(x) x(mod p) 作为 x 的 指纹 , 其中 p 是小于 2n 2 的 素数 , p 二进制长度: log 2 p ≤ log 2 (2n 2 ) +1=O(log 2 n ), f(x) 的二进制长度 ≤ log 2 p ,即 传输长度可大大缩短 x 的二进制是 10 6 位, 即 n=10 6 , 则 p < 2 × 10 12 ≈ 2 40.8631 f(x) 位数 不超过 41 位 , 传输一 次 指纹 f 可 节省约 2.5 万倍 根据 下面所做的分析,错判率小于 若取 5 次指纹,错判率小于 22
23 .判断字符串是否相等 (Monte Carlo) 错判 率分析 B 接到 指纹 f(x ) 后 与 f(y ) 比较, 若 f(x ) ≠ f(y ) ,当然有 x ≠ y 。 若 f(x)=f(y ) 而 x y ,此 时是 一个 错 误匹配 错误 匹配 的概率有多大 ? 随机取 一个 小于 2n 2 的 素数 p ,则 对于给定的 x 和 y , 错 判率 P fail = 23 f(x) x(mod p) 作为 x 的指纹
24 .判断字符串是否相等 (Monte Carlo) 错判 率分析 错 判率 P fail = 24 f(x) x(mod p) 作为 x 的指纹 使得 f(x)=f(y ) 的 素数的个数 = 能够整除 |x-y| 的素数的个数 数论定理 1 :设 (n) 是小于 n 的素数个数,则 (n) ≈ 则 小于 2n 2 的素数 的总个数为: (2n 2 ) ≈ 数论定理 2 : a ≡ b (mod p) iff p 整除 |a-b| 数论 定理 3 : 若 a < 2 n ,则能整除 a 的素数个数不超过 (n) 个 ∵ |x-y|<max{ x,y } ≤ 2 n -1 ,∴能整除 |x-y| 的素数个数 ≤ (n) 错判率 P fail = =
25 .判断字符串是否 相等 (Monte Carlo) 25 n=500 1000 10 4 10 5 10 6 10 7 10 8 10 9 (n)= 95 168 1229 9592 78498 664579 5761445 50847478 数论定理 1 :设 (n) 是小于 n 的素数个数,则 (n) ≈
26 .子串匹配问题 给定两个字符串: X = “ x 1 x 2 … x n ” Y = “ y 1 y 2 … y m ” 判断 Y 是否为 X 的子串? 26 X=“main ten ance” , Y =“ten” 是 S 的子串, Y 在 X 中的位置为 4
27 .子串匹配问题 判断 Y 是否为 X 的子串 ? 记 X(j)= x j x j + 1 … x j+m-1 逐一比较 X(j) 的 指纹 f(X(j)) 与 Y 的 指纹 f(Y) f(X(j+1)) 可根据 f(X(j)) 计算,故算法可很快 完 成 不失一般性,令 X 和 Y 都是 0-1 串 ( 二进制编码 ) f(X(j+1 )) = (x j+1 … x j+m )(mod p) = ( 2(x j+1 … x j+m-1 )+ x j+m )(mod p) = ( 2(x j+1 … x j+m-1 )+ 2 m x j - 2 m x j + x j+m )(mod p) = ( 2(x j x j+1 … x j+m-1 ) - 2 m x j + x j+m )(mod p ) = (2 ( (x j x j+1 … x j+m-1 )mod p ) - 2 m x j + x j+m )(mod p) = (2*f(X(j)) – (2 m mod p) x j + x j+m ) ( mod p) 数论定理 4 : ( xy+z )(mod p) =(x(y mod p)+z)(mod p) 被余数都在 p 附近,与 p 相差很小,只需一两次加减法即可求余 [-(p-1), 2p-1]
28 .子串匹配问题 出错的概率 当 Y ≠ X(j) , 但 f(Y)=f(X(j )) 时 产生错误 而 f(Y)=f(X(j )) 当且仅当 p 能整除 |Y-X(j )| 当 p 能整除 |Y-X(j)| 时, p 当然也能 整除 Z = |Y-X(1)|×| Y-X(2 )| × … × | Y-X(j )|× … × | Y-X(n-m+1 )| ∵ | Y-X(j)|<2 m 。 ∴ Z = |Y-X(1 )| |Y-X(2)| … |Y-X(n-m+1)| < ( 2 m ) n-m+1 ≤ 2 mn ∴ 能整除 Z 的素数 的 个数不 超过 ( mn ) 个 P fail = = = 数论 定理 3 : 若 a < 2 n ,则能整除 a 的素数个数不超过 (n) 个
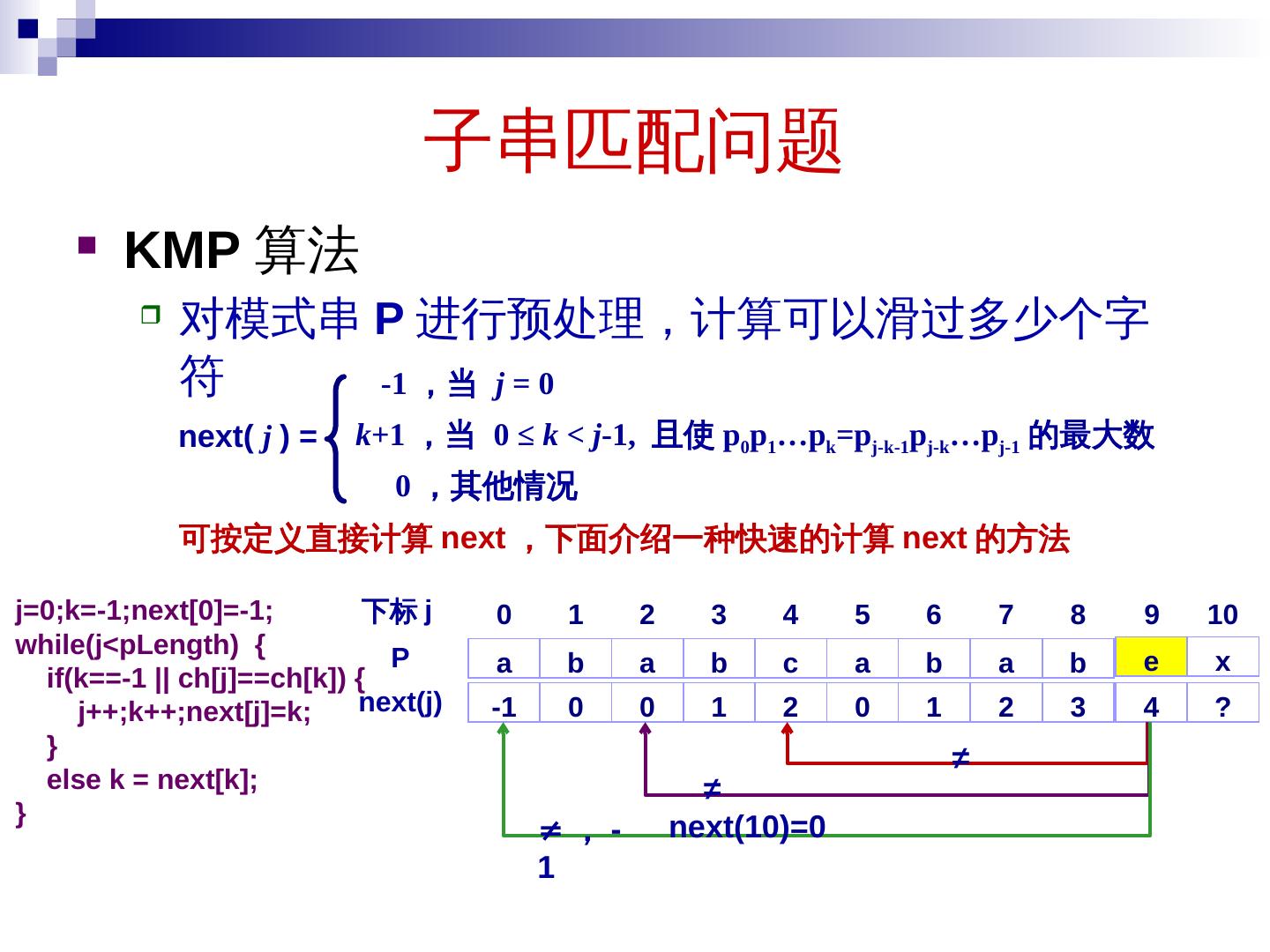
29 .子串匹配问题 字符串的穷举模式匹配算法 匹配失败时,目标串 T 回溯,模式串 P 从头开始 29 P T p 2 p 3 … p m-3 p m-2 p m-1 p 1 p 0 t 2 t 3 … t m-3 t m-2 t m-1 … t 1 t 0 t n-1 p 2 p 3 … p m-3 p m-2 p m-1 p 1 p 0 p 2 p 3 … p m-3 p m-2 p m-1 p 1 p 0 P P 第 1 趟 第 2 趟 第 3 趟 … 时间复杂度 O(m*n) …