05算法设计与分析---贪心算法

1 .东南大学计算机学院 方效林 贪心 算法

2 .本章内容 贪心 算法要素 活动 选择问题 哈夫曼 编码问题 最小生成树 问题 单源 最短路径问题 2

3 .贪心算法要素 贪心算法 的基本思想 求解 最优化问题的算法包含一系列 步骤 每 一步都有一组 选择 作出 在当前看来最好的 选择 希望 通过作出 局部最优选择 达到 全局 最优 选择 贪心算法 不一定总产 生最优解 贪心算法 是否产生优化解，需严格 证明 贪心算法产生最优解的条件 最优子结构 贪心选择性 3

4 .贪心算法要素 最优子结构 当 一个问题的最优解 包含子 问题的最优解时，称这个问题具有最优 子结构 贪心选择性 当一个问题的全局最优解可以通过局部最优解得到，称这个问题具有贪心选择性 证明思路： 假定 首选元素不是贪心选择所要的元素，证明将首元素替换成贪心选择所需元素，依然得到 最优解 数学归纳法 证明每一步均可通过贪心选择得到最优解 4

5 .贪心算法要素 动态规划方法可用的条件 最优子结构 子问题重叠性 贪心算法产生最优解的条件 最优子结构 贪心选择性 适 用贪心算法时，动态规划可能不适用 适用动态规划时，贪心算法可能 不适用 5

6 .活动选择问题 活动 S={1,2,…,n} 是 n 个活动的集合，活动共用同一资源，同一时间只有一个活动 使用 。活动 i 有起始时间 s i ， 终止时间 f i ，s i  f i ，表示为 x i =[ s i， f i ] 相容 活动 活动 i 和 j 是相容的， 若 s j  f i 或 s i  f j 6 s i f i s j f j s i s j f i f j

7 .活动选择问题 问题定义 输入： S={1, 2, …, n}，x i =[ s i， f i ]，1  i  n 输出： S 的最大相容集合 贪心 思想 为了选择更多活动，每次选择 f i 最小的活动 7

8 .活动选择问题 8 S 按结束时间排序， f 1  f 2  ….  f n Greedy-Activity-Selector(S , F) n = length(S ); A = {1}; j = 1; for i = 2 to n do if s i  f j then A = A ∪{i }； j = i ； return A T(n) =  (n)+  ( nlogn ) =  ( nlogn )

9 .活动选择问题 最优子结构性质 设活动 S ={1, 2, …, n } 已按结束时间递增排序 ， 即 f 1  f 2  ….  f n ，设 A 是包括活动 1 的最优解，则 A’=A-{1} 是 S ’ ={i  S|s i  f 1 } 的最优解。 证明： 显然 A’ 中的活动是相容的，只需证 A’ 是最大的。 若不然，假设 B’ 是最大的，且 | B’| > | A’| 。 那么 B={1}∪B ’ 是最优解，但 |B| =1+ | B’| > 1+| A’|=| A| 这与 A 是最大的（最优解）矛盾。 9 问题的最优解包含子问题的最优解

10 .活动选择问题 贪心选择 性 设活动 S={1, 2, …, n} 已按结束时间递增排序 ， 即 f 1  f 2  ….  f n 。每次选 结束时间最小的相容活动，可得最优解 A 。 证明： 设贪心最优解 A 也按结束时间递增排序，设其第一个活动为 k ，第二个活动为 j 若 k=1 ，则成立 若 k1 ，由于 A 中活动相容，有 f k  s j ，由于 f 1  f k ，因此，可以用活动 1 代替活动 k 10

11 .哈夫曼编码 带权路径长度 假设二叉树中每个叶结点有一个权值 w i ， 到根的路径长度为 l i ， 其他结点权值为 0 ，则有 n 个叶子结点的树的带权路径长度为 11 2 4 5 7 2 5 7 4 7 4 2 5 WPL=2*(2+4+5+7)=36 WPL=2+2*4+3*(5+7)=46 WPL=7+2*5+3*(4+2)=35 带权路径长度达到最小的二叉树即为 Huffman 树。 在 Huffman 树中，权值越大的结点离根越近。

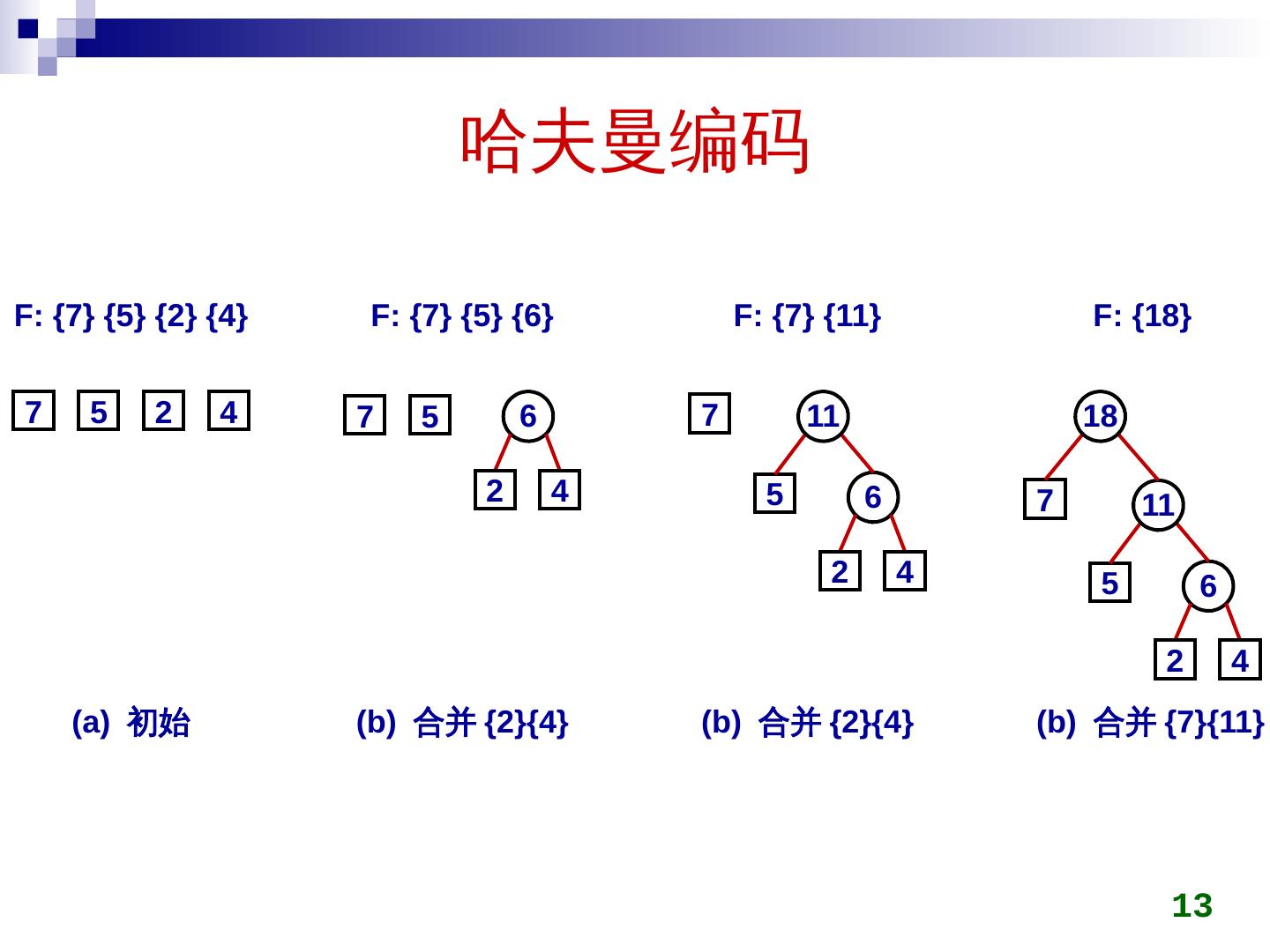
12 .哈夫曼编码 构造权值为 {w 1 ,w 2 , …, w n } 的 Huffman 树 构造 n 棵二叉树的森林 F={T 1 ,T 2 , …, T n } ，每棵二叉树 T i 只有一个带权值为 w i 的根结点 重复以下步骤，直到只剩一棵树为止： 1. 在 F 中选两棵根结点权值最小的二叉树，作为左、右子树构造一棵新的二叉树，新树的根结点权值等于其左、右子树根结点权值之和 2. 在 F 中删除这两棵二叉树 3. 把新构造的二叉树加入 F 12

13 .哈夫曼编码 13 F: {7} {5} {2} {4} 7 5 2 4 (a) 初始 F: {7} {5} {6} (b) 合并 {2}{4} F: {7} {11} (b) 合并 {2}{4} F: {18} (b) 合并 {7}{11} 6 7 5 2 4 6 7 5 2 4 11 6 7 5 2 4 11 18

14 .哈夫曼编码 Huffman 编码，进行数据压缩 计算机领域数据用二进制表示 若已统计出某文本中各字符出现的概率，可以用 Huffman 编码进行数据压缩 14

15 .哈夫曼编码 Huffman 编码，进行数据压缩 假设某文本共有 1000 个字符，且只由 a, b, c, d, e 5 种字符组成 固定长度编码可将每个字符用 3 比特表示，整个文本要 3 * 1000=3000 比特表示，平均编码长度 3 比特 15 符号 定长编码 a 000 b 001 c 100 d 101 e 110

16 .哈夫曼编码 Huffman 编码，进行数据压缩 假设某文本共有 1000 个字符，且只由 a, b, c, d, e 5 种字符组成 若已统计出各字符出现的概率分别为 0.12, 0.40, 0.15, 0.08, 0.25 ，则整个文本可用 2150 比特表示 16 0.2 0.25( e ) 0.15( c ) 0.08( d ) 0.12( a ) 0.35 0.6 0.40( b ) 1.0 0 0 0 0 1 1 1 1 符号 概率 Huffman 编码 a 0.12 1111 b 0.40 0 c 0.15 110 d 0.08 1110 e 0.25 10 平均编码长度 ( 带权路径长度 ) B(T) = 0.12*4 + 0.08*4 + 0.15*3 + 0.25*2 + 0.40*1 = 2.15

17 .哈夫曼编码 17 最 优子结构 T 是字符表 C 一棵哈夫曼树。设字符 x 和 y 是 T 中任意两个相邻叶结点， z 是其父结点， f(x) 和 f(y) 是其频率。将 z 看作频率 是 f(z)=f(x)+f(y) 的字符 ， T ’= T- { x,y } 是字母表 C’= C- { x,y }∪{z} 的哈夫曼树 证明： 若 T’ 不是 C’ 的哈夫曼树 ( 最优 解 ) ， 则必存在 T’’， 使 B(T’’)<B(T’) 。因为 z 是 C’ 中字符，它必为 T’’ 中的 叶子。把 结点 x 与 y 加入 T’’， 作为 z 的子结点 ，得到 C 的哈夫曼树 T’’’ ， B(T’’’)= B(T ’’)+f(x)+f(y)< B(T ’)+ f(x)+f(y )<B(T) 。这与 T 是 C 的哈夫曼树矛盾。 z x y T T’ z 问题的最优解包含子问题的最优解

18 .哈夫曼编码 18 贪心选择性 设 C 是字符表，字符 x 和 y 是 C 中频率最小的两个字符，则存在一棵哈夫曼树，使得 x 与 y 编码长度最长 ( 即到根路径长度最长 ) 证明： 假设一哈夫曼树编码长度最长的不是 x 和 y ，是 a 和 b ，且 f(a)≥f(x), f(b) ≥ f(y), 则 L(a ) ≥L(x), L(b ) ≥L(y), L 指编码长度，如左图所示。分别将 a 和 x ， b 和 y 交换，得到 B(T’) = B(T) -f(x)L(x)-f(y)L(y)-f(a)L(a)-f(b)L(b) +f(x)L(a)+f(y)L(b)+f(a)L(x)+f(b)L(y) =B(T)+( fx-fa )(La-Lx)+( fy-fb )( Lb -Ly) ≤ B(T) x y a b T a b x y T’ 优先选择频率最小的 x 和 y 结果并不会变坏

19 .并查集 互不相交的集合 ( 等价类的划分 ) 需要经常合并集合 ( 等价类的合并 ) 需要经常查找元素属于哪个集合 19

20 .并查集 并查集支持以下操作 初始化 UFSets(s) : 将 s 中每个元素自成一个集合 合并 Union(Root1,Root2) : 集合 Root2 并入 Root1 查找 Find(x) : 查找元素 x 属于哪个集合 20

21 .并查集 用树表示集合 初始化时，每个元素自成为一棵树 21 3 4 1 2 5 6 7 8 9 0 全集合 S 初始化时形成的森林 初始化时形成的父指针表示 负数表示没有父结点 -1 表示树中有 1 个结点 -2 表示有 2 个结点， 以此类推 下标 父指针 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 2 3 4 5 6 7 1 0 8 9

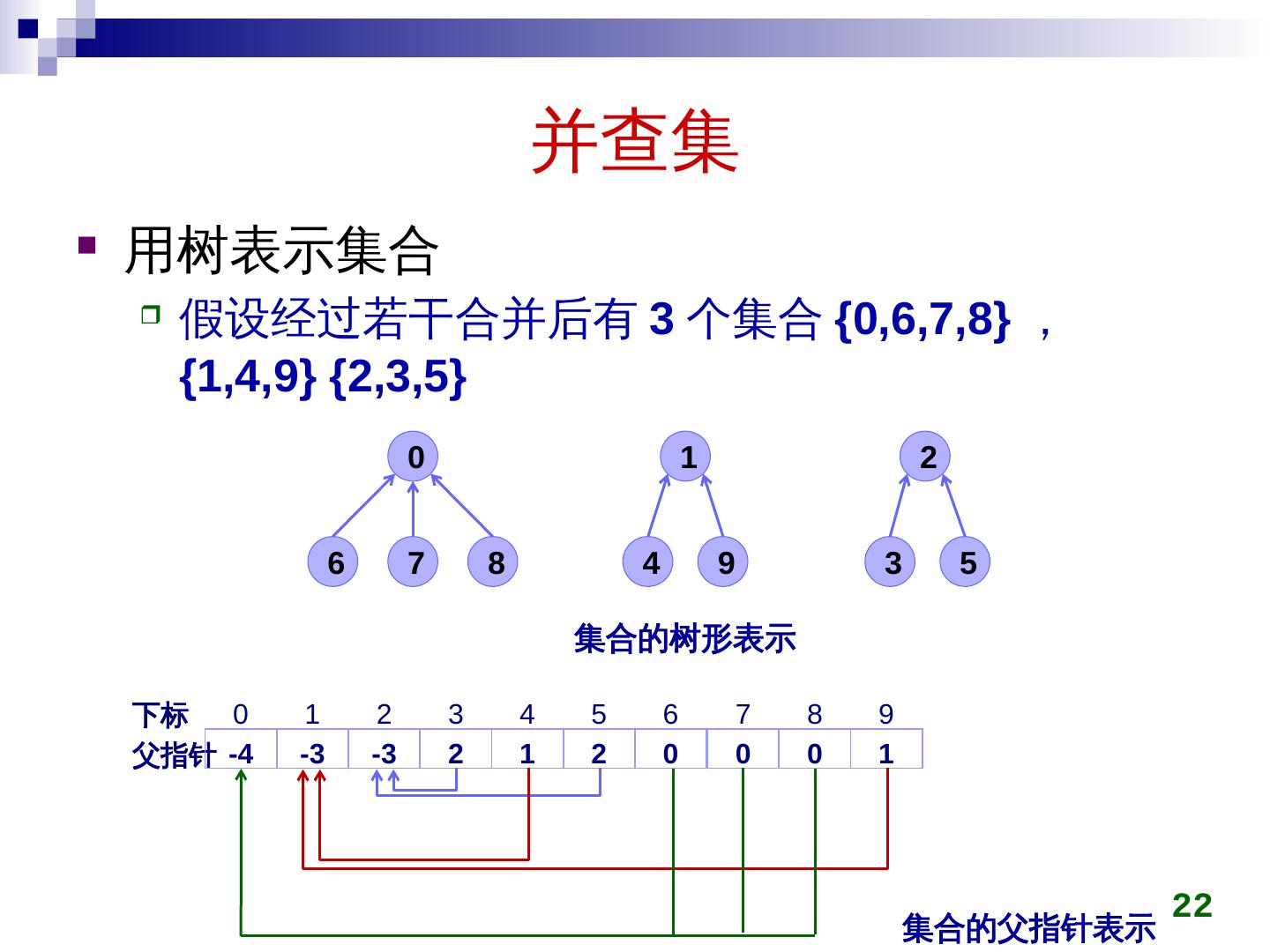
22 .并查集 用树表示集合 假设经过若干合并后有 3 个集合 {0,6,7,8} ， {1,4,9} {2,3,5} 22 8 6 7 0 集合的树形表示 集合的父指针表示 2 3 5 1 4 9 下标 父指针 2 3 4 5 6 7 1 0 8 9 -3 2 1 2 0 0 -3 -4 0 1

23 .并查集 用树表示集合 合并 s 1 ={0,6,7,8}  s 2 = {1,4,9} s 2 作为 s 1 根的子树，或相反 23 8 6 7 0 合并集合 8 1 6 7 4 9 0 8 1 6 7 4 9 0 第一种合并方式 第二种合并方式 1 4 9  第一种合并的父指针表示 下标 父指针 2 3 4 5 6 7 1 0 8 9 -3 2 0 2 0 0 0 -7 0 0

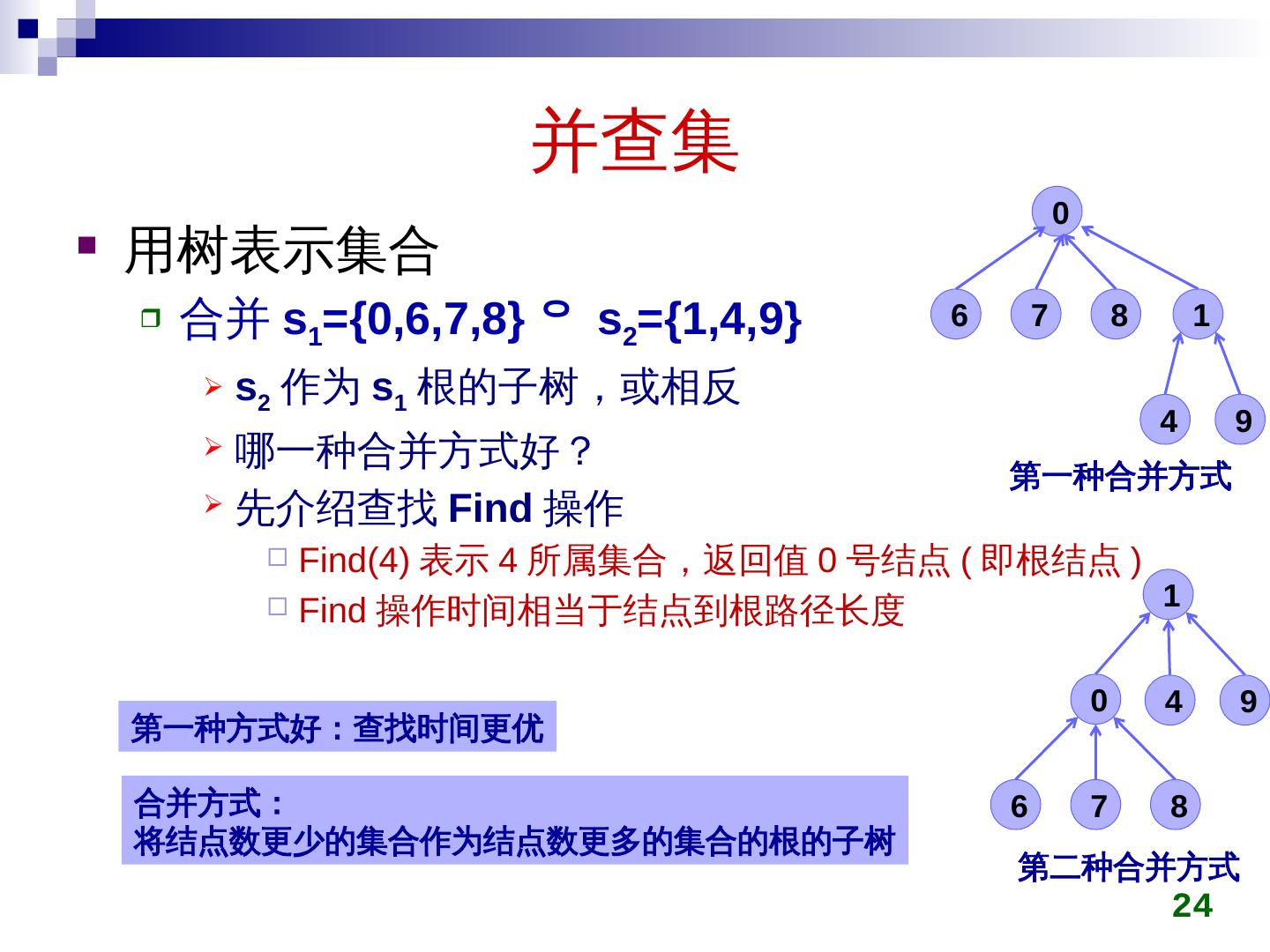
24 .并查集 用树表示集合 合并 s 1 ={0,6,7,8}  s 2 = {1,4,9} s 2 作为 s 1 根的子树，或相反 哪一种合并方式好？ 先介绍查找 Find 操作 Find(4) 表示 4 所属集合，返回值 0 号结点 ( 即根结点 ) Find 操作时间相当于结点到根路径长度 24 8 1 6 7 4 9 0 8 1 6 7 4 9 0 第一种合并方式 第二种合并方式 第一种方式好：查找时间更优 合并方式： 将结点数更少的集合作为结点数更多的集合的根的子树

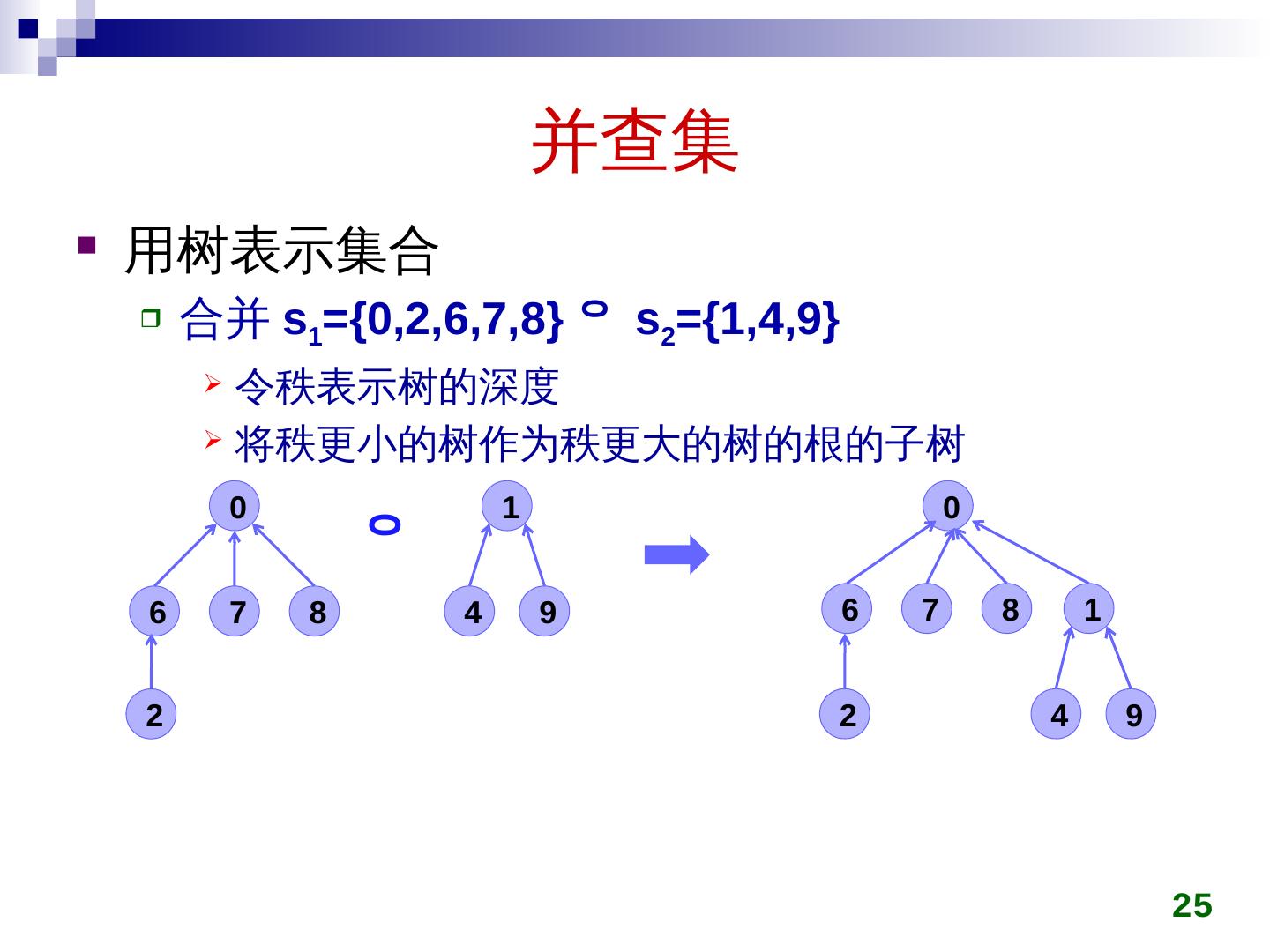
25 .并查集 用树表示集合 合并 s 1 ={0,2,6,7,8}  s 2 = {1,4,9} 令秩表示树的深度 将秩更小的 树 作为秩更大的 树的根的子树 25 8 6 7 0 1 4 9  2 8 1 6 7 4 9 0 2

26 .并查集 用树表示集合 路径压缩，在 find 过程中顺便压缩 26 1 0 2 3 3 1 2 0 按秩合并与路径压缩方式， 操作的平均代价为

27 .最小生成树 生成树 设 G=(V, E) 是一个边加权无向连通图。 G 的生成树是无向树 S=(V, T), T  E 。 W 是 G 的权函数 , T 权 值 定义为 W(T )=  ( u,v )T W( u,v ) 最小生成树 G 的最小生成树是 W(T) 最小的 G 的生成树 问题 的 定义 输入 : 无向连通图 G=(V, E), 权函数 W 输出 : G 的最小生成树 27

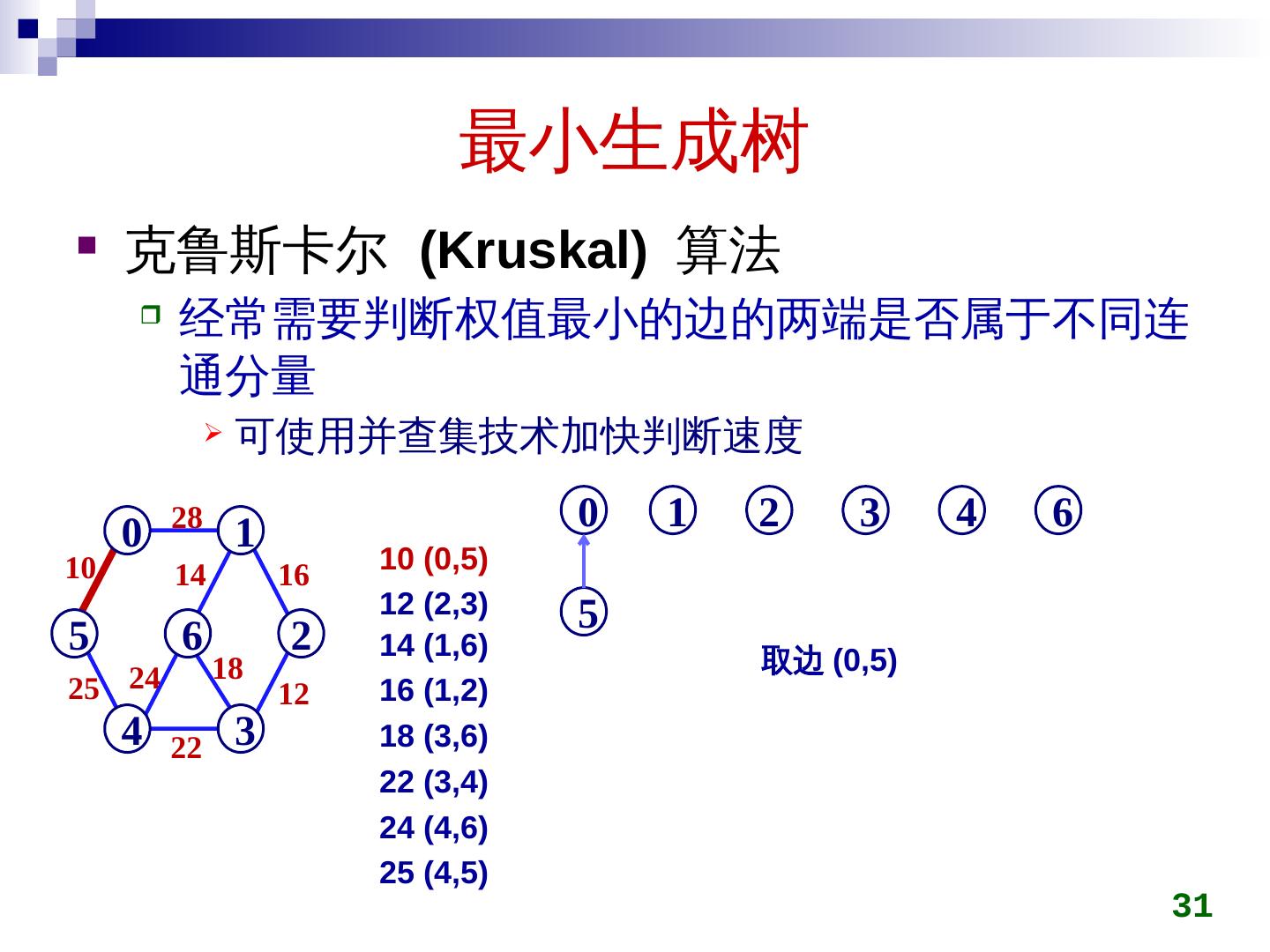
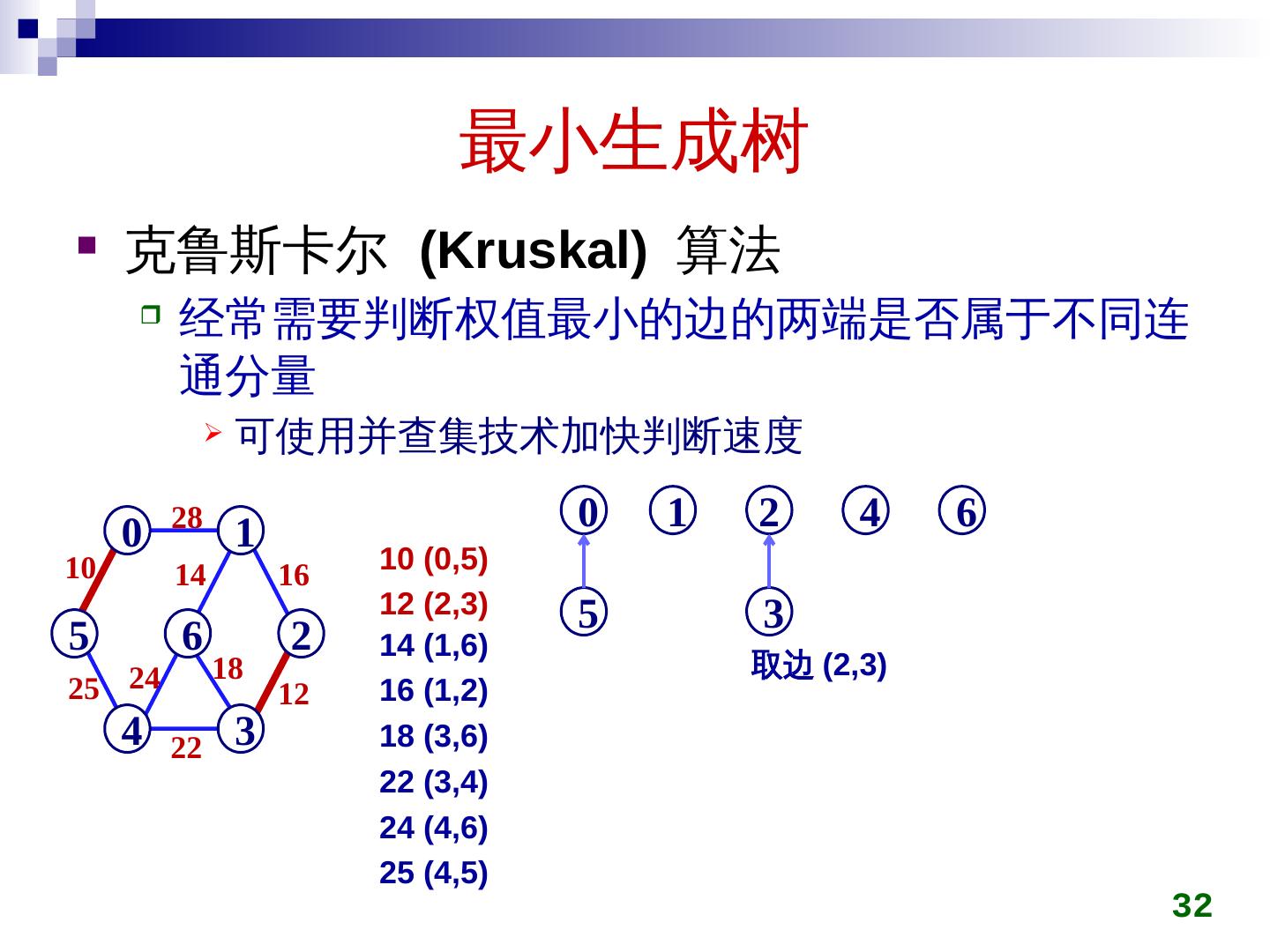
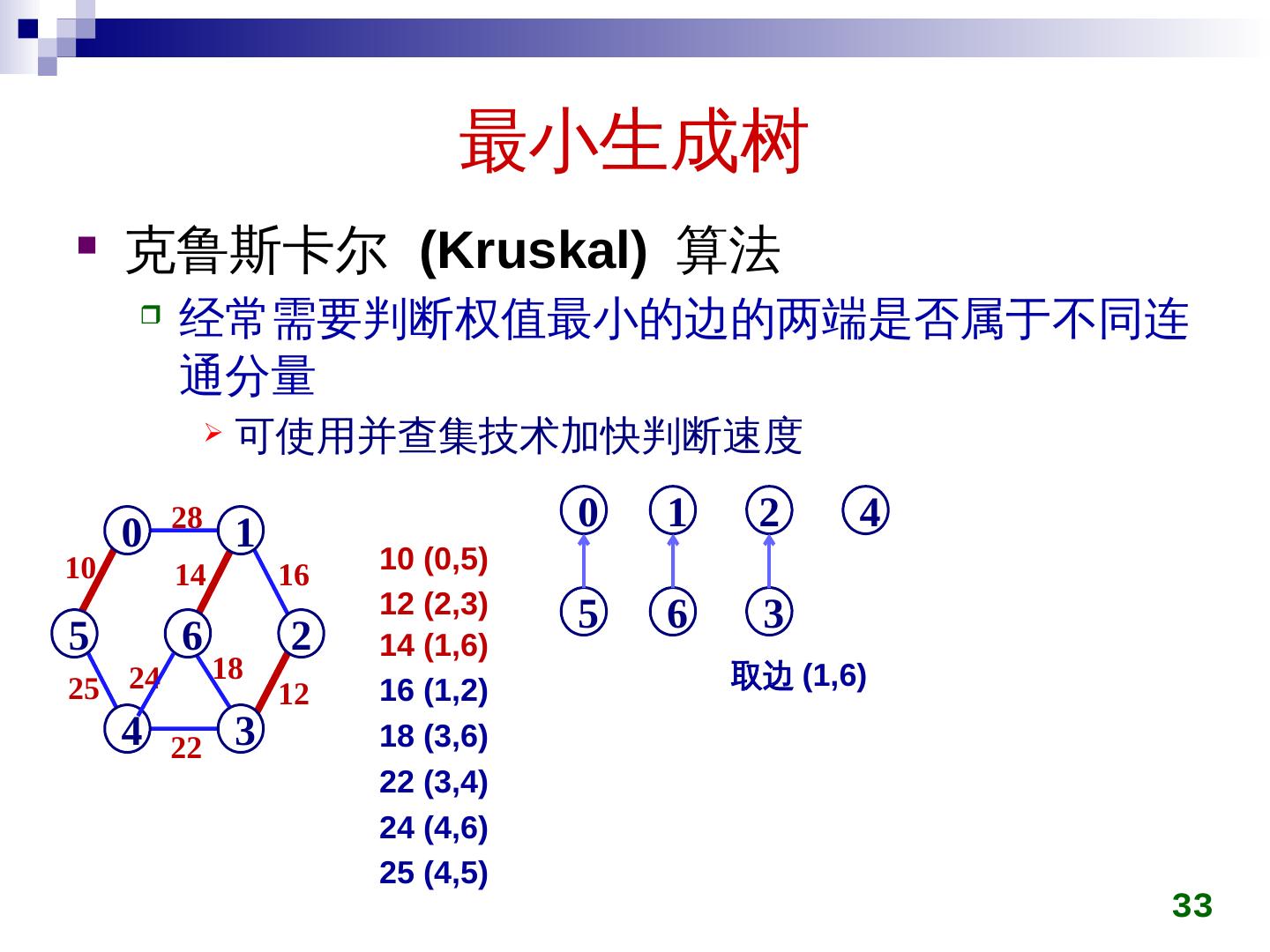
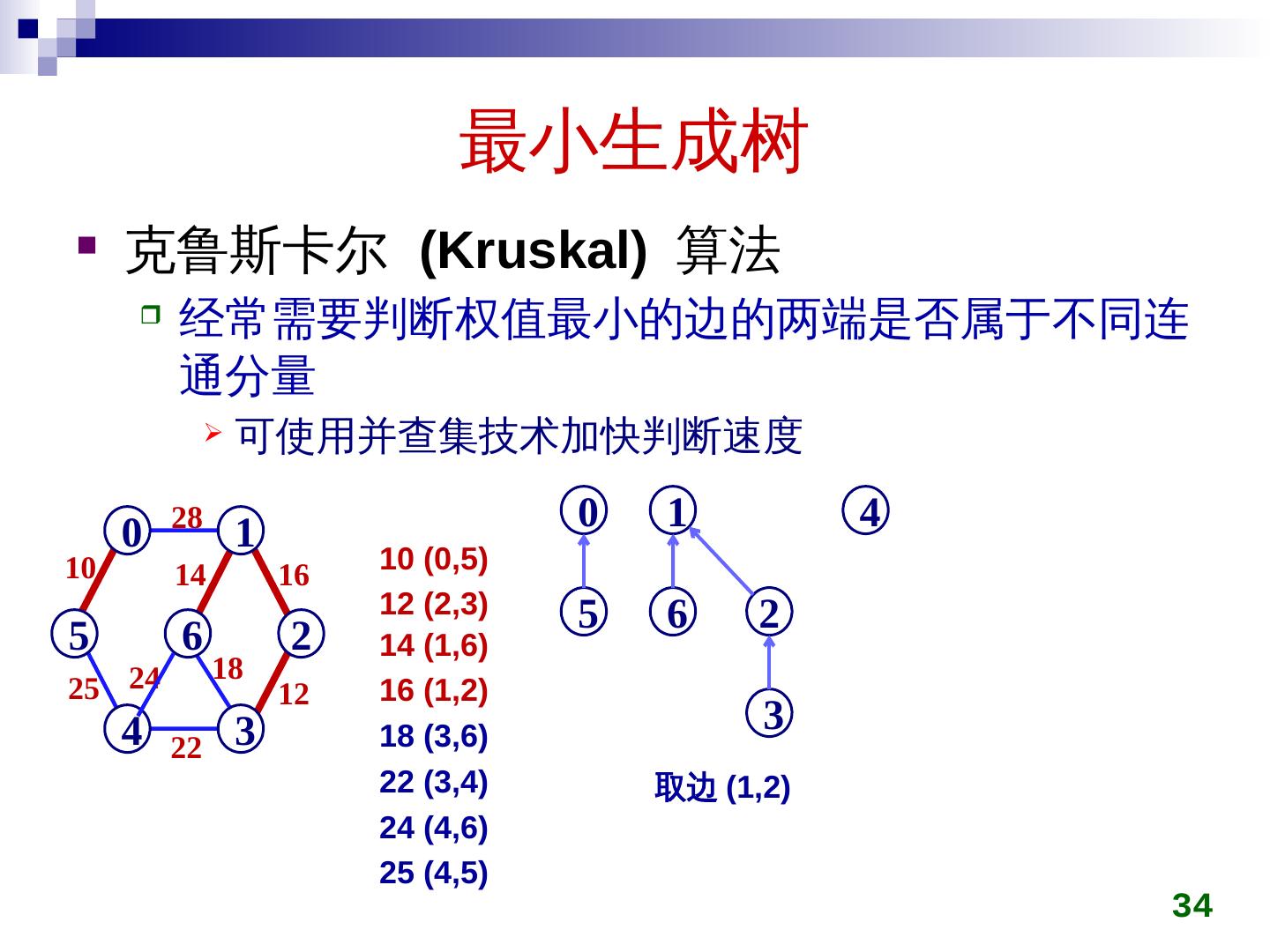
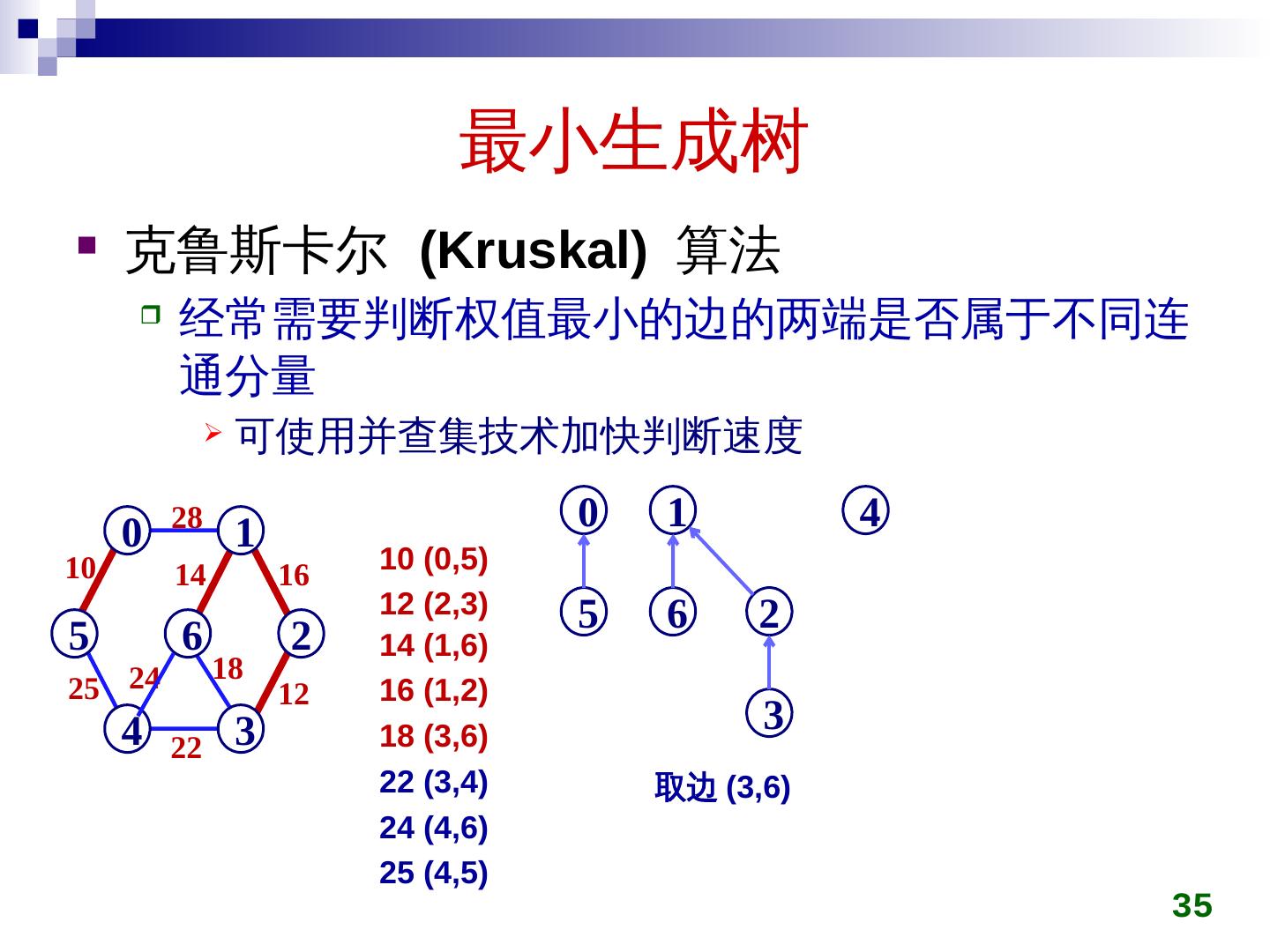
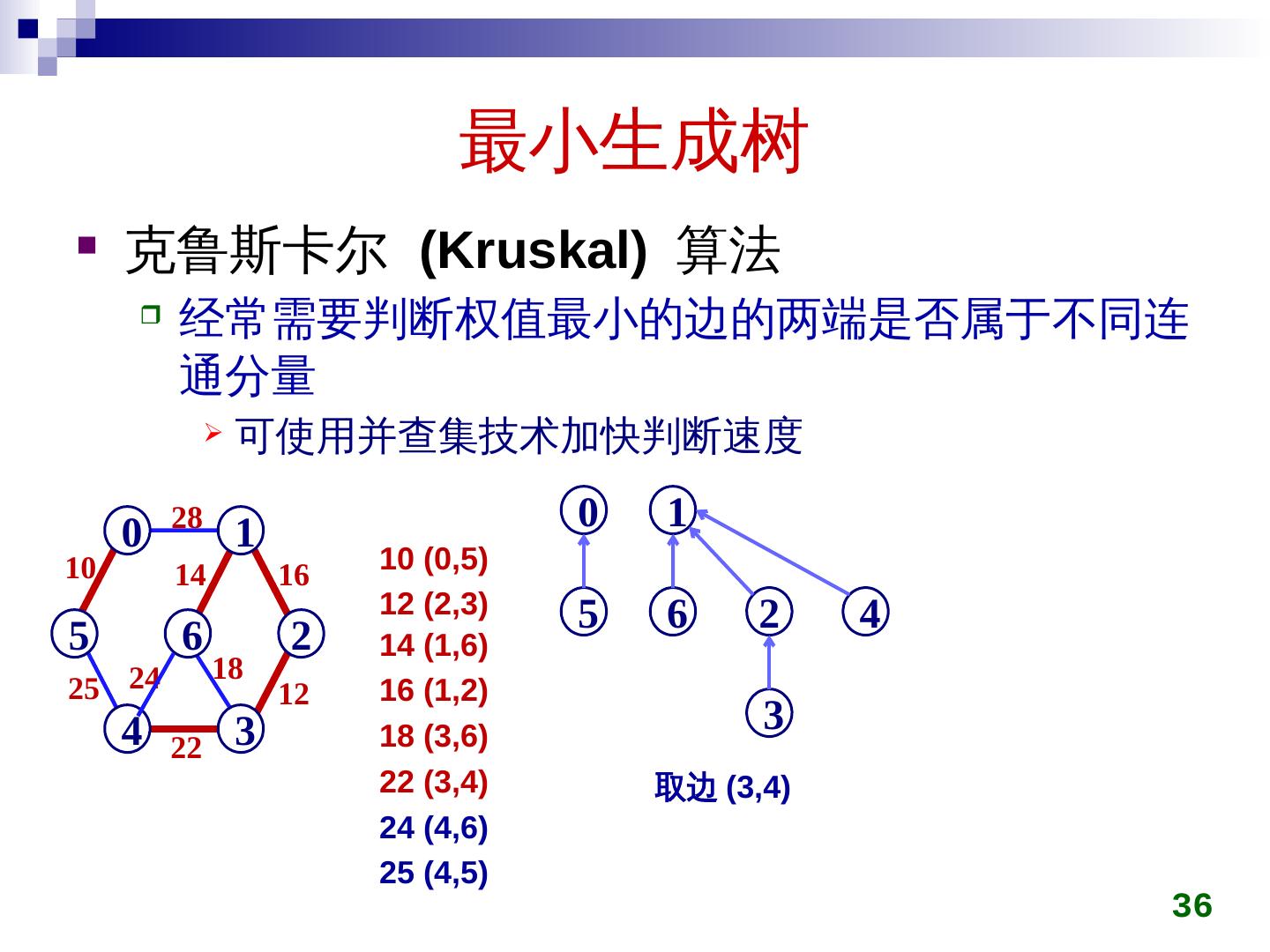
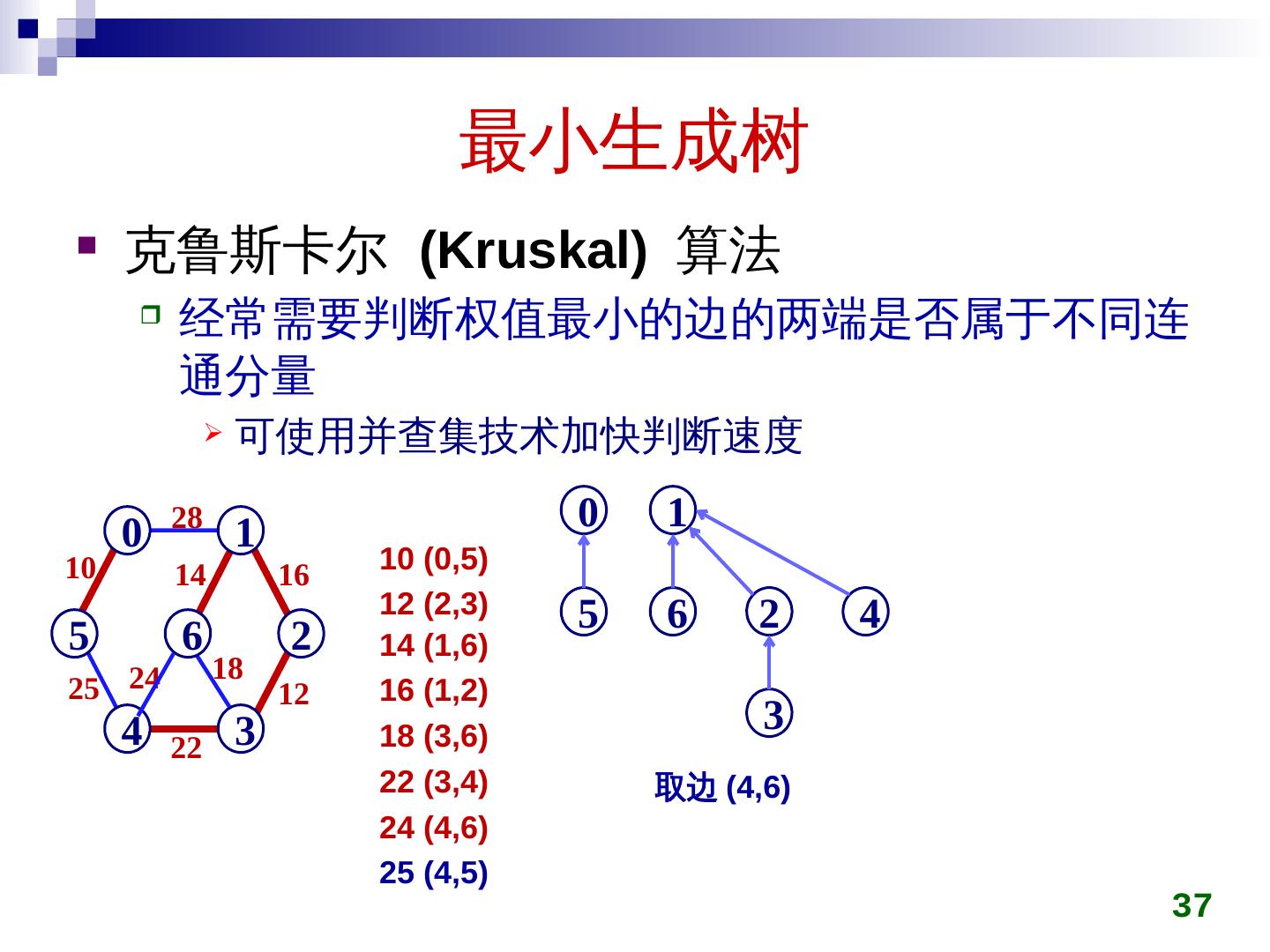
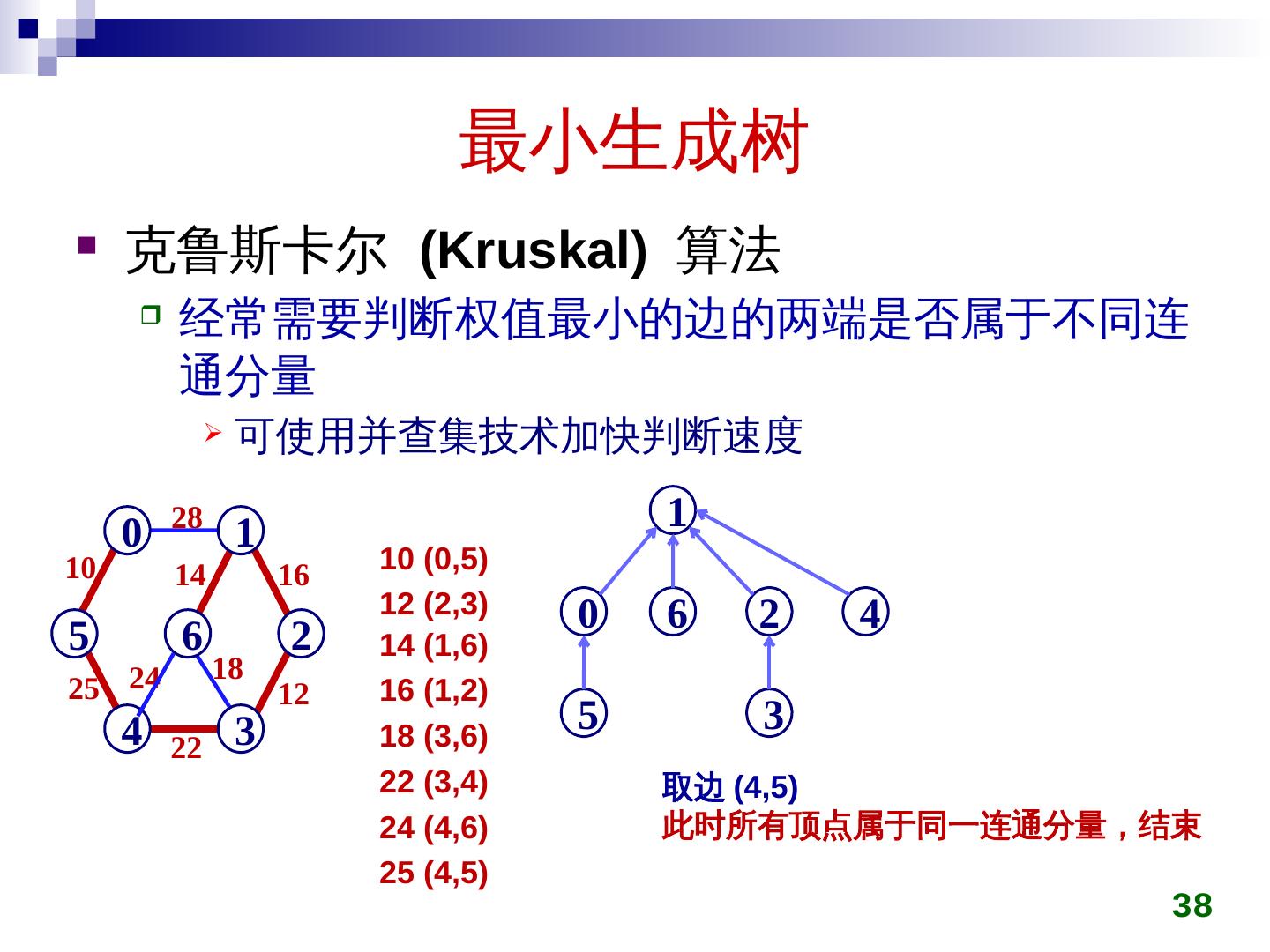
28 .最小生成树 克鲁斯卡尔 ( Kruskal ) 算法 初始时所有顶点自成一集合 在图上选权值最小的边 e min ，判断 e min 两端点是否属于不同集合 c i ,c j 若是，将 c i ,c j 用 e min 连接成同一个集合 否则，舍弃 e min 重复上一过程，直到所有顶点在同一集合 28

29 .最小生成树 克鲁斯卡尔 (Kruskal) 算法 29 28 5 0 4 6 1 3 2 10 25 14 24 22 16 18 12 5 0 4 6 1 3 2 5 0 4 6 1 3 2 10 5 0 4 6 1 3 2 10 12 5 0 4 6 1 3 2 10 14 12 5 0 4 6 1 3 2 10 14 16 12 5 0 4 6 1 3 2 10 14 22 16 12 5 0 4 6 1 3 2 10 25 14 22 16 12