04算法设计与分析---动态规划

1 .东南大学计算机学院 方效林 动态规划

2 .本章内容 动态规划原理 矩阵连乘 钢条切割 最长公共子序列 最优二叉搜索树 流水作业调度 0/1 背包问题 2

3 .动态规划原理 与 分治法类似，动态规划法也是把 问题一 层一层地分解为规模逐渐减小的同类型的子 问题 分 治法 子问题是相互独立的 若不独立，将重复计算 动态规划 可分为多个相关子 问题 子问题的解被重复 使用 子问题 只 求解一 次 ，结果 保存 在表 中，以后用到时直接存取 3

4 .动态规划原理 动态规划的条件 最优 子结构 当一个问题 的 最优 解 包含了子问题 的 最优 解时， 称 这个 问题 具有 最优 子结构 重叠子问题 在 问题的求解过程中，很多子问题的解将被多次使用 4

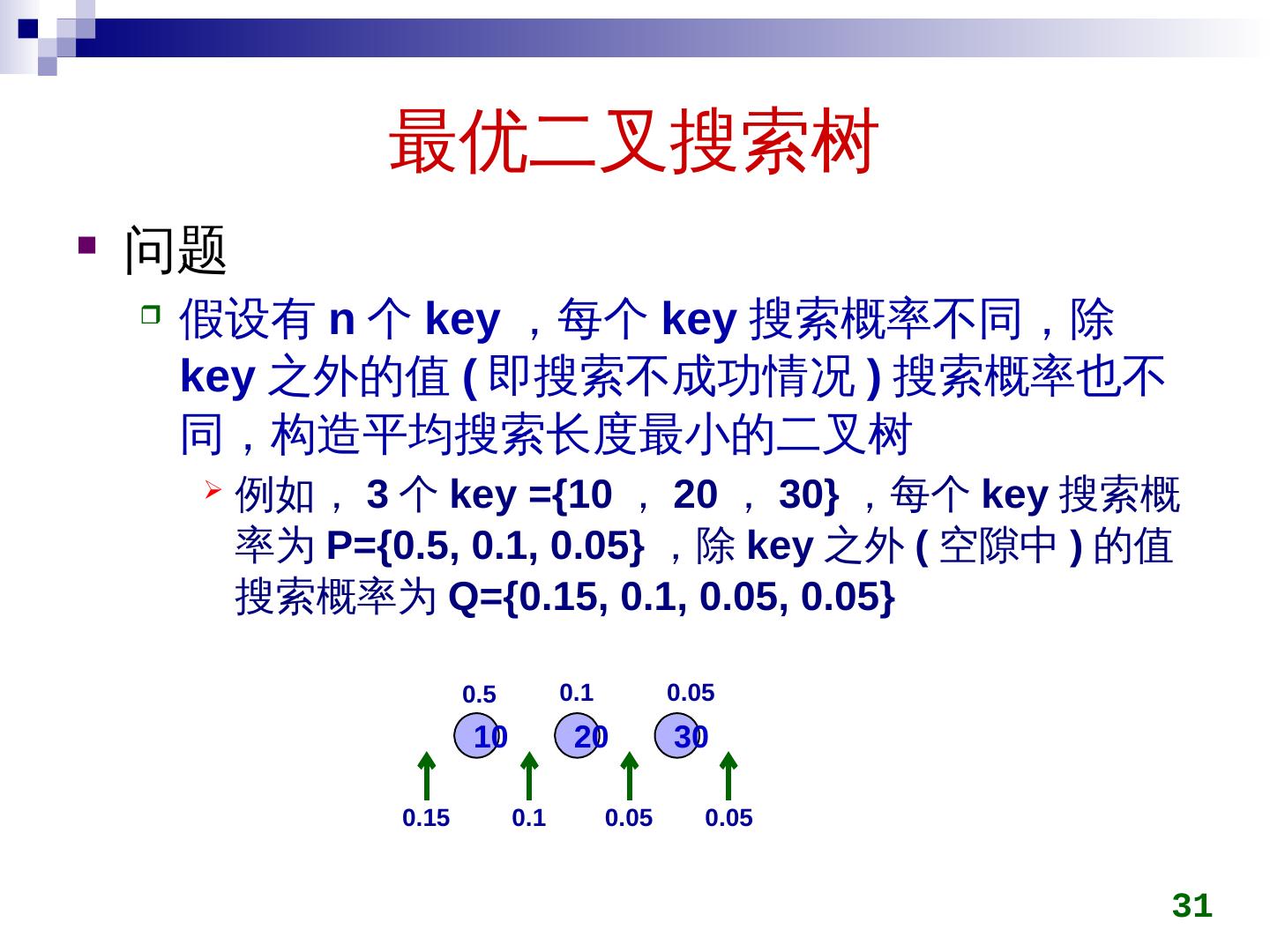
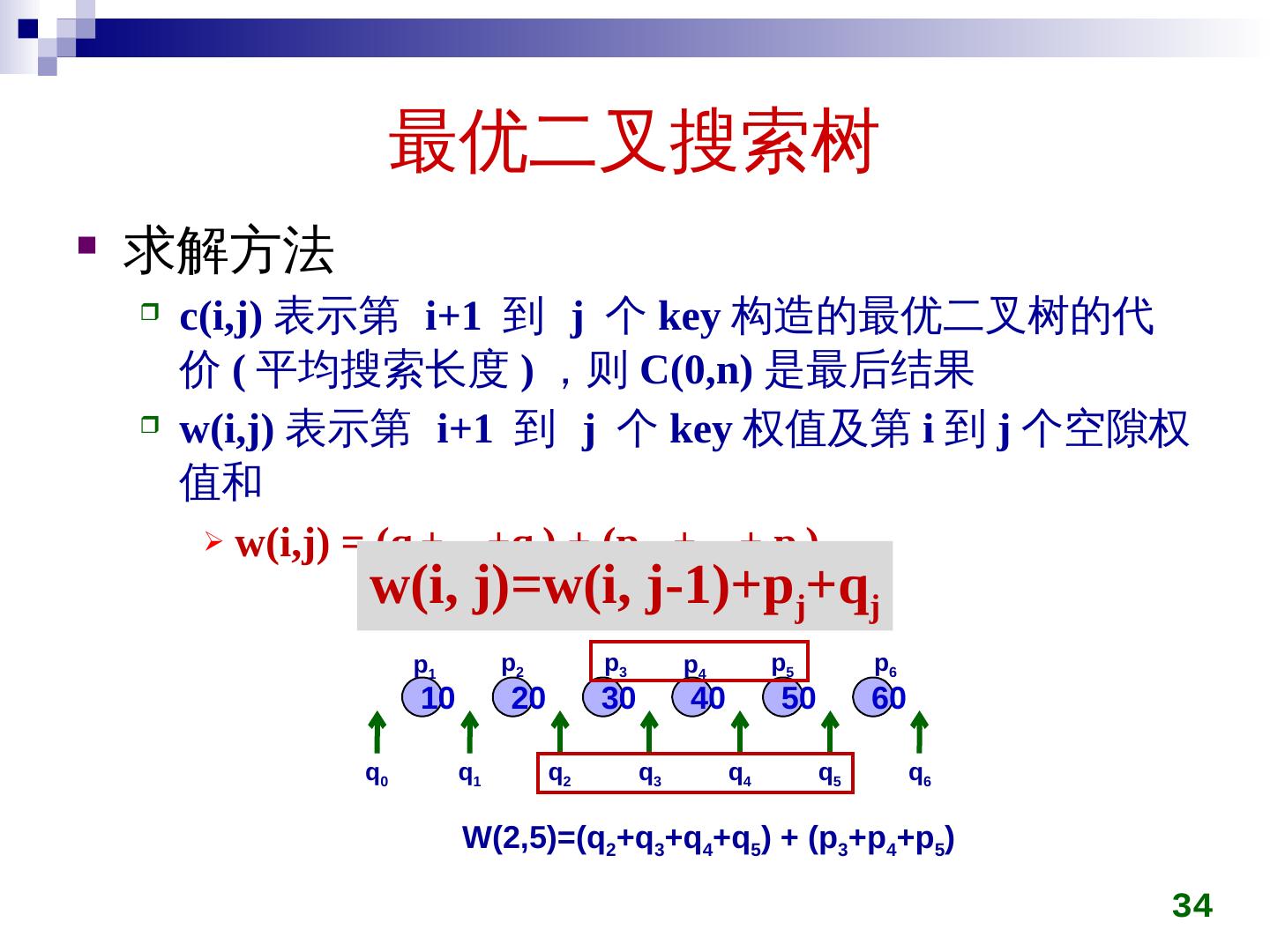
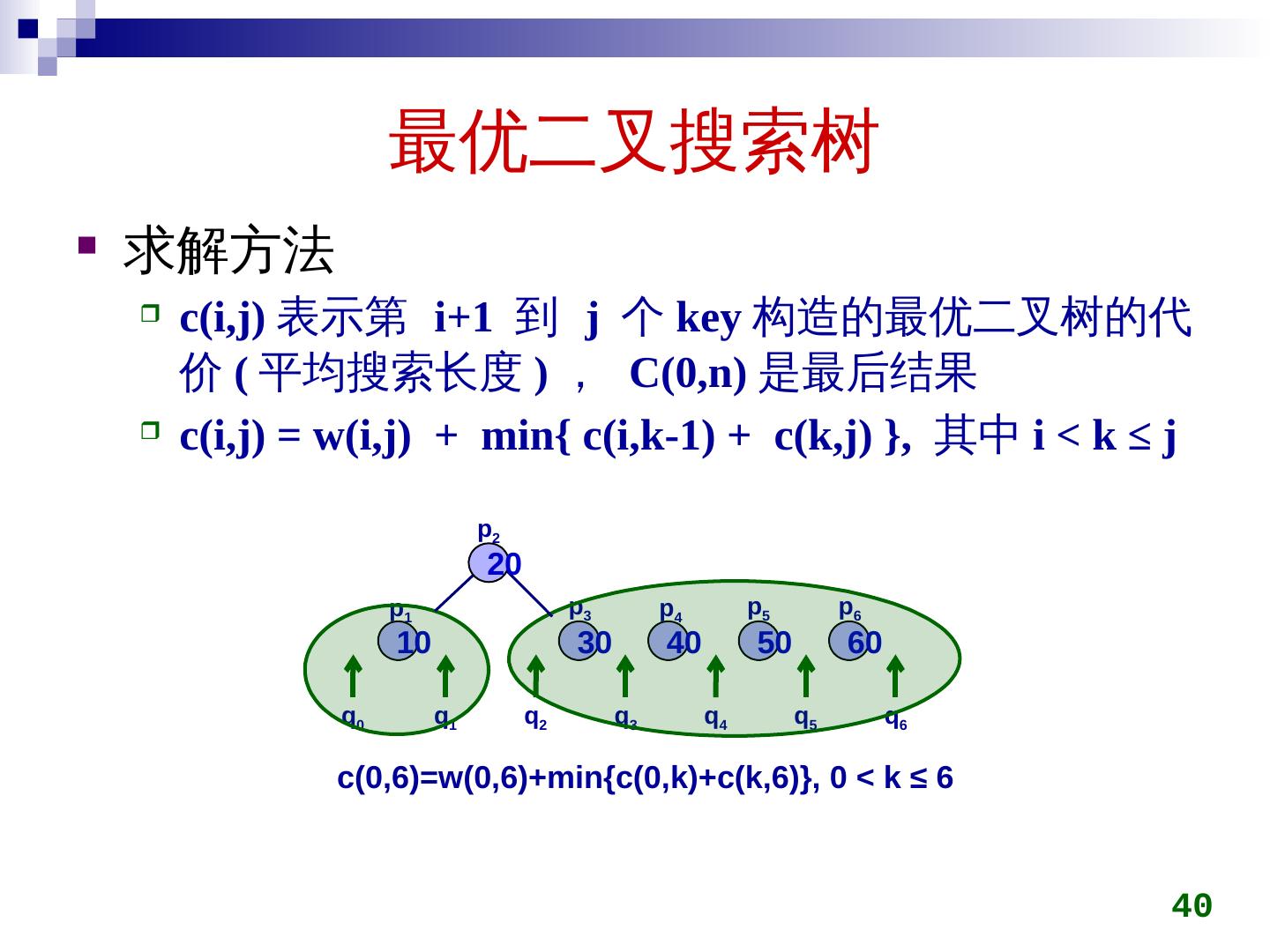
5 .矩阵连乘 两矩阵 A 和 B ， 其 维数分别 是 p  q 和 q  r ， 这 两 矩阵相乘 需进行 p  q  r 次乘法 5

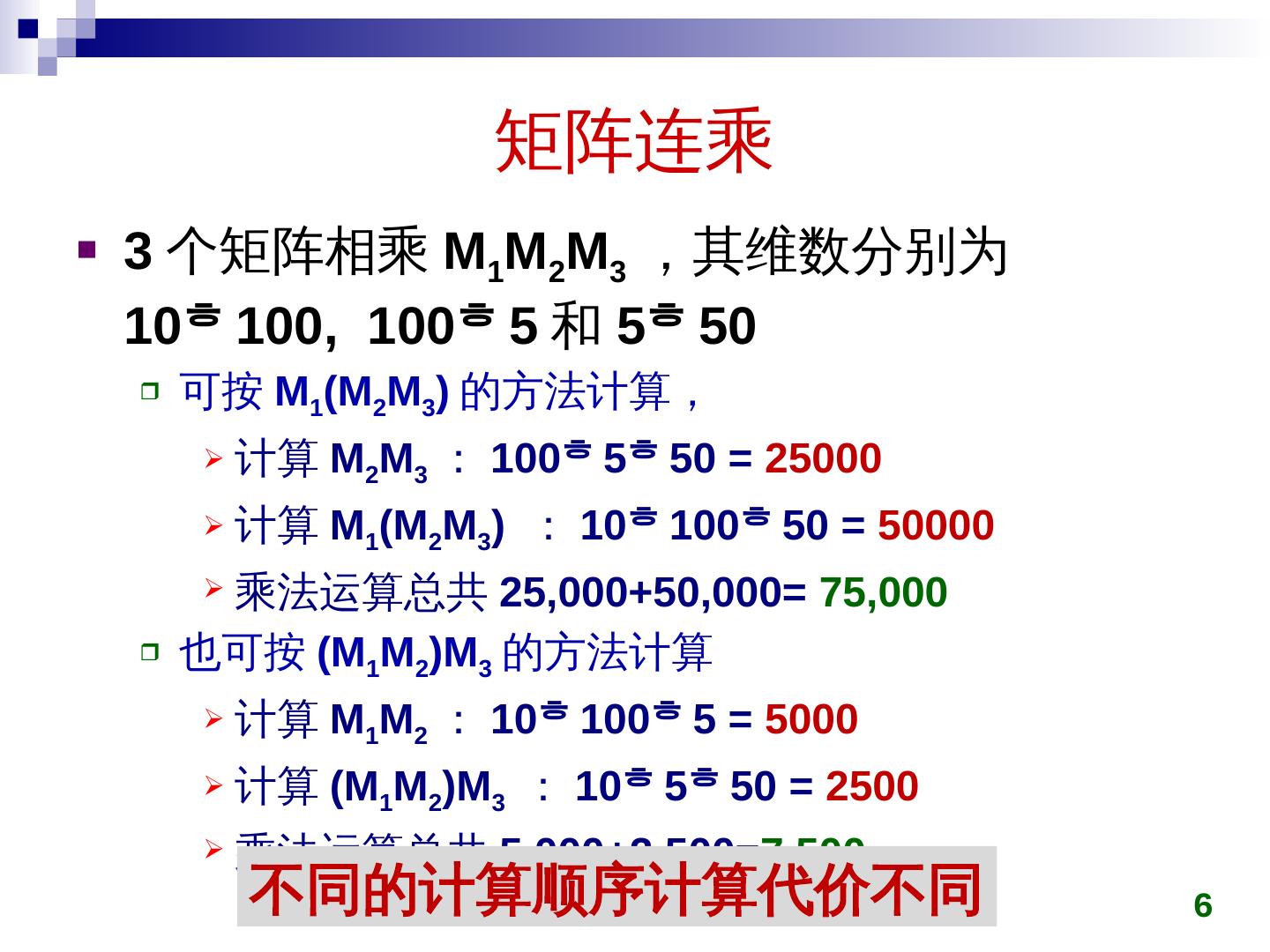
6 .矩阵连乘 3 个矩阵 相乘 M 1 M 2 M 3 ， 其 维数 分别 为 10  100, 100  5 和 5  50 可按 M 1 (M 2 M 3 ) 的 方法 计算， 计算 M 2 M 3 ： 100  5 50 = 25000 计算 M 1 (M 2 M 3 ) ： 10  100  50 = 50000 乘法运算 总共 25,000+50,000= 75,000 也可按 ( M 1 M 2 )M 3 的 方法 计算 计算 M 1 M 2 ： 10 100 5 = 5000 计算 (M 1 M 2 )M 3 ： 10  5  50 = 2500 乘法运算 总共 5,000+2,500= 7,500 6 不同的计算顺序计算代价不同

7 .矩阵连乘 n 个矩阵 相乘，最小化乘法运算次数 ? 解空间大小 令 p(n) 为 n 个矩阵 相乘不同计算方法的总数，则有 p(n) = 1 if n=1 p(n) = if n>1 p(n ) 正好是 catalan 数 =   7 (M 1 M 2 … M k )( M k+1 M k+2 … M n ) 解空间巨大无法枚举

8 .矩阵连乘 n 个矩阵 相乘，最小化乘法运算次数 ? 但是，若可分别得到 M 1 M 2 … M k 和 M k+1 M k+2 … M n 的最小乘法次数，则可以得到在 k 处断开的连乘方法 ( M 1 M 2 … M k )(M k+1 M k+2 … M n ) 的最小乘法次数 令 M 1 M 2 … M k 的最小乘法次数 为 m[1,k] M k+1 M k+2 … M n 的 最小乘法次数 为 m[k+1,n] 则 k 处断开的最少乘法数 m[1,k] + m[k+1,n] +r 1  r k  r n 8 具有 最优 子结构 ： 问题 的 最优 解 包括子 问题 最优 解

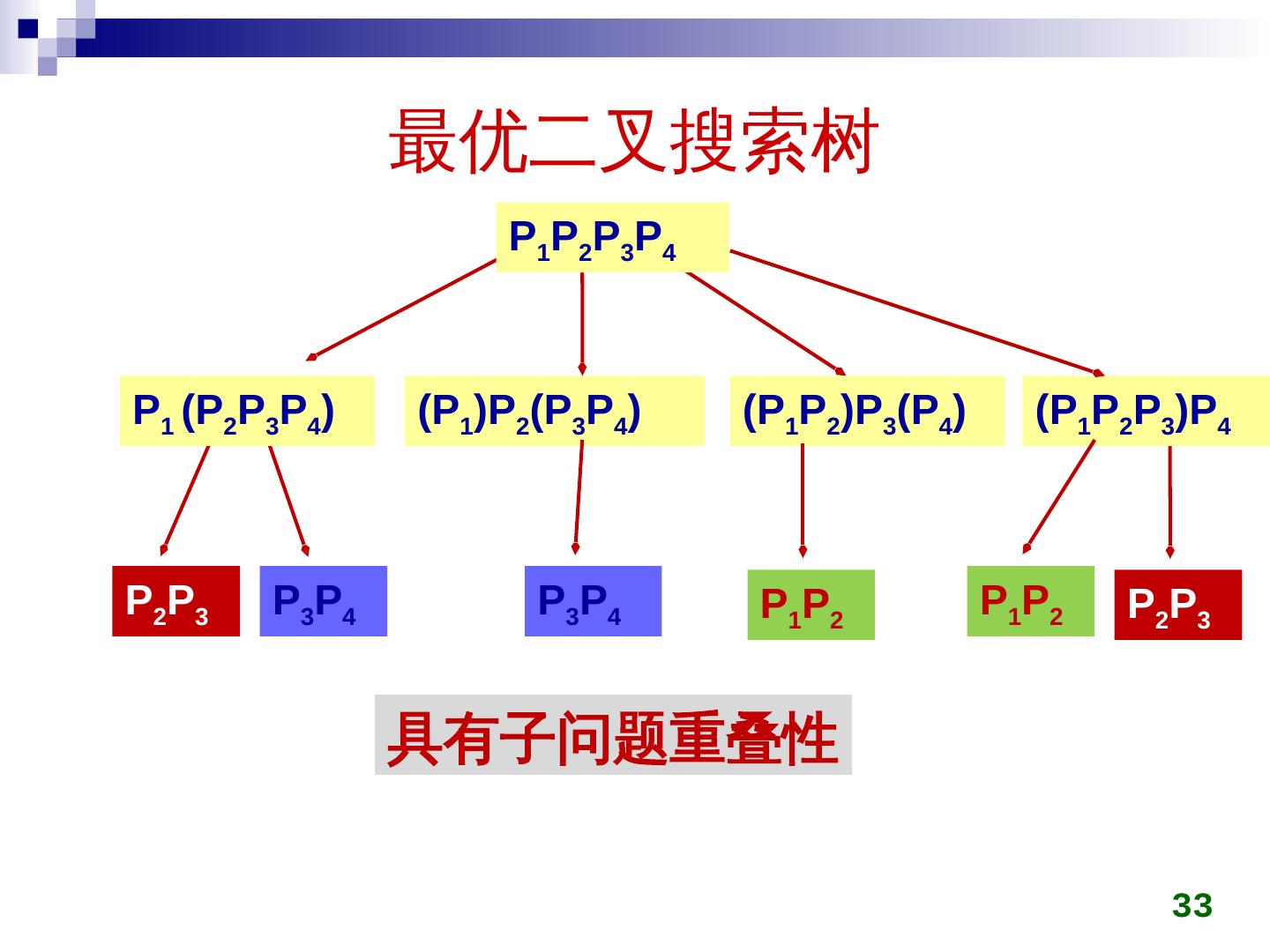
9 .矩阵连乘 9 M 1 M 2 M 3 M 4 M 1 (M 2 M 3 M 4 ) (M 1 M 2 ) (M 3 M 4 ) (M 1 M 2 M 3 ) M 4 M 2 M 3 M 3 M 4 M 1 M 2 M 3 M 4 M 1 M 2 M 2 M 3 具有子问题重叠性

10 .矩阵连乘 令 m[ i,j ] 表示 M i M i+1 … M j 的 最小乘法 次数 则 m[1,n] 表示 M 1 M 2 … M n 的最小乘法 次数 在 k 处 断开 m[ i,j ] = m[ i,k ] + m[k+1,j]+ r i  r k  r j 考虑所有 k ，则有 m[ i,j ] = min i≤k <j {m[ i,k ] + m[k+1,j] + r i  r k  r j }, if i<j m[ i,j ] = 0, if i=j 10

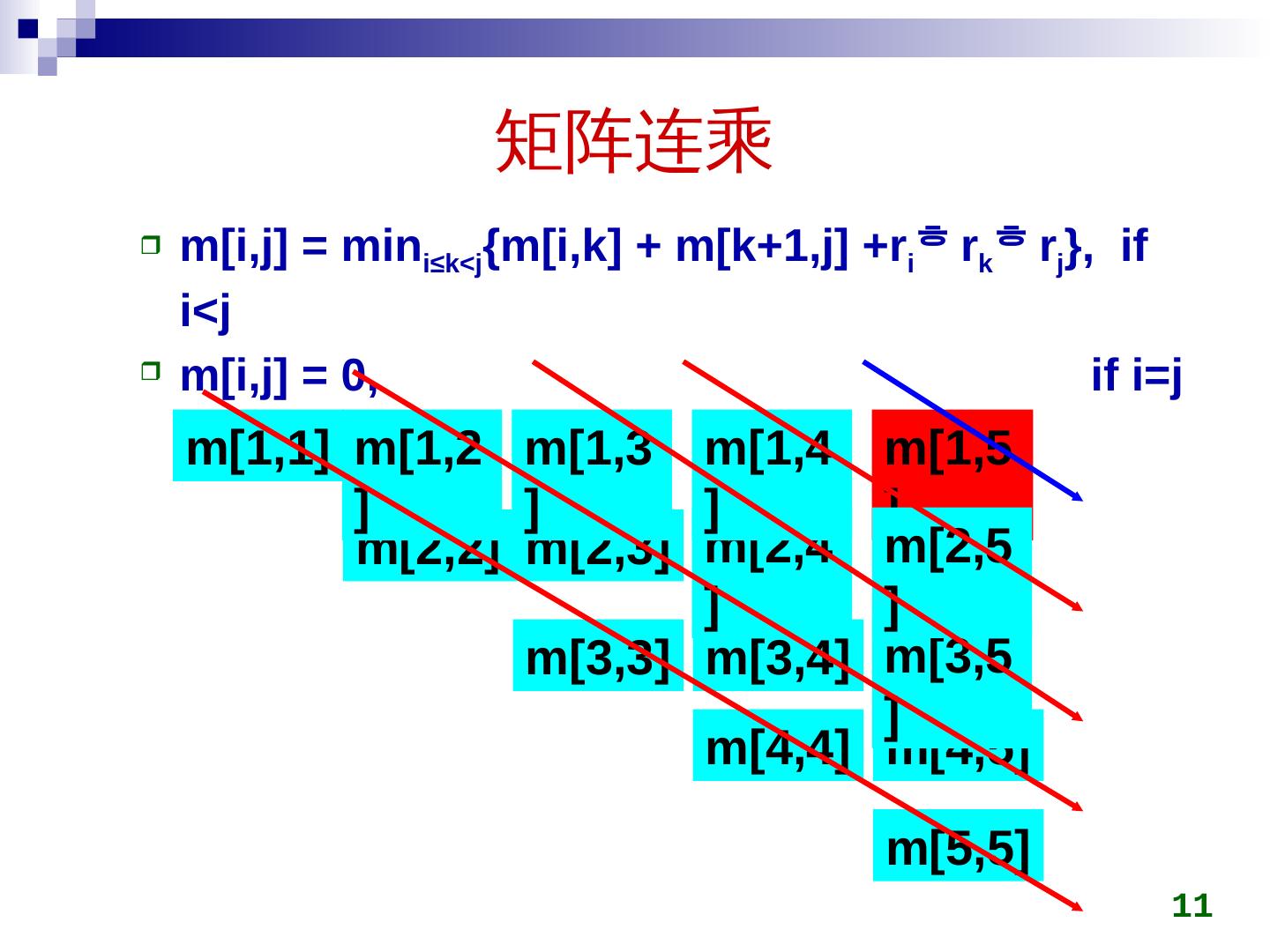
11 .矩阵连乘 m[ i,j ] = min i≤k <j {m[ i,k ] + m[k+1,j] + r i  r k  r j }, if i<j m[ i,j ] = 0, if i=j 11 m[1,5] m[1,1] m[4,4] m[5,5] m[2,2] m[3,3] m[4,5] m[3,4] m[2,3] m[1,2] m[1,3] m[2,4] m[3,5] m[1,4] m[2,5]

12 .矩阵连乘 12 Matrix-Chain-Order(r) n=length(r)； for i=1 to n do m[i, i]=0; for x=1 to n-1 do for i=1 to n-x do j = i+x ; m[i, j] = ∞; for k = i to j-1 do q = m[i, k]+ m[k+1, j]+r i-1 r k r j if q<m[i, j] then m[ i,j ]=q; s[ i,j ]= k; return m and s 自底向上方法

13 .矩阵连乘 13 m[N,N], s[N,N] 赋 -1; MatrixChain (i, j) if i=j then m[i , j]= 0 ; return ; m[i , j] = ∞; for k = i to j-1 do a = m[i, k]; b = m[k+1, j]; if a == -1 then a = MatrixChain (i, k); if b == -1 then b = MatrixChain (k+1, j); q = a + b + r i-1 r k r j if q<m[i, j] then m[ i,j ]=q; s[ i,j ]= k; 递归备忘录方法

14 .钢条切割 长度为 n 英寸的钢条进行切割，可有很多切法 1 段 4 英寸 4 段 1 英寸 2 段 2 英寸 1 段 3 英寸 1 段 1 英寸 假设有一张价格表 14 1 2 3 4 长度 i 1 5 8 9 价格 pi 将这 4 英寸的钢条切成 2 段 2 英寸的，收益最大，为 10

15 .钢条切割 问题定义 给定一段长度为 n 英寸的钢条和一个价格表 pi (i=1,2,…,n) ，给定切割方案，使收益最大 15

16 .钢条切割 令 r(n) 为长度为 n 英寸的钢条的最大收益，则 16   含义：从一端切一段长度为 i 的钢条下来后，可获得的最大收益 即切下来的钢条价格 pi ，加上剩下长度为 n-i 的钢条的最大收益 具有 最优 子结构 ： 问题 的 最优 解 包括子 问题 最优 解

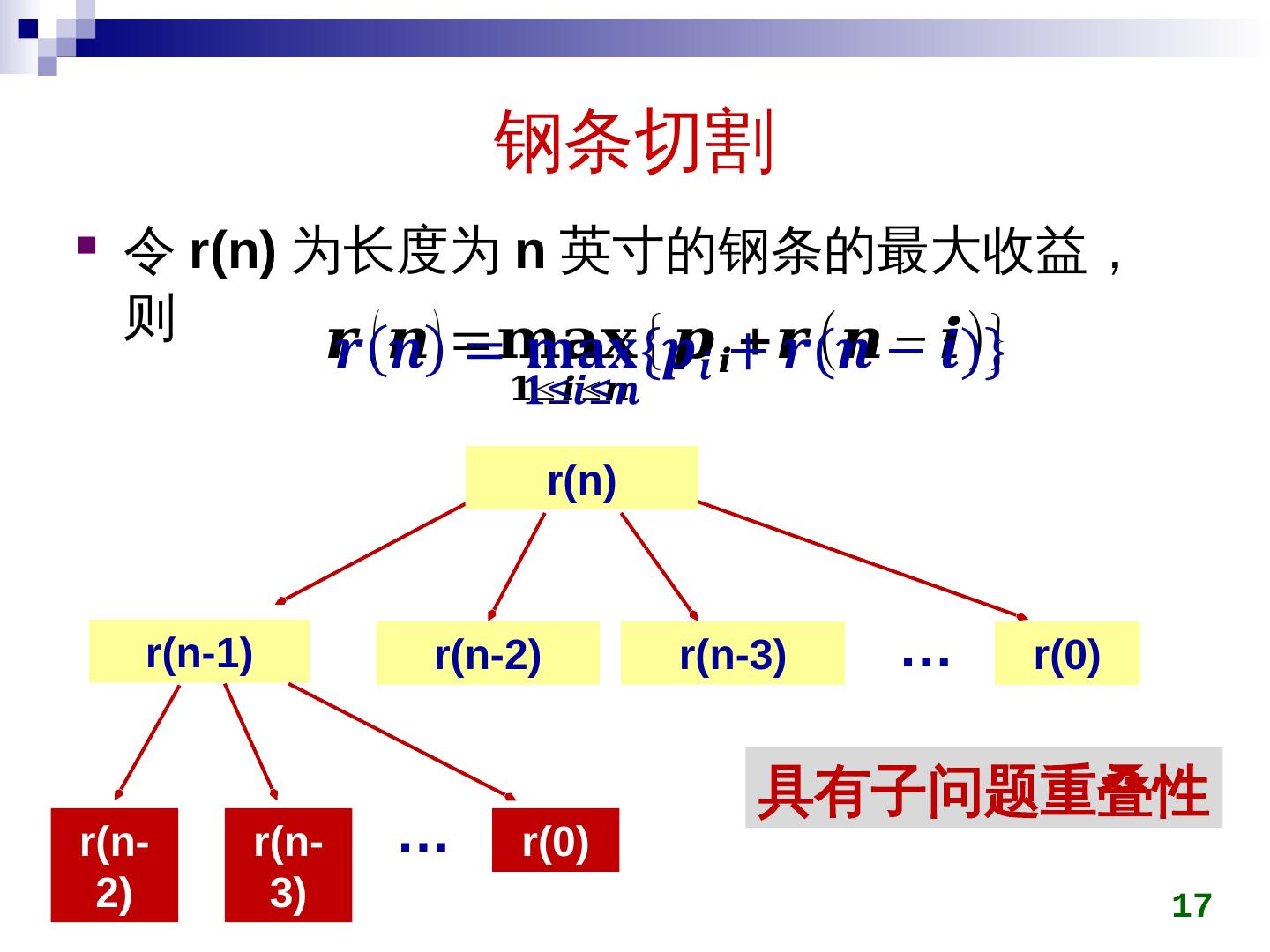
17 .钢条切割 令 r(n) 为长度为 n 英寸的钢条的最大收益，则 17   具有子问题重叠性 r(n) r(n-1) r(n-2) r(0) r(n-2) r(n-3) r(n-3) r(0) … …

18 .钢条切割 18 CUT(p, n, r) r[0] = 0 for j=1 to n temp = - ∞ for i=1 to j temp = max(temp, p[i]+r[j-i]) r[j] = temp 自底向上方法 r[0] 不用计算，依次计算 r[1],r[2],r[3],r[4]

19 .钢条切割 19 预处理 r[ ] ，使 r[i]= - ∞ CUT(p, n, r) if r[n]≥0 then return r[n] if n == 0 then temp = 0 else temp = -∞ for i=1 to n do temp = max(temp , p[i]+CUT(p, n-i)) r[n] = temp return temp 递归备忘录方法 //r[n] 不用重复计算了

20 .最长公共子序列 子序列 X =< x 1 , x 2 , … , x m >, 若 1 ≤i 1 <i 2 < ┅ < i k ≤m ，使 Z =< z 1 , z 2 ,┅, z k > = <x i1 , x i2 ,┅, x ik >, 称 Z 是 X 的子序列 X=(A, B, C, D , E , F , G ) Z=(B, C, E , F ) 是 X 的 子序例 W=(B, D, A) 不是 X 的子序例 公共子序列 Z 是序列 X 与 Y 的 公共子 序列 Z 是 X 的子 序列 Z 也 是 Y 的子 序列 20

21 .最长公共子序列 最 长公共子序列（ LCS） 问题 输入 ： X = (x 1 ,x 2 ,..., x n )，Y = (y 1 ,y 2 ,... y m ) 输出： Z = X 与 Y 的最长公共子序列 21

22 .最长公共子序列 第 i 前缀 设 X=(x 1 , x 2 , ..., x n ) 是一个序列 X 的第 i 前缀 X(i) ，定义 为 X(i)=( x 1 , ..., x i ) 例如： X=(A, B, D, C, A), X(1 )=(A), X(2)=(A, B), X(3)=(A, B, D) 22

23 .最长公共子序列 最优 子结构性质 设 X=(x 1 , ..., x m ) 、 Y=(y 1 , ..., y n ) 是 两个序列 ， Z =(z 1 , ..., z k ) 是 X 与 Y 的 LCS ，则有有： ⑴ 如果 x m = y n , 则 z k = x m = y n , Z(k-1) 是 X(m-1) 和 Y(n-1) 的 LCS， 即 LCS( m,n ) = LCS(m-1,n-1) + 1 . ⑵ 如果 x m  y n 若最终 z k  x m ， 则 LCS( m,n )= LCS(m-1,n) 若最终 z k  y n ， 则 LCS( m,n )= LCS(m,n-1) LCS( m,n )=max{LCS(m-1,n), LCS(m,n-1 )} 23 X=(x 1 , x 2 , ... , x m-1 , x m ) Y =(y 1 , y 2 , ... , y n-1 , y n ) 问题 最优 解 包括 子 问题 最优 解

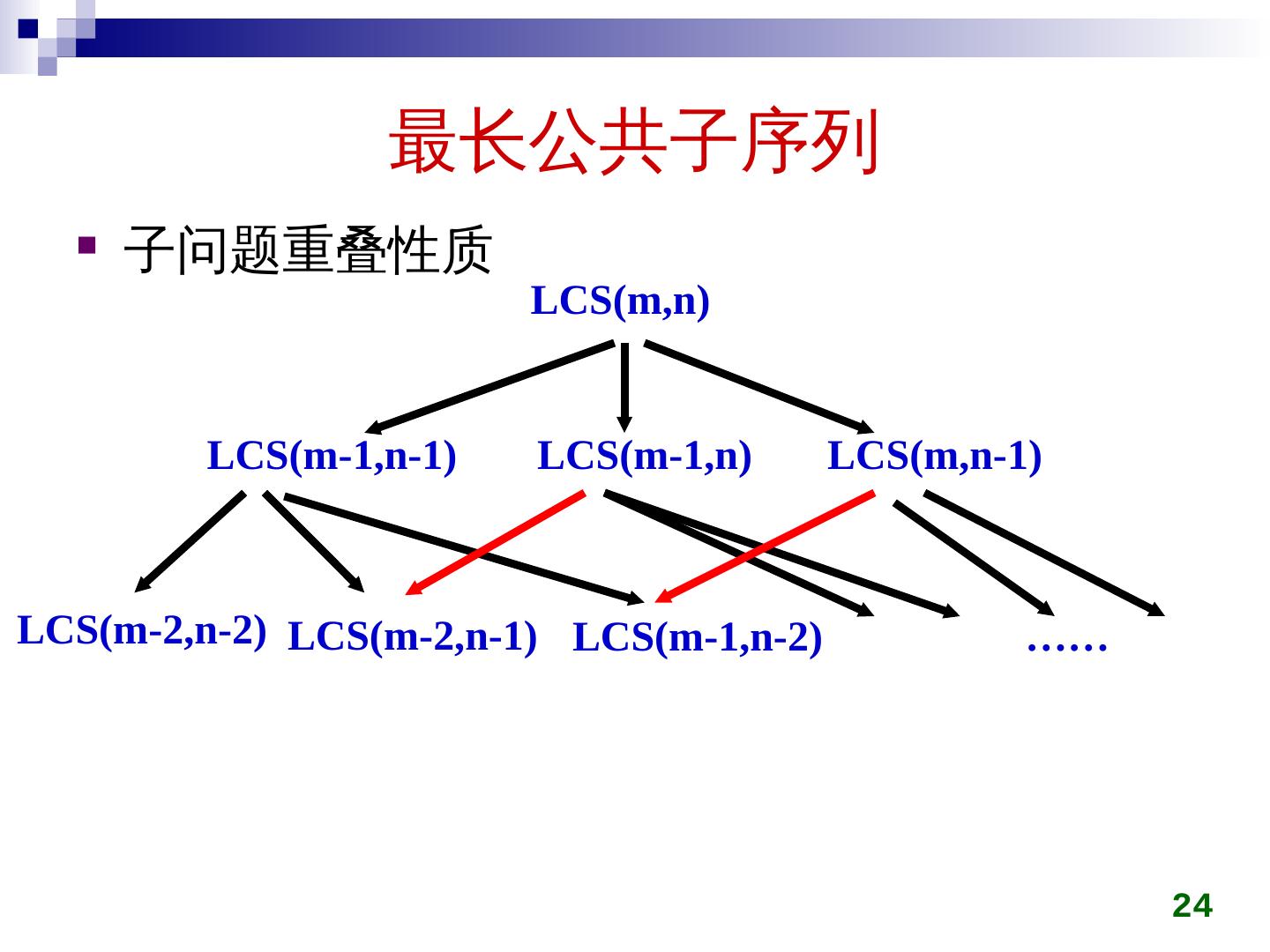
24 .最长公共子序列 子问题重叠性质 24 LCS( m,n ) LCS(m-1,n-1) LCS(m-1,n) LCS(m,n-1) LCS(m-2,n-2) LCS(m-2,n-1) LCS(m-1,n-2) ……

25 .最长公共子序列 LCS 递归方程 LCS[ i,j ]=0 if i=0 or j=0 LCS[ i,j ]=LCS[i-1 , j-1] + 1 if i, j>0 , x i = y j LCS[ i,j ]=Max(LCS[i,j-1],LCS[i-1,j]) if i,j >0,x i  y j 25

26 .最长公共子序列 基本思想 26 LCS[i-1 , j-1] LCS [i-1,j ] LCS [i , j-1] LCS [i , j]

27 .最长公共子序列 自底向上计算过程 27 LCS[0,0 ] LCS[0,1 ] LCS[0,3 ] LCS[0,2 ] LCS[0,4 ] LCS[1,0 ] LCS[2,0 ] LCS[3,0 ] LCS[1,1 ] LCS[2,1 ] LCS[3,1 ] LCS[1,2 ] LCS[1,3 ] LCS[1,4 ] LCS[2,2 ] LCS[2,3 ] LCS[2,4 ] LCS[3,2 ] LCS[3,3 ] LCS[3,4 ]

28 .最长公共子序列 递归计算过程 28 LCS[0,0 ] LCS[0,1 ] LCS[0,3 ] LCS[0,2 ] LCS[0,4 ] LCS[1,0 ] LCS[2,0 ] LCS[3,0 ] LCS[1,1 ] LCS[2,1 ] LCS[3,1 ] LCS[1,2 ] LCS[1,3 ] LCS[1,4 ] LCS[2,2 ] LCS[2,3 ] LCS[2,4 ] LCS[3,2 ] LCS[3,3 ] LCS[3,4 ]

29 .最长公共子序列 29 for i=0 to m do LCS[i,0 ]←0 for j=1 to n do LCS[0,j ]←0 for i=1 to m do for j=1 to n do if X[i]=Y[j] then LCS[ i,j ] = LCS[i-1,j-1 ]+ 1; b[ i,j ] = “ ↖” ; else if LCS[i-1,j ]≥C[i,j-1] then LCS[ i,j ] = LCS[i-1,j ] ； b[ i,j ] = “ ↑” ; else LCS[ i,j ] = LCS[i,j-1 ] ； b[ i,j ] = “ ←” ; 时间复杂度 O( mn ) 空间复杂度 O( mn )