- 快召唤伙伴们来围观吧
- 微博 QQ QQ空间 贴吧
- 文档嵌入链接
- 复制
- 微信扫一扫分享
- 已成功复制到剪贴板
03算法设计与分析---分治算法
展开查看详情
1 .东南大学计算机学院 方效林 分治算法
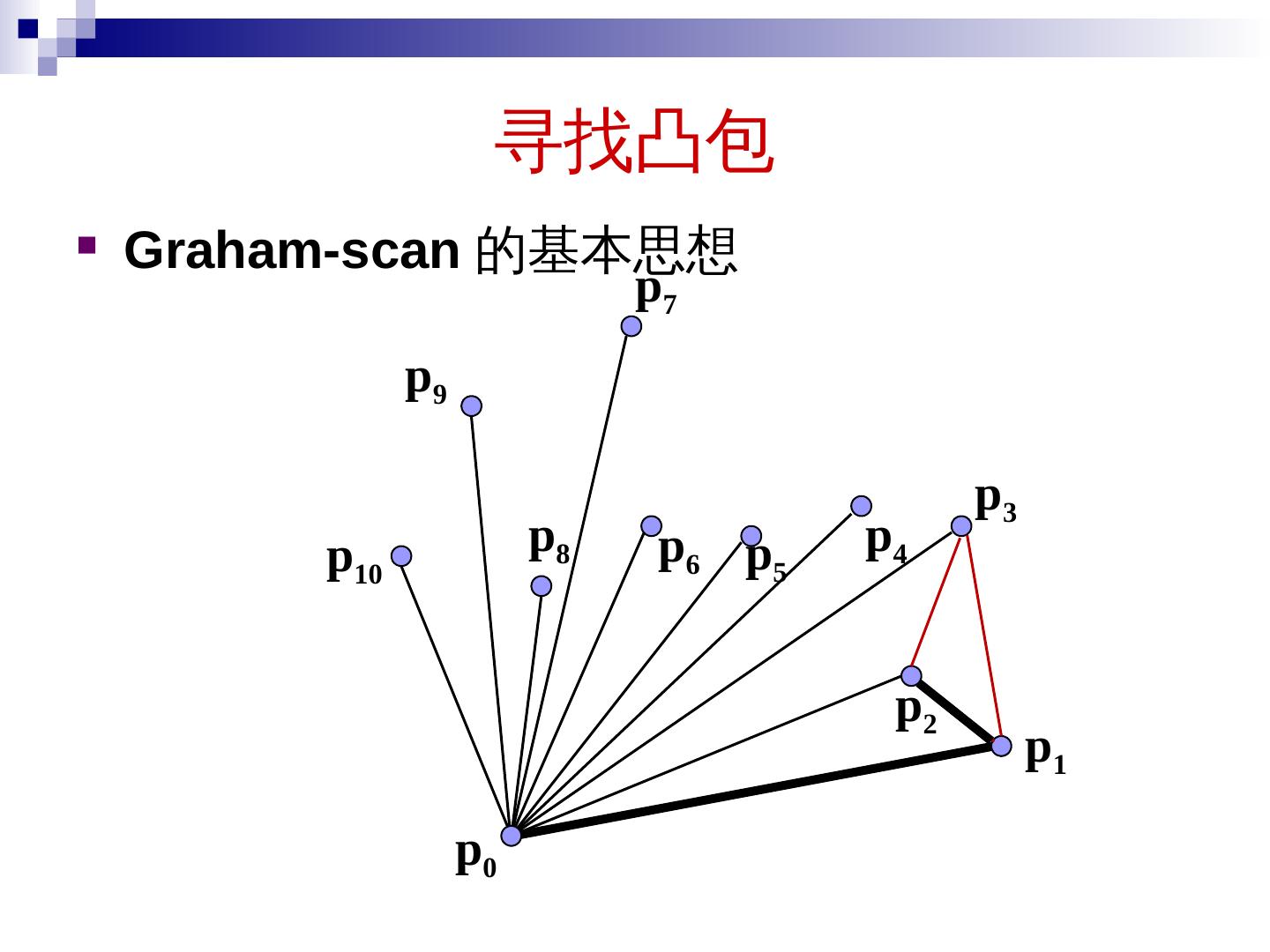
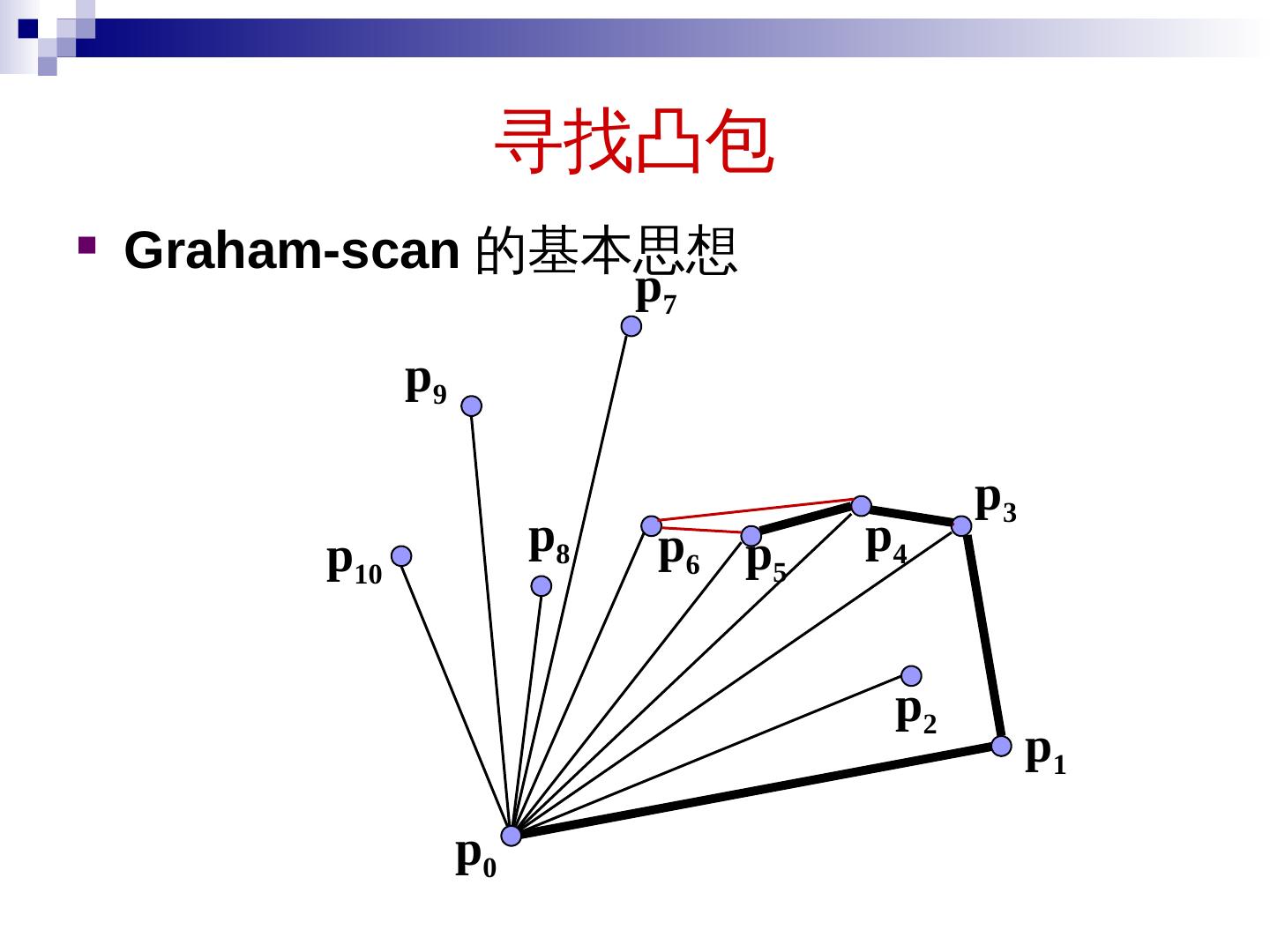
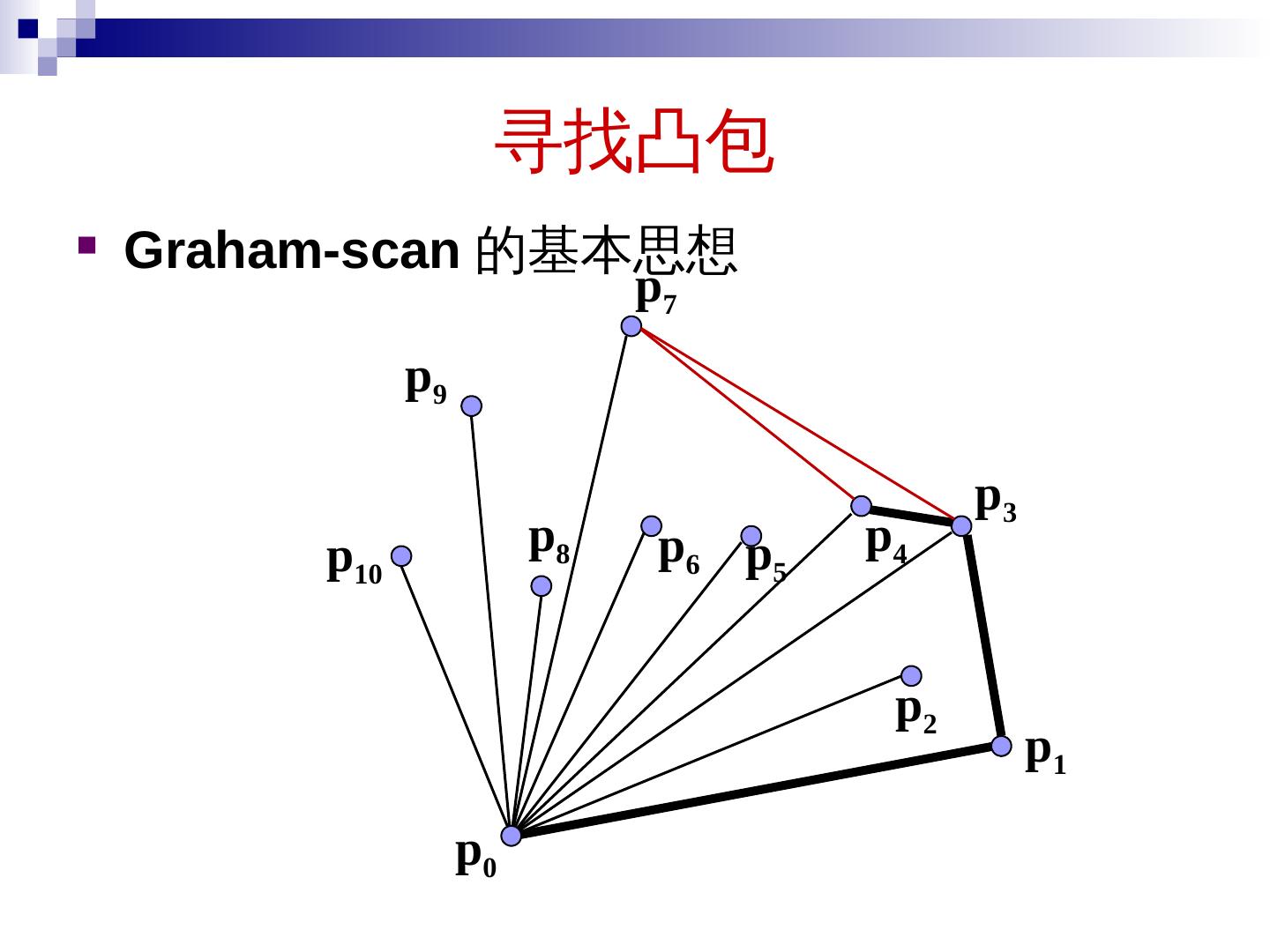
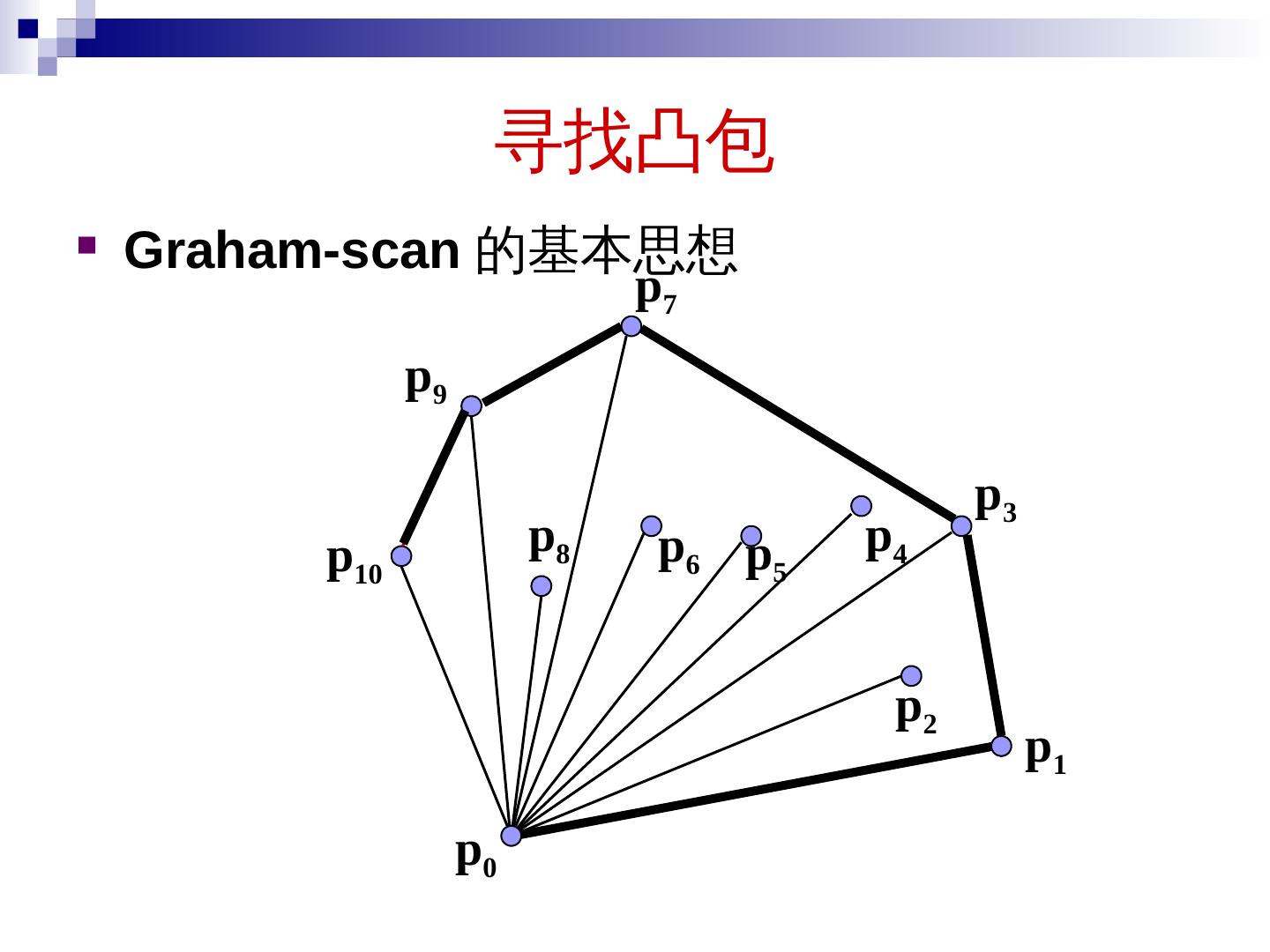
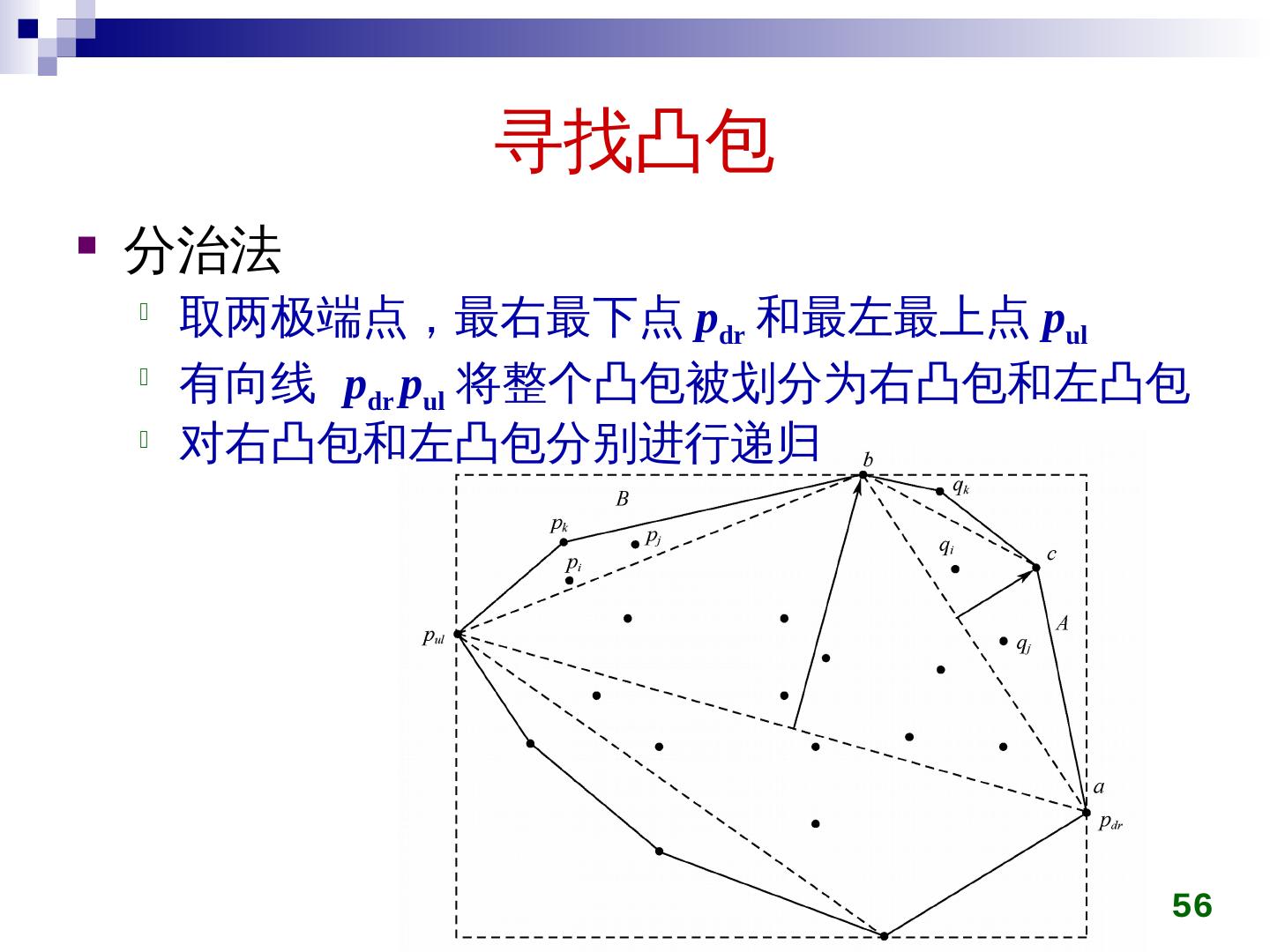
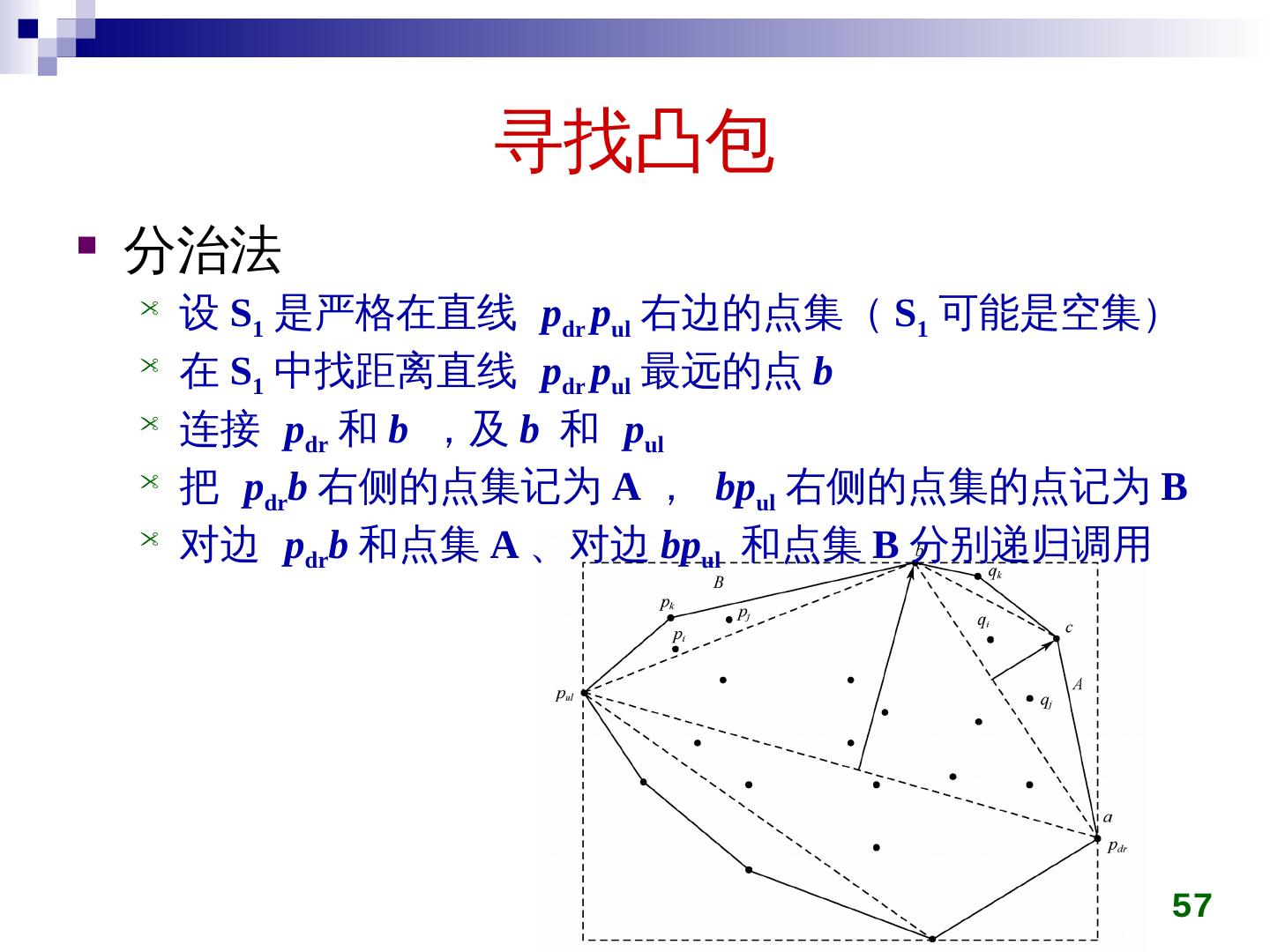
2 .本章内容 分治算法的原理 大整数乘法 矩阵乘法 求第 k 小元素问题 寻找 最近点对 快速 傅立叶 变换 寻找凸包 2
3 .分 治算法的原理 设计过程 Divide :整个 问题划分为多个子问题 Conquer :求解各子问题(递归 调用子问题的 算法) Combine :合并子问题的解, 形成原始问题的解 3
4 .分 治算法的原理 分析过程 建立 递归 方程 T(n)= aT (n/b)+D(n)+C(n) Divide 时间复杂度: D(n) Conquer 时间复杂度: aT (n/b) Combine : C(n) 当 n<c, T(n)= (1) 递归方程求解 4
5 .分 治算法的原理 例 1 :归并排序 5 21 25 49 25 * 16 08 31 41 21 25 49 25 * 16 08 31 41 21 25 49 25 * 16 08 31 41 21 25 49 25 * 16 08 31 41 21 25 49 25 * 16 08 31 41 08 16 21 25 25 * 31 41 49 21 25 25 * 49 08 16 31 41 21 25 25 * 49 08 16 31 41
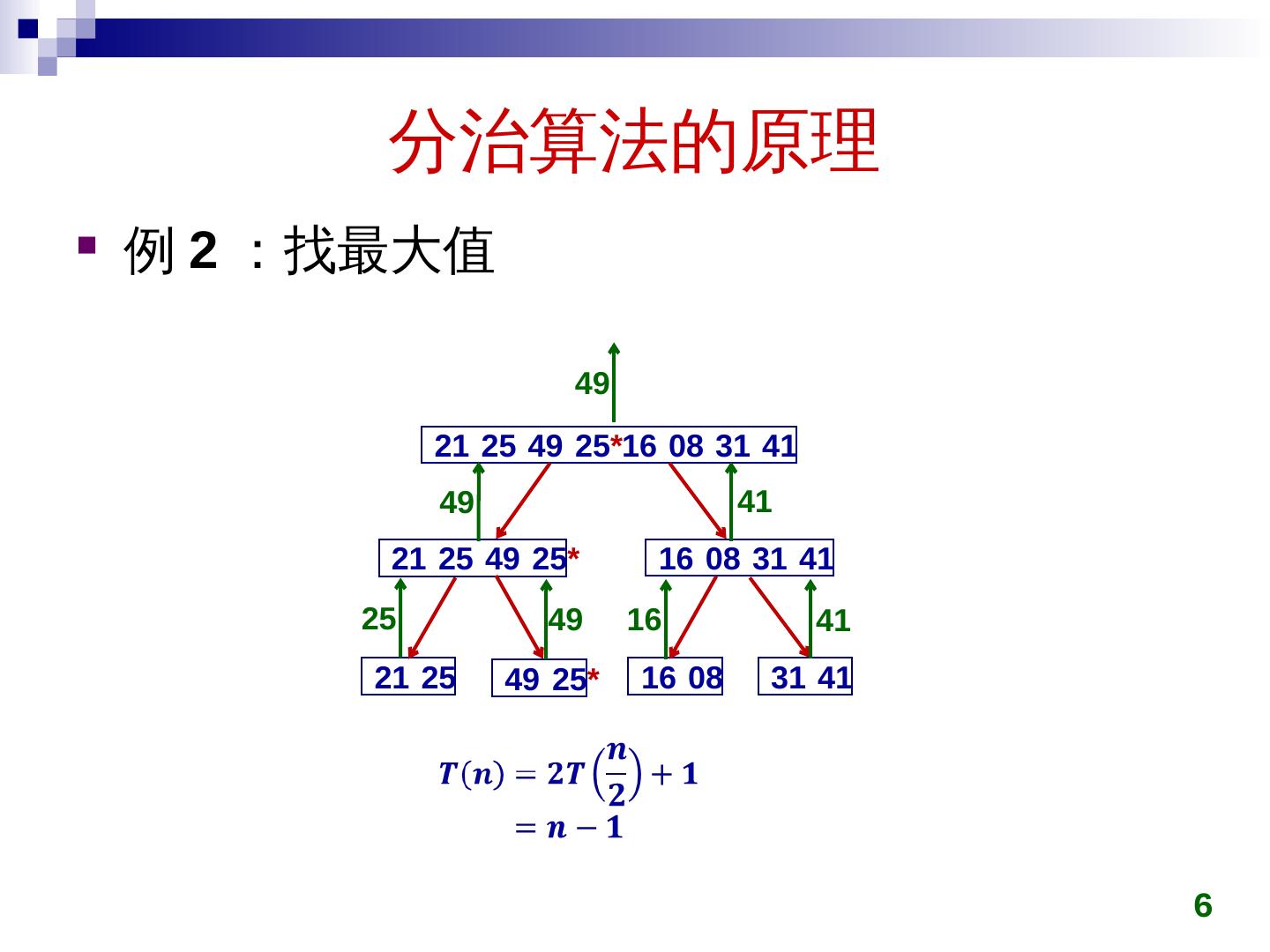
6 .分 治算法的原理 例 2 :找最大值 6 21 25 49 25 * 16 08 31 41 21 25 49 25 * 16 08 31 41 21 25 49 25 * 16 08 31 41 25 49 16 41 49 41 49
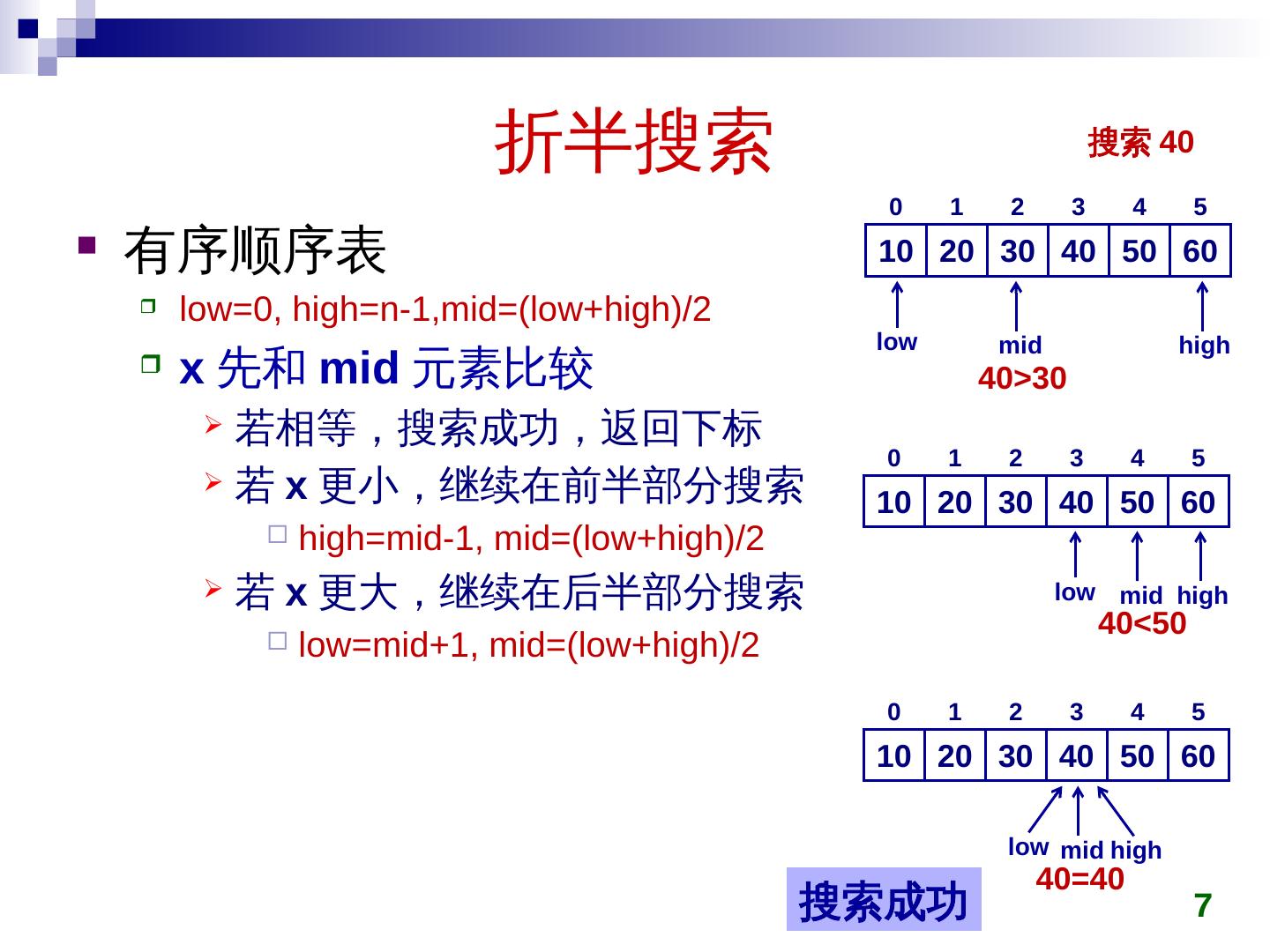
7 .折半 搜索 有序顺序表 low=0, high=n-1,mid=( low+high )/2 x 先和 mid 元素比较 若相等,搜索成功,返回下标 若 x 更小,继续在前半部分搜索 high=mid-1, mid=( low+high )/2 若 x 更大,继续在后半部分搜索 low=mid+1, mid=( low+high )/2 7 搜索 40 low mid high 10 20 30 40 50 60 0 1 2 3 4 5 low mid high 10 20 30 40 50 60 0 1 2 3 4 5 low mid high 10 20 30 40 50 60 0 1 2 3 4 5 40>30 40<50 40=40 搜索成功
8 .折半搜索 有序顺序表 low=0, high=n-1,mid=( low+high )/2 x 先和 mid 元素比较 若相等,搜索成功,返回下标 若 x 更小,继续在前半部分搜索 high=mid-1, mid=( low+high )/2 若 x 更大,继续在后半部分搜索 low=mid+1, mid=( low+high )/2 8 搜索 25 low mid high 10 20 30 40 50 60 0 1 2 3 4 5 low mid high 10 20 30 40 50 60 0 1 2 3 4 5 low mid high 10 20 30 40 50 60 0 1 2 3 4 5 25<30 25>10 25>20 low mid high 10 20 30 40 50 60 0 1 2 3 4 5 low>high ,搜索失败
9 .折半搜索 有序顺序表 折半搜索构造的判定树 设满二叉树 n=2 h -1 则有 2 h =n+1 , h=log 2 (n+1) 平均搜索长度 9 50 = = = = = = 30 < < < < < < > > > > > > 20 40 60 10 错位相减法
10 .大整数乘法 n 位 二进制整数 X 和 Y 相乘 通常算法时间复杂性性为 分 治 算法时间 复杂 度可降至 10
11 .大整数乘法 11 A B n/2 位 X= n/2 位 C D n/2 位 Y = n/2 位 XY = (A2 n/2 + B)(C2 n/2 + D) = AC2 n + (AD+BC)2 n/2 + BD 复杂性没有改善 , 乘以 2 n 表示左移 n 位
12 .大 整数乘法 12 A B n/2 位 X= n/2 位 C D n/2 位 Y = n/2 位 XY = (A2 n/2 + B)(C2 n/2 + D) = AC2 n + (( A+B )( C+D)-AC-BD)2 n/2 + BD 复杂性降低了 , 乘以 2 n 表示左移 n 位
13 .矩阵乘法 两个 的矩阵 和 相乘 通常算法时间复杂性性为 分治算法时间复杂度可降至 13
14 .矩阵乘法 两个 的矩阵 和 相乘 将 和 分成 4 个大小为 的子矩阵运算 14 = C 11 =A 11 B 11 +A 12 B 21 , C 12 = A 11 B 12 + A 12 B 22 C 21 =A 21 B 11 +A 22 B 21 , C 22 = A 21 B 12 + A 22 B 22 复杂性没有改善 ,
15 .矩阵乘法 两个 的矩阵 和 相乘 将 和 分成 4 个大小为 的子矩阵运算 15 = 将 8 个矩阵相乘转变成 7 个矩阵相乘 M 1 = A 11 (B 12 - B 22 ) M 2 = (A 11 + A 12 ) B 22 M 3 = (A 21 + A 22 ) B 11 M 4 = A 22 (B 21 - B 11 ) M 5 = (A 11 + A 22 ) (B 11 + B 22 ) M 6 = (A 12 - A 22 ) (B 21 + B 22 ) M 7 = (A 11 – A 21 ) (B 11 + B 12 ) C 11 = M 5 + M 4 - M 2 + M 6 C 12 = M 1 + M 2 C 21 = M 3 + M 4 C 22 = M 5 + M 1 – M 3 – M 7
16 .矩阵乘法 两个 的矩阵 和 相乘 将 和 分成 4 个大小为 的子矩阵运算 16 = 将 8 个矩阵相乘转变成 7 个矩阵相乘 C 11 = M 5 + M 4 - M 2 + M 6 C 12 = M 1 + M 2 C 21 = M 3 + M 4 C 22 = M 5 + M 1 – M 3 – M 7 复杂性降低 ,
17 .矩阵乘法 两个 的矩阵 和 相乘 还有更好的算法,复杂度可降至 可否 继续降低复杂度? 还没有定论 17
18 .快速排序 基本思想 Partition :任取一元素 x 为基准 ( 如选第 1 个 ) ,小于 x 的元素放在 x 左边,大于等于 x 的元素放在 x 右边 对左、右部分递归执行上一步骤直至只有一个元素 18 21 25 49 25 * 16 08 初始 第 1 层 第 2 层 第 3 层 选 21 为基准 左部选 08 ,右部选 25 *为基准 左部选 16 ,右部选 25 为基准 08 16 21 25 49 25 * 08 16 21 25 * 25 49 08 16 21 25 * 25 49 第 4 层 右部选 49 为基准 08 16 21 25 * 25 49
19 .快速排序 Partition(low,high) 初始时基准坐标 p = low, x=a[low]=21 从 i=low+1 位置开始判断,比 x 小的元素与 p 下一个位置交换, p 自加 1 循环直至 i > high ,最后 a[low] 与 a[p] 交换 19 p p p i p i>high, 停止 i a[low] 与 a[p] 交换 a[i] 与 a[p+1] 交换 , p++ a[i] 与 a[p+1] 交换 , p++ 21 25 49 25 * 16 08 21 16 49 25 * 25 08 21 16 08 25 * 25 49 08 16 21 25 * 25 49
20 .快速排序 基于比较的排序方法,最好的算法不会好于 O( nlogn ) , 因为 比较搜索树中 2 h >=n! ,从而 h>= nlogn 20
21 .第 k 小元素 在有 个元素的数组中,找第 小的元素 可采用 堆 排序方法 找 第 小元素 每 获得一个 元素 , 最坏 情况 下要 次比较 故此 方法的时间复杂度在最坏情况下是 当 接近 时 , 此 方法 需要 次 比较。 21
22 .第 k 小元素 在有 个元素的数组 S 中,找第 小的元素 给出一复杂度为 的算法 Select(S, k) 若 | S |< 50 , 采用 堆排序的方法找出 第 k 小元素 否则, 将 个元素 分为 组 ,每 组 5 个元素 ,每组 排序 , 将每组第 3 个元素取出,得到大小为 的数组 M 最后 一组中的元素可能不足 5 个 1 个取出 ; 2 个取 较小; 3 个取中间 ; 4 个取第 2 小 m = Select( , ) , 代价 S 中至少有 大于等于 m 类似地, S 中至少有 小于 m 22
23 .第 k 小元素 在有 个元素的数组 S 中,找第 小的元素 给出一复杂度为 的算法 Select(S, k) 若 | S |< 50 , 采用 堆排序的方法找出 第 k 小元素 否则, 依次 扫描整个数组 S , 代价 si m 时放入 S 1 ; si =m 时放入 S 2 ; si m 时放入 S 3 ; 当 k S 1 时,调用 Select(S 1 , k) , S 1 大小最多为 , 代价 当 S 1 k S 1 + S 2 时, 返回 m 当 k S 1 + S 2 时 ,调用 Select(S 3 , k - S 1 - S 2 ) S 3 大小 最多为 , 代价 23
24 .第 k 小元素 在有 个元素的数组 S 中,找第 小的元素 给出一复杂度为 的算法 Select(S, k) 第二数学归纳法 证明: n<50 时显然成立 假设 n m 时, , n=m+1 时 , 24
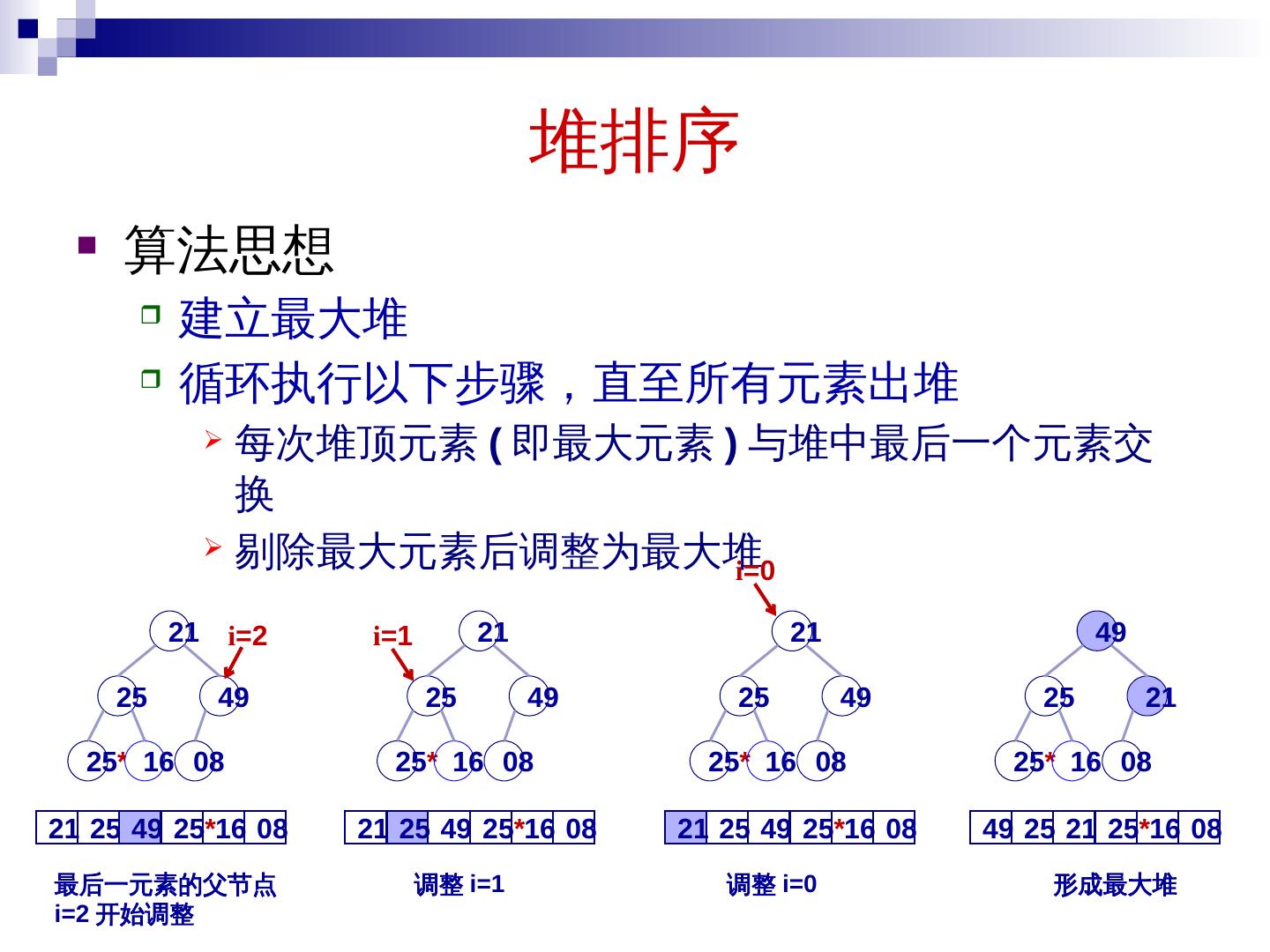
25 .堆排序 算法思想 建立最大堆 循环执行以下步骤,直至所有元素出堆 每次堆顶元素 ( 即最大元素 ) 与堆中最后一个元素交换 剔除最大元素后调整为最大堆 49 08 25 25 * 16 21 i =2 21 25 49 25 * 16 08 最后一元素的父节点 i=2 开始调整 i =1 21 25 49 25 * 16 08 调整 i=1 i =0 调整 i=0 21 25 49 25 * 16 08 49 08 25 25 * 16 21 49 08 25 25 * 16 21 形成最大堆 49 25 21 25 * 16 08 21 08 25 25 * 16 49
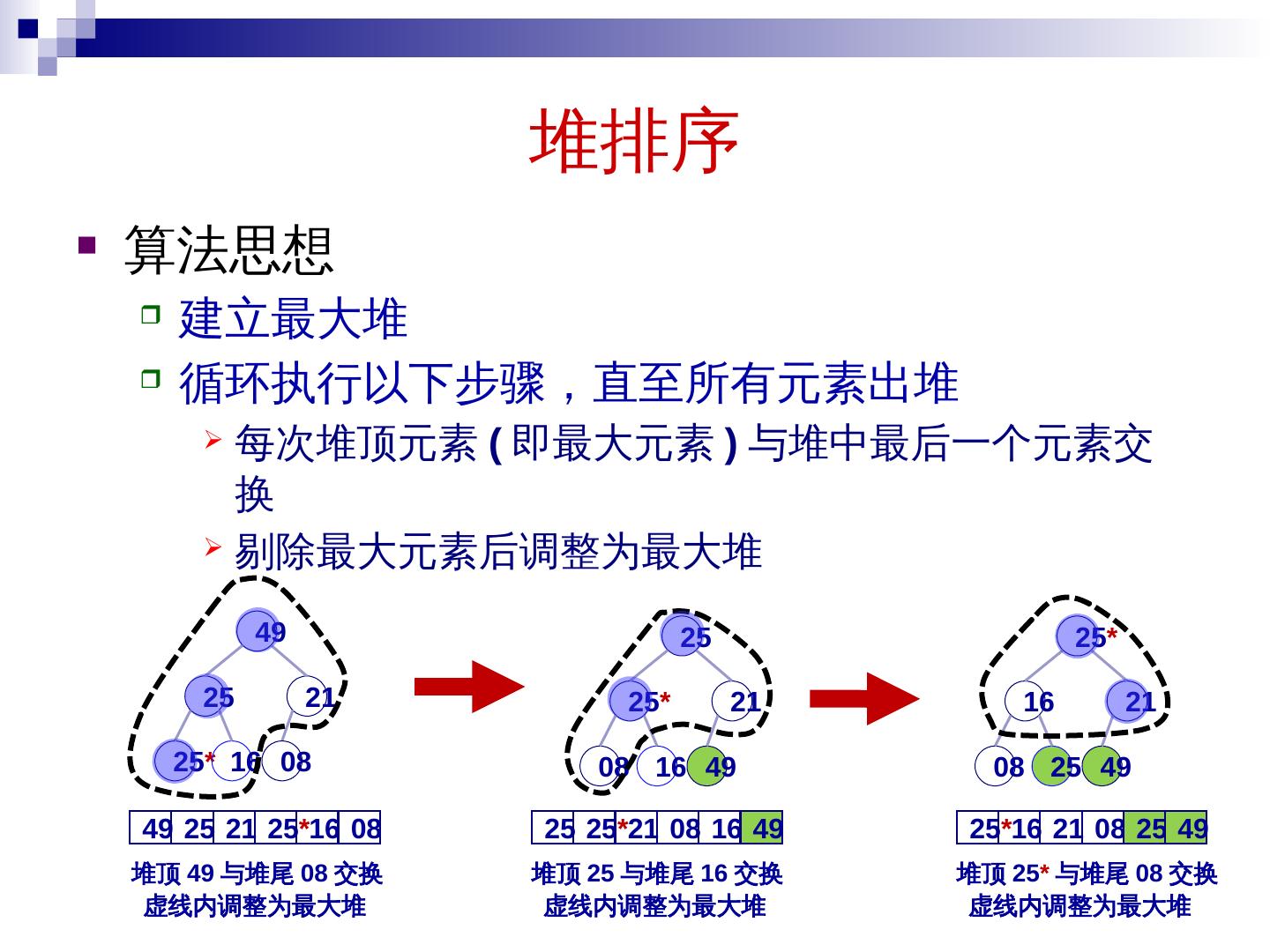
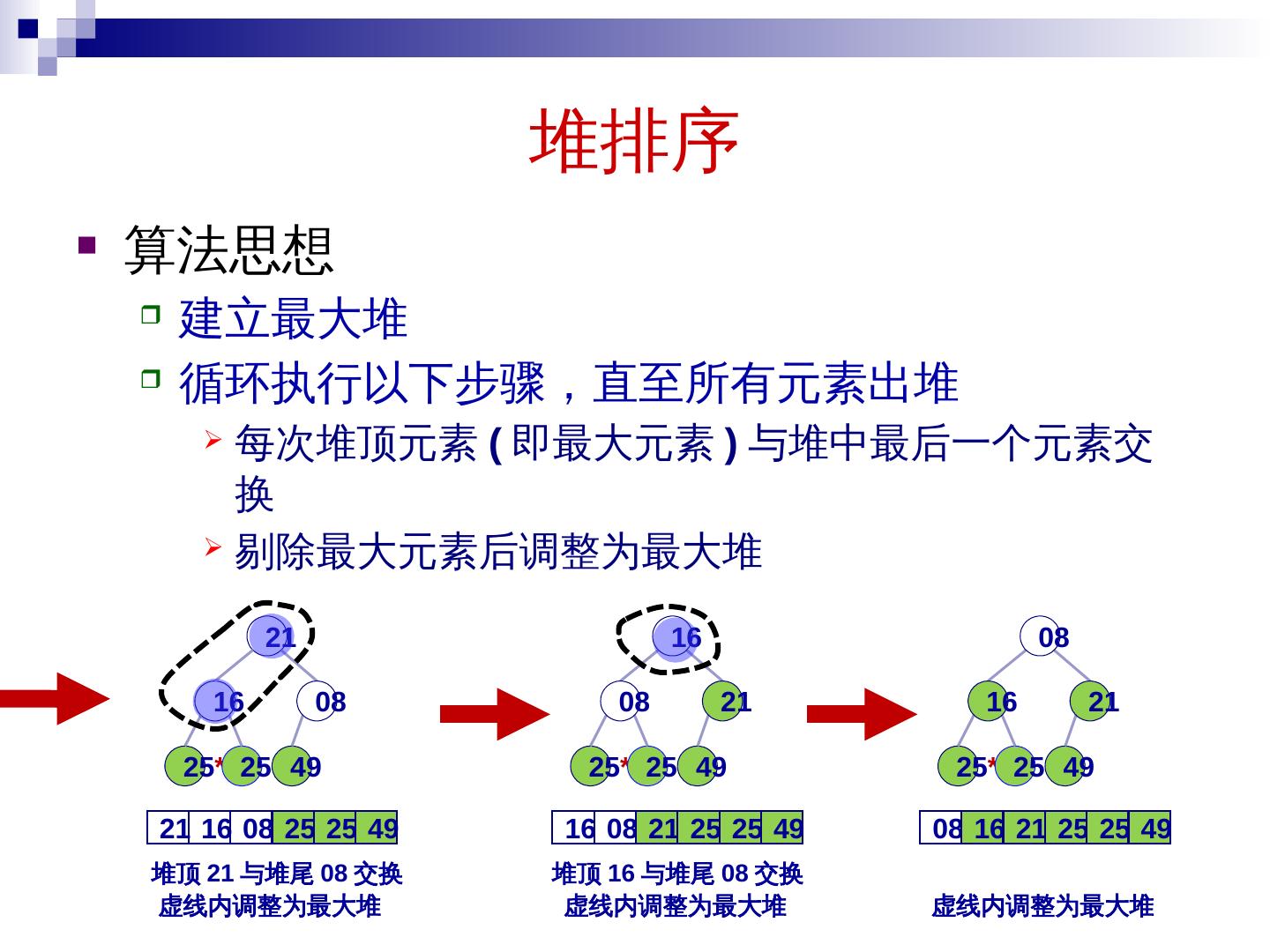
26 .堆排序 算法思想 建立最大堆 循环执行以下步骤,直至所有元素出堆 每次堆顶元素 ( 即最大元素 ) 与堆中最后一个元素交换 剔除最大元素后调整为最大堆 堆顶 49 与堆尾 08 交换 49 25 21 25 * 16 08 21 25 25 * 16 49 08 21 49 25 * 08 16 25 25 25 * 21 08 16 49 虚线内调整为最大堆 堆顶 25 与堆尾 16 交换 虚线内调整为最大堆 21 49 16 08 25 25 * 25 * 16 21 08 25 49 堆顶 25 * 与堆尾 08 交换 虚线内调整为最大堆
27 .堆排序 算法思想 建立最大堆 循环执行以下步骤,直至所有元素出堆 每次堆顶元素 ( 即最大元素 ) 与堆中最后一个元素交换 剔除最大元素后调整为最大堆 49 16 25 * 25 21 21 16 08 25 * 25 49 堆顶 21 与堆尾 08 交换 虚线内调整为最大堆 08 49 25 * 25 16 08 21 25 * 25 49 堆顶 16 与堆尾 08 交换 虚线内调整为最大堆 21 08 16 49 25 * 25 08 16 21 25 * 25 49 虚线内调整为最大堆 21 16 08
28 .堆排序 堆排序算法分析 建立最大堆 设堆中有 n 个元素 , 对应完全二叉树有 k 层 (2 k-1 ≤n < 2 k ) 第 i 层向下调整移动距离最大为 (k-i), 第 i 层节点数为 2 i-1 总移动次数 循环弹出堆顶元素 执行 n-1 次向下调整,每次调整距离 log 2 (n+1) 总调整时间 O(nlog 2 n)
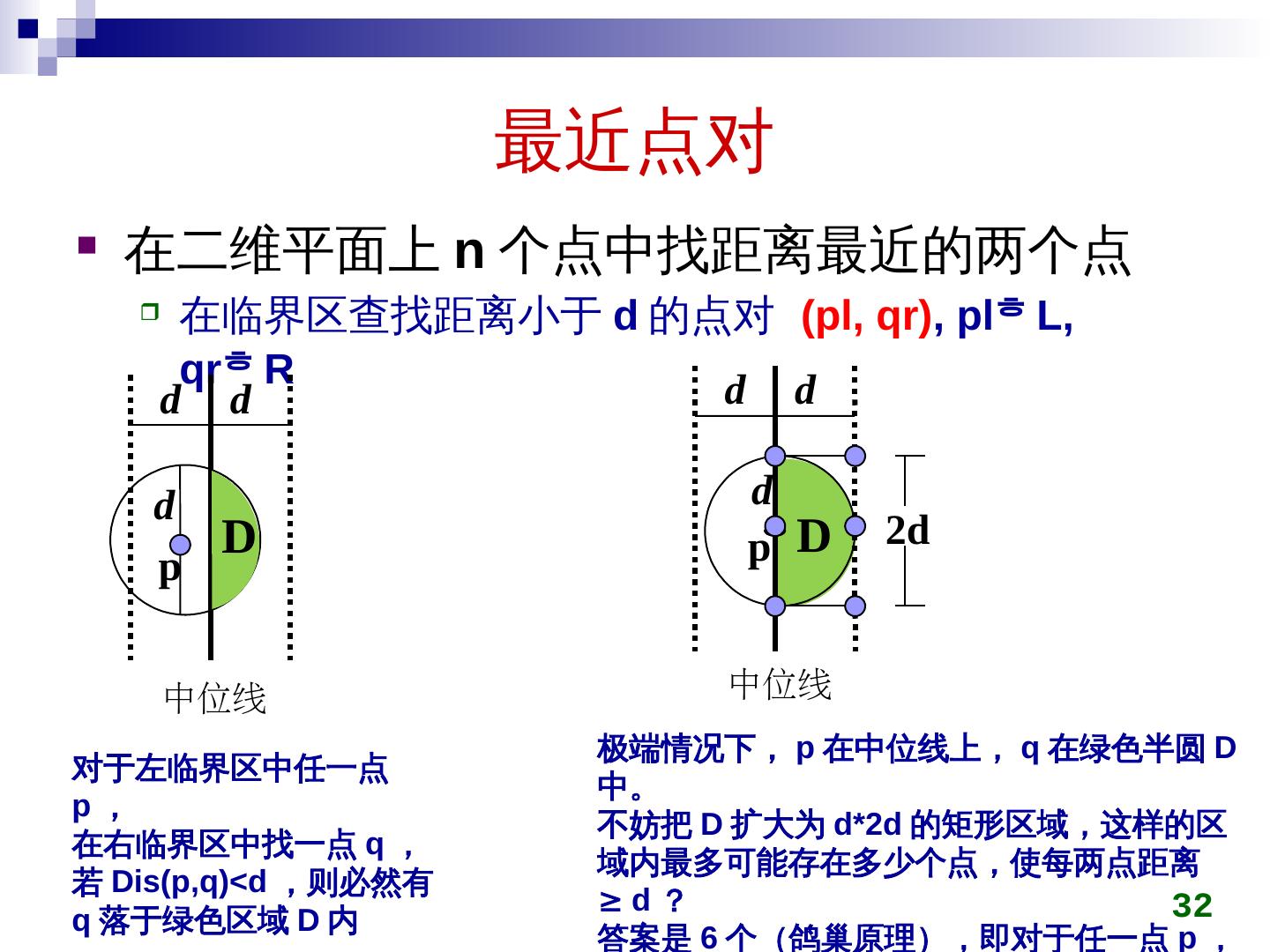
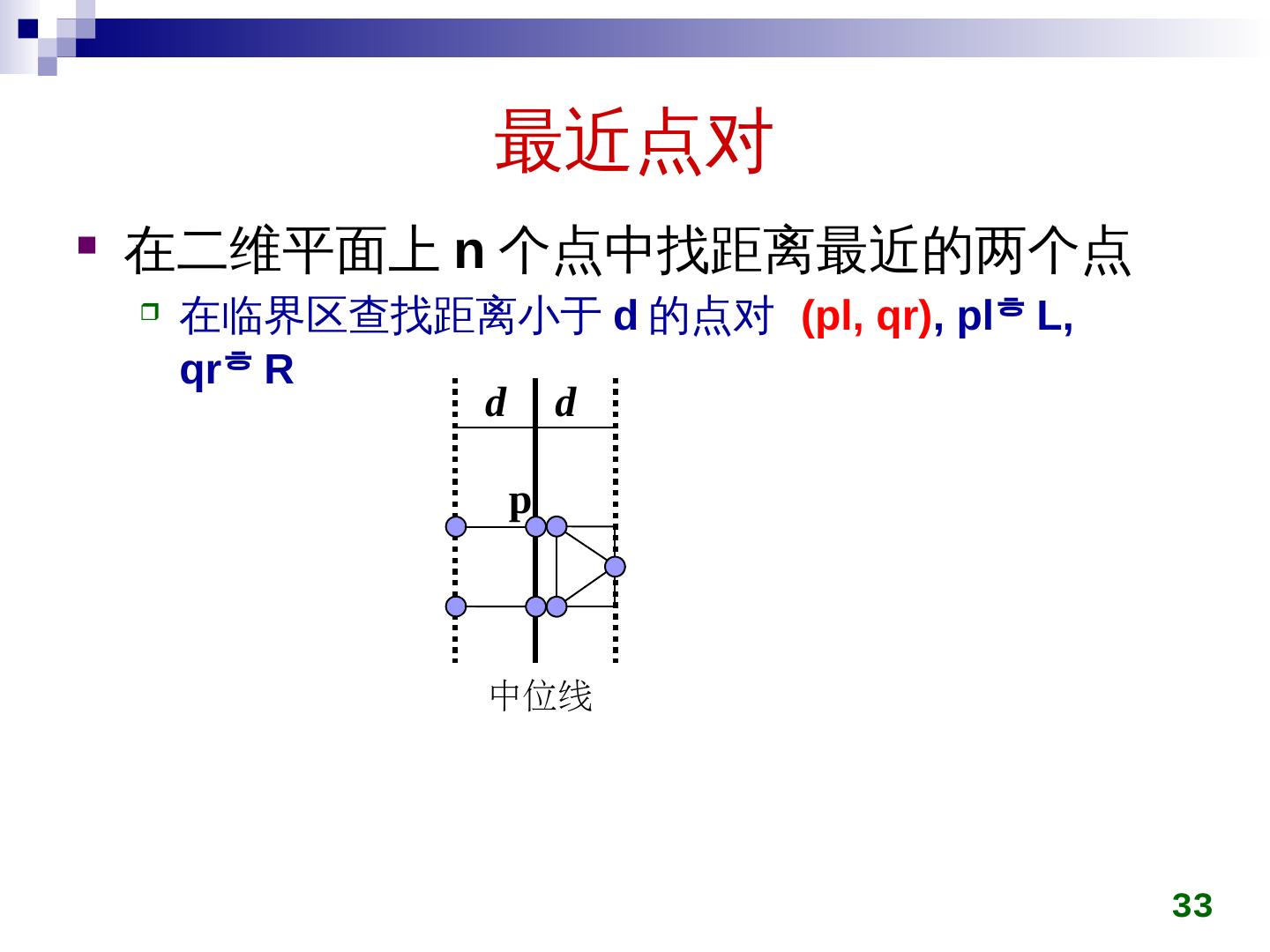
29 .最近点对 在二维平面上 n 个点中找距离最近的两个点 输入 输出距离最近的两个点 为 Euclidean 距离, 令 29