展开查看详情
1 .Data Structures and Algorithms in Parallel Computing Lecture 10
2 .Numerical algorithms Algorithms that use numerical approximation to solve mathematical problems They do not seek exact solutions because this would be nearly impossible in practice Much work has been done on parallelizing numerical algorithms Matrix operations Particle physics Systems of linear equations … Note: https://courses.engr.illinois.edu/cs554/fa2015/notes/index.html
3 .Matrix operations Inner product: Outer product: Matrix vector product: Matrix matrix product:
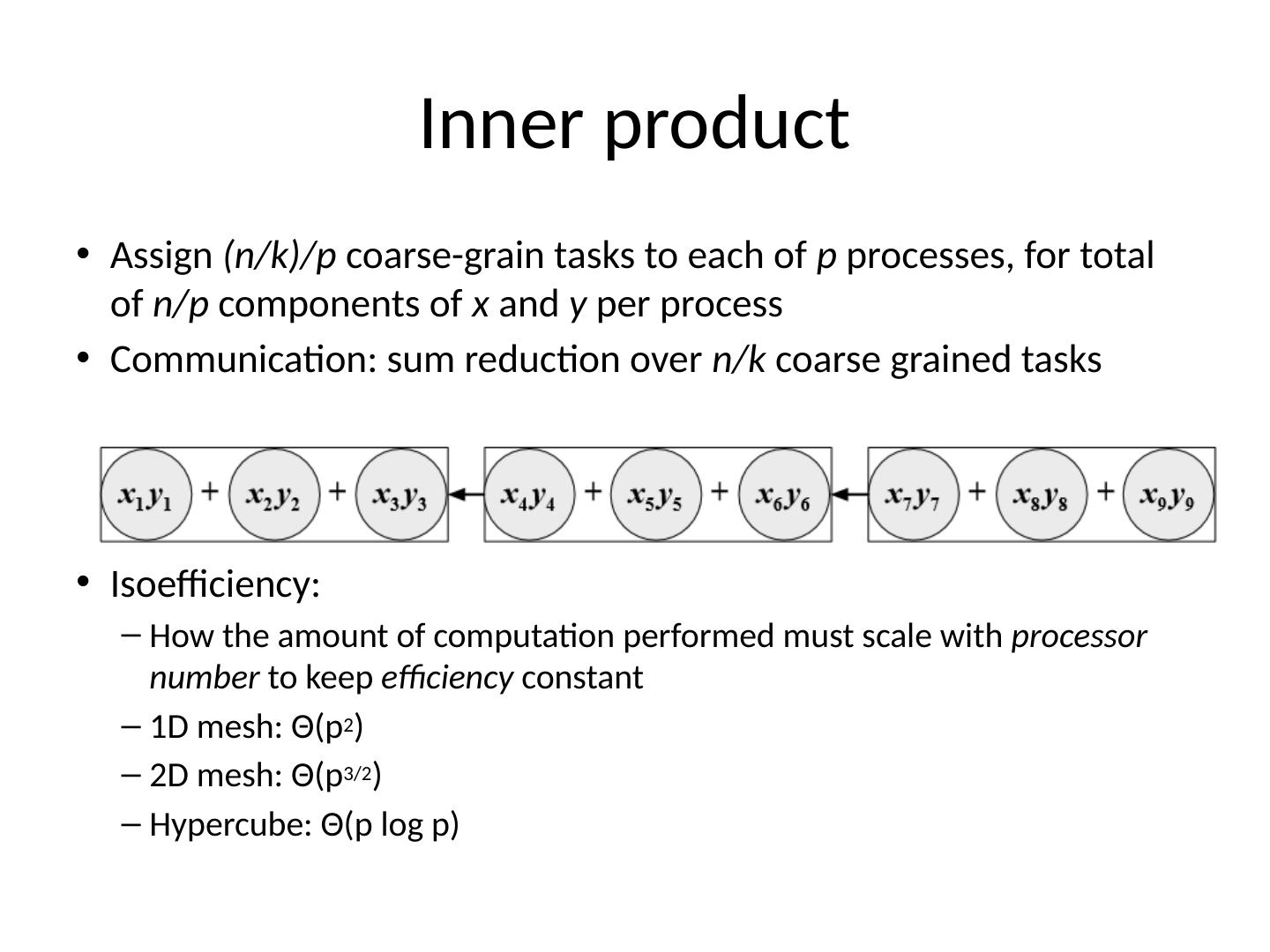
4 .Inner product Assign (n/k)/p coarse-grain tasks to each of p processes, for total of n/p components of x and y per process Communication: sum reduction over n/k coarse grained tasks Isoefficiency : How the amount of computation performed must scale with processor number to keep efficiency constant 1D mesh: Θ (p 2 ) 2D mesh: Θ (p 3/2 ) Hypercube: Θ (p log p)
5 .Outer product At most n tasks store components of x and y: for some j, task ( i,j ) stores x i and task ( j,i ) stores y i , or task ( i,i ) stores both x i and y i , i = 1,...,n Communication: For i = 1,...,n, task that stores x i broadcasts it to all other tasks in ith task row For j = 1,...,n, task that stores y j broadcasts it to all other tasks in jth task column
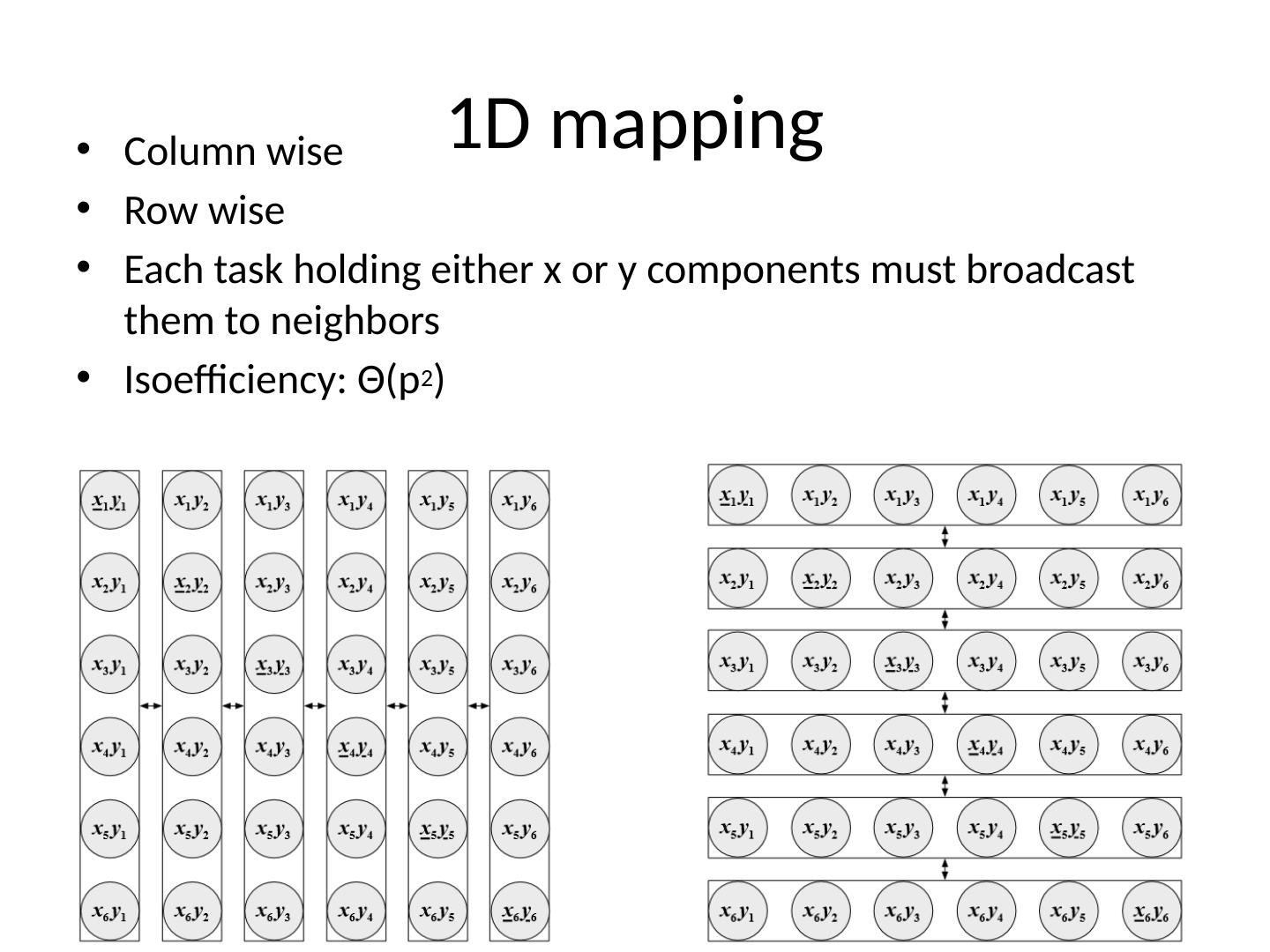
6 .1D mapping Column wise Row wise Each task holding either x or y components must broadcast them to neighbors Isoefficiency : Θ (p 2 )
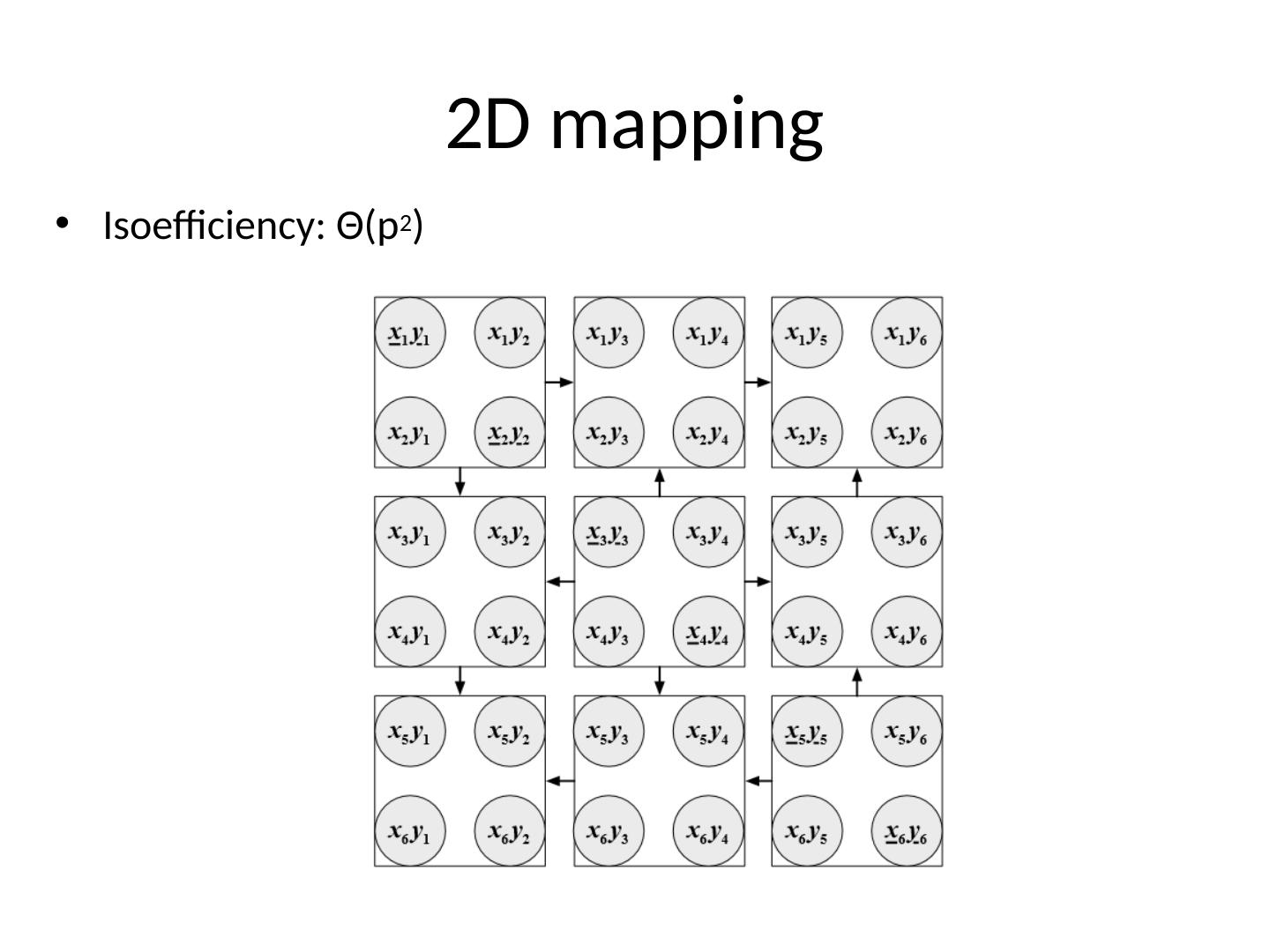
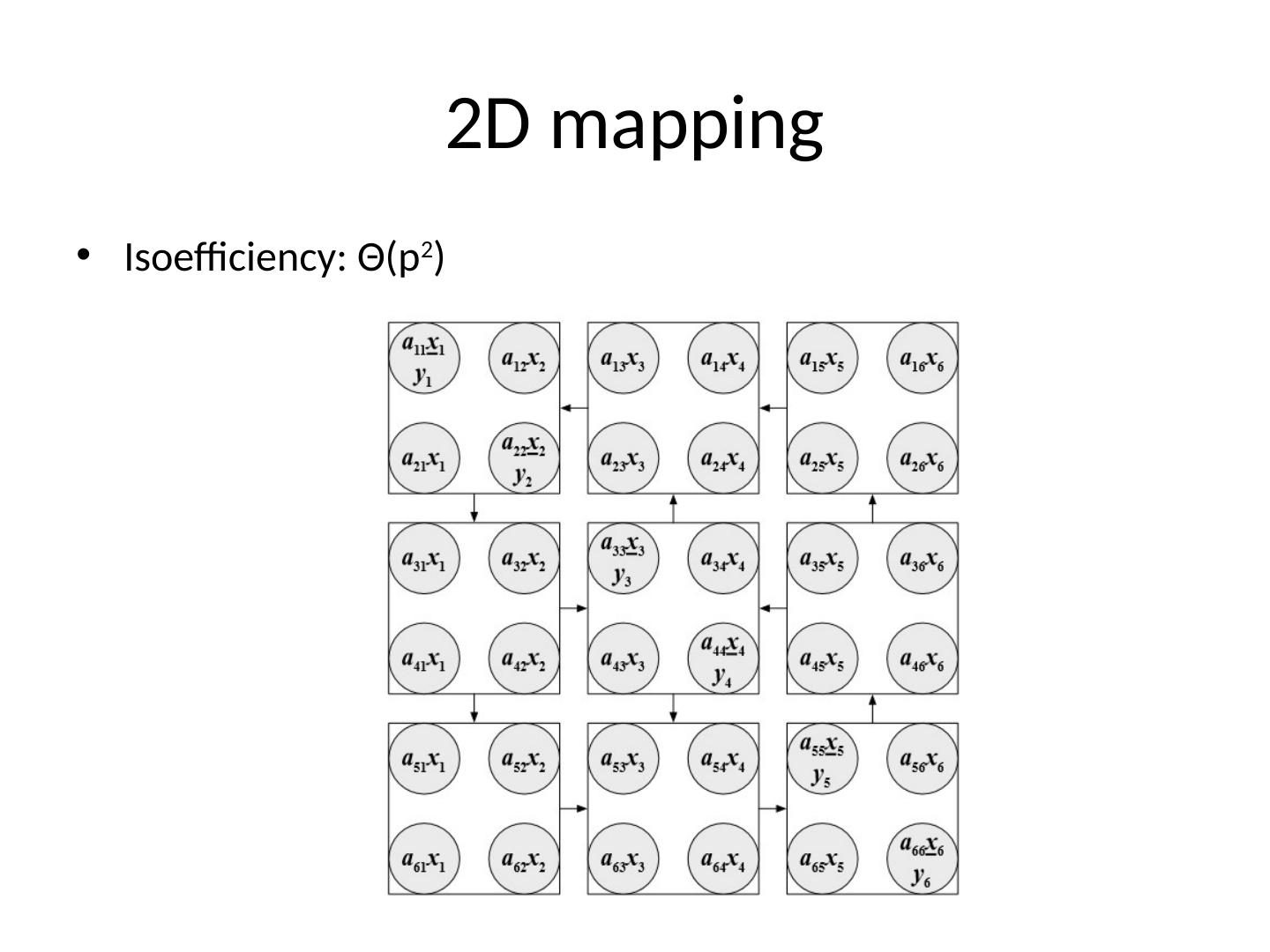
7 .2D mapping Isoefficiency : Θ (p 2 )
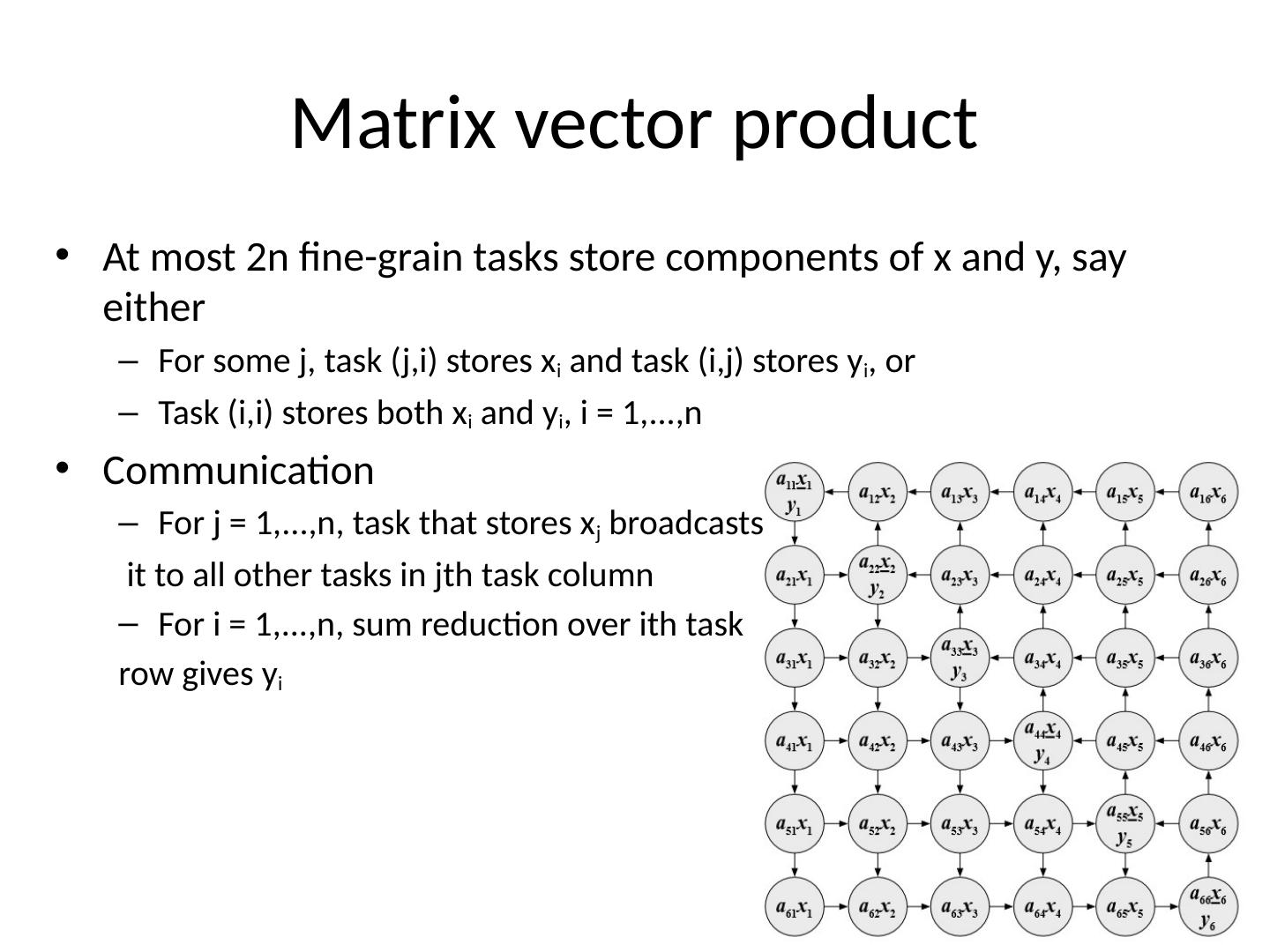
8 .Matrix vector product At most 2n fine-grain tasks store components of x and y, say either F or some j, task ( j,i ) stores x i and task ( i,j ) stores y i , or T ask ( i,i ) stores both x i and y i , i = 1,...,n Communication For j = 1,...,n, task that stores x j broadcasts it to all other tasks in jth task column For i = 1,...,n, sum reduction over ith task row gives y i
9 .Matrix vector product Steps Broadcast x j to tasks ( k,j ), k = 1,...,n Compute y i = a ij x j Reduce y i across tasks ( i,k ), k = 1,..., n
10 .Matrix vector product Steps Broadcast x j to tasks ( k,j ), k = 1,...,n Compute y i = a ij x j Reduce y i across tasks ( i,k ), k = 1,..., n
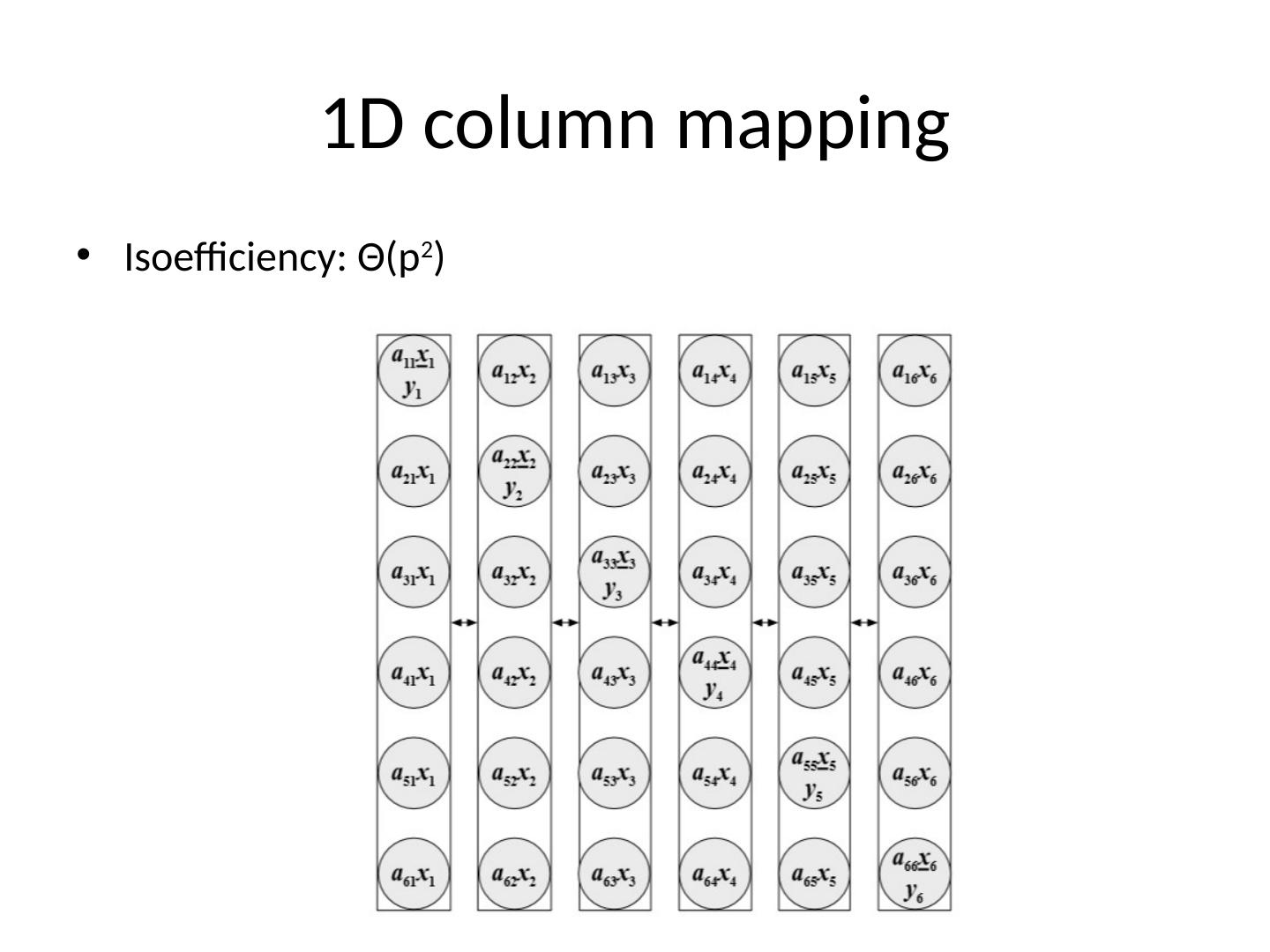
11 .1D column mapping Isoefficiency : Θ (p 2 )
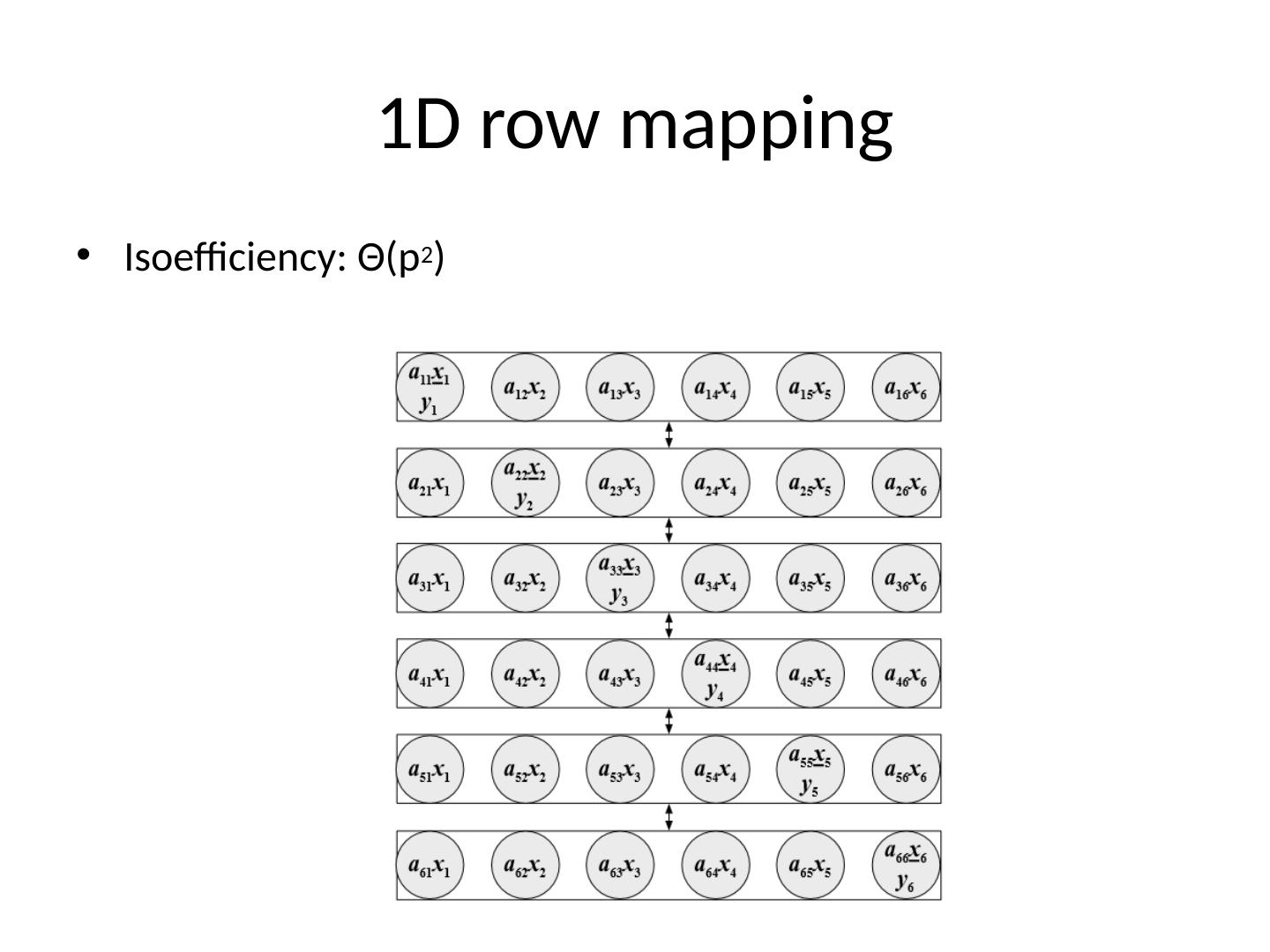
12 .1D row mapping Isoefficiency : Θ (p 2 )
13 .Matrix matrix product Matrix-matrix product can be viewed as: n 2 inner products, or sum of n outer products, or n matrix-vector products Each viewpoint yields different algorithm One way to derive parallel algorithms for matrix-matrix product is to apply parallel algorithms already developed for inner product, outer product, or matrix-vector product We will investigate parallel algorithms for this problem directly
14 .Matrix matrix product At most 3n 2 fine-grain tasks store entries of A, B, or C, say task ( i,j,j ) stores a ij , task ( i,j,i ) stores b ij , and task ( i,j,k ) stores c ij for i,j = 1,...,n and some fixed k ( i ,j,k ) = (row, column, layer) Communication Broadcast entries of jth column of A horizontally along each task row in jth layer Broadcast entries of ith row of B vertically along each task column in ith layer For i,j = 1,...,n, result c ij is given by sum reduction over tasks ( i,j,k ), k = 1,...,n
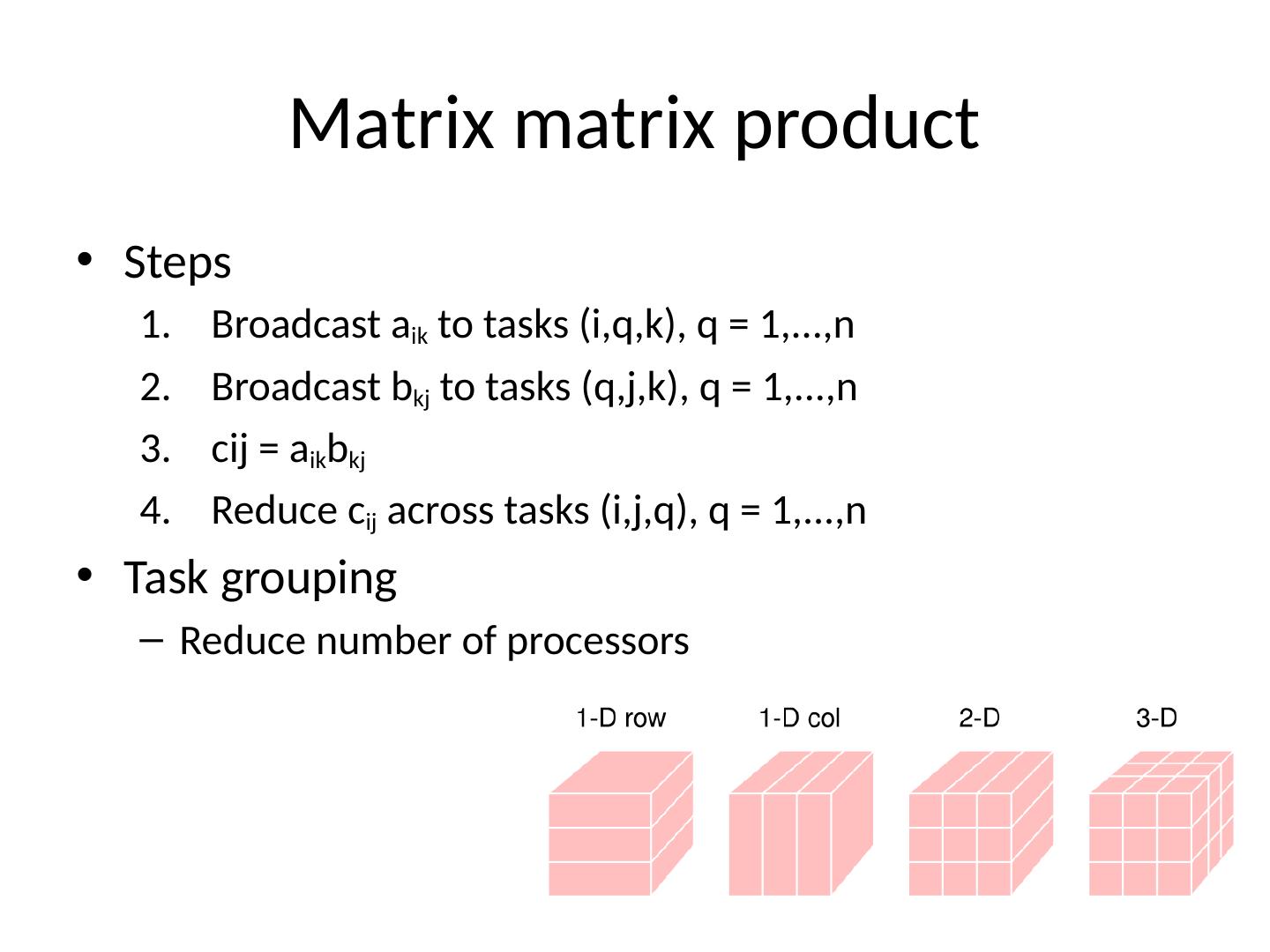
15 .Matrix matrix product Steps B roadcast a ik to tasks (i,q,k), q = 1,...,n B roadcast b kj to tasks (q,j,k), q = 1,...,n cij = a ik b kj R educe c ij across tasks (i,j,q), q = 1,..., n Task grouping Reduce number of processors
16 .Particle systems Many physical systems can be modeled as a collection of interacting particles Atoms in molecule Planets in solar system Stars in galaxy Galaxies in clusters Particles exert mutual forces on each other Gravitational Electrostatic
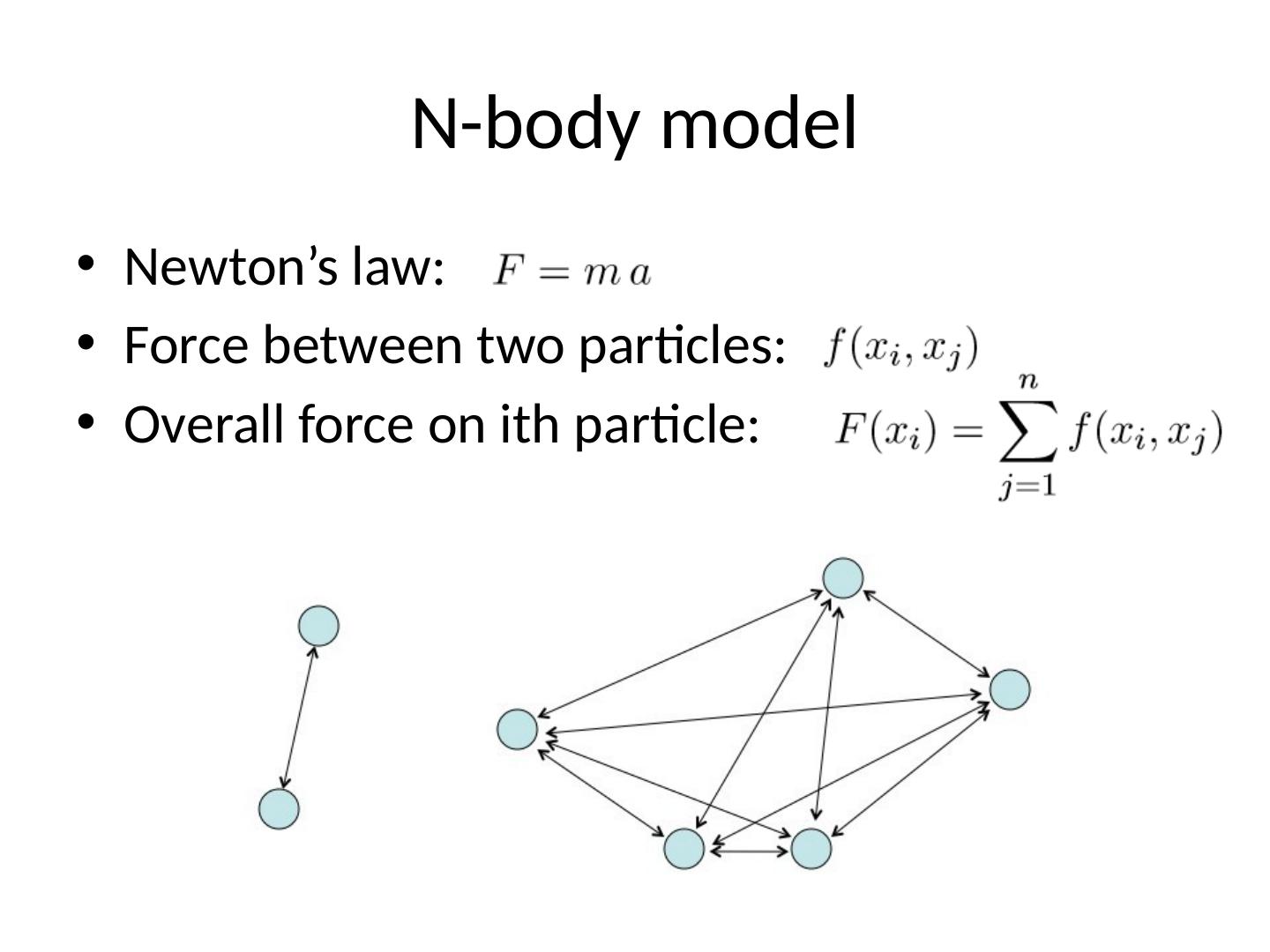
17 .N-body model Newton’s law: Force between two particles: Overall force on ith particle:
18 .Complexity O(n 2 ) due to particle-particle interactions Can be reduced to O(n log n) or O(n) through Hierarchical trees Multipole methods Pay penalty of accuracy
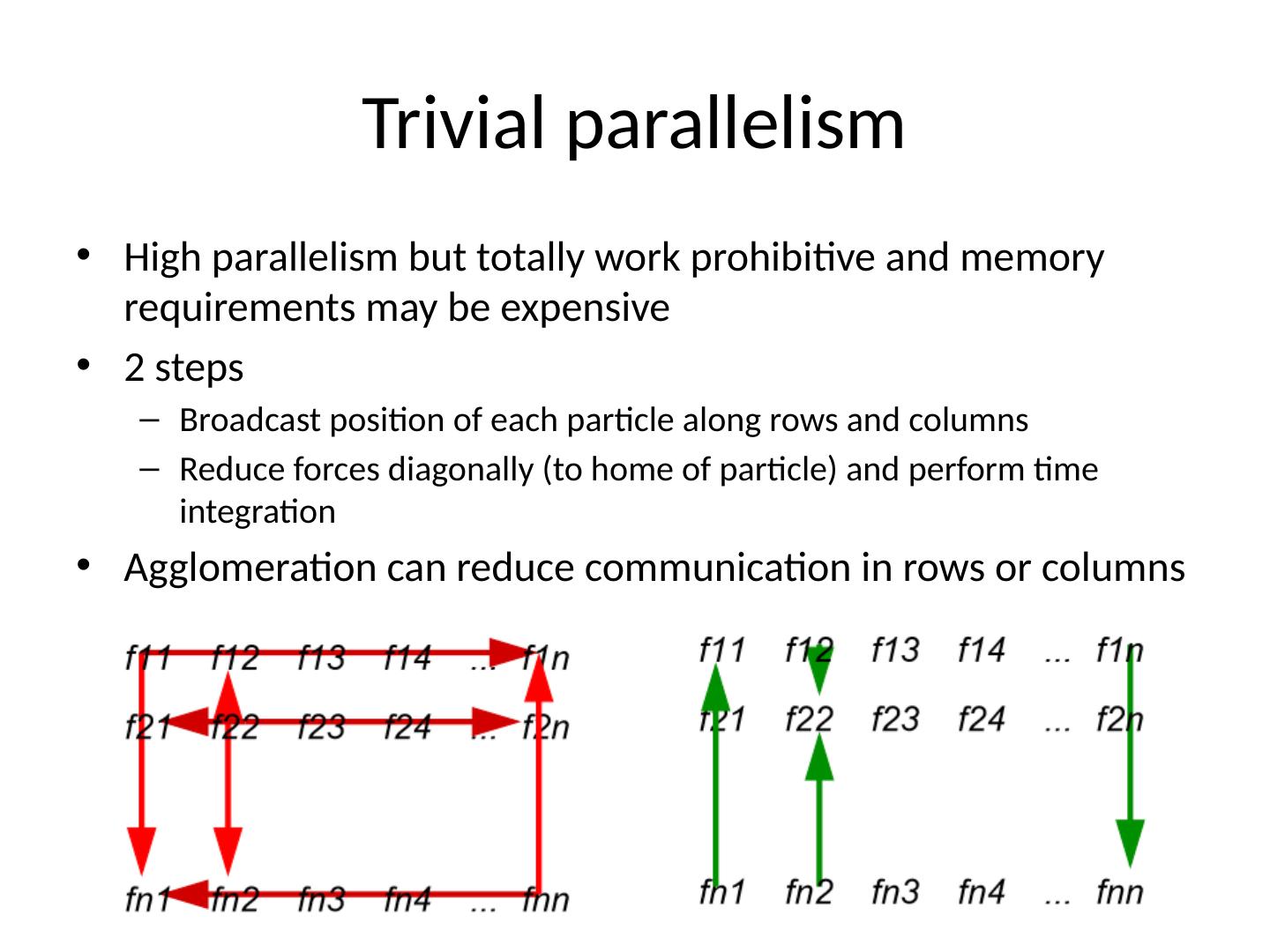
19 .Trivial parallelism High parallelism but totally work prohibitive and memory requirements may be expensive 2 steps Broadcast position of each particle along rows and columns Reduce forces diagonally (to home of particle) and perform time integration Agglomeration can reduce communication in rows or columns
20 .Reducing complexity Forces have infinite range, but with declining strength Three major options Perform full computation at O(n 2 ) cost Discard forces from particles beyond certain range, introducing error that is bounded away from zero Approximate long-range forces, exploiting behavior of force and/or features of problem
21 .Approach Monopole representation Or tree code Method: Aggregate distant particles into cells and represent effect of all particles in a cell by monopole (first term in multipole expansion) evaluated at center of cell Replace influence of far away particles with aggregate approximation of force Use larger cells at greater distances Approximation is relatively crude
22 .Parallel Approach Divide domain into patches, with each patch assigned to a process Tree code replaces communication with all processes by communication with fewer processes To avoid accuracy problem of monopole expansion, use full multipole expansion
23 .What’s next? Discuss some recent papers on parallel algorithms dealing with classes of problems discussed during this lecture
热门城市
