09Data Structures and Algorithms-Parallel computational geometry

1 .Data Structures and Algorithms in Parallel Computing Lecture 9

2 .Computational geometry Computational geometry problems involve calculating properties of sets of objects in k-dimensional space Classic problems include Minimum distance between any two points Finding the smallest convex region that encloses a set of points (convex-hull) Finding line or polygon intersections

3 .Parallel computational geometry Most standard problems have been solved thru efficient parallel algorithms Many sequential problems are based on divide-and-conquer techniques Straightforward parallelism Others are based on plane sweeping Do not parallelize well Solvable in parallel using the plane sweep tree

4 .Closest pair Set of k-dimensional points Return the 2 points closest to each other 2D case Planar closest pair Work O(n log n) Same as sequential version  optimal Depth O(log 2 n) Divide and conquer Split points along lines parallel to the y axis

5 .Algorithm δ L – closest distance in L δ R – closest distance in R

6 .Boundary-merge Points sorted by y axis δ = min ( δ R, δ L ,) δ M – closest distance in M Closest points can be either at δ L , δ R , or a distance δ between a point in L and one in R from the line x m δ P = min ( δ R, δ L , δ M )

7 .Convex hull Take a set ok k-dimensional points and return the smallest convex region For 2D the problem is planar convex hull Algorithms QuickHull MergeHull

8 .QuickHull Idea: Pick “pivot”, split data, recurse on each split set Steps Pick 2 points p 1 and p 2 Remove points which are on the right of the p 1 p 2 line If remaining set has at most one element stop Else find point p m farthest from p 1 p 2 which is on the hull Apply algorithm recursively on p 1 , p m and p m , p 2

9 .Algorithm

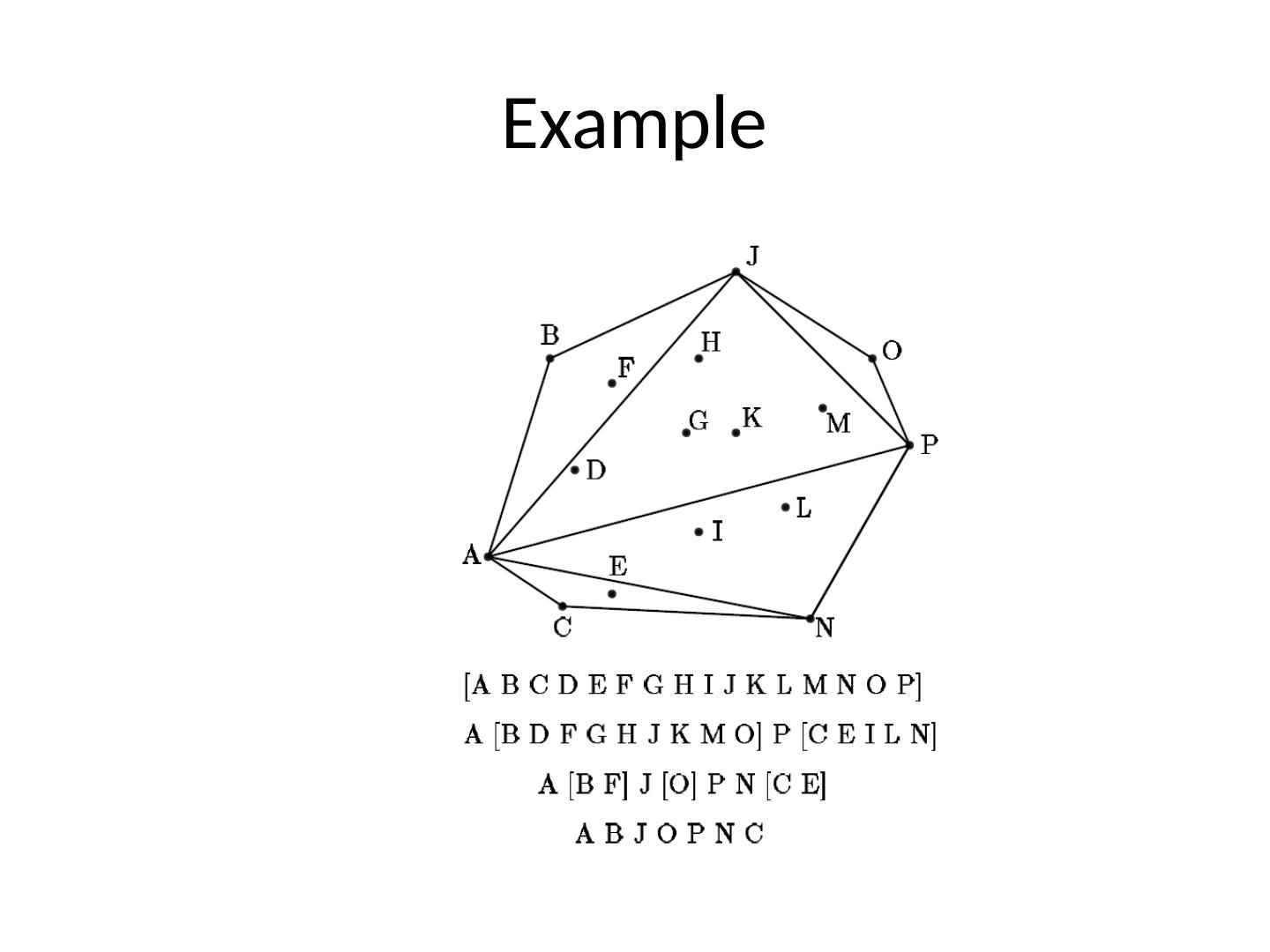
10 .Example

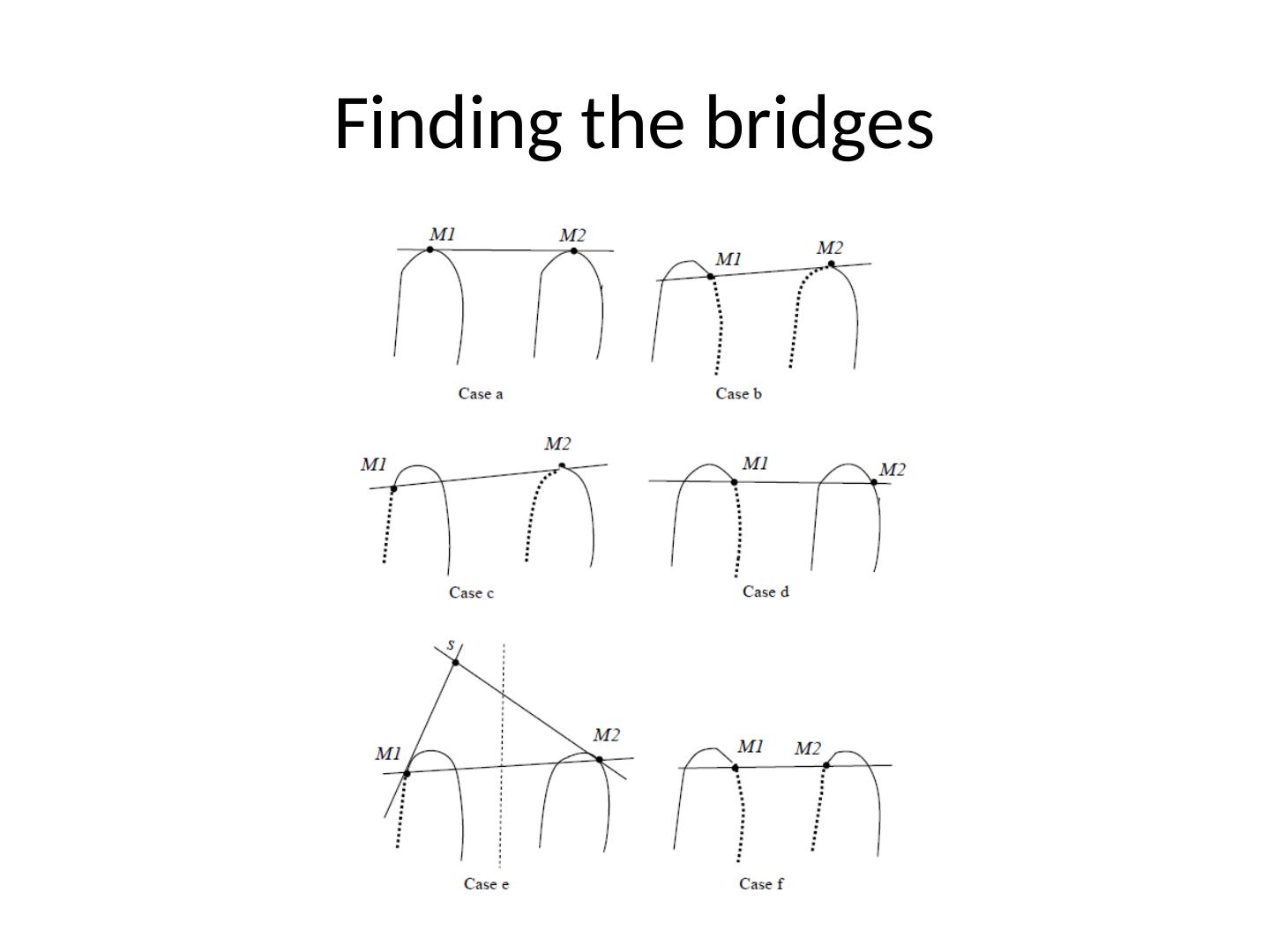
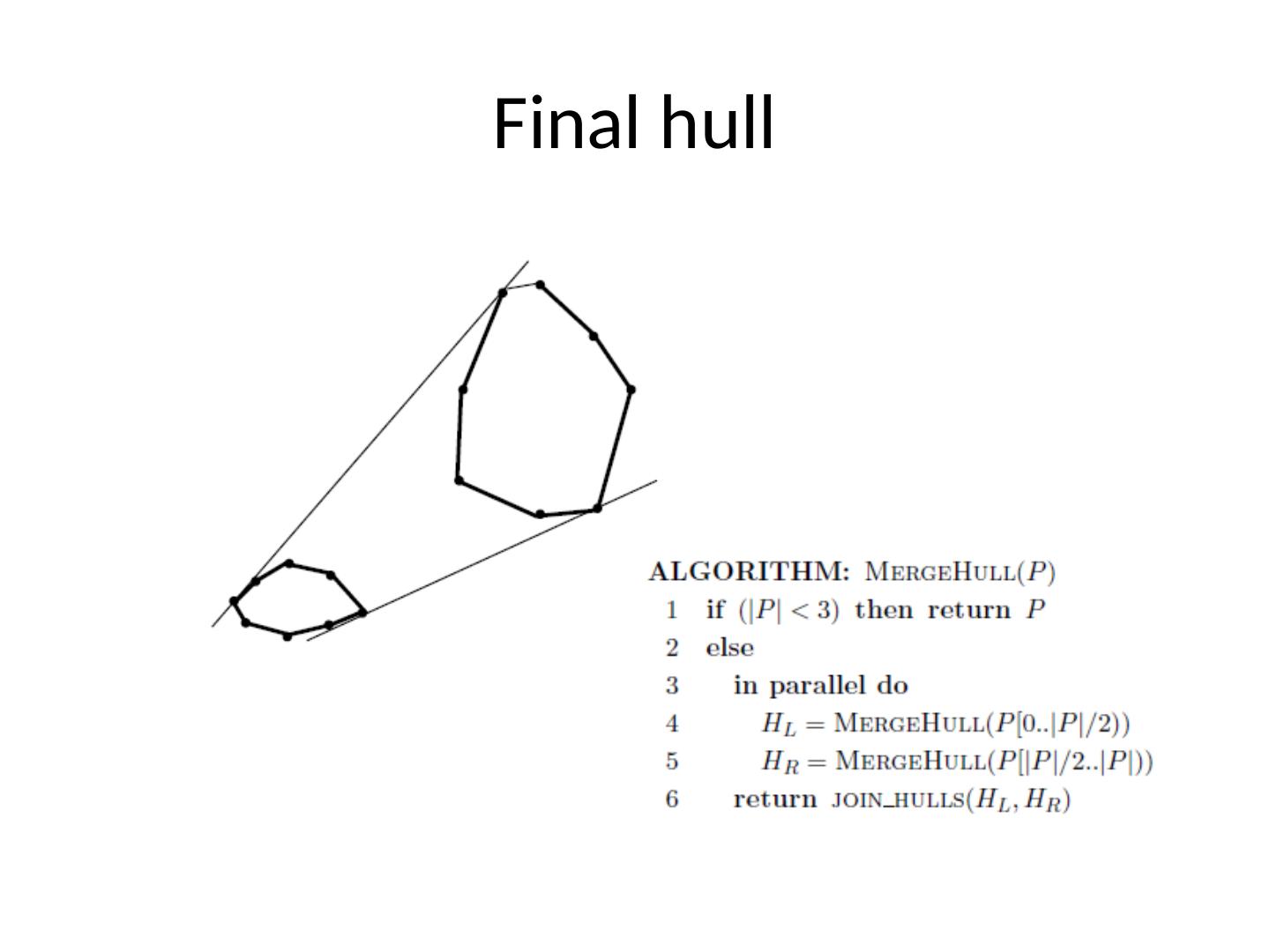
11 .MergeHull Unlike QuickHull most work is done after returning from the recursive calls Steps Input points sorted by x coordinates H L is a convex hull on the left H R is a convez hull on the right Merge the two hulls Find upper and lower points on each and link them Upper and lower bridges Recursively based on dual binary search Points on the outer sides of the hulls are on the final hull

12 .Finding the bridges

13 .Final hull

14 .What’s next? Parallel numerical algorithms …