1.Data Structures and Algorithms in Parallel Computing Lecture 8

2.Parallel sorting Sorting is a problem that admits a variety of parallel solutions Goal Sorting a sequence of values in increasing order using n processors Why in parallel? Frequent operation in many applications Best sequential algorithm is O(n log n) In parallel on n processors we can aim for O ( log n)

3.Compare and swap with message exchange Sequential version requires comparing and swapping values Parallel version requires an extra communication step

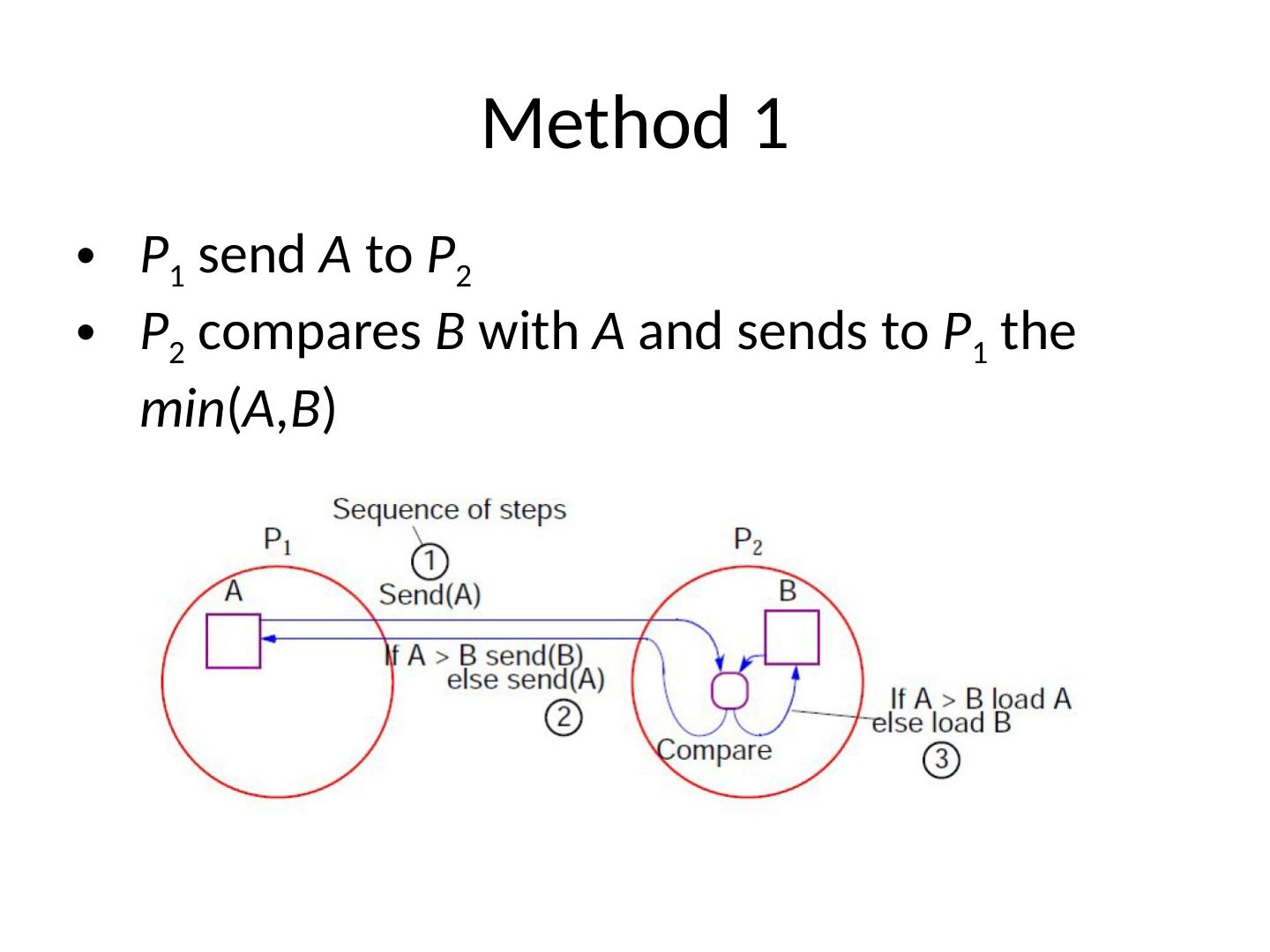
4.Method 1 P 1 send A to P 2 P 2 compares B with A and sends to P 1 the min ( A,B )

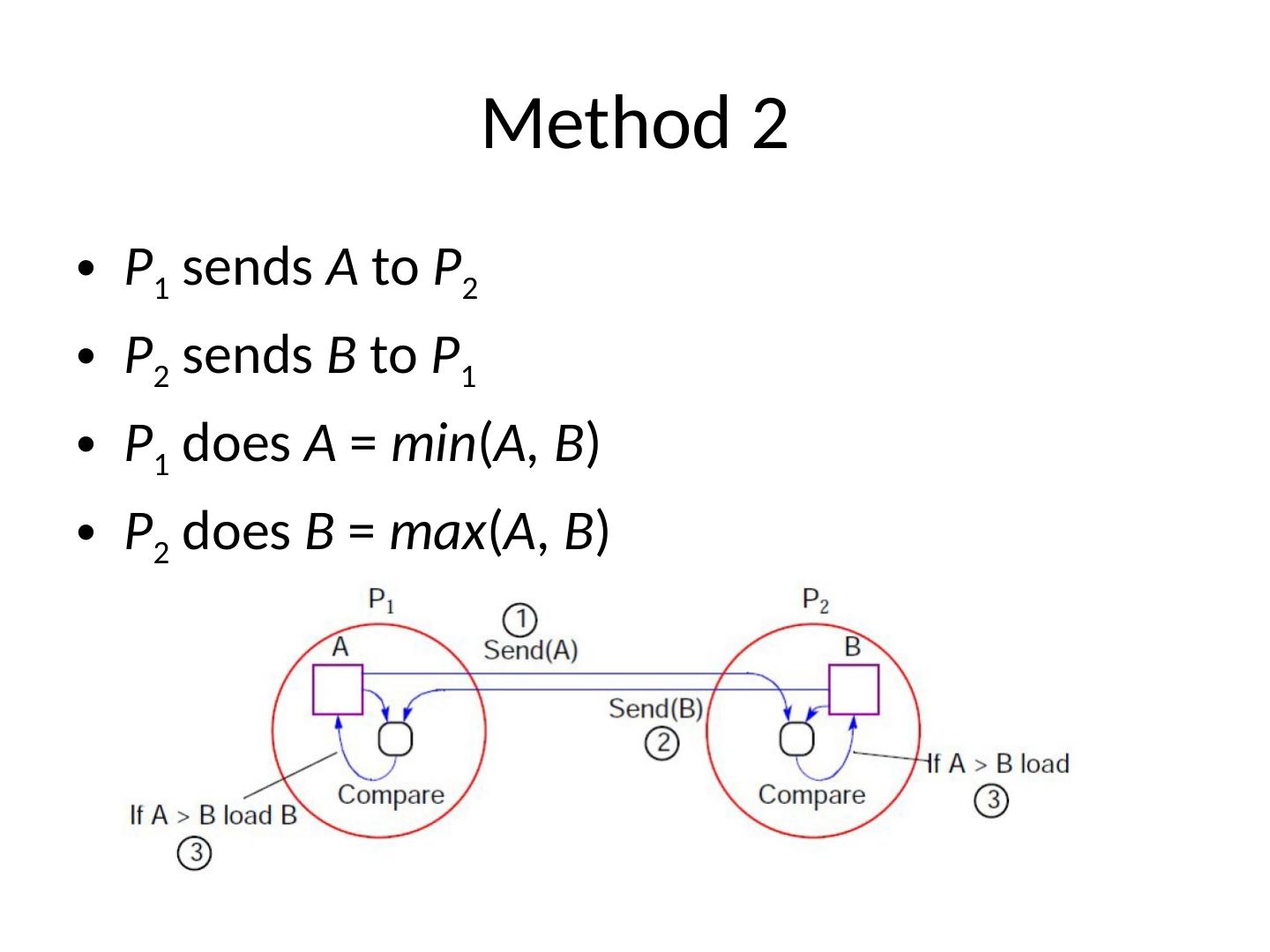
5.Method 2 P 1 sends A to P 2 P 2 sends B to P 1 P 1 does A = min ( A, B ) P 2 does B = max ( A, B )

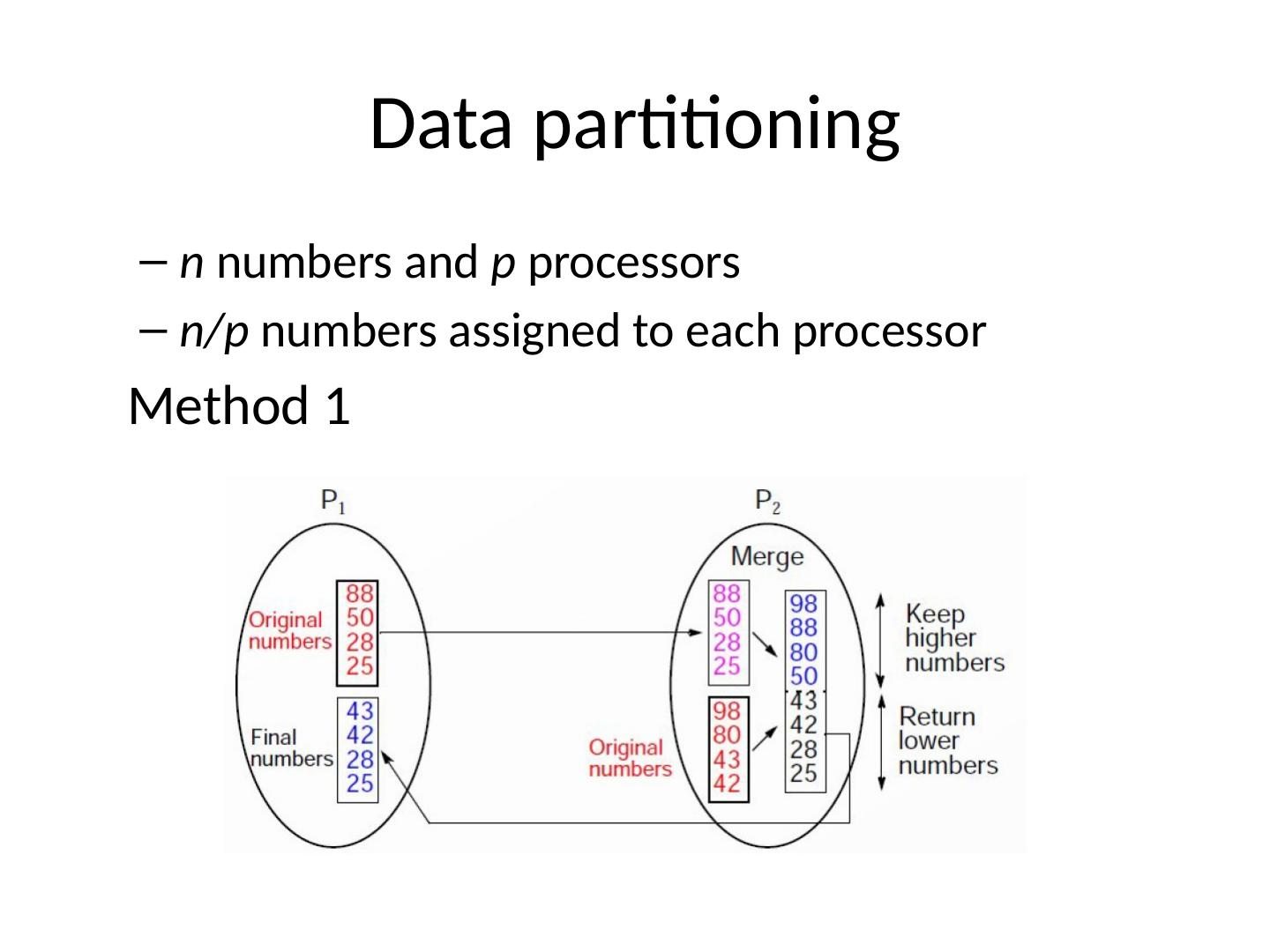
6.Data partitioning n numbers and p processors n/p numbers assigned to each processor Method 1

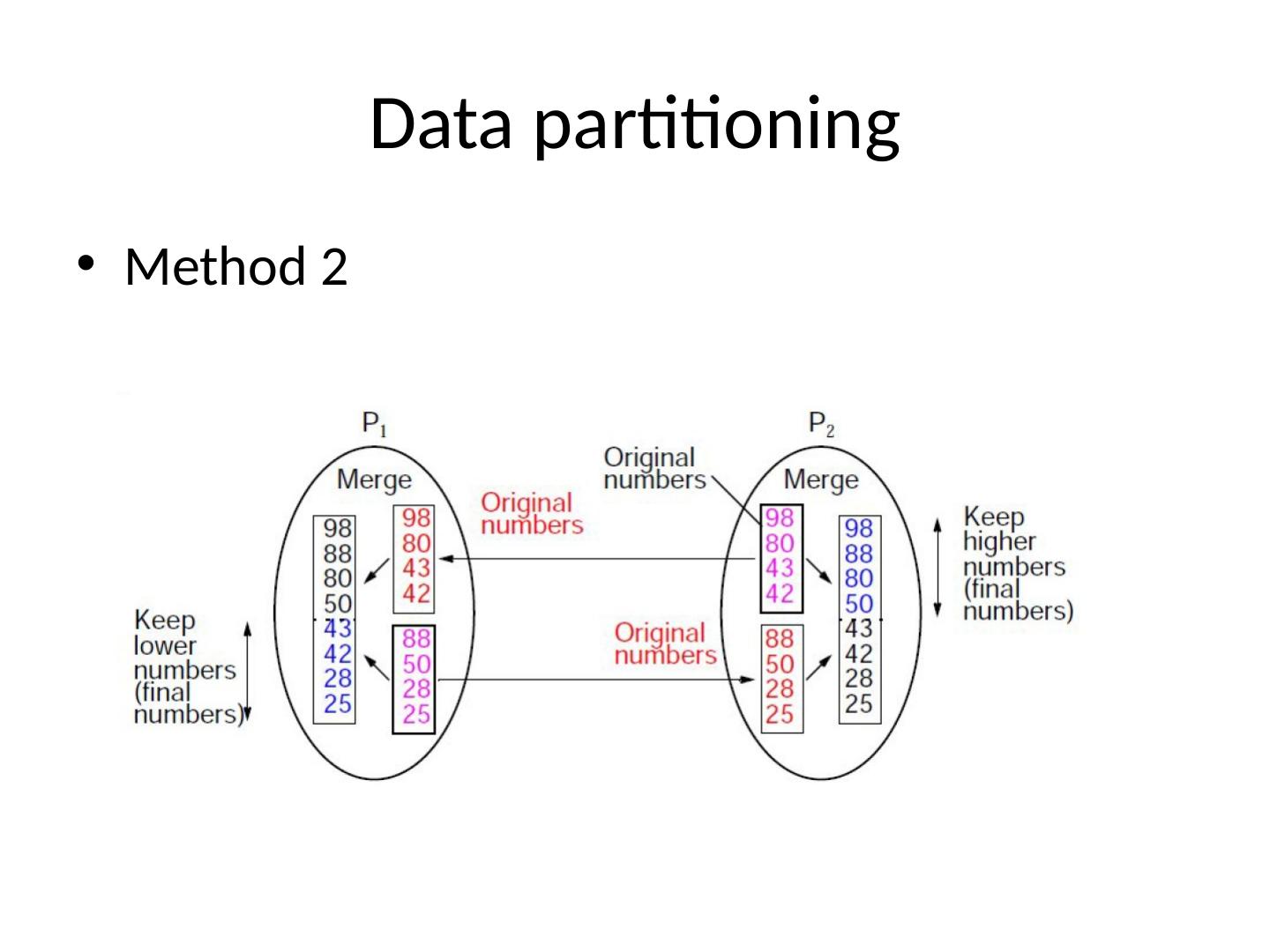
7.Data partitioning Method 2

8.Algorithms Bubblesort Mergesort Quicksort Bitonic sort

9.Sequential bubblesort

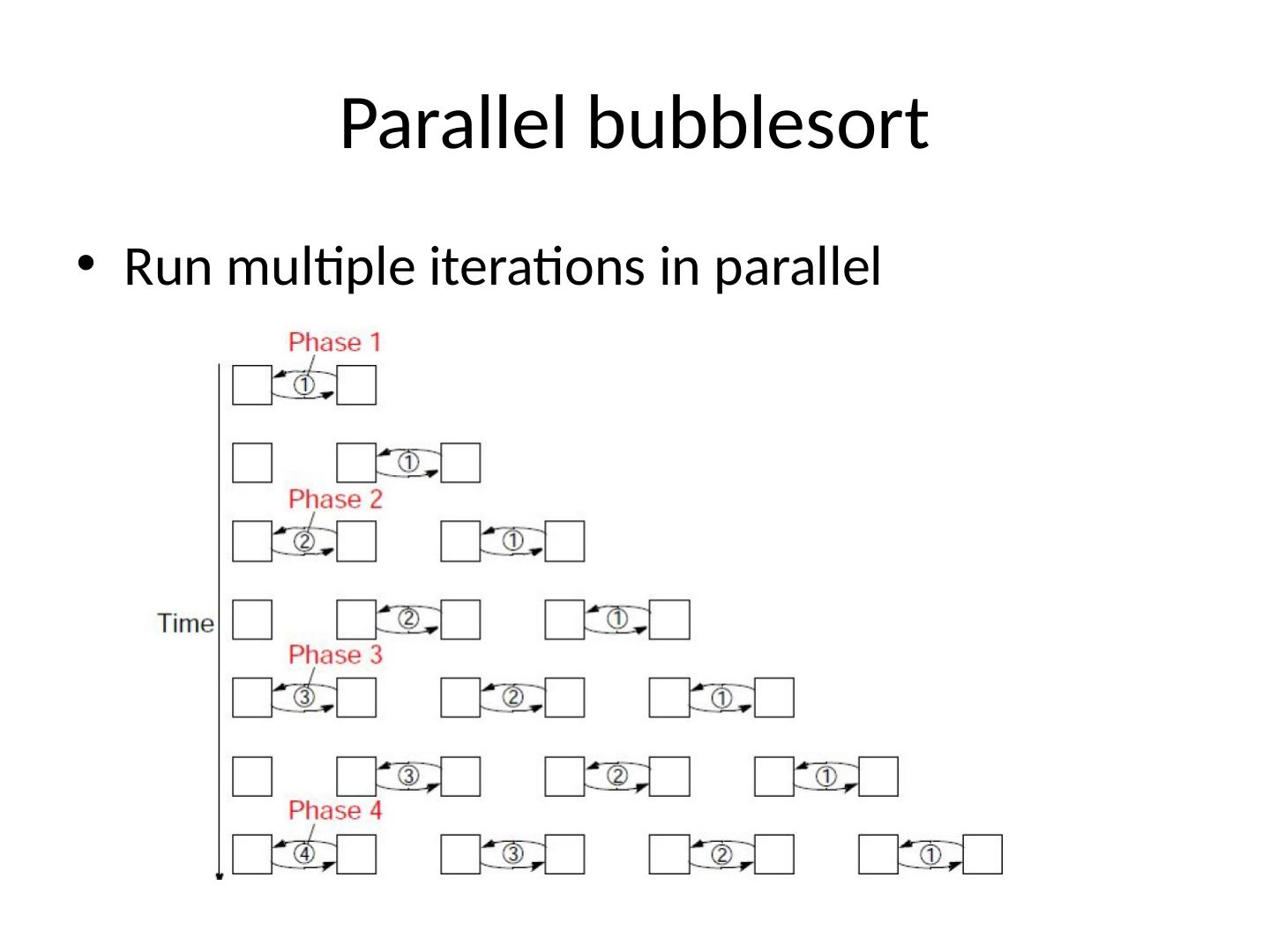
10.Parallel bubblesort Run multiple iterations in parallel

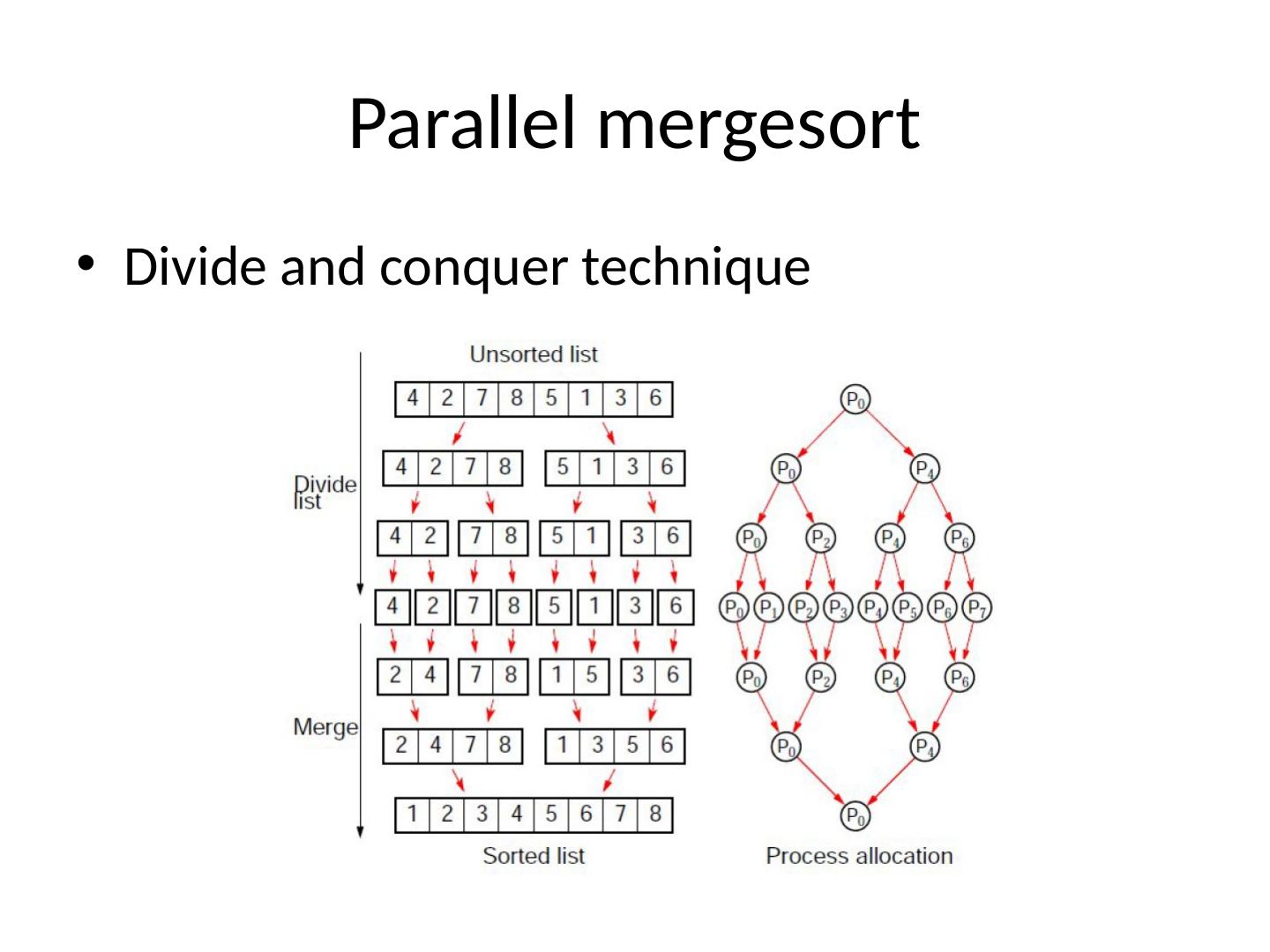
11.Parallel mergesort Divide and conquer technique

12.Parallel quicksort

13.Bitonic sort Bitonic sequences complexity: O(log 2 n ) a sequence is bitonic if it contains two sequences, one increasing and one decreasing, i.e. a 1 < a 2 < . . . < a i−1 < a i > a i+1 > a i+2 > . . . > a n for some i such that (0 ≤ i ≤ n ) a sequence is bitonic if the property described is attained by a circular rotation to the right of its elements.

14.Bitonic sorting network Unsorted sequence  bitonic sequence  sorted sequence https:// www.youtube.com/watch?v=GEQ8y26blEY

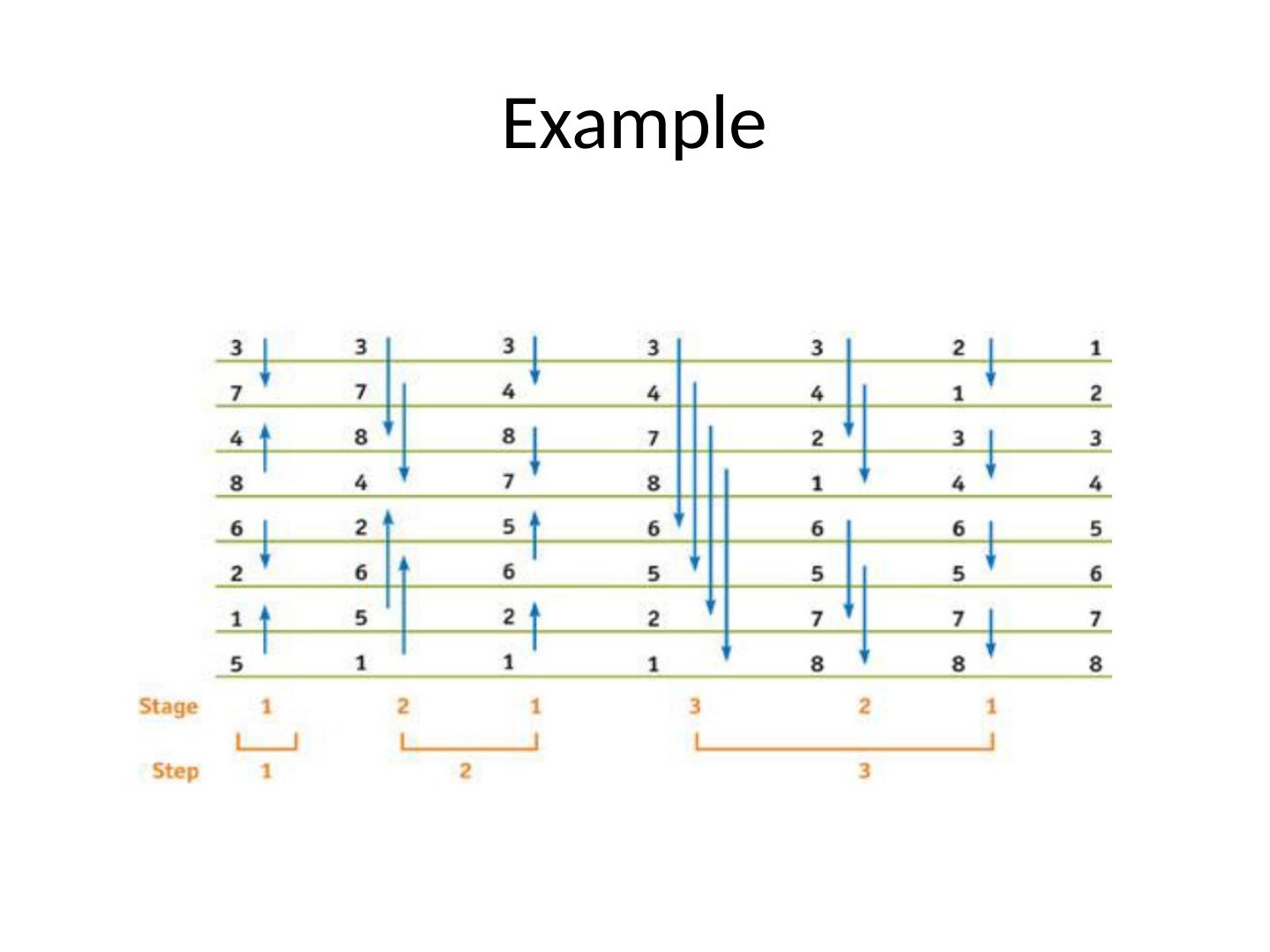
15.Example

16.What’s next? Parallel computational geometry Parallel numerical algorithms …