- 快召唤伙伴们来围观吧
- 微博 QQ QQ空间 贴吧
- 文档嵌入链接
- 复制
- 微信扫一扫分享
- 已成功复制到剪贴板
07Data Structures and Algorithms--Load balancing
展开查看详情
1 .Data Structures and Algorithms in Parallel Computing Lecture 7
2 .Parallel scientific computing How to assign work to machines? Static (at the start) vs. dynamic (during run time) Objective is to minimize total solution time Traditional approaches Graph partitioning Geometric partitioning Good for applications lacking graph connectivity (e.g., particle methods)
3 .Traditional approaches Recursive Spectral Bisection Splits vertices into groups based on eigenvectors of the Laplacian matrix associated with the graph Slow but effective Multilevel partitioning Diffusive partitioning Transfers work from heavily loaded processors to their more lightly loaded neighbors Faster than multilevel but require more iterations to achieve global balance
4 .Applications Multilevel partitioning Effective on finite element and finite volume methods Cells are divided among processors Diffusive and geometric partitioning Used in dynamic computations such as adaptive finite element methods Physical locality of geometric partitioning exploited by particle methods
5 .Beyond traditional approaches Traditional methods do not work well for higher connectivity and less homogeneity and symmetry Clustering Used in data mining Similarity and object-attributed based graph models Direct (look for connected components) and partitioning (min-cut) based clustering Other methods Devine et al., Partitioning and Load Balancing for Emerging Parallel Applications and Architectures , Parallel Processing for Scientific Computing, 2006
6 .Distributed graph processing Minimize communication costs between nodes Load balance the execution among nodes Subgraph centric reduced communication overhead by increasing local computations However efficiency depends on the graph type and partitioning technique
7 .Graph partitioning Key component in any distributed graph processing platform Performed before running graph algorithms Reduce communication and balance computation Partitioning depends on graph type Sparse graphs Better load balance with reduced communication Sparse graphs with skewed distributions Difficult to load balance with minimum communication Dense graphs Difficult to reduce communication overhead
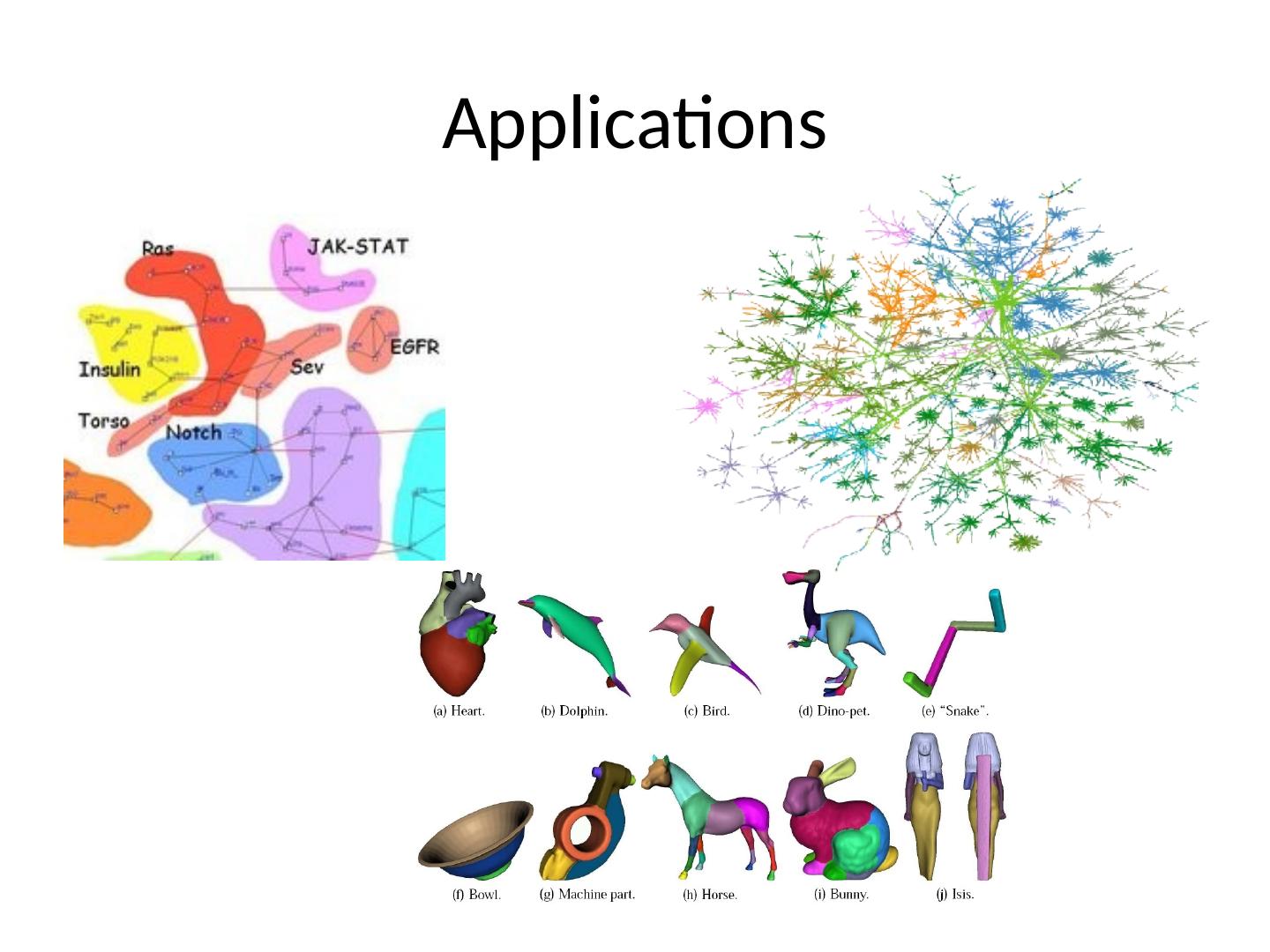
8 .Applications Load balancing while minimizing communication Structured and unstructured mesh distribution for distributed memory parallel computing Sparse matrix times vector multiplication VLSI Layout Telephone network design Sparse Gaussian Elimination
9 .Applications
10 .1D and 2D data distribution Represent graph as sparse matrix 1D – distribute vertices with their edges to processors Example : Parallel Boost Graph Library 2D – distribute subgraphs to processors Reduces communication overhead Allows higher degree of concurrency Example : various solutions for IBM BlueGene /L and Cray machines
11 .Balance computation vs. reduce communication Case study: Breadth First Search communication-intensive graph computations Used as subroutine for other sophisticated algorithms Connected components, spanning forests, testing for bipartites , maximum flows, betweenness centrality Chosen as representative benchmark for ranking supercomputers Bluc et al., Graph Partitioning for Scalable Distributed Graph Computations , DIMACS, 2004
12 .BFS algorithms In 2D case communication happens only along one processor dimension Buluc et al., Parallel Breadth-First Search on Distributed Memory Systems , SC, 2011
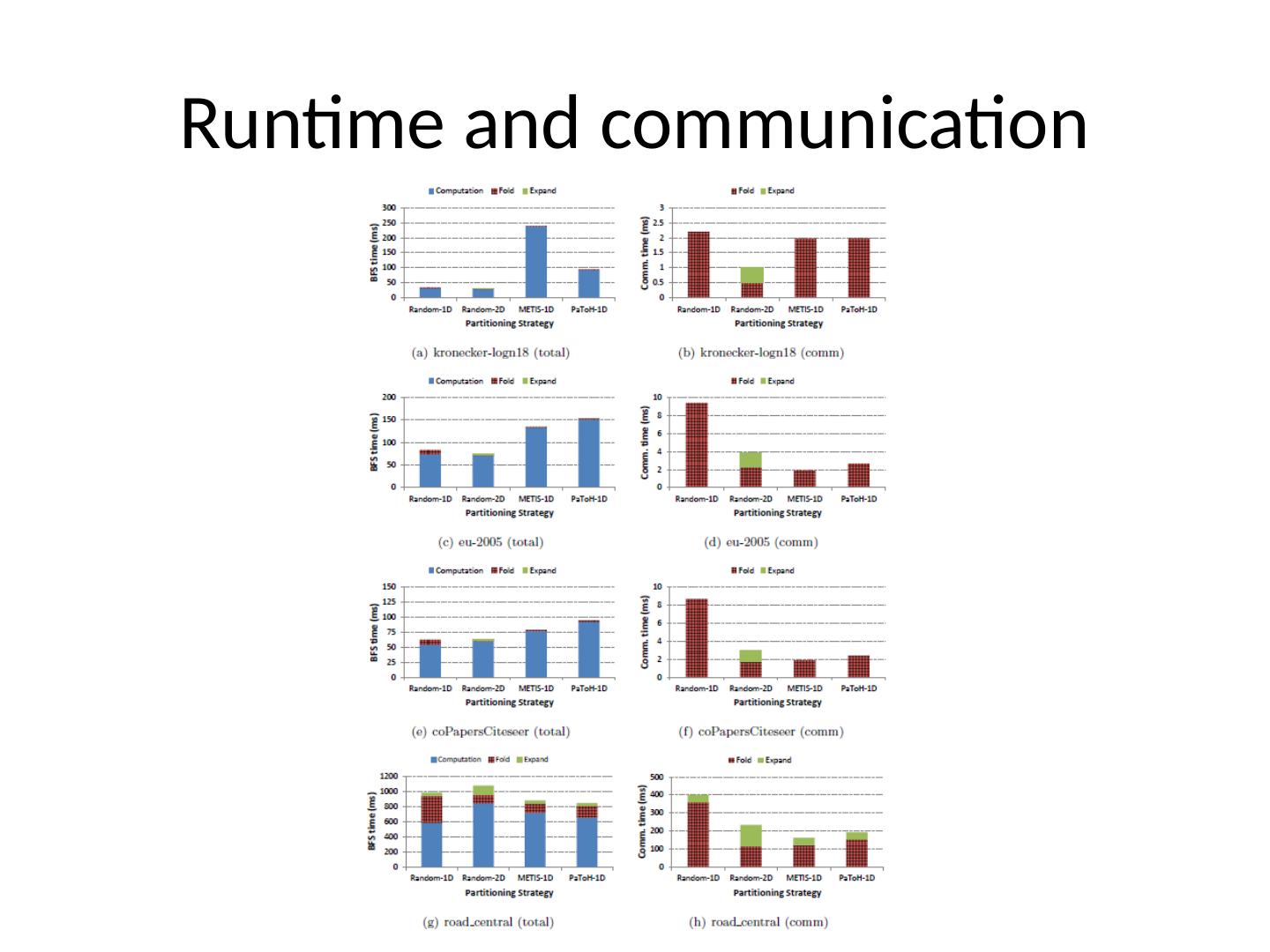
13 .Analysis METIS 1D partitioning balanced vertices per partition and simultaneously minimizing the number of cut edges K-way multilevel partitioning PaToH 1D and 2D partitioning Multilevel hypergraph partitioning
14 .Runtime and communication
15 .Overall conclusion Reducing work and communication imbalance among partitions is more important than minimizing the total edge cut Even well balanced vertex and edge partitions do not guarantee load-balanced execution for real-world graphs
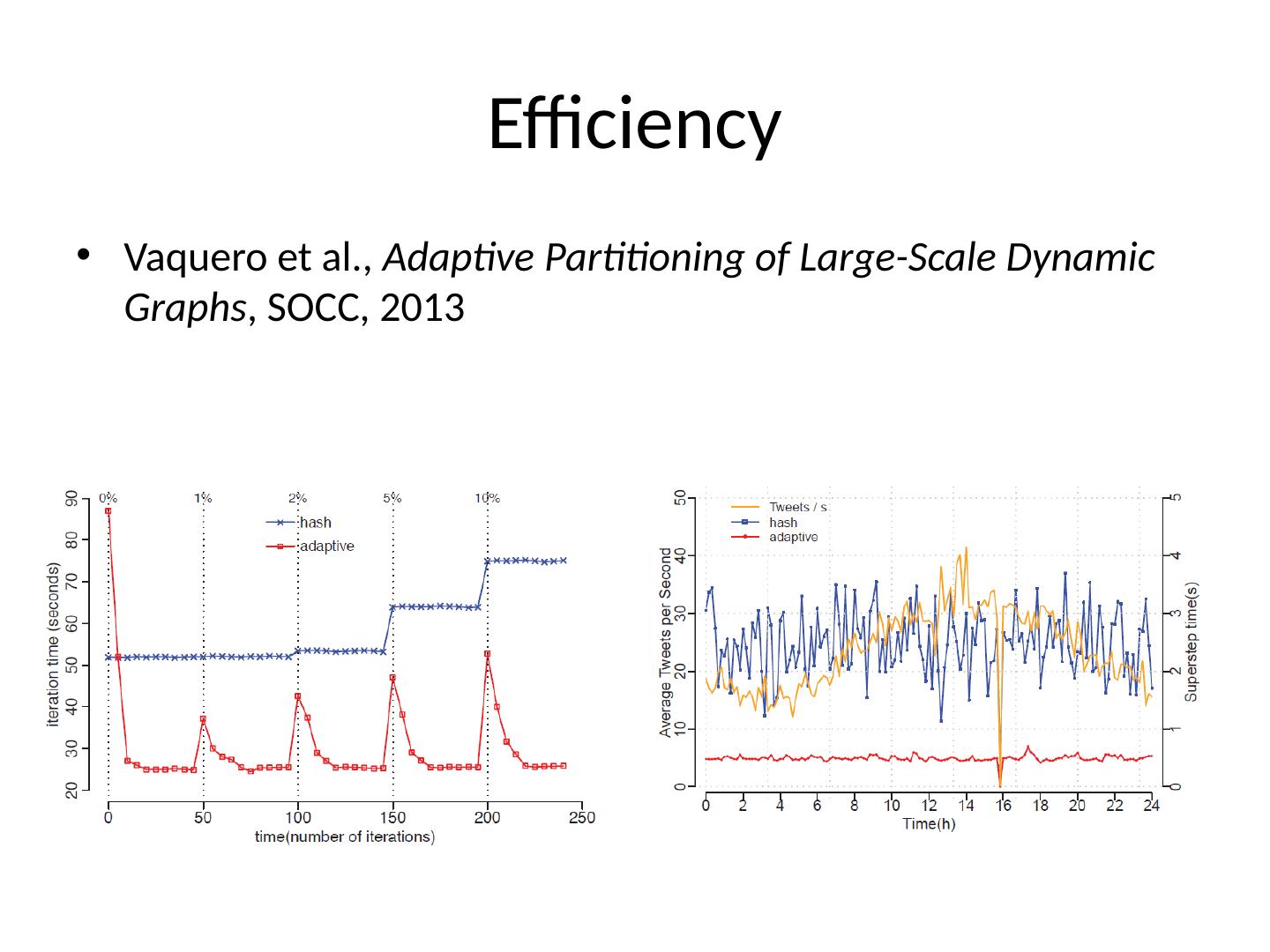
16 .Dynamic graphs Real world graphs are not static Edges and vertices are constantly added/removed Twitter, trace route, social network graphs Partitions need to be updated constantly Repartitioning may be required to rebalance load and reduce communication Repartitioning done in parallel with the graph processing algorithm Online, without restarting from scratch
17 .Efficiency Vaquero et al., Adaptive Partitioning of Large-Scale Dynamic Graphs , SOCC, 2013
18 .What’s next? Parallel sorting Parallel computational geometry Parallel numerical algorithms …