04Data Structures and Algorithms--BSP model

1 .Data Structures and Algorithms in Parallel Computing Lecture 4

2 .Parallel computer A parallel computer consists of a set of processors that work together on solving a problem Moore’s law has broken down in 2007 because of increasing power consumption O(f 3 ) where f is the frequency Tianhe-2 has 3.12 million processor cores and consumes 17.8 MW It is as cheap to put 2 cores on the same chip as putting just one 2 cores running at f/2 consume only ¼ of the power of a single core running at f However it is hard to achieve the same total computational speed in practice

3 .Bulk Synchronous Parallelism BSP model 1 st proposed in 1989 Alternative to the PRAM model Used for distributed memory computers Fast local memory access Algorithm developers need not worry about network details, only about global performance Efficient algorithms which can be run on many different parallel computers

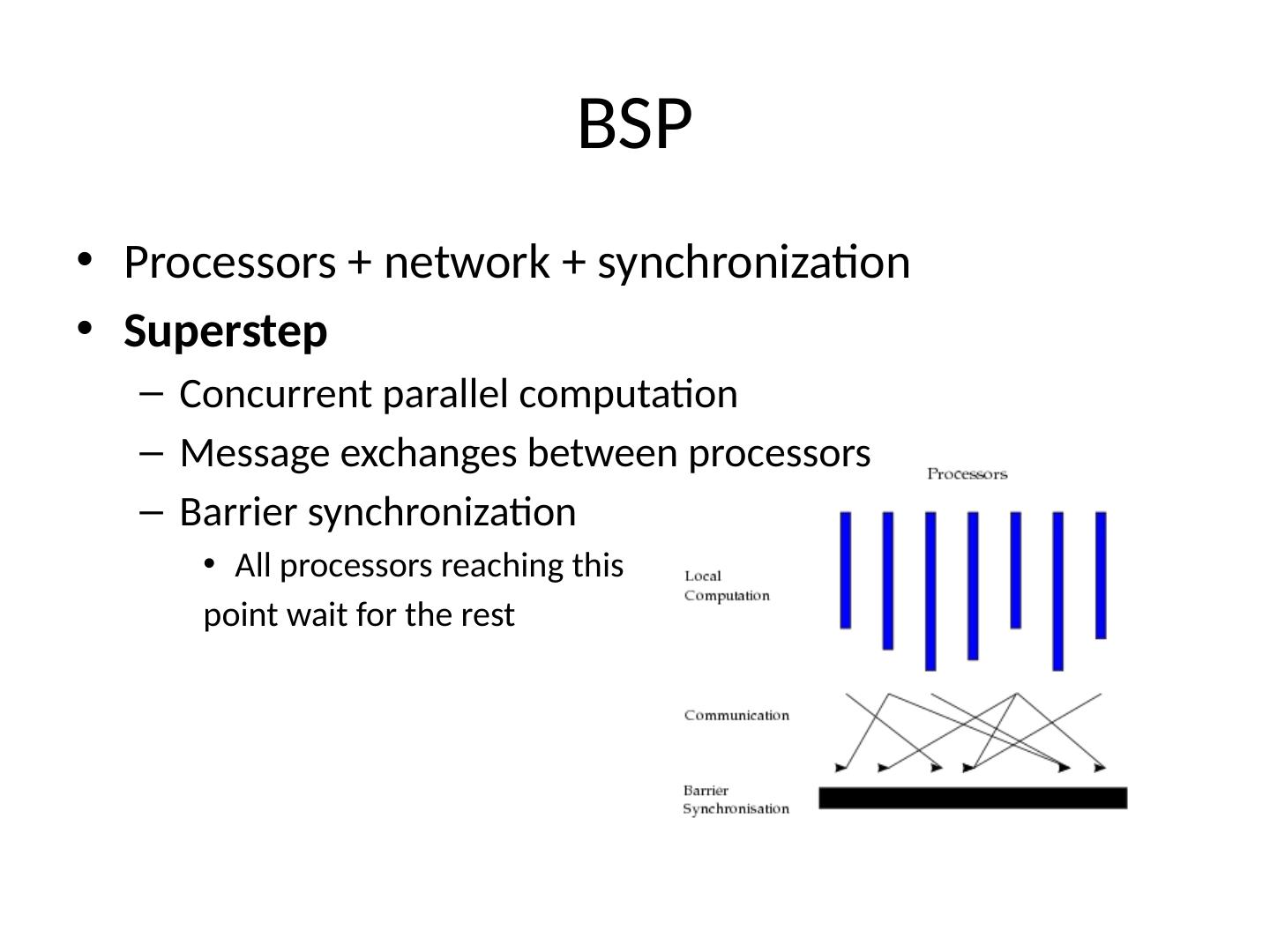
4 .BSP Processors + network + synchronization Superstep Concurrent parallel computation Message exchanges between processors Barrier synchronization All processors reaching this point wait for the rest

5 .Supersteps A BSP algorithm is a sequence of supersteps Computation superstep Many small steps Example: floating point operations (addition, subtraction, etc.) Communication superstep Communication operations each transmitting a data word Example: transfer a real number between 2 processors In theory we distinguish between the 2 types of supersteps In practice we assume a single superstep

6 .Communication superstep h-relation Superstep in which every processor sends and receives at most h data words h=max{ h s , h r } h s is the maximum number of data words sent by a processor h d is the maximum number of data words received by a processor Cost T(h)= hg+l Where g is the time per data word and l is the global synchronization time

7 .Time of an h-relation on a 4-core Apple iMac desktop Taken from www.staff.science.uu.nl/~bisse101/Book/PSC/psc1_2.pdf

8 .Computation superstep T= w+l Where w is the maximum number of flops of a processor in a superstep , and l is the global synchronization time Processors with less than w flops wait idle

9 .Total cost of a BSP algorithm Add cost of all supersteps a+bg+cl g and l are a function of the number of processors a , b , and c depend on p and the problem size n

10 .BSP implementations Google Pregel MapReduce Apache Giraph Open source implementation of Pregel Apache Hama Inspired from Pregel BSPLib …

11 .Pregel framework Computations consist of a sequence of iterations called supersteps During a superstep , the framework invokes a user defined function for each vertex which specifies the behavior at a single vertex V and a single superstep S The function can: Read messages sent to V in superstep S-1 Send messages to other vertices that will be received in superstep S+1 Modify the state of V and of the outgoing edges Make topology changes (add/remove/update edges/vertices) http ://people.apache.org/~edwardyoon/documents/pregel.pdf

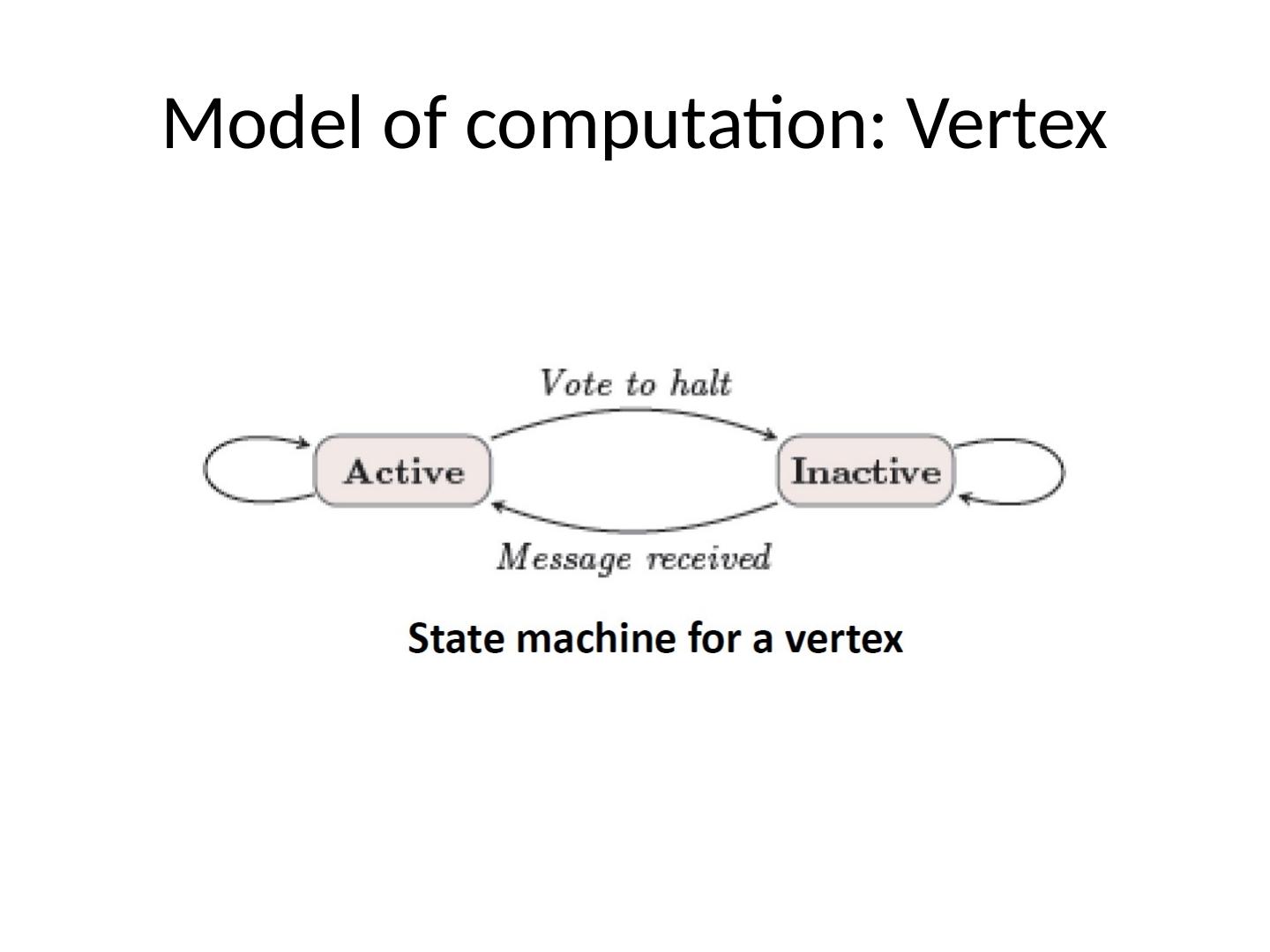
12 .Model of computation: Progress I n superstep 0 all vertices are active Only active vertices participate in a superstep They can go inactive by voting for halt They can be reactivated by an external message from another vertex The algorithm terminates when all vertices have voted for halt and there are no messages in transit

13 .Model of computation: Vertex

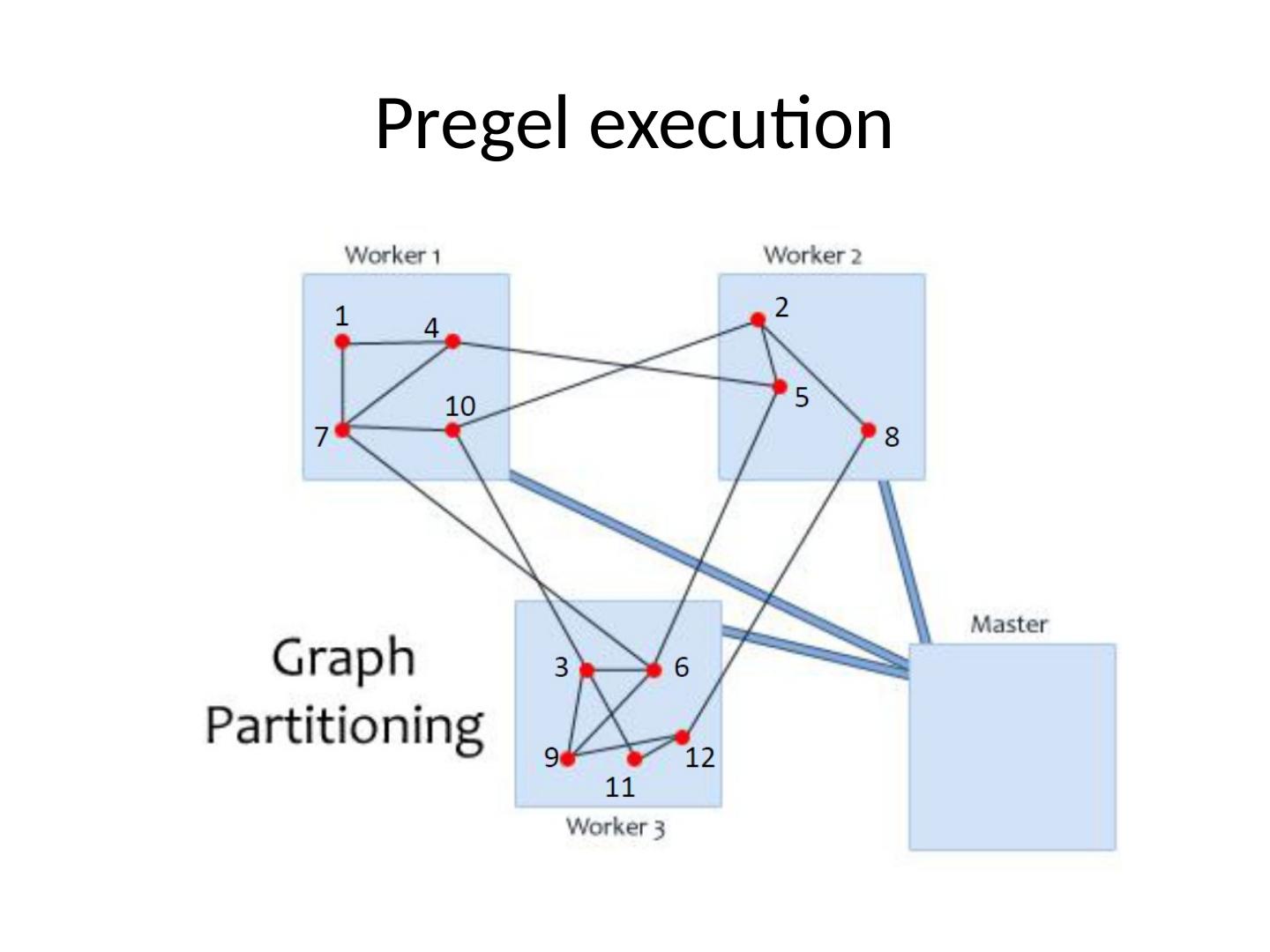
14 .Pregel execution

15 .Pregel execution Master-worker paradigm Partition graph Random hash based Custom ( mincut , …) Assign vertices to workers (processors) Mark all vertices as active Each active vertex executes a Compute() function and delivers messages which were sent in the previous superstep Get/Modify current vertex value using GetValue ()/ MutableValue () Respond to master with active vertices for the next superstep All workers execute the same code! Master is used for coordination

16 .Fault tolerance At the start of each superstep the master instructs workers to save their state Master pings workers to see who is running If failure is detected, master reasigns partitions to available workers

17 .Example: find largest value in a graph

18 .What’s next? BSP model SSSP, connected components, pagerank Vertex centric vs. subgraph centric Load balancing Importance of partitioning and graph type ...