展开查看详情
1 .Data Structures and Algorithms in Parallel Computing Lecture 2
2 .Parallel algorithmic techniques Techniques used in parallel algorithm design Some are extensions of sequential algorithms’ design approaches Others are specific to parallel algorithms Methods: Divide-and-conquer Randomization Parallel pointer manipulation
3 .Divide-and-conquer Split problem in subproblems Easier to solve than original problem Merge solutions to construct global solution Improves program modularity May lead to simple but efficient algorithms Powerful tool in sequential algorithm design
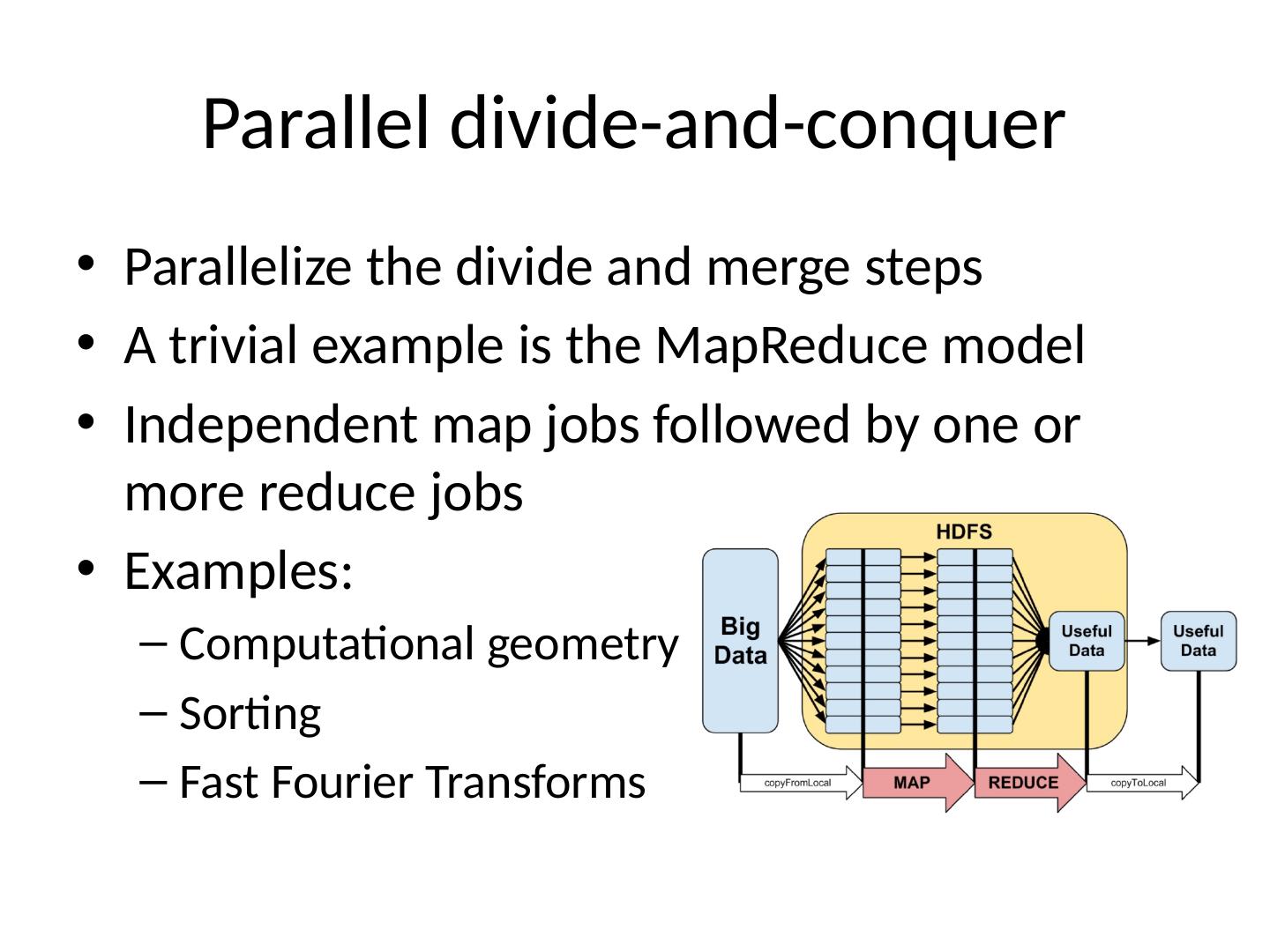
4 .Parallel divide-and-conquer Parallelize the divide and merge steps A trivial example is the MapReduce model Independent map jobs followed by one or more reduce jobs Examples: Computational geometry Sorting Fast Fourier Transforms
5 .Example: mergesort Takes a sequence of n keys and returns the ordered list Split sequence in two sequences of n/2 keys Recursively sort the two sequences Merge the two sorted n/2 keys sequence O(n) time complexity Runtime
6 .Parallel mergesort Recursive calls are independent
7 .Complexity analysis Hence the complexity is W(n)/D(n) = O(n log n)/O(n) = O(log n) Merge phase is sequential bottleneck Need to improve the depth of the merge phase
8 .Improvements Parallel merge C . P. Kruskal . Searching, merging, and sorting in parallel computation. IEEE Trans . Comput ., C–32(10 ):942–946, Oct. 1983 Pipelined divide-and-conquer : O(log n ) Start the merge phase at the top level before the recursive calls complete R . Cole. Parallel merge sort. SIAM Journal of Computing, 17(4):770–785, Aug . 1988
9 .Randomization Random numbers used in parallel algorithms to ensure that processors make local decisions which with high probability add up to global decisions Techniques Sampling Symmetric breaking Load balancing
10 .Sampling Select a representative sample from a set of elements Solve the problem on that sample Use the solution to guide the solution for the original set Example: sorting
11 .Number sorting Partition the keys into non-overlapping intervals and sort each interval Each interval must contain approximatively the same number of keys Random sampling used to determine the interval boundaries Select a random sample of keys All selected keys are sorted together Sorted keys are used as boundaries Example s : computational geometry, graphs, string matching
12 .Symmetry breaking Phenomenon in which small fluctuations acting on a system crossing a critical point decide the system’s fate Example: Select a large number of independent graph vertices in parallel Vertices are not neighbors If one vertex joins the set all of its neighbors must deny to join Difficult if the structure of each vertex is the same Randomness is used to break the symmetry between vertices
13 .Load balancing Evenly distribute a large number of items across processors Randomly assign each element to a subset Good results if the average size of a subset is at least logarithmic in the size of the original set
14 .Parallel pointer techniques Sequential techniques for manipulating lists, trees, graphs, do not translate easily into parallel techniques Examples: Traversing the elements of a linked list Visiting the list of nodes in postorder Performing a depth first search Solution: replace them with equivalent parallel techniques
15 .Pointer jumping In each step, each node in parallel replaces its pointer with that of its successor (or parent for trees) Example Label each node of an n-node list with the label of the last node (or root) Log n steps for each node to point to the same node
16 .Euler tour A path through the graph in which every edge is traversed exactly once Example Euler tour of an undirected tree is computed by following the perimeter of the tree visiting each edge twice (on the way down and then up) Keeping the Euler tour it is possible to compute many functions on the tree O(n) - independent on the depth of the tree
17 .Graph contraction Reduce size of a graph while keeping some of its original structure Example Graph partitioning Collapse high density vertices recursively Find connected components Expand the connected components to original graph
18 .Ear decomposition Partition a graph into an ordered collection of paths First path is a cycle The rest are called ears End-points of each ear are anchored on previous paths Can be used to determine of 2 edges are on a common cycle Example Determining biconnectivity , triconnectivity , 4-connectivity, planarity, replace depth first search Logarithmic depth and linear work
19 .What’s next? Graph parallel algorithms BSP model SSSP, connected components , pagerank Vertex centric vs. subgraph centric Load balancing Importance of partitioning and graph type ...
热门城市
