13Data Structures---Gridge Graph

1 .What is a Graph? A graph G consists of a set of nodes (also called vertices) V, and a set of edges E, each edge connecting a pair of nodes in V. Numerous real-life problems can be represented using graphs. The Seven Bridges of Königsberg Is it possible to walk along a route that crosses each bridge exactly once? 

2 .Problem proposed by Euler Such a path is known as Euler path Suppose there is such a path. Then there is a starting point and there is an end point. For every intermediate edge v, there must be an equal number of incoming and outgoing edges. Is it true for the bridge graph? 

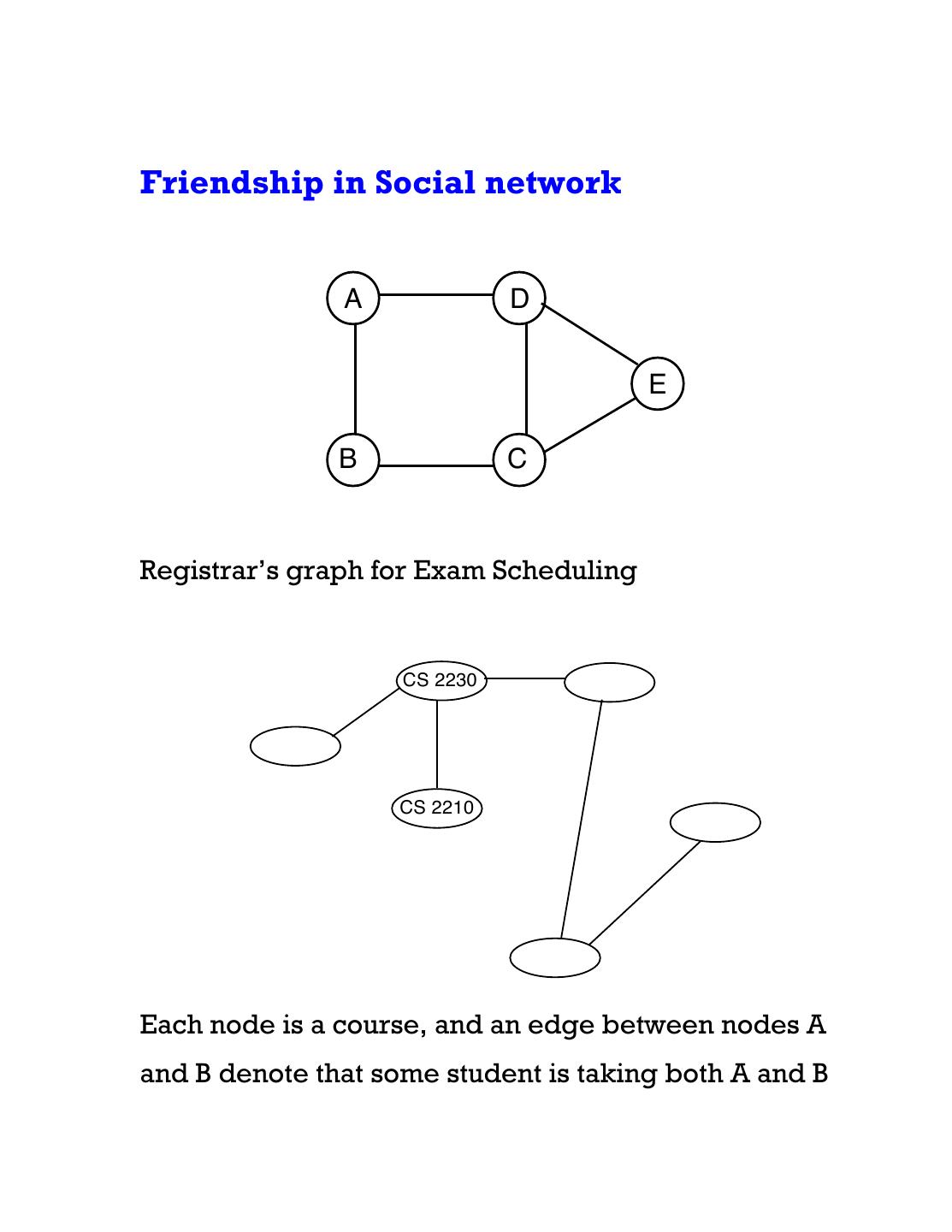
3 .Friendship in Social network A D E B C Registrar’s graph for Exam Scheduling CS 2230 CS 2210 Each node is a course, and an edge between nodes A and B denote that some student is taking both A and B 

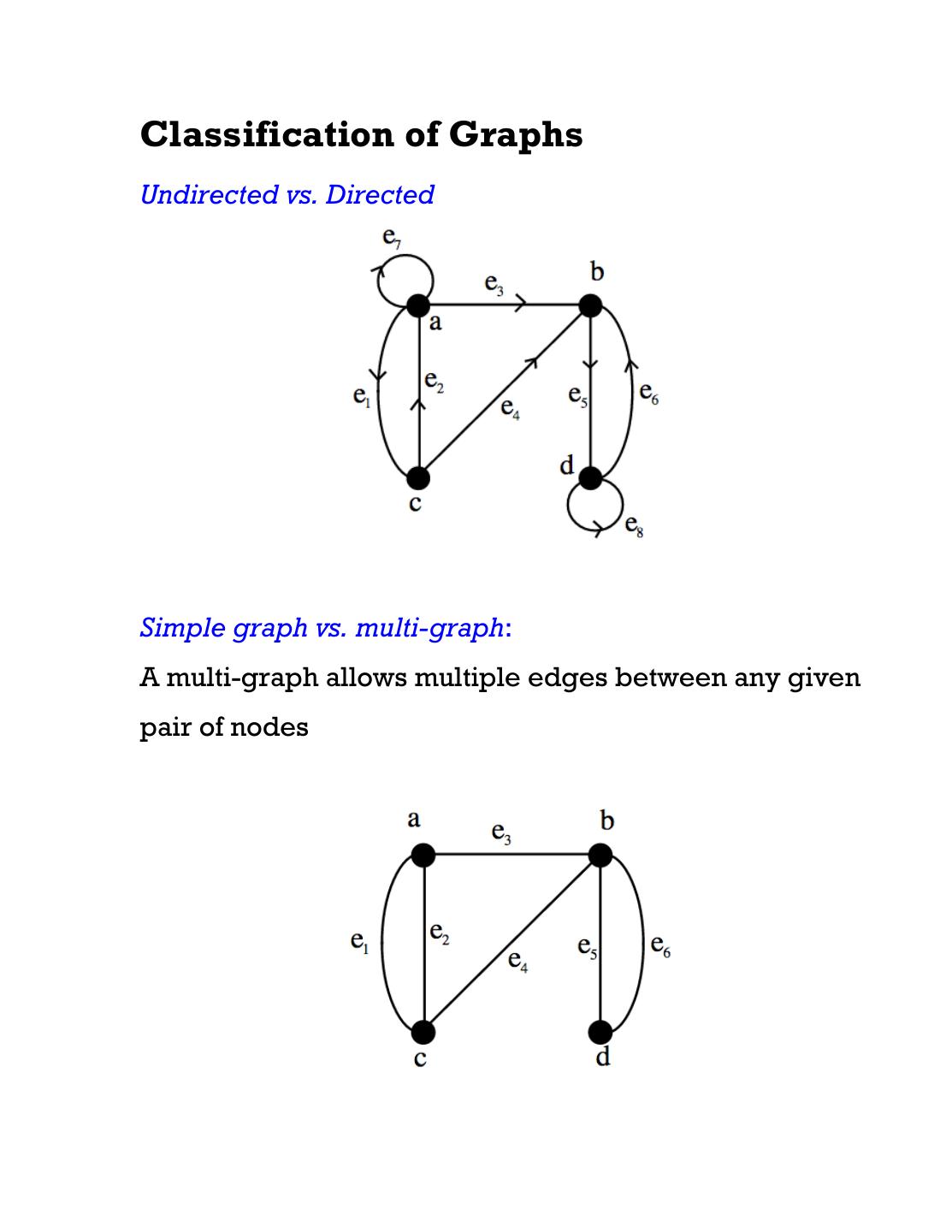
4 .Classification of Graphs Undirected vs. Directed Simple graph vs. multi-graph: A multi-graph allows multiple edges between any given pair of nodes 

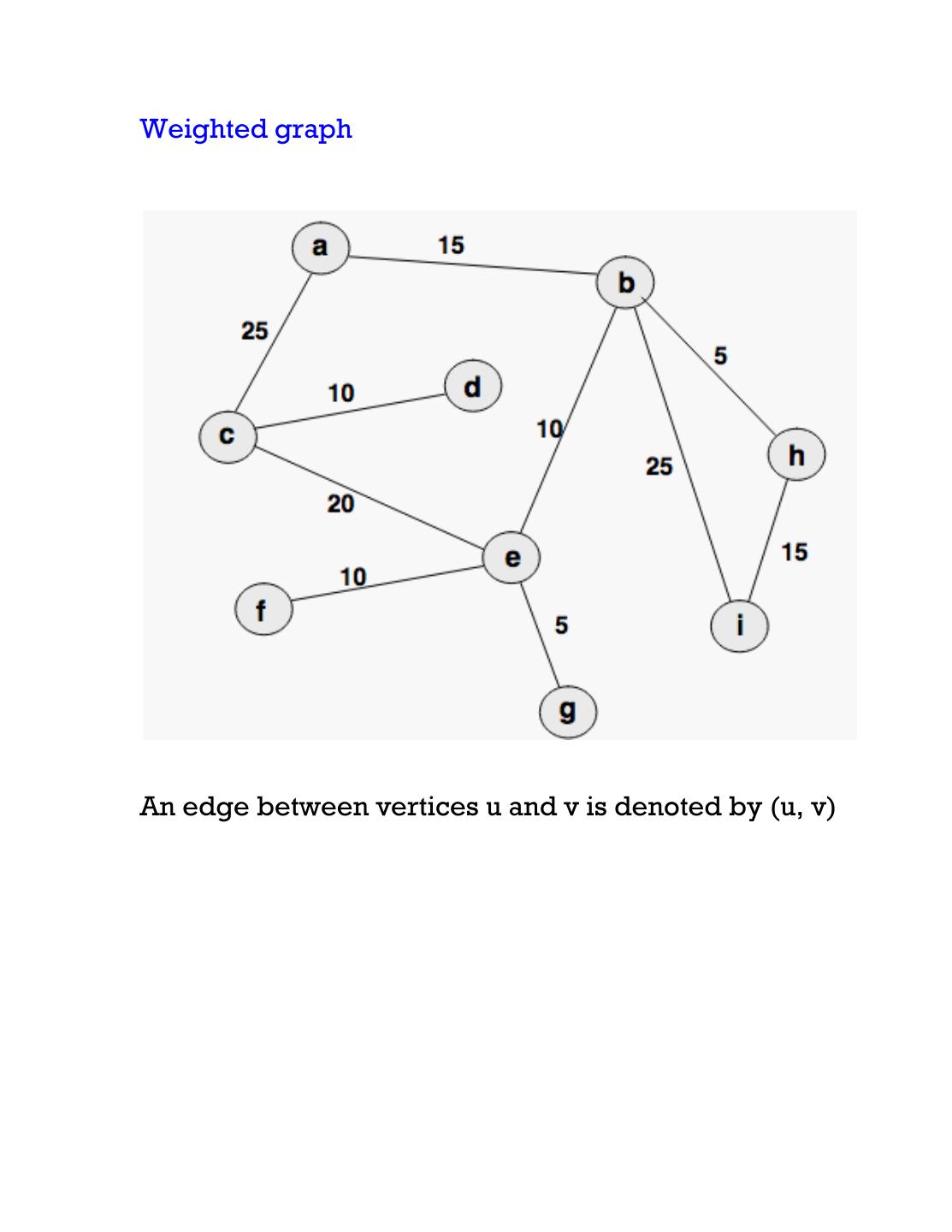
5 .Weighted graph An edge between vertices u and v is denoted by (u, v) 

6 .Graph ADT Partial list of methods Vertices(), NumberVertices() Edges(), NumEdges(), Degree() Outdegree(v), Indegree(v) {for directed graphs) OutgoingEdges(), IncomingEdges() InsertVertex(x), InsertEdge(u,v,x) RemoveVertex(x), RemoveEdge(e) How efficiently the graph can be stored and these methods can be computed, will depend on the data structure used to represent the graph. 

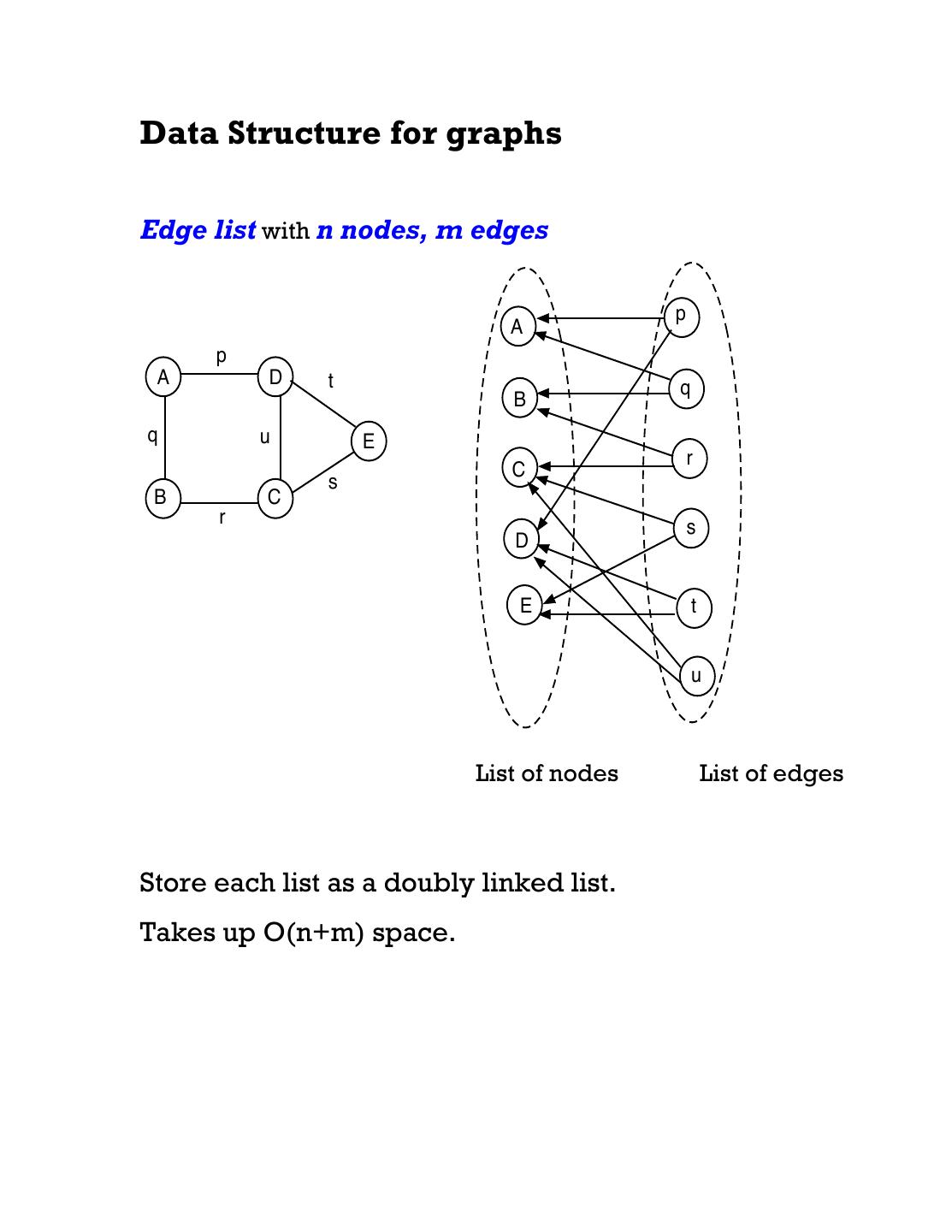
7 .Data Structure for graphs Edge list with n nodes, m edges p A p A D t q B q u E r C s B C r s D E t u List of nodes List of edges Store each list as a doubly linked list. Takes up O(n+m) space. 

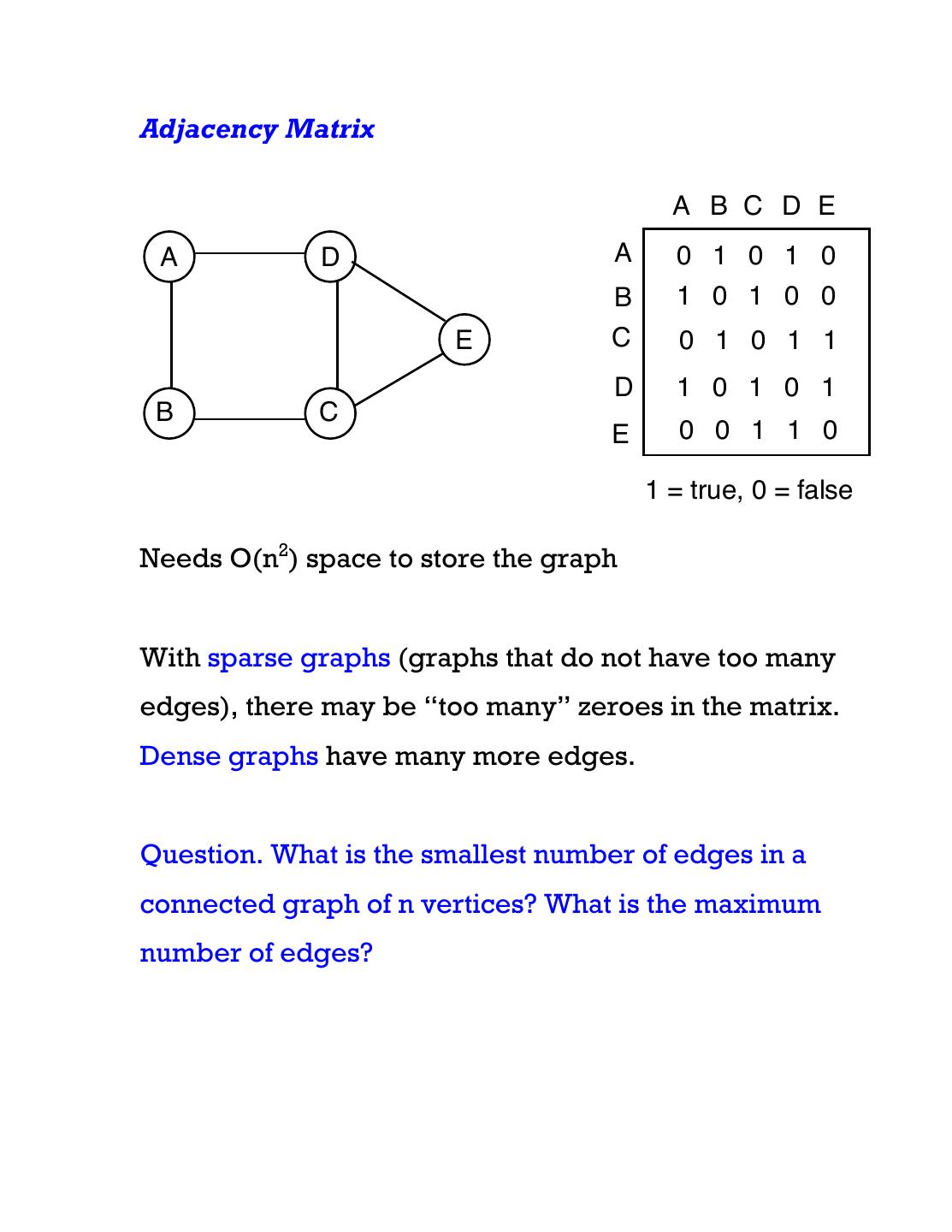
8 .Adjacency Matrix A B C D E A D A 0 1 0 1 0 B 1 0 1 0 0 E C 0 1 0 1 1 D 1 0 1 0 1 B C E 0 0 1 1 0 1 = true, 0 = false Needs O(n2) space to store the graph With sparse graphs (graphs that do not have too many edges), there may be “too many” zeroes in the matrix. Dense graphs have many more edges. Question. What is the smallest number of edges in a connected graph of n vertices? What is the maximum number of edges? 

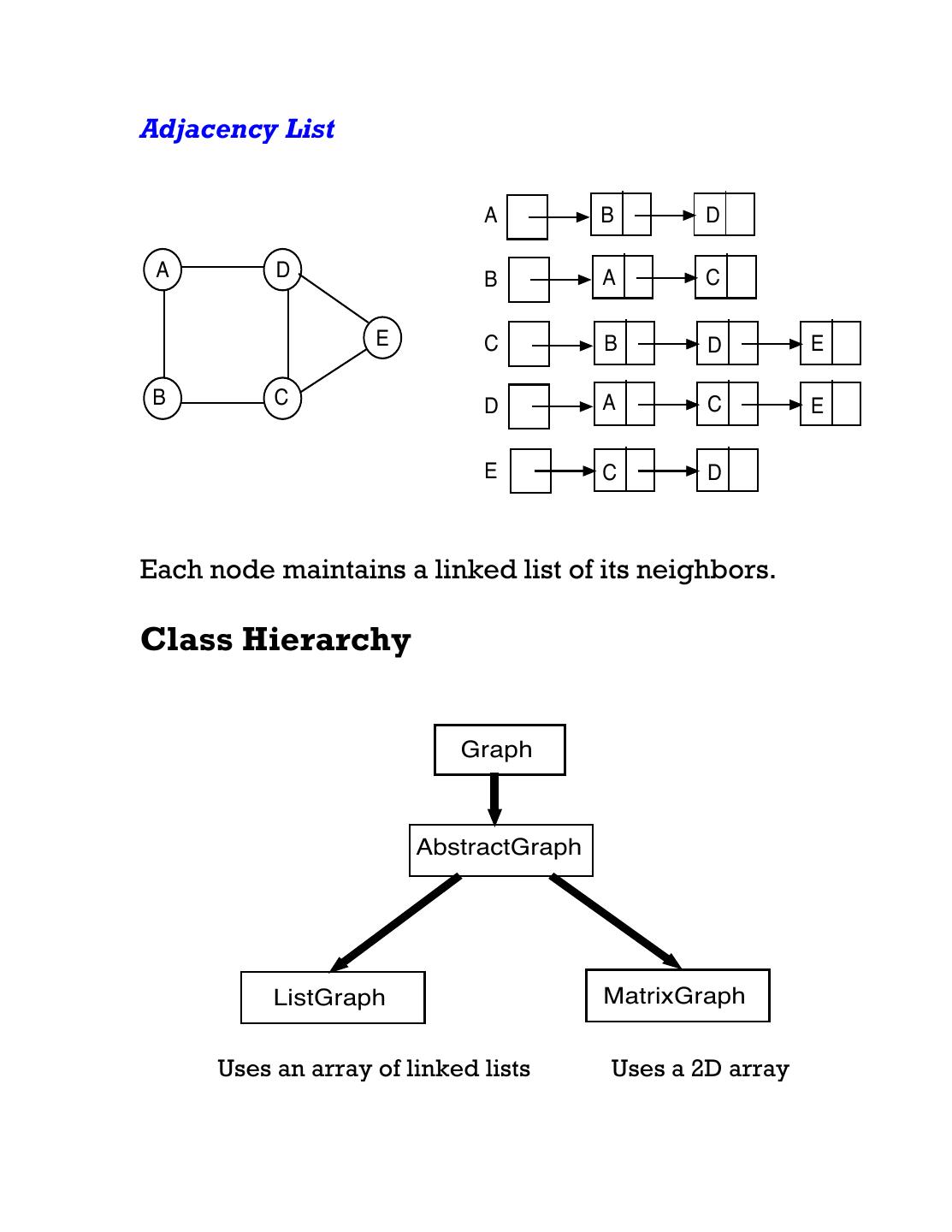
9 .Adjacency List A B D A D B A C E C B D E B C D A C E E C D Each node maintains a linked list of its neighbors. Class Hierarchy Graph AbstractGraph ListGraph MatrixGraph Uses an array of linked lists Uses a 2D array 

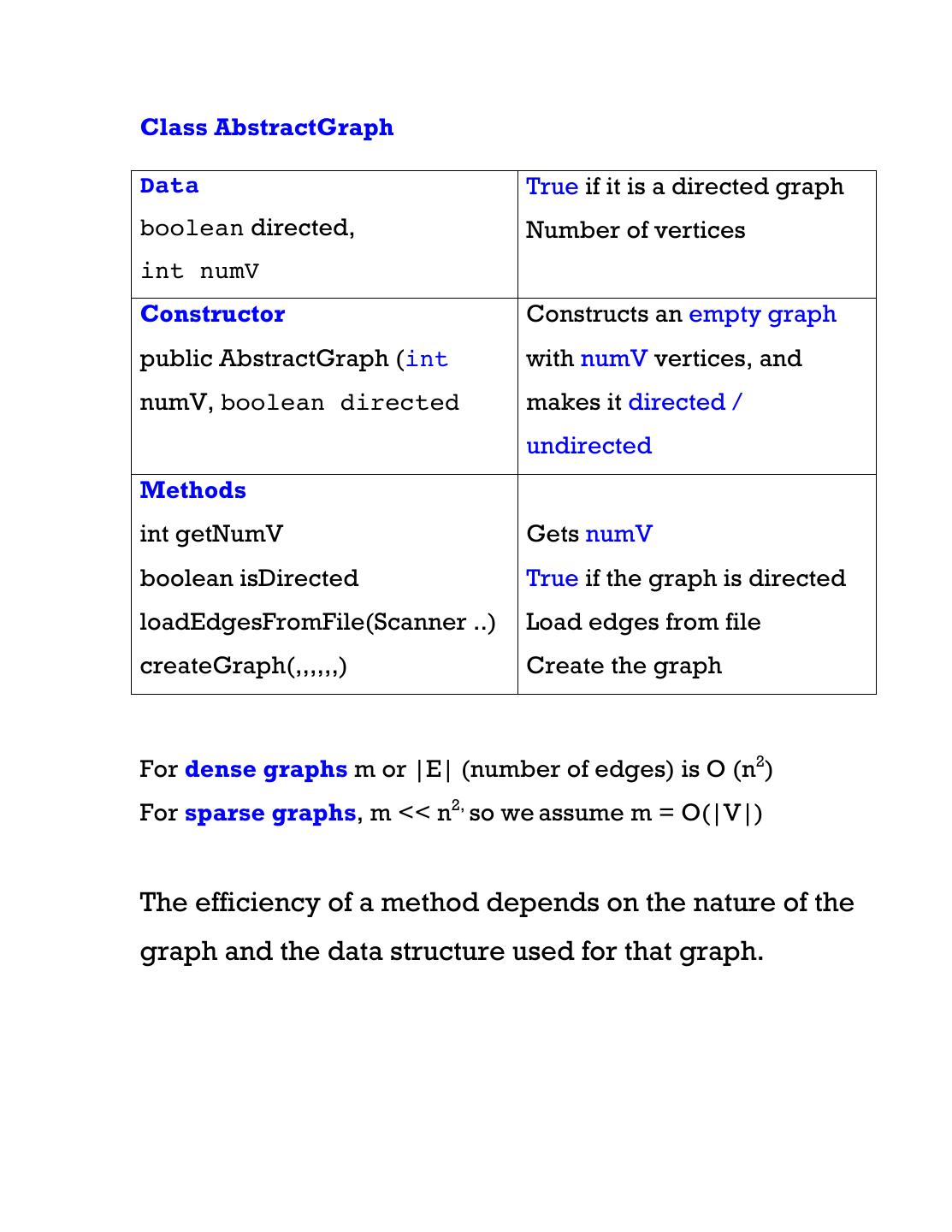
10 .Class AbstractGraph Data True if it is a directed graph boolean directed, Number of vertices int numV Constructor Constructs an empty graph public AbstractGraph (int with numV vertices, and numV, boolean directed makes it directed / undirected Methods int getNumV Gets numV boolean isDirected True if the graph is directed loadEdgesFromFile(Scanner ..) Load edges from file createGraph(,,,,,,) Create the graph For dense graphs m or |E| (number of edges) is O (n2) For sparse graphs, m << n2, so we assume m = O(|V|) The efficiency of a method depends on the nature of the graph and the data structure used for that graph. 

11 .Consider an operation as follows 1. For each vertex u 2. For each vertex v adjacent to u 3. Do something with edge (u, v) Example: • Count the number of edges, or • Find the edge with the minimum weight Using adjacency list representation, Step 1 takes O(n) time and for each node u Step 2 takes O(Eu) time, where Eu= the edges incident on vertex u. The combined time will be O(m), where m = total number of edges (Why is this true? Take any graph as an example) Using adjacency matrix representation, for each node u, Step 2 also takes also takes O(n) time, so the overall algorithm takes O(n2) time. 

12 .Graph traversal Graph traversal is a systematic way of visiting all the vertices of a graph. There are two kinds of traversals: Bread-First-Search (BFS) and Depth-First-Search (DFS) Breadth-First-Search Given a starting node v, the idea is to first visit all nodes at distance 1 from v, then visit all nodes at distance 2 from v, then visit all nodes at distance 3 from v, and so on. The implementation uses a queue as shown below: Put v into an empty queue Q; While Q is not empty { Remove the head u of Q; Mark u as visited; Enqueue all unvisited neighbors of u } 

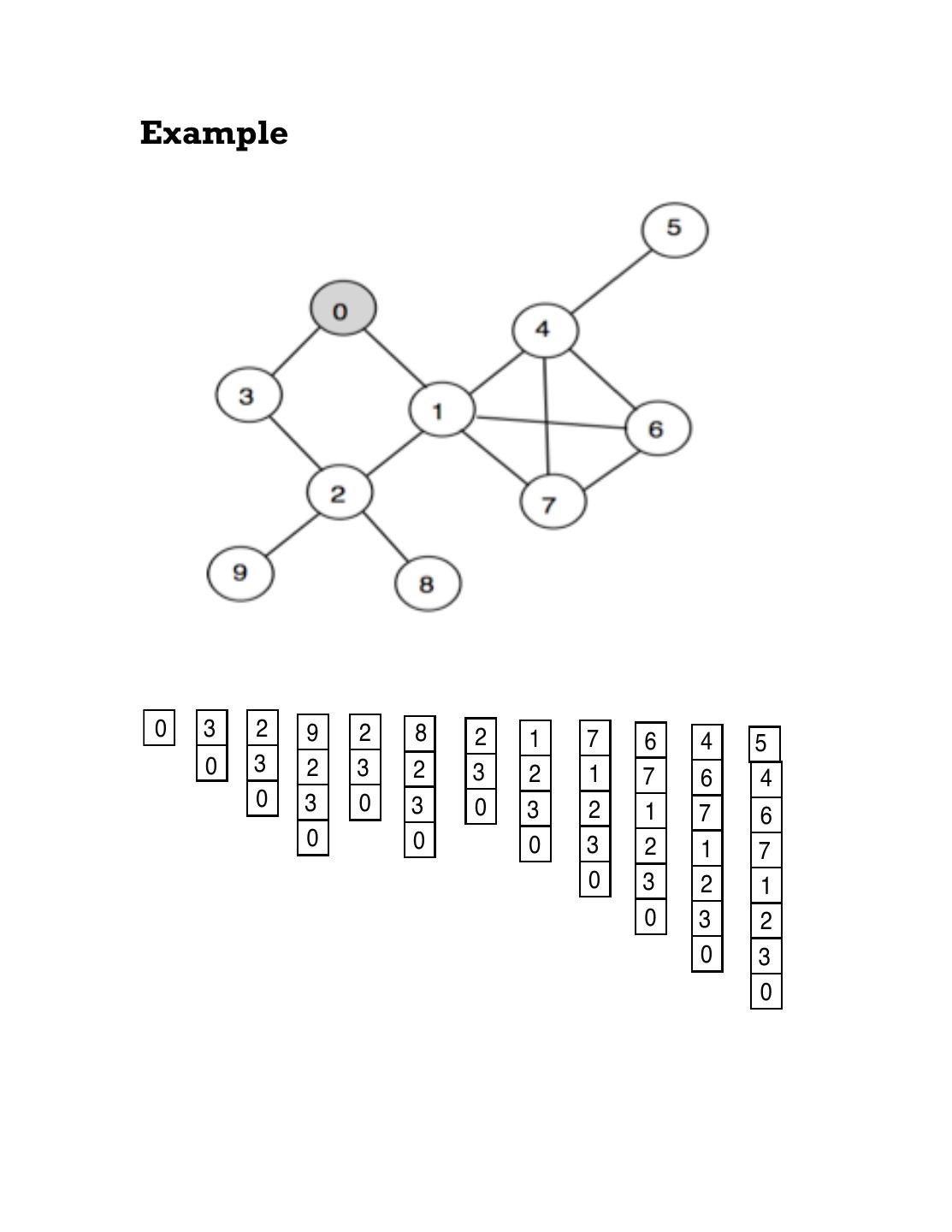
13 .Example 

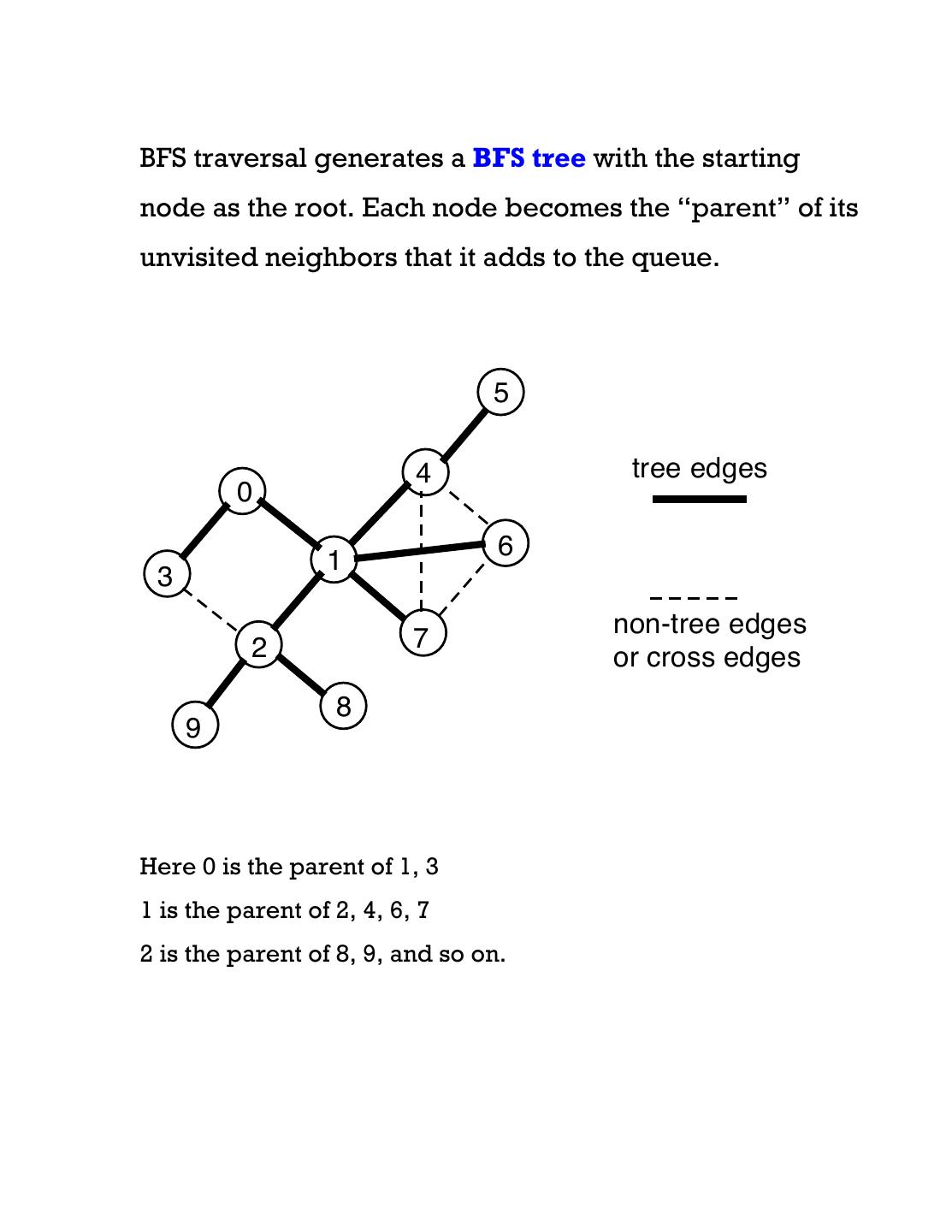
14 .BFS traversal generates a BFS tree with the starting node as the root. Each node becomes the “parent” of its unvisited neighbors that it adds to the queue. 5 4 tree edges 0 1 6 3 7 non-tree edges 2 or cross edges 8 9 Here 0 is the parent of 1, 3 1 is the parent of 2, 4, 6, 7 2 is the parent of 8, 9, and so on. 

15 .Applications of Breadth-First Tree Find the shortest path from one node to another node. (Heard about “six degrees of separation?”) Computing the routing table in a network Find the diameter of a graph Broadcast a message in a graph In directed graphs, one can check if a graph is strongly connected (i.e., whether there is exists a path between each pair of nodes) 

16 .Depth-First-Search (DFS) Given a starting node v, the idea is to first visit one neighbor u, u’s unvisited neighbor w, w’s unvisited neighbor x, and so on until you can progress no further. Then retract and visit another unvisited neighbor of the last visited node. Continue until all nodes are visited. The implementation uses a stack as shown below: Put v into an empty stack S; While Q is not empty { Peek at the top u of S; Mark u as visited; If u has an unvisited neighbor w then push w into S else pop S } 

17 .Example 0 3 2 9 2 8 2 1 7 6 4 5 0 3 2 3 2 3 2 1 7 6 4 0 3 0 3 0 3 2 1 7 6 0 0 0 3 2 1 7 0 3 2 1 0 3 2 0 3 0 

18 .DFS traversal generates a DFS tree. A visited node that pushes a neighbor into the stack becomes the parent of that neighbor. So how will the DFS tree look like? 5 4 tree edges 0 1 6 3 7 non-tree edges 2 or cross edges 8 9 For directed graphs, such tree constructions have to follow the edge directions (i.e., each tree edge must be in the same direction as in the original graph) 

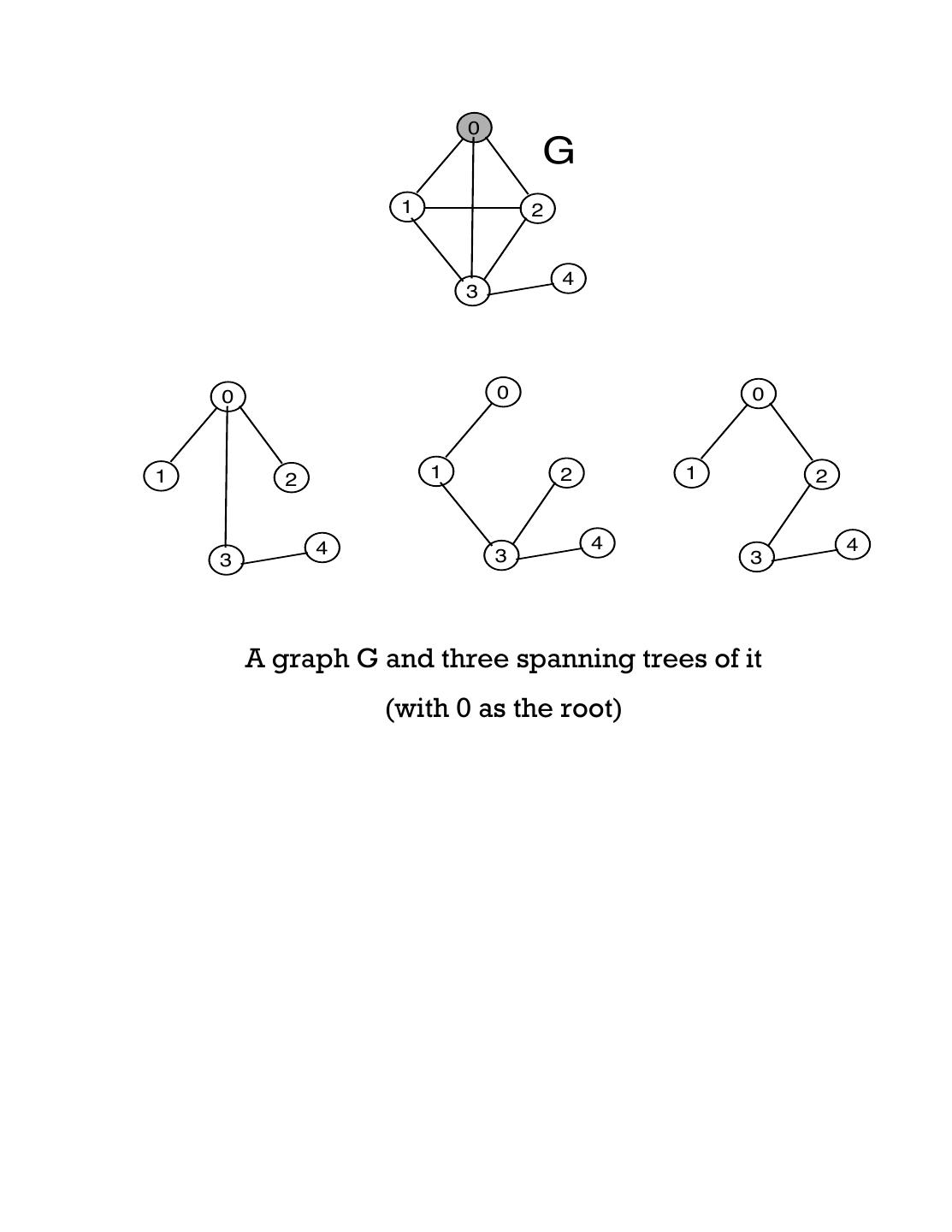
19 .Applications of Depth-First Tree Finding a path from one node to another (for both directed and undirected graphs). Detecting a cycle in a directed graph Spanning tree A spanning tree of a Graph G is a sub-graph that connects all the vertices with the minimum possible number of edges. There can be many spanning trees of a graph G. Both BFS tree and DFS tree are spanning trees of G. 

20 . 0 G 1 2 4 3 0 0 0 1 2 1 2 1 2 4 4 4 3 3 3 A graph G and three spanning trees of it (with 0 as the root) 

21 .Minimum Spanning Tree (MST) In a weighted graph, computing a minimum spanning tree is an important problem. The weight of a spanning tree is the sum of the weights of all of the tree edges. Of all the spanning trees, the one with the smallest weight is the minimum spanning tree. 0 90 10 0 90 10 1 3 15 25 1 3 15 25 20 2 7 20 2 7 50 10 8 10 50 8 Graph G Minimum Spanning Tree of G Two well-known algorithms for computing MST are 1. Kruskal’s Algorithm 2. Prim’s Algorithm 

22 .Kruskal's algorithm 1. Create an empty graph T with the vertices as G, but without any edges. 2. Form a priority queue Q with all the edges of G (a smaller weight has higher priority) 3. While number of edges in T < n-1 Remove edge (u, v) from Q If u and v are not connected, then add (u, v) to T. Follow the example in the class. 

23 .Prim's algorithm 1. Start with an arbitrarily chosen single vertex. 2. Grow the tree by one edge at a time: Find the minimum weight outgoing edge (use a priority queue for this) and add it to the tree, until no outgoing edge is left. (An edge is outgoing if it connects a node in the tree to another node not yet in the tree. Find such an edge with the minimum weight). Follow the example in the class. 

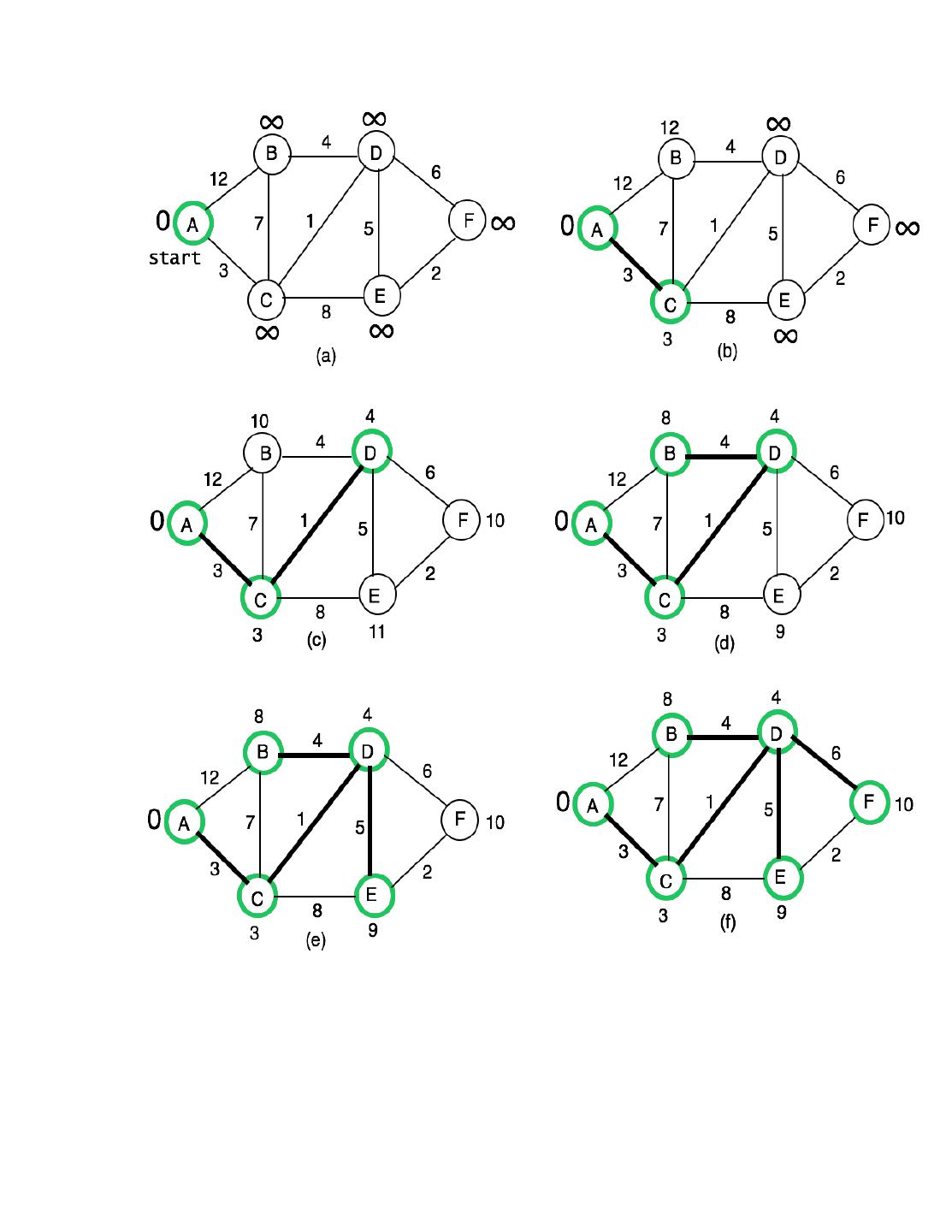
24 .Computing the shortest path Given a weighted graph, what is the shortest path from node u to node v (or to every other node in the garph) is an important question of great practical importance. One of the important algorithms for computing the shortest path is Dijkstra’s algorithm. Dijkstra’s Algorithm First, try to mentally compute the shortest path from A to every other node. 

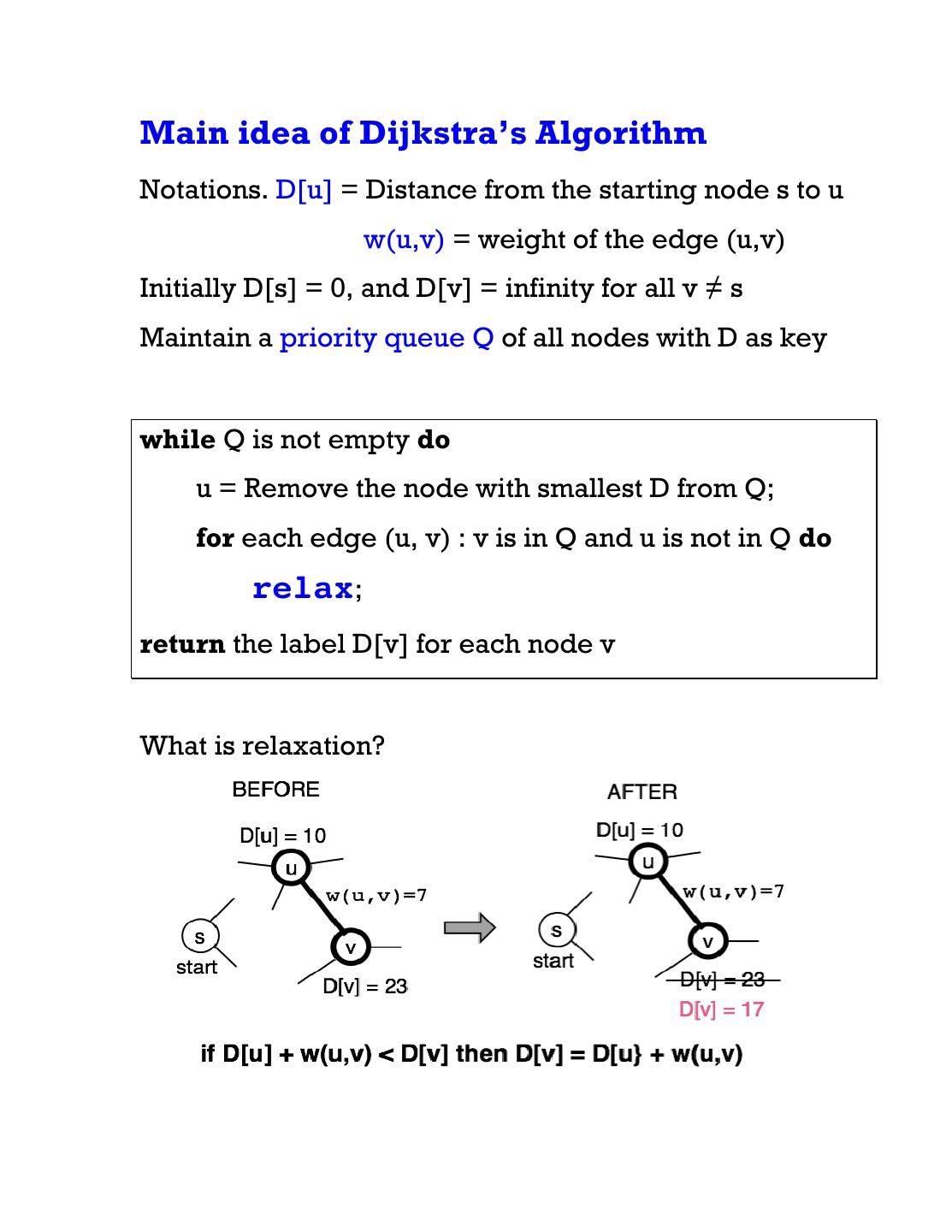
25 .Main idea of Dijkstra’s Algorithm Notations. D[u] = Distance from the starting node s to u w(u,v) = weight of the edge (u,v) Initially D[s] = 0, and D[v] = infinity for all v ≠ s Maintain a priority queue Q of all nodes with D as key while Q is not empty do u = Remove the node with smallest D from Q; for each edge (u, v) : v is in Q and u is not in Q do relax; return the label D[v] for each node v What is relaxation? 

26 .