- 快召唤伙伴们来围观吧
- 微博 QQ QQ空间 贴吧
- 文档嵌入链接
- 复制
- 微信扫一扫分享
- 已成功复制到剪贴板
11-1Data Structures---HuffmanCoding
展开查看详情
1 .Huffman coding An exercise in the use of priority queue Symbol Frequency Symbol Frequency Symbol Frequency space 186 b 47 g 15 e 103 d 32 p 15 t 80 l 32 b 13 a 64 u 23 v 8 o 63 c 22 k 5 i 57 f 21 j 1 n 57 m 20 q 1 s 51 w 18 x 1 r 48 y 16 z 1 Source: Donald Knuth, The Art of Computer Programming (Volume 3) p 441 This table shows the average occurrence of individual letters in every 1000 letters. Each letter can be encoded by a custom binary code. The problem. How will you encode these symbols so that the binary file has the smallest size?
2 .Straight ASCII (that will use n bytes for coding n characters is not the optimal solution, when you know the frequencies of these characters. An efficient solution will use only a few bits for the frequently used characters, but may use more bits to encode less frequently used characters. Of course this will be a custom encoding scheme. [Application: saving the transmission bandwidth] A naïve solution is as follows. Suppose the frequencies of the following five letters satisfy the order e > a> c > b > d 0 1 e 0 1 a 0 1 c 0 1 b d Here are the codes: e = 0, a = 10, c = 110, b= 1110, d = 1111 This is ok, but may not be optimal when the frequencies are known.
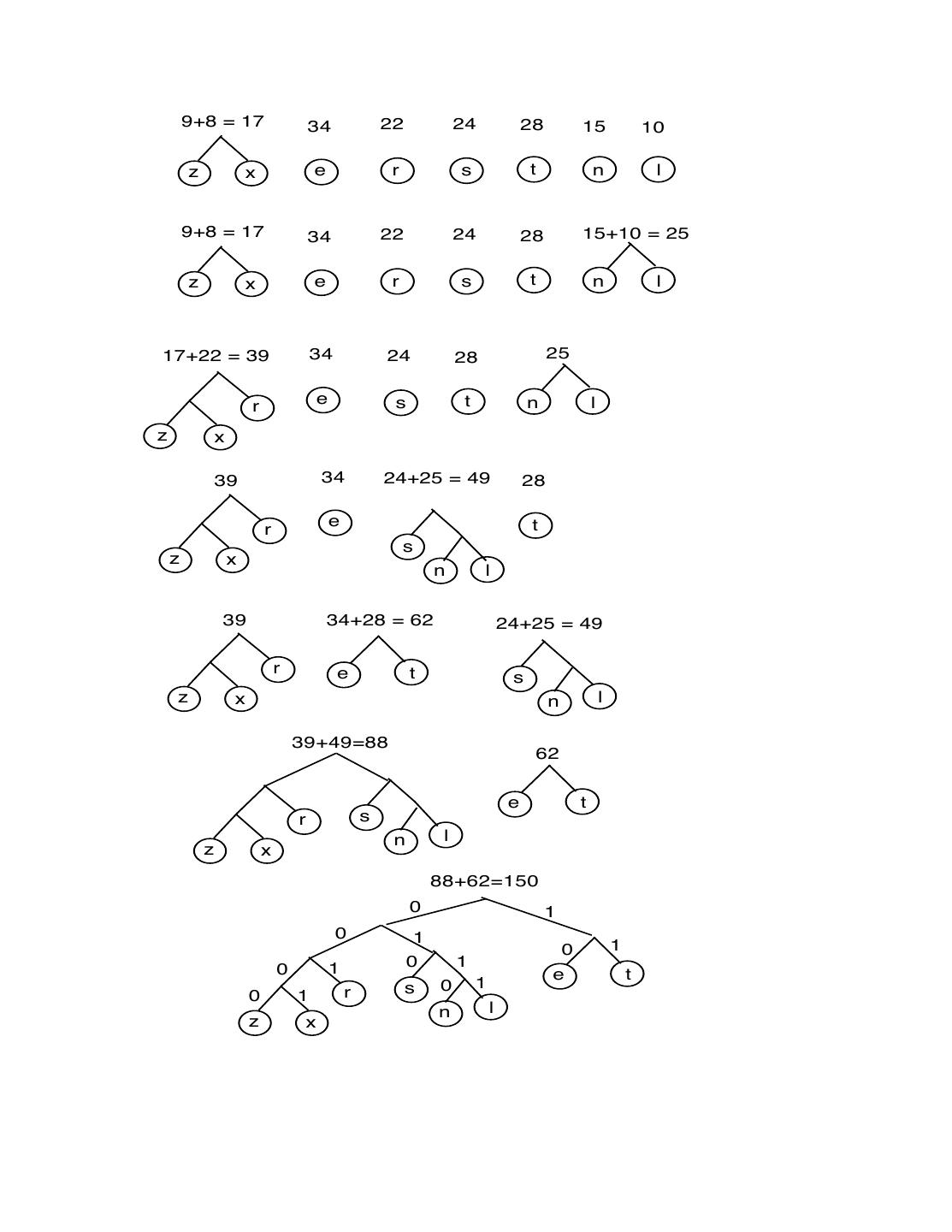
3 .A smaller scale example e r s t n l z x 34 22 24 28 15 10 9 8 Frequency in an average sample of size 150 letters Enqueue these in a priority queue Dequeue (the letter/subtree with smallest count) Dequeue (the letter/subtree with smallest count) Form a subtree by adding a common parent to the above two and enqueue into the priority queue again Repeat these steps till a binary tree is formed. The tree is shown in the next page. This leads to the following codes. z = 0000 n = 0110 x = 0001 l = 0111 r = 001 e = 10 s = 010 t = 11
4 . 9+8 = 17 34 22 24 28 15 10 z x e r s t n l 9+8 = 17 34 22 24 28 15+10 = 25 z x e r s t n l 17+22 = 39 34 24 28 25 e s t n l r z x 39 34 24+25 = 49 28 e t r s z x n l 39 34+28 = 62 24+25 = 49 r e t s z x n l 39+49=88 62 e t r s n l z x 88+62=150 0 1 0 1 0 1 1 0 1 0 e t s 0 1 0 1 r n l z x