11Data Structures---The Set ADT

1 .The Set ADT List vs. SET Set = Unordered collection of elements – no duplicates. {1, 3, 8} is the same as {3, 8, 1} List = Ordered collection of elements, does not care about duplicates. Main methods in the Set ADT Add (e) Adds e to the set (if not present) Remove (e) Removes e if it is present Contains (e) Checks if the set contains e Size( ) Returns the number of elements isEmpty Is the set empty? 

2 .Also, set union ( S ∪ T ), set intersection ( S ∩ T ) and set difference (i.e. subtraction) ( S − T ) are important operations. Java.util.Set interface provides the following methods to support these operations. When executed on a set S, • addAll(T) implements S ∪ T • retainAll(T) implements S ∩ T • removeAll(T) implements S − T A multi-set (also called a bag) is a generalization of set -- it allows duplicates. Sorted set is an extension of set, when elements come from a comparable class 

3 .Binary Search Tree An ordered map is one in which the keys have a total order, just like in a heap. You can insert, find, and delete entries, just as with a hash table. But unlike a hash table, you can quickly find the entry with minimum or maximum key, or the entry nearest another entry in the total order (i.e. successor and predecessor). A simple implementation of an ordered map is a binary search tree. Two invariants hold for every node X 1. Every key in its left subtree is ≤ X 2. Every key in its right subtree is > X 

4 .Observation. In-order traversal of a BST leads to a sorted array Lookup time Depends on the height of the tree. For a balanced tree, it is O(log n). Here is a worst case 20 8 16 10 12 11       The height is O(n), so is the search time. For efficient lookup, we need a balanced binary tree. 

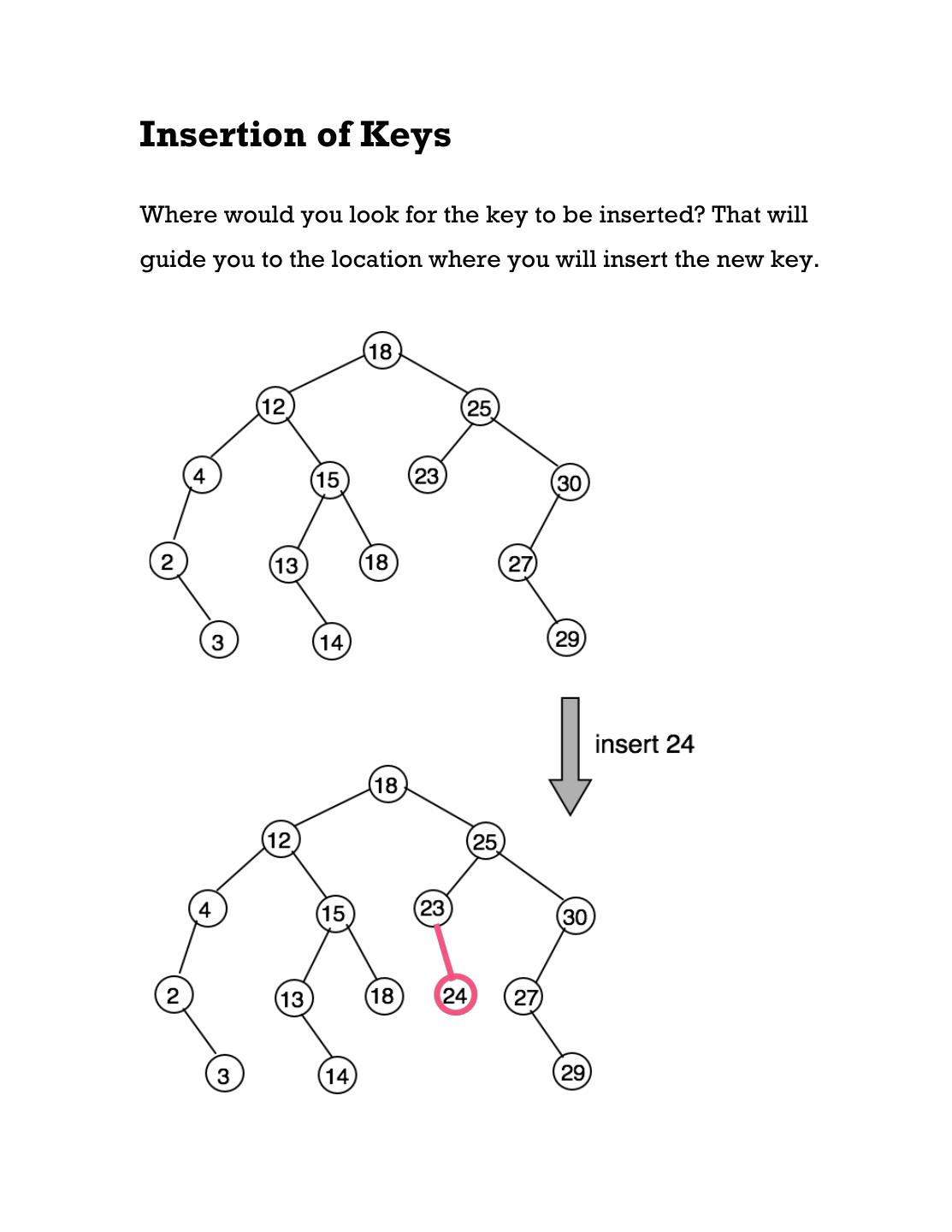
5 .Insertion of Keys Where would you look for the key to be inserted? That will guide you to the location where you will insert the new key.   

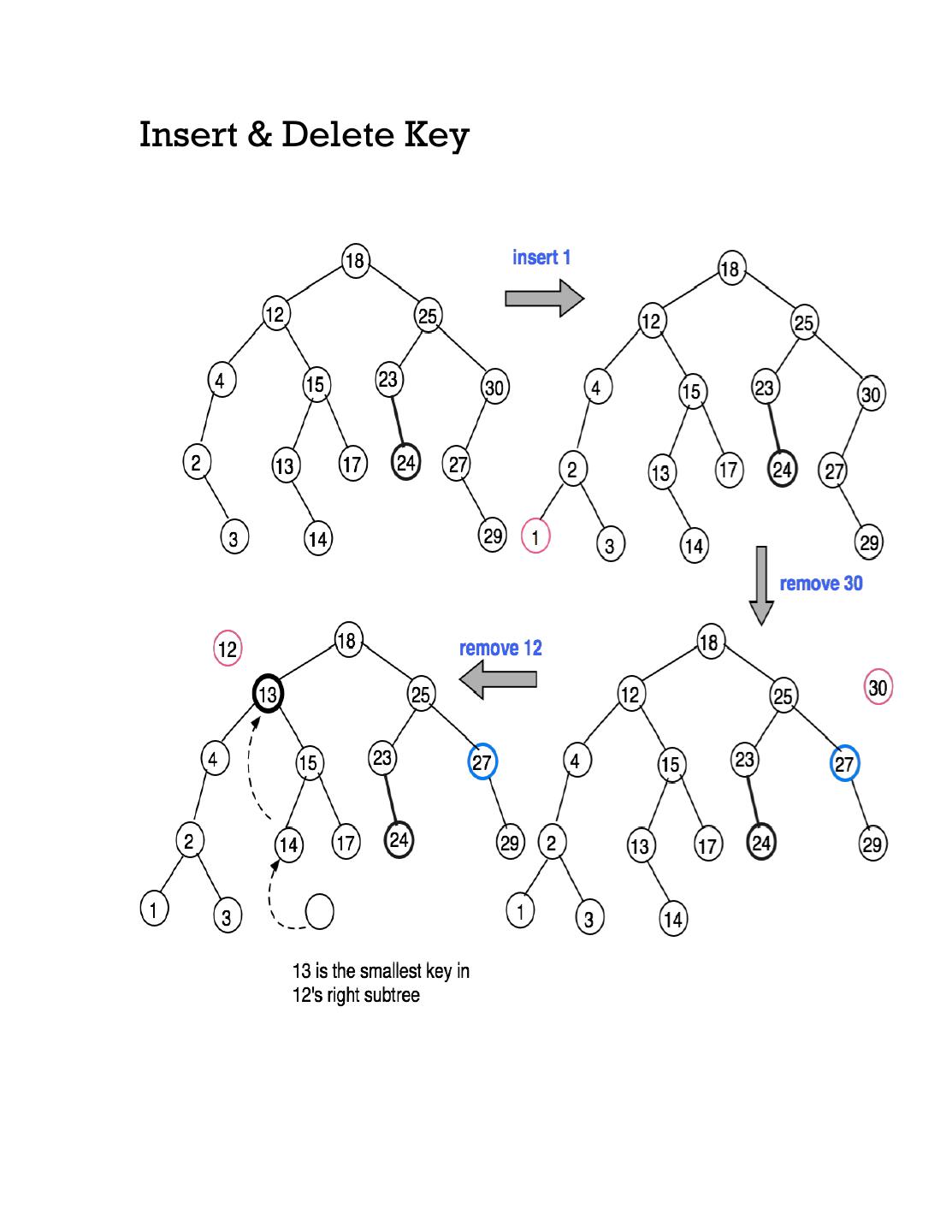
6 .Insert & Delete Key 

7 .Delete key K Three different cases of removal of node n with key K. Case 1. If K is a leaf node then just detach the node with key K from its parent Case 2. If node n has one child, move n's child up to take n's place. Node n's parent becomes the parent of n's child, and n's child becomes the child of n's parent. Case 3. Let x be the node with the smallest key in n's right subtree. Remove x; since x has the minimum key in the subtree (i.e., its successor of n) x has no left child and is easily removed. Replace n by x. x has the key closest to k that isn't smaller than k, so the binary search tree invariant still holds See the example. [You can also pick the largest key from the left subtree, since the node containing such a key will not have a right child] 

8 .Successor of node x The successor of the largest key is NIL. Otherwise, consider two cases. Case 1. If node x has a non-empty right subtree, then x’s successor is the minimum in the right subtree of x. Case 2. If node x has an empty right subtree then: Node x’s successor y is the node that x is the predecessor of (x is the maxim in y’s left subtree). Therefore, x’s successor y, is the lowest ancestor of x whose left child is also an ancestor of x. y = successor(x) 18 12 25 4 15 23 30 2 13 17 24 27 x 3 14 29 

9 .Problem with unbalanced search trees If you create a binary search tree by inserting the given keys in a random order, then with high probability the tree will have height O(log n), and operations on the tree will take O(log n) time. Explore what happens if the keys are inserted in a sorted order 2, 3, 5, 7, 10 into an empty tree. It is important to devise algorithms that keep a BST balanced. AVL tree is a binary search tree that can balance itself.