- 快召唤伙伴们来围观吧
- 微博 QQ QQ空间 贴吧
- 文档嵌入链接
- 复制
- 微信扫一扫分享
- 已成功复制到剪贴板
10Data Structures---Hash Tables
展开查看详情
1 .Hash Tables A map (also called dictionary) is an ADT that contains key-value pairs. It helps retrieve the value using the key as the “address.” As an example, consider a set of two-letter words. You want to build a dictionary so that you can look up the definition of any two-letter word, very quickly. The two- letter word is the key that addresses the definition of the word. Key Definition am First person singular number indicative of be, also, before noon an The form of ‘a’ before a vowel sound … be To exist or to live by (Preposition) near or next to …
2 .More applications of maps (University record) Key = student id. Value = information about the student (Social media) Key = user name / email id. Value = user information. So, how will you implement a dictionary of all two-letter words? Take an array with 26x26= 676 elements. Each two-letter will map to a unique index of the array. The content of that array index will be the definition. Is this scalable? NO. Consider large words … Hash tables implement dictionaries Number of keys = n Array size = N, and The number of possible keys M >> N > n
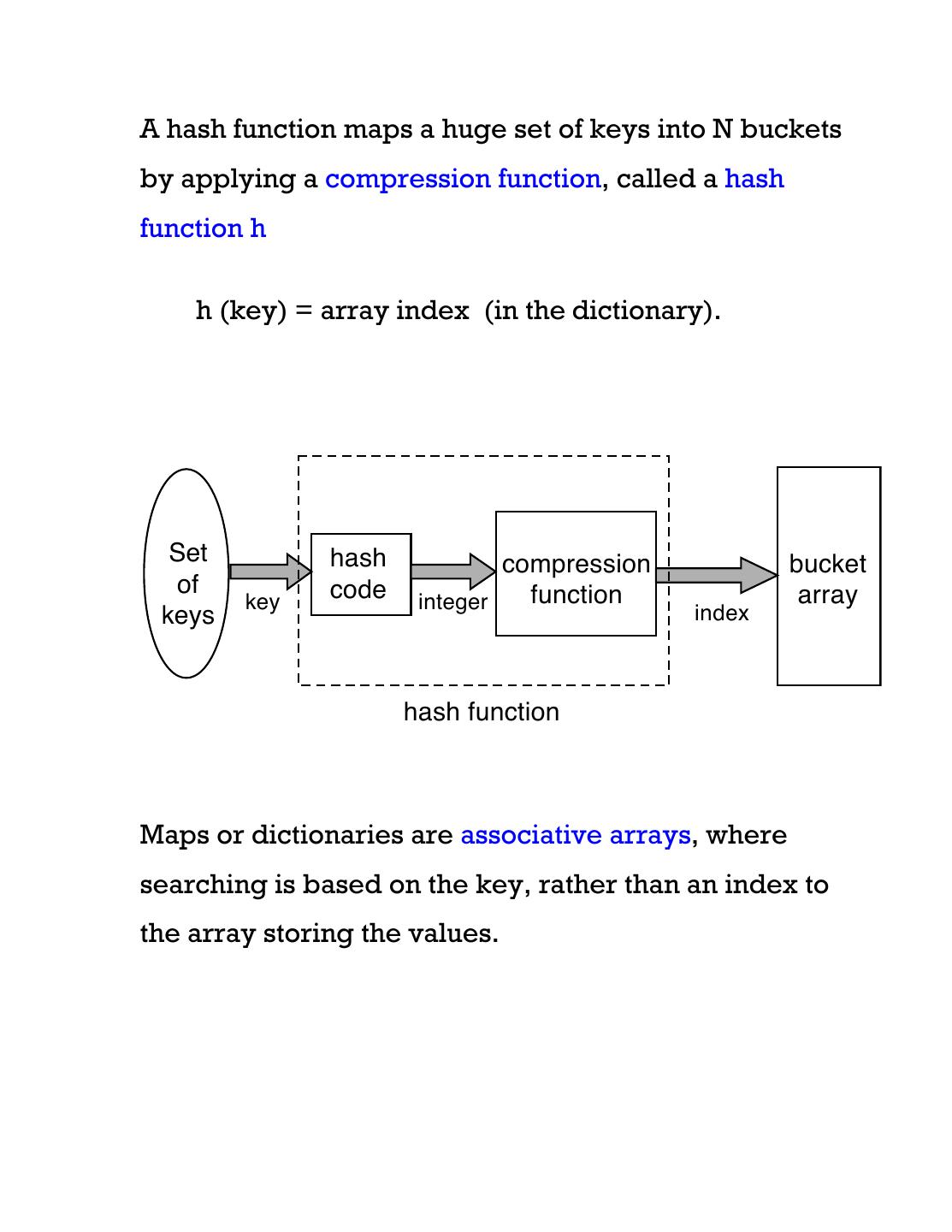
3 .A hash function maps a huge set of keys into N buckets by applying a compression function, called a hash function h h (key) = array index (in the dictionary). Set hash compression bucket of code function array key integer keys index hash function Maps or dictionaries are associative arrays, where searching is based on the key, rather than an index to the array storing the values.
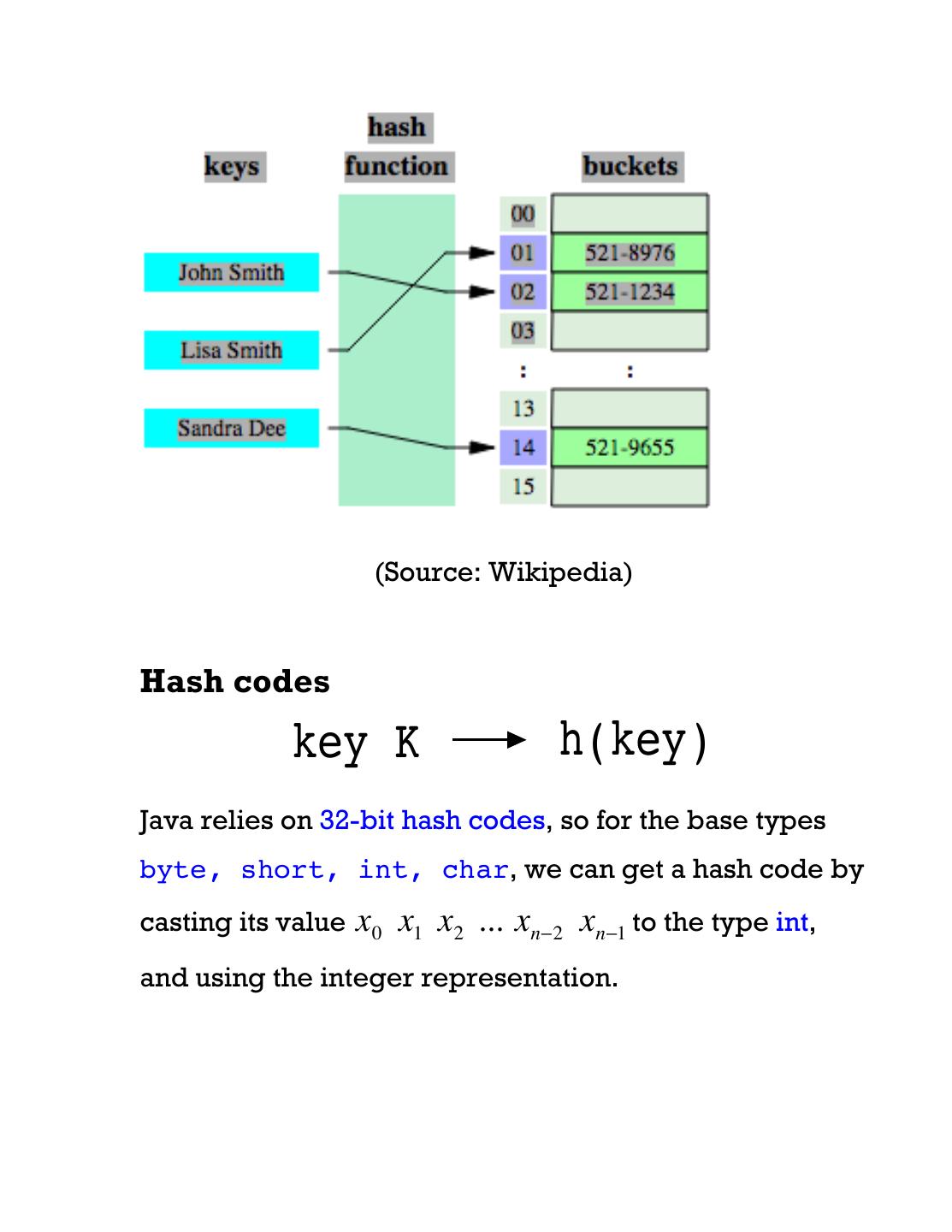
4 . (Source: Wikipedia) Hash codes key K h(key) Java relies on 32-bit hash codes, so for the base types byte, short, int, char, we can get a hash code by casting its value x0 x1 x2 ... xn−2 xn−1 to the type int, and using the integer representation.
5 .For a string object s = s[0] s[1] … s[n-1], the following method is used to compute the hash code h(s): h(s) = s[0]*31^(n-1)+s[1]*31^(n-2)+ ... + s[n-1] This is called polynomial hash code. When using a hash table to implement a map, for consistency, equivalent keys must map to the same bucket. So, if x.equals(y) then x.hashCode == y.hashCode Compression functions Let us get back to the dictionary of all 2-letter words. There are 26 x 26 = 676 possible keys, but perhaps 70 possible meaningful words. Let us convert each 2-letter word xy to an integer i as follows (using f(a) = 0, f(b) = 1, f(c) = 2, …, f(z) = 25): i = 26.f(x) + f(y)
6 .Division method. If we plan on storing these words in an array of size 100 (i.e. N=100) then a simple compression function is mod 100 (if N = bucket array size, then use mod N). Thus, the integer i will be placed in location i mod N of the hash table MAD (Multiply-Add-Divide) method Map i to [(a.i + b) mod p] mod N Here p is a prime number and a, b are random integers chosen from the interval [0..p-1] Depending on the value of n/N, it works in most cases, but what if there are two words xy and pq such that h(xy) = h(pq)? This is called collision. Computing the compression function for collision avoidance is a form of black art. Use a function so that two different keys do not map to the same index of the hash table.
7 .Hash table operations A hash table supports at least three operations: insert(key, value) Compute the key's hash code. Compress it to determine the entry's bucket. Insert the entry (key and value together) into that bucket (and deal with collision) find(key) Hash the key to determine its bucket. Search the entry with the given key. If found, return the entry, else, return null. delete(key) Hash the key to determine its bucket. Search the list for an entry with the given key. Remove it from the list if found. Return the entry or null if not found.
8 .Collision avoidance Hashing with separate chaining (Also called Chain hashing) Each bucket entry references a linked list of entries, called a chain. If several keys are mapped to the same bucket, their definitions all reside in that bucket's linked list. 0 1 2 3 4 5 6 7 8 9 10 But how do we know which definition corresponds to which word? The answer is that we must store each key in the table along with its definition (i.e. both key and value).
9 .Open addressing Linear Probing i hash Key Let i be the hash function of an entry X, but assume that slot i of the hash table is not free, since it has been allocated to entry Y (so that is a collision). Try looking for slots i+1, i+2, i+3, … until a free slot is found. Quadratic Probing In case of a collision at slot i, try looking for slots i+12, i+22, i+32, … until a free slot is found.
10 .Typically we expect O(1) time performance for each of the operations. This may not be feasible if the load factor n/N is large (> 0.75) or there are too many collisions. The performance can slowly degenerate towards O(n). Resizing the hash table It is not always possible to foresee the number of entries we'll need to store. So, what to do when the load factor increases? One option is to enlarge the hash table when the load factor becomes too large. Allocate a new array (typically at least twice as long as the old), and then walk through all the entries in the old array and “rehash” them into the new. [Note: you just can’t copy the entries of the old array into the slots of the new array, because the compression functions of the two arrays will be different. You have to rehash each entry individually.] For best performance, hash codes often need to be designed specially for each new object.
11 .Complexities of insert, delete, search Initially all empty buckets contain “null”. To insert a key K, first find if it K already exists. If so, the new value will replace the old value. Otherwise insert it into a blank slot. To delete a key, first find it, and then replace it by null. Case 1. Chain hashing Needs additional space. Each bucket has to maintain an independent linked list. The lengths of these lists should be as small as possible otherwise search complexity will increase. If the space is tight, this can scale up to O(n).
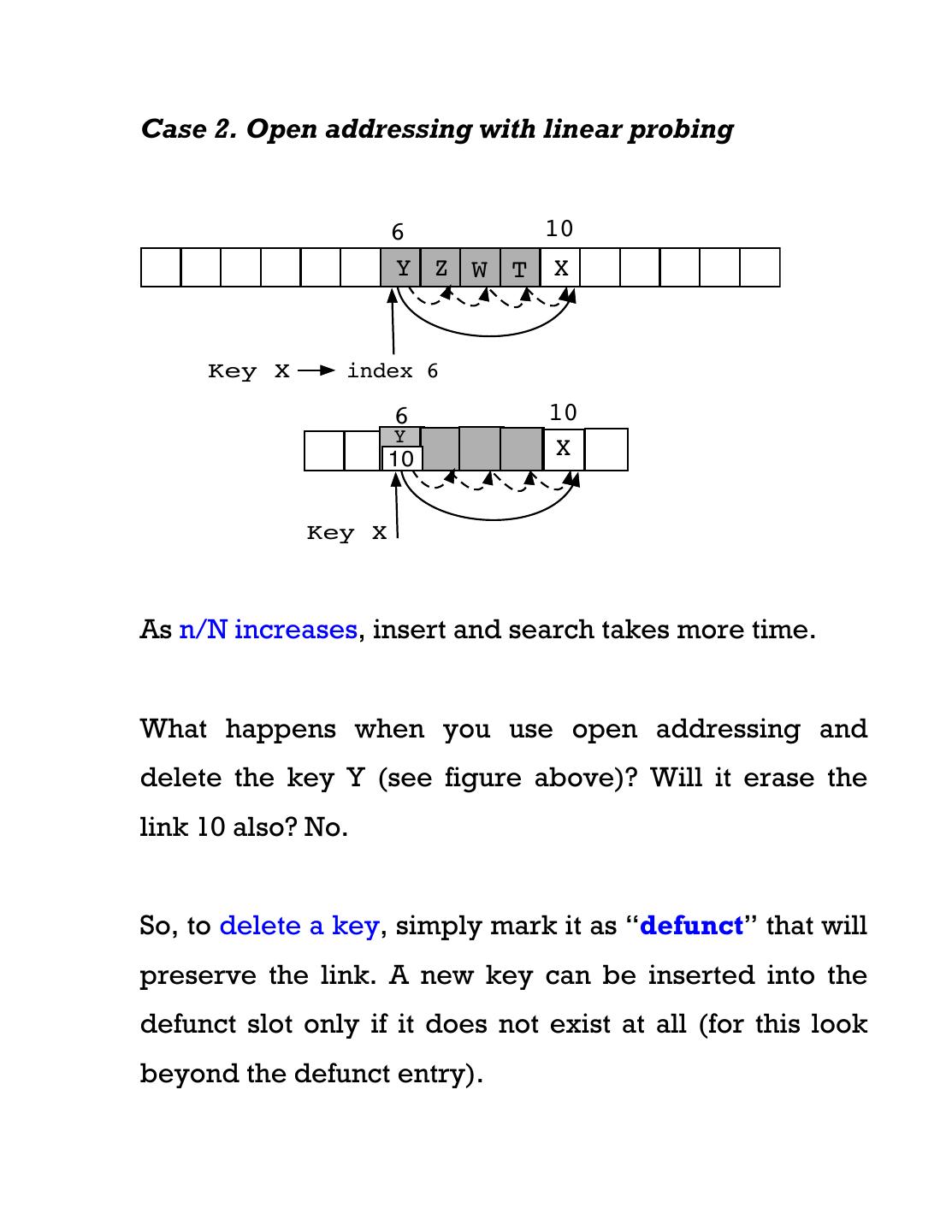
12 .Case 2. Open addressing with linear probing 6 10 Y Z W T X Key X index 6 6 10 Y 10 X Key X As n/N increases, insert and search takes more time. What happens when you use open addressing and delete the key Y (see figure above)? Will it erase the link 10 also? No. So, to delete a key, simply mark it as “defunct” that will preserve the link. A new key can be inserted into the defunct slot only if it does not exist at all (for this look beyond the defunct entry).
13 .Computing the hashCode of a given key should be fast, while minimizing the probability of collision. For a string s, the hash is computed as follows: int hash = 0; for (int i = 0; i < s.length(); i++) hash = (31 * hash + s.charAt(i)) % N Why can it be computed fast? Because it avoids the use of a multiplier (which is slow)! How? Horner’s Rule for computing polynomials h(s) = s[0]*31^(n-1)+s[1]*31^(n-2)+ ... + s[n-1] y0 = s[0] y1 = 31*y0 + s[1] y2 = 31*y1 + s[2] y3 = 31*y2 + s[3] … … … h(s) = yn-‐1 = 31*yn-‐2 + s[n-‐1]
14 .Example. Consider the following keys to be entered into a hash table, first into a table of size 5. “Tom”, “Dick”, “Harry”, “Sam”, “Pete” Key hashCode() hashCode()%5 Tom 84274 4 Dick 2129869 4 Harry 69496448 3 Sam 82879 4 Pete 2484038 3 The load factor is 100%. Try with a larger table of size 11
15 .Tidbits If you use hashCode()%N as compression function, then note that it may sometimes return a negative value (when the argument is negative) leading to an array out-‐of-‐bound exception. Add N to make it +ve. Also, the function Math.abs(s.hashCode()%N can return a negative integer when the 32-‐bit argument is 10000000000…00, since its positive version cannot be represented using 32 bits (needs 33 bits)! One way out is the following private int hash(Key key) { return (key.hashCode() & 0x7fffffff) % M; } It masks the sign bit and converts it into a positive integer.
16 .Quadratic probing is slow since it involves multiplication. Here is how you can speed it up to calculate the next index. Initially k= -‐1 k = k+2 index = (index + k) % hashTableSize Why does it work?