- 快召唤伙伴们来围观吧
- 微博 QQ QQ空间 贴吧
- 文档嵌入链接
- 复制
- 微信扫一扫分享
- 已成功复制到剪贴板
05Data Structure and Algorithm---Graph
展开查看详情
1 . Graph Graphs and graph theory can be used to model: – Computer networks – Social networks – Communications networks – Information networks – Software design – Transportation networks – Biological networks 1
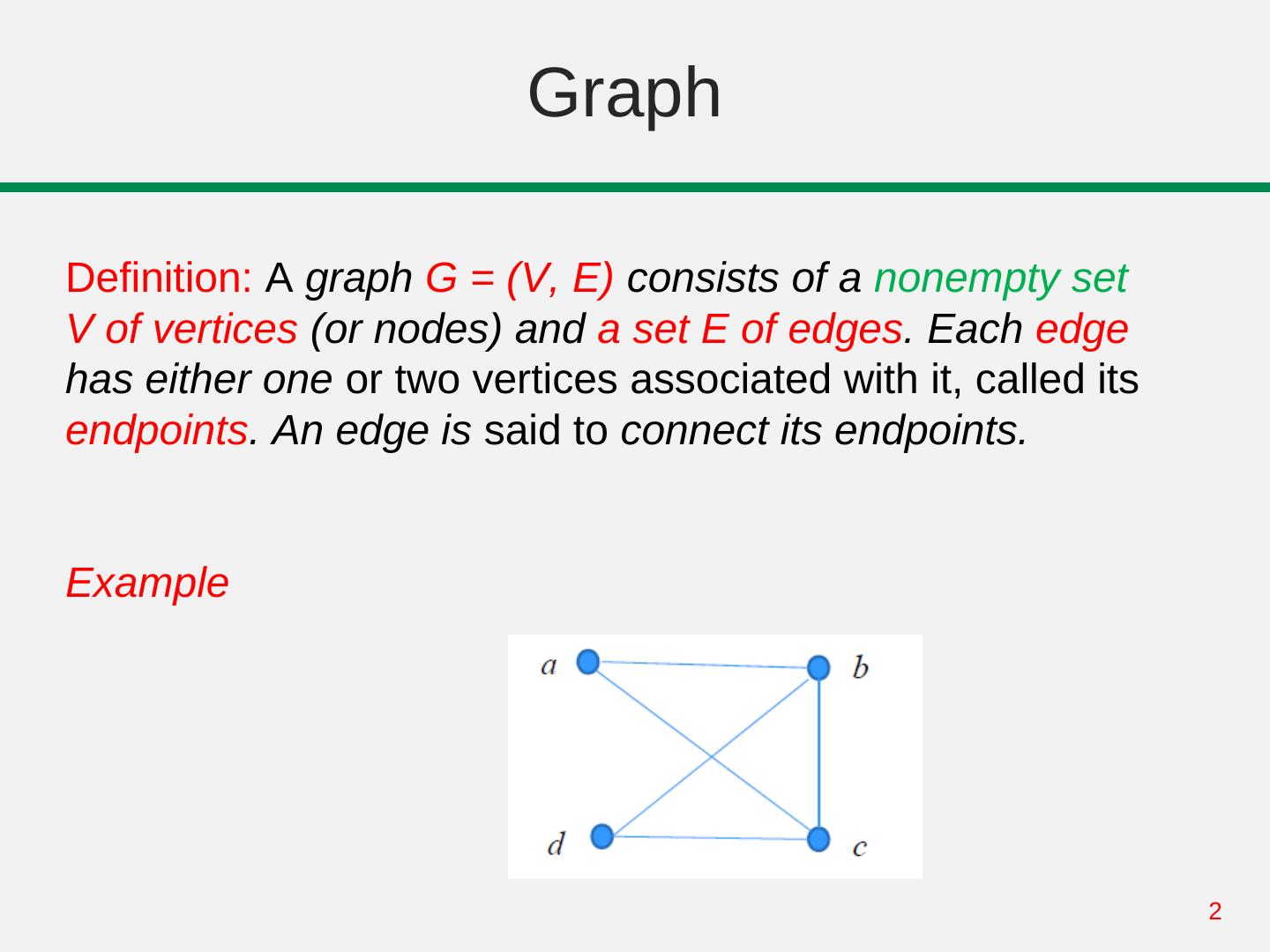
2 . Graph Definition: A graph G = (V, E) consists of a nonempty set V of vertices (or nodes) and a set E of edges. Each edge has either one or two vertices associated with it, called its endpoints. An edge is said to connect its endpoints. Example 2
3 . Terminology In a simple graph each edge connects two different vertices and no two edges connect the same pair of vertices. Multigraphs may have multiple edges connecting the same two vertices. When m different edges connect the vertices u and v, we say that {u,v} is an edge of multiplicity m. • An edge that connects a vertex to itself is called a loop. • A pseudograph may include loops, as well as multiple edges connecting the same pair of vertices. 3
4 . Directed graph Definition: A directed graph (or digraph) G = (V, E) consists of a nonempty set V of vertices (or nodes) and a set E of directed edges (or arcs). Each edge is associated with an ordered pair of vertices. The directed edge associated with the ordered pair (u,v) is said to start at u and end at v. Remark: – Graphs where the end points of an edge are not ordered are said to be undirected graphs. 4
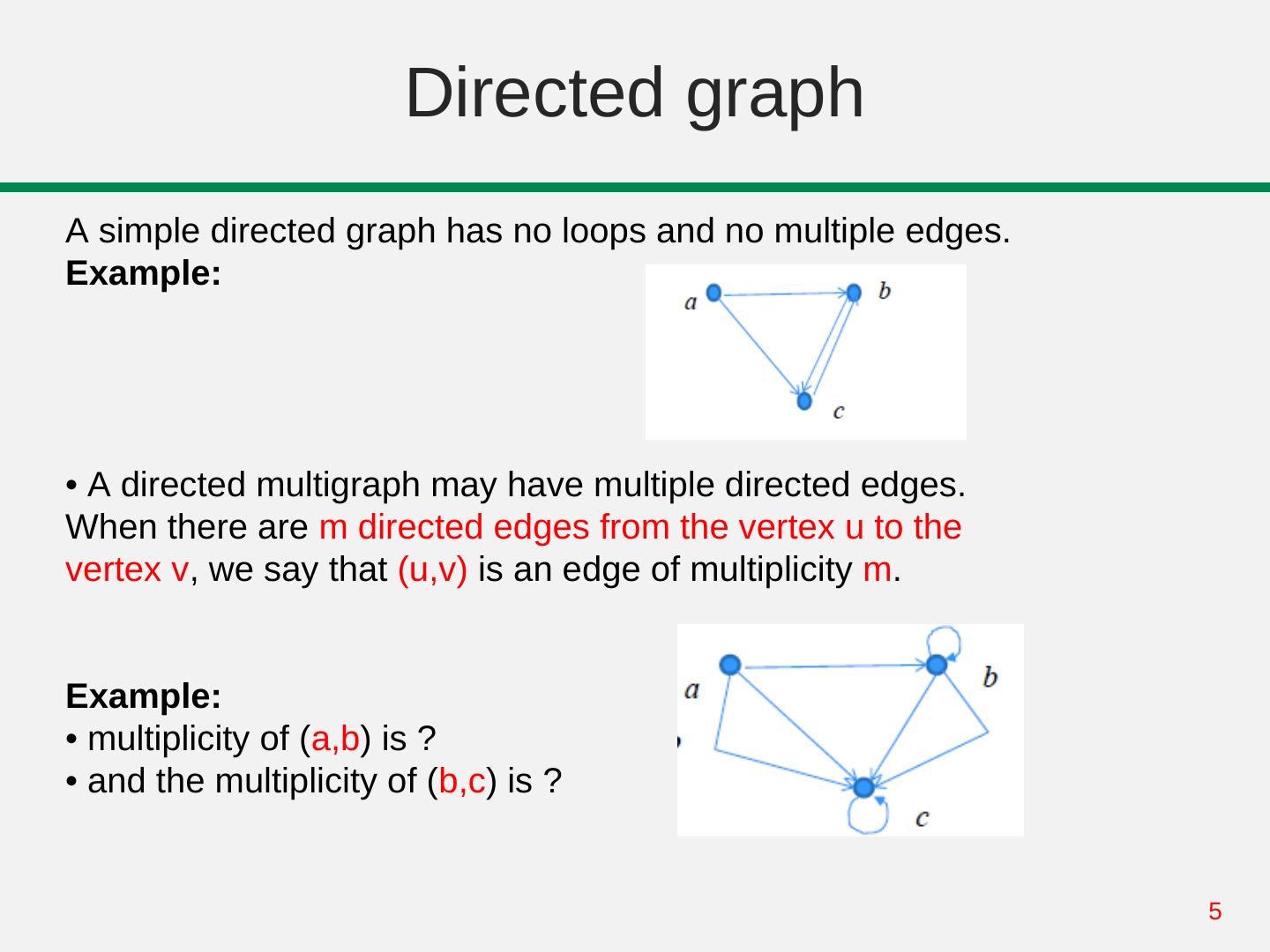
5 . Directed graph A simple directed graph has no loops and no multiple edges. Example: • A directed multigraph may have multiple directed edges. When there are m directed edges from the vertex u to the vertex v, we say that (u,v) is an edge of multiplicity m. Example: • multiplicity of (a,b) is ? • and the multiplicity of (b,c) is ? 5
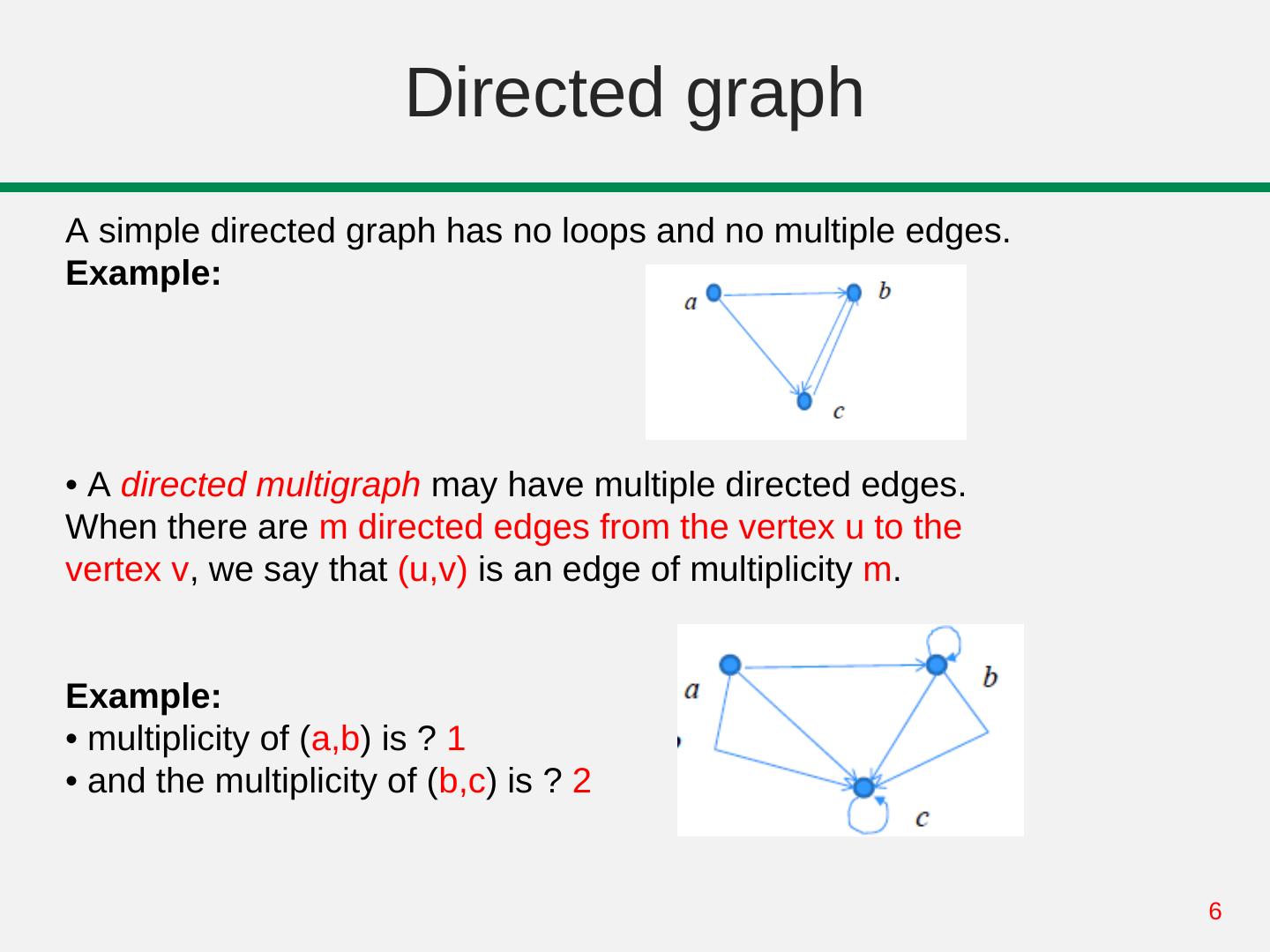
6 . Directed graph A simple directed graph has no loops and no multiple edges. Example: • A directed multigraph may have multiple directed edges. When there are m directed edges from the vertex u to the vertex v, we say that (u,v) is an edge of multiplicity m. Example: • multiplicity of (a,b) is ? 1 • and the multiplicity of (b,c) is ? 2 6
7 . Undirected graph Definition 1. Two vertices u, v in an undirected graph G are called adjacent (or neighbors) in G if there is an edge e between u and v. Such an edge e is called incident with the vertices u and v and e is said to connect u and v. Definition 2. The set of all neighbors of a vertex v of G = (V, E), denoted by N(v), is called the neighborhood of v. If A is a subset of V, we denote by N(A) the set of all vertices in G that are adjacent to at least one vertex in A. So, Definition 3. The degree of a vertex in a undirected graph is the number of edges incident with it, except that a loop at a vertex contributes two to the degree of that vertex. The degree of the vertex v is denoted by deg(v). 7
8 . Undirected graph Example: What are the degrees and neighborhoods of the vertices in the graphs G? Solution: G: deg(a) = 2, deg(b) = deg(c) = deg(f ) = 4, deg(d ) = 1, deg(e) = 3, deg(g) = 0. N(a) = {b, f }, N(b) = {a, c, e, f }, N(c) = {b, d, e, f }, N(d) = {c}, N(e) = {b, c , f }, N(f) = {a, b, c, e}, N(g) = Ø . 8
9 . Undirected graph Example: What are the degrees and neighborhoods of the vertices in the graphs H? Solution: H: deg(a) = 4, deg(b) = deg(e) = 6, deg(c) = 1, deg(d) = 5. N(a) = {b, d, e}, N(b) = {a, b, c, d, e}, N(c) = {b}, N(d) = {a, b, e}, N(e) = {a, b ,d}. 9
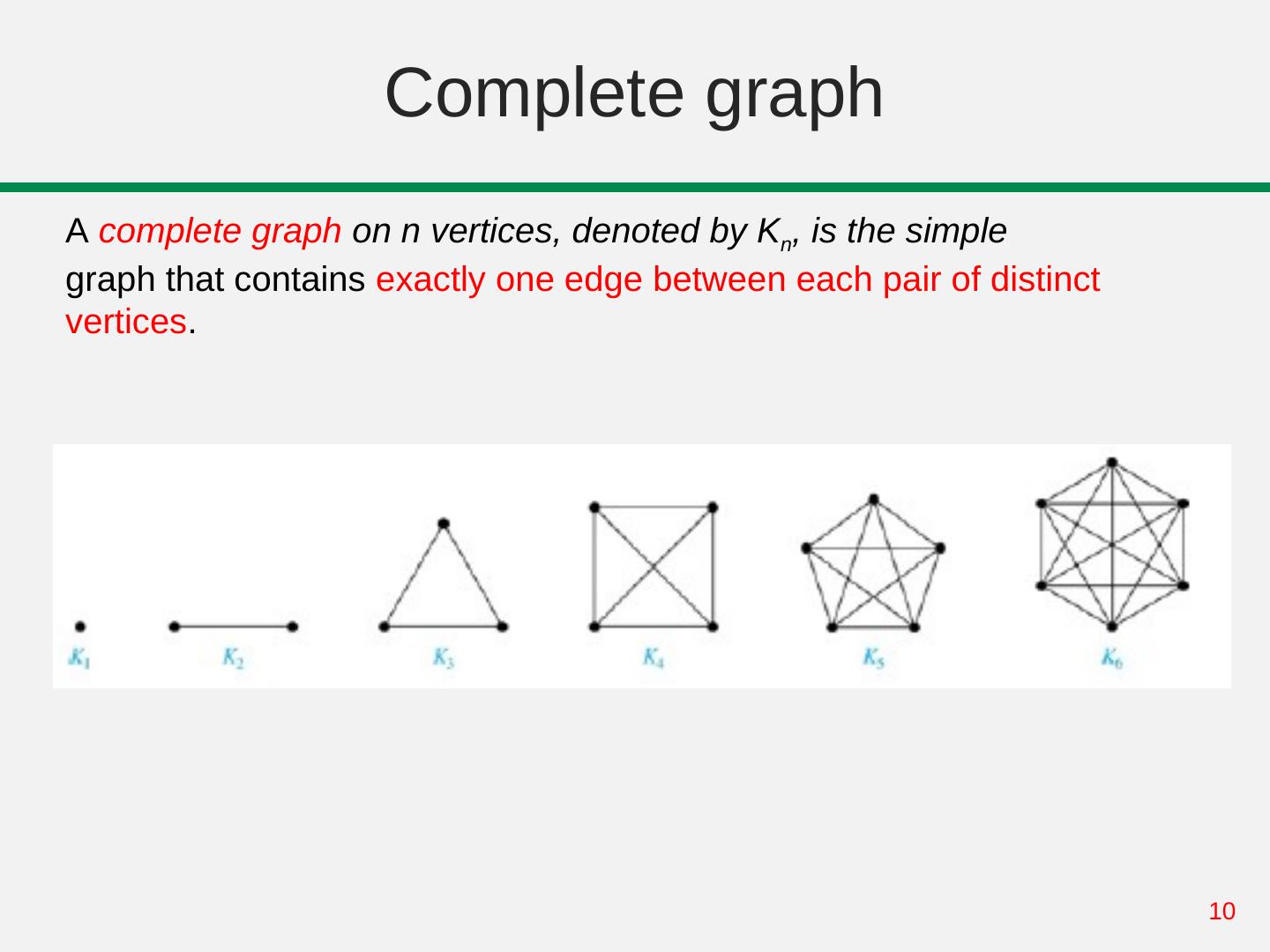
10 . Complete graph A complete graph on n vertices, denoted by Kn, is the simple graph that contains exactly one edge between each pair of distinct vertices. 10
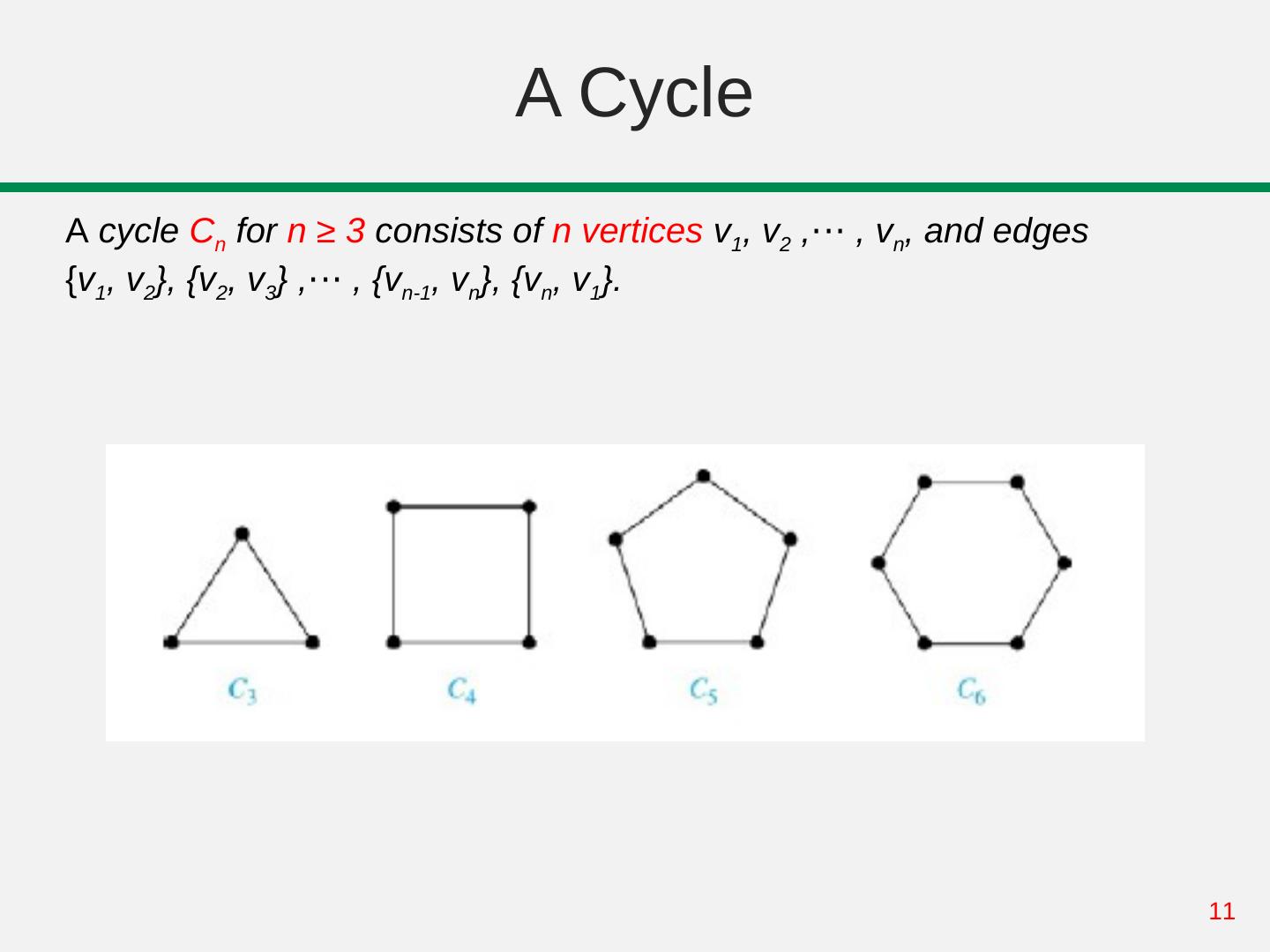
11 . A Cycle A cycle Cn for n ≥ 3 consists of n vertices v1, v2 ,⋯ , v , vn, and edges {v1, v2}, {v2, v3} ,⋯ , v , {vn-1, vn}, {vn, v1}. 11
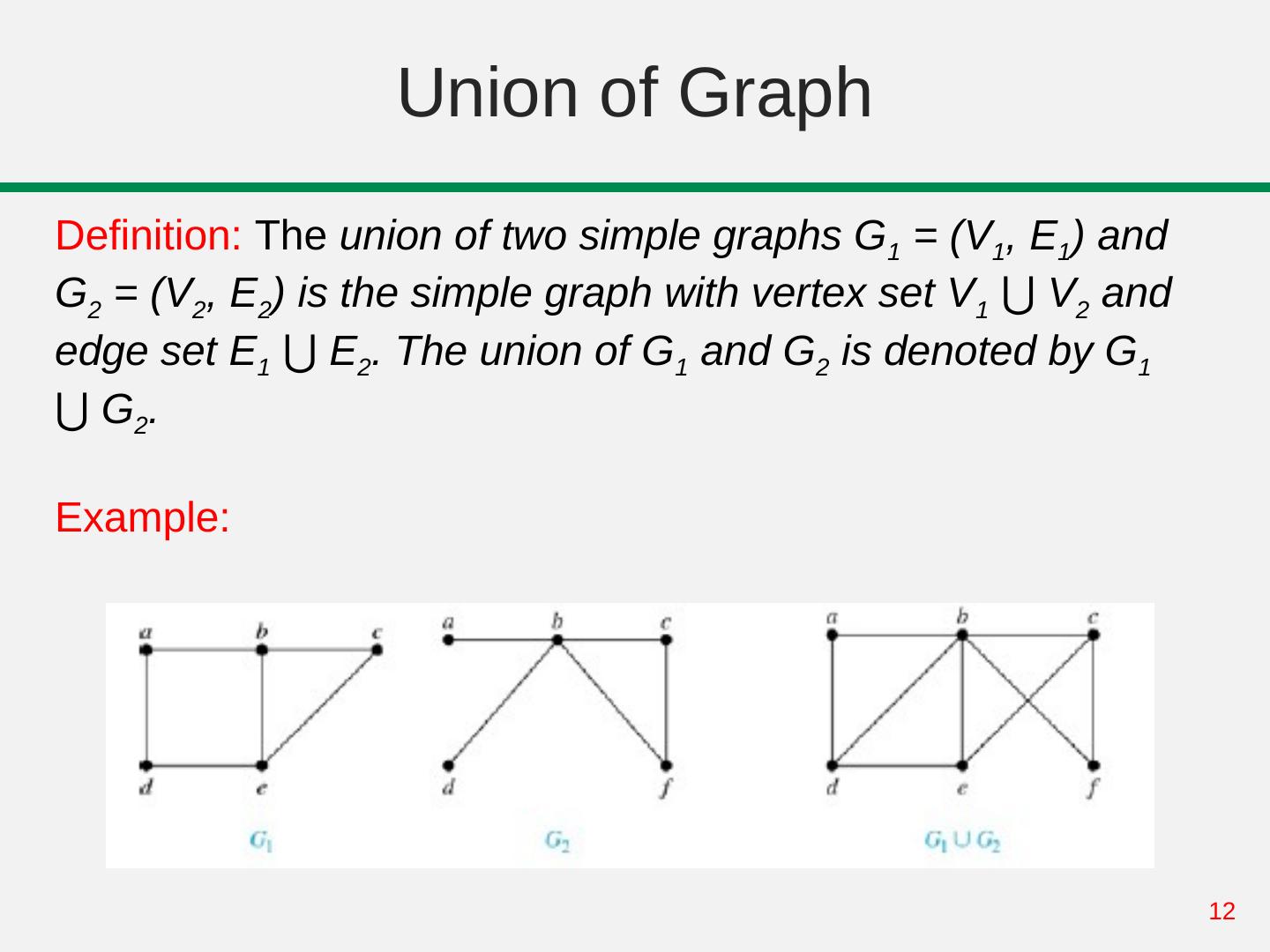
12 . Union of Graph Definition: The union of two simple graphs G1 = (V1, E1) and G2 = (V2, E2) is the simple graph with vertex set V1 ⋃ V V2 and edge set E1 ⋃ V E2. The union of G1 and G2 is denoted by G1 ⋃ V G2. Example: 12
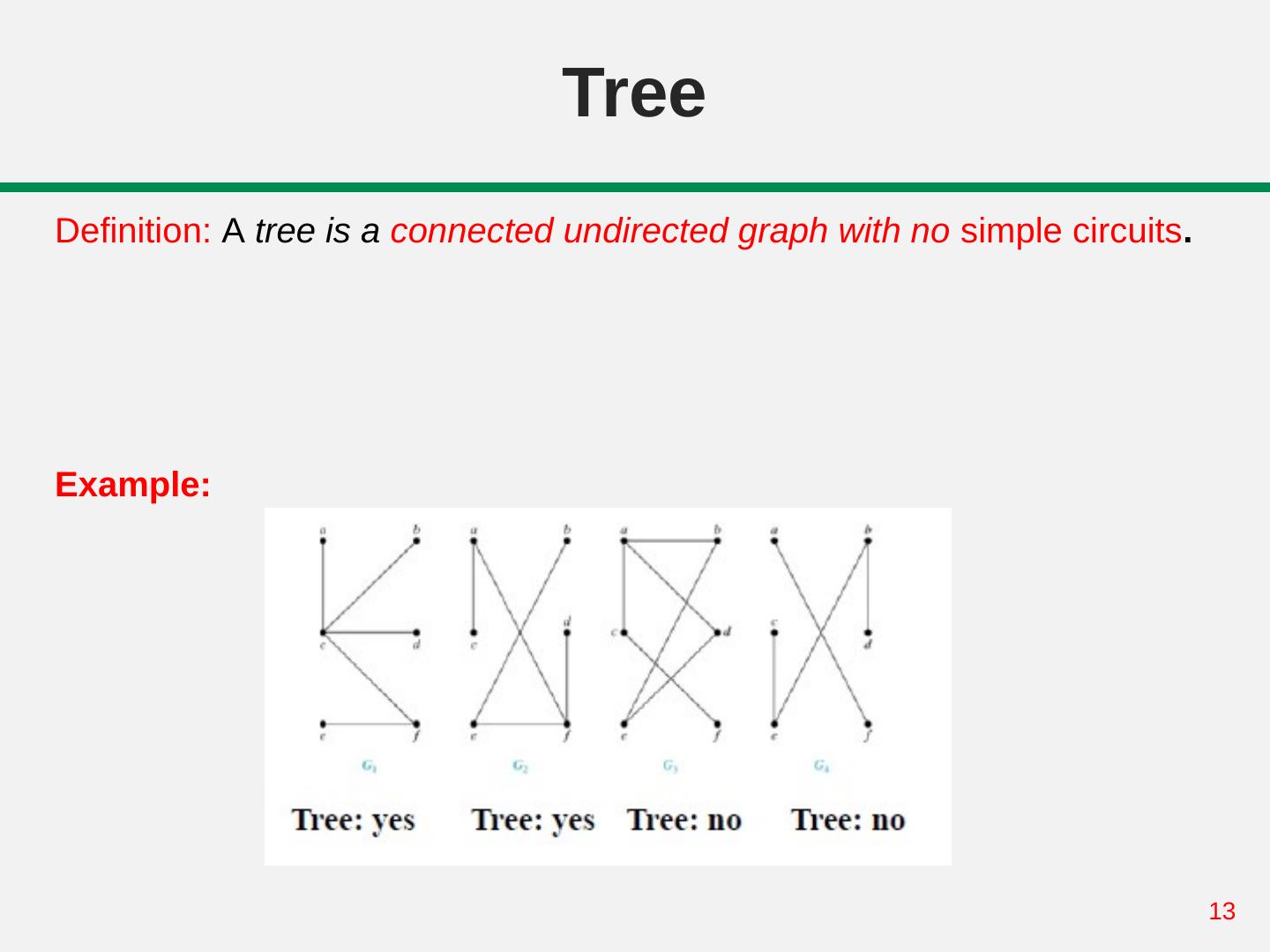
13 . Tree Definition: A tree is a connected undirected graph with no simple circuits. Example: 13
14 . Tree Definition: A forest is a graph that has no simple circuit, but is not connected. Each of the connected components in a forest is a tree. Example: 14
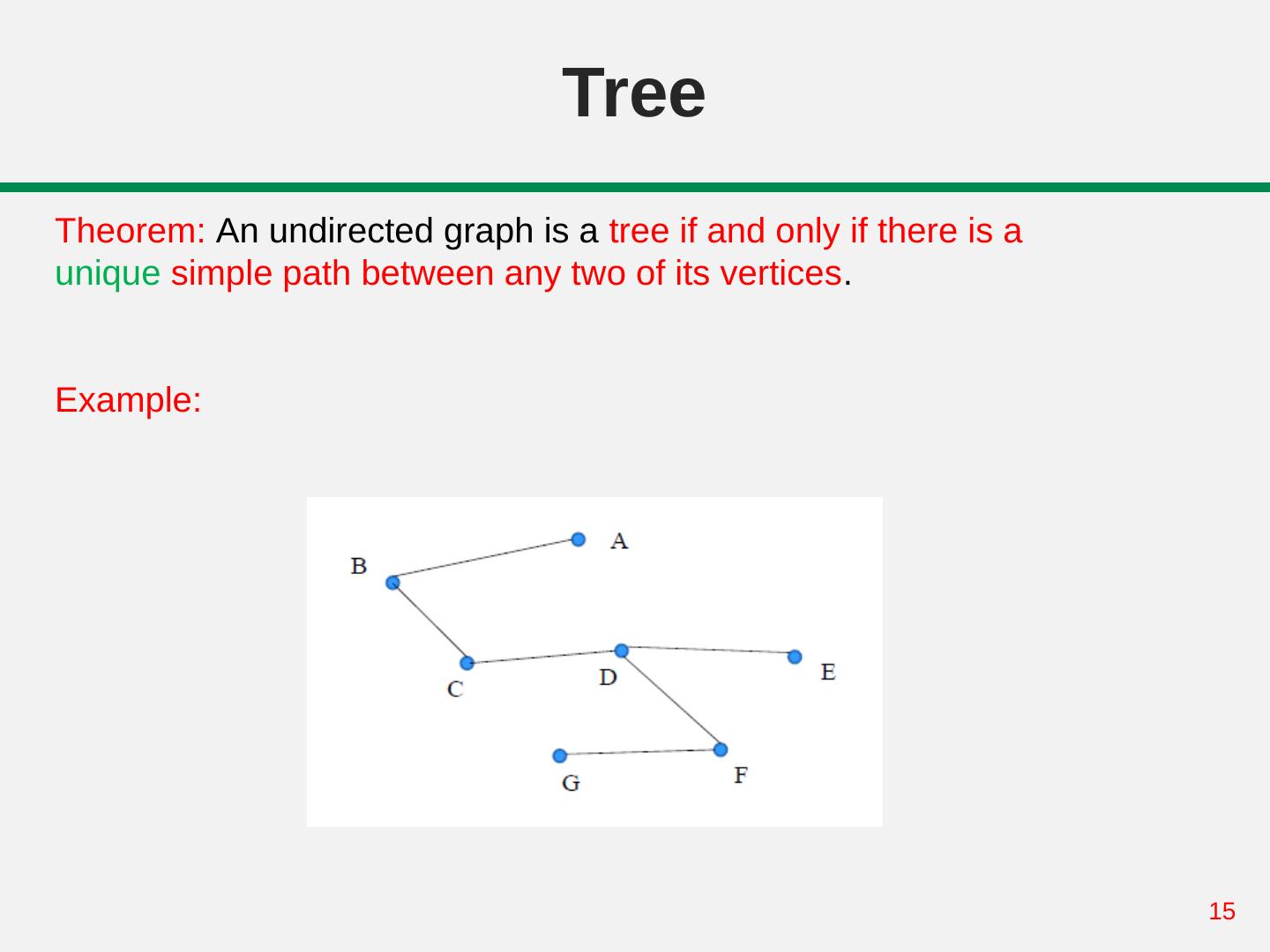
15 . Tree Theorem: An undirected graph is a tree if and only if there is a unique simple path between any two of its vertices. Example: 15
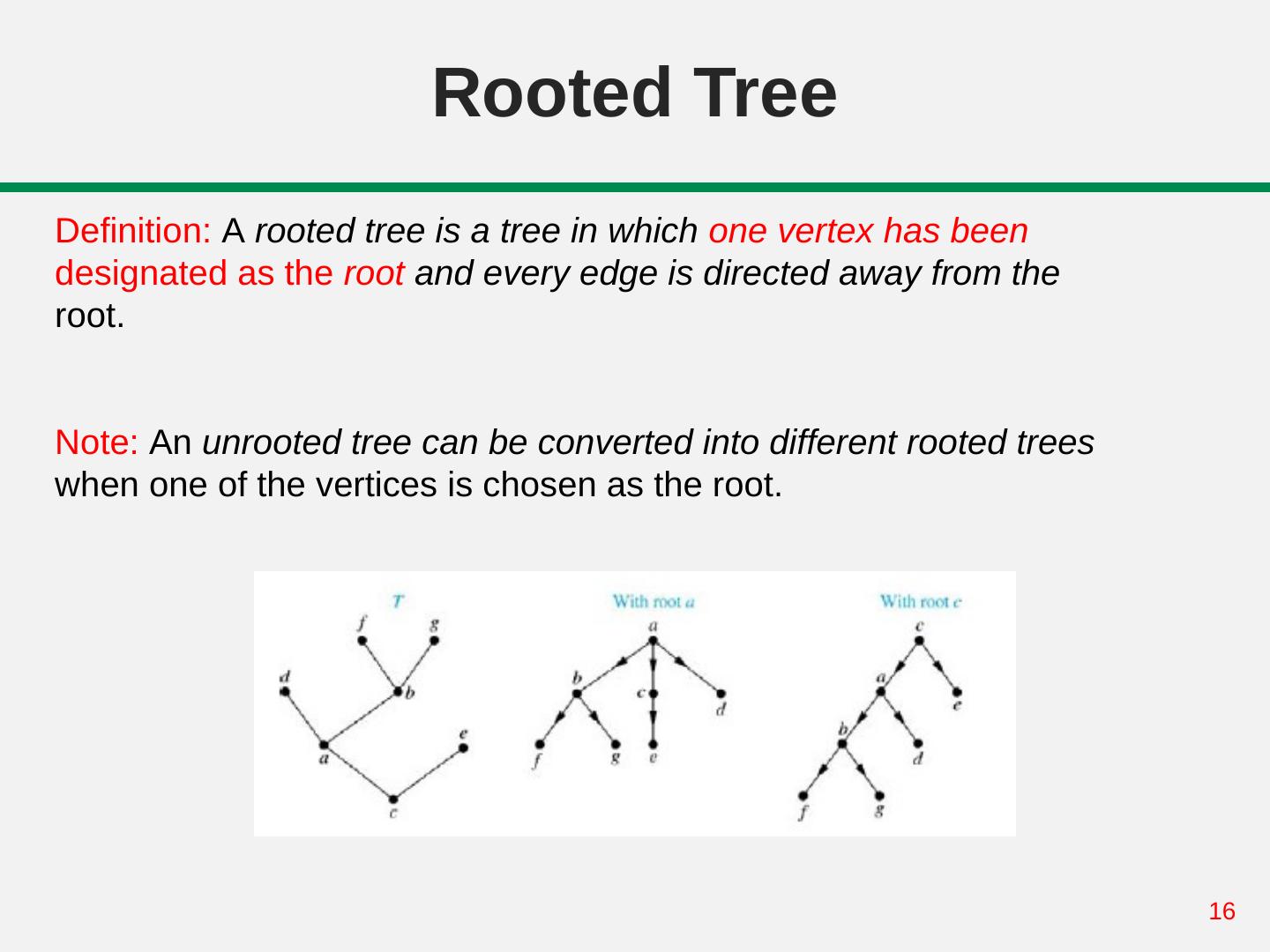
16 . Rooted Tree Definition: A rooted tree is a tree in which one vertex has been designated as the root and every edge is directed away from the root. Note: An unrooted tree can be converted into different rooted trees when one of the vertices is chosen as the root. 16
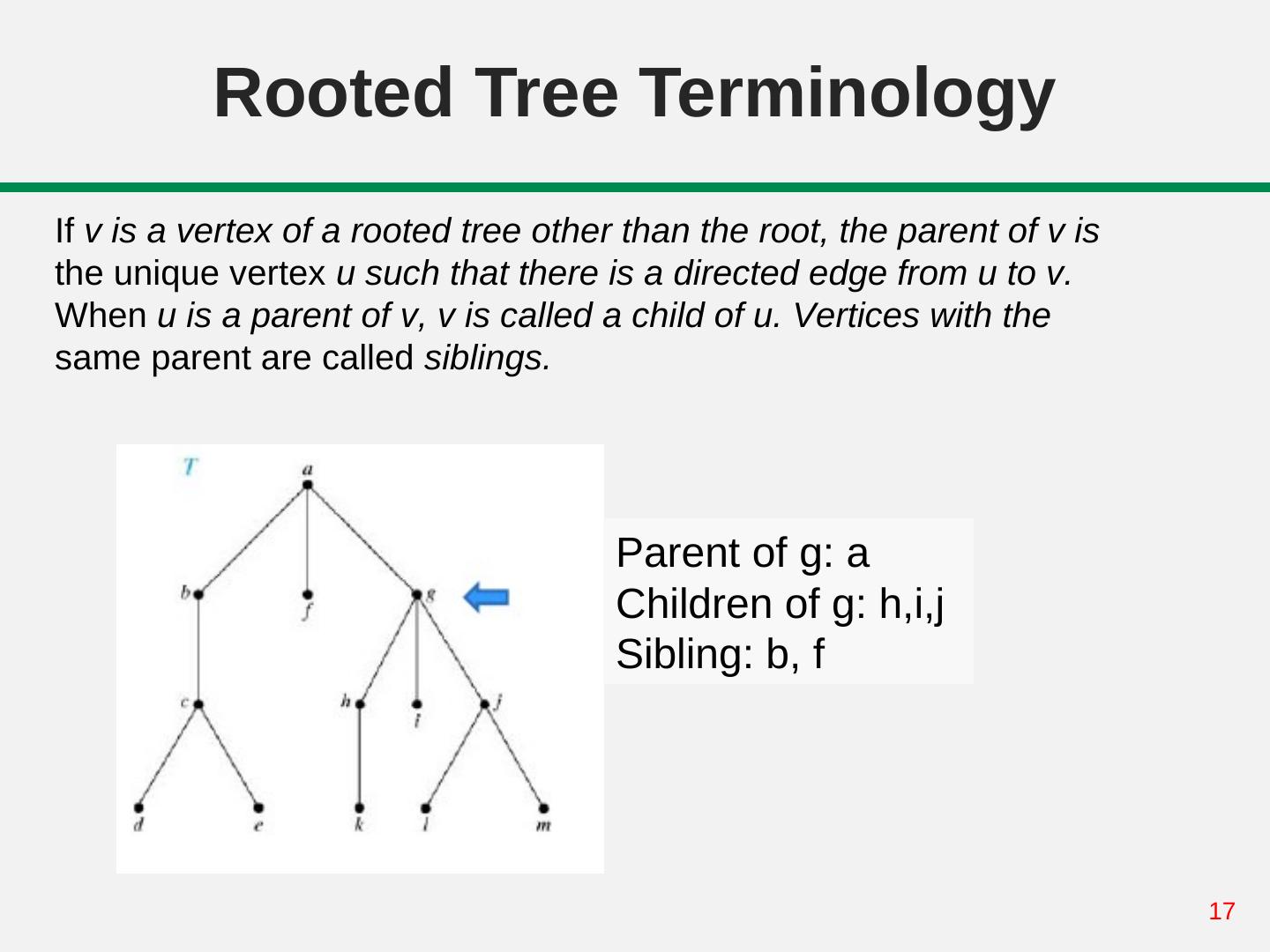
17 . Rooted Tree Terminology If v is a vertex of a rooted tree other than the root, the parent of v is the unique vertex u such that there is a directed edge from u to v. When u is a parent of v, v is called a child of u. Vertices with the same parent are called siblings. Parent of g: a Children of g: h,i,j Sibling: b, f 17
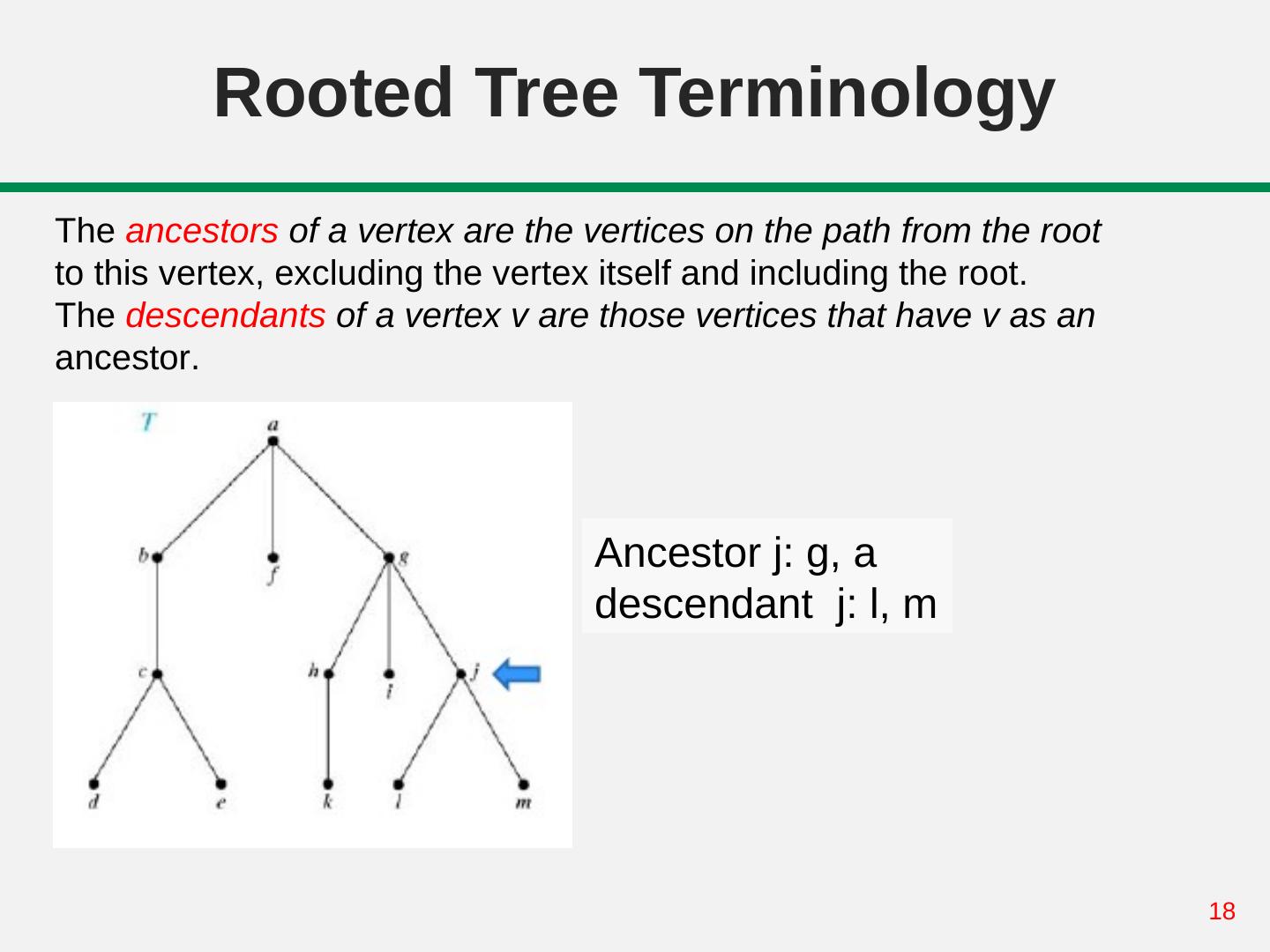
18 . Rooted Tree Terminology The ancestors of a vertex are the vertices on the path from the root to this vertex, excluding the vertex itself and including the root. The descendants of a vertex v are those vertices that have v as an ancestor. Ancestor j: g, a descendant j: l, m 18
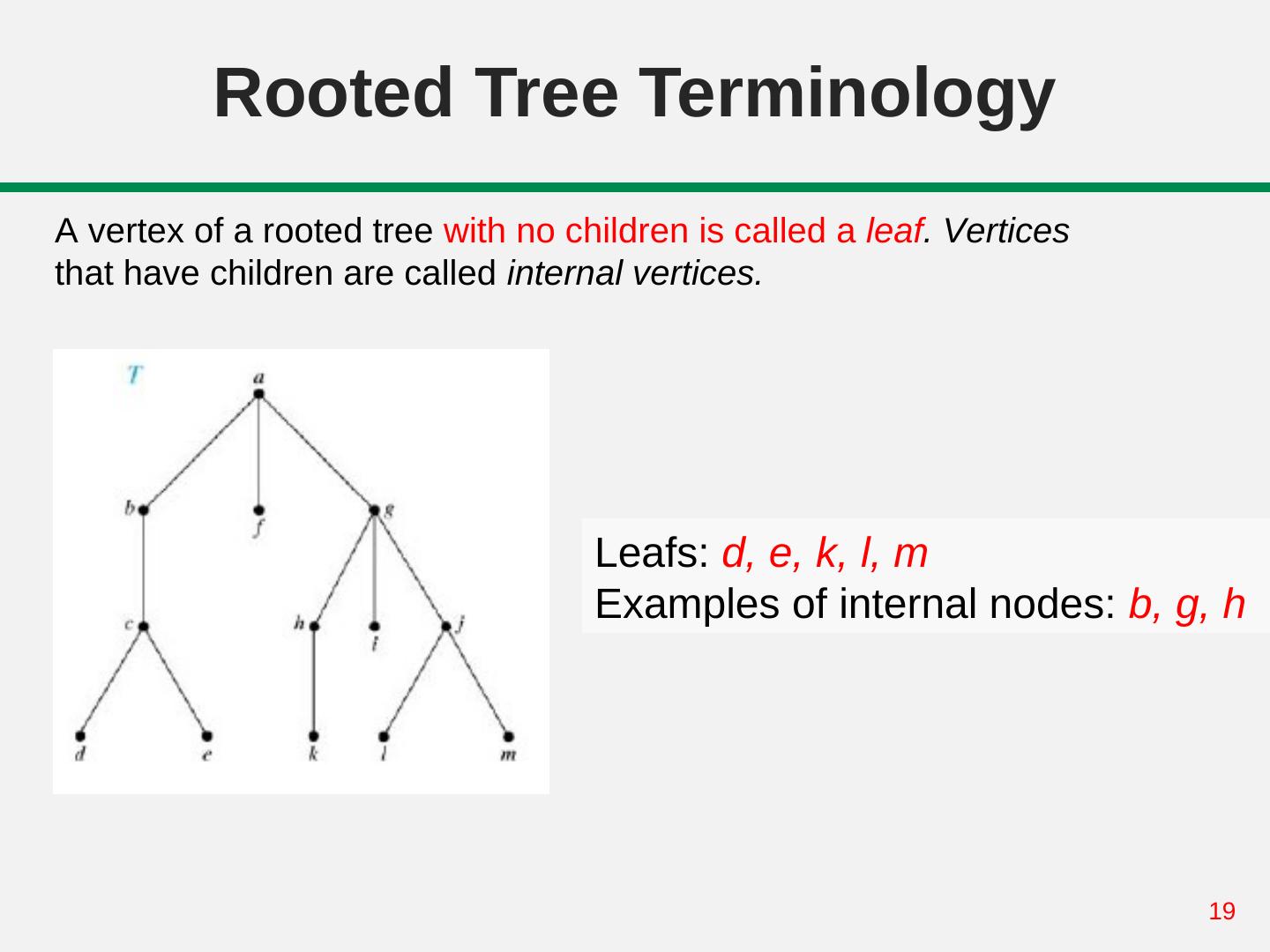
19 . Rooted Tree Terminology A vertex of a rooted tree with no children is called a leaf. Vertices that have children are called internal vertices. Leafs: d, e, k, l, m Examples of internal nodes: b, g, h 19
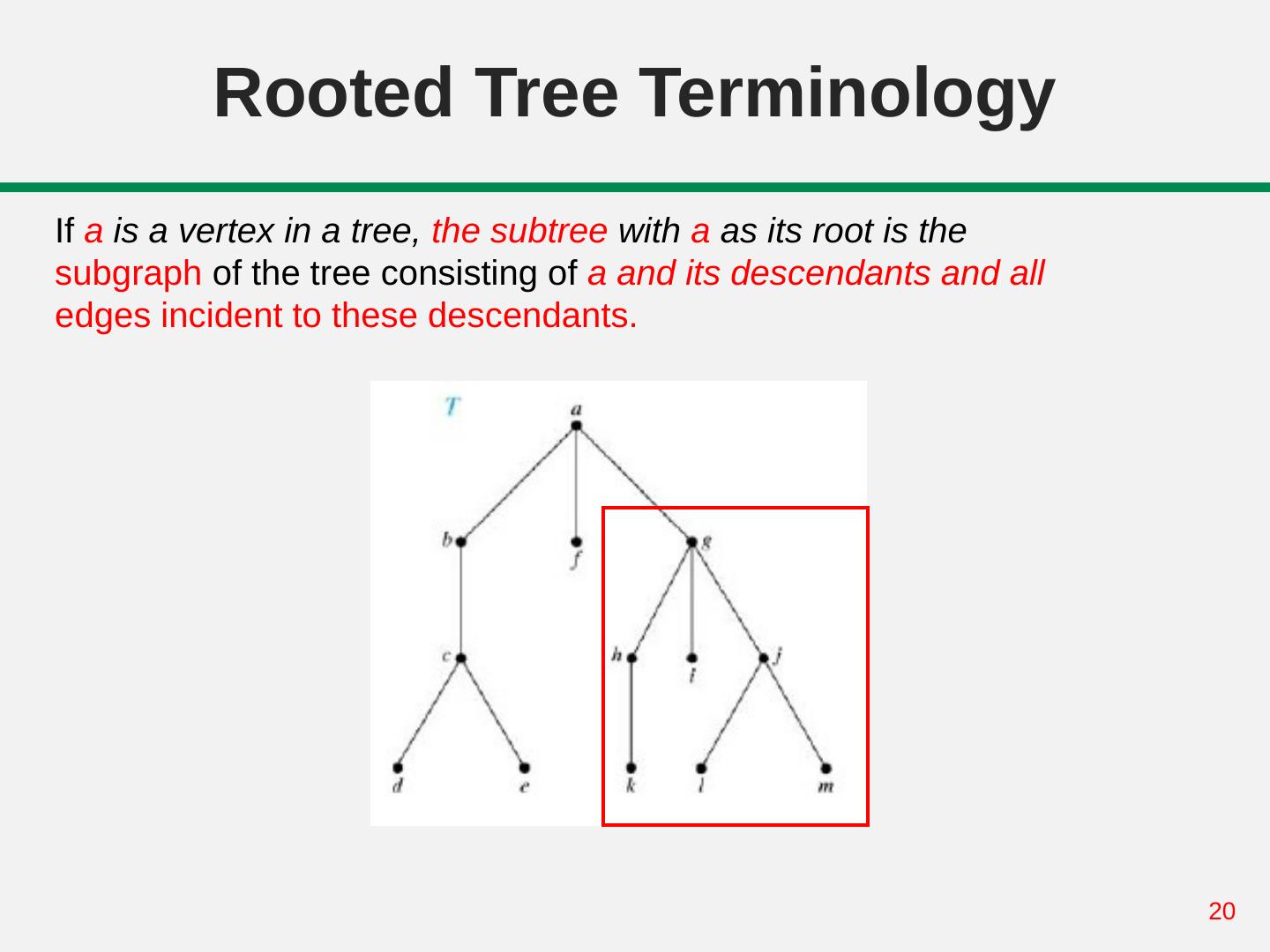
20 . Rooted Tree Terminology If a is a vertex in a tree, the subtree with a as its root is the subgraph of the tree consisting of a and its descendants and all edges incident to these descendants. 20
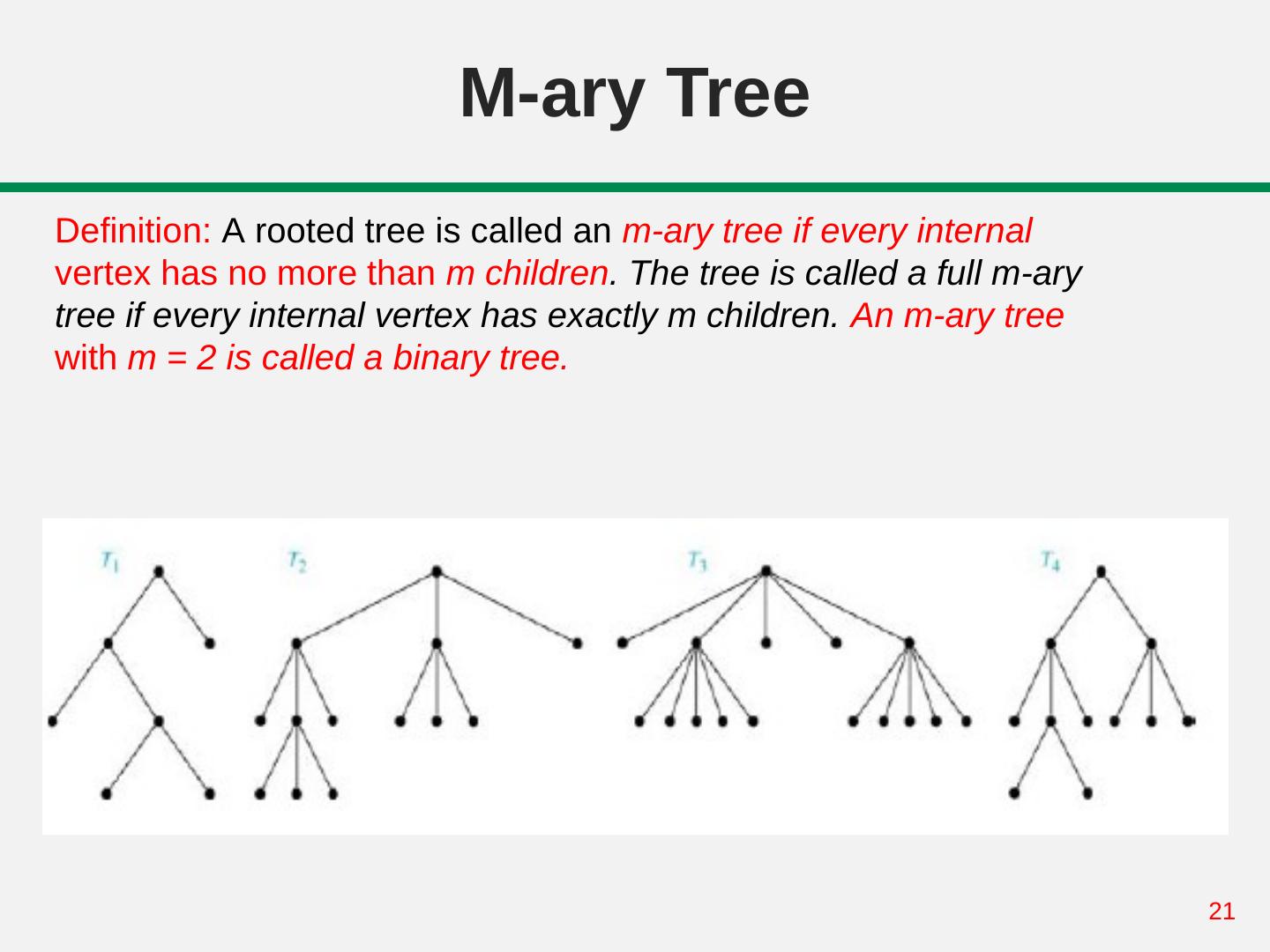
21 . M-ary Tree Definition: A rooted tree is called an m-ary tree if every internal vertex has no more than m children. The tree is called a full m-ary tree if every internal vertex has exactly m children. An m-ary tree with m = 2 is called a binary tree. 21
22 . Binary Tree A binary tree is an ordered rooted where each internal vertex has at most two children. If an internal vertex of a binary tree has two children, the first is called the left child and the second the right child. The tree rooted at the left child of a vertex is called the left subtree of this vertex, and the tree rooted at the right child of a vertex is called the right subtree of this vertex. 22