4Data Structure and Algorithm---Binary Search Trees

1 .Source Code for Data Structures and Algorithm Analysis in C (Second Edition) – by Weiss http://users.cis.fiu.edu/~weiss/dsaa_c2e/files.html

2 .http://en.wikipedia.org/wiki/Binary_tree http://en.wikipedia.org/wiki/Binary_search_tree Graph - http:// xlinux.nist.gov/dads/HTML/graph.html

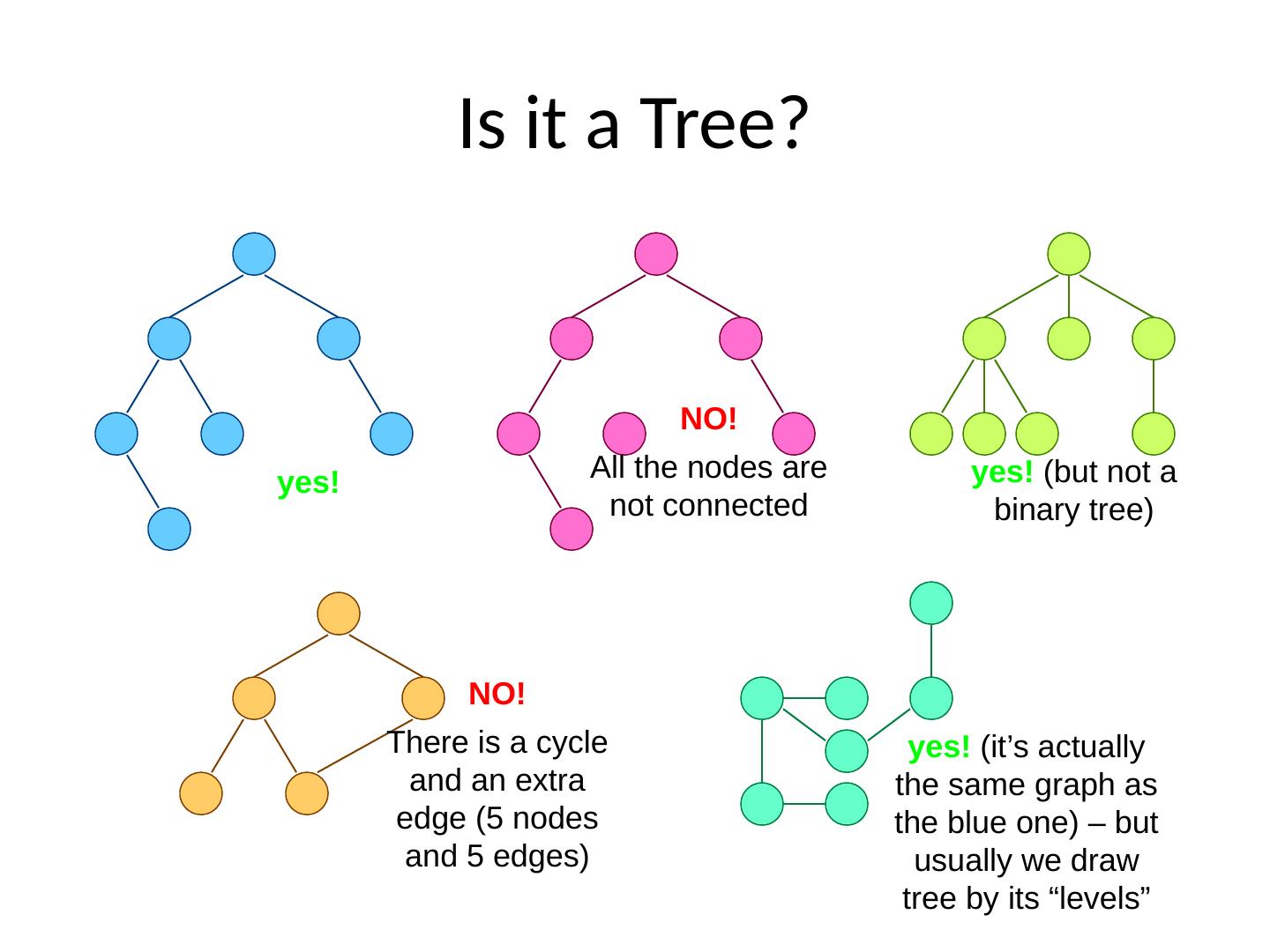
3 .Is it a Tree? yes! NO! All the nodes are not connected NO! There is a cycle and an extra edge (5 nodes and 5 edges) yes! (but not a binary tree) yes! (it’s actually the same graph as the blue one) – but usually we draw tree by its “levels”

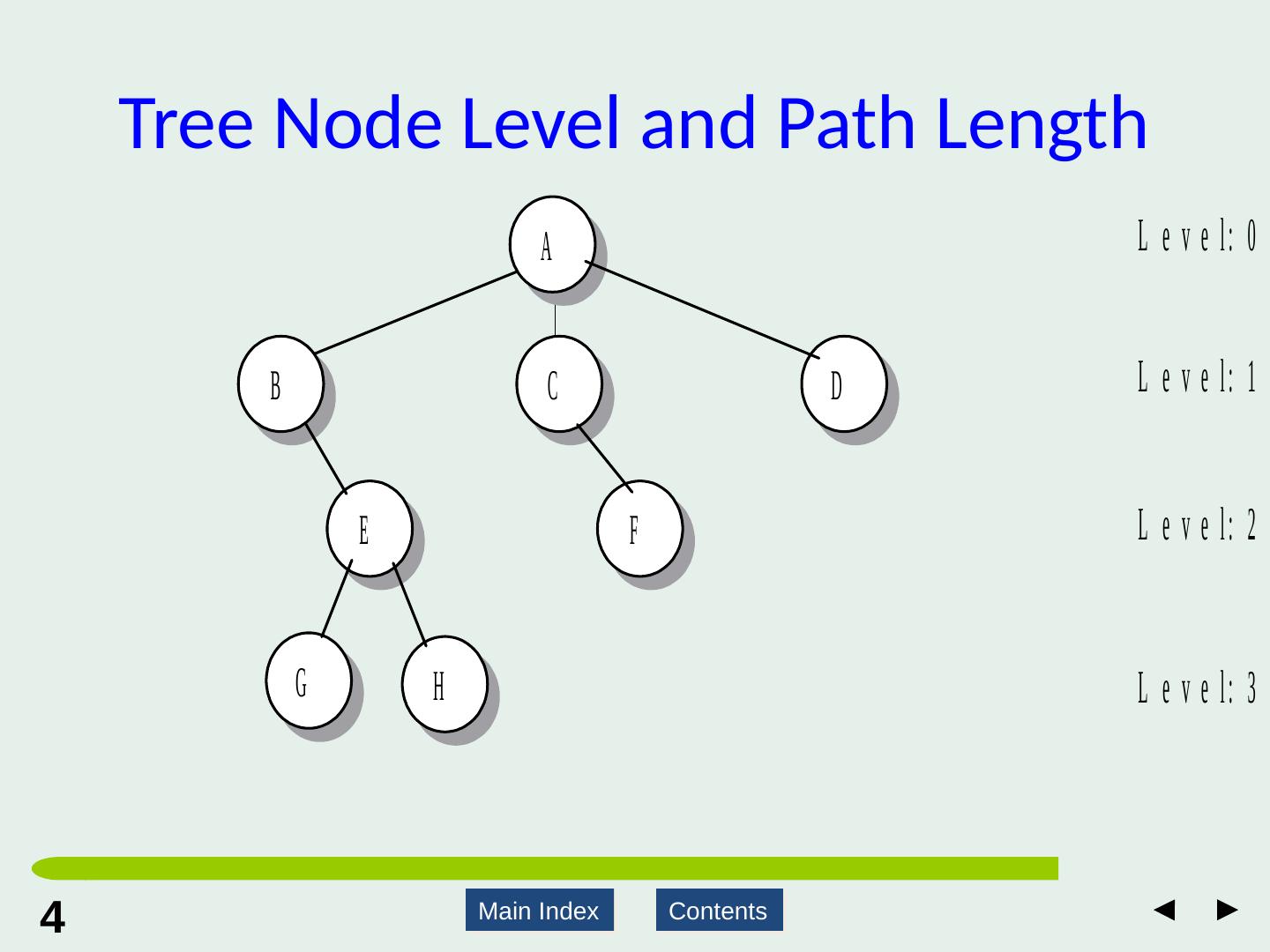
4 .4 4 Main Index Contents Tree Node Level and Path Length

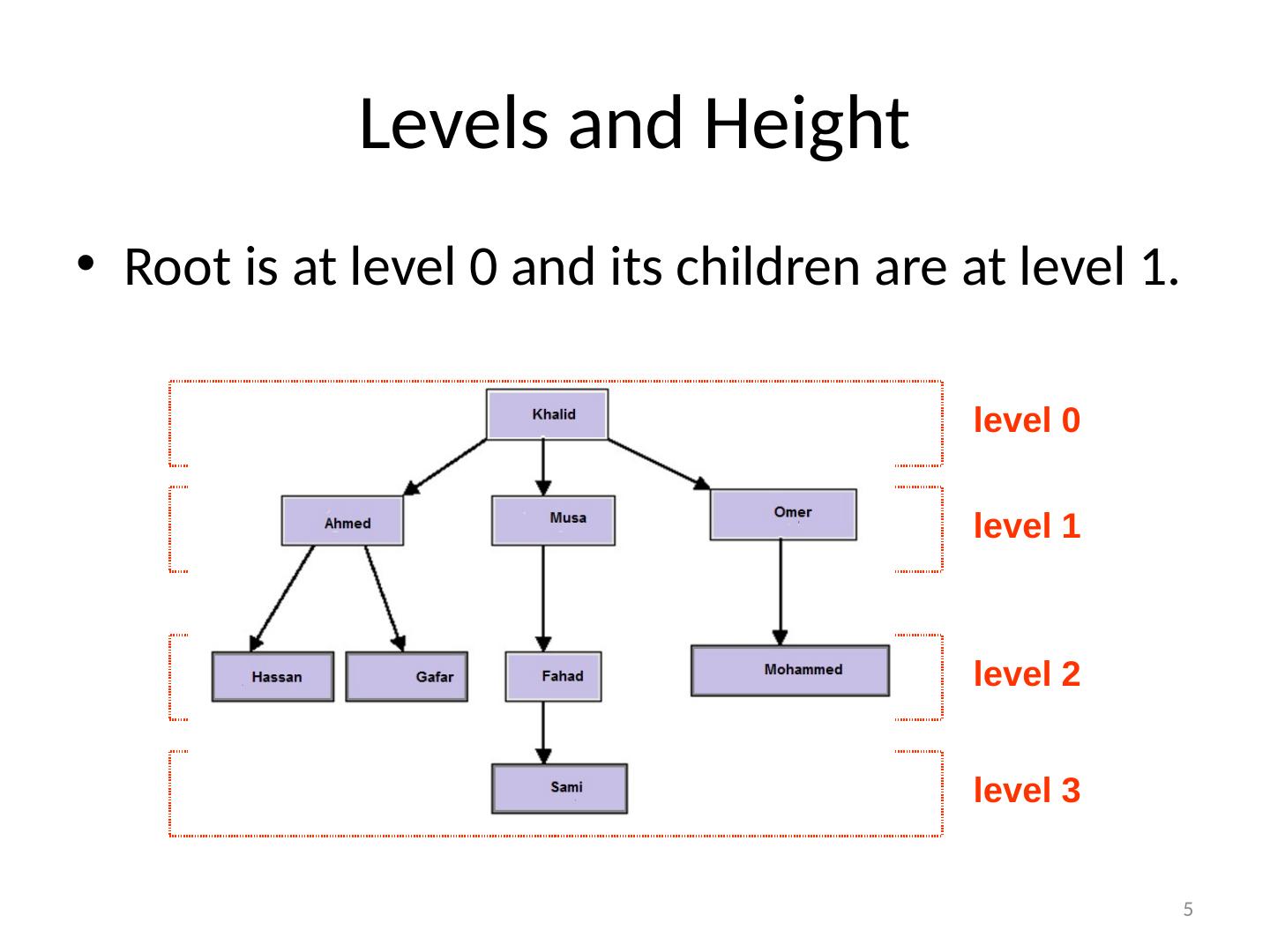
5 .5 Levels and Height Root is at level 0 and its children are at level 1. level 0 level 1 level 2 level 3

6 .Measuring Trees The height of a node v is the number of nodes on the longest path from v to a leaf The height of the tree is the height of the root, which is the number of nodes on the longest path from the root to a leaf The depth of a node v is the number of nodes on the path from the root to v This is also referred to as the level of a node Note that there are slightly different formulations of the height of a tree Where the height of a tree is said to be the length (the number of edge) on the longest path from node to a leaf

7 .Trees - Example E R T E L P M E A S A root Leaves or terminal nodes Child (of root) Depth of T: 2 Height of T: 1 Level 0 1 3 2

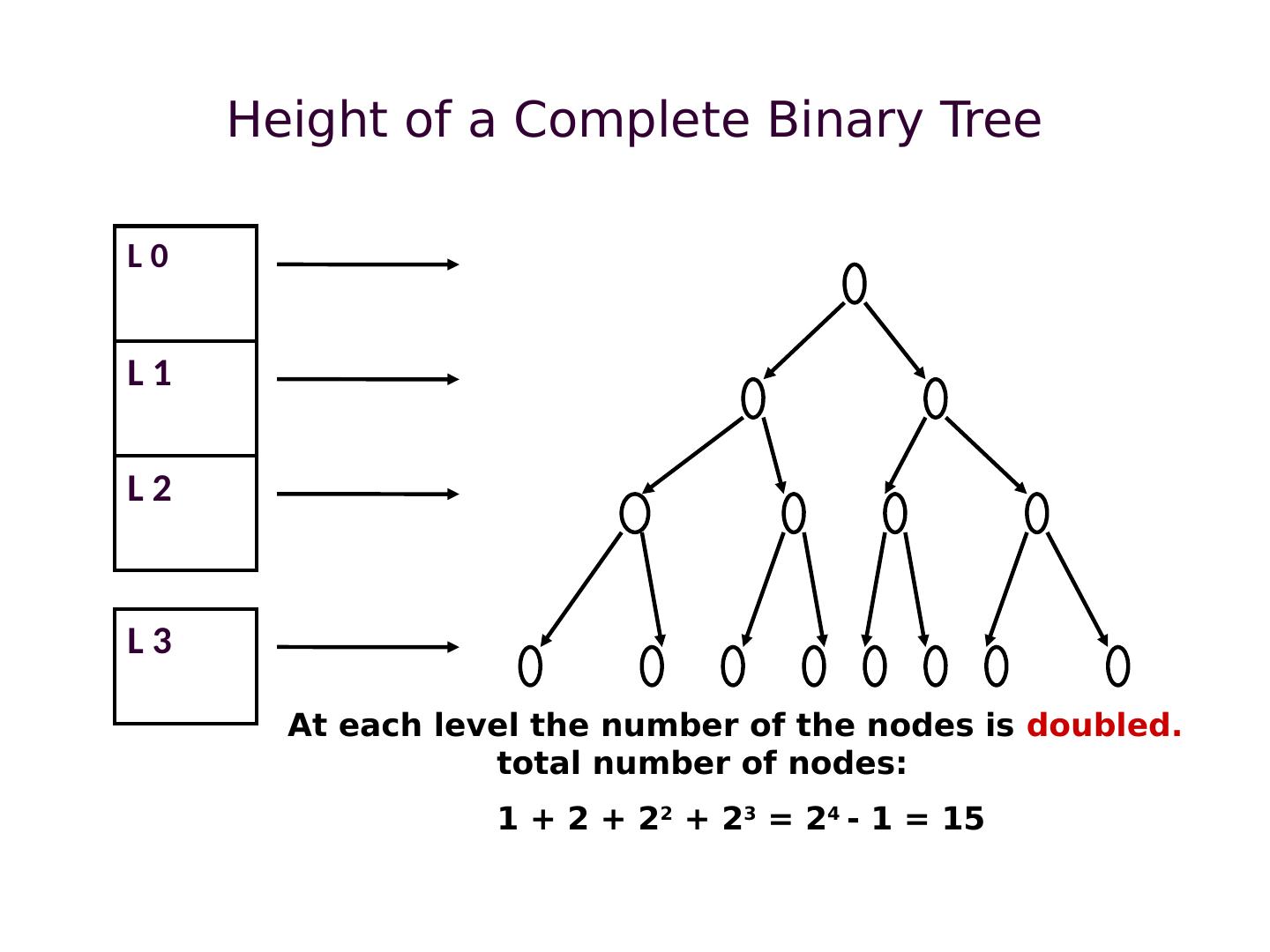
8 .Height of a Complete Binary Tree L 0 L 1 L 2 L 3 At each level the number of the nodes is doubled. total number of nodes: 1 + 2 + 2 2 + 2 3 = 2 4 - 1 = 15

9 .Example: Expression Tree How do you construct an expression tree from a postfix expression? E.g a b + c d e + * *

10 .1 3 7 5 Binary Search Tree Also known as Totally Ordered Tree Definition: A binary tree B is called a binary search tree iff: There is an order relation ≤ defined for the vertices of B For any vertex v , and any descendant u of v.left , u ≤ v For any vertex v , and any descendent w of v.right , v ≤ w 4 root 2 6

11 .Binary Search Tree Consequences: The smallest element in a binary search tree (BST) is the “left-most” node The largest element in a BST is the “right-most” node Inorder traversal of a BST encounters nodes in increasing order 4 2 6 1 3 7 5 root

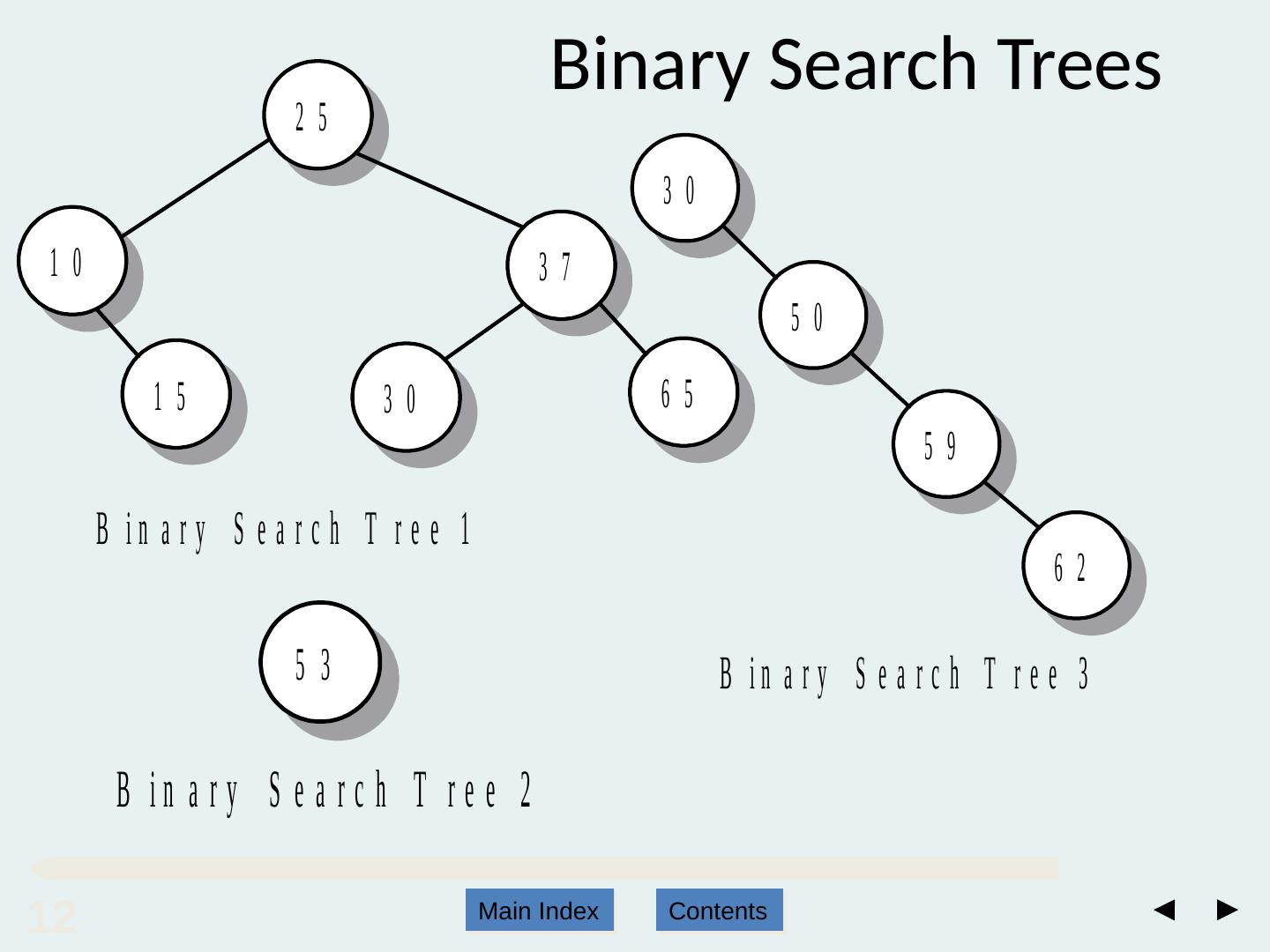
12 .12 12 Main Index Contents Binary Search Trees

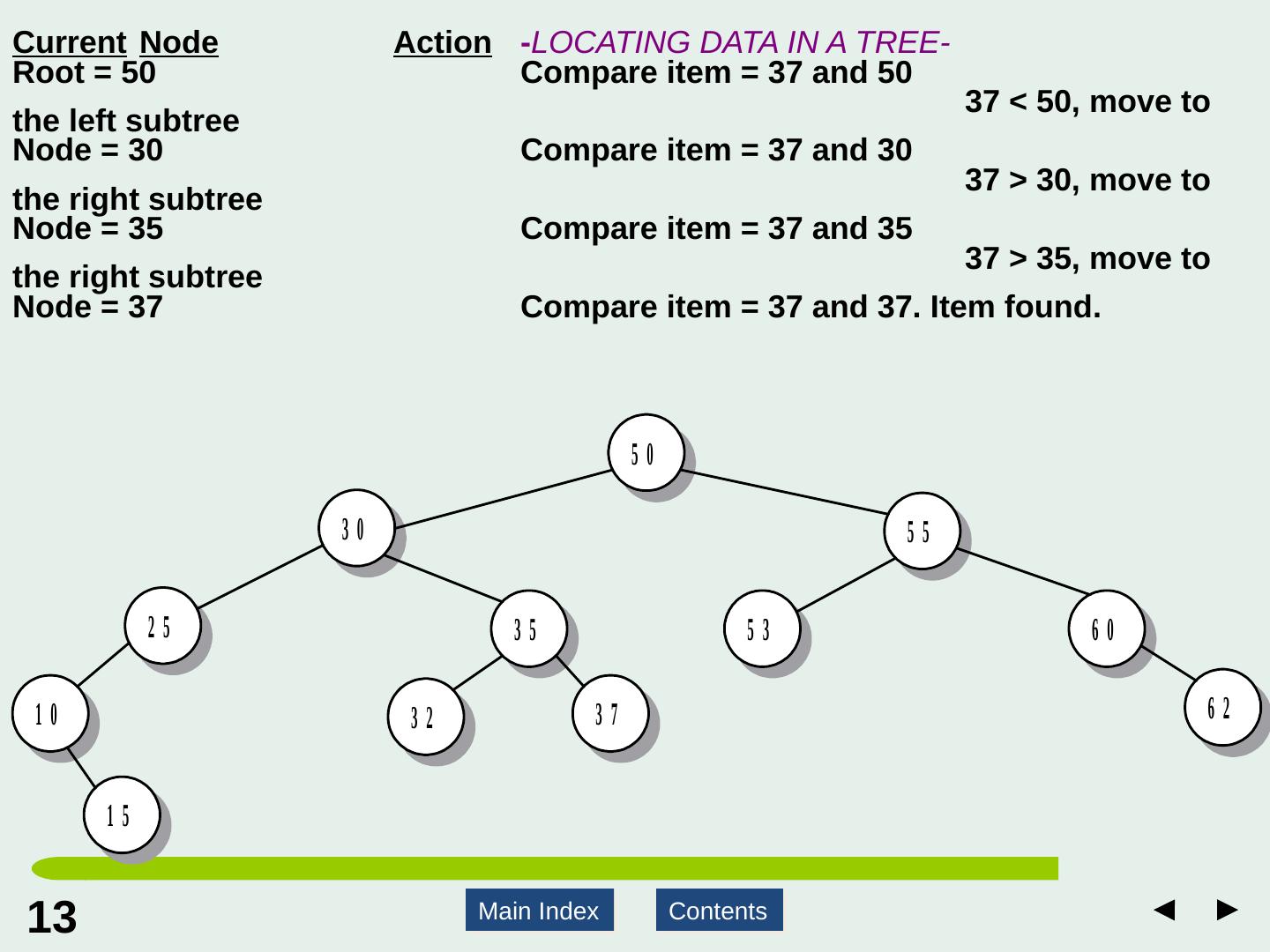
13 .13 13 Main Index Contents Current Node Action - LOCATING DATA IN A TREE- Root = 50 Compare item = 37 and 50 37 < 50, move to the left subtree Node = 30 Compare item = 37 and 30 37 > 30, move to the right subtree Node = 35 Compare item = 37 and 35 37 > 35, move to the right subtree Node = 37 Compare item = 37 and 37. Item found.