03Data Structure and Algorithm---Binary Trees

1 .Binary Trees "A tree may grow a thousand feet tall, but its leaves will return to its roots." -Chinese Proverb

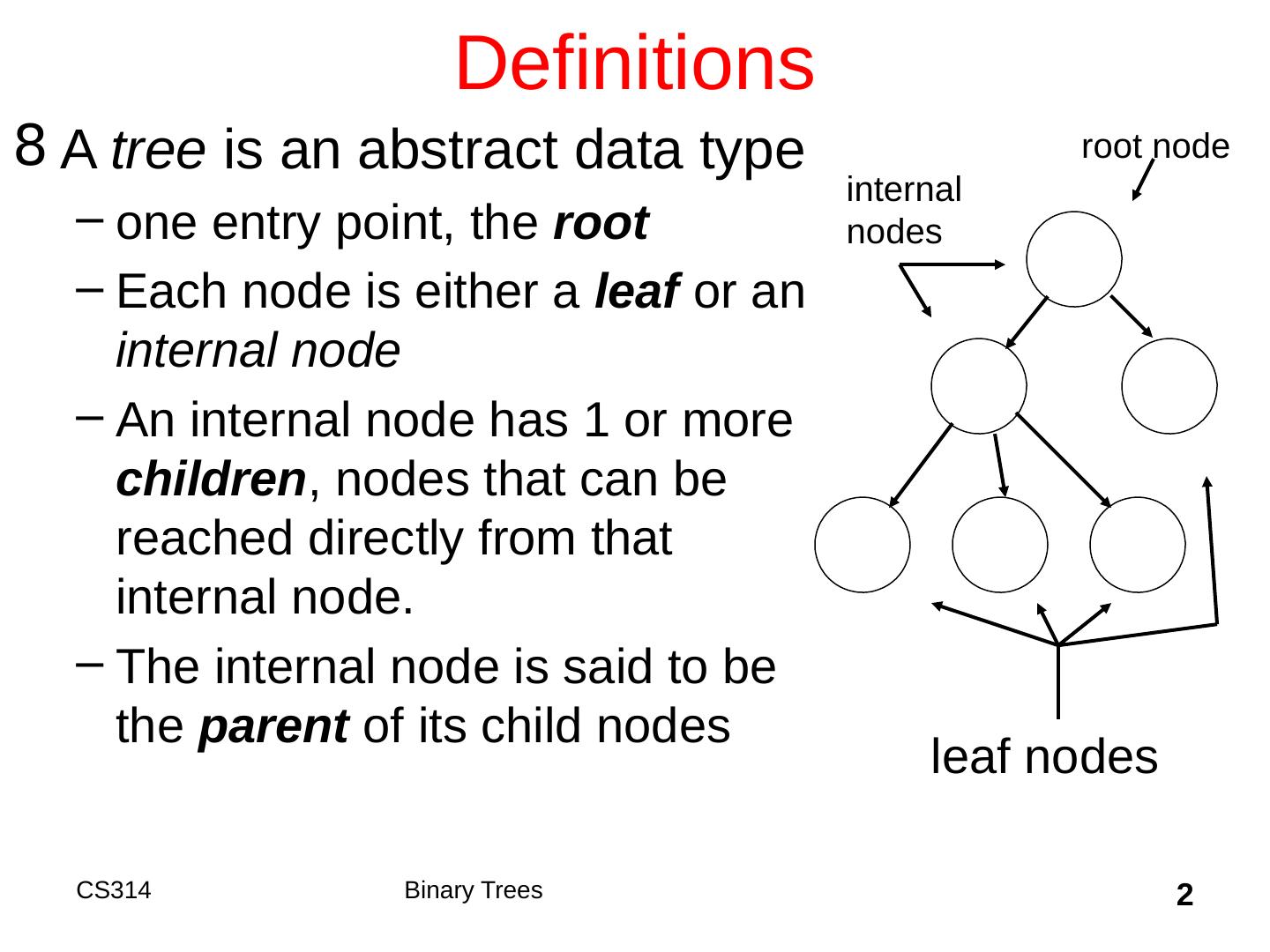
2 .2 Definitions A tree is an abstract data type one entry point, the root Each node is either a leaf or an internal node An internal node has 1 or more children , nodes that can be reached directly from that internal node. The internal node is said to be the parent of its child nodes root node leaf nodes internal nodes Binary Trees CS314

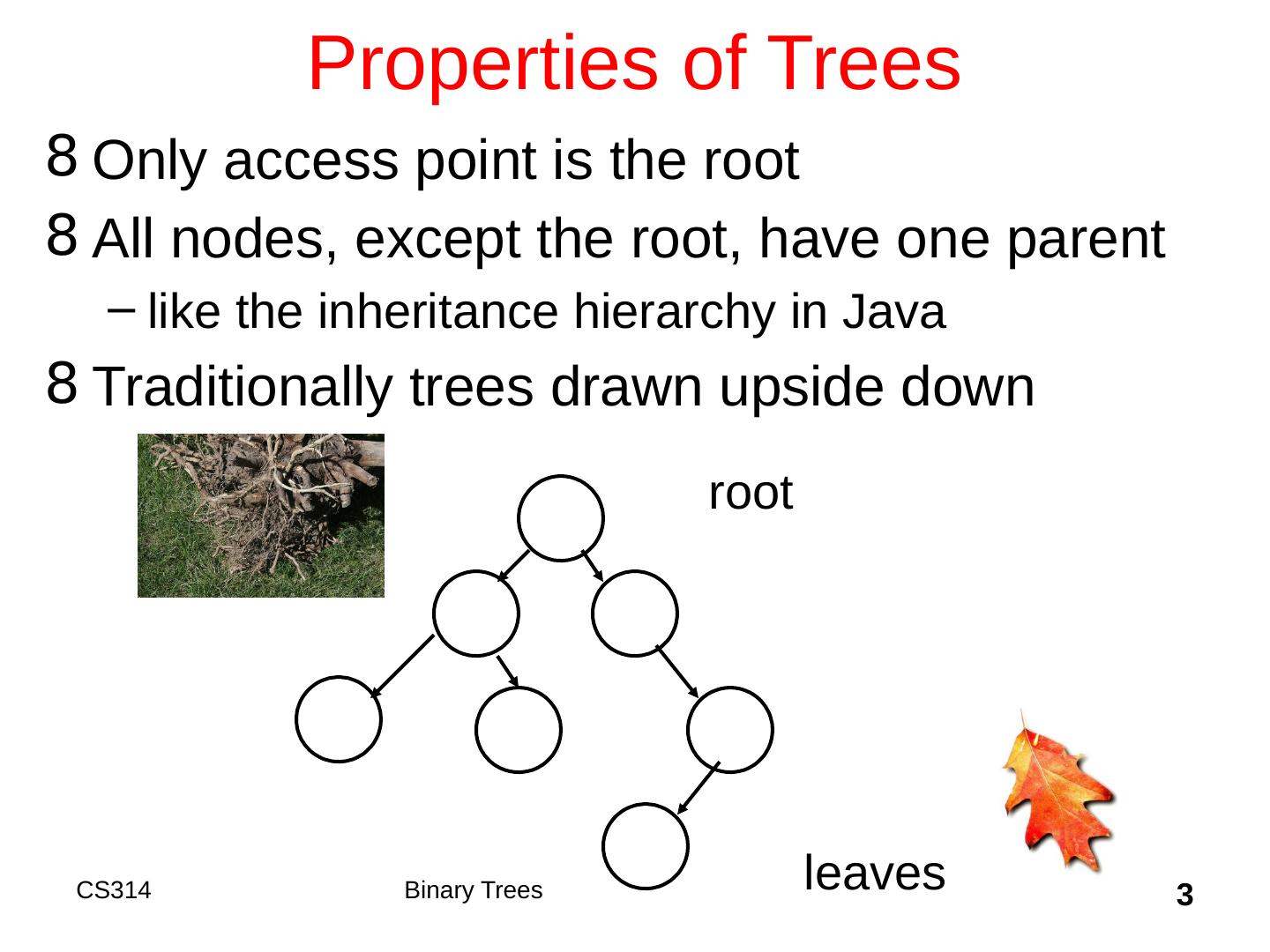
3 .3 Properties of Trees Only access point is the root All nodes, except the root, have one parent like the inheritance hierarchy in Java Traditionally trees drawn upside down root leaves Binary Trees CS314

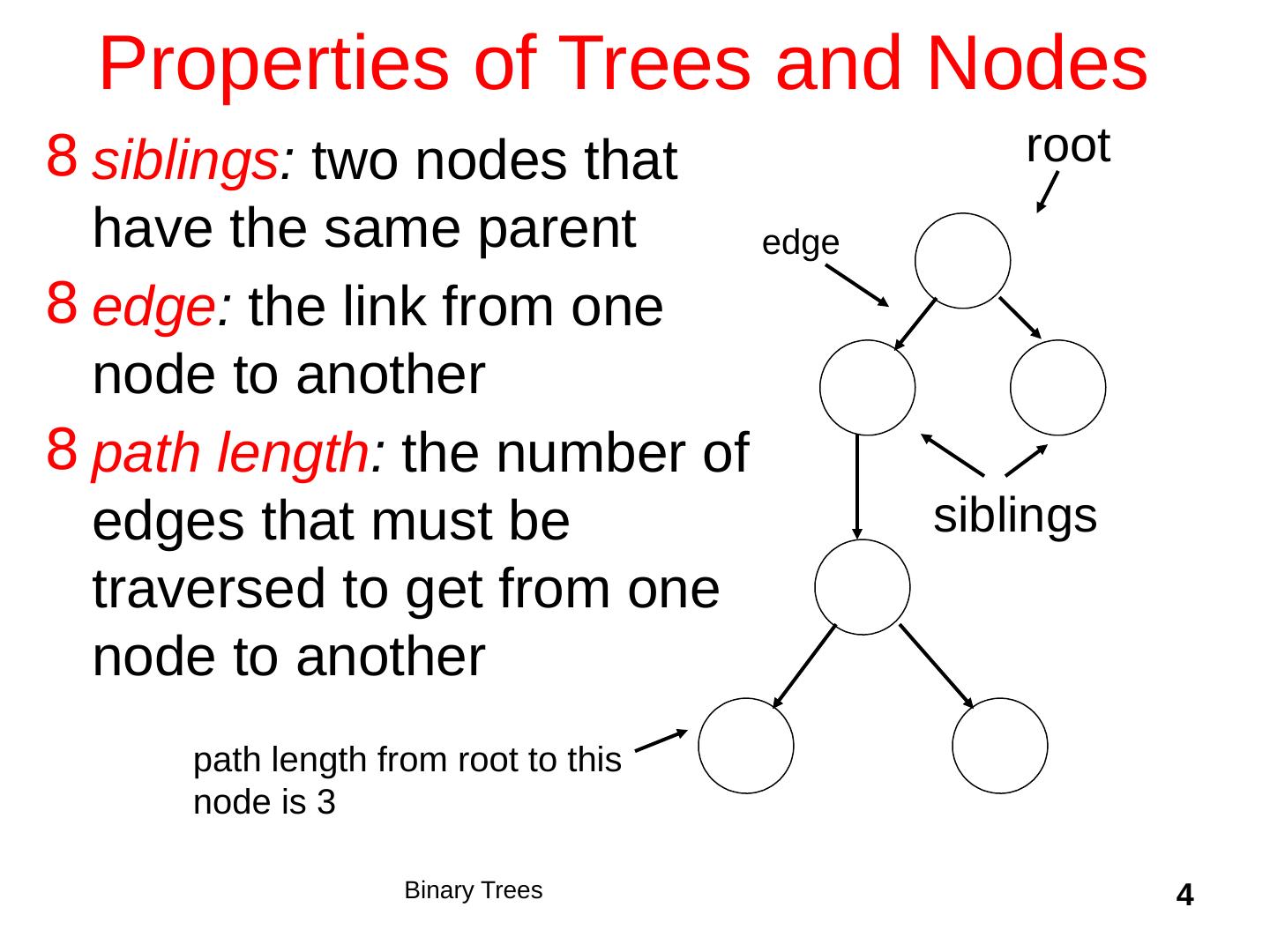
4 .4 Properties of Trees and Nodes siblings : two nodes that have the same parent edge : the link from one node to another path length : the number of edges that must be traversed to get from one node to another root siblings edge path length from root to this node is 3 Binary Trees

5 .5 More Properties of Trees depth : the path length from the root of the tree to this node height of a node: The maximum distance (path length) of any leaf from this node a leaf has a height of 0 the height of a tree is the height of the root of that tree descendants : any nodes that can be reached via 1 or more edges from this node ancestors: any nodes for which this node is a descendant Binary Trees CS314

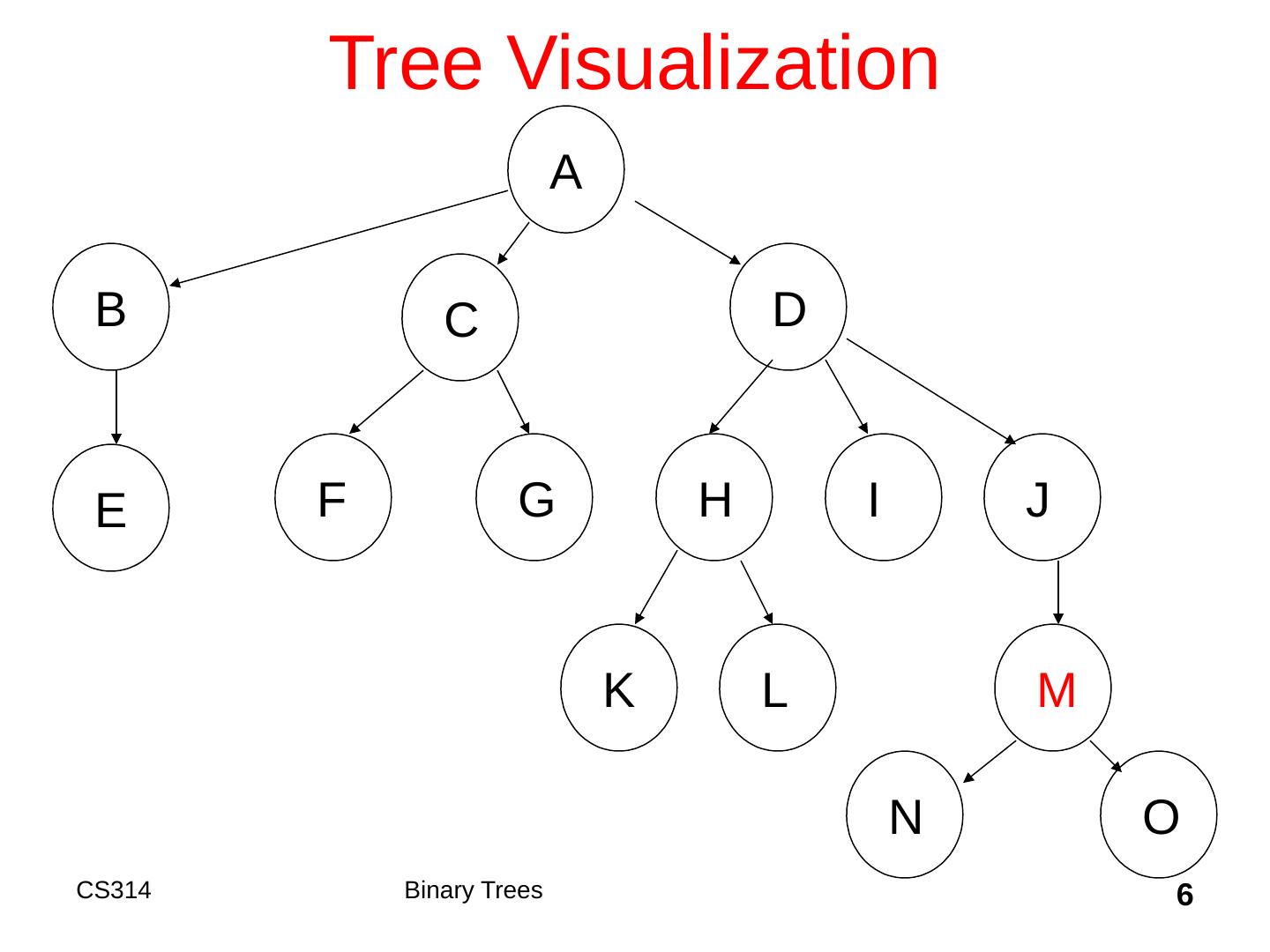
6 .6 Tree Visualization D B C F E A G H J I K L M N O Binary Trees CS314

7 .Clicker Question 1 What is the depth of the node that contains M on the previous slide? 0 1 2 3 4 7 Binary Trees CS314

8 .8 Binary Trees There are many variations on trees but we will start with binary trees binary tree: each node has at most two children the possible children are usually referred to as the left child and the right child parent left child right child Binary Trees CS314

9 .9 Full Binary Tree full binary tree: a binary tree is which each node was exactly 2 or 0 children Binary Trees CS314

10 .10 Complete Binary Tree complete binary tree: a binary tree in which every level, except possibly the deepest is completely filled. At depth n, the height of the tree, all nodes are as far left as possible Where would the next node go to maintain a complete tree? Binary Trees CS314

11 .11 Binary Tree Traversals Many algorithms require all nodes of a binary tree be visited and the contents of each node processed or examined. There are 4 traditional types of traversals preorder traversal: process the root, then process all sub trees (left to right) in-order traversal: process the left sub tree, process the root, process the right sub tree post order traversal: process the left sub tree, process the right sub tree, then process the root level order traversal: starting from the root of a tree, process all nodes at the same depth from left to right, then proceed to the nodes at the next depth. Binary Trees CS314

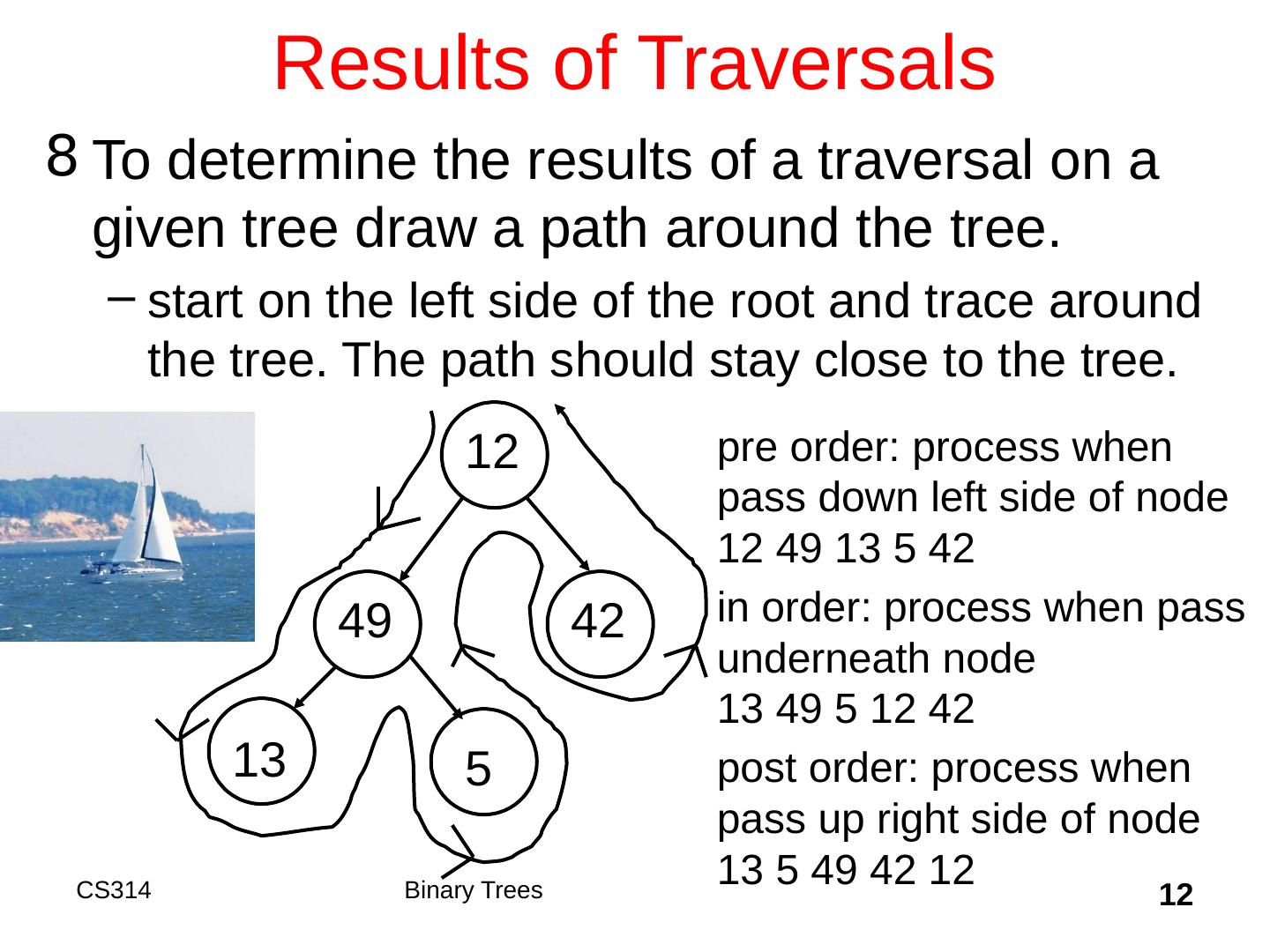
12 .12 Results of Traversals To determine the results of a traversal on a given tree draw a path around the tree. start on the left side of the root and trace around the tree. The path should stay close to the tree. 12 49 42 5 13 pre order: process when pass down left side of node 12 49 13 5 42 in order: process when pass underneath node 13 49 5 12 42 post order: process when pass up right side of node 13 5 49 42 12 Binary Trees CS314