- 快召唤伙伴们来围观吧
- 微博 QQ QQ空间 贴吧
- 文档嵌入链接
- 复制
- 微信扫一扫分享
- 已成功复制到剪贴板
09数据结构---排序
展开查看详情
1 . 第九章 排序 东南大学计算机学院 方效林 方效林 本课件借鉴了清华大学殷人昆老师 和哈尔滨工业大学张岩老师的课件
2 . 本章主要内容 排序的概念 插入排序 顺序插入排序 折半插入排序 希尔排序 快速排序 选择排序 归并排序 分配排序 内部排序算法分析 2
3 . 排序的概念 定义 将一组杂乱无章的数据按一定规律顺次排列 数据表 (dataList)dataList) 待排序数据元素的有限集合 排序码 (dataList)key)) 通常数据元素有多个属性,作为排序依据的属性称 为排序码 学生成绩表,按学号小到大排序,按成绩高到低排序 3
4 . 排序的概念 排序的稳定性 两数据元素排序码相同,排序前后两元素先后顺序 初始 2(dataList)c) 1(dataList)a) 3(dataList)d) 2(dataList)b) 若相同,则是稳定的 若不同,则不稳定 排序 1 1(dataList)a) 2(dataList)b) 2(dataList)c) 3(dataList)d) 稳定的 内排序和外排序 排序 2 1(dataList)a) 2(dataList)c) 2(dataList)b) 3(dataList)d) 不稳定 内排序 所有元素都在存在内存的排序 外排序 数据太多,内存放不下,而存放在外部存储器,排序 时需要经常在内、外存之间读写数据 4
5 . 排序的概念 排序的时间开销 内排序一般用数据比较次数和数据移动次数衡量 外排序一般用外存的读写次数衡量 (dataList) 外存慢 ) 排序的空间开销 执行排序算法需要的存储空间 5
6 . 顺序插入排序 顺序插入排序算法 将待排序元素,从后向前寻找适当的插入位置,直 到所有元素都插入为止 初始 21 25 49 25* 16 08 第1步 21 25 49 25* 16 08 插入 25 , 25 ≥ 21 ,无需移动 第2步 21 25 49 25* 16 08 插入 49 , 49 ≥ 25 ,无需移动 第3步 21 25 49 25* 16 08 插入 25* , 25* < 49 , 21 25 25* 49 16 08 49 后移, 25* 填入 第4步 21 25 25* 49 16 08 插入 16 , 16 < 49,25*,25,21 , 16 21 25 25* 49 08 49,25*,25,21 后移, 16 填入 第5步 16 21 25 25* 49 08 插入 08 , 08 < 49,25*,25,21,16 , 08 16 21 25 25* 49 49,25*,25,21,16 后移, 08 填入 6
7 . 顺序插入排序 算法分析 最好情况 (dataList)n 个元素 ) 原数据是按小到大顺序排好的 每步只需与前一个数据比较一次,而不用移动数据 总比较次数 n-1 ,总移动次数 0 最坏情况 (dataList)n 个元素 ,i=0,1,…,n-1) 原数据按大到小顺序排好的 元素 i 需要比较 i 次,每比较 1 次移动 1 次,元素 i 移 动2次 n 1 temp = a[i] 总比较次数和总移动次数 KCN i n(n 1)/2 n /2, 2 a[0] = temp i 1 n 1 比较和移动最坏最好平均值约为 n2/4 2 RMN (i 2) (n 4)(n 1)/2 n /2 i 1 时间复杂度 O(dataList)n2)
8 . 顺序插入排序 算法分析 是稳定的算法, key) 相同元素原来的顺序不会打 乱 初始 21 25 49 25* 16 08 排序后 08 16 21 25 25* 49 需要额外一个存储空间 temp = a[i] a[0] = temp 8
9 . 折半插入排序 折半插入排序算法 将待排序元素,按折半搜索法寻找适当的插入位置 ,直到所有元素都插入为止 0 1 2 3 4 5 0 1 2 3 4 5 16 21 25 25* 49 23 16 21 25 25* 49 23 low mid high mid high low mid>23,high=mid-1,mid=(dataList)low+high)/2 0 1 2 3 4 5 low>high , 49,25*,25 后移, 23 填入 16 21 25 25* 49 23 16 21 23 25 25* 49 low mid high mid≤23,low=mid+1,mid=(dataList)low+high)/2 0 1 2 3 4 5 16 21 25 25* 49 23 low mid high 9 mid≤23,low=mid+1,mid=(dataList)low+high)/2
10 . 折半插入排序 算法分析 平均情况下,折半搜索比顺序搜索快 搜索元素 i 需比较 log2i +1 次 总比较次数 n 1 ( log i 1) 1 2 2 3 3 k k k i 1 2 20 21 22 2k 1 1 * 2 0 2 * 2 1 3 * 2 2 k * 2 k 1 (k - 1) * 2 k 1 n * (log 2 n - 1) 1 n * log 2 n n 1 移动的时间复杂度 O(dataList)n2) 比较的时间复杂度 O(dataList)n*log2n) 是稳定的排序算法,需额外一个存储空间 10
11 . 希尔排序 基本思想 设定不同 gap 值,距离 gap 的元素放一起插入排 初始序 21 25 49 25* 16 08 第1步 21 25 49 25* 16 08 gap= n/3+1 = 3 21 25 49 25* 16 08 21 25 49 25* 16 08 结果 21 16 08 25* 25 49 第2步 21 16 08 25* 25 49 gap= gap/3+1 = 2 21 16 08 25* 25 49 结果 08 16 21 25* 25 49 第3步 08 16 21 25* 25 49 gap= gap/3+1 = 1 结果 08 16 21 25* 25 49 最后 1 步是 n 个元素进行插入排序 11 是不是很慢?
12 . 希尔排序 算法分析 设定不同 gap 值,距离 gap 的元素放一起插入排序 gap 值越来越小,由于前面的排序过程,使得大多数数 据已经基本有序,因此希尔排序速度仍然很快 gap 的取值方法有很多种 gap= gap/3+1 gap= gap/2 …… 希尔排序复杂度分析很困难,还没有完整的数学分析 统计得出,平均比较和移动次数在 [n1.25,1.6n1.25] 内 是不稳定的排序算法 12
13 . 快速排序 基本思想 Partition :任取一元素任取一元素 x 为基准 (dataList) 如选第 1 个 ) , 小于 x 的元素放在 x 左边,大于等于 x 的元素放 在 x 右边 初始对左、右部分递归执行上一步骤直至只有一个元素 21 25 49 25* 16 08 第1层 08 16 21 25* 25 49 选 21 为基准 第2层 08 16 21 25* 25 49 左部选 08 ,右部选 25* 为基准 第3层 08 16 21 25* 25 49 左部选 16 ,右部选 25 为基准 第4层 08 16 21 25* 25 49 右部选 49 为基准 13
14 . 快速排序 Partition(dataList)low,high) 初始时基准坐标 p = low, x=a[low]=21 从 i=low+1 位置开始判断,比 x 小的元素与 p 下 一个位置交换, p 自加 1 循环直至 i > high ,最后 a[low] 与 a[p] 交换 21 25 49 25* 16 08 21 16 49 25* 25 08 i i p p a[i] 与 a[p+1] 交换 , p++ a[i] 与 a[p+1] 交换 , p++ 21 16 08 25* 25 49 08 16 21 25* 25 49 i>high, 停止 p p 14 a[low] 与 a[p] 交换
15 .作业:任取一元素 对数据 a[N] 进行快速排序的程序 qsort(dataList)a[ ], 0, n-1) 15
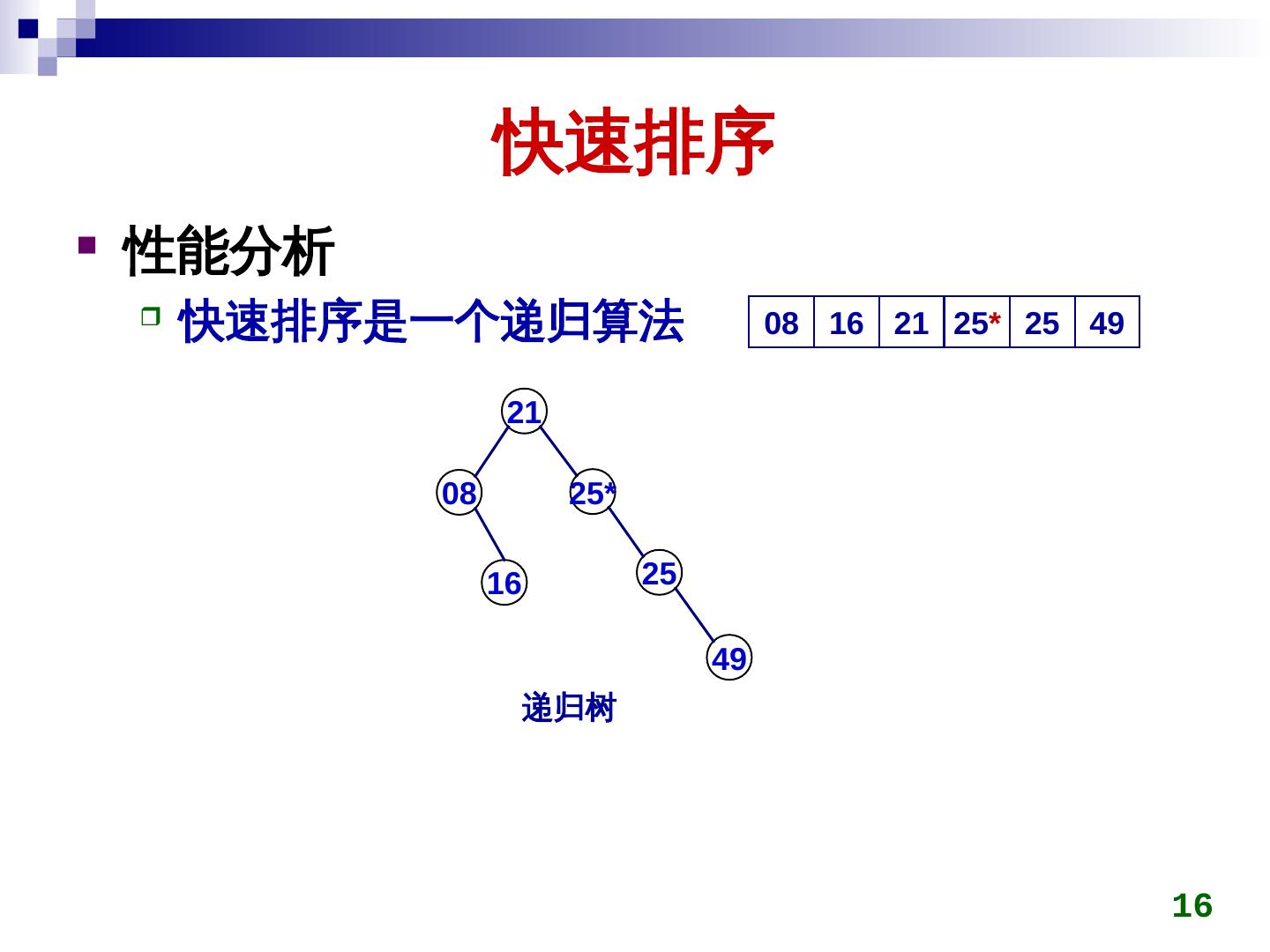
16 . 快速排序 性能分析 快速排序是一个递归算法 08 16 21 25* 25 49 21 08 25* 16 25 49 递归树 16
17 . 21 快速排序 08 25* 性能分析 16 25 快速排序的趟数取决于递归树的深度 49 若每次选取的基准可将序列划分成长度相近的左、 右两部分,则下一层将对两个长度减半的序列排序 设原序列有 n 个元素,选基准和划分所需时间为 O(dataList)n) 设整个快速排序所需时间为 T(dataList)n) ,则有:任取一元素 T(dataList)n) ≤ cn + 2T(dataList)n/2) // c 是一个常数 ≤ cn + 2(dataList)cn/2 + 2T(dataList)n/4)) = 2cn + 4T(dataList)n/4) ≤ 2cn + 4(dataList)cn/4 +2T(dataList)n/8)) = 3cn + 8T(dataList)n/8) ……… ≤ cn log2n + nT(dataList)1) = O(dataList)nlog2n ) 17
18 . 快速排序 性能分析 快速排序平均计算时间为 O(dataList)nlog2n) 平均计算时间是所有内部排序方法中最好的 递归算法每层需保存递归调用的指针和参数 平均情况下 最大递归层数为 log2(dataList)n+1) 存储开销为 O(dataList)log2n) 18
19 . 08 16 快速排序 21 性能分析 25* 最坏情况 25 单枝树,每次划分只得到比上一次少一个元素的序列 49 比较次数 n 1 1 n2 (n i) 2 n(n 1) 2 i 1 递归树有 n 层,存储开销为 O(dataList)n) 快速排序是不稳定的算法 19
20 . 快速排序 改进算法 快速排序对长度很小的序列排序并不比直接插入快 长度取 5~25 时,直接插入法比快速排序法快 10% 改进方法 1 :任取一元素 在快速排序递归过程中,当序列长度小于一定值时,使 用直接插入排序法 改进方法 2 :任取一元素 在快速排序递归过程中,当序列长度小于一定值时,退 出排序 得到一个整体上几乎已经排好序的序列 对这个几乎已经排好序的序列使用直接插入排序法 20
21 . 快速排序 改进算法 基准元素的选取对算法性能有很大影响 改进方法 1 :任取一元素 可随机选择一个元素作为基准,避免最坏情况发生 改进方法 2 :任取一元素 取左端点、右端点、中点 (dataList)mid=(dataList)left+right)/2) 这三 个元素中的中间值作为基准 21 25 49 25* 16 35 08 左端点 中点 右端点 取 21 , 25* , 08 三个元素中的 21 为基准 21
22 . 选择排序 直接选择排序 在待排序序列中选择最小的元素 x x 与第一个元素对换 剔除 x ,对剩下元素执行以上步骤 初始 21 25 49 25* 16 08 第1步 08 25 49 25* 16 21 第2步 08 16 49 25* 25 21 第3步 08 16 21 25* 25 49 第4步 08 16 21 25* 25 49 第5步 08 16 21 25* 25 49 22
23 . 选择排序 直接选择排序 算法分析 设有 n 个元素,第 i 趟比较次数为 n-i-1 次 总比较次数为 n 2 n(n 1) KCN (n i 1) i 0 2 移动次数 最好情况为 0 最坏情况为 3(dataList)n-1) 直接选择排序是不稳定算法 23
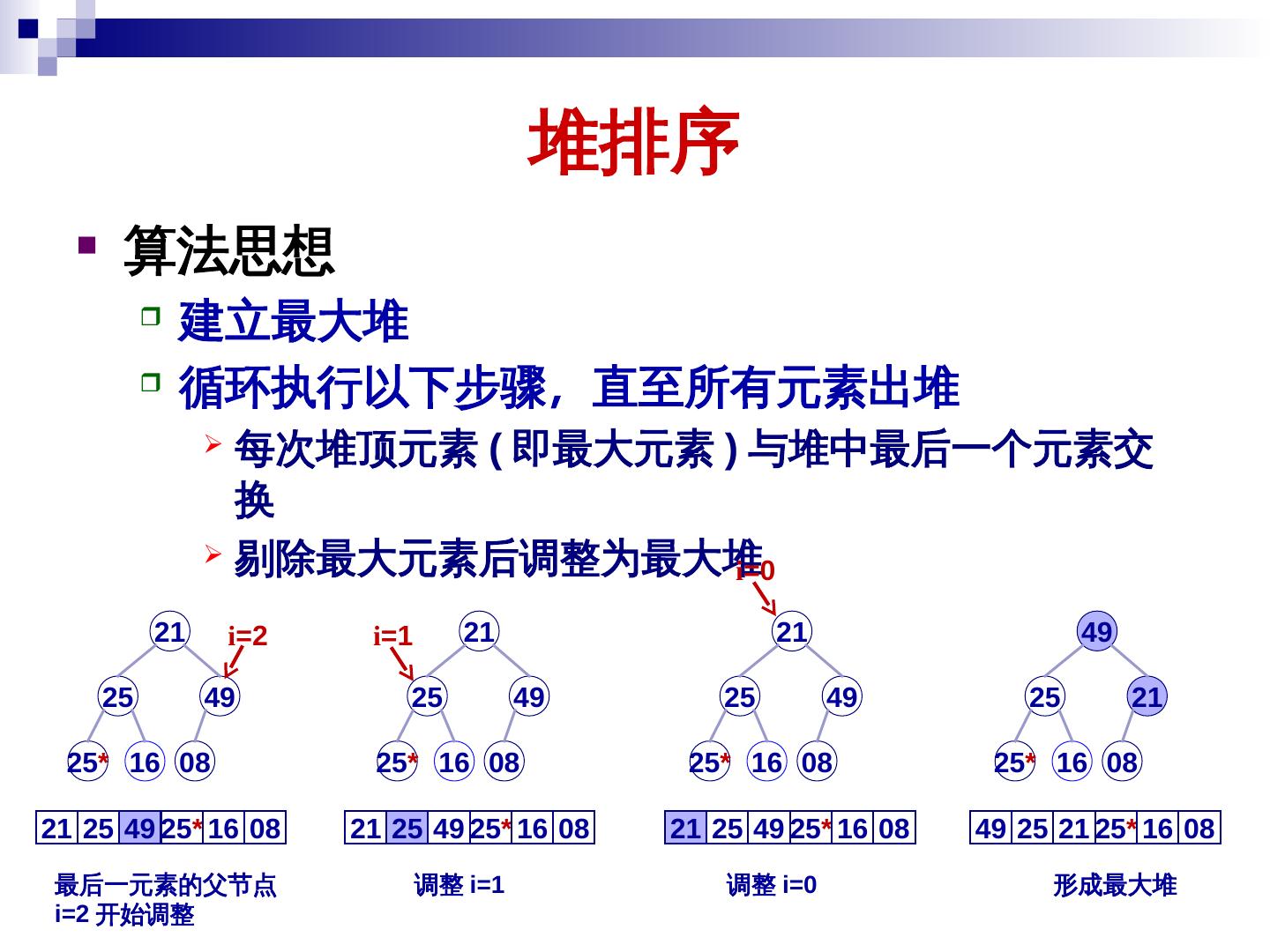
24 . 堆排序 算法思想 建立最大堆 循环执行以下步骤,直至所有元素出堆 每次堆顶元素 (dataList) 即最大元素 ) 与堆中最后一个元素交 换 剔除最大元素后调整为最大堆 i=0 21 i=2 i=1 21 21 49 25 49 25 49 25 49 25 21 25* 16 08 25* 16 08 25* 16 08 25* 16 08 21 25 49 25* 16 08 21 25 49 25* 16 08 21 25 49 25* 16 08 49 25 21 25* 16 08 最后一元素的父节点 调整 i=1 调整 i=0 形成最大堆 i=2 开始调整
25 . 堆排序 算法思想 建立最大堆 循环执行以下步骤,直至所有元素出堆 每次堆顶元素 (dataList) 即最大元素 ) 与堆中最后一个元素交 换 剔除最大元素后调整为最大堆 49 25 25* 25 21 25* 21 16 21 25* 16 08 08 16 49 08 25 49 49 25 21 25* 16 08 25 25* 21 08 16 49 25* 16 21 08 25 49 堆顶 49 与堆尾 08 交换 堆顶 25 与堆尾 16 交换 堆顶 25* 与堆尾 08 交换 虚线内调整为最大堆 虚线内调整为最大堆 虚线内调整为最大堆
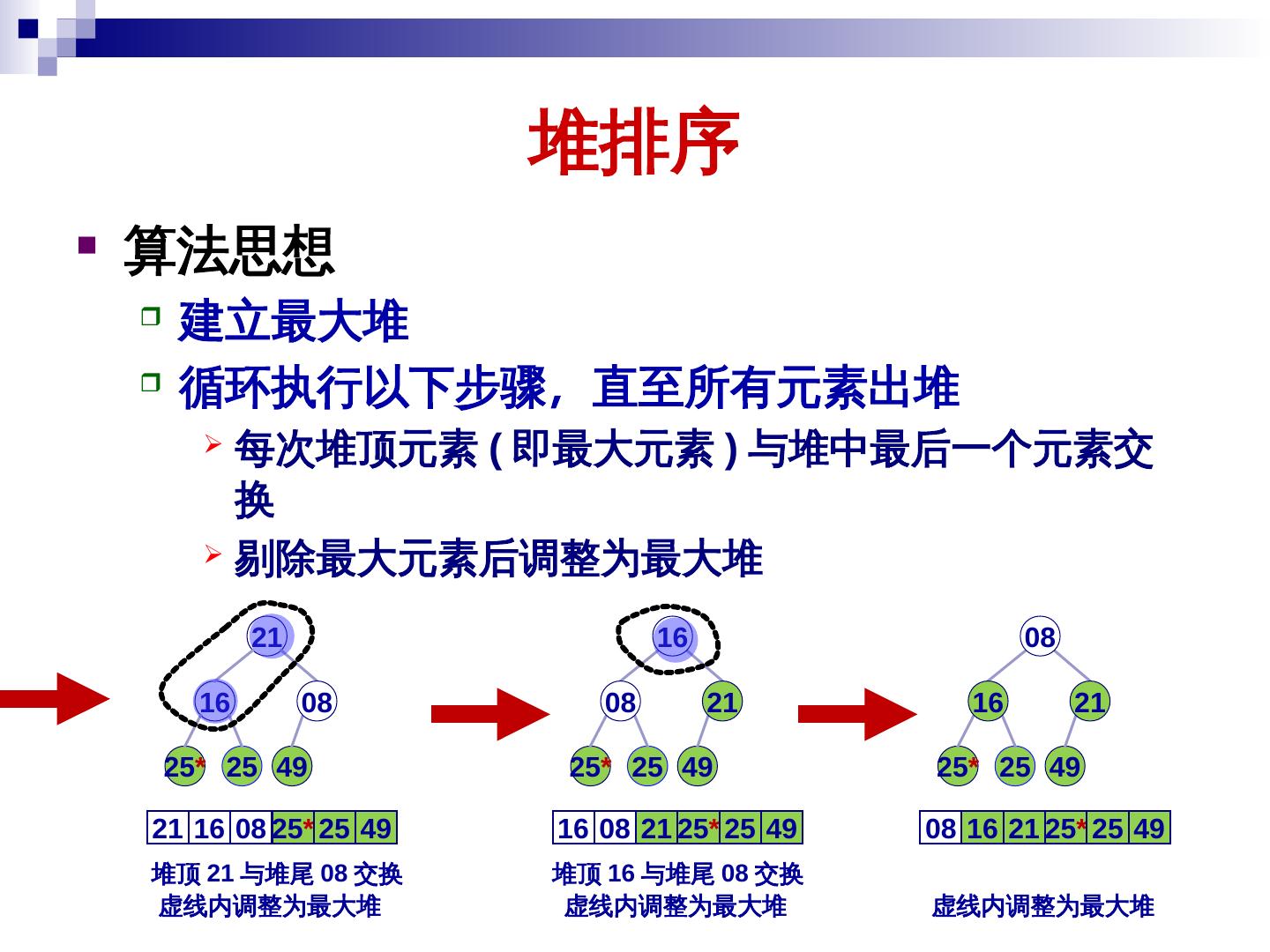
26 . 堆排序 算法思想 建立最大堆 循环执行以下步骤,直至所有元素出堆 每次堆顶元素 (dataList) 即最大元素 ) 与堆中最后一个元素交 换 剔除最大元素后调整为最大堆 21 16 08 16 08 08 21 16 21 25* 25 49 25* 25 49 25* 25 49 21 16 08 25* 25 49 16 08 21 25* 25 49 08 16 21 25* 25 49 堆顶 21 与堆尾 08 交换 堆顶 16 与堆尾 08 交换 虚线内调整为最大堆 虚线内调整为最大堆 虚线内调整为最大堆
27 . 堆排序 堆排序算法分析 建立最大堆 设堆中有 n 个元素 , 对应完全二叉树有 k 层 (dataList)2k-1≤n < 2k) 第 i 层向下调整移动距离最大为 k 1 (dataList)k-i), 第 i 层节点数为 2i-1 2 2 i -1 k i O(n ) i 1 总移动次数 循环弹出堆顶元素 执行 n-1 次向下调整,每次调整距离 log2(dataList)n+1) 总调整时间 O(dataList)nlog n) 堆排序算法的计算时间复杂度为 2 O(dataList)nlog2n) 是不稳定排序
28 . 归并排序 算法思想 将序列分成两个长度相等的子序列 分别对两个子序列排序 将排好序的两个子序列合并 21 25 49 25* 16 08 31 41 08 16 21 25 25* 31 41 49 21 25 49 25* 16 08 31 41 21 25 25* 49 08 16 31 41 21 25 49 25* 16 08 31 41 21 25 25* 49 08 16 31 41 21 25 49 25* 16 08 31 41 21 25 49 25* 16 08 31 41 28
29 . 归并排序 算法分析 计算时间包括 对两个子序列分别排序时间 归并的时间 T(dataList)n) = cn+2T(dataList)n/2) = O(dataList)nlog2n) 最好、最坏、平均时间复杂度均为 O(dataList)nlog2n) 是稳定排序 29