08数据结构---搜索结构

1 .第七章 搜索结构 东南大学计算机学院 方效林 方效林 本课件借鉴了清华大学殷人昆老师 和哈尔滨工业大学张岩老师的课件 

2 . 本章主要内容  搜索的概念  静态搜索结构  顺序搜索  有序顺序表  顺序搜索  折半搜索  斐波那契搜索  二叉搜索树 2 

3 . 搜索的概念  在数据集合中寻找满足某种条件的数据元素  搜索可能成功  也可能不成功  可唯一标识一个元素的属性称为关键字 (key)key))  基于关键字的搜索结果是唯一的  基于其他属性的搜索结果可能不唯一  衡量搜索算法时间效率的标准  平均比较次数，或平均搜索长度 (key)ASL)) 3 

4 . 顺序搜索  从表头 (key) 或尾 ) 开始，依次用各对象的关键字 与给定值 x 比较  若值相等，搜索成功，返回下标  若整个表都未找到，搜索失败 搜索成功的平均搜索长度： n -1 n -1 pi: 搜索第 i 个元素概率 ASL succ   i 0 pi  c i . 其 中(  pi  1 ) i 0 ci: 搜索到第 i 个元素所需比较次数 n -1 1 1 n ( n  1) n  1 pi=1/n ASLsucc   ( i  1)    . i 0 n n 2 2 ci=i+1 n 个元素 搜索不成功的平均搜索长度 … ASLunsucc = n+1 4 

5 . 有序顺序表  顺序搜索  从表头 (key) 或尾 ) 开始，依次用各对象的关键字与给 定值 x 比较  若值相等，搜索成功，返回下标  若 x 比关键字大时，搜索失败 搜索成功的平均搜索长度： n -1 1 1 n ( n  1) n  1 ASLsucc   ( i  1)    . i 0 n n 2 2 n 个元素， n+1 个空档 搜索不成功的平均搜索长度 … 1  n -1  1  n ( n  1)  ASLunsucc   n   ( i  1)   n   n 1  i 0  n 1  2  5 

6 . 有序顺序表 搜索 40 0 1 2 3 4 5  折半搜索 10 20 30 40 50 60  low=0, high=n-1,mid=(low+high)/2 low mid high  x 先和 mid 元素比较 40>30  若相等，搜索成功，返回下标 0 1 2 3 4 5  若 x 更小，继续在前半部分搜索 10 20 30 40 50 60  high=mid-1, mid=(key)low+high)/2  若 x 更大，继续在后半部分搜索 low mid high 40<50  low=mid+1, mid=(key)low+high)/2 0 1 2 3 4 5 10 20 30 40 50 60 low mid high 40=40 搜索成功 6 

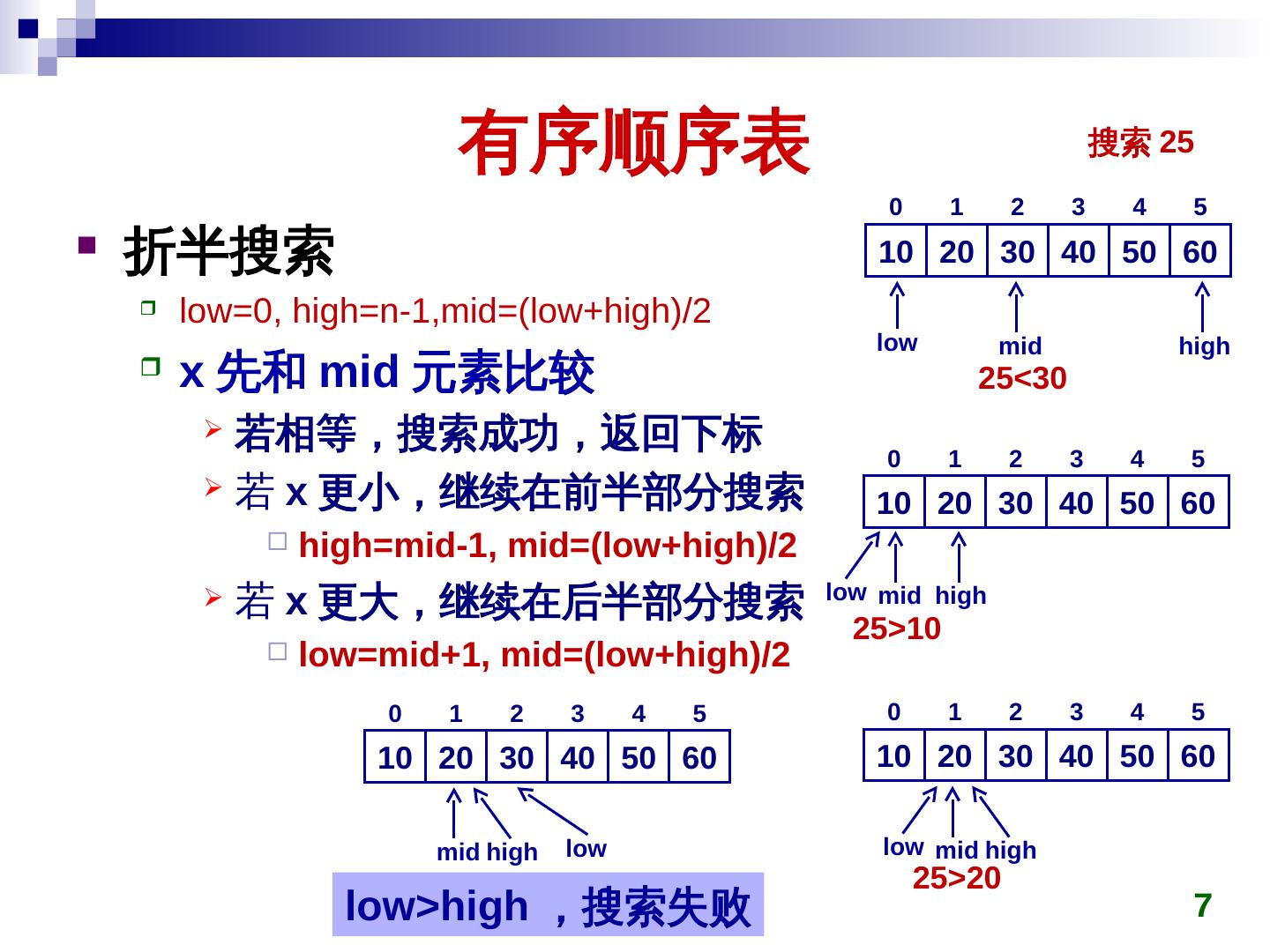
7 . 有序顺序表 搜索 25 0 1 2 3 4 5  折半搜索 10 20 30 40 50 60  low=0, high=n-1,mid=(low+high)/2 low mid high  x 先和 mid 元素比较 25<30  若相等，搜索成功，返回下标 0 1 2 3 4 5  若 x 更小，继续在前半部分搜索 10 20 30 40 50 60  high=mid-1, mid=(key)low+high)/2  若 x 更大，继续在后半部分搜索 low mid high 25>10  low=mid+1, mid=(key)low+high)/2 0 1 2 3 4 5 0 1 2 3 4 5 10 20 30 40 50 60 10 20 30 40 50 60 mid high low low mid high 25>20 low>high ，搜索失败 7 

8 . 有序顺序表 < 30 = > 10 50  折半搜索 < = > < = >  折半搜索构造的判定树 20 < = > 40 60 < = > < = >  设满二叉树 n=2h-1  则有 2h=n+1 ， h=log2(key)n+1)  平均搜索长度 1 ASLsucc  (1 * 20  2 * 21  3 * 2 2    ( h  1) * 2 h  2  h * 2 h - 1 ) n 错位相减法 1  (( h  1)  2 h  1) n n1  log 2 ( n  1)  1  log 2 ( n  1)  1 n 8 

9 . 有序顺序表  斐波那契搜索 n, n=0,1 F(key)n) = F(key)n-1)+F(key)n-2), n≥2 n 0 1 2 3 4 5 6 7 8 9 10 11 F(key)n) 0 1 1 2 3 5 8 13 21 34 55 89 9 

10 . 有序顺序表 n 0 1 2 3 4 5 6 7 8 9 10 11  斐波那契搜索 F(key)n) 0 1 1 2 3 5 8 13 21 34 55 89  low=1, high=n,mid=F(x-1), F(x) 是最小的≥ n 的斐波那契数  x 先和 mid 元素比较  若相等，搜索成功，返回下标  若 x 更小，继续在前半部分搜索  high=mid-1, mid=low+F(key)x-2)-1  若 x 更大，继续在后半部分搜索  low=mid+1, mid=low+F(key)x-3)-1 1 2 3 4 5 6 7 8 9 10 11 12 10 15 20 25 30 35 40 45 50 55 60 65 low mid high 搜索 25 10 

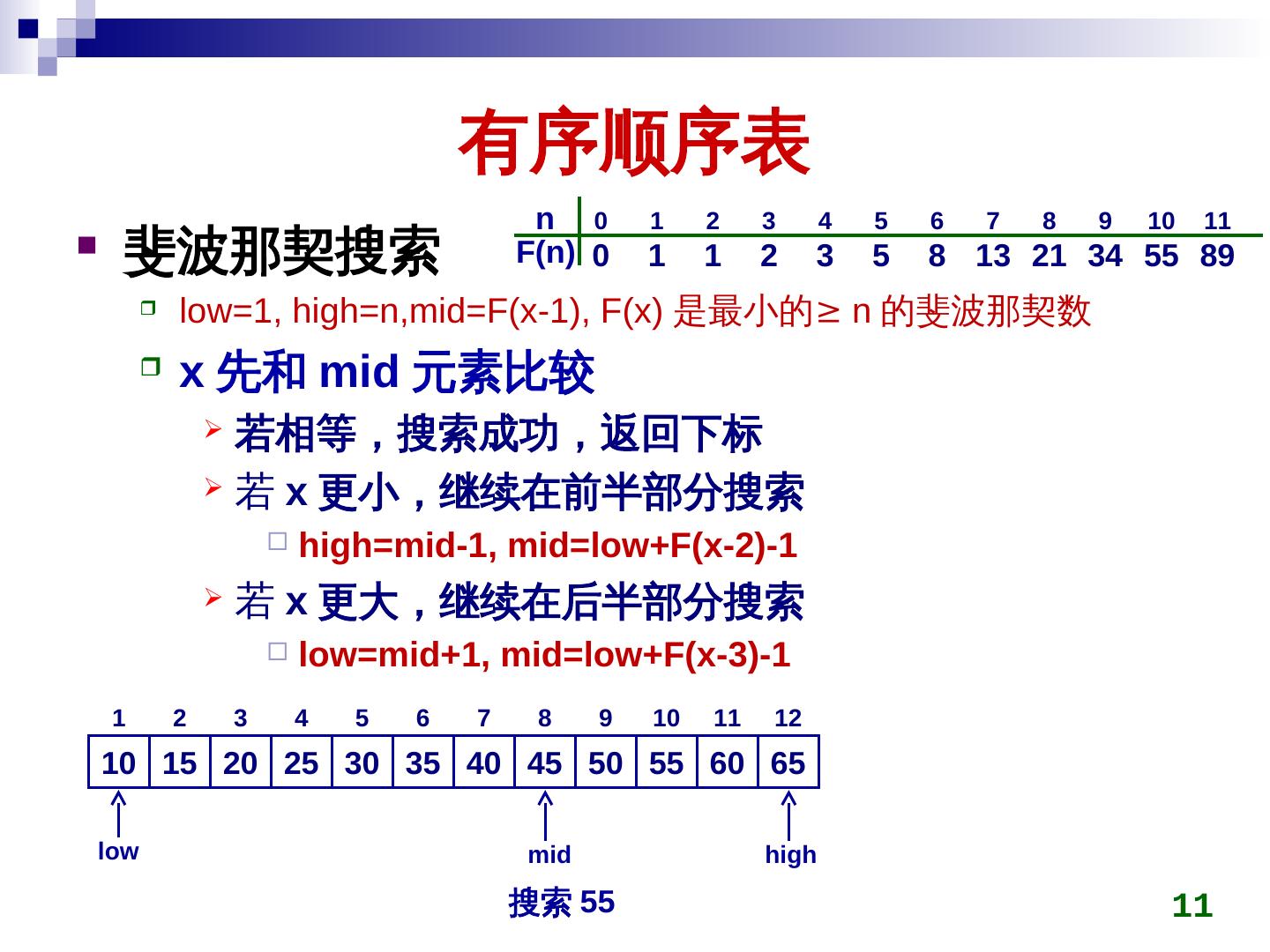
11 . 有序顺序表 n 0 1 2 3 4 5 6 7 8 9 10 11  斐波那契搜索 F(key)n) 0 1 1 2 3 5 8 13 21 34 55 89  low=1, high=n,mid=F(x-1), F(x) 是最小的≥ n 的斐波那契数  x 先和 mid 元素比较  若相等，搜索成功，返回下标  若 x 更小，继续在前半部分搜索  high=mid-1, mid=low+F(key)x-2)-1  若 x 更大，继续在后半部分搜索  low=mid+1, mid=low+F(key)x-3)-1 1 2 3 4 5 6 7 8 9 10 11 12 10 15 20 25 30 35 40 45 50 55 60 65 low mid high 搜索 55 11 

12 . 二叉搜索树  二叉搜索树的概念  或者是空树  或者具有以下性质  每个结点都有一个关键字 (key)key))  左子树上所有结点的 key) 小于根结点的 key)  右子树上所有结点的 key) 大于根结点的 key)  左子树和右子树也是二叉搜索树 12 

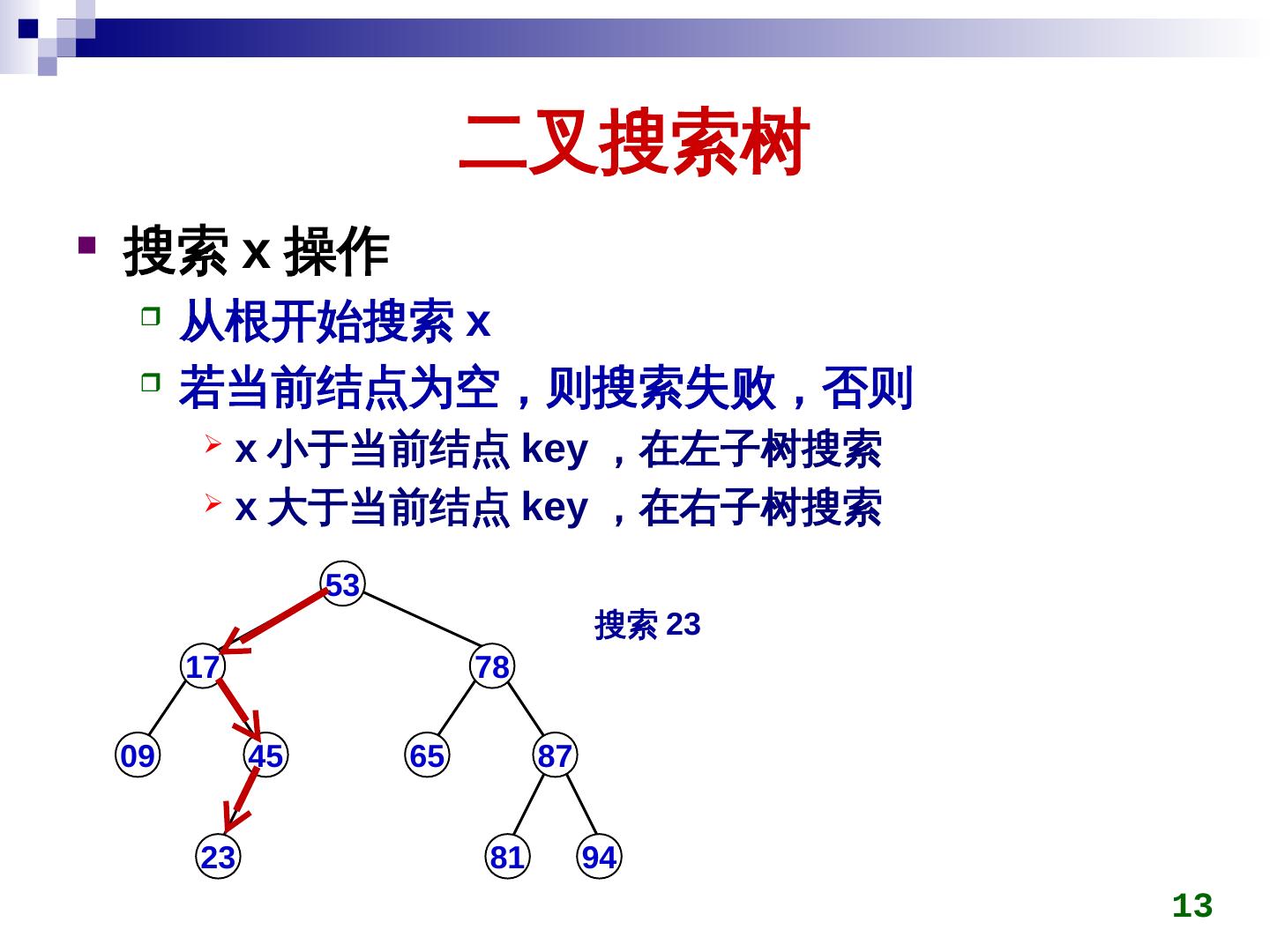
13 . 二叉搜索树  搜索 x 操作  从根开始搜索 x  若当前结点为空，则搜索失败，否则  x 小于当前结点 key) ，在左子树搜索  x 大于当前结点 key) ，在右子树搜索 53 搜索 23 17 78 09 45 65 87 23 81 94 13 

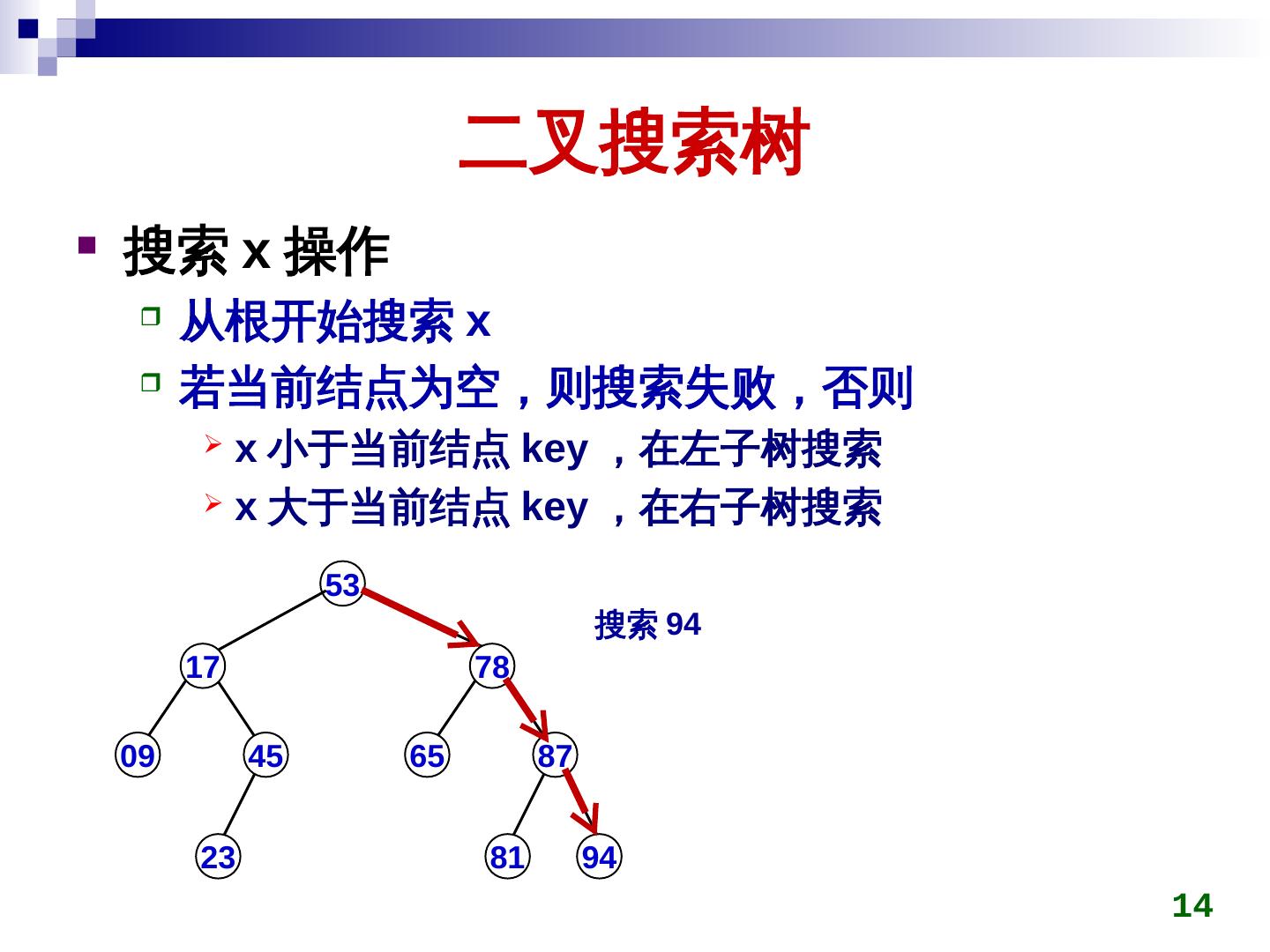
14 . 二叉搜索树  搜索 x 操作  从根开始搜索 x  若当前结点为空，则搜索失败，否则  x 小于当前结点 key) ，在左子树搜索  x 大于当前结点 key) ，在右子树搜索 53 搜索 94 17 78 09 45 65 87 23 81 94 14 

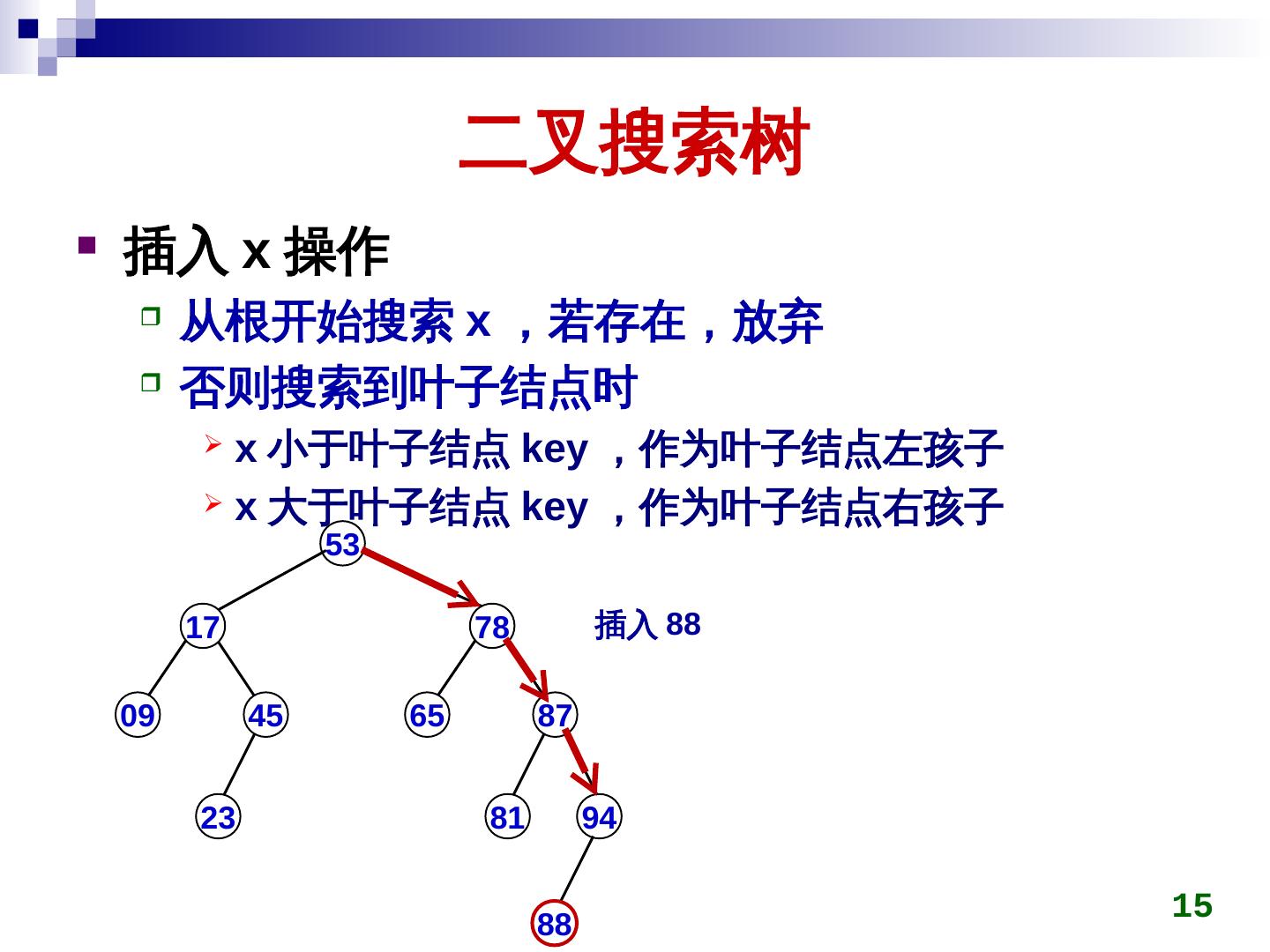
15 . 二叉搜索树  插入 x 操作  从根开始搜索 x ，若存在，放弃  否则搜索到叶子结点时  x 小于叶子结点 key) ，作为叶子结点左孩子  x 大于叶子结点 key) ，作为叶子结点右孩子 53 17 78 插入 88 09 45 65 87 23 81 94 15 88 

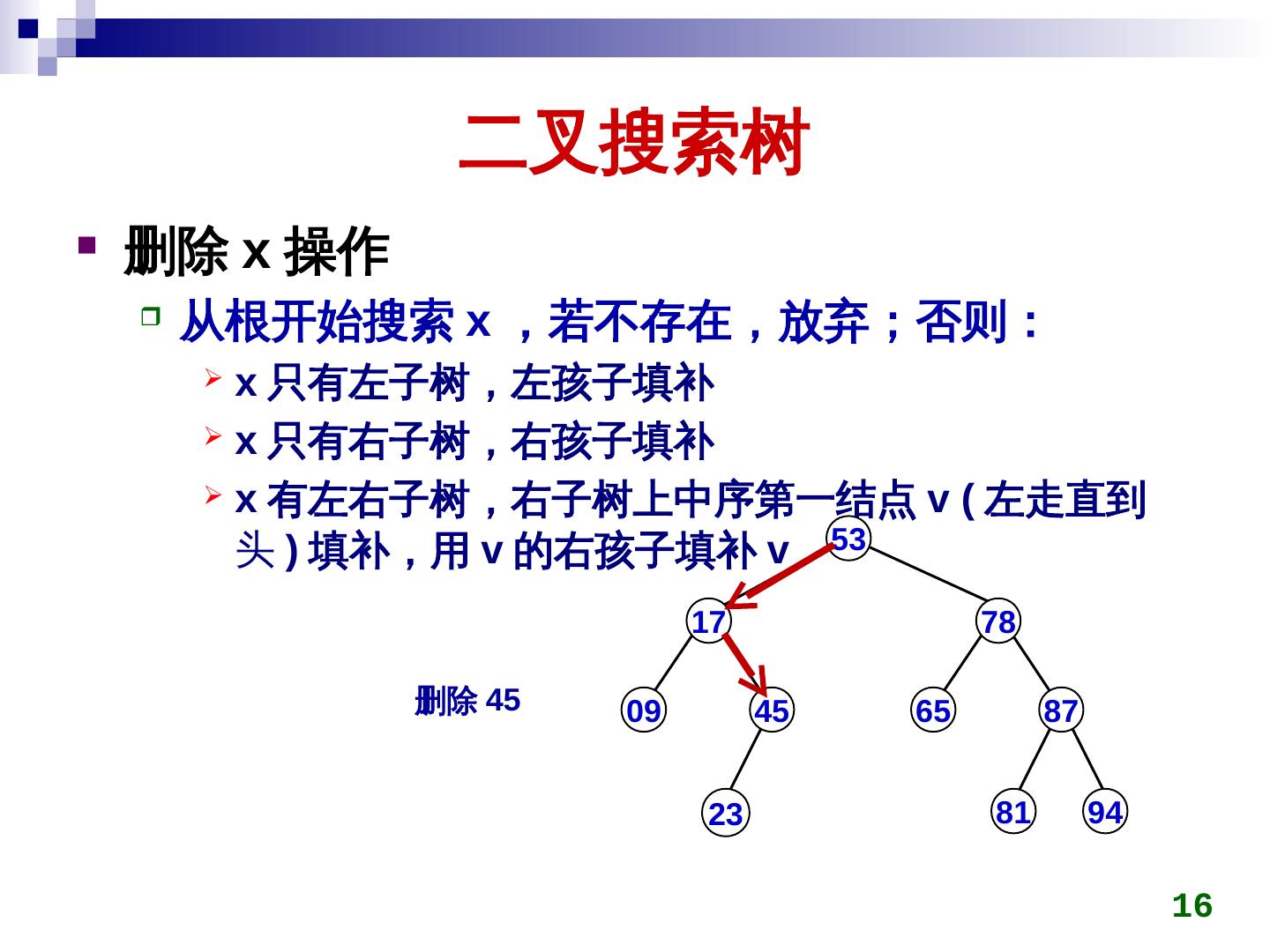
16 . 二叉搜索树  删除 x 操作  从根开始搜索 x ，若不存在，放弃；否则：  x 只有左子树，左孩子填补  x 只有右子树，右孩子填补  x 有左右子树，右子树上中序第一结点 v (key) 左走直到 头 ) 填补，用 v 的右孩子填补 v 53 17 78 删除 45 09 45 65 87 23 81 94 16 

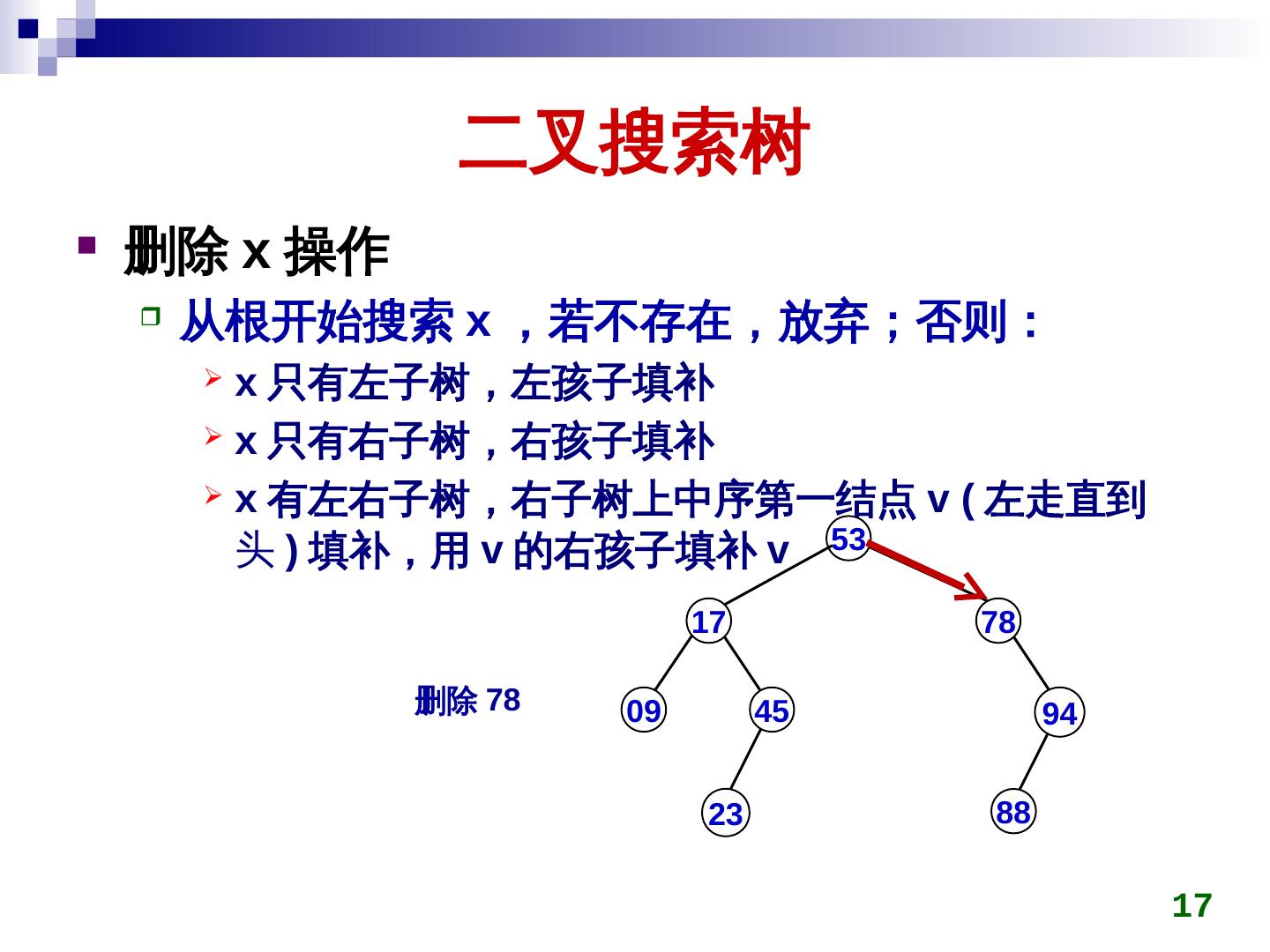
17 . 二叉搜索树  删除 x 操作  从根开始搜索 x ，若不存在，放弃；否则：  x 只有左子树，左孩子填补  x 只有右子树，右孩子填补  x 有左右子树，右子树上中序第一结点 v (key) 左走直到 头 ) 填补，用 v 的右孩子填补 v 53 17 78 删除 78 09 45 94 23 88 17 

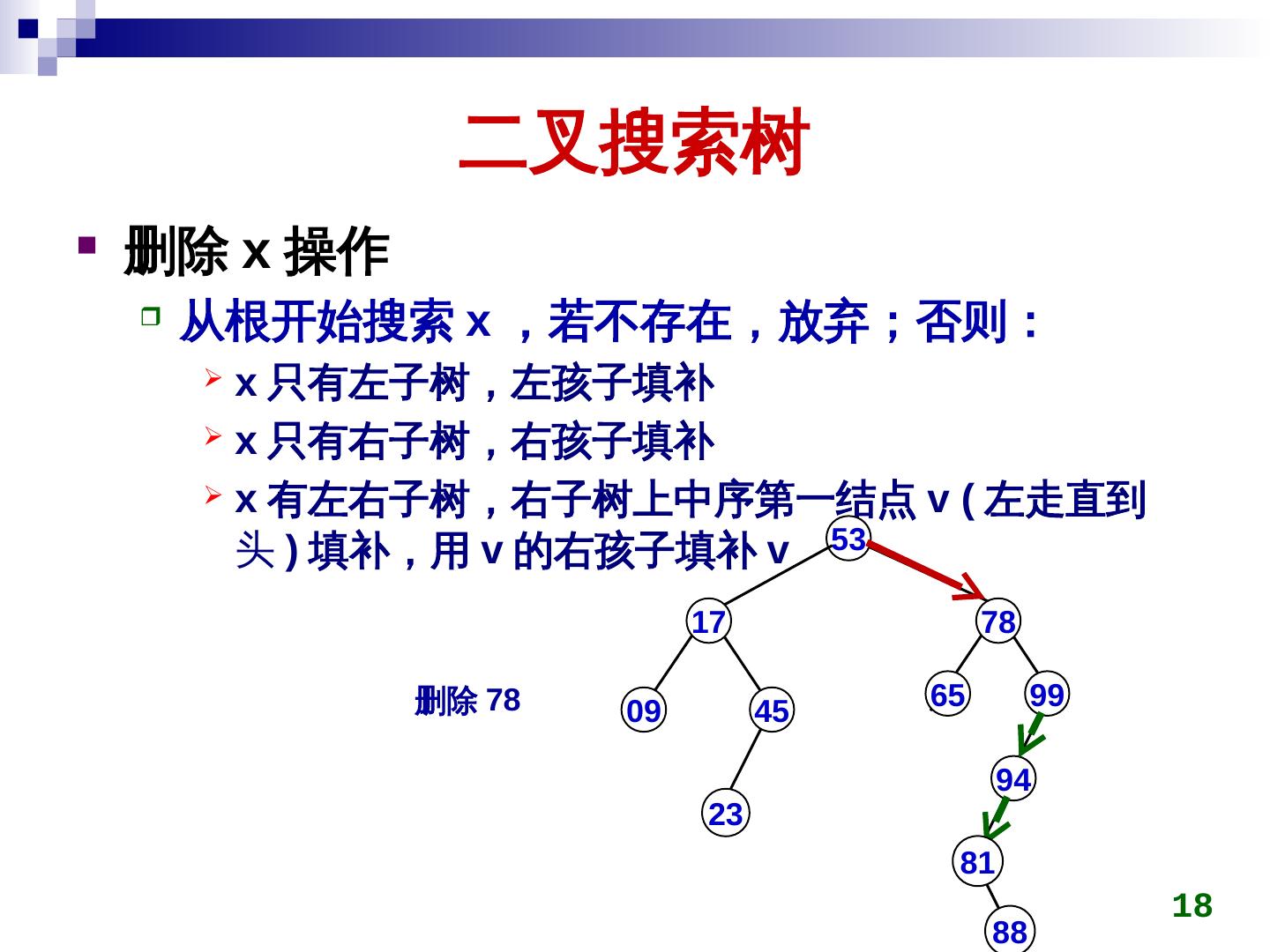
18 . 二叉搜索树  删除 x 操作  从根开始搜索 x ，若不存在，放弃；否则：  x 只有左子树，左孩子填补  x 只有右子树，右孩子填补  x 有左右子树，右子树上中序第一结点 v (key) 左走直到 头 ) 填补，用 v 的右孩子填补 v 53 17 78 删除 78 65 99 09 45 94 23 81 18 88 

19 . 二叉搜索树  性能分析  满二叉树 n 1 ASLsucc  n  log i  i 1 2 中间结点等概率搜索， 中间结点数为 n 叶子为搜索失败情况 其他为 key) 1 2n1 ASLunsucc   n  1 i n 1  log 2 i  叶子结点等概率搜索， 叶子结点数为 n+1 19 

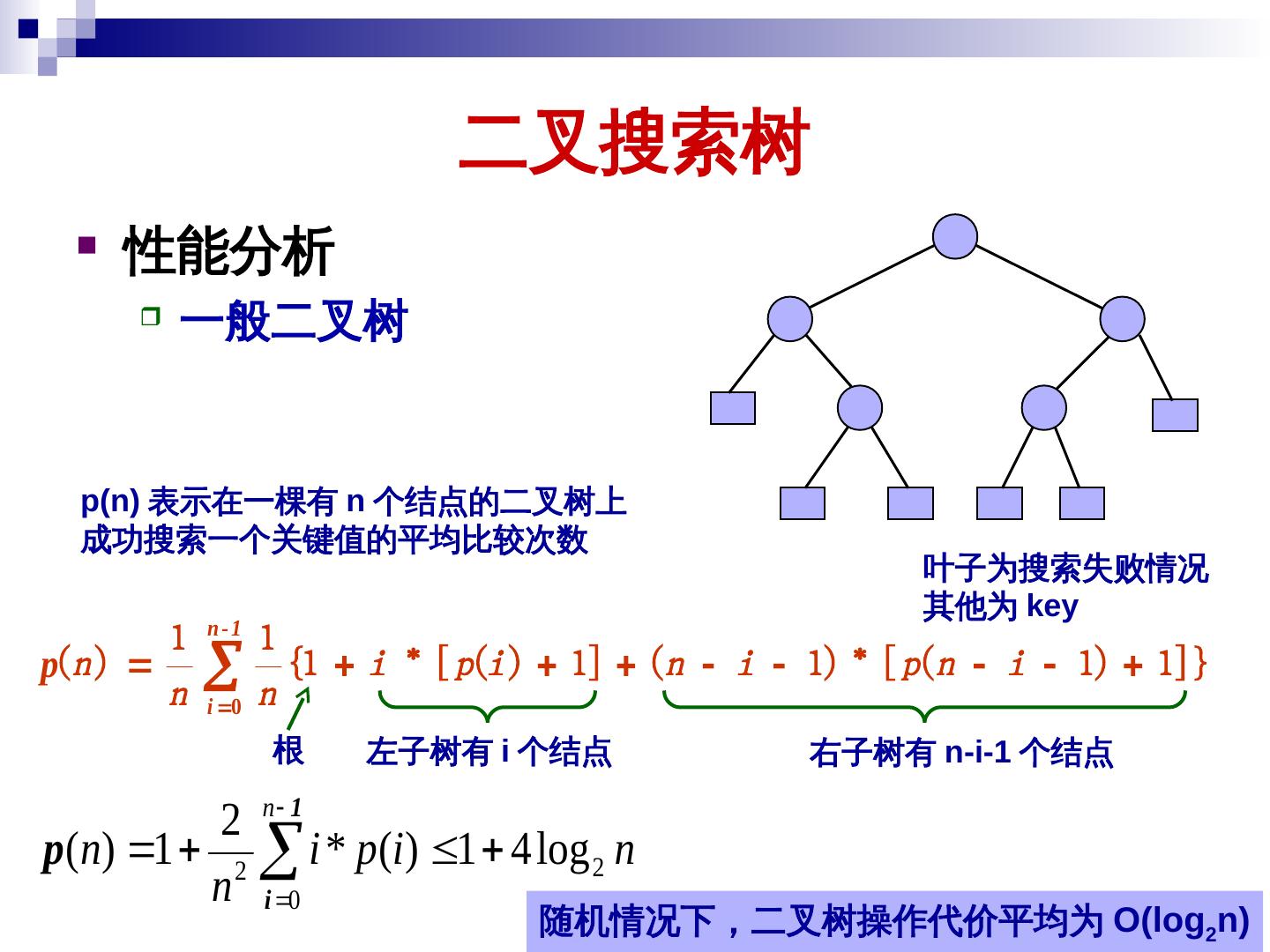
20 . 二叉搜索树  性能分析  一般二叉树 p(key)n) 表示在一棵有 n 个结点的二叉树上 成功搜索一个关键值的平均比较次数 叶子为搜索失败情况 其他为 key) n-1 1 1 p(n )  n  i 0 n {1  i * [ p(i )  1]  (n  i  1) * [ p(n  i  1)  1]} 根 左子树有 i 个结点 右子树有 n-i-1 个结点 2 n 1 p(n) 1  2  i * p(i ) 1  4 log 2 n n i 0 20 n) 随机情况下，二叉树操作代价平均为 O(key)log 2 

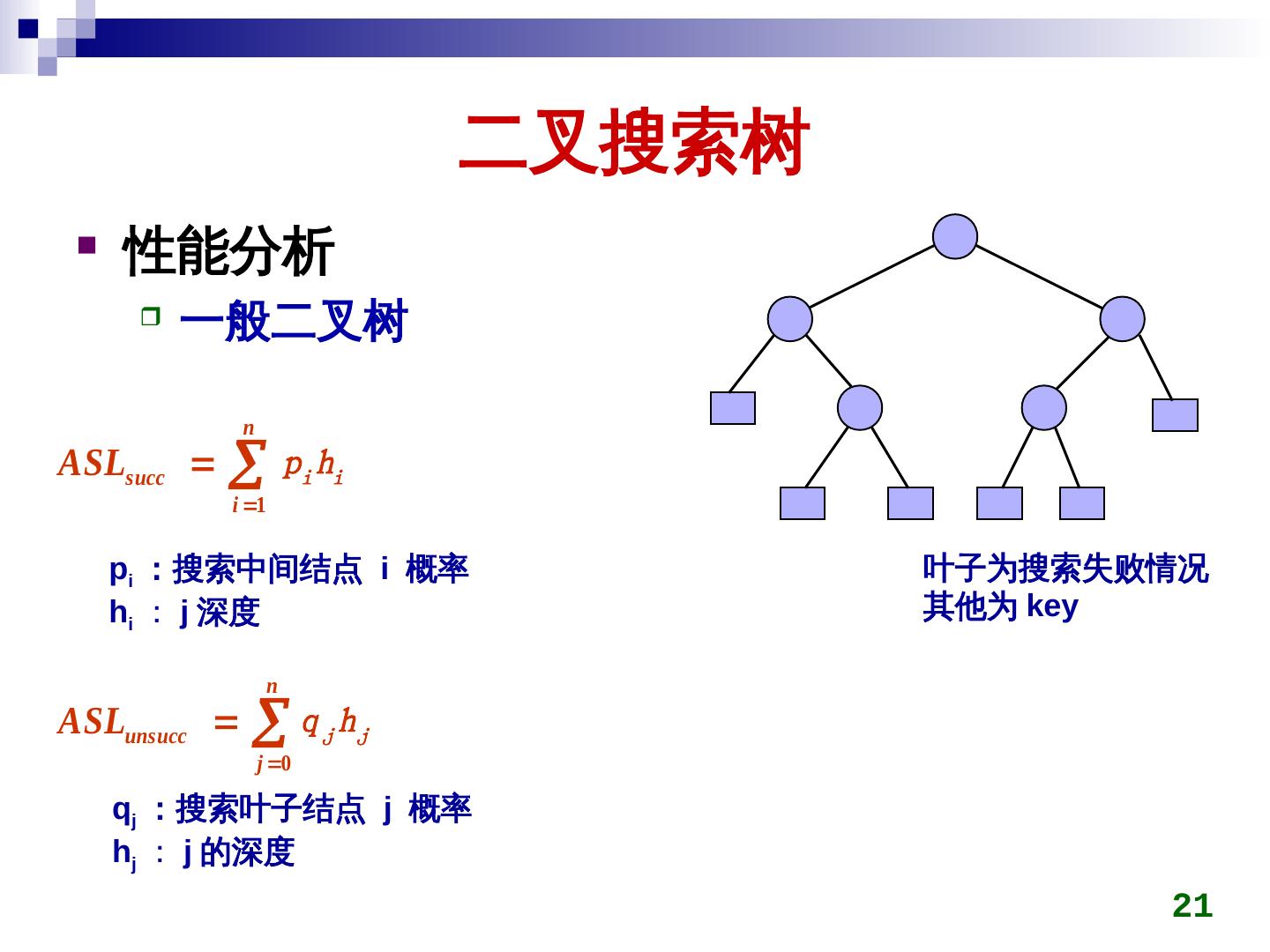
21 . 二叉搜索树  性能分析  一般二叉树 n ASLsucc   pi hi i 1 pi ：搜索中间结点 i 概率 叶子为搜索失败情况 hi ： j 深度 其他为 key) n ASLunsucc  q j 0 j hj qj ：搜索叶子结点 j 概率 hj ： j 的深度 21 

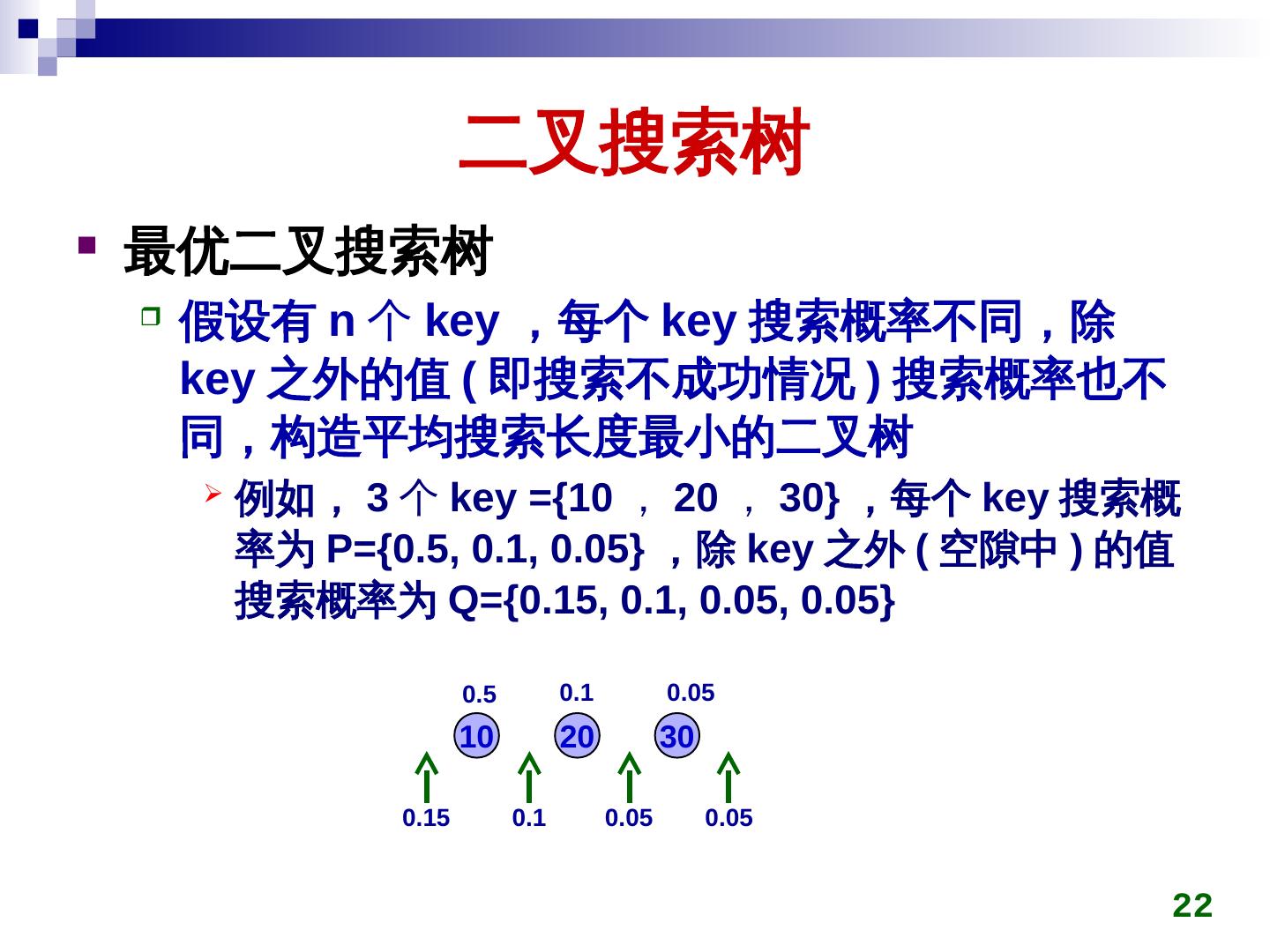
22 . 二叉搜索树  最优二叉搜索树  假设有 n 个 key) ，每个 key) 搜索概率不同，除 key) 之外的值 (key) 即搜索不成功情况 ) 搜索概率也不 同，构造平均搜索长度最小的二叉树  例如， 3 个 key) ={10 ， 20 ， 30} ，每个 key) 搜索概 率为 P={0.5, 0.1, 0.05} ，除 key) 之外 (key) 空隙中 ) 的值 搜索概率为 Q={0.15, 0.1, 0.05, 0.05} 0.5 0.1 0.05 10 20 30 0.15 0.1 0.05 0.05 22 

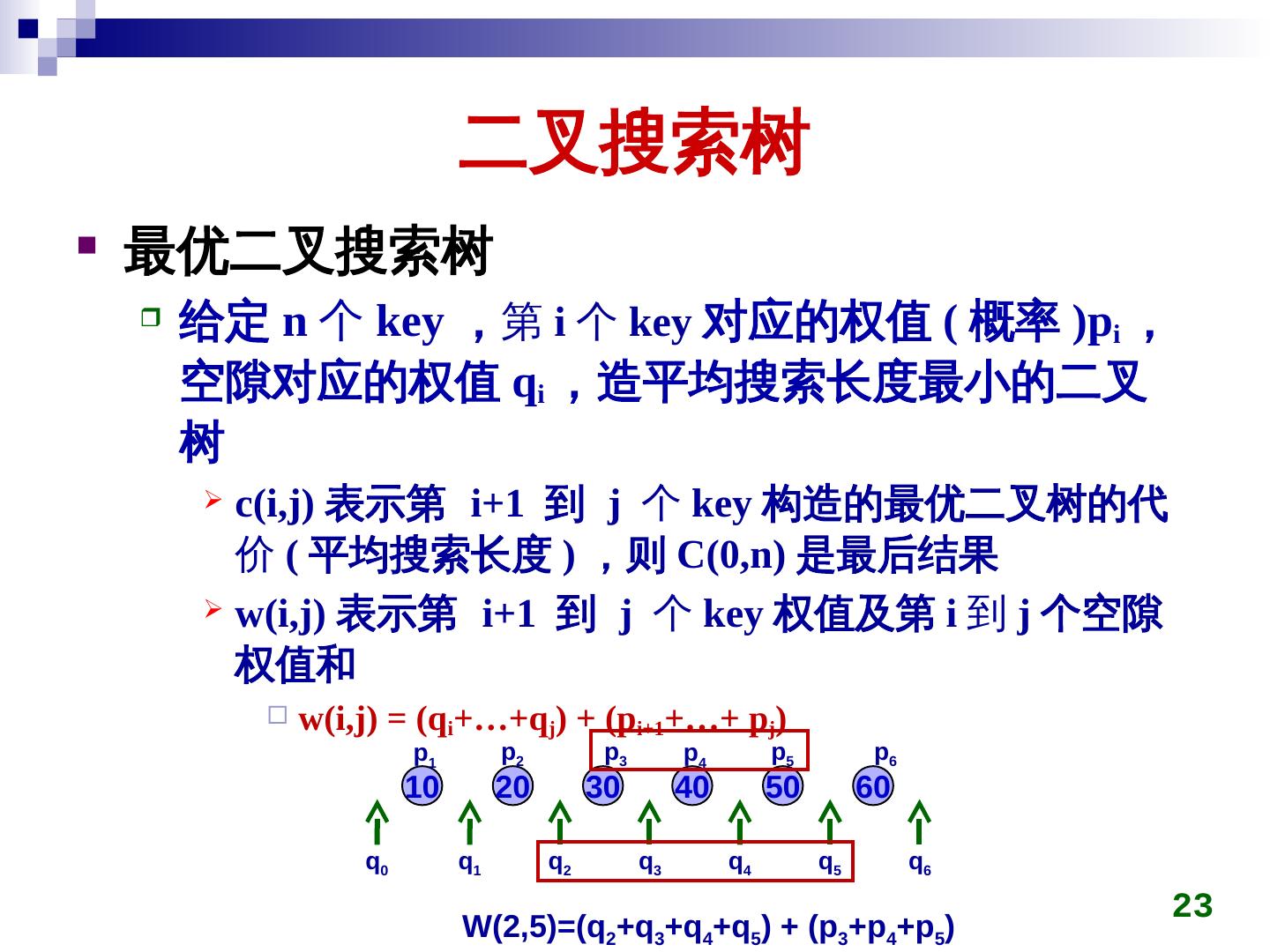
23 . 二叉搜索树  最优二叉搜索树  给定 n 个 key ，第 i 个 key 对应的权值 ( 概率 )pi ， 空隙对应的权值 qi ，造平均搜索长度最小的二叉 树  c(i,j) 表示第 i+1 到 j 个 key 构造的最优二叉树的代 价 ( 平均搜索长度 ) ，则 C(0,n) 是最后结果  w(i,j) 表示第 i+1 到 j 个 key 权值及第 i 到 j 个空隙 权值和  w(i,j) = (qi+…+qj) + (pi+1+…+ pj) p1 p2 p3 p4 p5 p6 10 20 30 40 50 60 q0 q1 q2 q3 q4 q5 q6 23 W(key)2,5)=(key)q2+q3+q4+q5) + (key)p3+p4+p5) 

24 . 二叉搜索树  最优二叉搜索树  给定 n 个 key ，第 i 个 key 对应的权值 ( 概率 )pi ， 空隙对应的权值 qi ，造平均搜索长度最小的二叉 树  c(i,j) 表示第 i+1 到 j 个 key 构造的最优二叉树的代 价 ( 平均搜索长度 ) ，则 C(0,n) 是最后结果  w(i,j) 表示第 i+1 到 j 个 key 权值及第 i 到 j 个空隙 权值和  w(i,j) = (qi+…+qj) + (pi+1+…+ pj)  i+1, … , j 以 k 为根的最优二叉树代价： 左子树的代价 右子树的代价 = pk + c(i,k-1)+w(i,k-1) + c(k,j)+w(k,j) 根的代价 左子树加一层的代价 右子树加一层的代价 

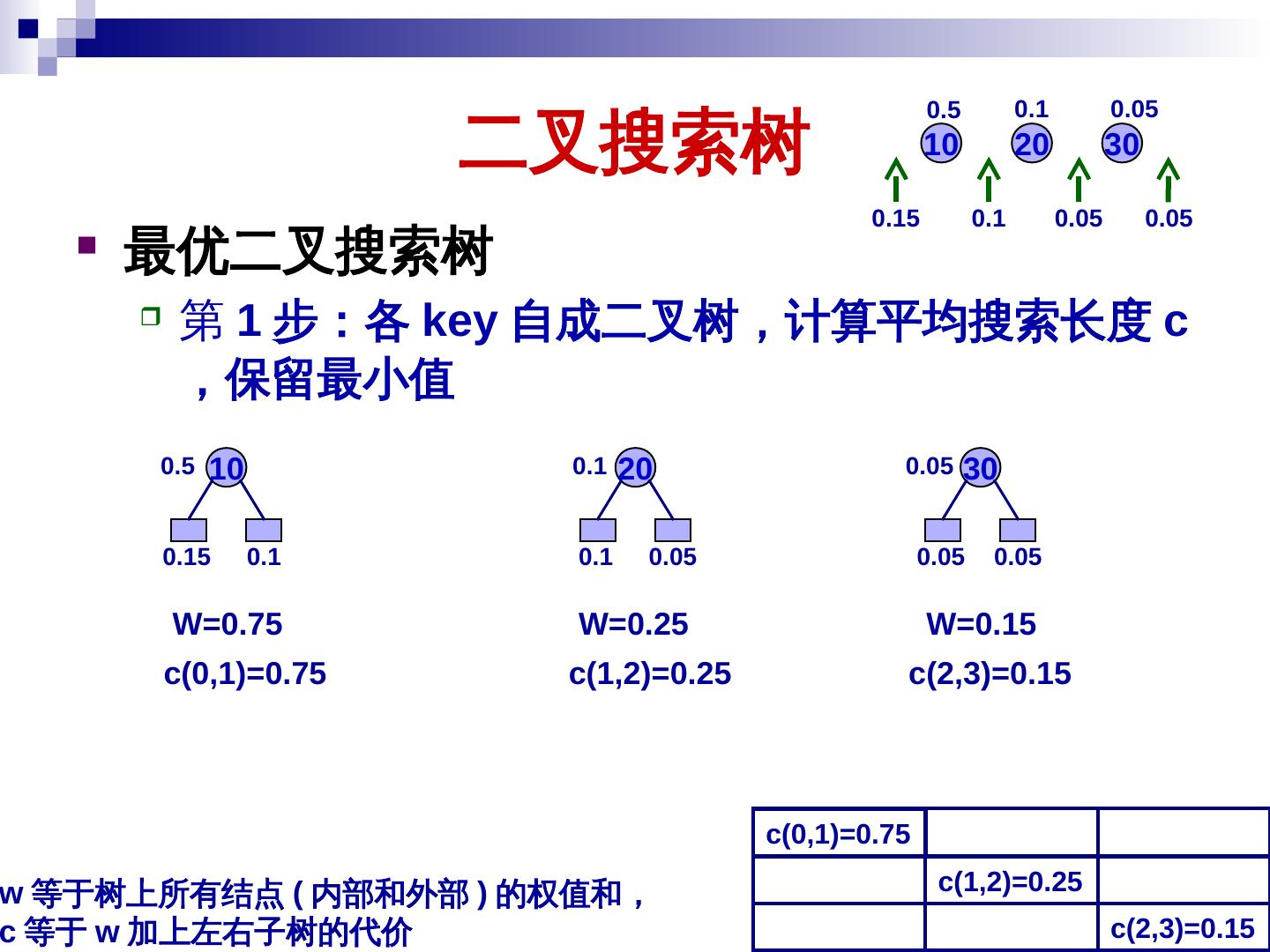
25 . 二叉搜索树  最优二叉搜索树  给定 n 个 key ，第 i 个 key 对应的权值 ( 概率 )pi ，空隙对 应的权值 qi ，造平均搜索长度最小的二叉树  c(i,j) 表示第 i+1 到 j 个 key 构造的最优二叉树的代价 ( 平均 搜索长度 ) ，则 C(0,n) 是最后结果  w(i,j) 表示第 i+1 到 j 个 key 权值及第 i 到 j 个空隙权值和  w(i,j) = (qi+…+qj) + (pi+1+…+ pj)  i+1, … , j 以 k 为根的最优二叉树代价： = pk + c(i,k-1)+w(i,k-1) + c(k,j)+w(k,j) = w(i,j) + c(i,k-1) + c(k,j) 左子树的代价 树上权值和 25 右子树的代价 

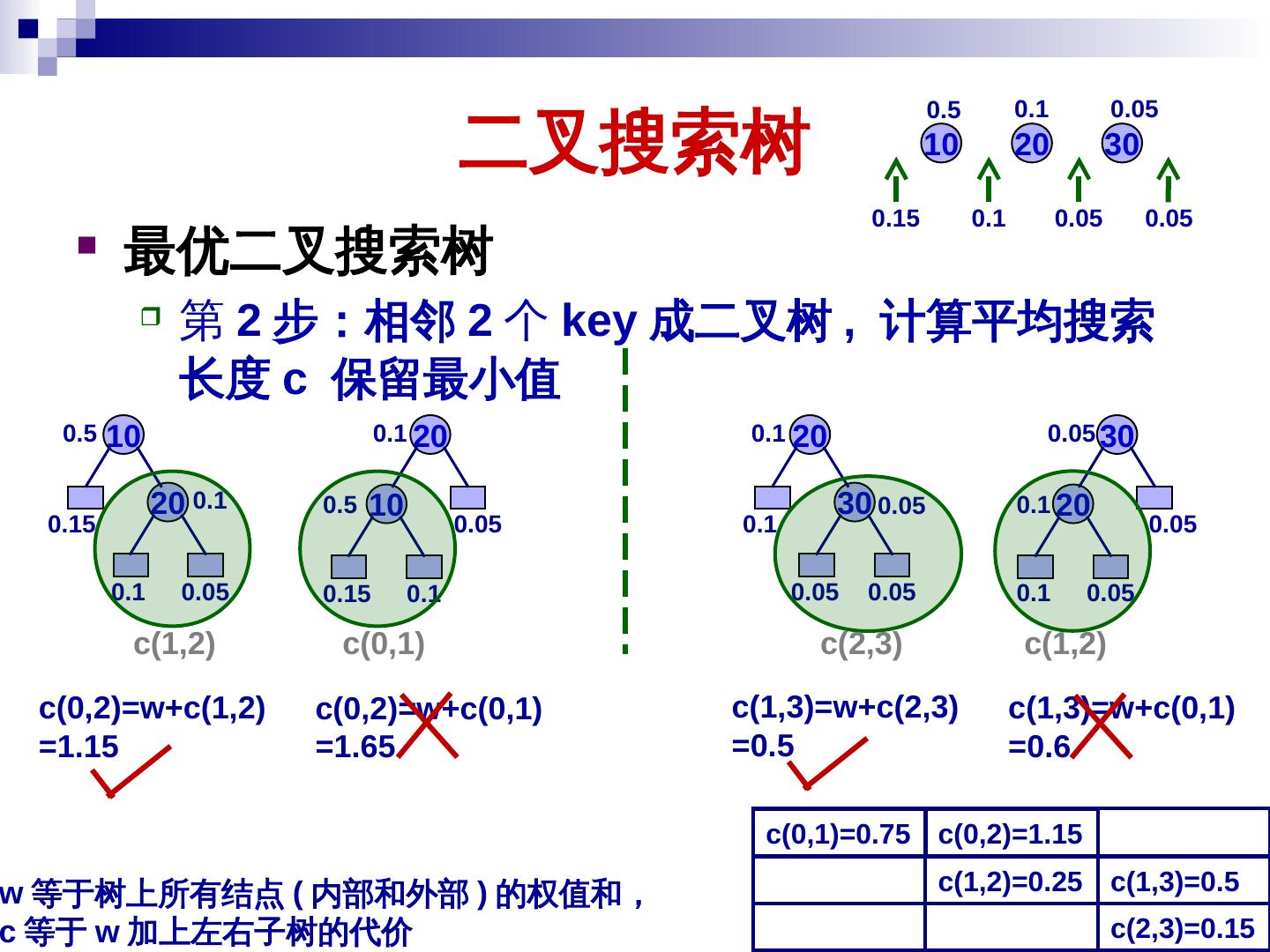
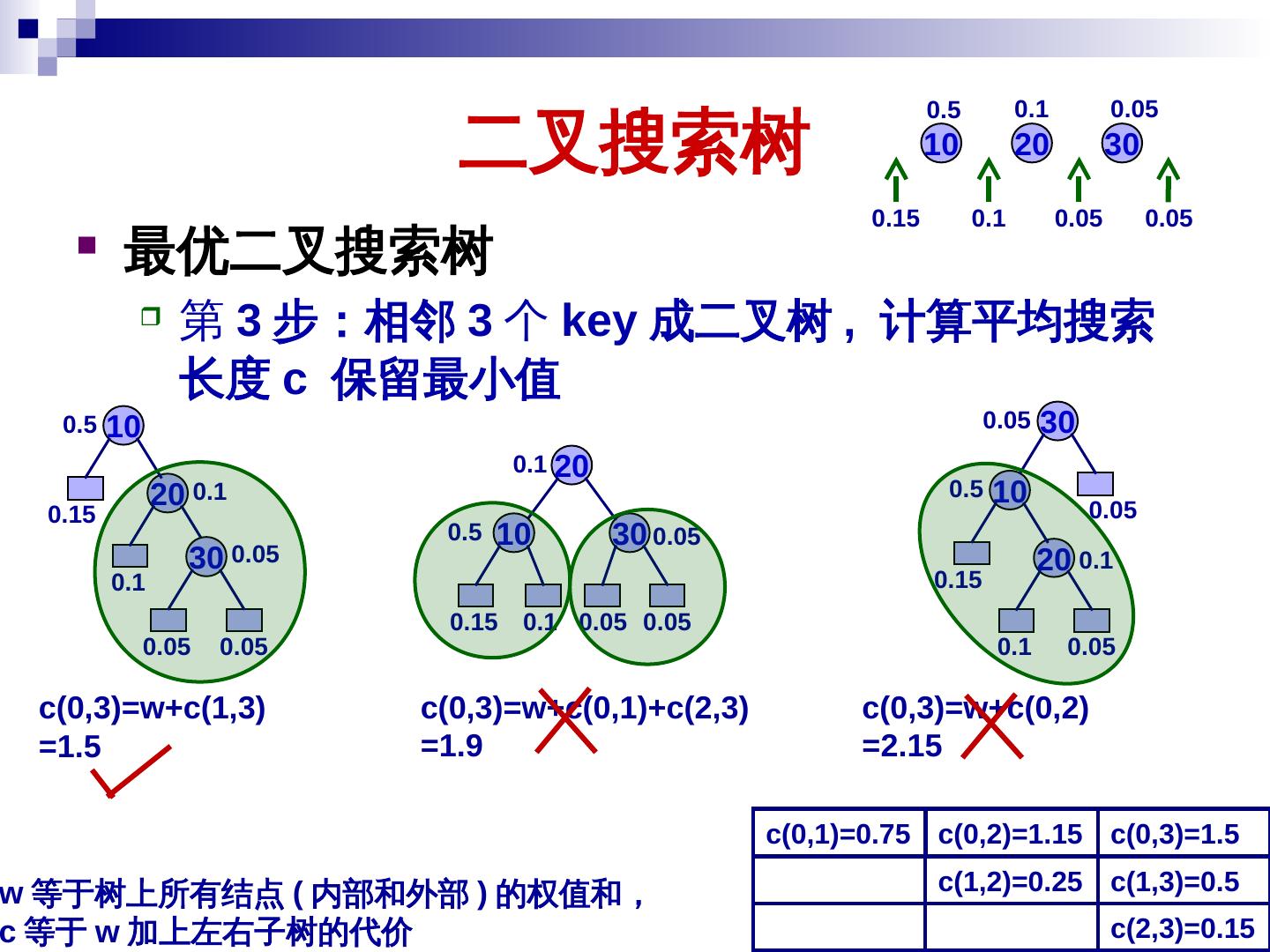
26 . 二叉搜索树  最优二叉搜索树  给定 n 个 key ，第 i 个 key 对应的权值 ( 概率 )pi ，空隙对应的权值 qi ，造平均搜索长度最小的二叉树  c(i,j) 表示第 i+1 到 j 个 key 构造的最优二叉树的代价 ( 平均搜索长度 ) ，则 C(0,n) 是最后结果  w(i,j) 表示第 i+1 到 j 个 key 权值及第 i 到 j 个空隙权值和  w(i,j) = (qi+…+qj) + (pi+1+…+ pj)  i+1, … , j 以 k 为根的最优二叉树代价： = pk + c(i,k-1)+w(i,k-1) + c(k,j)+w(k,j) = w(i,j) + c(i,k-1) + c(k,j)  i+1, … , j 的最优二叉树代价： c(i,j) = w(i,j) + min{ c(i,k-1) + c(k,j) }, 其中 i < k ≤ j 26 树上权值和 左右子树代价和最小值 

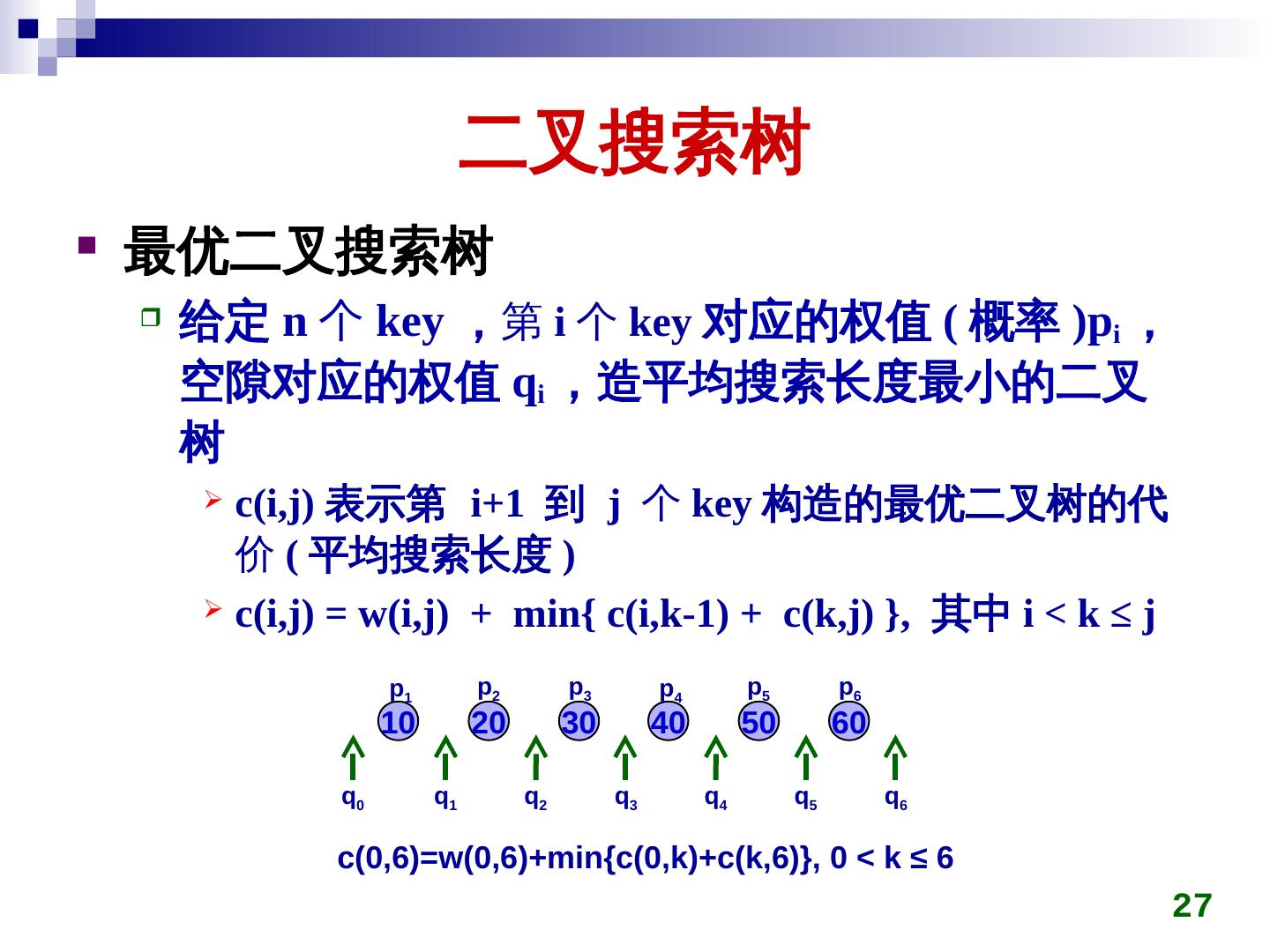
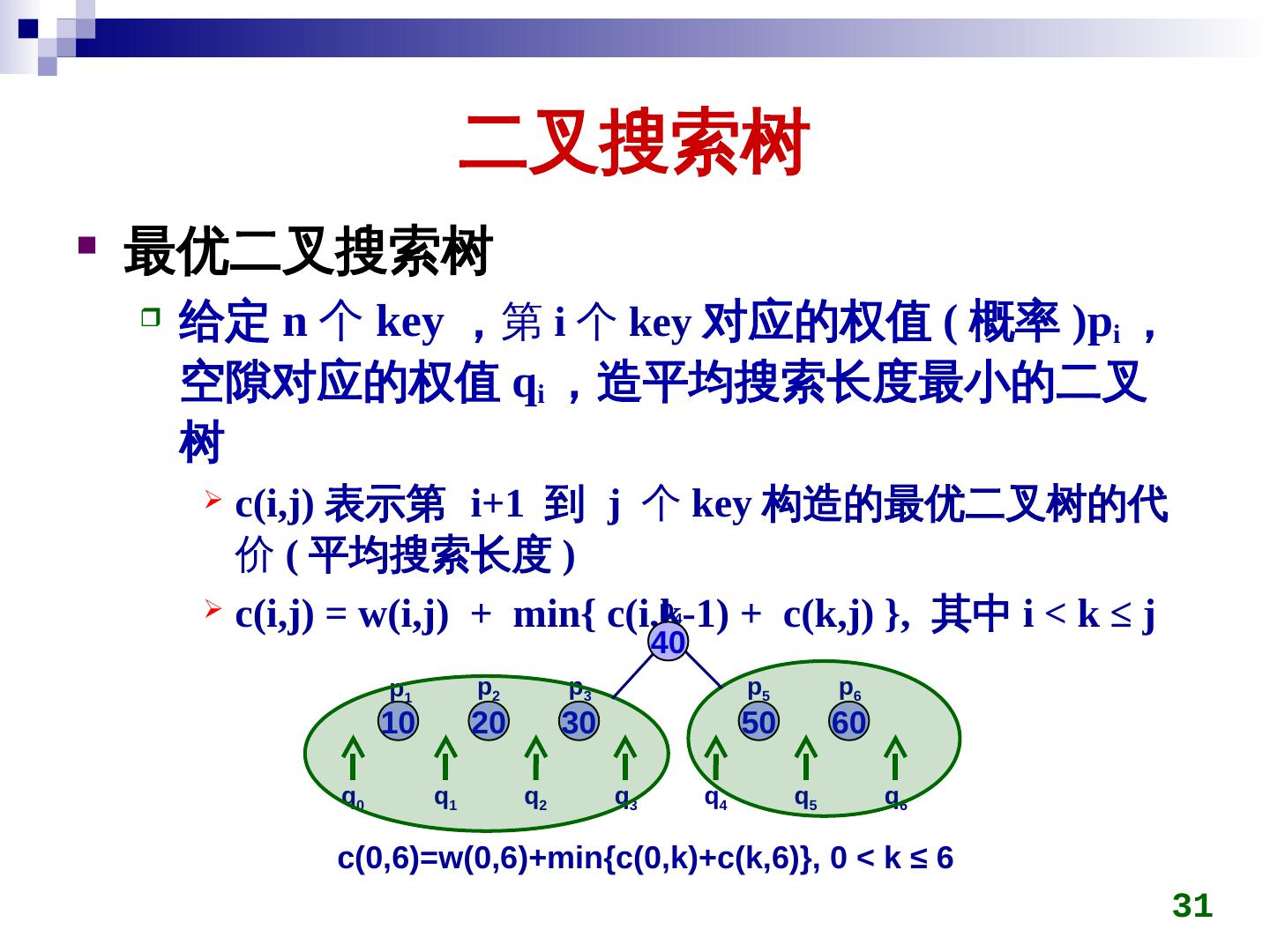
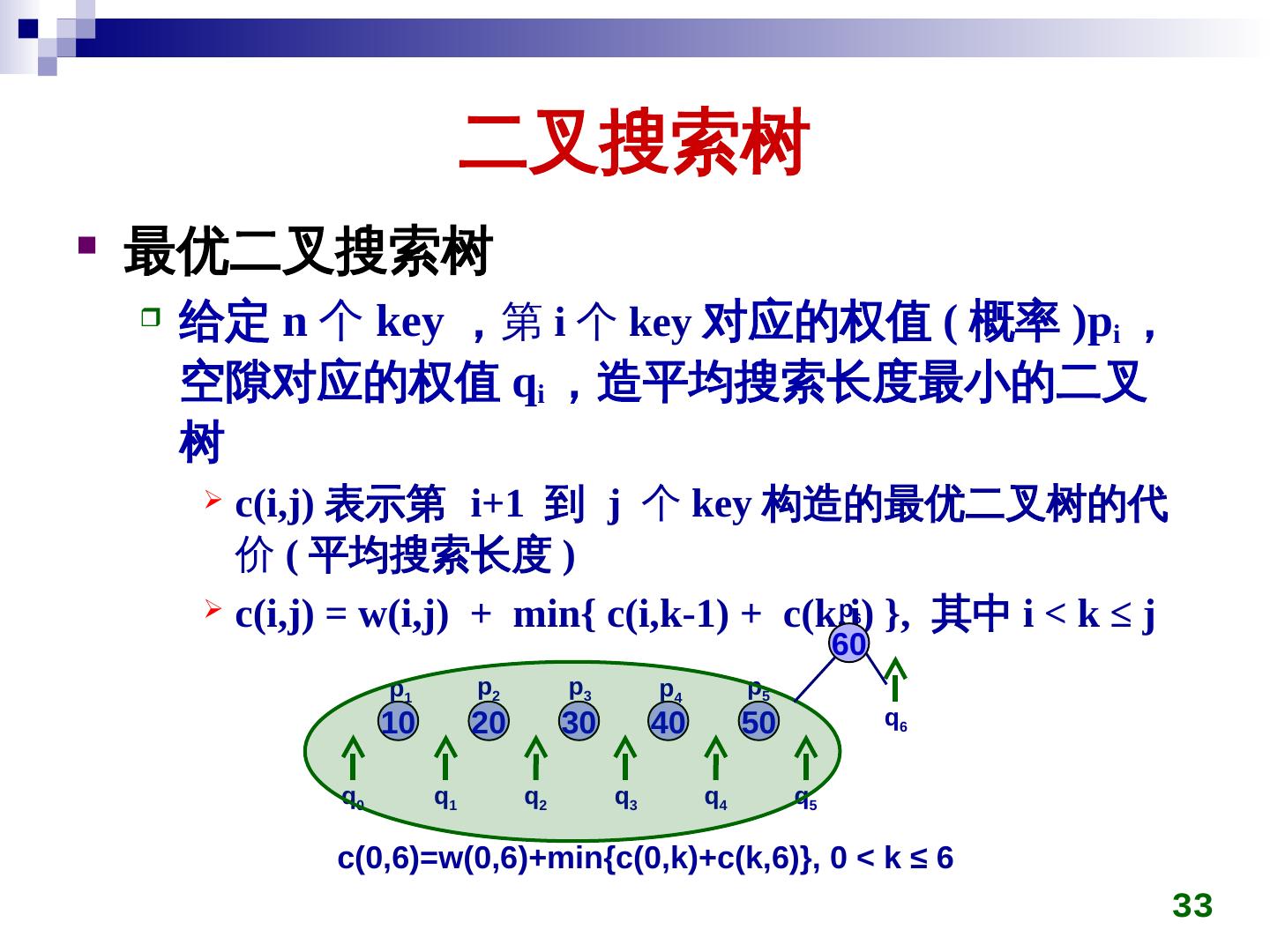
27 . 二叉搜索树  最优二叉搜索树  给定 n 个 key ，第 i 个 key 对应的权值 ( 概率 )pi ， 空隙对应的权值 qi ，造平均搜索长度最小的二叉 树  c(i,j) 表示第 i+1 到 j 个 key 构造的最优二叉树的代 价 ( 平均搜索长度 )  c(i,j) = w(i,j) + min{ c(i,k-1) + c(k,j) }, 其中 i < k ≤ j p1 p2 p3 p4 p5 p6 10 20 30 40 50 60 q0 q1 q2 q3 q4 q5 q6 c(key)0,6)=w(key)0,6)+min{c(key)0,k)+c(key)k,6)}, 0 < k ≤ 6 27 

28 . 二叉搜索树  最优二叉搜索树  给定 n 个 key ，第 i 个 key 对应的权值 ( 概率 )pi ， 空隙对应的权值 qi ，造平均搜索长度最小的二叉 树  c(i,j) 表示第 i+1 到 j 个 key 构造的最优二叉树的代 价 ( 平均搜索长度 ) p  c(i,j) = w(i,j) 1 + min{ c(i,k-1) + c(k,j) }, 其中 i < k ≤ j 10 p2 p3 p4 p5 p6 q0 20 30 40 50 60 q1 q2 q3 q4 q5 q6 c(key)0,6)=w(key)0,6)+min{c(key)0,k)+c(key)k,6)}, 0 < k ≤ 6 28 

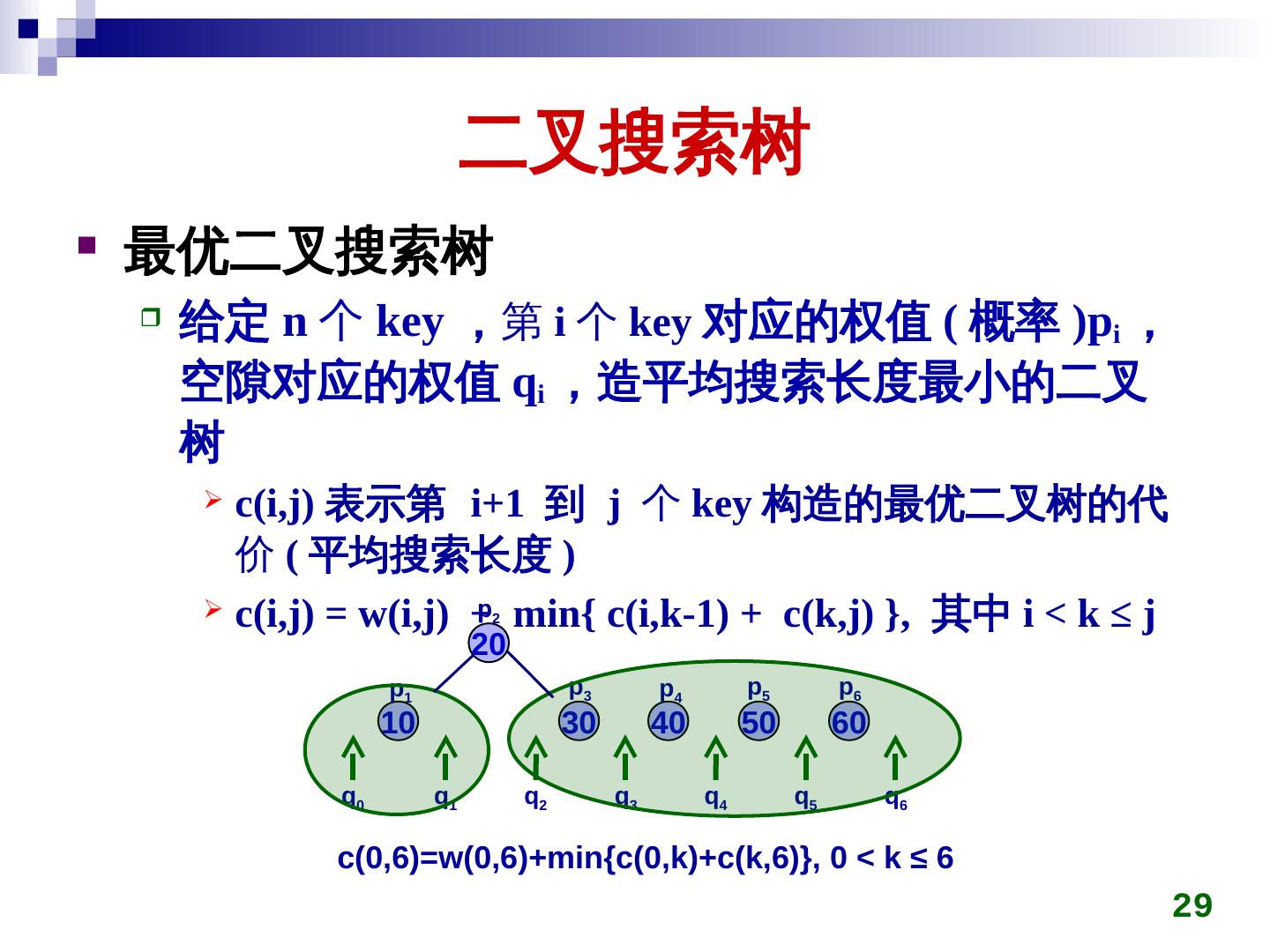
29 . 二叉搜索树  最优二叉搜索树  给定 n 个 key ，第 i 个 key 对应的权值 ( 概率 )pi ， 空隙对应的权值 qi ，造平均搜索长度最小的二叉 树  c(i,j) 表示第 i+1 到 j 个 key 构造的最优二叉树的代 价 ( 平均搜索长度 ) p min{ c(i,k-1) + c(k,j) }, 其中 i < k ≤ j  c(i,j) = w(i,j) + 2 20 p1 p3 p4 p5 p6 10 30 40 50 60 q0 q1 q2 q3 q4 q5 q6 c(key)0,6)=w(key)0,6)+min{c(key)0,k)+c(key)k,6)}, 0 < k ≤ 6 29