05数据结构---树2

1 . 第五章 树 东南大学计算机学院 方效林 方效林 本课件借鉴了清华大学殷人昆老师 和哈尔滨工业大学张岩老师的课件 

2 . 本章主要内容  树的基本概念  二叉树  二叉树的存储表示  二叉树的遍历及其应用  二叉树遍历的非递归算法  二叉树的计数  树与二叉树的转换  堆  Huffman 树及其应用 2 

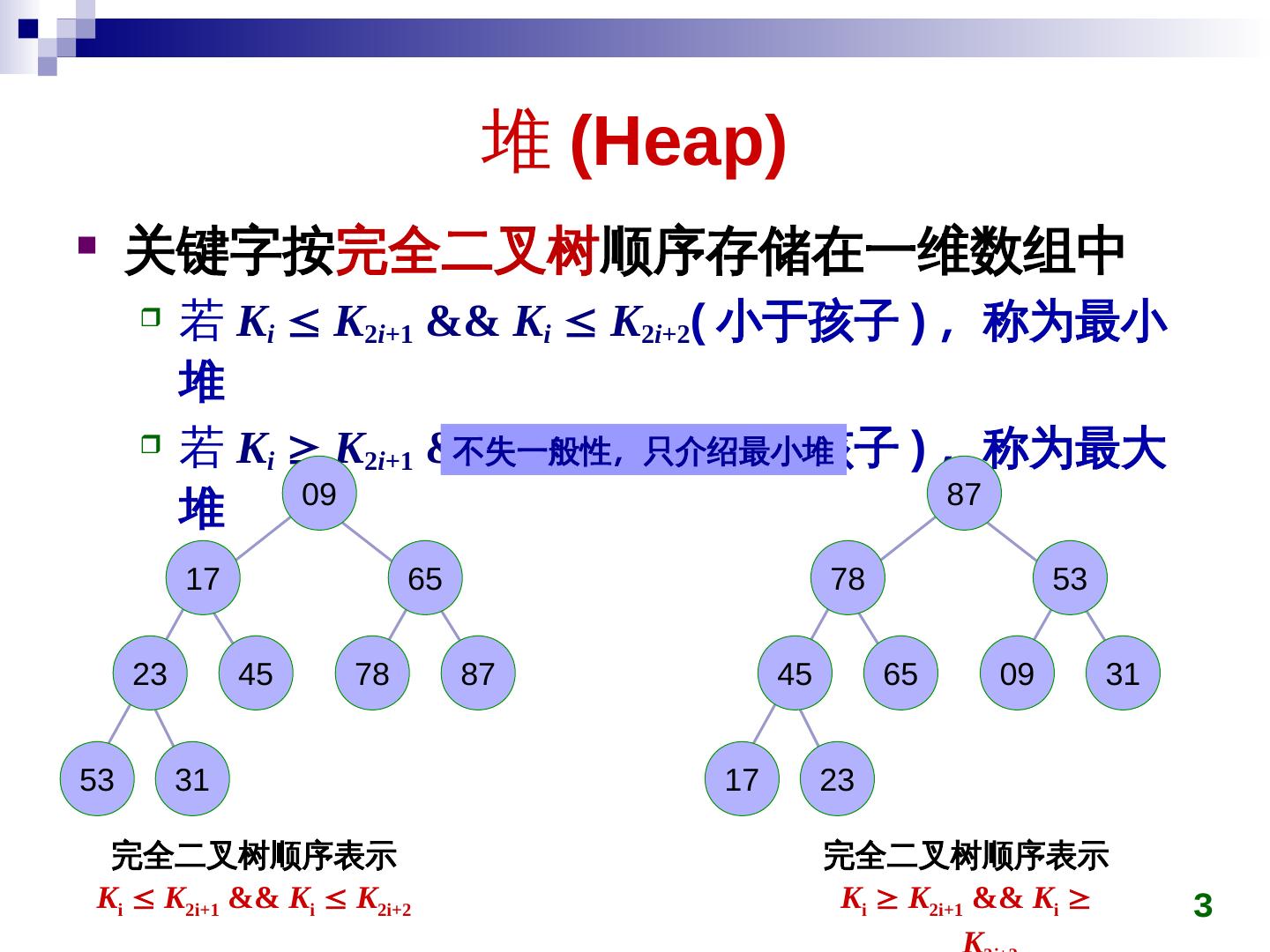
3 . 堆 (Heap)Heap))  关键字按完全二叉树顺序存储在一维数组中  若 Ki  K2i+1 && Ki  K2i+2(Heap) 小于孩子 ) ，称为最小称为最小 堆  若 Ki  K2i+1 && Ki  K2i+2(Heap) 大于孩子 ) ，称为最小称为最大 不失一般性，称为最小只介绍最小堆 09 87 堆 17 65 78 53 23 45 78 87 45 65 09 31 53 31 17 23 完全二叉树顺序表示 完全二叉树顺序表示 Ki  K2i+1 && Ki  K2i+2 Ki  K2i+1 && Ki  3 

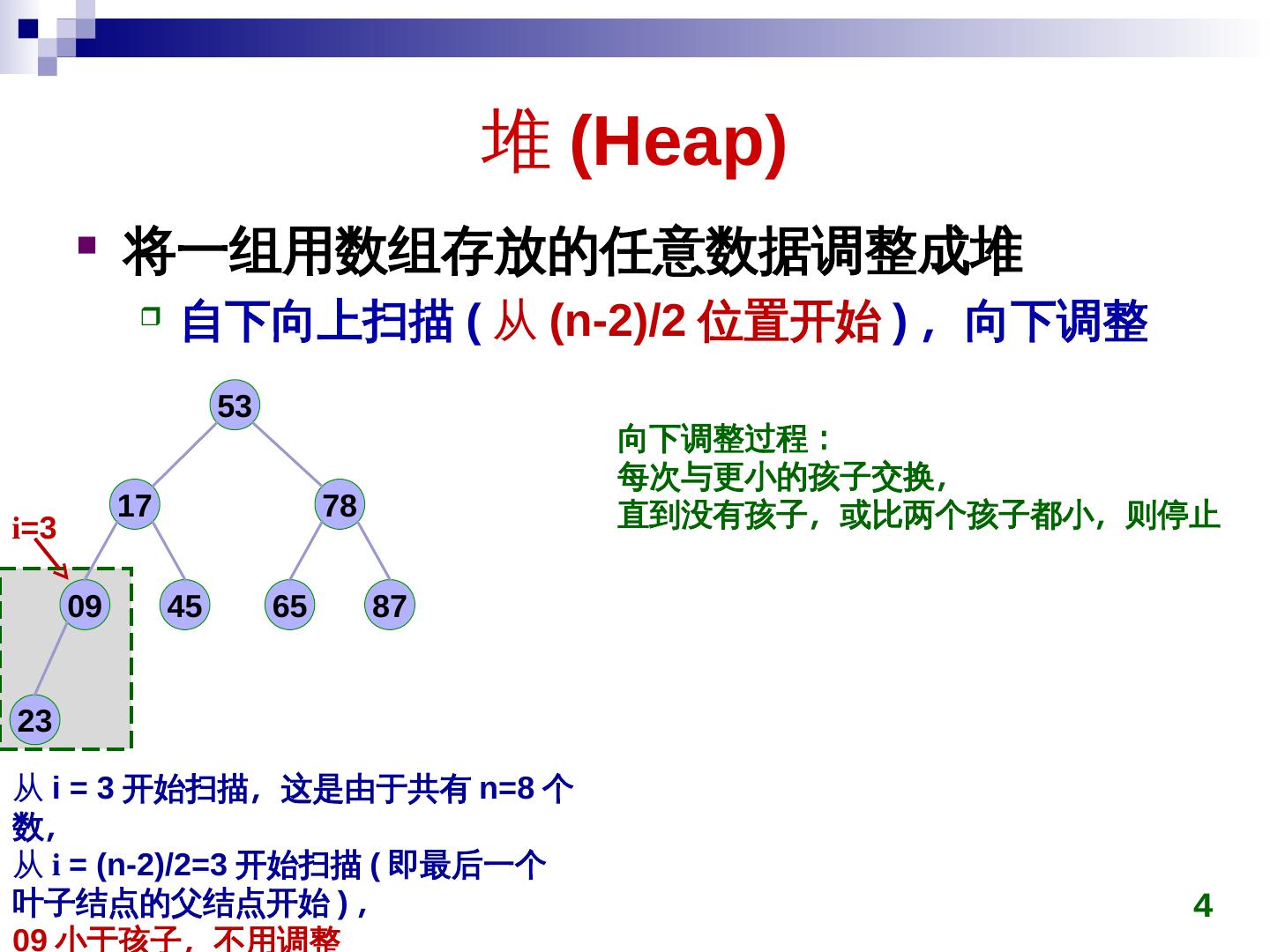
4 . 堆 (Heap)Heap))  将一组用数组存放的任意数据调整成堆  自下向上扫描 (Heap) 从 (Heap)n-2)/2)/2)/2 位置开始 ) ，称为最小向下调整 53 向下调整过程： 每次与更小的孩子交换，称为最小 17 78 直到没有孩子，称为最小或比两个孩子都小，称为最小则停止 i=3 09 45 65 87 2)/23 从 i = 3 开始扫描，称为最小这是由于共有 n=8 个 数，称为最小 从 i = (Heap)n-2)/2)/2)/2=3 开始扫描 (Heap) 即最后一个 叶子结点的父结点开始 ) ，称为最小 4 09 小于孩子，称为最小不用调整 

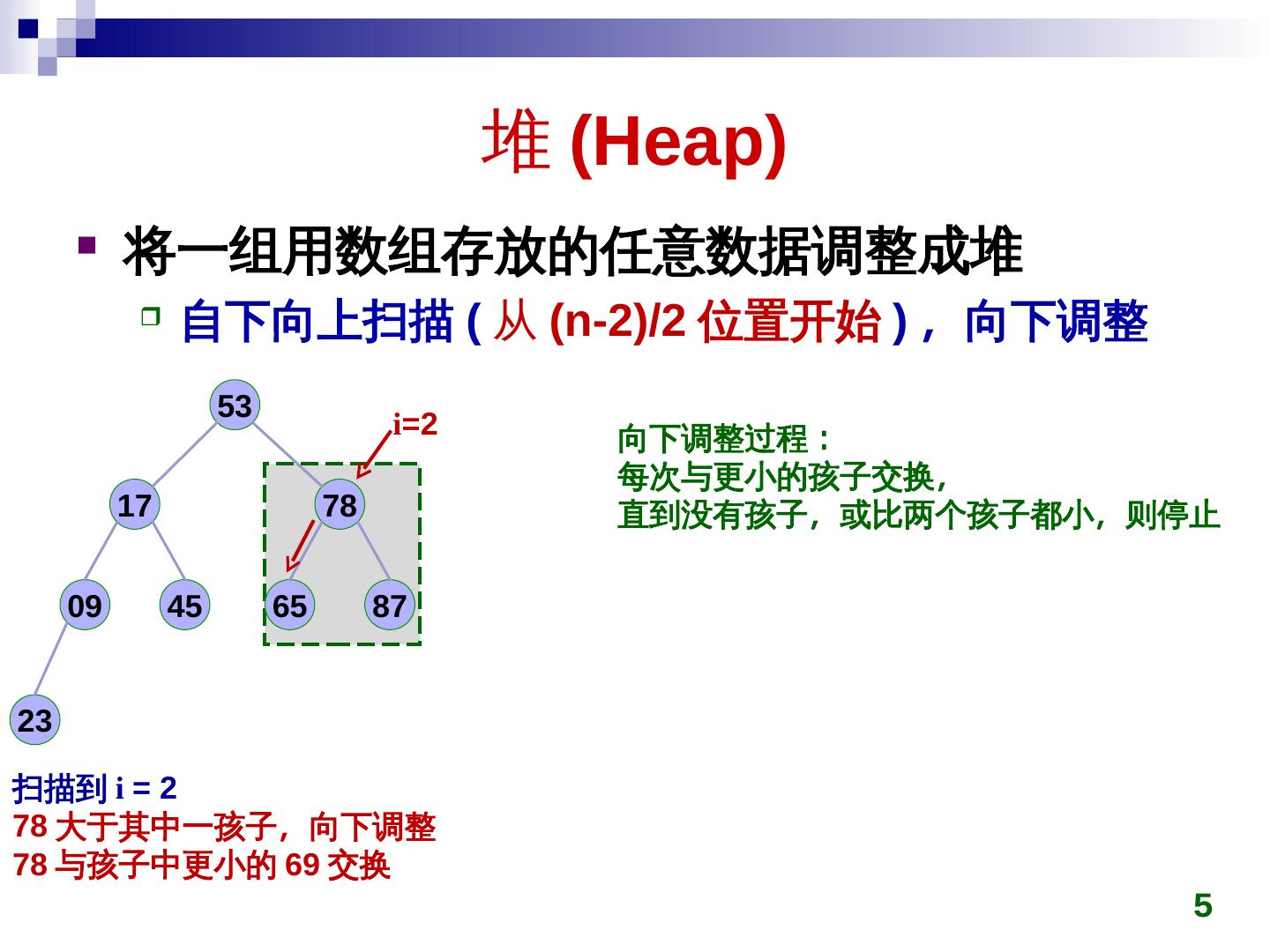
5 . 堆 (Heap)Heap))  将一组用数组存放的任意数据调整成堆  自下向上扫描 (Heap) 从 (Heap)n-2)/2)/2)/2 位置开始 ) ，称为最小向下调整 53 i=2)/2 向下调整过程： 每次与更小的孩子交换，称为最小 17 78 直到没有孩子，称为最小或比两个孩子都小，称为最小则停止 09 45 65 87 2)/23 扫描到 i = 2)/2 78 大于其中一孩子，称为最小向下调整 78 与孩子中更小的 69 交换 5 

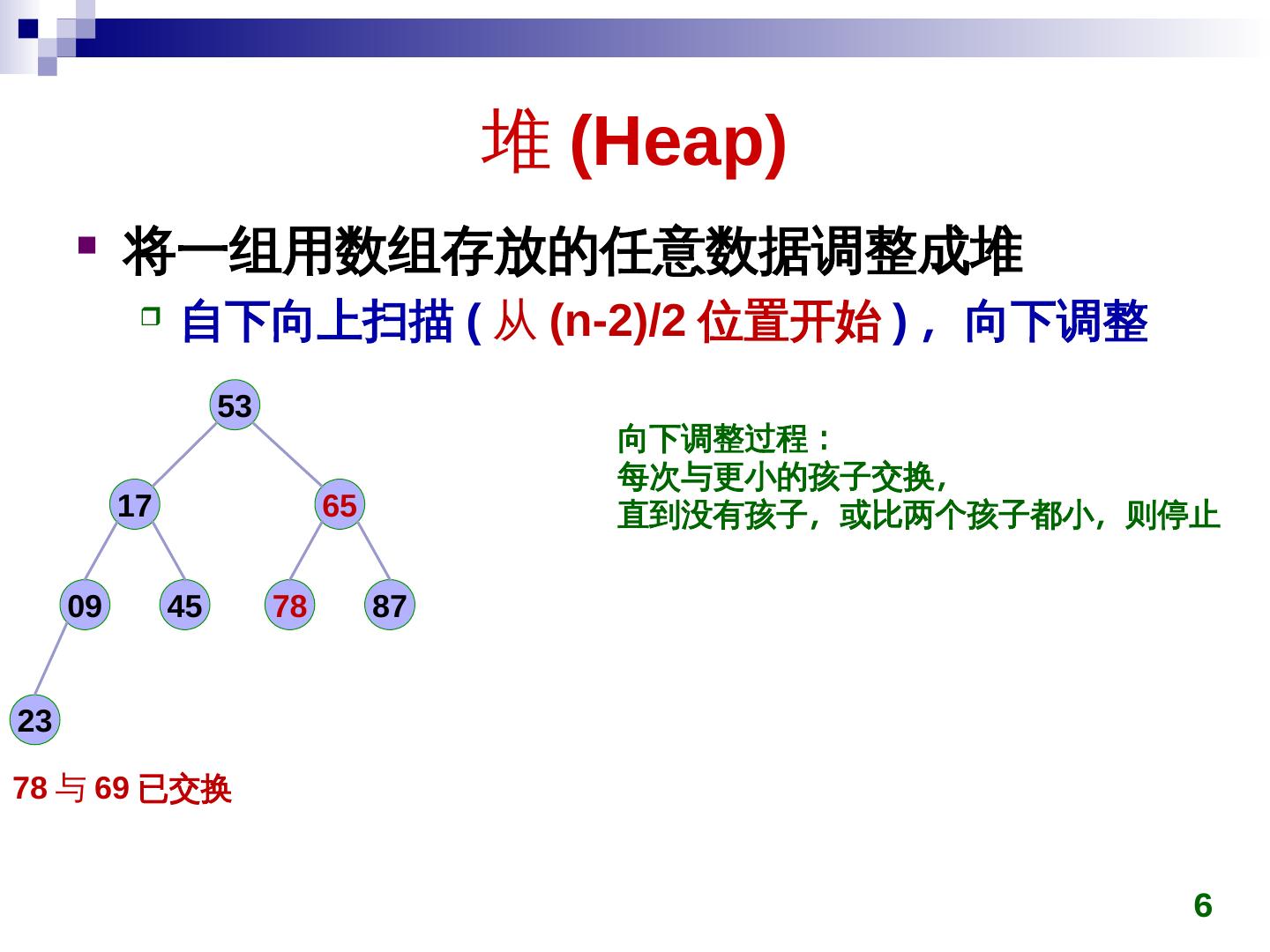
6 . 堆 (Heap)Heap))  将一组用数组存放的任意数据调整成堆  自下向上扫描 (Heap) 从 (Heap)n-2)/2)/2)/2 位置开始 ) ，称为最小向下调整 53 向下调整过程： 每次与更小的孩子交换，称为最小 17 65 直到没有孩子，称为最小或比两个孩子都小，称为最小则停止 09 45 78 87 2)/23 78 与 69 已交换 6 

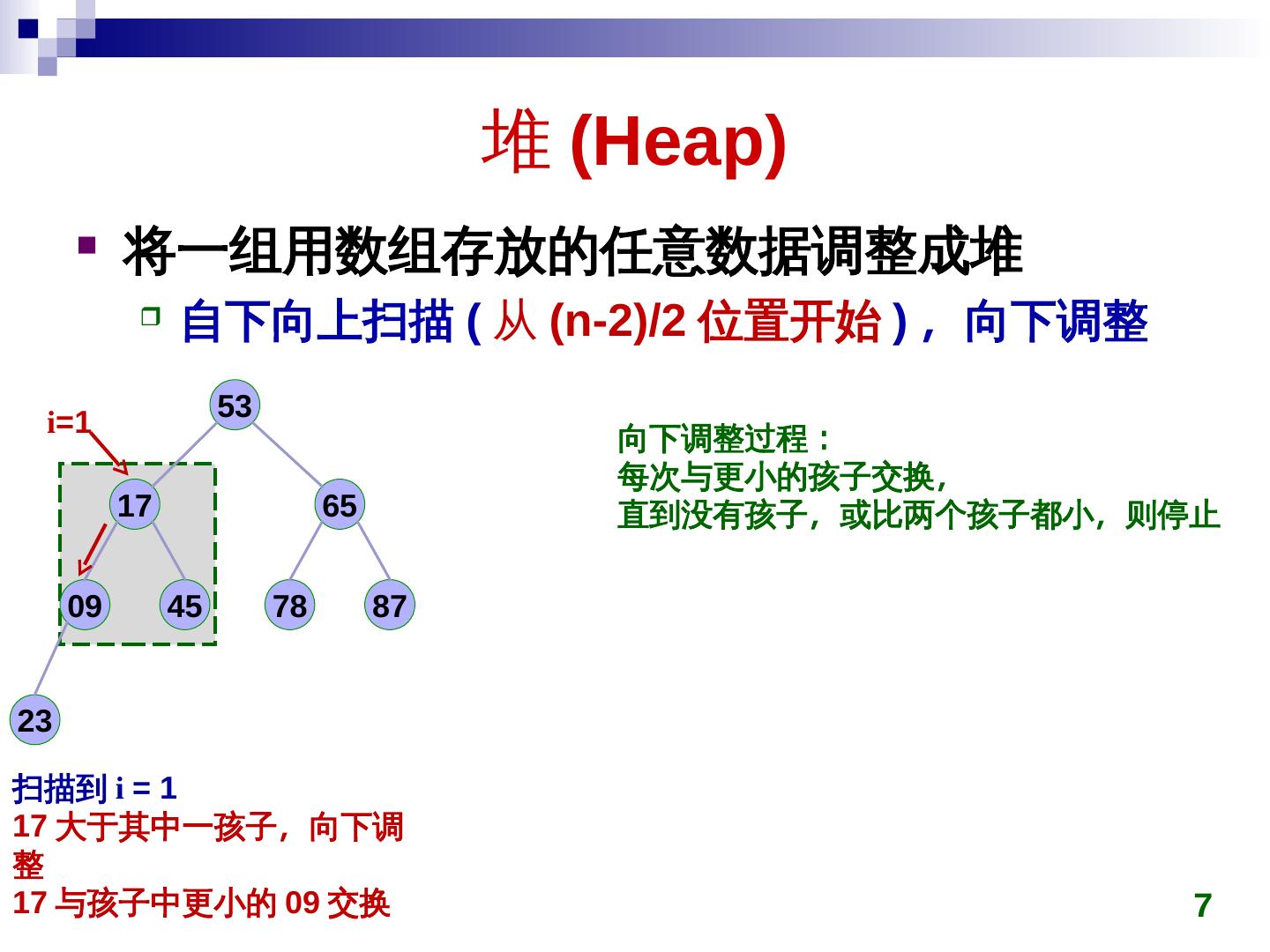
7 . 堆 (Heap)Heap))  将一组用数组存放的任意数据调整成堆  自下向上扫描 (Heap) 从 (Heap)n-2)/2)/2)/2 位置开始 ) ，称为最小向下调整 i=1 53 向下调整过程： 每次与更小的孩子交换，称为最小 17 65 直到没有孩子，称为最小或比两个孩子都小，称为最小则停止 09 45 78 87 2)/23 扫描到 i = 1 17 大于其中一孩子，称为最小向下调 整 17 与孩子中更小的 09 交换 7 

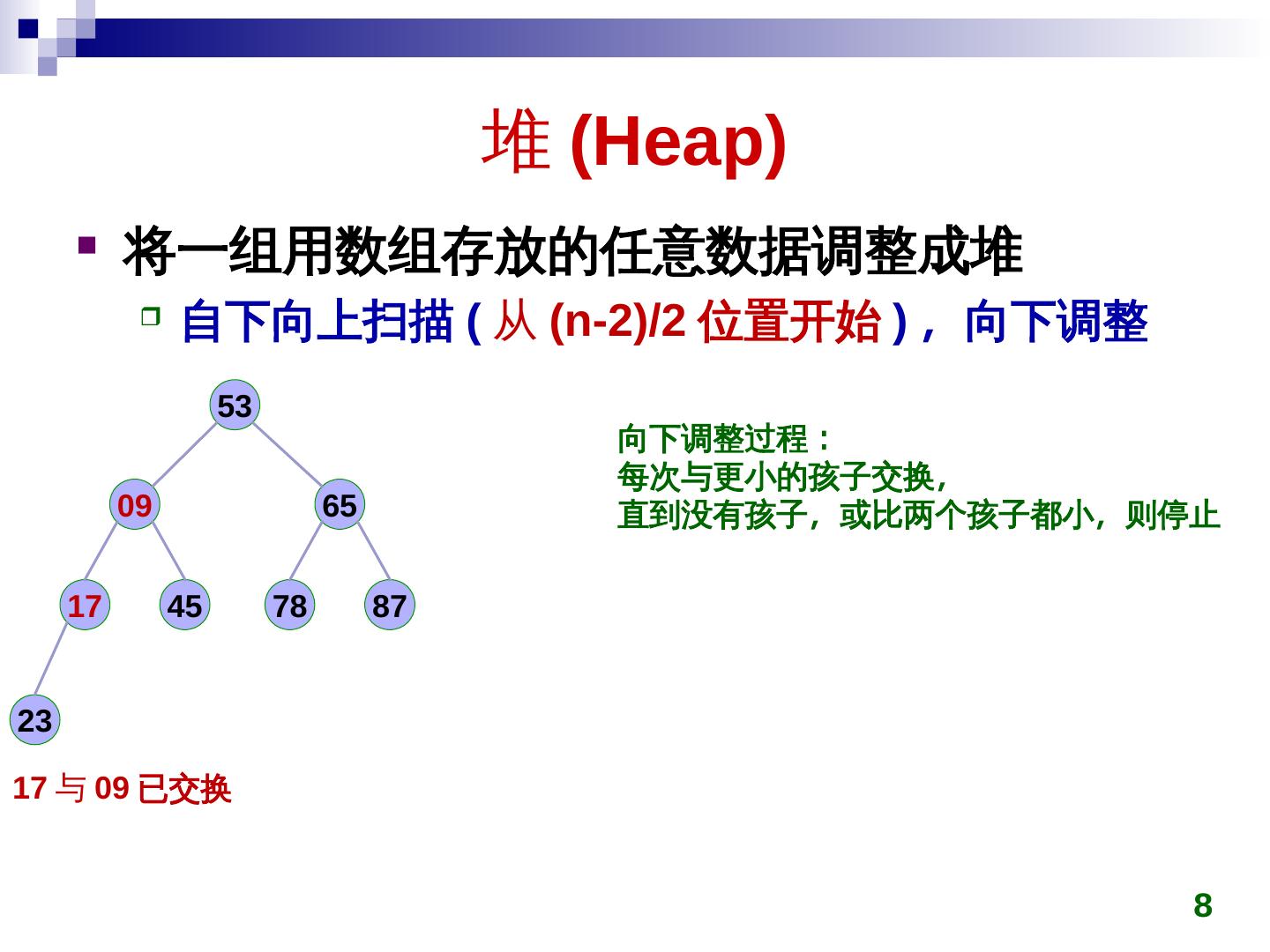
8 . 堆 (Heap)Heap))  将一组用数组存放的任意数据调整成堆  自下向上扫描 (Heap) 从 (Heap)n-2)/2)/2)/2 位置开始 ) ，称为最小向下调整 53 向下调整过程： 每次与更小的孩子交换，称为最小 09 65 直到没有孩子，称为最小或比两个孩子都小，称为最小则停止 17 45 78 87 2)/23 17 与 09 已交换 8 

9 . 堆 (Heap)Heap))  将一组用数组存放的任意数据调整成堆  自下向上扫描 (Heap) 从 (Heap)n-2)/2)/2)/2 位置开始 ) ，称为最小向下调整 53 向下调整过程： 每次与更小的孩子交换，称为最小 09 65 直到没有孩子，称为最小或比两个孩子都小，称为最小则停止 17 45 78 87 2)/23 继续向下进行判断 17 小于孩子，称为最小不用向下调整 9 

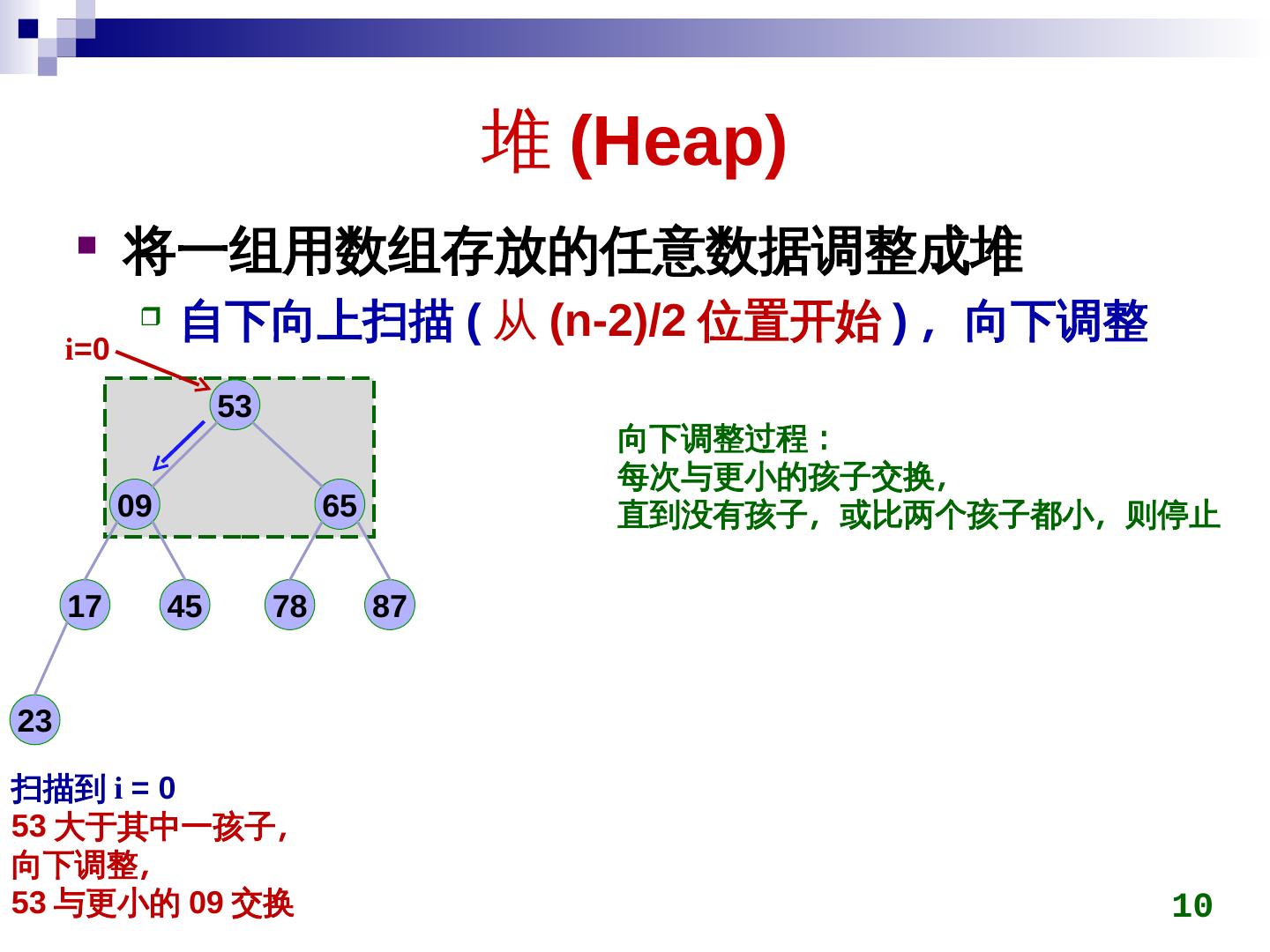
10 . 堆 (Heap)Heap))  将一组用数组存放的任意数据调整成堆  自下向上扫描 (Heap) 从 (Heap)n-2)/2)/2)/2 位置开始 ) ，称为最小向下调整 i=0 53 向下调整过程： 每次与更小的孩子交换，称为最小 09 65 直到没有孩子，称为最小或比两个孩子都小，称为最小则停止 17 45 78 87 2)/23 扫描到 i = 0 53 大于其中一孩子，称为最小 向下调整，称为最小 53 与更小的 09 交换 10 

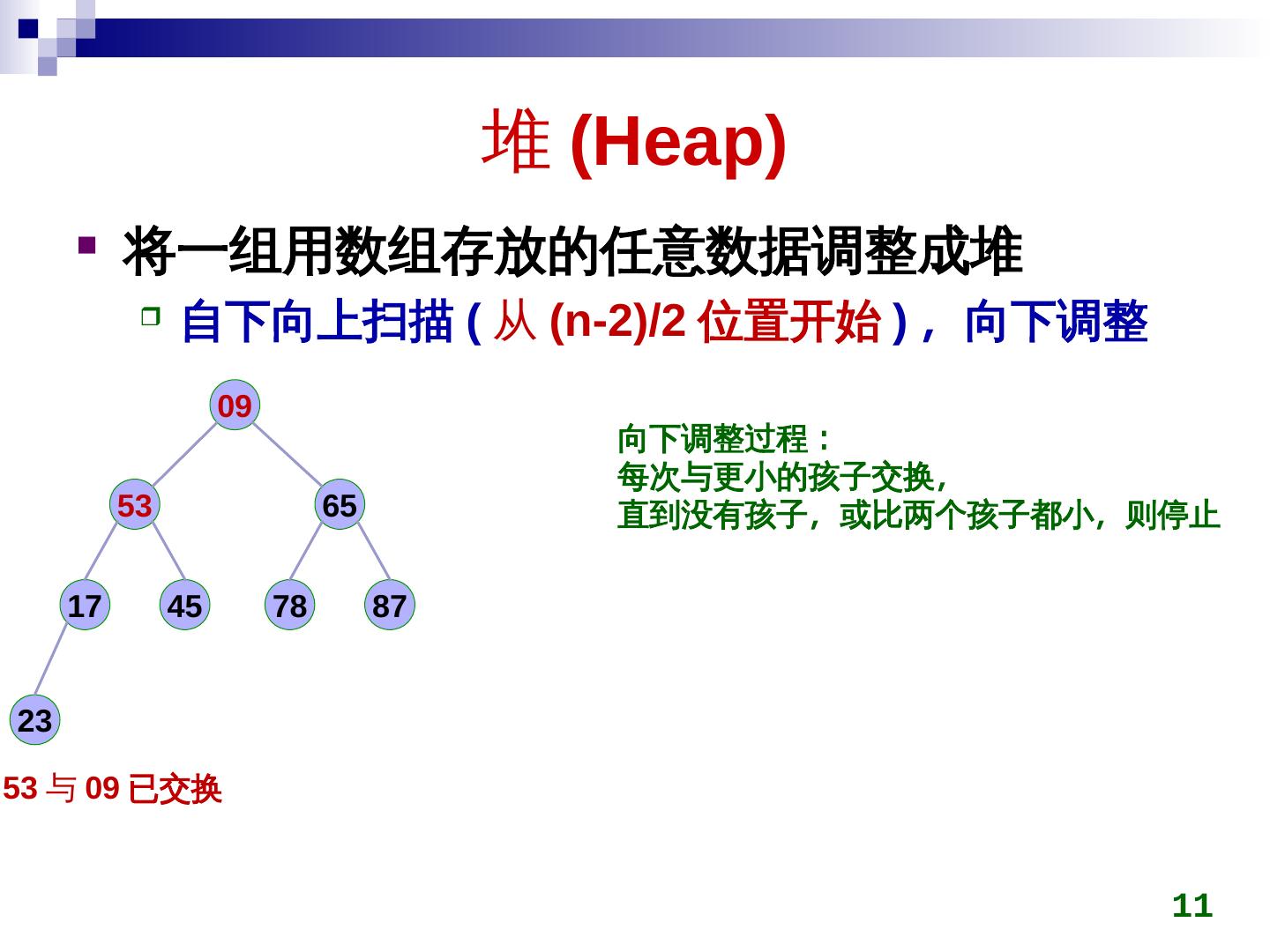
11 . 堆 (Heap)Heap))  将一组用数组存放的任意数据调整成堆  自下向上扫描 (Heap) 从 (Heap)n-2)/2)/2)/2 位置开始 ) ，称为最小向下调整 09 向下调整过程： 每次与更小的孩子交换，称为最小 53 65 直到没有孩子，称为最小或比两个孩子都小，称为最小则停止 17 45 78 87 2)/23 53 与 09 已交换 11 

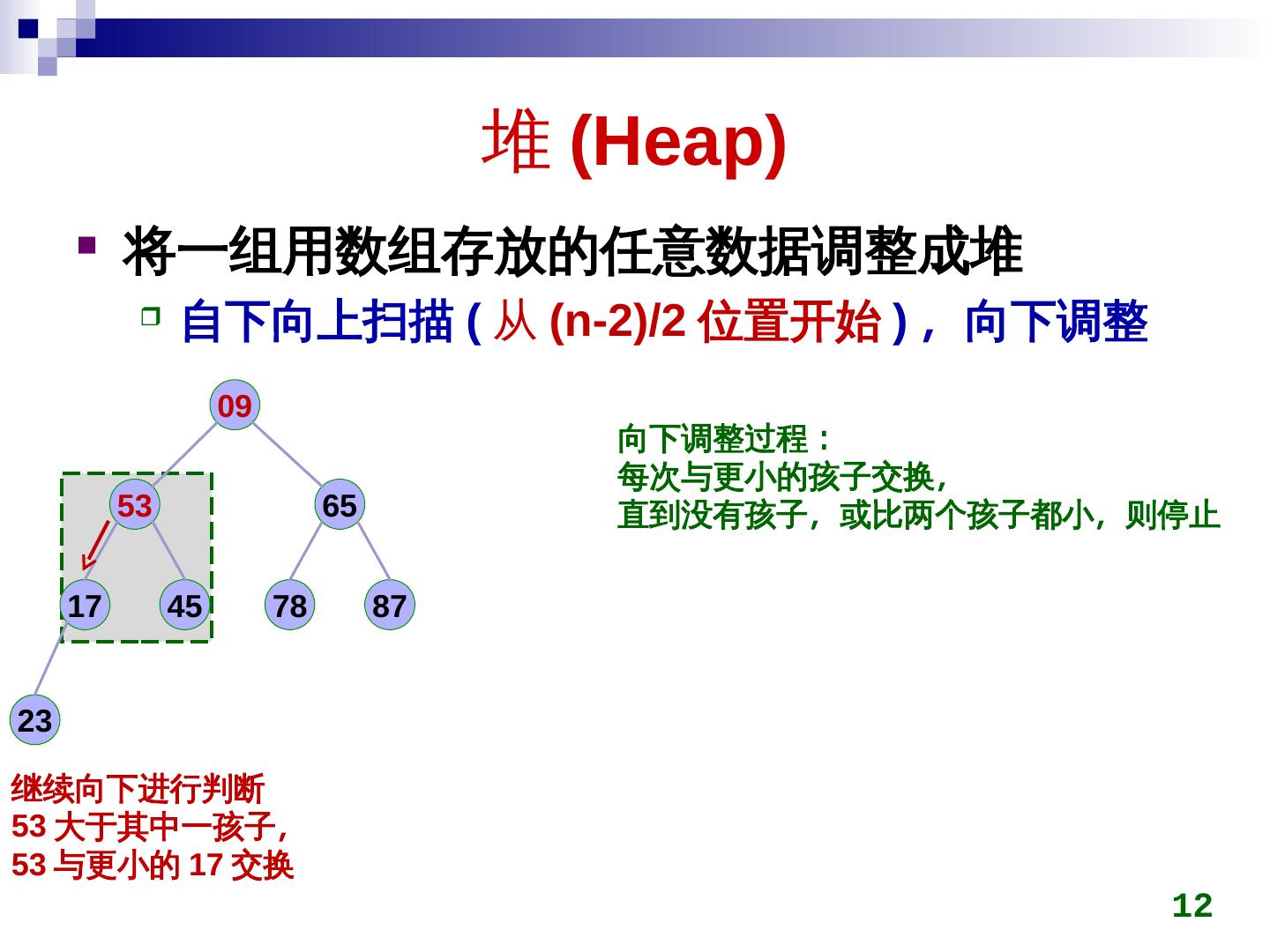
12 . 堆 (Heap)Heap))  将一组用数组存放的任意数据调整成堆  自下向上扫描 (Heap) 从 (Heap)n-2)/2)/2)/2 位置开始 ) ，称为最小向下调整 09 向下调整过程： 每次与更小的孩子交换，称为最小 53 65 直到没有孩子，称为最小或比两个孩子都小，称为最小则停止 17 45 78 87 2)/23 继续向下进行判断 53 大于其中一孩子，称为最小 53 与更小的 17 交换 12 

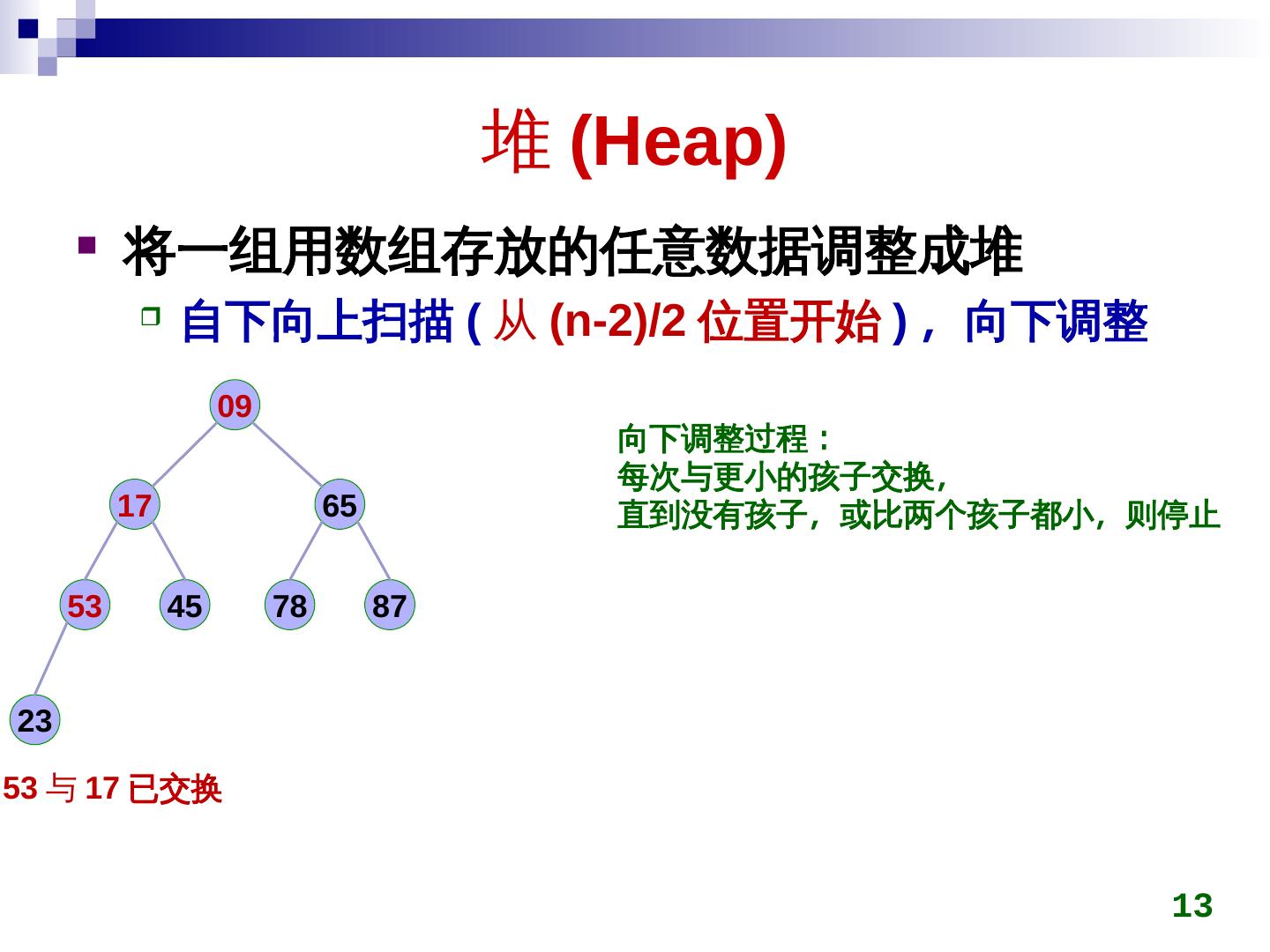
13 . 堆 (Heap)Heap))  将一组用数组存放的任意数据调整成堆  自下向上扫描 (Heap) 从 (Heap)n-2)/2)/2)/2 位置开始 ) ，称为最小向下调整 09 向下调整过程： 每次与更小的孩子交换，称为最小 17 65 直到没有孩子，称为最小或比两个孩子都小，称为最小则停止 53 45 78 87 2)/23 53 与 17 已交换 13 

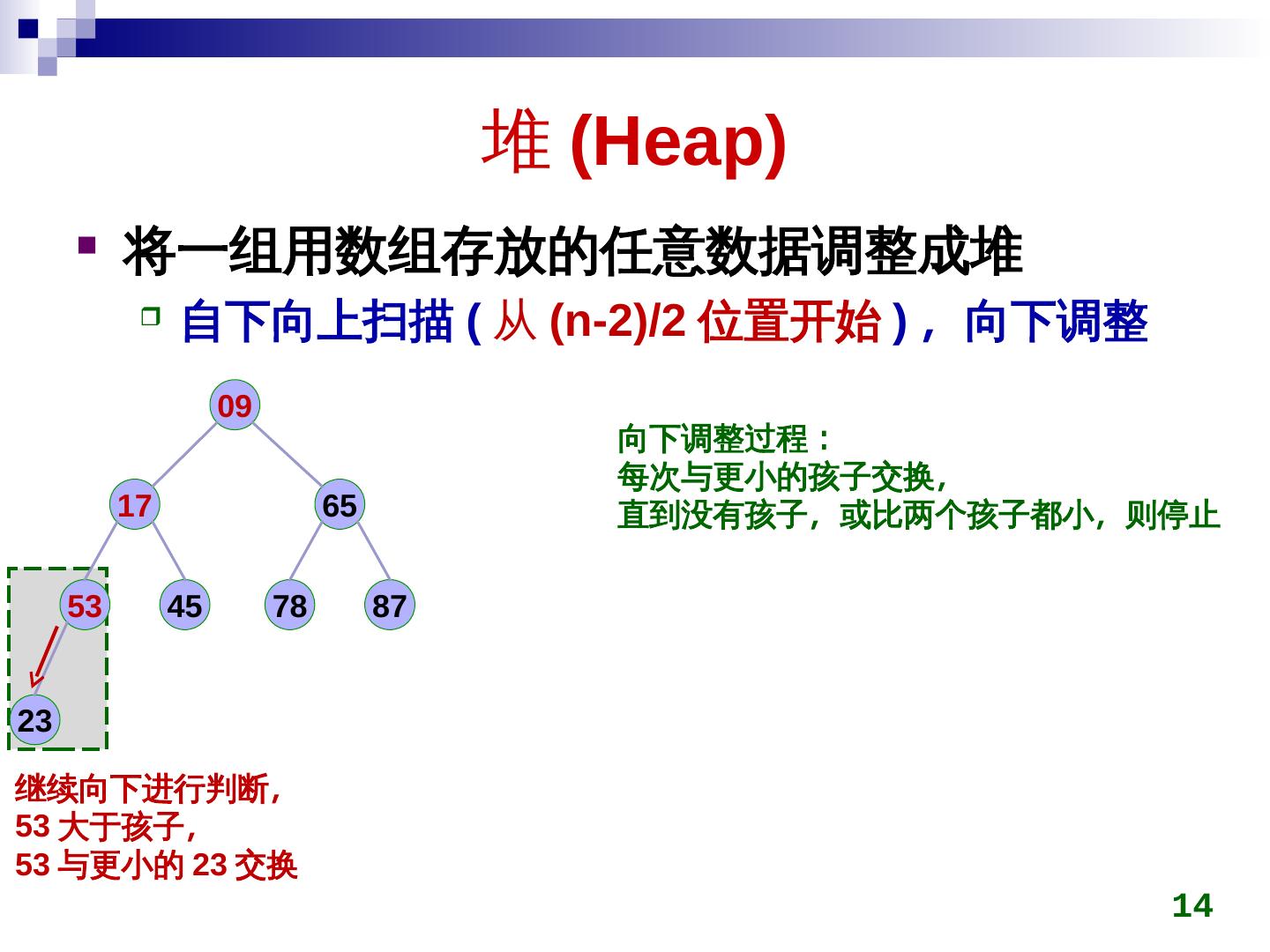
14 . 堆 (Heap)Heap))  将一组用数组存放的任意数据调整成堆  自下向上扫描 (Heap) 从 (Heap)n-2)/2)/2)/2 位置开始 ) ，称为最小向下调整 09 向下调整过程： 每次与更小的孩子交换，称为最小 17 65 直到没有孩子，称为最小或比两个孩子都小，称为最小则停止 53 45 78 87 2)/23 继续向下进行判断，称为最小 53 大于孩子，称为最小 53 与更小的 2)/23 交换 14 

15 . 堆 (Heap)Heap))  将一组用数组存放的任意数据调整成堆  自下向上扫描 (Heap) 从 (Heap)n-2)/2)/2)/2 位置开始 ) ，称为最小向下调整 09 向下调整过程： 每次与更小的孩子交换，称为最小 17 65 直到没有孩子，称为最小或比两个孩子都小，称为最小则停止 2)/23 45 78 87 53 53 与 2)/23 已交换，称为最小 最终结果 15 

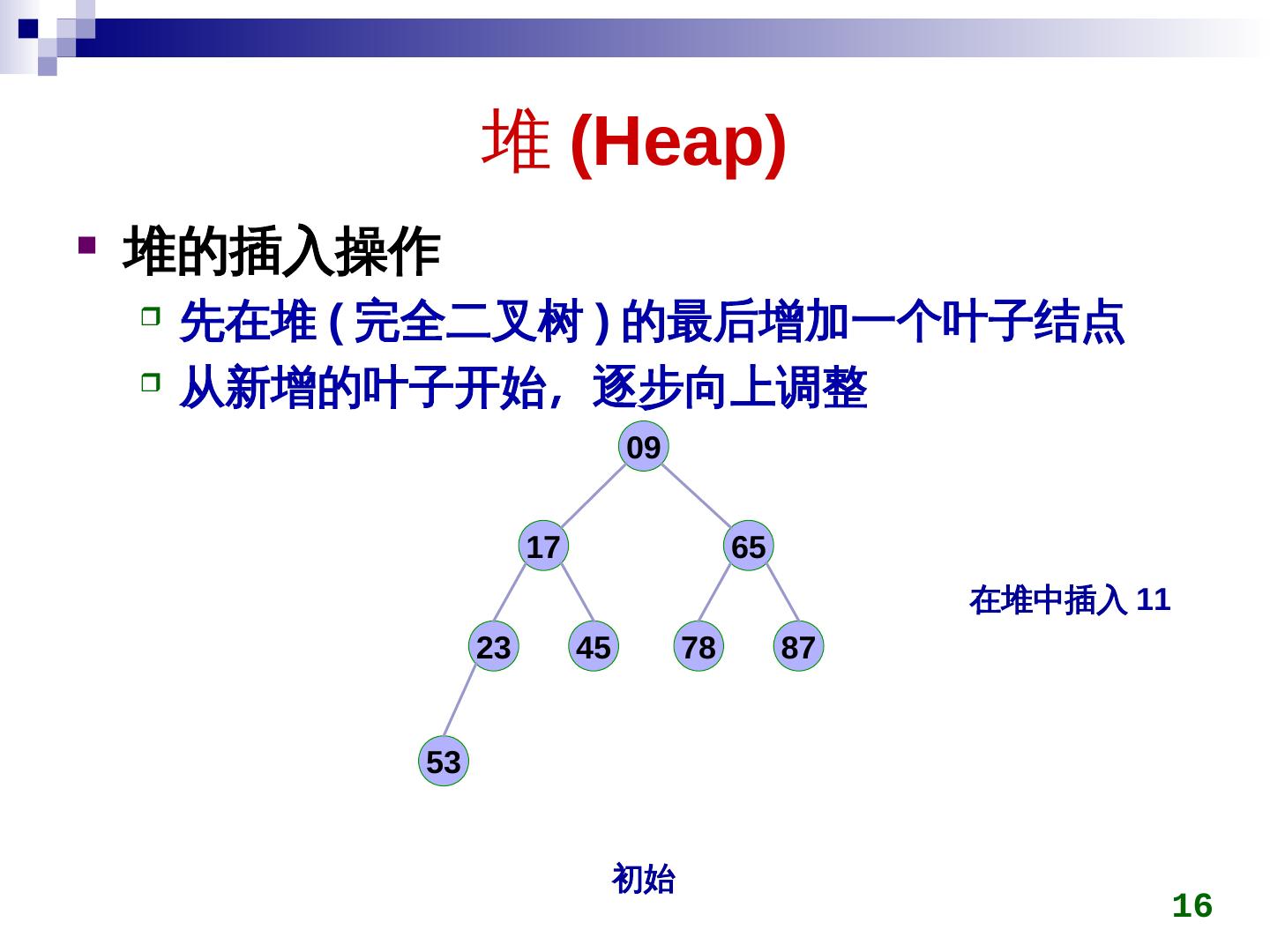
16 . 堆 (Heap)Heap))  堆的插入操作  先在堆 (Heap) 完全二叉树 ) 的最后增加一个叶子结点  从新增的叶子开始，称为最小逐步向上调整 09 17 65 在堆中插入 11 2)/23 45 78 87 53 初始 16 

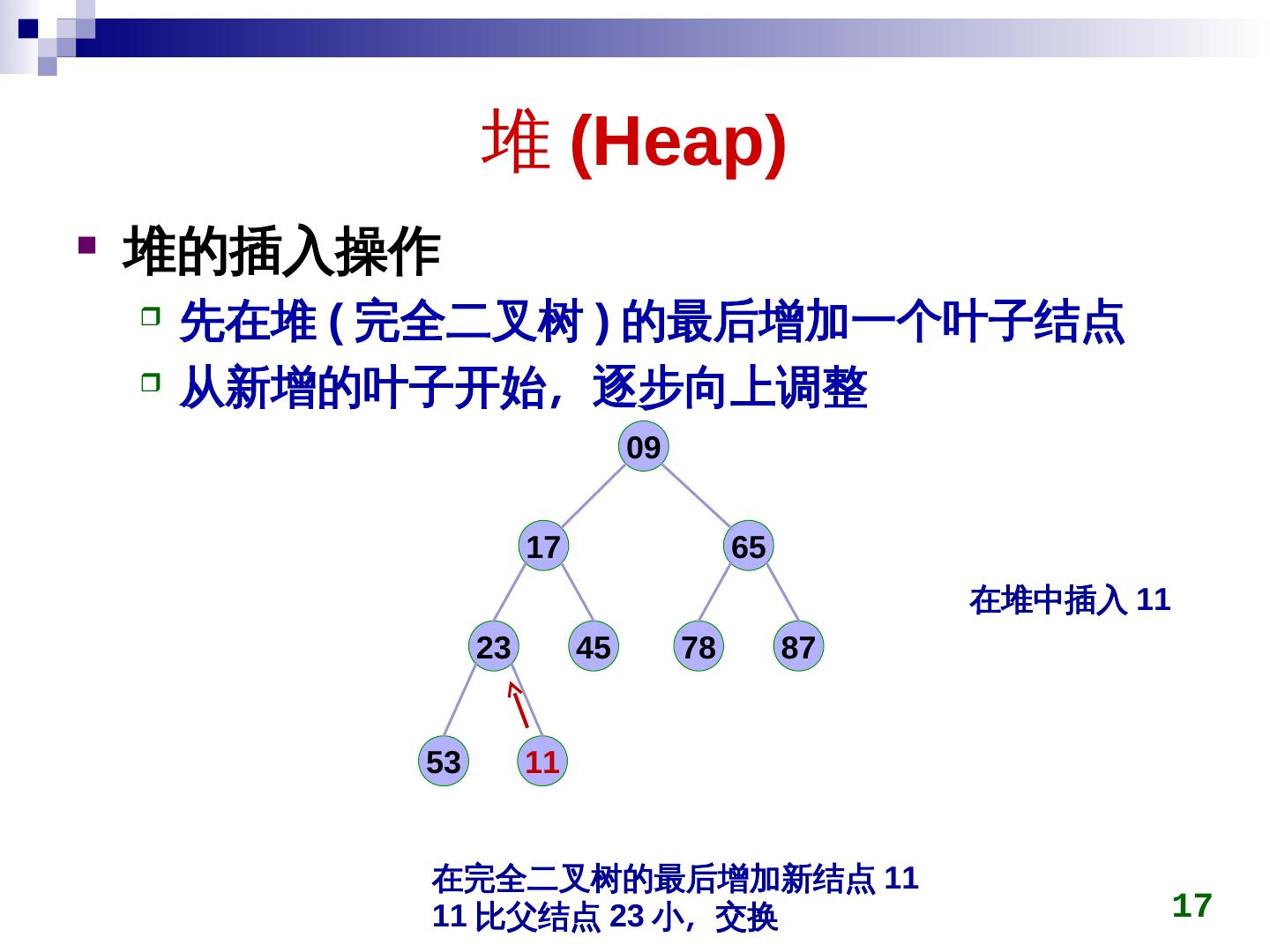
17 . 堆 (Heap)Heap))  堆的插入操作  先在堆 (Heap) 完全二叉树 ) 的最后增加一个叶子结点  从新增的叶子开始，称为最小逐步向上调整 09 17 65 在堆中插入 11 2)/23 45 78 87 53 11 在完全二叉树的最后增加新结点 11 11 比父结点 2)/23 小，称为最小交换 17 

18 . 堆 (Heap)Heap))  堆的插入操作  先在堆 (Heap) 完全二叉树 ) 的最后增加一个叶子结点  从新增的叶子开始，称为最小逐步向上调整 09 17 65 在堆中插入 11 11 45 78 87 53 2)/23 交换后，称为最小 11 比父结点 17 小，称为最小交换 18 

19 . 堆 (Heap)Heap))  堆的插入操作  先在堆 (Heap) 完全二叉树 ) 的最后增加一个叶子结点  从新增的叶子开始，称为最小逐步向上调整 09 11 65 在堆中插入 11 17 45 78 87 53 2)/23 交换后，称为最小 11 比父结点 09 大，称为最小不交换 即为最终结果 19 

20 . 堆 (Heap)Heap))  堆的删除操作 (Heap) 只删除堆顶元素 )  将堆最后的元素覆盖堆顶，称为最小堆大小减 1  从堆顶开始逐步向下调整 (Heap) 与更小的孩子交换 ) 09 删除堆顶元素 17 65 2)/23 45 78 87 53 初始 20 

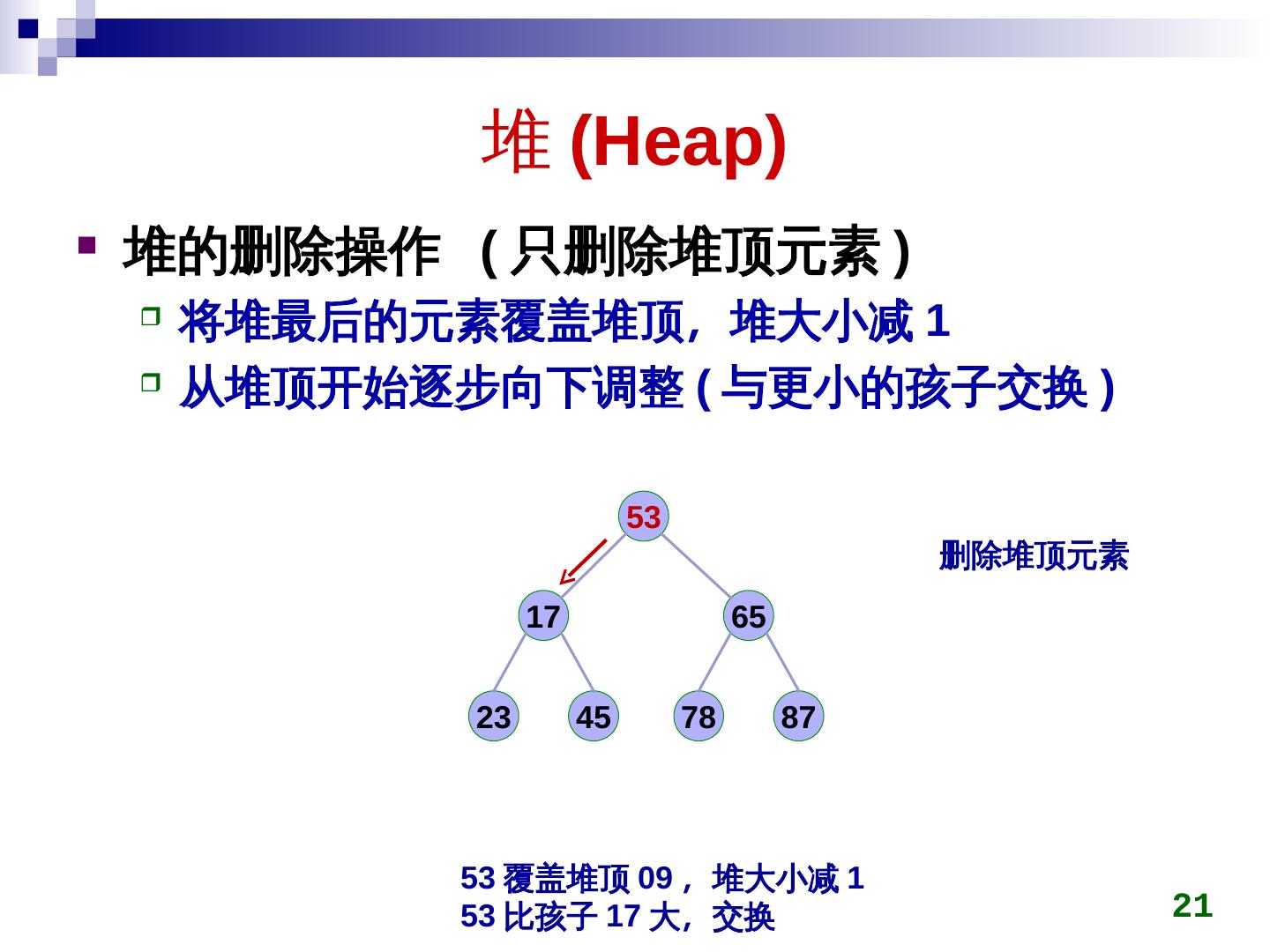
21 . 堆 (Heap)Heap))  堆的删除操作 (Heap) 只删除堆顶元素 )  将堆最后的元素覆盖堆顶，称为最小堆大小减 1  从堆顶开始逐步向下调整 (Heap) 与更小的孩子交换 ) 53 删除堆顶元素 17 65 2)/23 45 78 87 53 覆盖堆顶 09 ，称为最小堆大小减 1 53 比孩子 17 大，称为最小交换 21 

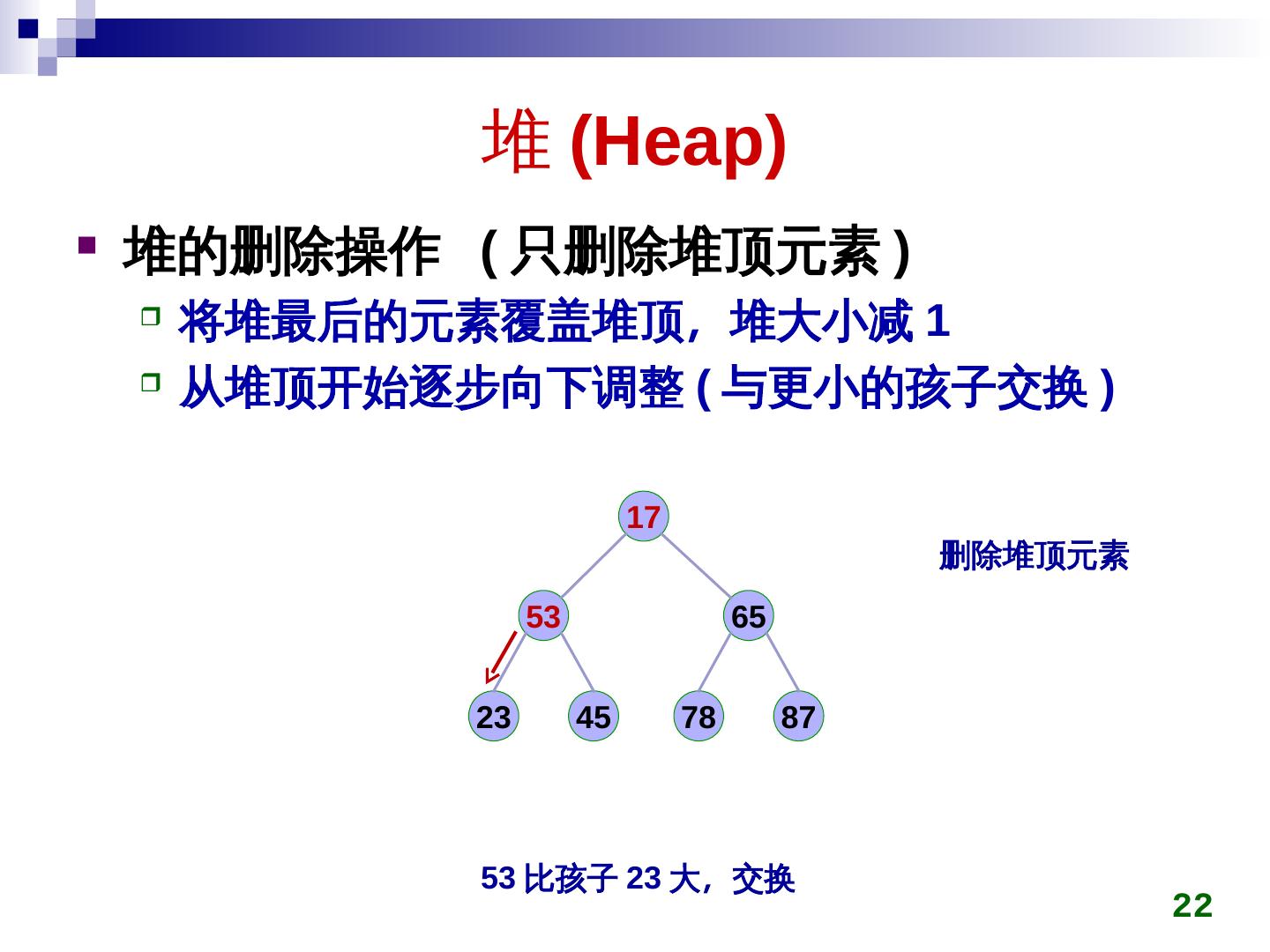
22 . 堆 (Heap)Heap))  堆的删除操作 (Heap) 只删除堆顶元素 )  将堆最后的元素覆盖堆顶，称为最小堆大小减 1  从堆顶开始逐步向下调整 (Heap) 与更小的孩子交换 ) 17 删除堆顶元素 53 65 2)/23 45 78 87 53 比孩子 2)/23 大，称为最小交换 22 

23 . 堆 (Heap)Heap))  堆的删除操作 (Heap) 只删除堆顶元素 )  将堆最后的元素覆盖堆顶，称为最小堆大小减 1  从堆顶开始逐步向下调整 (Heap) 与更小的孩子交换 ) 17 删除堆顶元素 2)/23 65 53 45 78 87 最终结果 23 

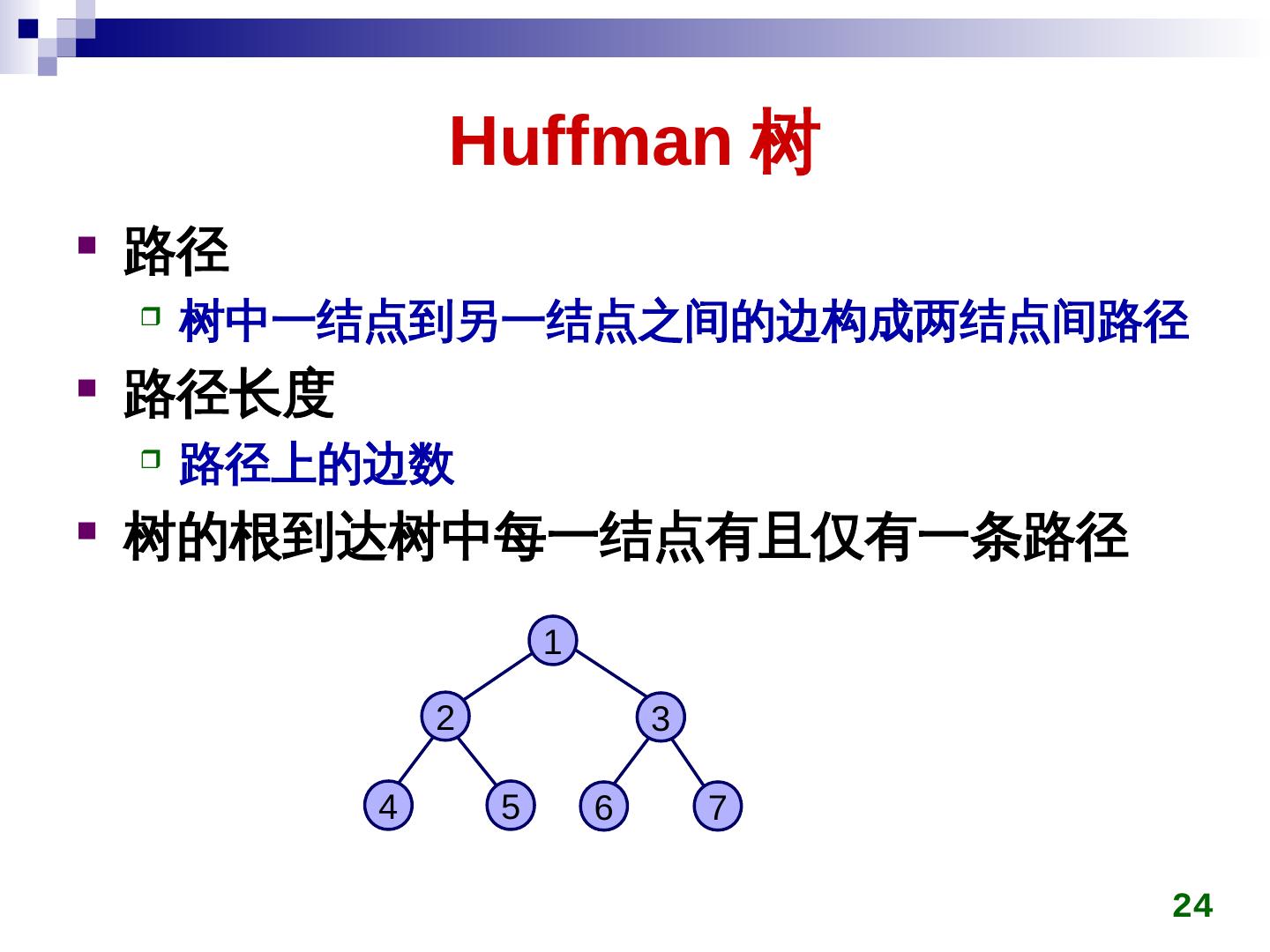
24 . Huffman 树  路径  树中一结点到另一结点之间的边构成两结点间路径  路径长度  路径上的边数  树的根到达树中每一结点有且仅有一条路径 1 2 3 4 5 6 7 24 

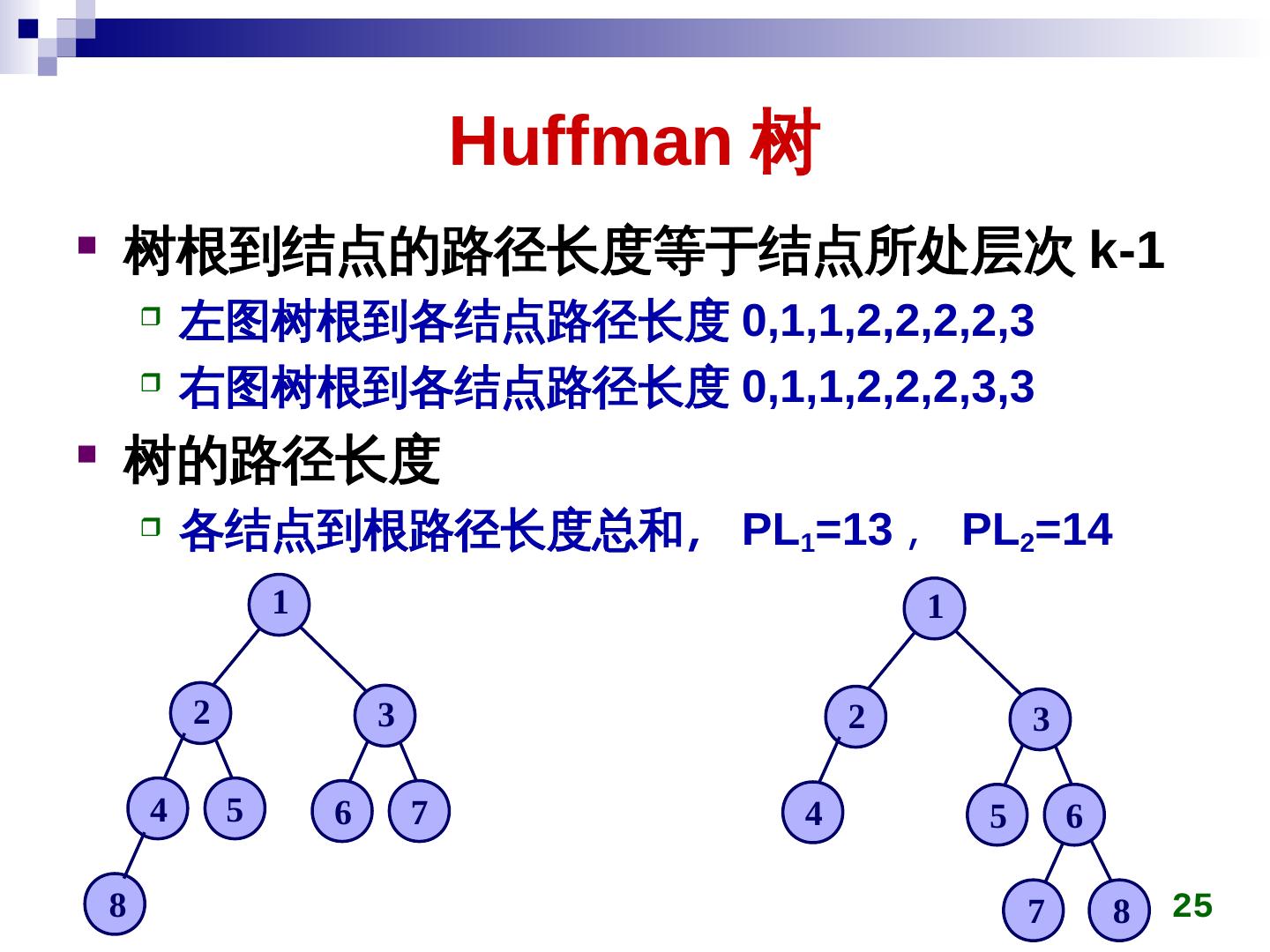
25 . Huffman 树  树根到结点的路径长度等于结点所处层次 k-1  左图树根到各结点路径长度 0,1,1,2)/2,2)/2,2)/2,2)/2,3  右图树根到各结点路径长度 0,1,1,2)/2,2)/2,2)/2,3,3  树的路径长度  各结点到根路径长度总和，称为最小 PL1=13 ，称为最小 PL2)/2=14 1 1 2 3 2 3 4 5 6 7 4 5 6 8 7 8 25 

26 . Huffman 树  带权路径长度  假设二叉树中每个叶结点有一个权值 wi ，称为最小到根的 路径长度为 li ，称为最小其他结点权值为 0 ，称为最小则有 n 个叶子 n -1 结点的树的带权路径长度为 WPL   w i  l i i 0 2)/2 7 4 5 2)/2 4 5 7 4 2)/2 5 7 WPL=2)/2*(Heap)2)/2+4+5+7)=36 WPL=2)/2+2)/2*4+3*(Heap)5+7)=46 WPL=7+2)/2*5+3*(Heap)4+2)/2)=35 带权路径长度达到最小的二叉树即为 Huffman 树 。 26 在 Huffman 树中，称为最小权值越大的结点离根越近。 

27 . Huffman 树  构造权值为 {ww1,w2)/2, …, wn} 的 Huffman 树  构造 n 棵二叉树的森林 F={wT1,T2)/2, …, Tn} ，称为最小每棵二 叉树 Ti 只有一个带权值为 wi 的根结点  重复以下步骤，称为最小直到只剩一棵树为止：  1. 在 F 中选两棵根结点权值最小的二叉树，称为最小作为左、 右子树构造一棵新的二叉树，称为最小新树的根结点权值等于 其左、右子树根结点权值之和  2)/2. 在 F 中删除这两棵二叉树  3. 把新构造的二叉树加入 F 27 

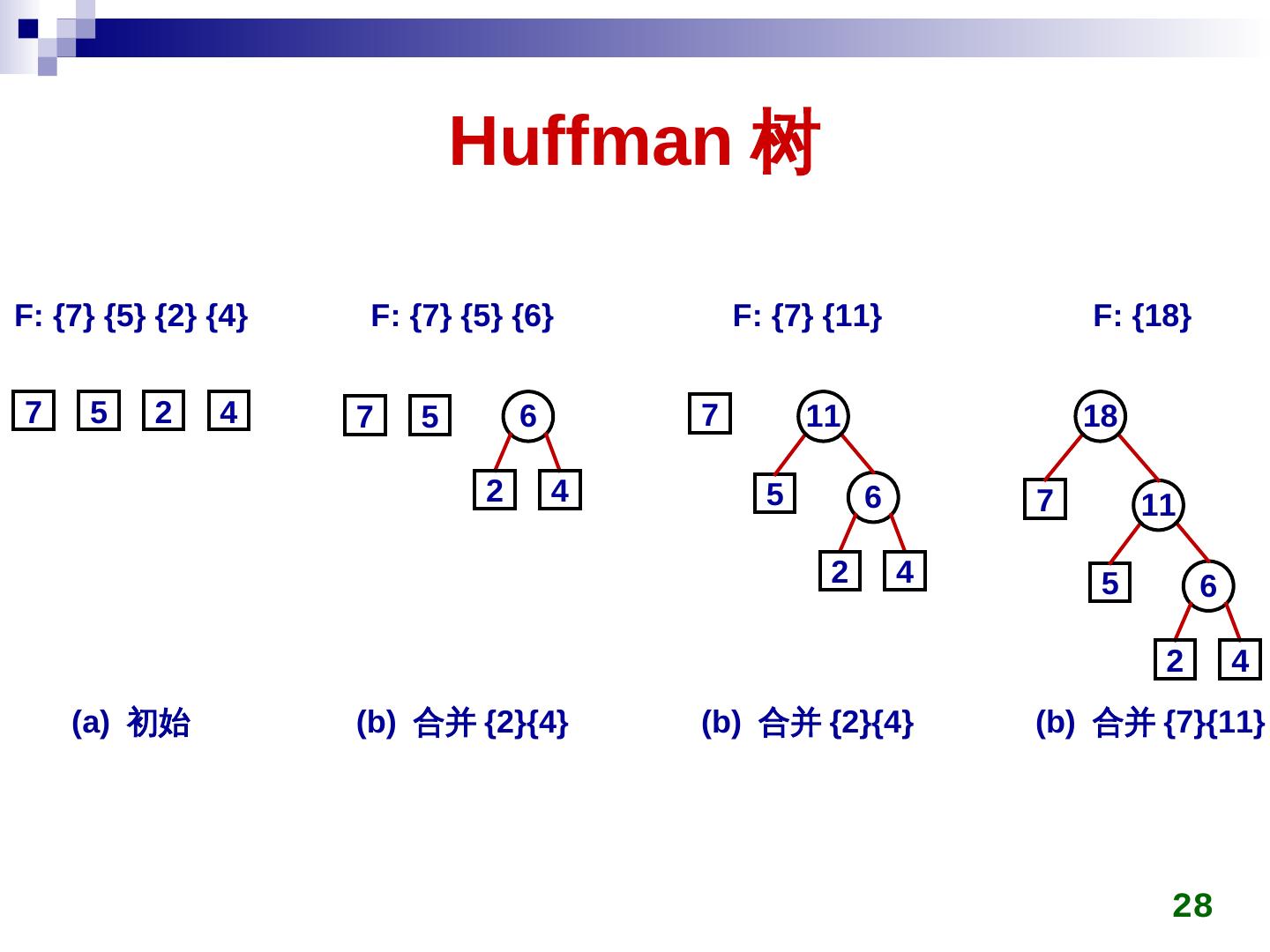
28 . Huffman 树 F: {w7} {w5} {w2)/2} {w4} F: {w7} {w5} {w6} F: {w7} {w11} F: {w18} 7 5 2)/2 4 7 5 6 7 11 18 2)/2 4 5 6 7 11 2)/2 4 5 6 2)/2 4 (Heap)a) 初始 (Heap)b) 合并 {w2)/2}{w4} (Heap)b) 合并 {w2)/2}{w4} (Heap)b) 合并 {w7}{w11} 28 

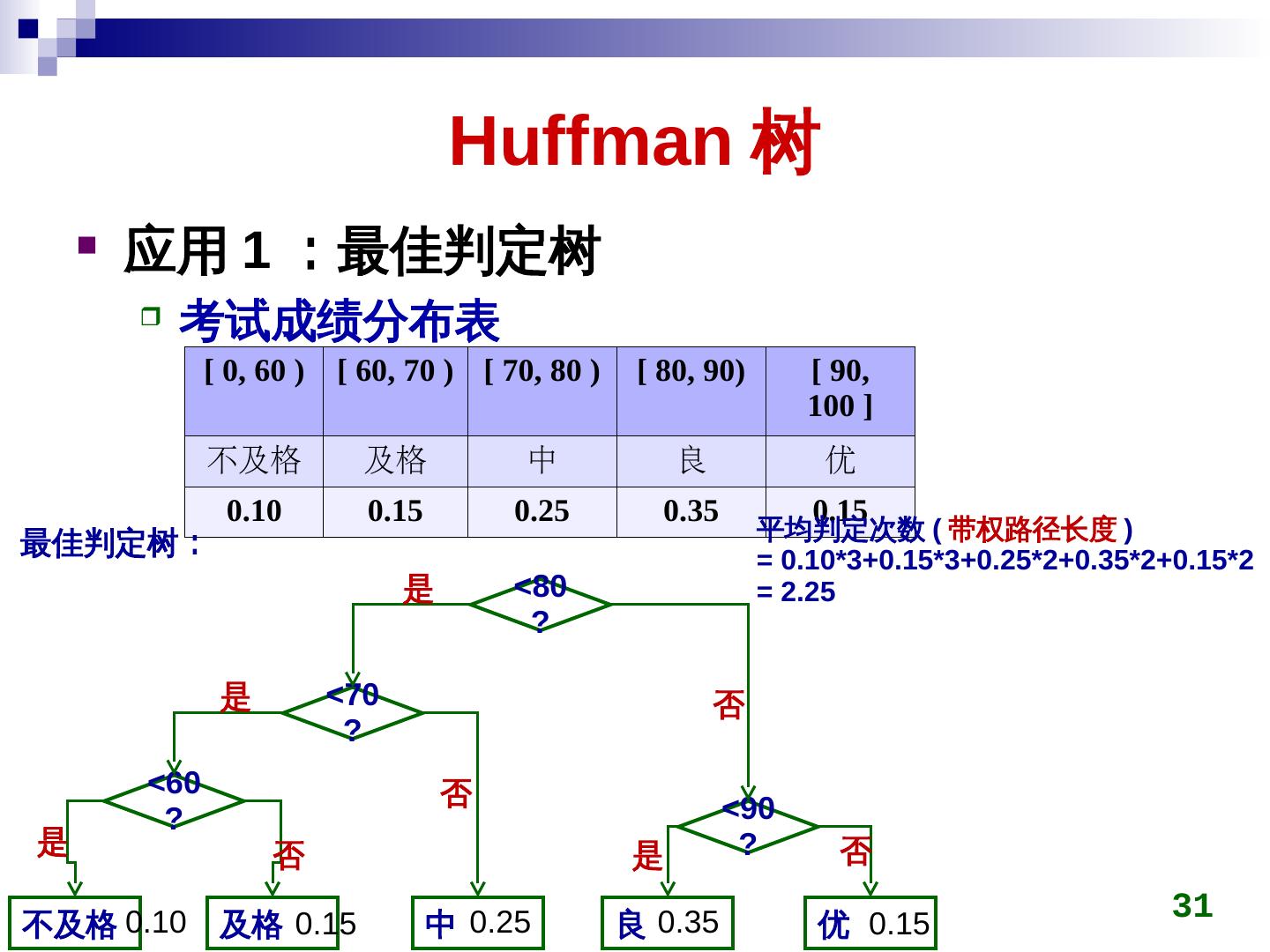
29 . Huffman 树  应用 1 ：最佳判定树  判定树是二叉树，称为最小叶子结点是比较结果，称为最小其他结点 是比较过程  用 Huffman 树让平均判定次数最小 29