05数据结构---树1

1 . 第五章 树 东南大学计算机学院 方效林 方效林 本课件借鉴了清华大学殷人昆老师 和哈尔滨工业大学张岩老师的课件 

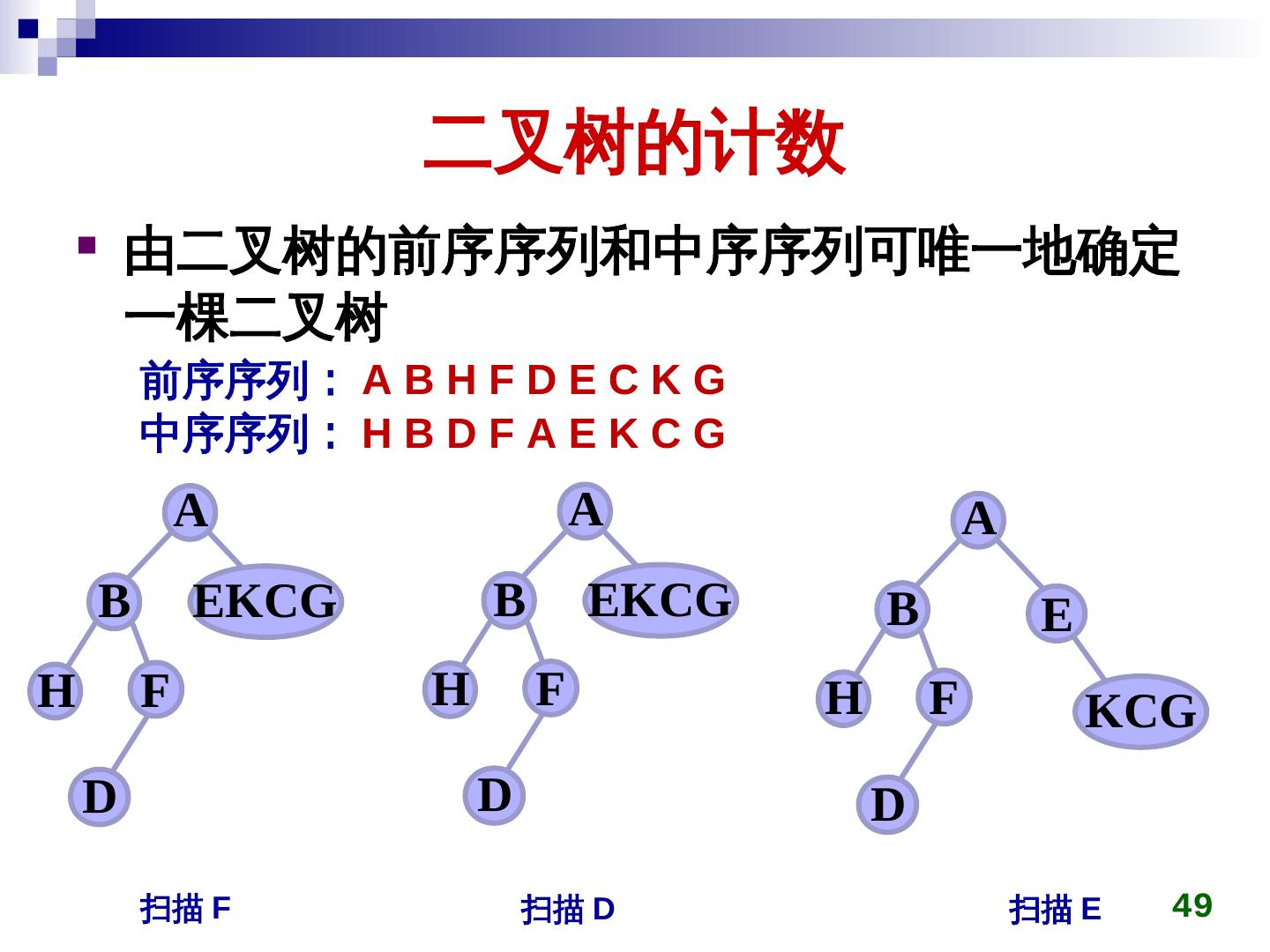
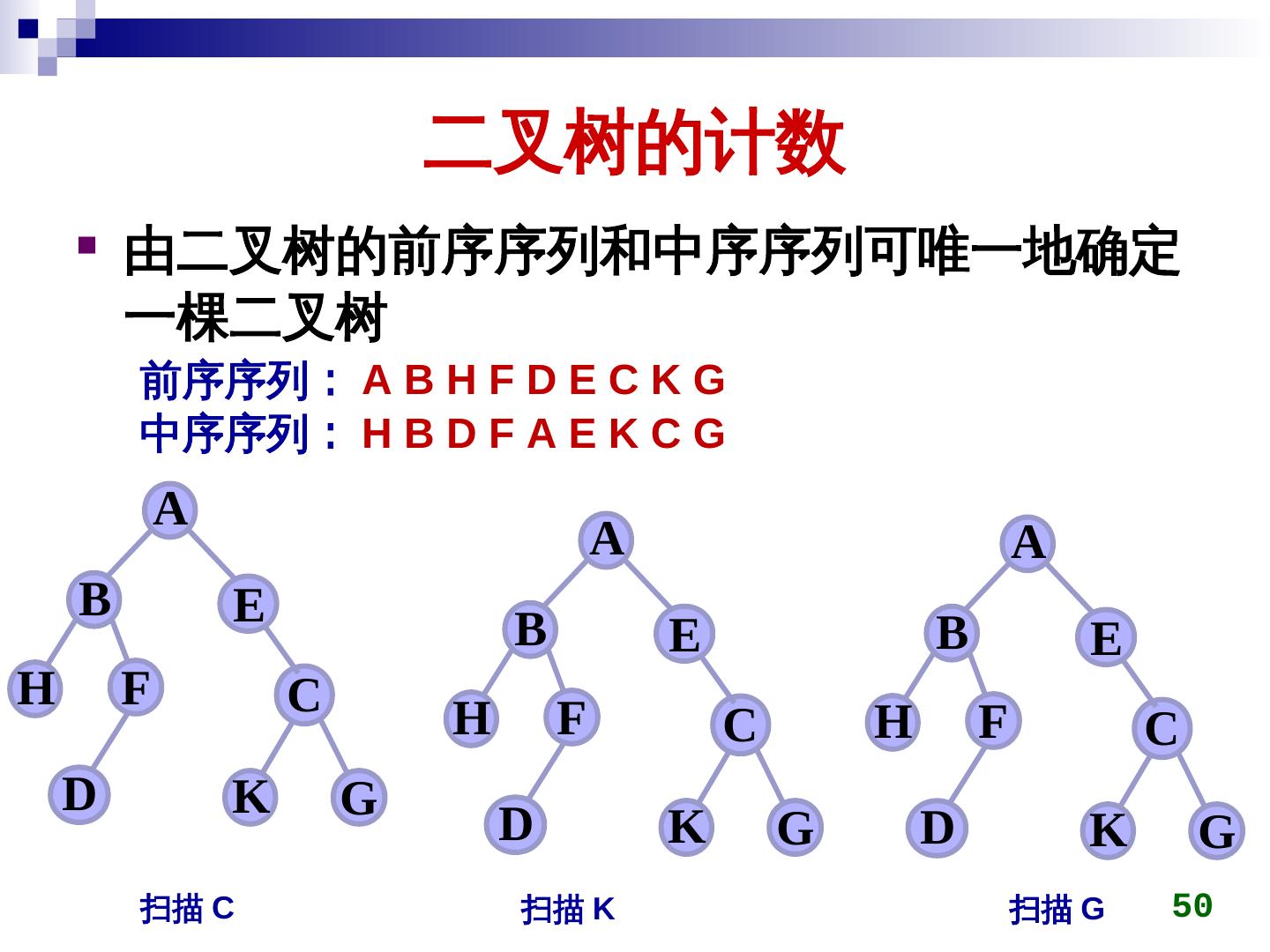
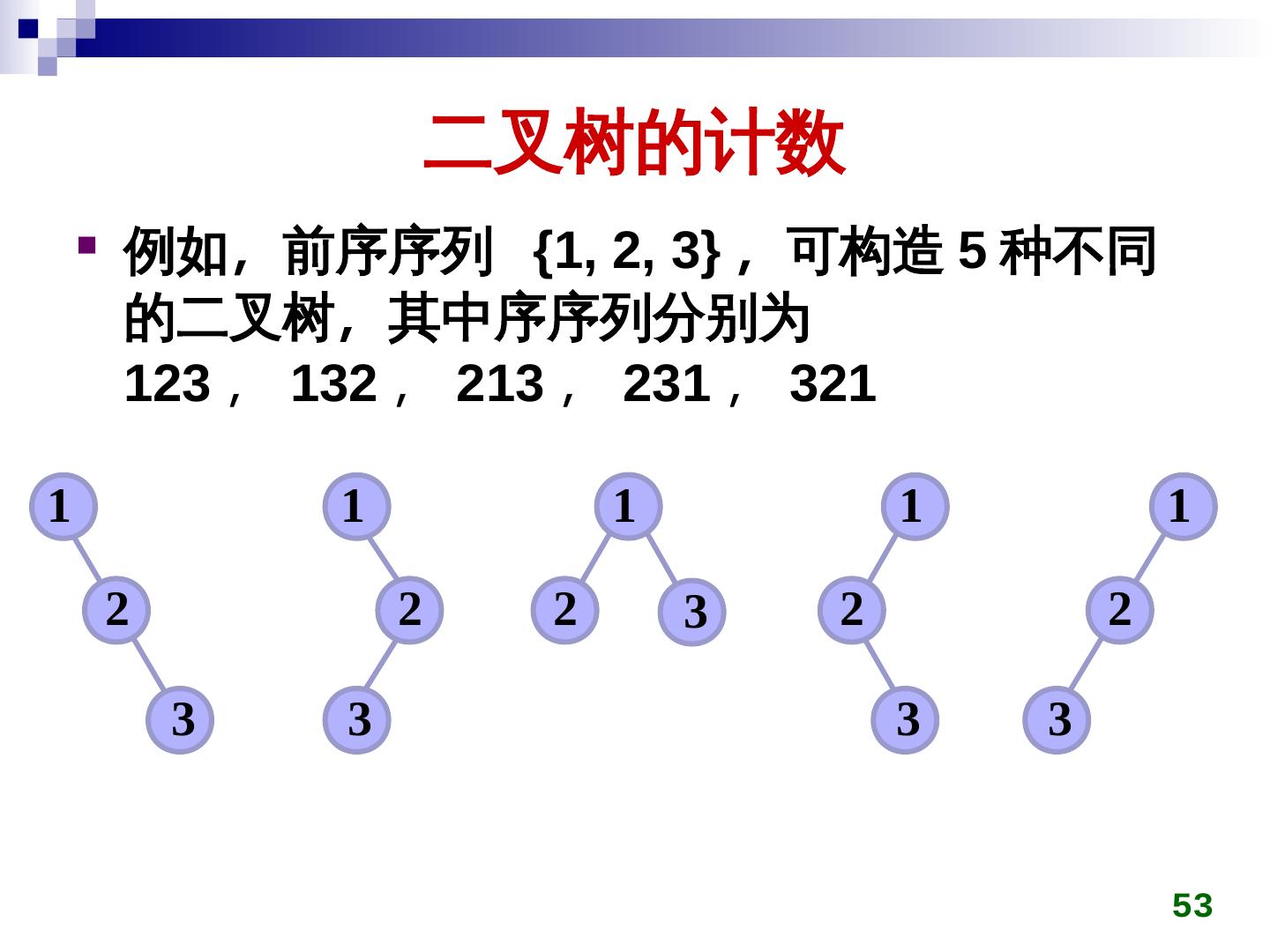
2 . 本章主要内容  树的基本概念  二叉树  二叉树的存储表示  二叉树的遍历及其应用  二叉树遍历的非递归算法  二叉树的计数  树与二叉树的转换  堆  Huffman 树及其应用 2 

3 . 树的基本概念  树是由 n (n>0) 个结点组成的有限集合：  有一个特定的称之为根 (root) ) 的结点；  除根以外的其它结点划分为 m (m≥0) 个互不相 交的有限集合 T1, T2, …, Tm ，其中每个集合也是一其中每个集合也是一 棵树，其中每个集合也是一并被称为根的子树。  这个定义是递归的 3 

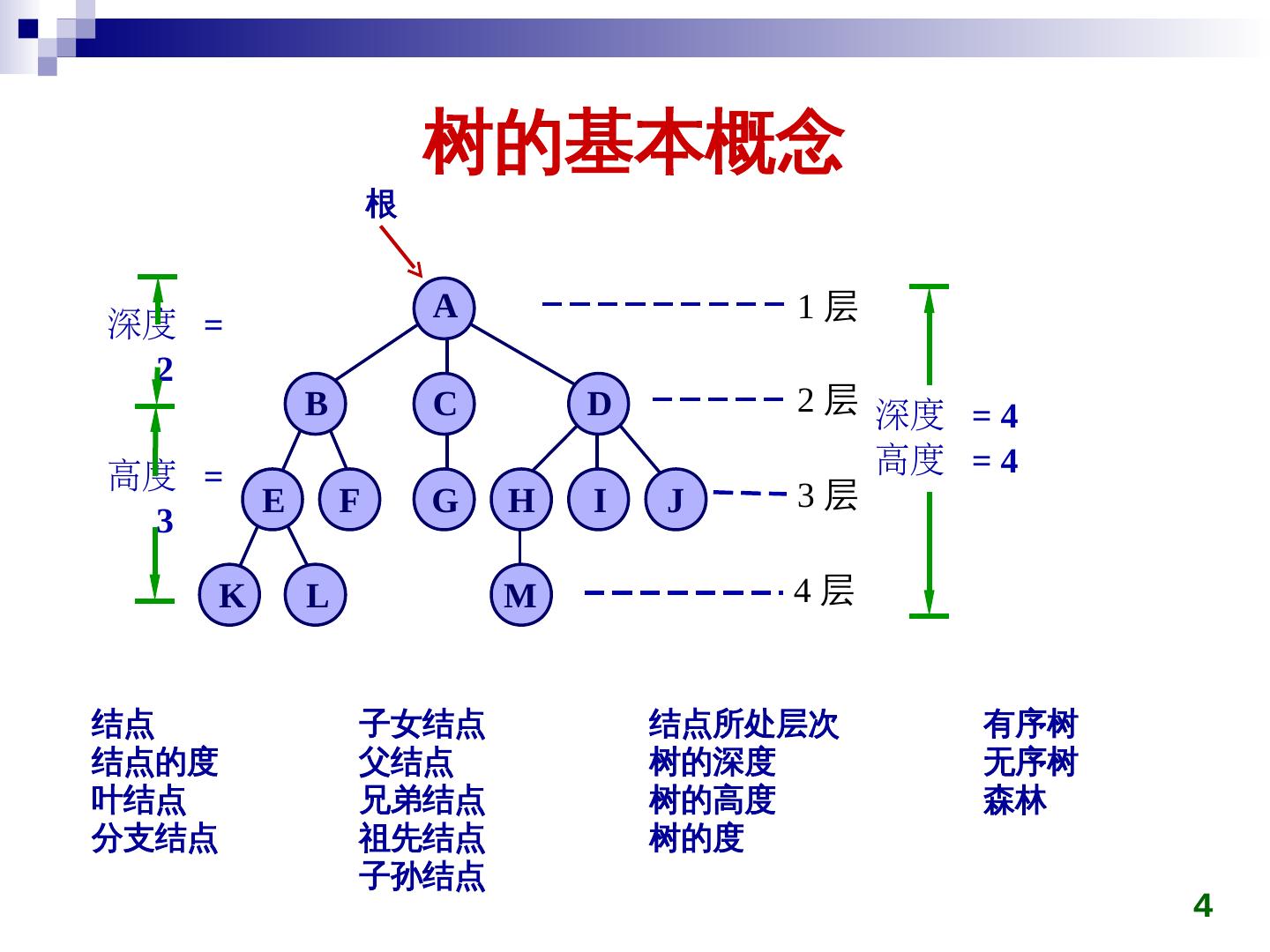
4 . 树的基本概念 根 A 1层 深度 = 2 B C D 2 层 深度 = 4 高度 = 高度 = 4 E F G H I J 3层 3 K L M 4层 结点 子女结点 结点所处层次 有序树 结点的度 父结点 树的深度 无序树 叶结点 兄弟结点 树的高度 森林 分支结点 祖先结点 树的度 子孙结点 4 

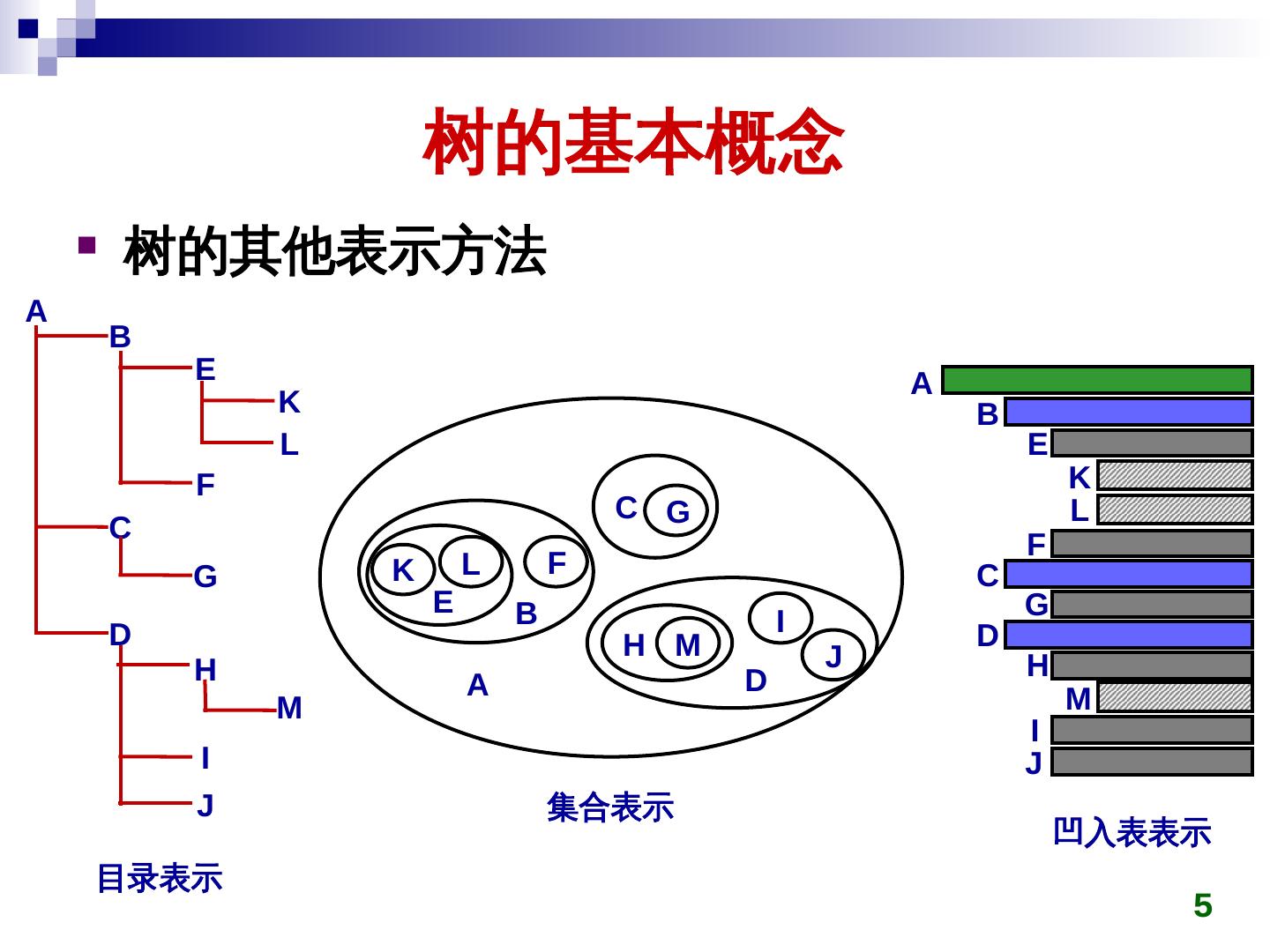
5 . 树的基本概念  树的其他表示方法 A B E A K B L E F K C G L C F G K L F C E B G D I D H M J H D H A M M I I J J 集合表示 凹入表表示 目录表示 5 

6 . 二叉树  二叉树是结点的有限集合：  该集合或者为空；  或者由一个根结点加上两棵分别称为左子树和右子 树的、互不相交的二叉树组成。  这个定义也是递归的 Ф L R L R 空 只有根 右子树为空 右子树为空 左右子树不为空 6 

7 . 二叉树  性质 1  若二叉树的层次从 1 开始 , 则在二叉树的第 i ( i≥1) 层最多有 2i-1 个结点。  证明： ( 用数学归纳法 )  i = 1 时，其中每个集合也是一根结点只有 1 个，其中每个集合也是一 21-1 = 20 =1 ；  若设 i = k 时性质成立，其中每个集合也是一即该层最多有 2k-1 个结点 ，其中每个集合也是一则当 i = k+1 时，其中每个集合也是一由于第 k 层每个结点最多可有 2 个子女，其中每个集合也是一第 k+1 层最多结点个数可有 2*2k-1 = 2k 个，其中每个集合也是一故性质成立。 7 

8 . 二叉树  性质 2  高度为 h (h≥1) 的二叉树最多有 2h -1 个结点。  证明： ( 用求等比级数前 k 项和的公式 )  高度为 h 的二叉树有 h 层，其中每个集合也是一各层最多结点个数相 加，其中每个集合也是一得到等比级数，其中每个集合也是一求和得：  20 + 21 + 22 + … + 2h-1 = 2h-1  空树的高度为 0 ，其中每个集合也是一只有根结点的树的高度为 1 。 8 

9 . 二叉树  性质 3  对任何一棵非空二叉树 , 如果其叶结点有 n0 个 , 度为 2 的非叶结点有 n2 个 , 则有 n0 ＝ n2 ＋ 1  证明：  若设度为 1 的结点有 n1 个，其中每个集合也是一总结点个数为 n ，其中每个集合也是一总 边数为 e ，其中每个集合也是一则根据二叉树的定义，其中每个集合也是一  n = n0+n1+n2 ，其中每个集合也是一且 e = 2n2+n1 = n-1  因此，其中每个集合也是一有 2n2+n1 = n0+n1+n2-1  n2 = n0-1 ，其中每个集合也是一 n0 = n2+1 9 

10 . 二叉树  满二叉树  深度为 k 的满二叉树是有 2k-1 个结点的二叉树  特点：每一层结点数都达到了最大数  完全二叉树  深度为 k 的完全二叉树中每一个结点的编号都与 深度为 k 的满二叉树中编号一一对应  特点：从第 1 层到第 k-1 层是满的，其中每个集合也是一仅最下面第 k 层或是满的，其中每个集合也是一或是从右到左缺若干结点 10 

11 . 二叉树 1 1 2 3 2 3 4 5 6 7 4 5 6 7 8 9 10 11 12 13 14 15 8 9 10 满二叉树 完全二叉树 11 

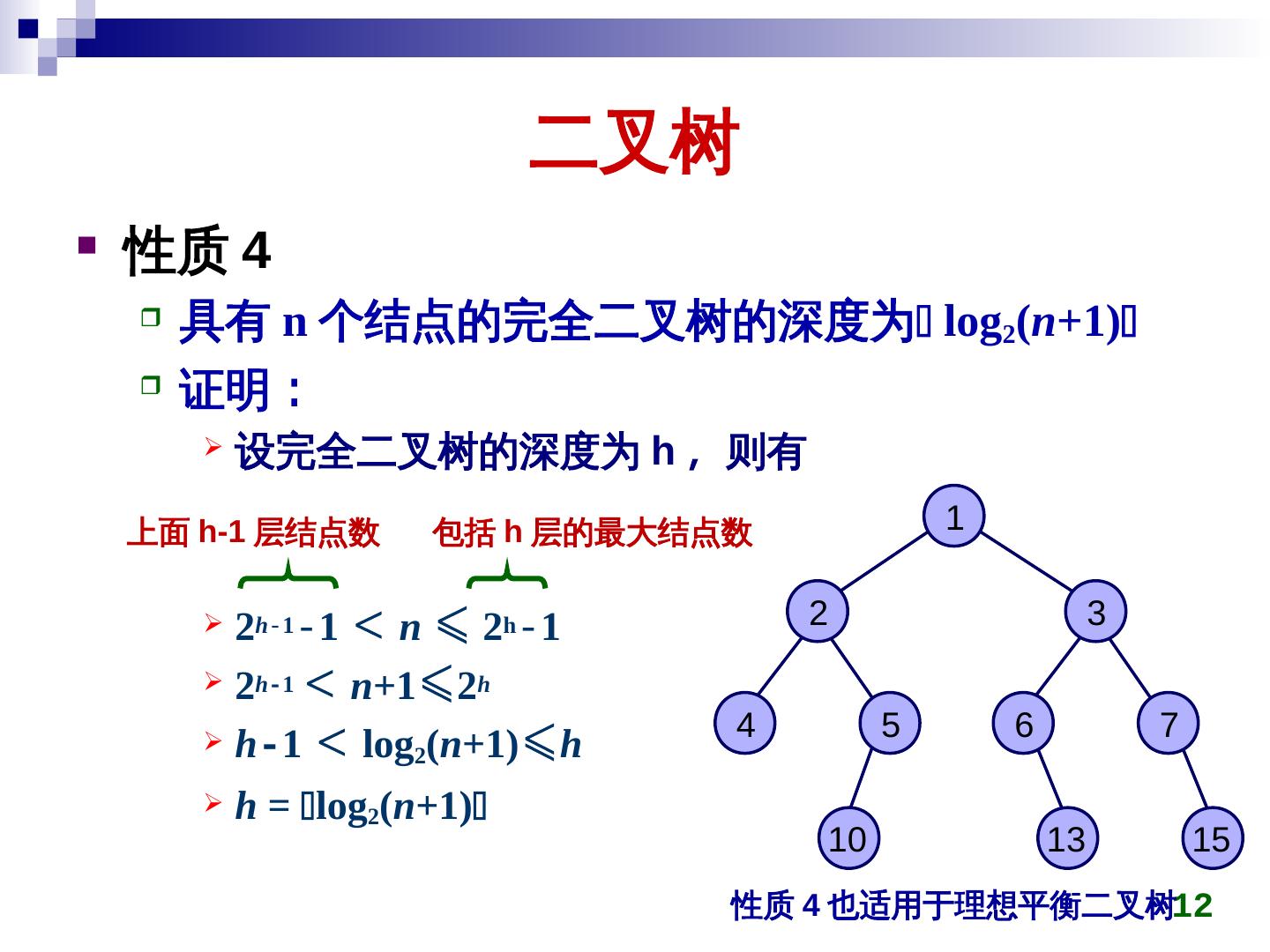
12 . 二叉树  性质 4  具有 n 个结点的完全二叉树的深度为 log2(n+1)  证明：  设完全二叉树的深度为 h ，其中每个集合也是一则有 上面 h-1 层结点数 包括 h 层的最大结点数 1  2h-1-1 ＜ n ≤ 2h-1 2 3  2h-1 ＜ n+1≤2h  h-1 ＜ log2(n+1)≤h 4 5 6 7  h = log2(n+1) 10 13 15 性质 4 也适用于理想平衡二叉树12 

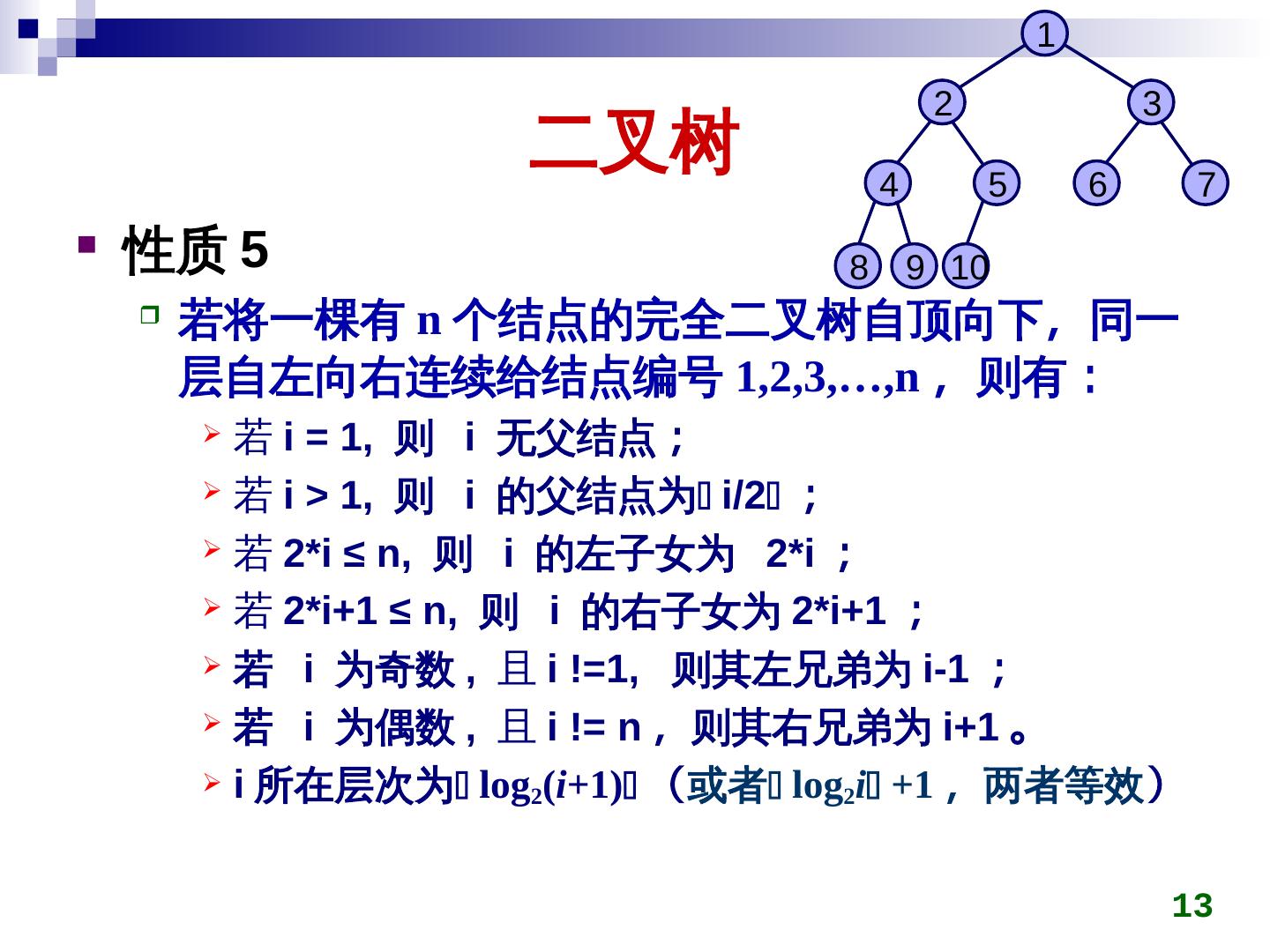
13 . 1 2 3 二叉树 4 5 6 7  性质 5 8 9 10  若将一棵有 n 个结点的完全二叉树自顶向下，其中每个集合也是一同一 层自左向右连续给结点编号 1,2,3,…,n ，其中每个集合也是一则有：  若 i = 1, 则 i 无父结点；  若 i > 1, 则 i 的父结点为 i/2 ；  若 2*i ≤ n, 则 i 的左子女为 2*i ；  若 2*i+1 ≤ n, 则 i 的右子女为 2*i+1 ；  若 i 为奇数 , 且 i !=1, 则其左兄弟为 i-1 ；  若 i 为偶数 , 且 i != n ，其中每个集合也是一则其右兄弟为 i+1 。  i 所在层次为 log2(i+1) （或者 log2i +1 ，其中每个集合也是一两者等效） 13 

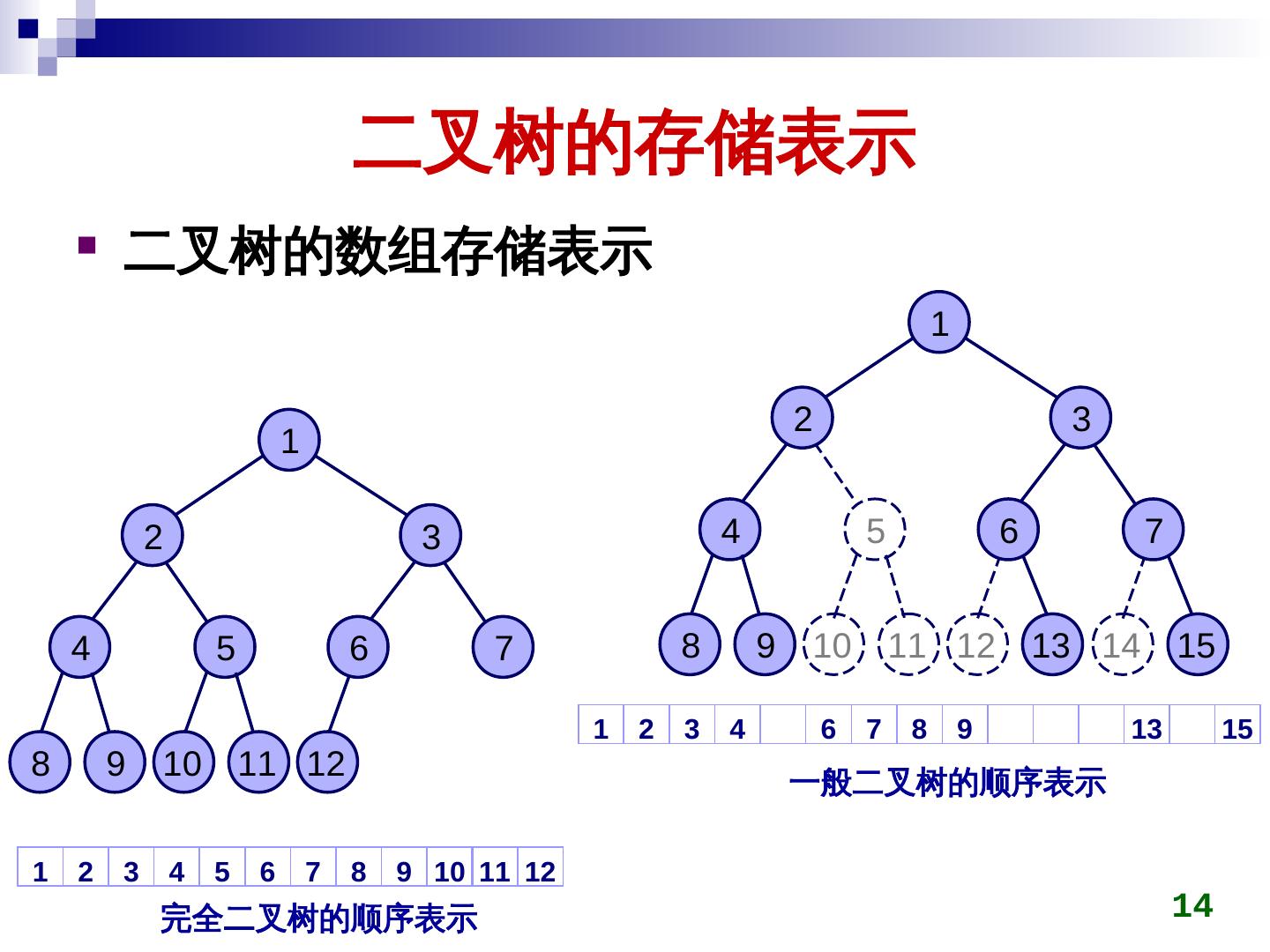
14 . 二叉树的存储表示  二叉树的数组存储表示 1 2 3 1 2 3 4 5 6 7 4 5 6 7 8 9 10 11 12 13 14 15 1 2 3 4 6 7 8 9 13 15 8 9 10 11 12 一般二叉树的顺序表示 1 2 3 4 5 6 7 8 9 10 11 12 完全二叉树的顺序表示 14 

15 . 二叉树的存储表示  二叉树的数组存储表示  完全二叉树适用于数组存储表示 1  一般二叉树不适用 2 3 4 5 6 7 8 9 10 11 12 13 14 15 1 3 7 15 单支树的顺序表示 15 

16 . St) ruct) TNode{ 二叉树的存储表示 Type Dat) a; TNode *left) Child; TNode *right) Child;  二叉树的链表存储表示 TNode *parent) ; }; 左孩子指针 右孩子指针 左孩子指针 右孩子指针 left) Child dat) a right) Child left) Child dat) a parent) right) Child parent) dat) a dat) a left) Child right) Child left) Child right) Child 二叉链表 三叉链表 找子女时间 O(1) ，其中每个集合也是一 找子女时间 O(1) ，其中每个集合也是一 找父亲要从根开始，其中每个集合也是一时间 O(log2i) 找父亲时间 O(1) 16 

17 . 二叉树的存储表示  二叉树的链表存储表示 root) root) root) A A ʌ A ʌ ʌ B B A C D ʌ C ʌ D ʌ A ʌ A E F ʌ E ʌ F ʌ ʌ A ʌ A ʌ ʌ G ʌ G ʌ A ʌ 二叉树 二叉链表 三叉链表 17 

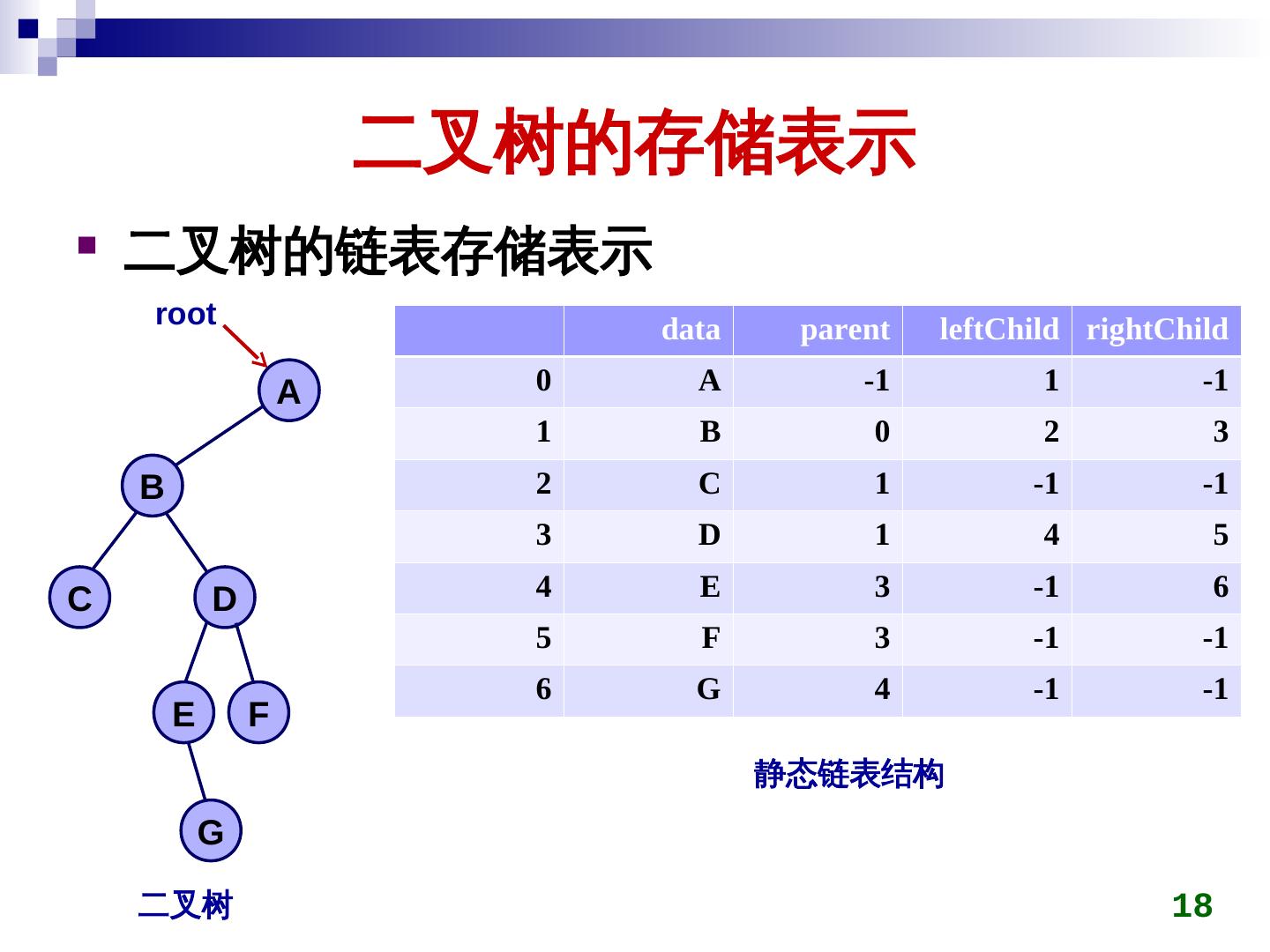
18 . 二叉树的存储表示  二叉树的链表存储表示 root) data parent leftChild rightChild A 0 A -1 1 -1 1 B 0 2 3 B 2 C 1 -1 -1 3 D 1 4 5 C D 4 E 3 -1 6 5 F 3 -1 -1 6 G 4 -1 -1 E F 静态链表结构 G 二叉树 18 

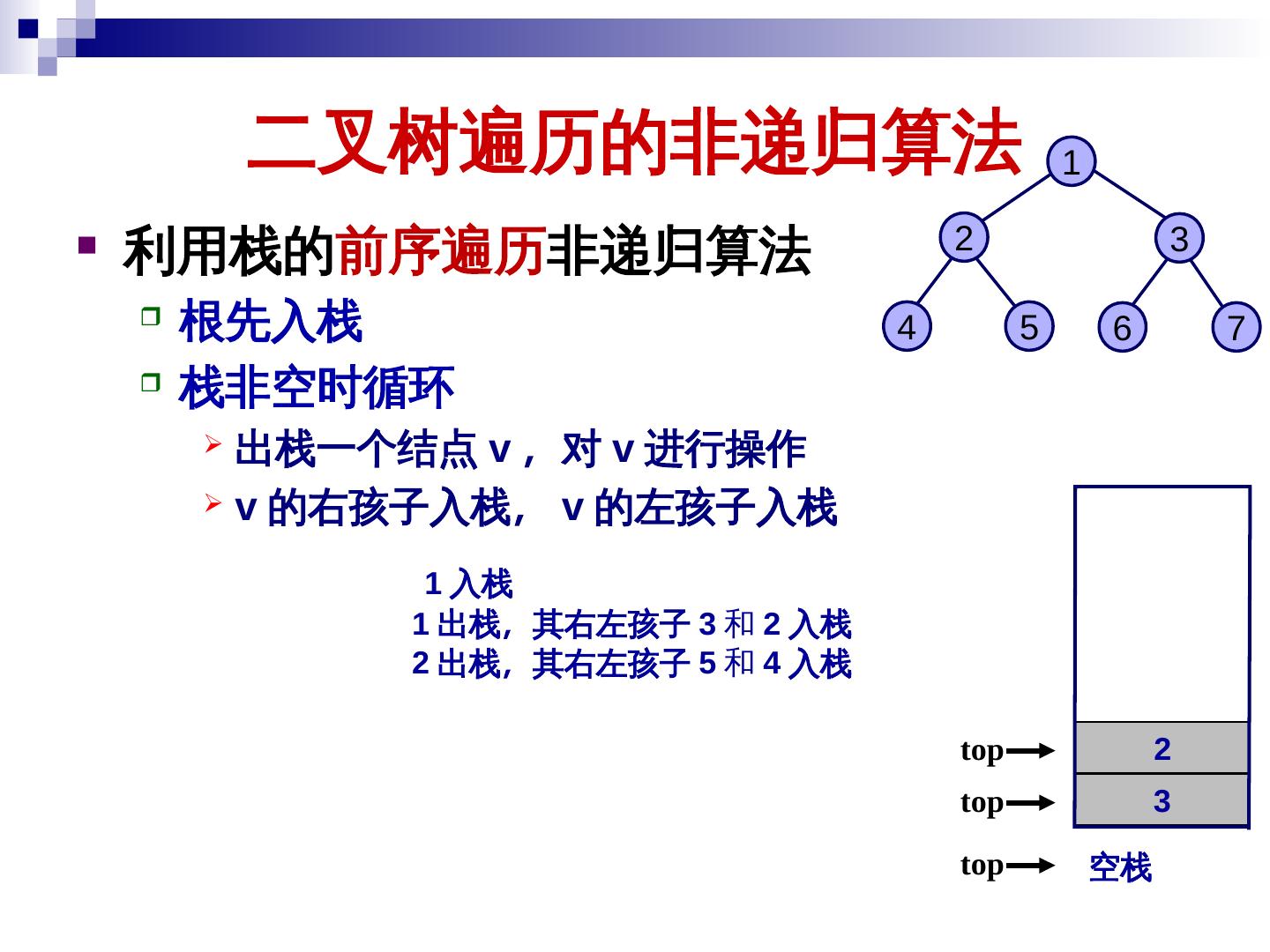
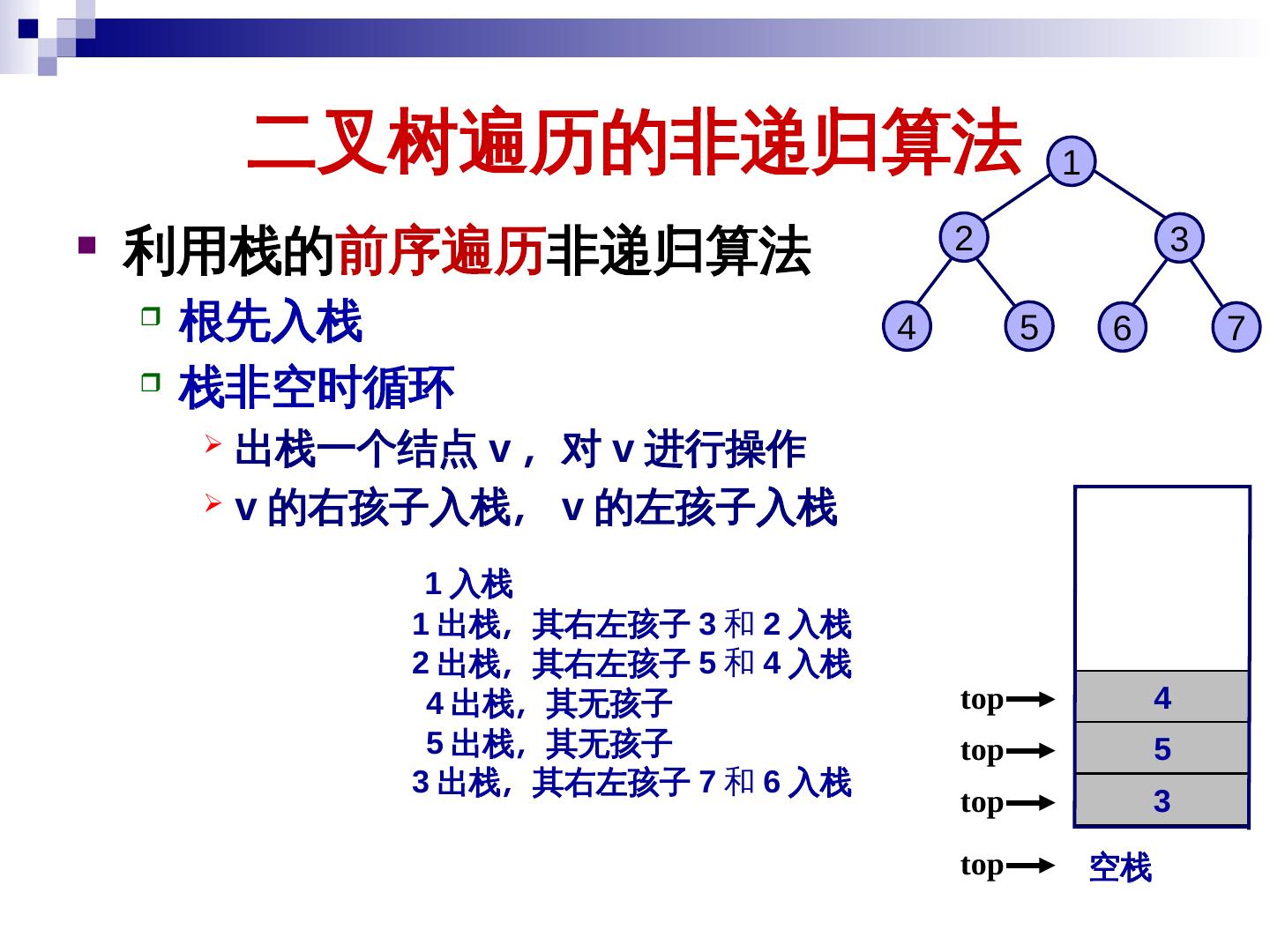
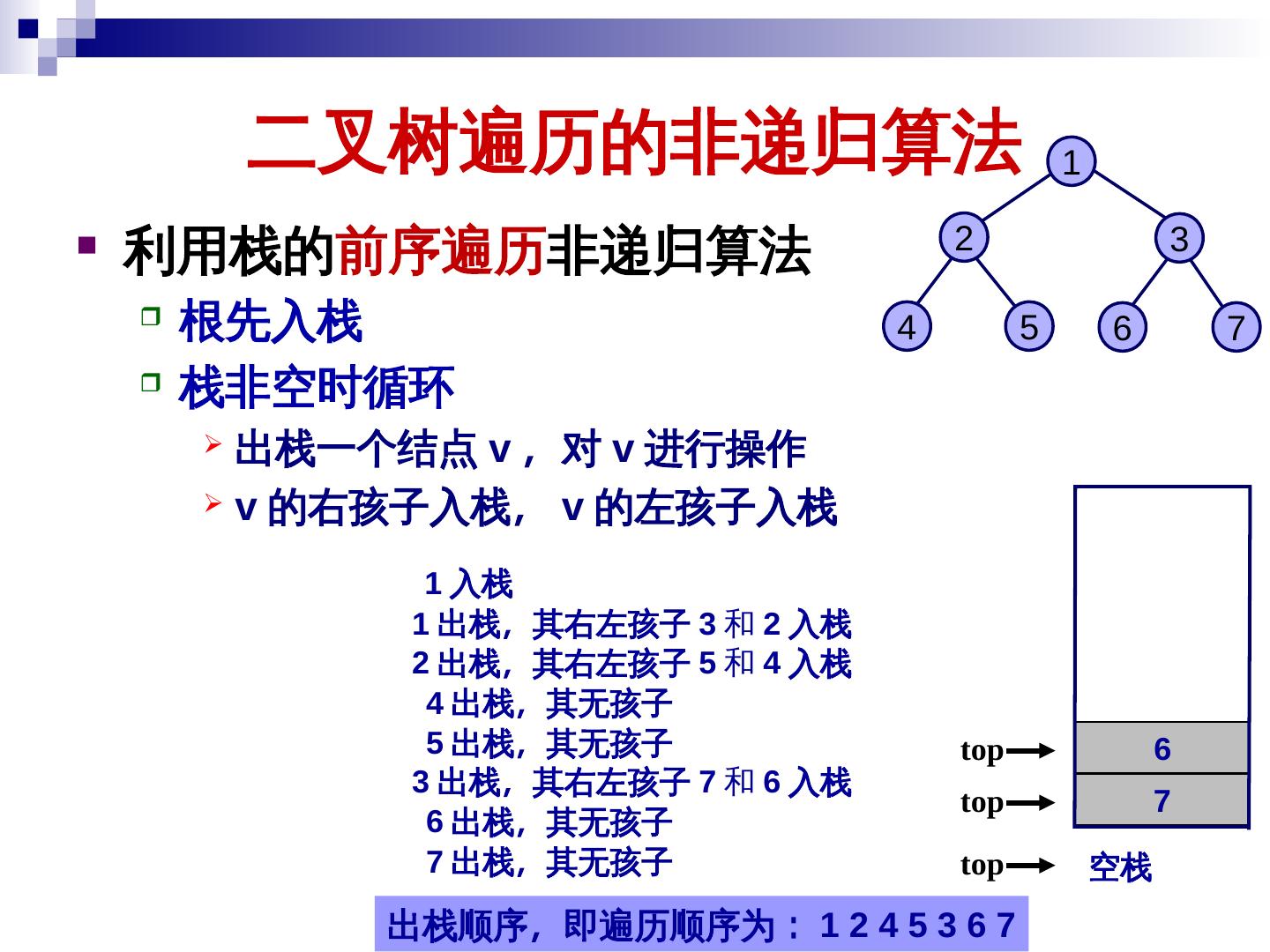
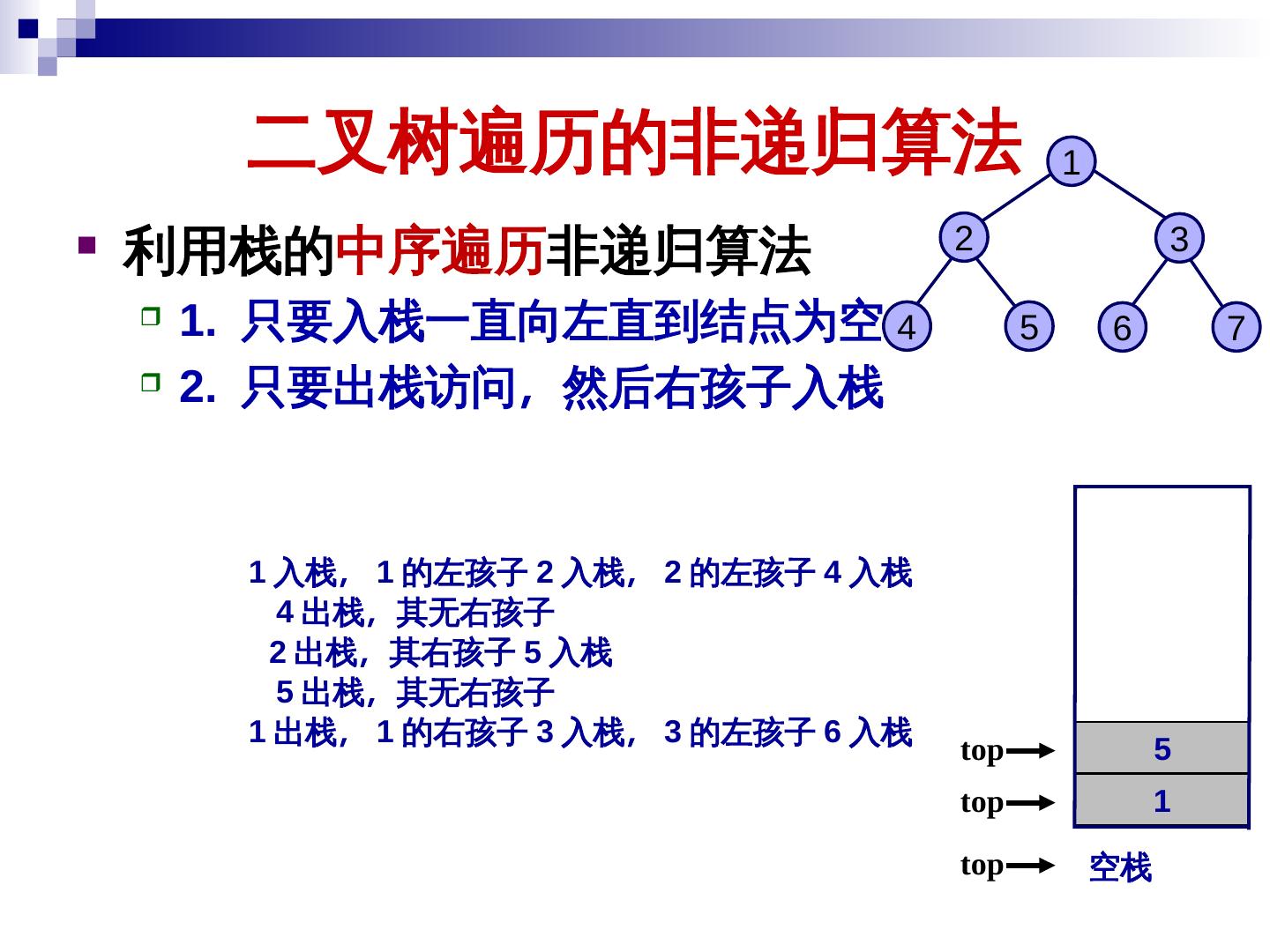
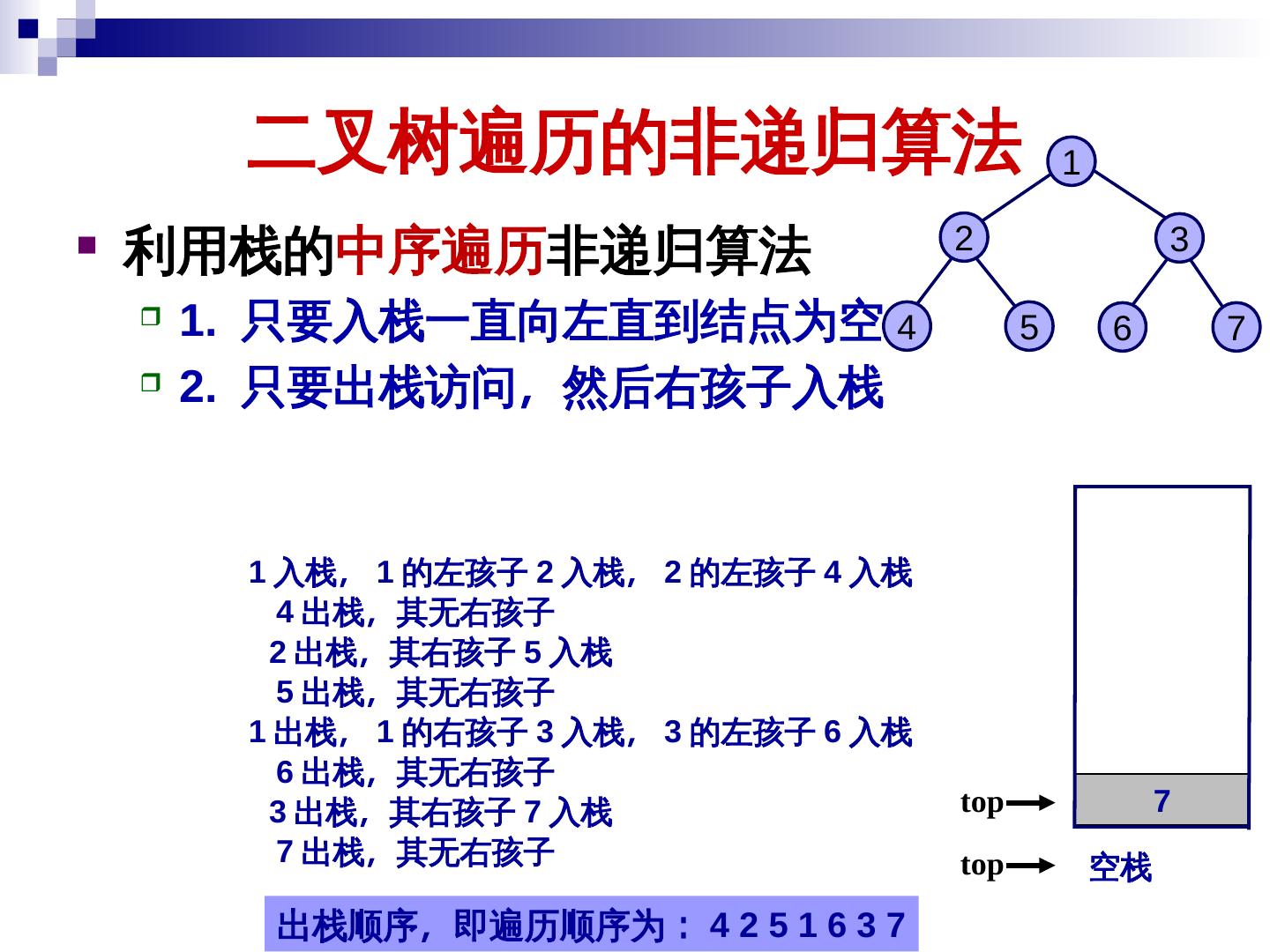
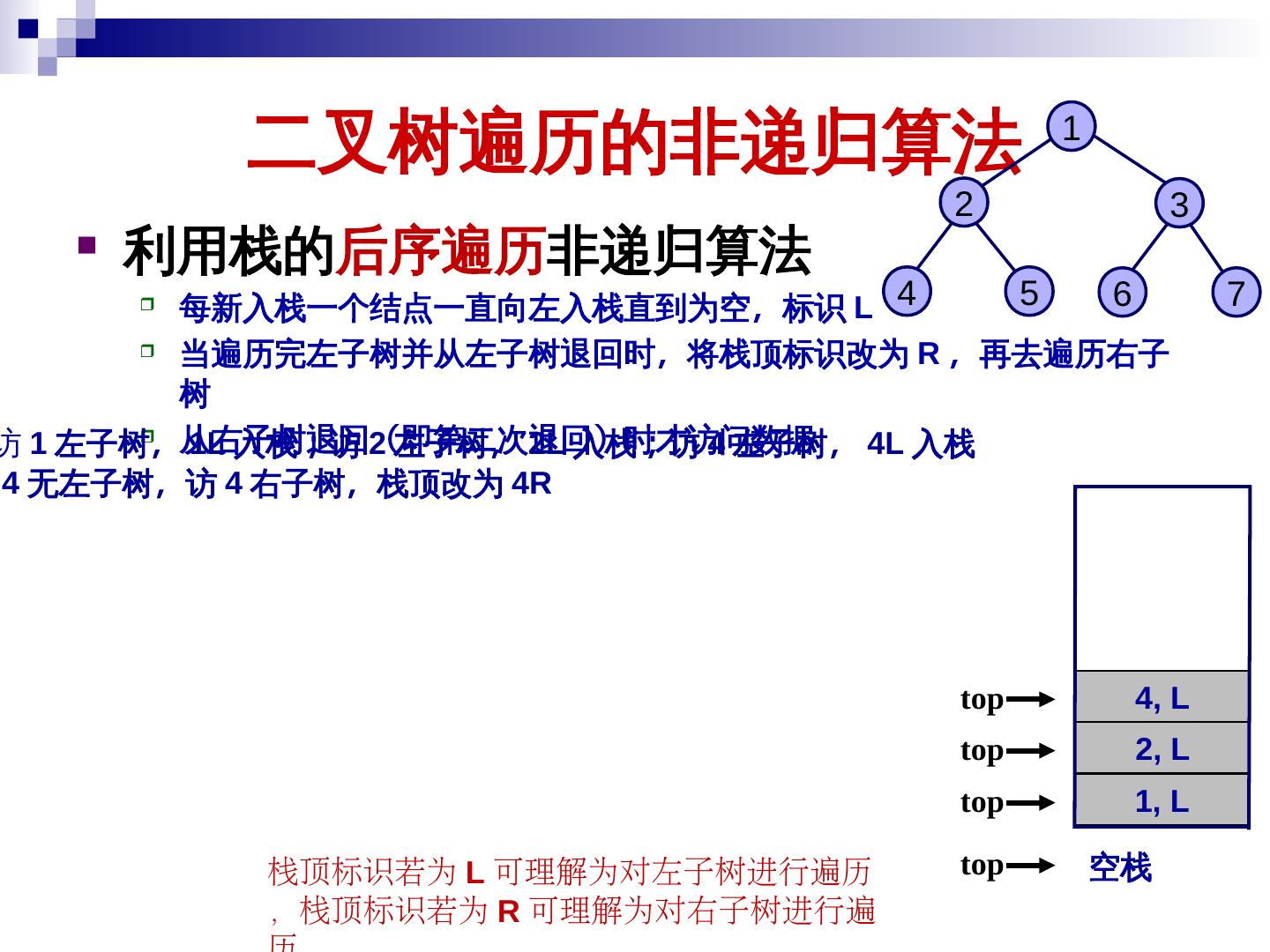
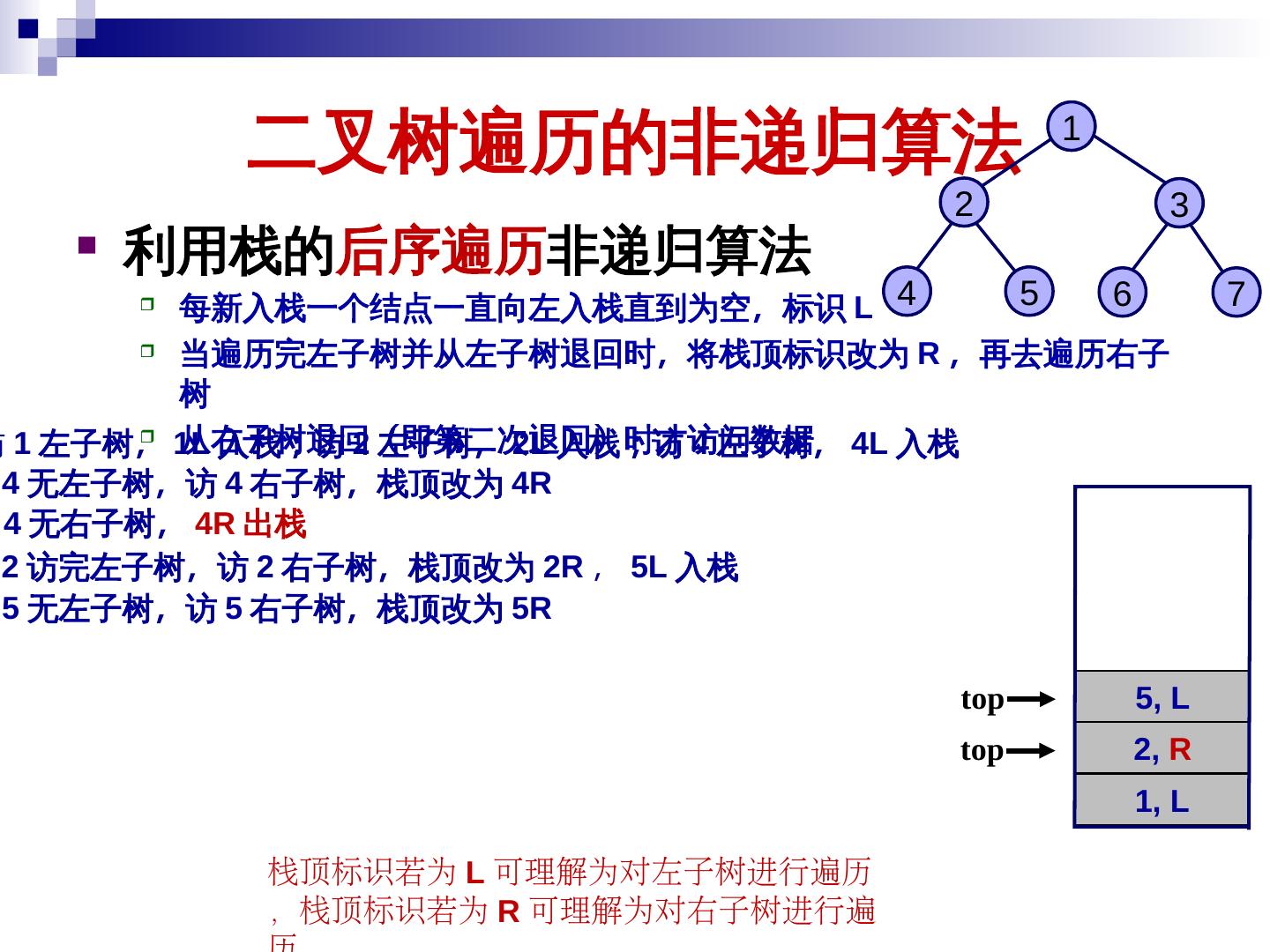
19 . 二叉树的遍历及其应用  二叉树的遍历就是按某种次序访问树中的结点 一次且仅一次  访问当前结点记为 V  访问结点的左子树记为 L  访问结点的右子树记为 R  遍历次序一般有  前序遍历 (VLR)  中序遍历 (LVR)  后序遍历 (LRV) 19 

20 . 二叉树的遍历及其应用  前序遍历 (VLR) -  首先访问当前结点 (V)  其次前序遍历左子树 (L) + /  最后前序遍历右子树 (R) a × e f void PreOrder ( BinTreeNode *T ) { if ( T != NULL ) { visit( T->data ); PreOrder ( T->leftChild ); b - PreOrder ( T->rightChild ); } } c d 前序遍历： – + a × b – c d / e f 20 

21 . 二叉树的遍历及其应用  中序遍历 (LVR) -  首先中序遍历左子树 (L)  其次访问当前结点 (V) + /  最后中序遍历右子树 (R) a × e f void InOrder ( BinTreeNode *T ) { if ( T != NULL ) { InOrder ( T->leftChild ); visit( T->data ); b - InOrder ( T->rightChild ); } } c d 中序遍历： a + b × c – d – e / f 21 

22 . 二叉树的遍历及其应用  后序遍历 (LRV) -  首先后序遍历左子树 (L)  其次后序遍历右子树 (R) + /  最后访问当前结点 (V) void PostOrder ( BinTreeNode *T ) { a × e f if ( T != NULL ) { PostOrder ( T->leftChild ); PostOrder ( T->rightChild ); b - visit( T->data ); } } c d 后序遍历： a b c d – × + e f / – 22 

23 . 二叉树的遍历及其应用  三种遍历路线相同，其中每个集合也是一结果不同  前序遍历： – + a × b – c d / e f  中序遍历： a + b × c – d – e / f -  后序遍历： a b c d – × + e f / – + / a × e f b - c d 23 

24 . 二叉树的遍历及其应用  计算二叉树的结点个数 ( 后序遍历 ) int Count ( BinTreeNode *T ) {  对左子树递归计数 a if ( T == NULL ) return 0;  对右子树递归计数 b else { int a = Count ( T->leftChild );  返回 1+a+b int b = Count ( T->rightChild ); return 1+a+b; } } 24 

25 . 二叉树的遍历及其应用  计算二叉树的深度 ( 后序遍历 ) int Height ( BinTreeNode *T ) {  计算左子树的深度 a if ( T == NULL ) return 0;  计算右子树的深度 b else { int a = Height ( T->leftChild );  返回 (a>b)?a+1:b+1 int b = Height ( T->rightChild ); return (a>b)?a+1:b+1; } } 25 

26 . 二叉树的遍历及其应用  二叉树的复制 ( 前序遍历 )  复制根结点数据 BinTreeNode * Copy( BinTreeNode *T ) { if ( T == NULL ) return NULL;  复制左子树 else { BinTreeNode * temp = new BinTreeNode;  复制右子树 temp->data = T->data;  返回根结点指针 Temp->leftChild = Copy ( T->leftChild ); Temp->rightChild = Copy( T->rightChild ); return temp; } } 26 

27 . 二叉树的遍历及其应用  判断两棵二叉树是否相等 ( 前序遍历 )  判断两棵树数据是否相等  判断两棵树左子树是否相等  判断两棵右子树是否相等 bool BinTreeNode * equal ( BinTreeNode *a, BinTreeNode *b ) { if ( a == NULL && b == NULL ) return true; else if ( a!=NULL && b!=NULL ) { bool r = ( a->data == b->data ); bool s = equal ( a->leftChild, b->leftChild ); bool t = equal ( a->rightChild, b->rightChild ); if (r && s && t) return true; else return false; } else return false; } 27 

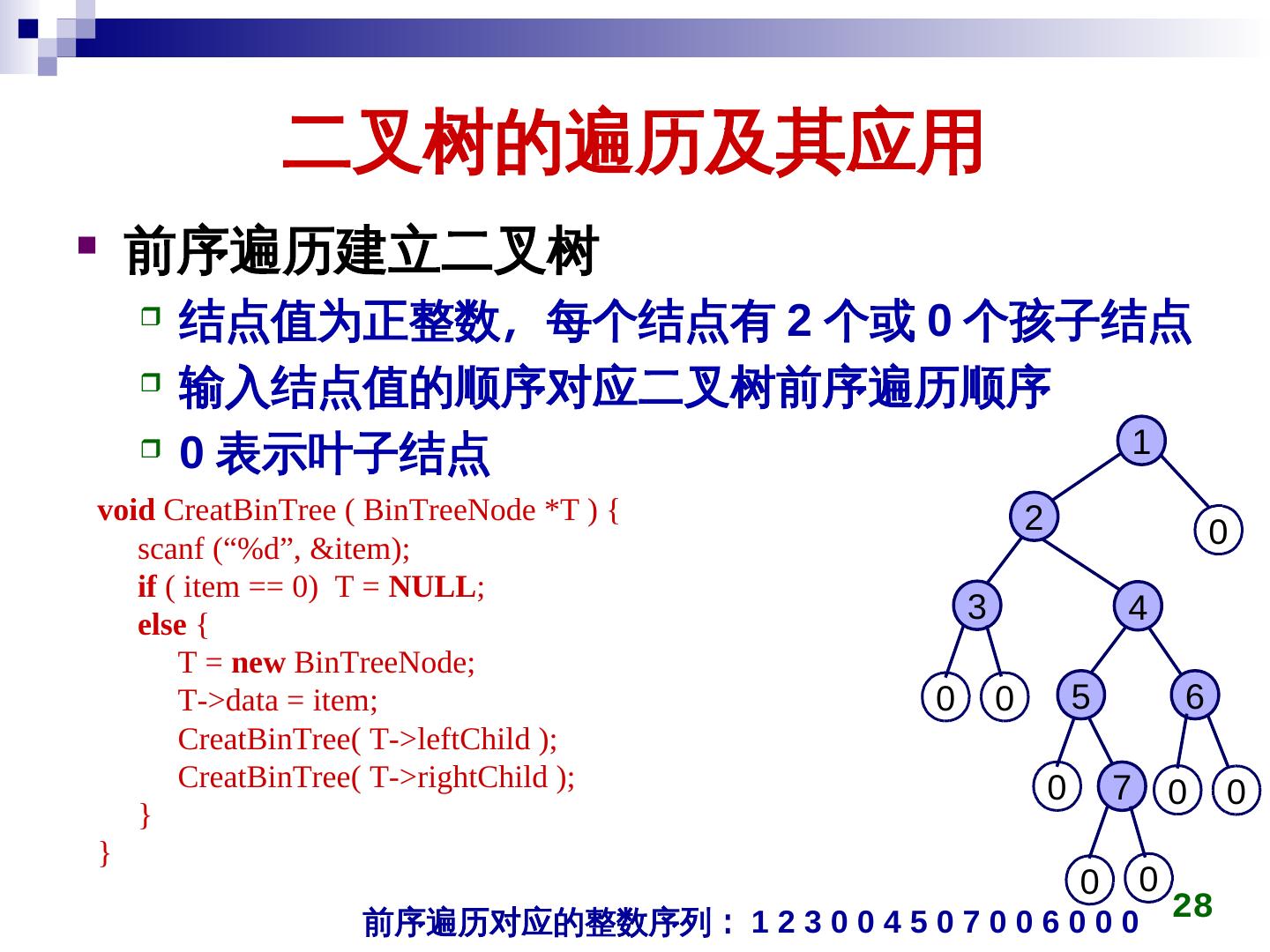
28 . 二叉树的遍历及其应用  前序遍历建立二叉树  结点值为正整数，其中每个集合也是一每个结点有 2 个或 0 个孩子结点  输入结点值的顺序对应二叉树前序遍历顺序  0 表示叶子结点 1 void CreatBinTree ( BinTreeNode *T ) { 2 scanf (“%d”, &item); 0 if ( item == 0) T = NULL; else { 3 4 T = new BinTreeNode; T->data = item; 0 0 5 6 CreatBinTree( T->leftChild ); CreatBinTree( T->rightChild ); 0 7 0 0 } } 0 0 前序遍历对应的整数序列： 1 2 3 0 0 4 5 0 7 0 0 6 0 0 0 28 

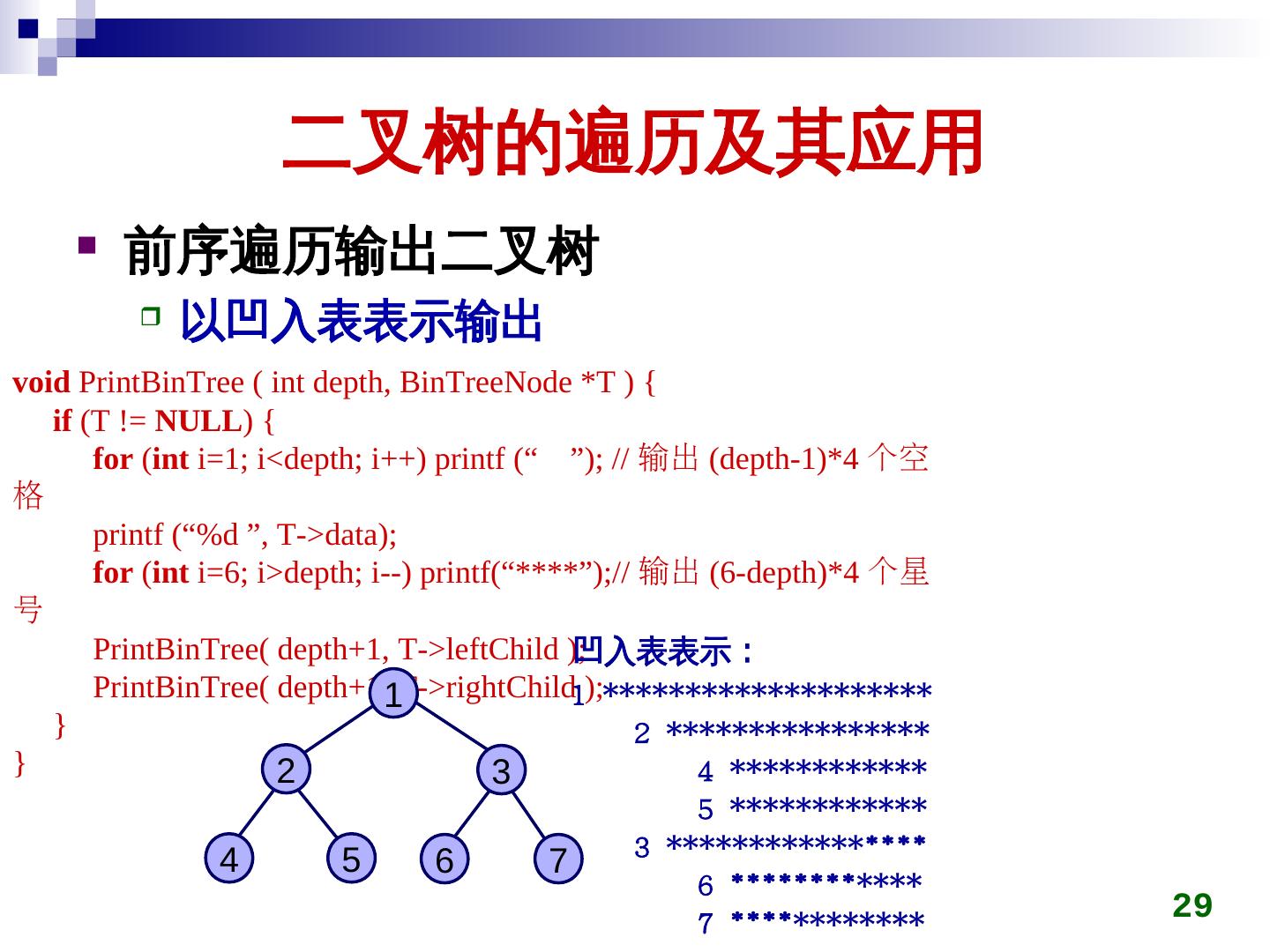
29 . 二叉树的遍历及其应用  前序遍历输出二叉树  以凹入表表示输出 void PrintBinTree ( int depth, BinTreeNode *T ) { if (T != NULL) { for (int i=1; i<depth; i++) printf (“ ”); // 输出 (depth-1)*4 个空 格 printf (“%d ”, T->data); for (int i=6; i>depth; i--) printf(“****”);// 输出 (6-depth)*4 个星 号 PrintBinTree( depth+1, T->leftChild );凹入表表示： PrintBinTree( depth+1,1T->rightChild1);******************** } 2 **************** } 2 3 4 ************ 5 ************ 4 5 6 7 3 **************** 6 ************ 29 7 ************