04-1Data Structures---Complexity of Algorithms

1 .Complexity of Algorithms Time complexity is abstracted to the number of steps or basic operations performed in the worst case during a computation. Now consider the following: 1. How much time does it take to read element A[m] of an array A? 2. How much time does it take to read the mth element of a singly linked list? 3. How much time does it take to insert an element after the mth element of a linked list? 4. How much time does it take to insert an element after A[m] in an array A? 5. How much time does it take to construct a string of size n by appending the individual characters one after another? 

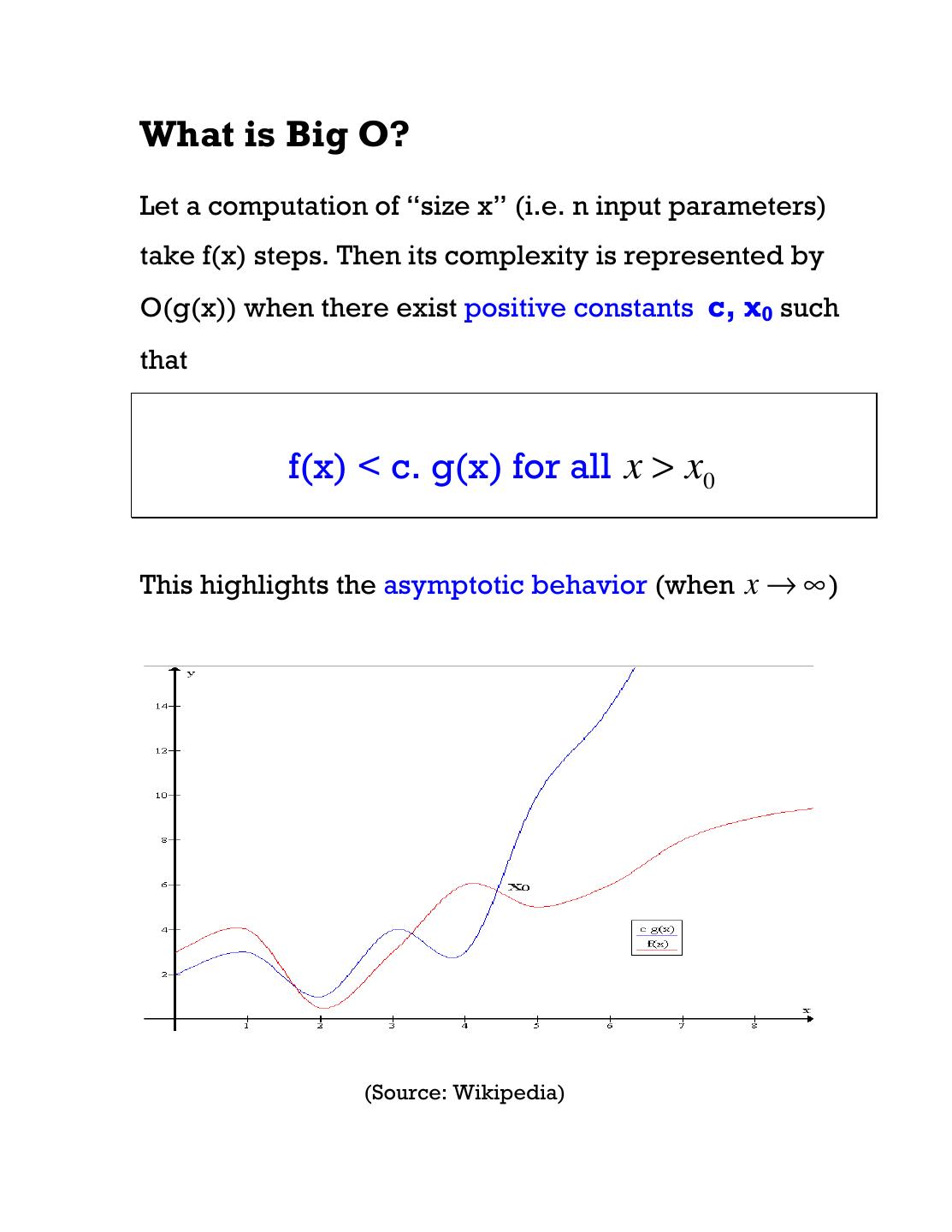
2 .What is Big O? Let a computation of “size x” (i.e. n input parameters) take f(x) steps. Then its complexity is represented by O(g(x)) when there exist positive constants c, x0 such that f(x) < c. g(x) for all x > x0 This highlights the asymptotic behavior (when x → ∞ )   (Source: Wikipedia) 

3 .Try to reason Why is n3 = O(2n), or n100 = O(2n)? Two issues Issue 1. Big-O gives a loose upper bound Consider the function f (n) = 3.n + 7 Is it O(n) or O(n2) or O(n3) or O(2n)? Issue 2. The constants are sometimes misleading A O(n) algorithm can have a running time c.n + d . What if c = 2100 or d= 2100 or both? Will you use this algorithm in place of another O(n2) algorithm that has a running time of 5n2 ? 

4 .Problem 1. Compute the time complexity of an algorithm that checks if the elements in a list are unique. Represent the list as an array arr public static boolean distinctValues(int[] arr){   for (int i = 0; i < arr.length-1; i++) { for (int j = i+1; j < arr.length; j++) { if (arr[i] == arr[j]) { return false; } } } return true; } The time complexity is O(n2). Why? 

5 .Problem 2. If you are given a sorted array, then how much time will it take for the same problem? What algorithm will you use -- the same algorithm or a different algorithm? Consider the following: public static boolean distinctValues(int[] arr){   for (int i = 0; i < arr.length-1; i++) { if (arr[i] == arr[i+1]) { return false; } } return true; } What is its time complexity in Big-O notation? 

6 .Think of this If you know of an algorithm that will sort n numbers in O(n log n) time, then will that be helpful? Is there such a sorting algorithm? Insertion sort has a complexity of O(n2) Merge sort has a complexity of O(n log n) 

7 .Sort a million items? On a slow machine Insertion sort takes roughly 70 hours Merge sort takes roughly 40 seconds The ratio is important. If the machine is 100 x faster then Insertion sort will take roughly 40 minutes Merge sort will take less than 0.5 seconds So, what is Merge Sort? 

8 .Merge Sort Uses Divide and Conquer. It solves sub-problems first, and then combines those solutions to solve the original problem. 3 1 4 9 6 8 7 2 Given array 3 1 4 9 6 8 7 2 split into two 1 3 4 9 2 6 7 8 sort each half 1 2 3 4 6 7 8 9 merge The algorithm is recursive. So, when do you stop? 

9 .private void doMergeSort(int low, int high) { //initially low = 0, high = array.legth-1; if (low < high) { int mid = low + (high - low) / 2; // Steps below sort the left side of the array doMergeSort(low, mid); // Steps below sort the right side of the array doMergeSort(mid + 1, high); // Now merge both sides mergeParts(low, mid, high); } }     

10 . Recursion One method can call another. When a method calls itself, then it is called recursion. Example 1. Factorial (n) = n×(n−1)×(n−2)×…×2×1     Base case: Factorial (1) = 1     Recursive step: factorial (n) = n × Factorial (n-1)         public static long factorial(int n) { if (n == 1) return 1; return n * factorial(n-1); } Two characteristics: 1. A base case with a solution and a return value. 2. A way of guiding the problem closer to the base case, and eventually hitting it. Why do we need a base case? Necessary for termination!   

11 .   factorial(5) factorial(4) factorial(3) factorial(2) factorial(1) return 1 return 2*1 = 2 return 3*2 = 6 return 4*6 = 24 return 5*24 = 120 Another way of calculating Factorial (n) public static int fact(int num) { int tmp = 1; for (int i = 1; i <= num; i++) { tmp *= i; } return tmp; } Is this recursive? No! Recursive programs are mathematically elegant, but not necessarily the only way to compute certain functions. 

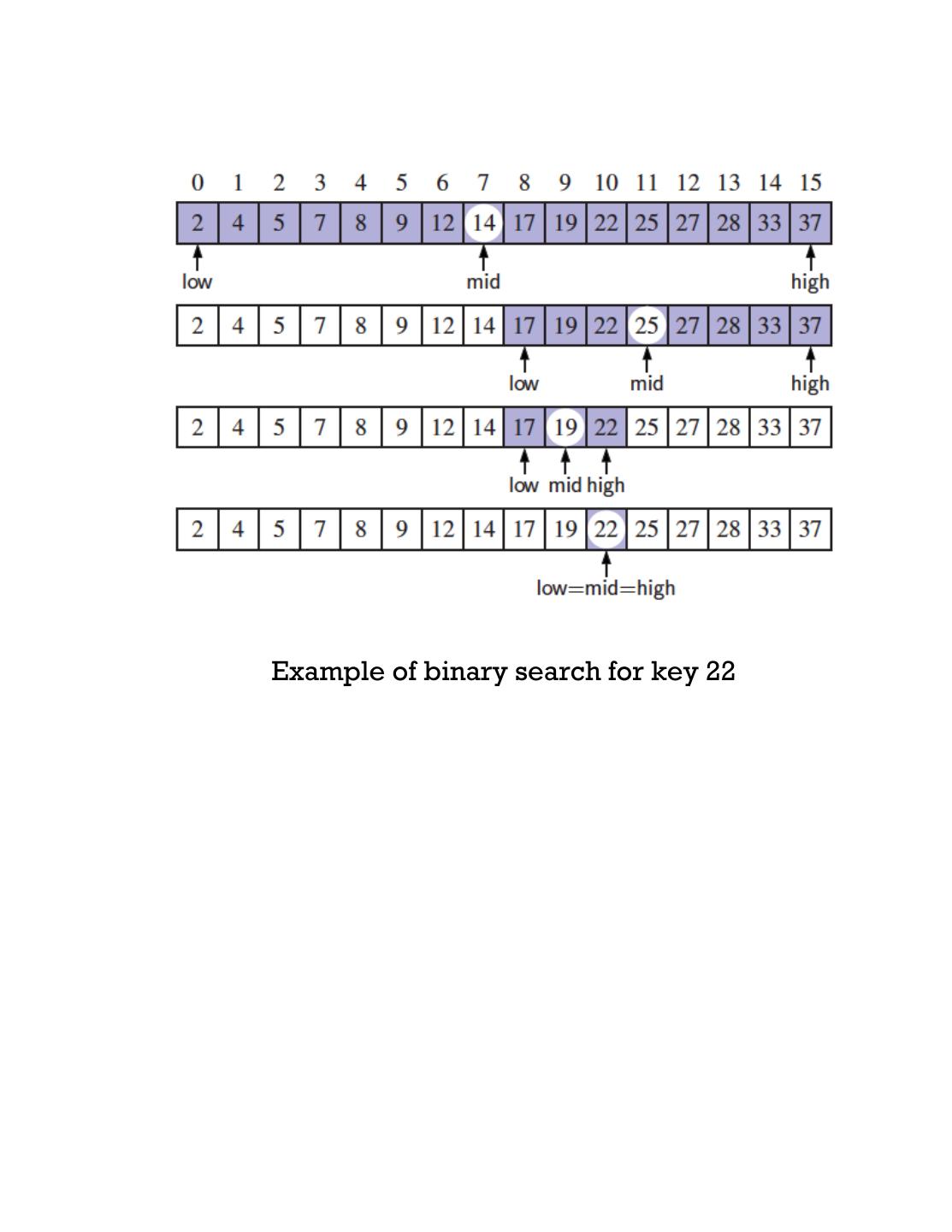
12 .Some more examples of recursion Binary search What is the complexity of searching an element in an unsorted array of length n? The obvious one is linear search. However, searching a sorted array is more efficient, and binary search is one such method. int[] data; int size; public boolean binarySearch(int key) { int low = 0; int high = size - 1; while(high >= low) { int middle = (low + high) / 2; if(data[middle] == key) { return true; // key found } if(data[middle] < key) { low = mid+1; return binarySearch(data, key, low, high); } else if(data[middle] > key) { high = mid return binarySearch(data, key, low, high); } return false; // key not found } 

13 .Example of binary search for key 22 

14 .Linear and Binary Recursion Linear Recursion. One recursive call initiates at most one other. Example. Factorial, LinearSum, ReverseArray etc Binary Recursion. Each recursive call triggers two others. Example. Fibonacci, MergeSort etc. Recursion, if not properly used, can lead to inefficient programs. First program public int fibBad(int n) { if(n == 0) return 0; else if(n == 1) return 1; else return fibBad(n - 1) + fibBad(n - 2); } Is there anything wrong with this? 

15 .A much better approach is as follows: Second program public static long[] fibGood(int n) { // Computes fib(n), fib(n-1) together if (n < = 1) { long[] answer = {n,0}; return answer; } else { long[] tmp = fibGood(n-1); long[] answer = {tmp[0] + tmp[1], tmp[0]}; return answer; } } Why is it better? How many recursive calls are made? 

16 .Array tmp[ ] of two elements F(n), F(n-1) F(n-1), F(n-2) à tmp[0] + tmp[1] = F(n), tmp[0] = F(n-1) F(n-2), F(n-3) à tmp[0] + tmp[1] = F(n-1), tmp[0] = F(n-2) F(n-3), F(n-4) à tmp[0] + tmp[1] = F(n-2), tmp[0] = F(n-3) … … … … … … How many recursive calls? Tail recursion Tail recursion refers to the case when the recursive call is the last statement. See this example. int f(int x, int y) { if (y == 0) { return x; } return f(x*y, y-1); } Why is it easier to handle? 

17 .Consider the following program import java.util.*; public class ArrayListDemo { public static void main(String args[]) { // create an array list ArrayList al = new ArrayList(); System.out.println("Initial size:" + al.size()); // add elements to the array list al.add("C"); al.add("A"); al.add("E"); al.add("B"); al.add("D"); al.add("F"); al.add(1, "A2"); System.out.println("Size after add: " + al.size()); // display the array list System.out.println("Contents of al: " + al); // Remove elements from the array list al.remove("F"); al.remove(2); System.out.println("Size after deletions: " + al.size()); System.out.println("Contents of al: " + al); } } 

18 .How many steps will it take for the list to grow to size n? If you were to do it, then you may consider the following approaches. 1. Pre-allocate the max amount of memory. May lead to poor memory utilization. 2. While adding a new element to a list of size k, allocate a separate space of size (k+1), and copy the first k elements to it. With proper garbage collection, the space utilization will be very good. How many copy operations will you need if the list grows to size n? 3. What about allocating a space of double size (i.e. 2.k) when the current space (of size k) is full? How many copy operations will you need if the list grows to size n? 

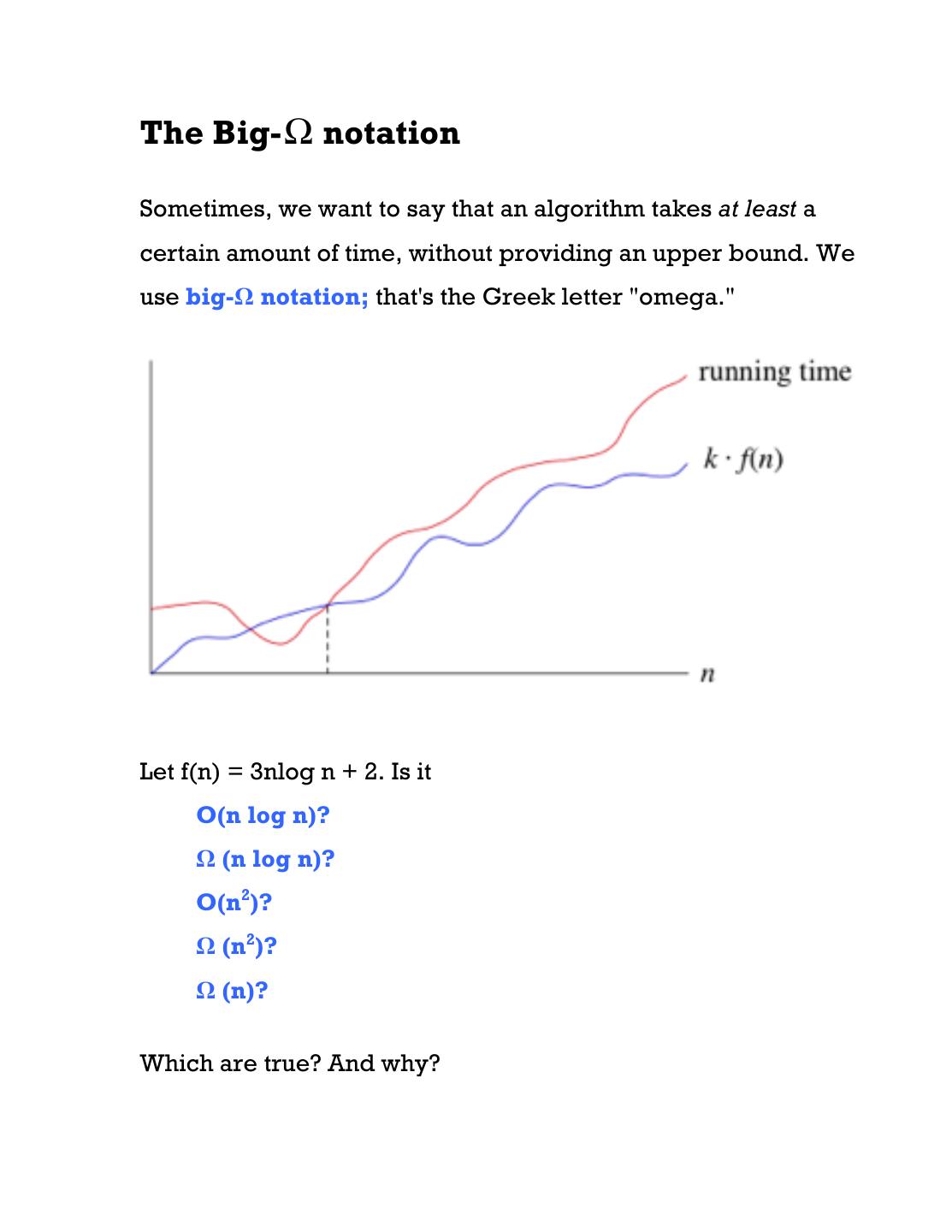
19 .The Big- Ω notation Sometimes, we want to say that an algorithm takes at least a certain amount of time, without providing an upper bound. We use big-Ω notation; that's the Greek letter "omega." Let f(n) = 3nlog n + 2. Is it O(n log n)? Ω (n log n)? O(n2)? Ω (n2)? Ω (n)? Which are true? And why?