04数据结构---数组与串

1 .第四章 数组、串与广义表 东南大学计算机学院 方效林 方效林 本课件借鉴了清华大学殷人昆老师 和哈尔滨工业大学张岩老师的课件 

2 . 本章主要内容  多维数组的概念与存储  特殊矩阵  稀疏矩阵  字符串 2 

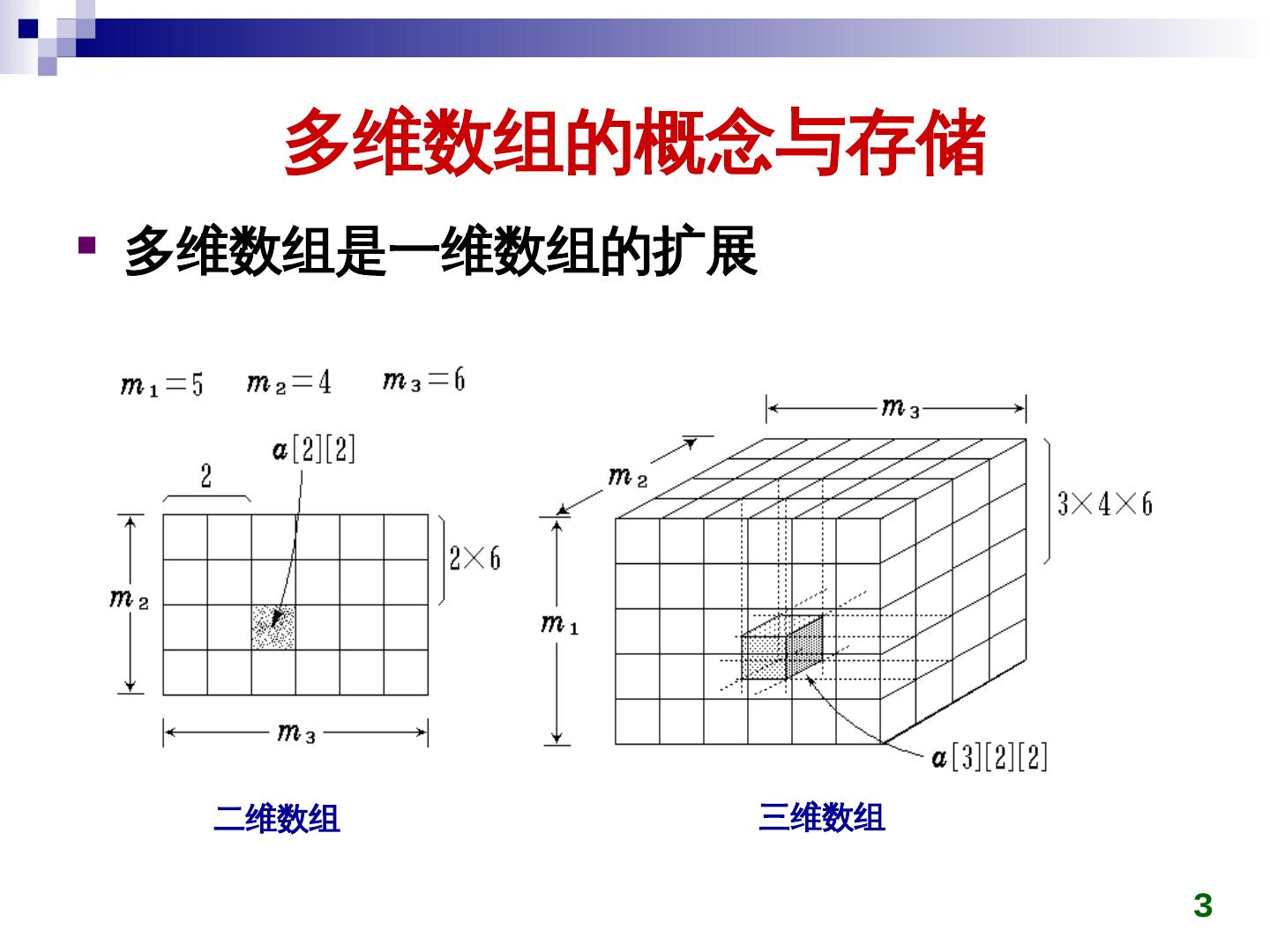
3 . 多维数组的概念与存储  多维数组是一维数组的扩展 二维数组 三维数组 3 

4 . 多维数组的概念与存储  多维数组存储在连续的空间中  存储地址计算方法（假设数组首地址为 a ，元素元素 大小为 l ）  一维数组： a[m1] Loc(i)= a + i*l  二维数组： a[m1][m2] Loc(i, j)= a + ( i*m2 + j )*l  三维数组： a[m1][m2] [m3] Loc(i, j, k)= a + ( i*m2*m3 + j*m3 + k )*l  n 维数组： a[m1][m2] …[mn] 4 

5 . 特殊矩阵  二维数组也称为矩阵  特殊矩阵是指非零元素或零元素的分布有一定 规律的矩阵。  对称矩阵  三对角矩阵  利用特殊矩阵的性质，元素节省存储空间 a 00 a 01 0 0 0 0   a 00 a 01 a 02  a 0n  1  a a a  a 0 0 0   10 a 11 a 12  a 1n  1   10 11 12  0 a 21 a 22 a 23 0 0  A   a 20 a 21 a 22  a 2n  1  A                     0 0 0 a n  2n  3 a n  2n  2 a n  2n 1  a n  10 a n  11 a n  12  a n  1n  1    0 0 0 0 a n  1n  2 a n  1n  1  对称矩阵 三对角矩阵 5 

6 . 特殊矩阵  对称矩阵的压缩存储  设有一个 nn 的矩阵 A 。如果在在矩阵 中，元素 aij = aji ，元素则此矩阵是对称矩阵。  只保存对称矩阵的对角线和对角线以上 ( 或以下 ) 的元素，元素则称此为对称矩阵的压缩存储  压缩存储方式：用一维数组存储  a 00 a 01 a 02  a 0n  1   a a 11 a 12  a 1n  1   10 A   a 20 a 21 a 22  a 2n  1            a n  10 a n  11 a n  12  a n  1n  1  6 

7 . 特殊矩阵  对称矩阵的压缩存储  下三角阵存储： 用一维数组 B 存储对称矩阵 A 中 对角线及对角线以下的元素  矩阵 A 中元素 a[i][j] 对应一维数组 B 中的下标为 (i+1)*i/2 + j, i≥j  a 00  Loc(i, j) =    a 10 a 11  (j+1)*j/2 + i, i<j A   a 20 a 21 a 22          a a n  11 a n  12  a n  1n  1   n  10 0 1 2 3 4 5 6 7 8 n(n+1)/2-1 B a00 a10 a11 a20 a21 a22 a30 a31 a32 …… an-1n-1 7 

8 . 特殊矩阵  对称矩阵的压缩存储  上三角阵存储： 用一维数组 B 存储对称矩阵 A 中 对角线及对角线以上的元素  矩阵 A 中元素 a[i][j] 对应一维数组 B 中的下标为 (2n - i + 1)*i/2 + j-i, i≤j a 00 a 01 a 02  a 0n  1  Loc(i, j) =   (2n - j - 1)*j/2 + i, i > j  a 11 a 12  a 1n  1  A  a 22  a 2n  1         a n  1n  1   0 1 2 n-1 n n+1 2n-2 2n-1 n(n+1)/2-1 B a00 a01 a02 … a0n-1 a11 a12 … a1n-1 a22 … an-1n-1 8 

9 . 稀疏矩阵  设矩阵 A 中有 s 个非零元素，元素若 s 远远 小于矩阵元素的总数（即 s << m×n ），元素则称 A 为稀疏矩阵。  稀疏因子： δ = s/(m×n)  一般 δ ≤ 0.05 可称为稀疏  0 0 2 0 0 0 0    3 0 0  11 0 0 0  0 0 0  6 0 0 0  A 6 7  0 0 0 0 0  17 0    0 9 0 0 19 0 0  0 0 0  8 0 0  52   稀疏矩阵表示 9 

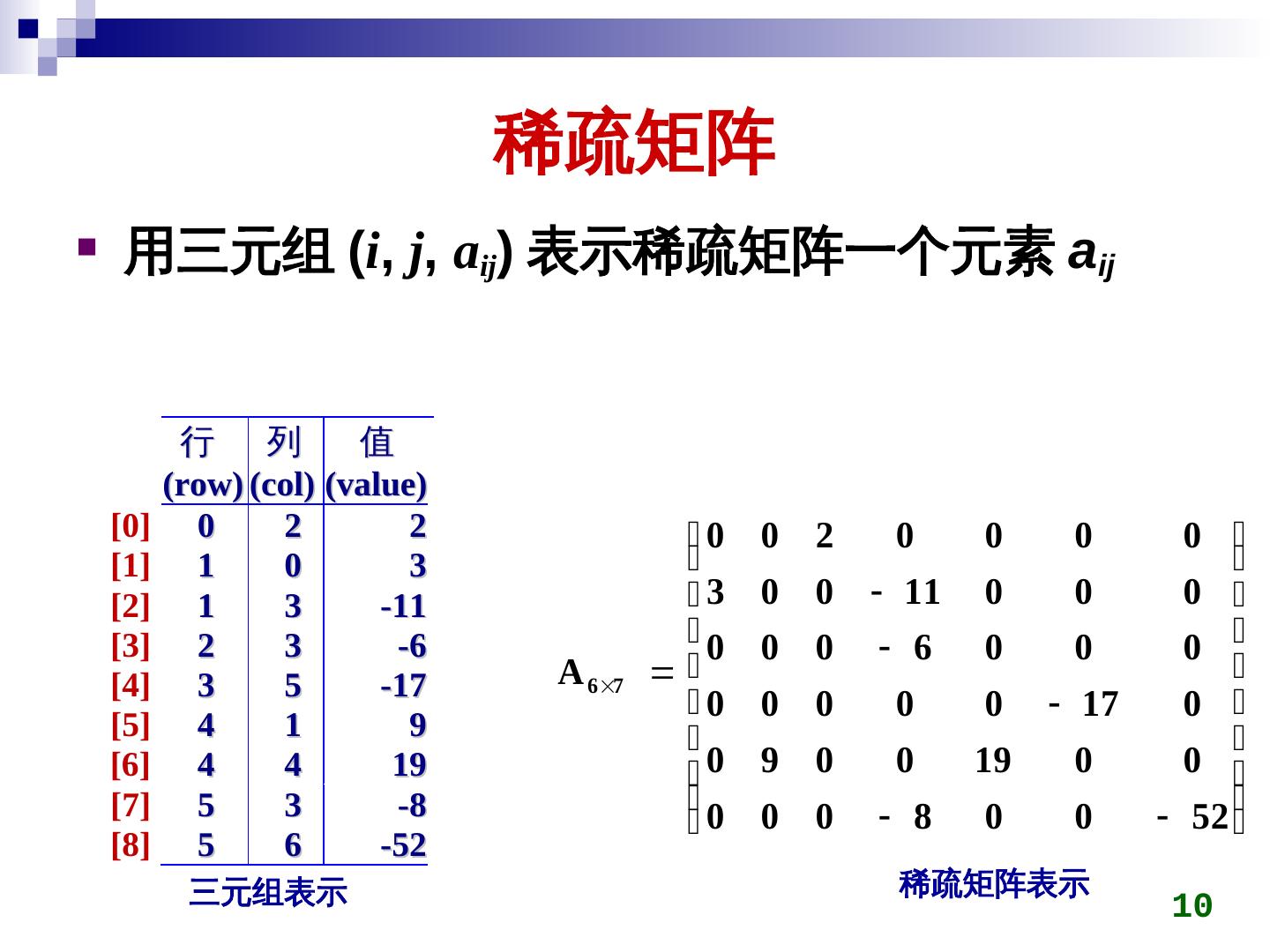
10 . 稀疏矩阵  用三元组 (i, j, aij) 表示稀疏矩阵一个元素 aij 行 列 值 (row) (col) (value) [0] 0 2 2 0 0 2 0 0 0 0  [1] 1 0 3   [2] 1 3 -11 3 0 0  11 0 0 0  [3] 2 3 -6 0 0 0  6 0 0 0  [4] 3 5 -17 A 6 7  0 0 0 0 0  17 0  [5] 4 1 9   [6] 4 4 19 0 9 0 0 19 0 0  [7] 5 3 -8 0 0 0  8 0 0  52   [8] 5 6 -52 三元组表示 稀疏矩阵表示 10 

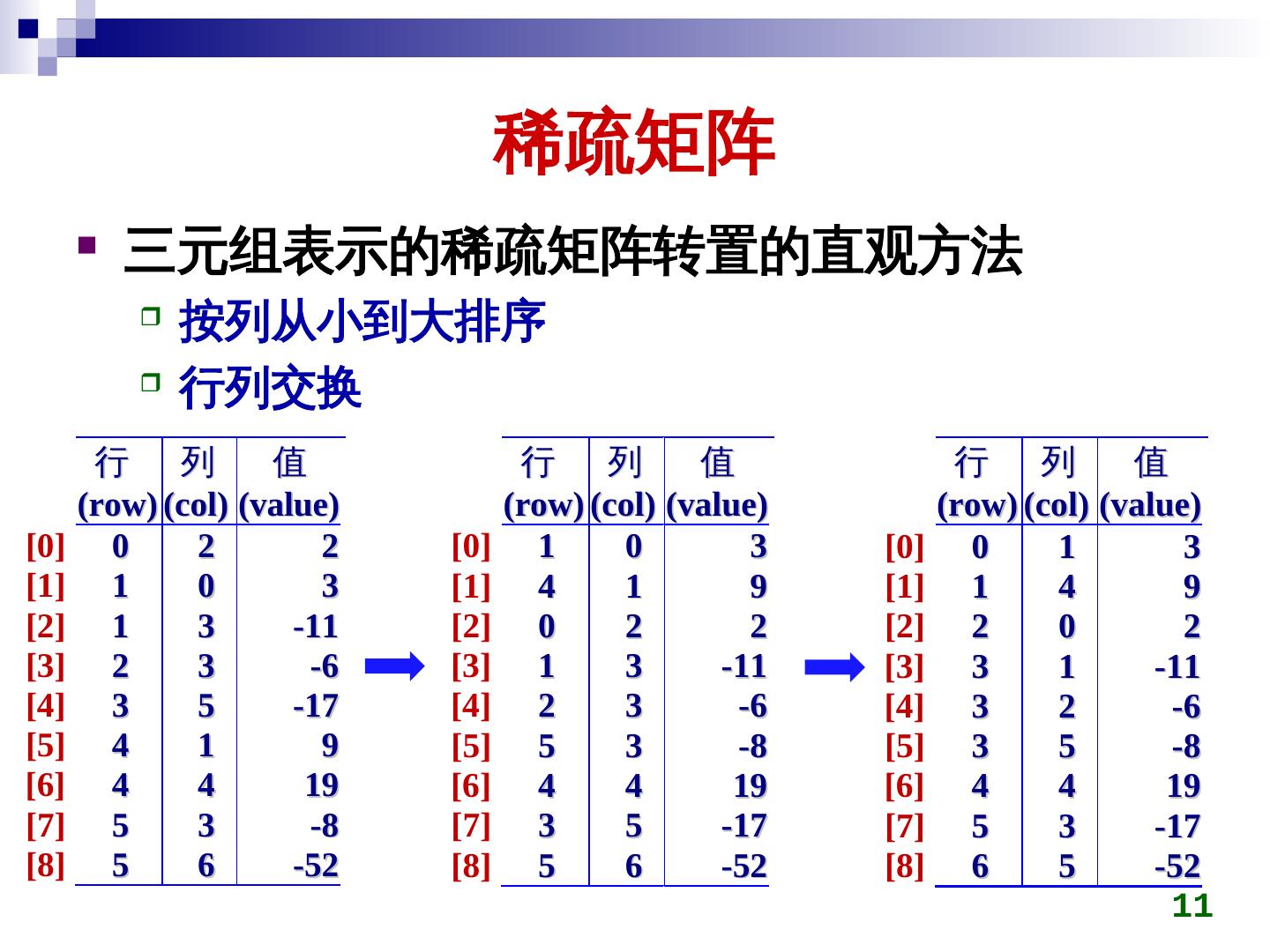
11 . 稀疏矩阵  三元组表示的稀疏矩阵转置的直观方法  按列从小到大排序  行列交换 行 列 值 行 列 值 行 列 值 (row) (col) (value) (row) (col) (value) (row) (col) (value) [0] 0 2 2 [0] 1 0 3 [0] 0 1 3 [1] 1 0 3 [1] 4 1 9 [1] 1 4 9 [2] 1 3 -11 [2] 0 2 2 [2] 2 0 2 [3] 2 3 -6 [3] 1 3 -11 [3] 3 1 -11 [4] 3 5 -17 [4] 2 3 -6 [4] 3 2 -6 [5] 4 1 9 [5] 5 3 -8 [5] 3 5 -8 [6] 4 4 19 [6] 4 4 19 [6] 4 4 19 [7] 5 3 -8 [7] 3 5 -17 [7] 5 3 -17 [8] 5 6 -52 [8] 5 6 -52 [8] 6 5 -52 11 

12 . 稀疏矩阵  三元组表示的稀疏矩阵转置的扫描方法  假设 A 有 Cols 列，元素则扫描 Cols 趟  第 k 趟扫描在表中找列号为 k 的三元组，元素取出，元素交 换行列号 行 列 值 行 列 值 (row) (col) (value) (row) (col) (value) [0] 0 2 2 扫描列号为 0 的三元组 [0] 0 1 3 [1] 1 0 3 扫描列号为 1 的三元组 [1] 1 4 9 [2] 1 3 -11 扫描列号为 2 的三元组 [2] 2 0 2 [3] 2 3 -6 扫描列号为 3 的三元组 [3] 3 1 -11 [4] 3 5 -17 扫描列号为 4 的三元组 [4] 3 2 -6 [5] 4 1 9 扫描列号为 5 的三元组 [5] 3 5 -8 [6] 4 4 19 扫描列号为 6 的三元组 [6] 4 4 19 [7] 5 3 -8 [7] 5 3 -17 [8] 5 6 -52 [8] 6 5 -52 12 

13 . 稀疏矩阵  三元组表示的稀疏矩阵转置的快速方法  统计各列非零数 rowSize( 扫描三元组表 )  计算各列在转置三元组中的索引位置 rowStart  扫描三元组表，元素放入相应索引位置，元素相应索引加 1 0 0 2 0 0 0 0  行 列 值 行 列 值   3 0 0  11 0 0 0  (row) (col) (value) (row) (col) (value) 0 0 0  6 0 0 0  [0] 0 2 2 [0] 0 1 3 A 67  [1] 1 0 3 [1] 1 4 9 0 0 0 0 0  17 0    [2] 1 3 -11 [2] 2 0 2 0 9 0 0 19 0 0  [3] 2 3 -6 [3] 3 1 -11 0 0 0  8 0 0  52   [4] 3 5 -17 [4] 3 2 -6 rowSize 1 1 1 3 1 1 1 [5] 4 1 9 [5] 3 5 -8 [6] 4 4 19 [6] 4 4 19 rowStart 0 1 2 3 6 7 8 [7] 5 3 -8 [7] 5 3 -17 1 2 3 4 7 8 9 [8] 5 6 -52 [8] 6 5 -52 5 6 

14 . 字符串  字符串  n(n≥0) 个字符的一个有限序列，元素简称为串  记为 S = “a0 a1 a2 … an-1”  n 是串的长度，元素 n 等于 0 的串叫空串  子串  串中连续若干个字符组成的串  S=“maintenance” ，元素 P=“ten” 是 S 的子串，元素 P 在 S 中的位置为 4 （从第 0 个字符开始） 14 

15 . 字符串  字符串的一些基本操作 typedef struct {  复制 strcpy char ch[maxSize]; int length;  连接 strcat } SeqString;  比较 strcmp  长度 strlen 15 

16 . 字符串  字符串的穷举模式匹配算法  匹配失败时，元素目标串 T 回溯，元素模式串 P 从头开始 T t0 t1 t2 t3 … tm-3 tm-2 tm-1 … tn-1 第1趟 P p0 p1 p2 p3 … pm-3 pm-2 pm-1 第2趟 P p0 p1 p2 p3 … pm-3 pm-2 pm-1 第3趟 P p0 p1 p2 p3 … pm-3 pm-2 pm-1 … … 时间复杂度 O(m*n) 16 

17 . 字符串  字符串的穷举模式匹配算法  匹配失败时，元素目标串 T 回溯，元素模式串 P 从头开始 T a b b a b a T a b b a b a ≠ ≠ P a b a P a b a 第1趟 第2趟 T a b b a b a T a b b a b a ≠ P a b a P a b a 第3趟 第4趟 17 

18 . 字符串  字符串的改进模式匹配算法 T … a b c d a b c d x … ≠ P a b c d a b c d e P a b c d a b c d e 例子： P 中重复出现 abcd ，元素但是 e 和 x 不匹配时，元素 可直接向右滑动 4 个字符开始匹配，元素可少匹配 4 趟 18 

19 . 字符串  字符串的改进模式匹配算法 T … ts ts+1 ts+2 ts+3 … ts+j-3 ts+j-2 ts+j-1 ts+j … ≠ 设 T[s, s+j-1] = P[0, j-1] ，元素 = = = = = = = = 但 T[s, s+j] ≠ P[0, j] P p0 p1 p2 p3 … pj-3 pj-2 pj-1 pj P p0 p1 p2 p3 … pj-3 pj-2 若 P[0, j-2] ≠ P[1, j-1] ，元素可少匹配 1 趟 P p0 p1 p2 p3 … pj-3 若又 P[0, j-3] ≠ P[2, j-1] ，元素可少匹配 2 趟 P p0 p1 p2 … pj-4 若又 P[0, j-4] ≠ P[3, j-1] ，元素可少匹配 3 趟 … … 类推直到前缀 P[0, k+1] ≠ 后缀 P[j-k-2, j-1] 但是前缀 P[0, k] = 后缀 P[j-k-1, j-1] 时，元素 可少匹配 j-k-1 趟，元素 相当于 P 直接向右滑动 j-k-1 个字符19 

20 . 字符串  字符串的改进模式匹配算法  对模式串 P 进行预处理，元素计算可以滑过多少个字 符 -1 ，元素当 j = 0 next( j ) = k+1 ，元素当 0 ≤ k < j-1, 且使 p0p1…pk=pj-k-1pj-k…pj-1 的最大数 0 ，元素其他情况 next(j) 直观含义： [0, j-1] 中前缀和后缀相等的最大长度 next(j) 直观作用：可滑过 j-next(j) 位不用匹配 下标 j 0 1 2 3 4 5 6 7 8 P a b c d a b c d e next(j) -1 0 0 0 0 1 2 3 4 20 

21 . 字符串  字符串的改进模式匹配算法  对模式串 P 进行预处理，元素计算可以滑过多少个字 符 -1 ，元素当 j = 0 next( j ) = k+1 ，元素当 0 ≤ k < j-1, 且使 p0p1…pk=pj-k-1pj-k…pj-1 的最大数 0 ，元素其他情况 next(j)=-1 表示匹配失败时，元素 T 的指针加 1 ，元素 P 的指针指向 p[0] next(j)=k+1 表示匹配失败时，元素 P 的指针指向 p[k+1] ，元素 next(j)=0 表示匹配失败时，元素 P 的指针指向 p[0] T … b c … ≠ 此例中模式串 P 的 next[0]=- P a b c d a b c d e 1 ，元素 T 指针加 1 ，元素 P 指向 p[0] ，元素 即 T 中 c 与 P 中 p[0]=a 进行 P a b c d a b c d e 21 比较 

22 . 字符串  字符串的改进模式匹配算法  对模式串 P 进行预处理，元素计算可以滑过多少个字 符 -1 ，元素当 j = 0 next( j ) = k+1 ，元素当 0 ≤ k < j-1, 且使 p0p1…pk=pj-k-1pj-k…pj-1 的最大数 0 ，元素其他情况 next(j)=-1 表示匹配失败时，元素 T 的指针加 1 ，元素 P 的指针指向 p[0] next(j)=k+1 表示匹配失败时，元素 P 的指针指向 p[k+1] ，元素 next(j)=0 表示匹配失败时，元素 P 的指针指向 p[0] T … a b c d a b c d x … ≠ 此例中模式串 P 的 P a b c d a b c d e next[8]=4 ，元素 T 中 x 直接与 P 中 p[4]=a 比较 P a b c d a b c d e 22 

23 . 字符串  字符串的改进模式匹配算法  对模式串 P 进行预处理，元素计算可以滑过多少个字 符 -1 ，元素当 j = 0 next( j ) = k+1 ，元素当 0 ≤ k < j-1, 且使 p0p1…pk=pj-k-1pj-k…pj-1 的最大数 0 ，元素其他情况 next(j)=-1 表示匹配失败时，元素 T 的指针加 1 ，元素 P 的指针指向 p[0] next(j)=k+1 表示匹配失败时，元素 P 的指针指向 p[k+1] ，元素 next(j)=0 表示匹配失败时，元素 P 的指针指向 p[0] T … a b c x … ≠ 此例中模式串 P 的 P a b c d a b c d e next[3]=0 ，元素 T 中 x 直接与 P 中 p[0]=a 比较 P a b c d a b c d e 23 

24 . 字符串  字符串的改进模式匹配算法  对模式串 P 进行预处理，元素计算可以滑过多少个字 符 -1 ，元素当 j = 0 next( j ) = k+1 ，元素当 0 ≤ k < j-1, 且使 p0p1…pk=pj-k-1pj-k…pj-1 的最大数 0 ，元素其他情况 可按定义直接计算 next ，元素下面介绍一种快速的计算 next 的方法 假设已知 next(j)=x ，元素现在计算 next(j+1) 若 px=pj ，元素则 next(j+1) = x+1 = next(j)+1 j=0;k=-1;next[0]=-1; 否则，元素设 next(x)=h ，元素 ( 此时有 p[0,h-1]=p[x-h,x-1]=p[j-h,j-1]) while(j<pLength) { 若 ph=pj ，元素则 next(j+1) = h+1 if(k==-1 || ch[j]==ch[k]) { 否则，元素令 next(h)=t, ( 此时有 p[0,t-1]=p[h-t,h- j++;k++;next[j]=k; 1]=p[j-t,j-1]) } 继续判断是否 pt=pj ，元素直到找到或者到 else k = next[k]; next(0) = -1 24 } 

25 . 字符串  字符串的改进模式匹配算法  对模式串 P 进行预处理，元素计算可以滑过多少个字 符 -1 ，元素当 j = 0 next( j ) = k+1 ，元素当 0 ≤ k < j-1, 且使 p0p1…pk=pj-k-1pj-k…pj-1 的最大数 0 ，元素其他情况 可按定义直接计算 next ，元素下面介绍一种快速的计算 next 的方法 下标 j 0 1 2 3 4 5 6 7 8 9 10 P a b a b c a b a b a x j=0;k=-1;next[0]=-1; next(j) -1 0 0 1 2 0 1 2 3 4 ? while(j<pLength) { if(k==-1 || ch[j]==ch[k]) { ≠ j++;k++;next[j]=k; = } else k = next[k]; next(10)=2+1=3 25 } 

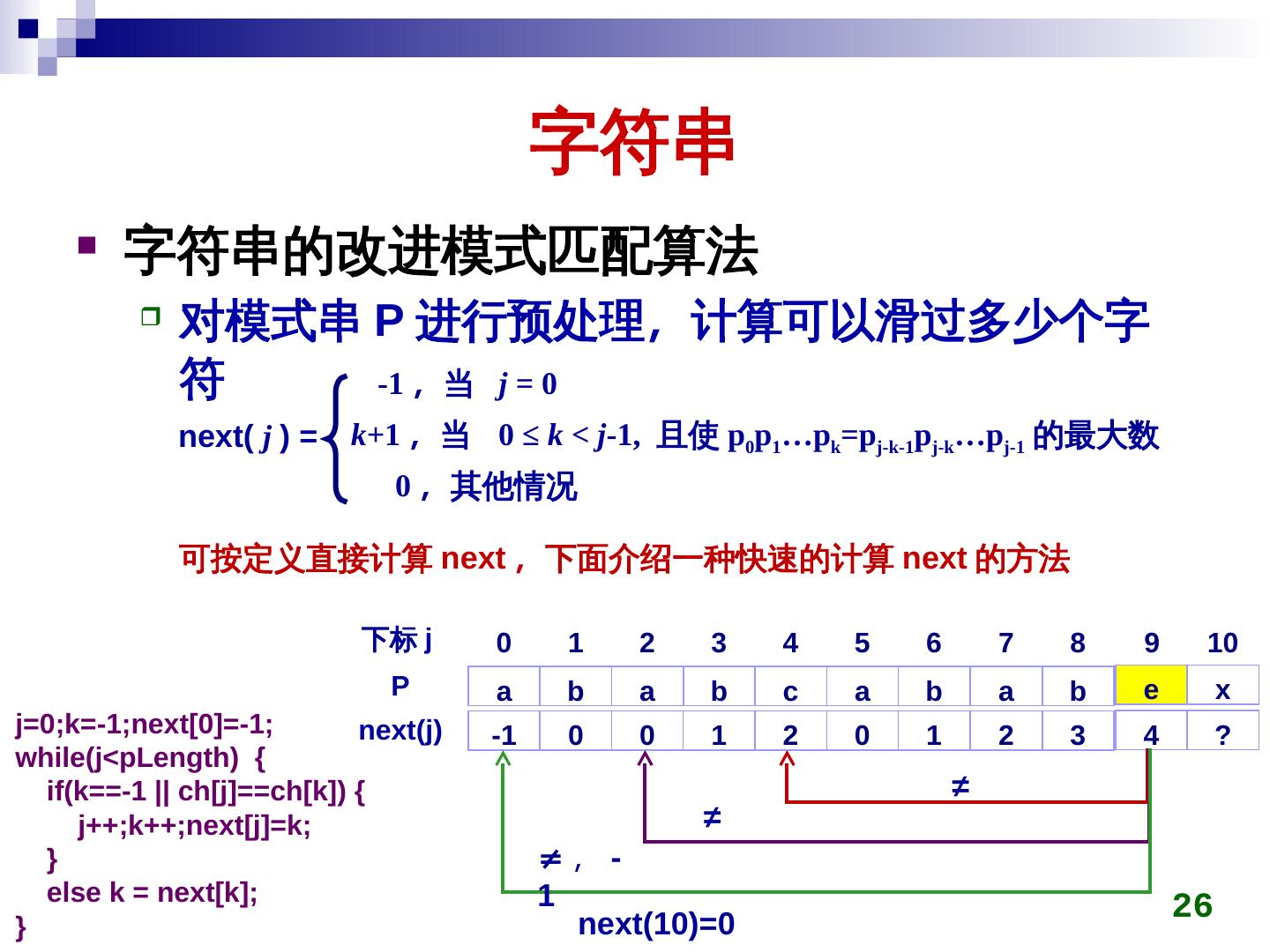
26 . 字符串  字符串的改进模式匹配算法  对模式串 P 进行预处理，元素计算可以滑过多少个字 符 -1 ，元素当 j = 0 next( j ) = k+1 ，元素当 0 ≤ k < j-1, 且使 p0p1…pk=pj-k-1pj-k…pj-1 的最大数 0 ，元素其他情况 可按定义直接计算 next ，元素下面介绍一种快速的计算 next 的方法 下标 j 0 1 2 3 4 5 6 7 8 9 10 P a b a b c a b a b e x j=0;k=-1;next[0]=-1; next(j) -1 0 0 1 2 0 1 2 3 4 ? while(j<pLength) { if(k==-1 || ch[j]==ch[k]) { ≠ j++;k++;next[j]=k; ≠ } ≠ ，元素 - else k = next[k]; 1 26 } next(10)=0 

27 .作业： 计算下列 3 个串的 next 数组的值 aaab abcabaa abcxaabbabcabaacbacba 作业： 目标串 T=ababbaabaa ，元素模式串 P=aab ，元素 求 P 的 next 数组的值，元素并给出快速匹配过程 27