03数据结构---栈与队列

1 .第三章 栈与队列 东南大学计算机学院 方效林 方效林 本课件借鉴了清华大学殷人昆老师 和哈尔滨工业大学张岩老师的课件 

2 . 本章主要内容  栈  栈的应用：表达式求值  栈与递归  队列  队列的应用：电路布线 2 

3 . 栈  定义：只允许在表的末端进行插入和删除的线性 表  特点：先进后出  栈的操作  进栈 push()  出栈 pop()  栈顶 top()  置空 setEmpty()  判断是否为空 isEmpty()  栈满 isFull() 3 

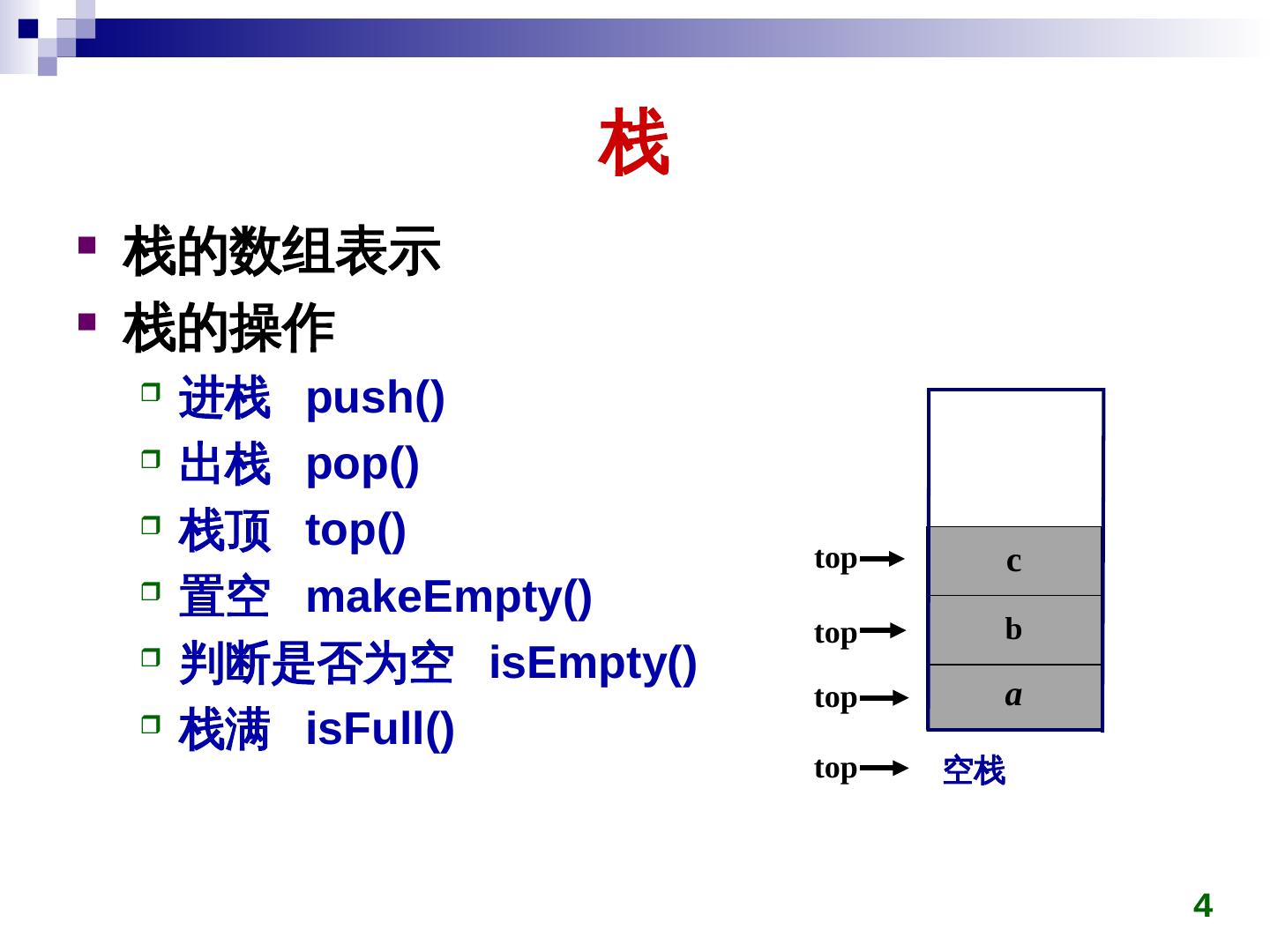
4 . 栈  栈的数组表示  栈的操作  进栈 push()  出栈 pop()  栈顶 top() top c  置空 makeEmpty() top b  判断是否为空 isEmpty() top a  栈满 isFull() top 空栈 4 

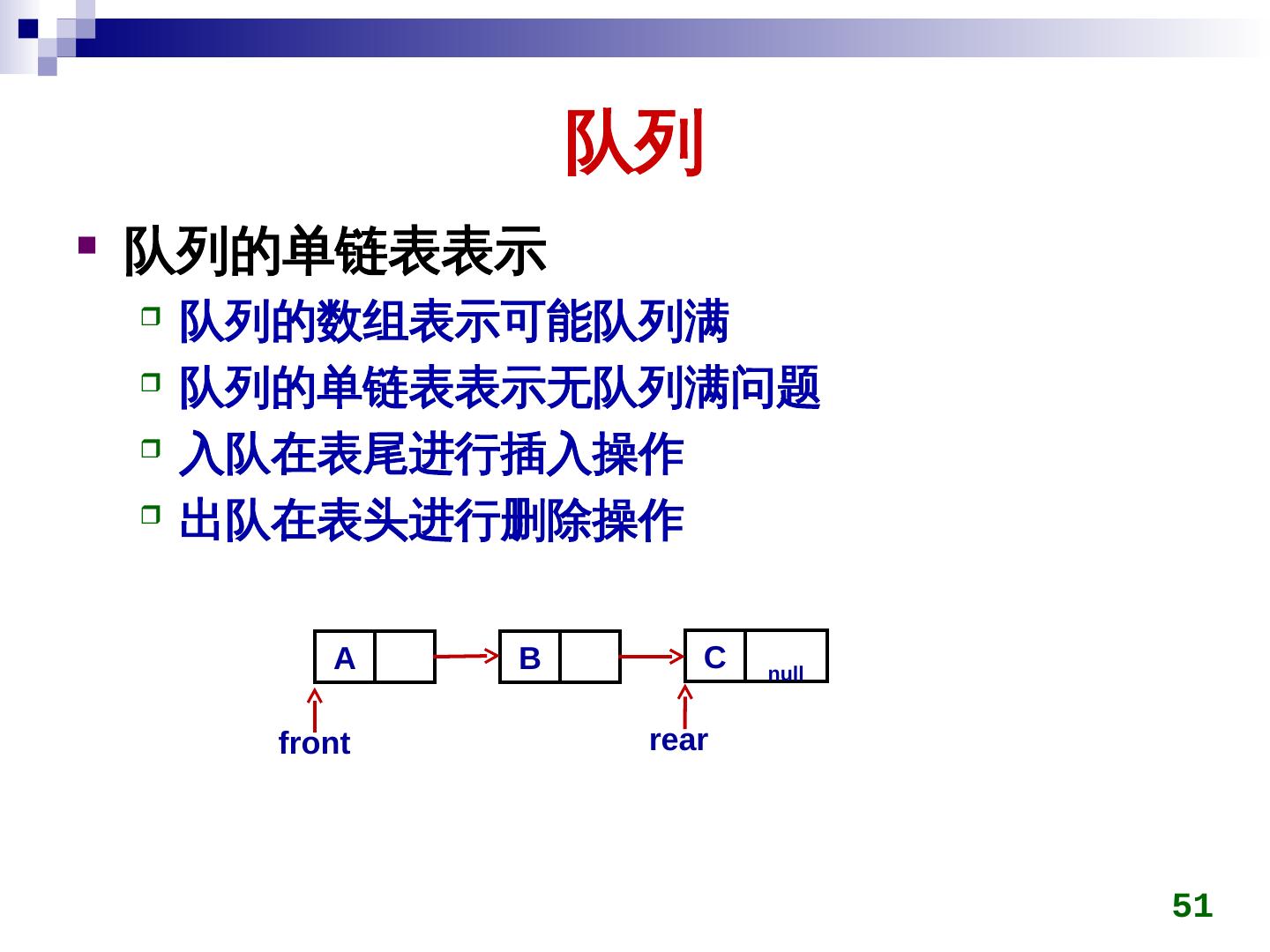
5 . 栈  栈的单链表表示  栈的数组表示可能栈满  栈的单链表表示无栈满问题 top c  入栈在表头进行插入操作  出栈在表头进行删除操作 b a null 5 

6 . 栈  进栈顺序为 (1,2,3) ，出栈顺序能否为 (3,1,2)?  不能， 3 出栈时，说明 2 和 1 都在栈里，而且 2 必须先于 1 出栈 top 3 2 1 作业： 1 ， 2 ， 3 ， 4 ， 5 ， 6 依次进栈，若出栈顺序为 2 ， 3 ， 4 ， 6 ， 5 ， 1 则栈大小至少为多少？ 6 

7 . 栈的应用：表达式求值  一个表达式由操作数 ( 亦称运算对象 ) 、操作 符 ( 亦称运算符 ) 和分界符组成。  算术表达式三种表示  中缀 (infix)) 表示  < 操作数 > < 操作符 > < 操作数 > ，如 A+B ；  前缀 (prefix)) 表示  < 操作符 > < 操作数 > < 操作数 > ，如 +AB ；  后缀 (postfix)) 表示  < 操作数 > < 操作数 > < 操作符 > ，如 AB+ ； 7 

8 . 栈的应用：表达式求值  中缀表达式： A + B * ( C - D ) - E / F  后缀表达式： A B C D - * + E F / -  表达式中相邻两个操作符的计算次序为：  优先级高的先计算；  优先级相同的自左向右计算；  当使用括号时从最内层括号开始计算。  前缀和中缀表达式求值需要两个栈；后缀表达 式求值只需一个栈，相对简单些。 8 

9 . 栈的应用：表达式求值  从左向右扫描表达式，用一个栈暂存扫描到的 操作数或计算结果。  后缀表达式的计算顺序中已隐含了加括号的优 先次序，括号在后缀表达式中不出现 中缀表达式： 后缀表达式： A+B*(C-D)-E/F ABCD-*+EF/- R1 R4 R1 R4 R2 R2 R3 R3 R5 R5 9 

10 .作业： 写出下列中缀表达式的后缀表达式 1.A*B*C 2.-A+B-C+D 3.A*(-B)+C 4.(A+B)*D+E/(F+A*D)+C 5.A&&B||!(E>F) 6.!(A && !((B<C) || (C>D))) || (C<E) 10 

11 . 栈的应用：表达式求值  后缀表达式求值过程  顺序扫描后缀表达式每一项  若该项是操作数，则进栈  若该项是操作符 <op> ，  若是单目运算符，则出栈一个操作数 X ，并将计算结 果 <op>X 进栈  若是双目运算符，则连续出栈两个操作数 X 和 Y ，并 将计算结果 X <op> Y 进栈  当表达式的所有项都扫描并处理完后，栈顶存放的 就是最后的计算结果。 11 

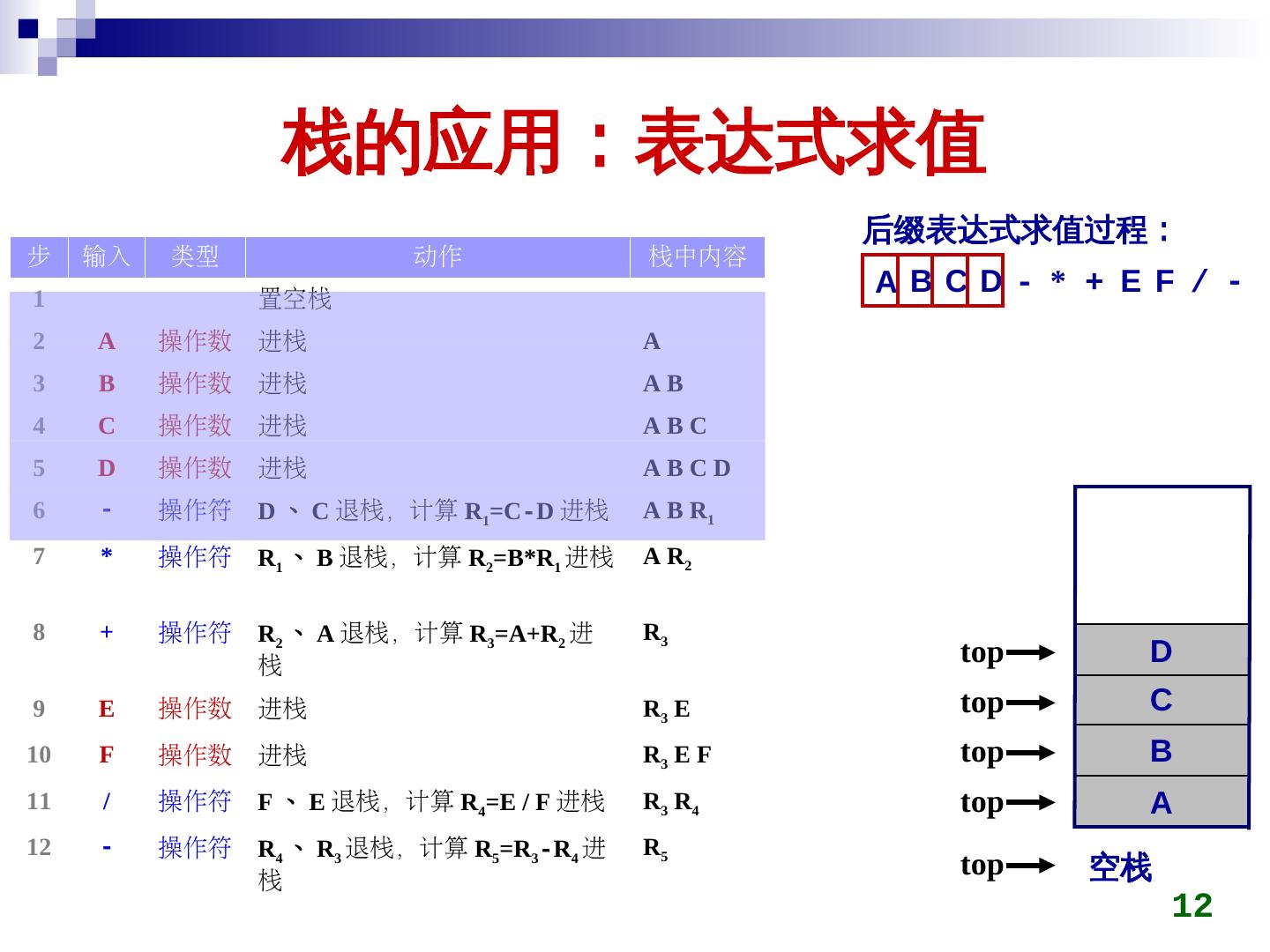
12 . 栈的应用：表达式求值 后缀表达式求值过程： 步 输入 类型 动作 栈中内容 1 置空栈 ABCD- * + E F / - 2 A 操作数 进栈 A 3 B 操作数 进栈 AB 4 C 操作数 进栈 ABC 5 D 操作数 进栈 ABCD 6 - 操作符 D 、 C 退栈，计算 R1=C-D 进栈 A B R1 7 * 操作符 R1 、 B 退栈，计算 R2=B*R1 进栈 A R2 8 + 操作符 R2 、 A 退栈，计算 R3=A+R2 进 R3 栈 top D 9 E 操作数 进栈 R3 E top C 10 F 操作数 进栈 R3 E F top B 11 / 操作符 F 、 E 退栈，计算 R4=E / F 进栈 R3 R4 top A 12 - 操作符 R4 、 R3 退栈，计算 R5=R3-R4 进 R5 栈 top 空栈 12 

13 . 栈的应用：表达式求值 后缀表达式求值过程： 步 输入 类型 动作 栈中内容 1 置空栈 ABCD- * + E F / - 2 A 操作数 进栈 A 3 B 操作数 进栈 AB 4 C 操作数 进栈 ABC 5 D 操作数 进栈 ABCD 6 - 操作符 D 、 C 退栈，计算 R1=C-D 进栈 A B R1 R1=C-D 7 * 操作符 R1 、 B 退栈，计算 R2=B*R1 进栈 A R2 8 + 操作符 R2 、 A 退栈，计算 R3=A+R2 进 R3 栈 top D 9 E 操作数 进栈 R3 E top C 10 F 操作数 进栈 R3 E F top B 11 / 操作符 F 、 E 退栈，计算 R4=E / F 进栈 R3 R4 A 12 - 操作符 R4 、 R3 退栈，计算 R5=R3-R4 进 R5 栈 13 

14 . 栈的应用：表达式求值 后缀表达式求值过程： 步 输入 类型 动作 栈中内容 1 置空栈 ABCD- * + E F / - 2 A 操作数 进栈 A 3 B 操作数 进栈 AB 4 C 操作数 进栈 ABC 5 D 操作数 进栈 ABCD 6 - 操作符 D 、 C 退栈，计算 R1=C-D 进栈 A B R1 R2=B*R1 7 * 操作符 R1 、 B 退栈，计算 R2=B*R1 进栈 A R2 8 + 操作符 R2 、 A 退栈，计算 R3=A+R2 进 R3 栈 9 E 操作数 进栈 R3 E top R1=C-D 10 F 操作数 进栈 R3 E F top B 11 / 操作符 F 、 E 退栈，计算 R4=E / F 进栈 R3 R4 top A 12 - 操作符 R4 、 R3 退栈，计算 R5=R3-R4 进 R5 栈 14 

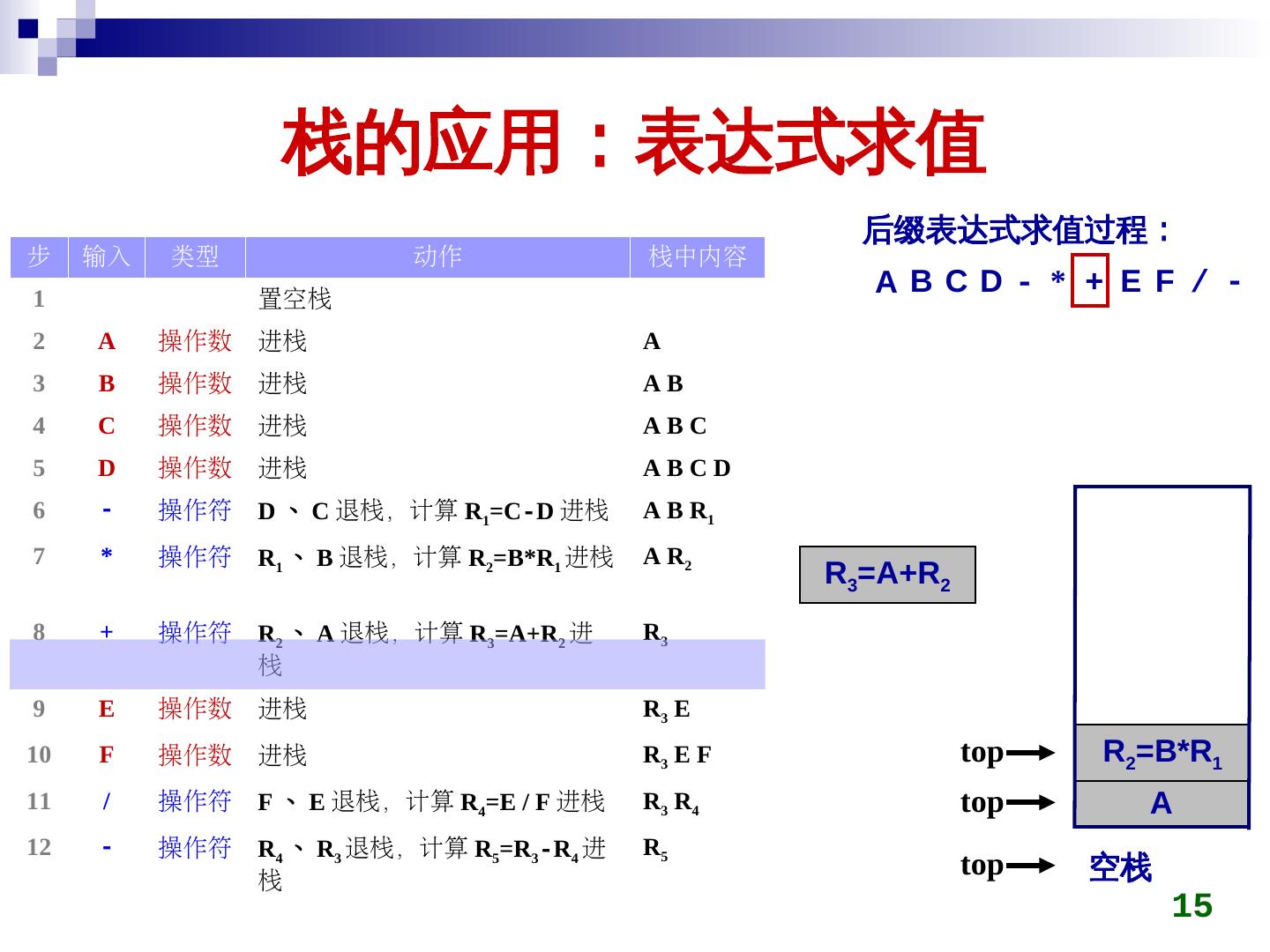
15 . 栈的应用：表达式求值 后缀表达式求值过程： 步 输入 类型 动作 栈中内容 1 置空栈 ABCD- * + E F / - 2 A 操作数 进栈 A 3 B 操作数 进栈 AB 4 C 操作数 进栈 ABC 5 D 操作数 进栈 ABCD 6 - 操作符 D 、 C 退栈，计算 R1=C-D 进栈 A B R1 7 * 操作符 R1 、 B 退栈，计算 R2=B*R1 进栈 A R2 R3=A+R2 8 + 操作符 R2 、 A 退栈，计算 R3=A+R2 进 R3 栈 9 E 操作数 进栈 R3 E 10 F 操作数 进栈 R3 E F top R2=B*R1 11 / 操作符 F 、 E 退栈，计算 R4=E / F 进栈 R3 R4 top A 12 - 操作符 R4 、 R3 退栈，计算 R5=R3-R4 进 R5 栈 top 空栈 15 

16 . 栈的应用：表达式求值 后缀表达式求值过程： 步 输入 类型 动作 栈中内容 1 置空栈 ABCD- * + E F / - 2 A 操作数 进栈 A 3 B 操作数 进栈 AB 4 C 操作数 进栈 ABC 5 D 操作数 进栈 ABCD 6 - 操作符 D 、 C 退栈，计算 R1=C-D 进栈 A B R1 7 * 操作符 R1 、 B 退栈，计算 R2=B*R1 进栈 A R2 8 + 操作符 R2 、 A 退栈，计算 R3=A+R2 进 R3 栈 9 E 操作数 进栈 R3 E top F 10 F 操作数 进栈 R3 E F top E 11 / 操作符 F 、 E 退栈，计算 R4=E / F 进栈 R3 R4 top R3=A+R2 12 - 操作符 R4 、 R3 退栈，计算 R5=R3-R4 进 R5 栈 16 

17 . 栈的应用：表达式求值 后缀表达式求值过程： 步 输入 类型 动作 栈中内容 1 置空栈 ABCD- * + E F / - 2 A 操作数 进栈 A 3 B 操作数 进栈 AB 4 C 操作数 进栈 ABC 5 D 操作数 进栈 ABCD 6 - 操作符 D 、 C 退栈，计算 R1=C-D 进栈 A B R1 7 * 操作符 R1 、 B 退栈，计算 R2=B*R1 进栈 A R2 R4=E/F 8 + 操作符 R2 、 A 退栈，计算 R3=A+R2 进 R3 栈 9 E 操作数 进栈 R3 E top F 10 F 操作数 进栈 R3 E F top E 11 / 操作符 F 、 E 退栈，计算 R4=E / F 进栈 R3 R4 top R3=A+R2 12 - 操作符 R4 、 R3 退栈，计算 R5=R3-R4 进 R5 栈 17 

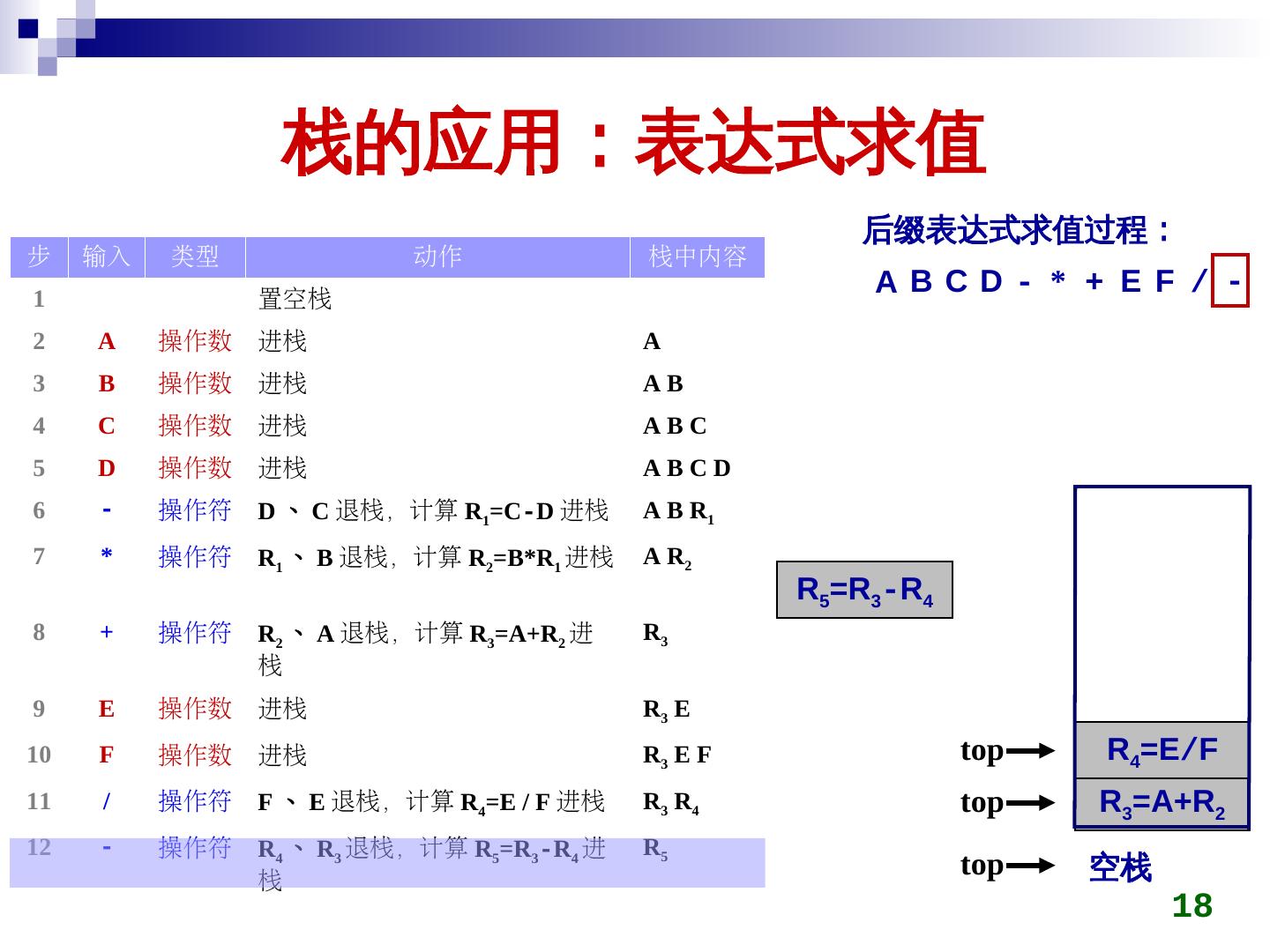
18 . 栈的应用：表达式求值 后缀表达式求值过程： 步 输入 类型 动作 栈中内容 1 置空栈 ABCD- * + E F / - 2 A 操作数 进栈 A 3 B 操作数 进栈 AB 4 C 操作数 进栈 ABC 5 D 操作数 进栈 ABCD 6 - 操作符 D 、 C 退栈，计算 R1=C-D 进栈 A B R1 7 * 操作符 R1 、 B 退栈，计算 R2=B*R1 进栈 A R2 R5=R3-R4 8 + 操作符 R2 、 A 退栈，计算 R3=A+R2 进 R3 栈 9 E 操作数 进栈 R3 E 10 F 操作数 进栈 R3 E F top R4=E/F 11 / 操作符 F 、 E 退栈，计算 R4=E / F 进栈 R3 R4 top R3=A+R2 12 - 操作符 R4 、 R3 退栈，计算 R5=R3-R4 进 R5 栈 top 空栈 18 

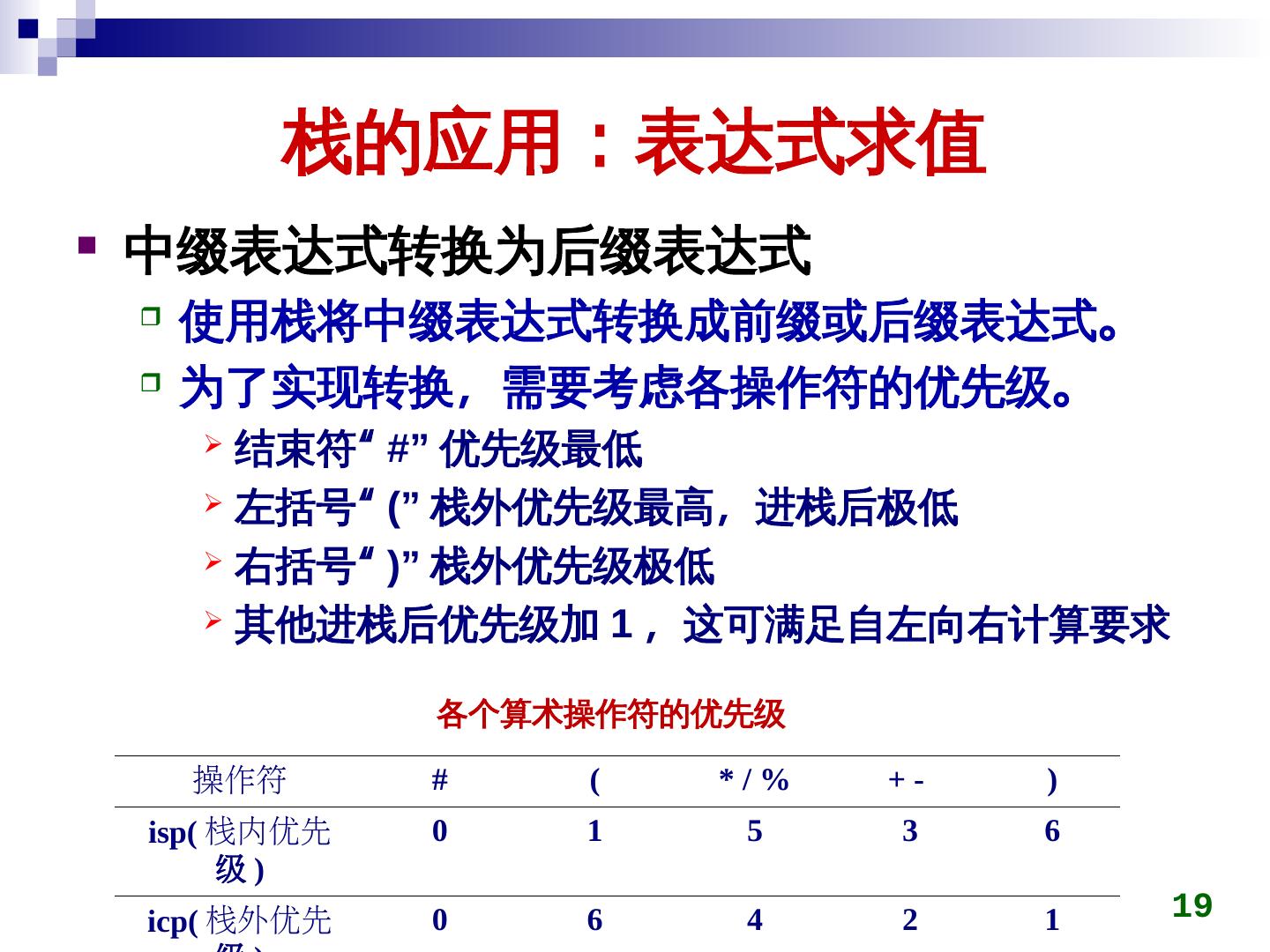
19 . 栈的应用：表达式求值  中缀表达式转换为后缀表达式  使用栈将中缀表达式转换成前缀或后缀表达式。  为了实现转换，需要考虑各操作符的优先级。  结束符“ #” 优先级最低  左括号“ (” 栈外优先级最高，进栈后极低  右括号“ )” 栈外优先级极低  其他进栈后优先级加 1 ，这可满足自左向右计算要求 各个算术操作符的优先级 操作符 # ( */% +- ) isp( 栈内优先 0 1 5 3 6 级) icp( 栈外优先 0 6 4 2 1 19 

20 . 栈的应用：表达式求值  中缀表达式转换为后缀表达式算法  操作符栈初始化，结束符 # 进栈，读入中缀表达式的 首字符 ch  重复执行以下步骤，直到 ch=# ，同时栈顶操作符也是 # ，停止循环  若 ch 是操作数直接输出，读入下一字符 ch  若 ch 是操作符，比较 ch 和栈顶操作符 op 优先级：  若 icp(ch) > isp(op) ，令 ch 进栈，读入下一字符 ch  若 icp(ch) < isp(op) ，退栈，并输出  若 icp(ch)==isp(op) ，退栈不输出；若退出的是 ( ，则读入下一 个字符 ch  算法结束，输出序列即为所得后缀表达式 20 

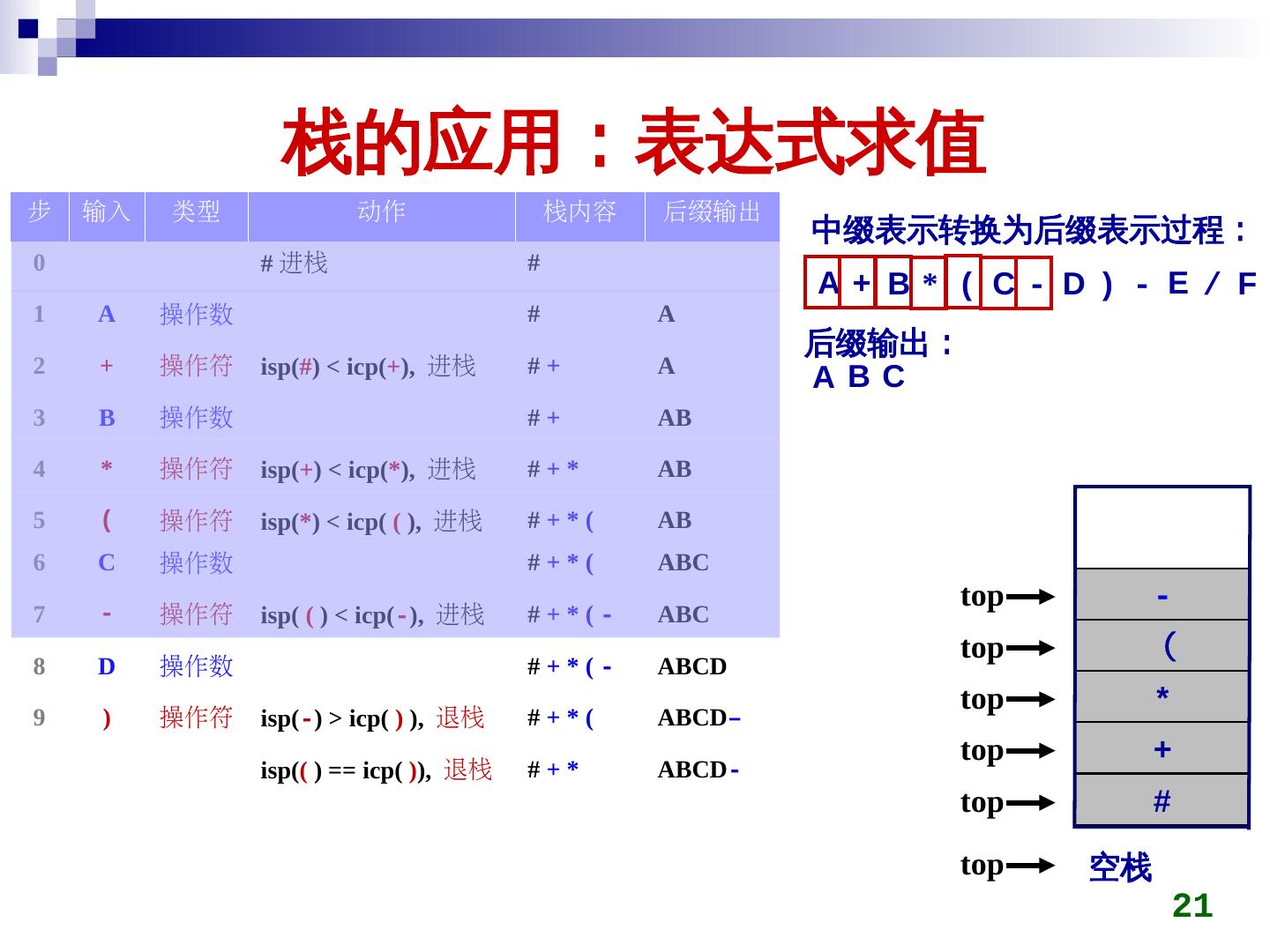
21 . 栈的应用：表达式求值 步 输入 类型 动作 栈内容 后缀输出 中缀表示转换为后缀表示过程： 0 # 进栈 # A+ B* ( C- D) - E / F 1 A 操作数 # A 后缀输出： 2 + 操作符 isp(#) < icp(+), 进栈 #+ A ABC 3 B 操作数 #+ AB 4 * 操作符 isp(+) < icp(*), 进栈 #+* AB 5 ( 操作符 isp(*) < icp( ( ), 进栈 #+*( AB 6 C 操作数 #+*( ABC top - 7 - 操作符 isp( ( ) < icp(-), 进栈 #+*(- ABC top （ 8 D 操作数 #+*(- ABCD top * 9 ) 操作符 isp(-) > icp( ) ), 退栈 #+*( ABCD– top + isp(( ) == icp( )), 退栈 #+* ABCD- top # top 空栈 21 

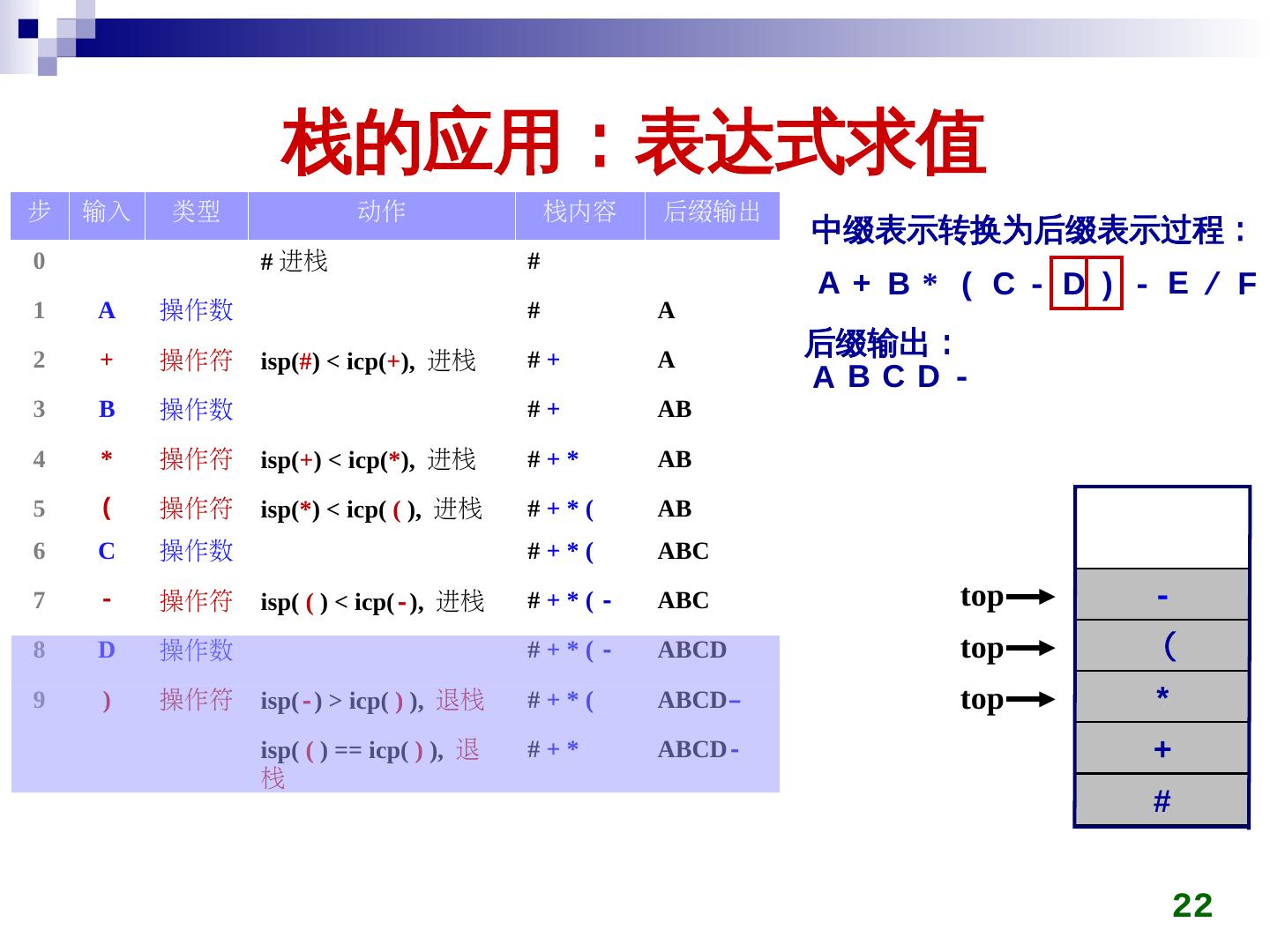
22 . 栈的应用：表达式求值 步 输入 类型 动作 栈内容 后缀输出 中缀表示转换为后缀表示过程： 0 # 进栈 # A+ B* ( C- D) - E / F 1 A 操作数 # A 2 + #+ A 后缀输出： 操作符 isp(#) < icp(+), 进栈 ABCD- 3 B 操作数 #+ AB 4 * 操作符 isp(+) < icp(*), 进栈 #+* AB 5 ( 操作符 isp(*) < icp( ( ), 进栈 #+*( AB 6 C 操作数 #+*( ABC 7 - 操作符 isp( ( ) < icp(-), 进栈 #+*(- ABC top - 8 D 操作数 #+*(- ABCD top （ 9 ) 操作符 isp(-) > icp( ) ), 退栈 #+*( ABCD– top * isp( ( ) == icp( ) ), 退 #+* ABCD- + 栈 # 22 

23 . 栈的应用：表达式求值 步 输入 类型 动作 栈内容 后缀输出 中缀表示转换为后缀表示过程： 10 - 操作符 isp(*) > icp(-), 退栈 #+ ABCD-* A+ B* ( C- D) - E / F isp(+) > icp(-), 退栈 # ABCD-*+ 后缀输出： isp(#) > icp(-), 进栈 #- ABCD-*+ ABCD- * + 11 E 操作数 #- ABCD-*+E 12 / 操作符 isp(-) < icp(/), 进栈 #- / ABCD-*+E 13 F 操作数 #- / ABCD-*+EF 14 # 操作符 isp(/) < icp(#), 退栈 #- ABCD-*+EF/ isp(-) < icp(#), 退栈 # ABCD-*+EF- 结束 top * top + top # 23 

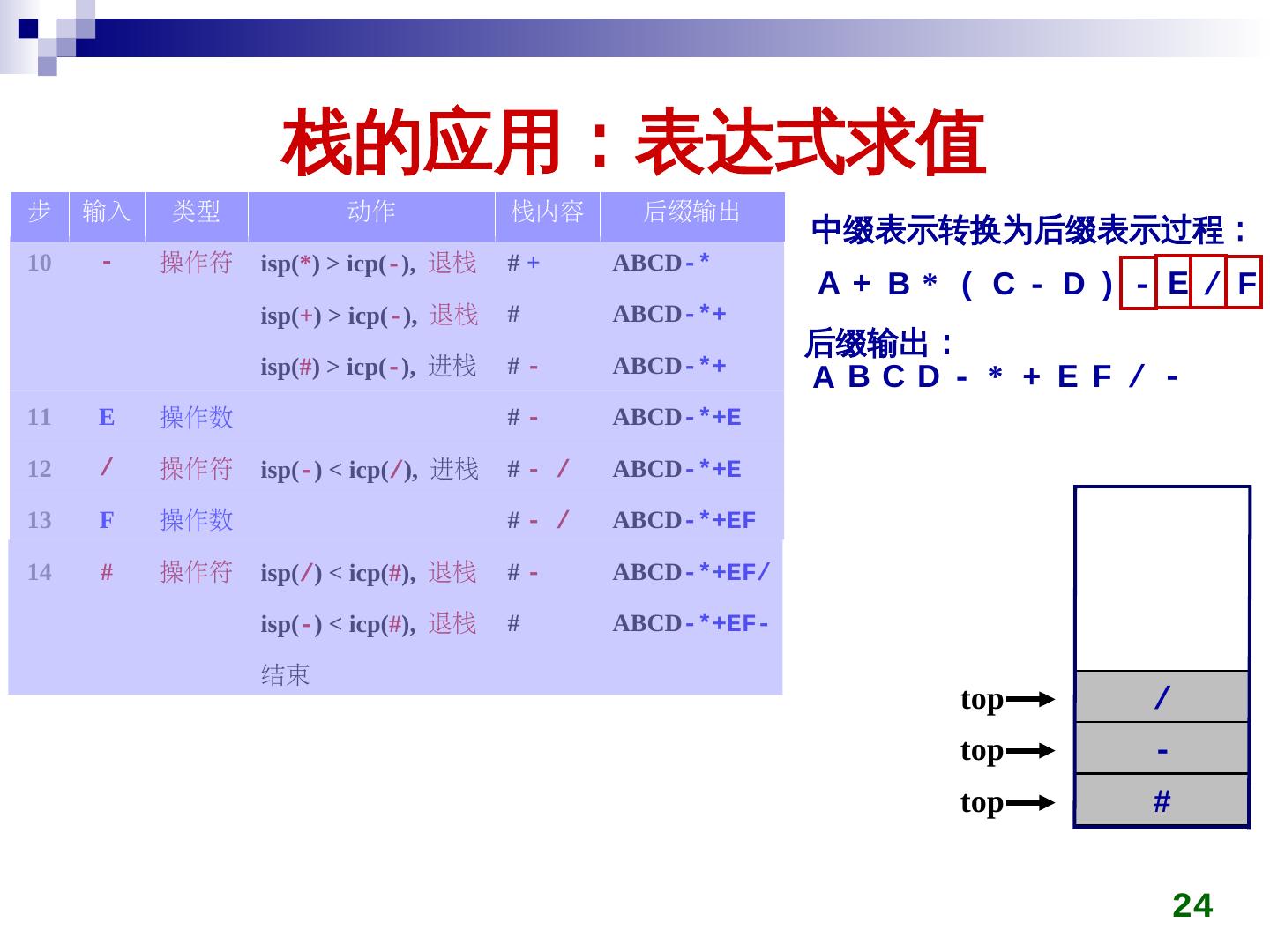
24 . 栈的应用：表达式求值 步 输入 类型 动作 栈内容 后缀输出 中缀表示转换为后缀表示过程： 10 - 操作符 isp(*) > icp(-), 退栈 #+ ABCD-* A+ B* ( C- D) - E / F isp(+) > icp(-), 退栈 # ABCD-*+ 后缀输出： isp(#) > icp(-), 进栈 #- ABCD-*+ ABCD- * + E F / - 11 E 操作数 #- ABCD-*+E 12 / 操作符 isp(-) < icp(/), 进栈 #- / ABCD-*+E 13 F 操作数 #- / ABCD-*+EF 14 # 操作符 isp(/) < icp(#), 退栈 #- ABCD-*+EF/ isp(-) < icp(#), 退栈 # ABCD-*+EF- 结束 top / top - top # 24 

25 . 作业  程序实现简单的中缀表达式求值  数字均为一位数，即 0-9  运算符只有 + - * / ( ) 25 

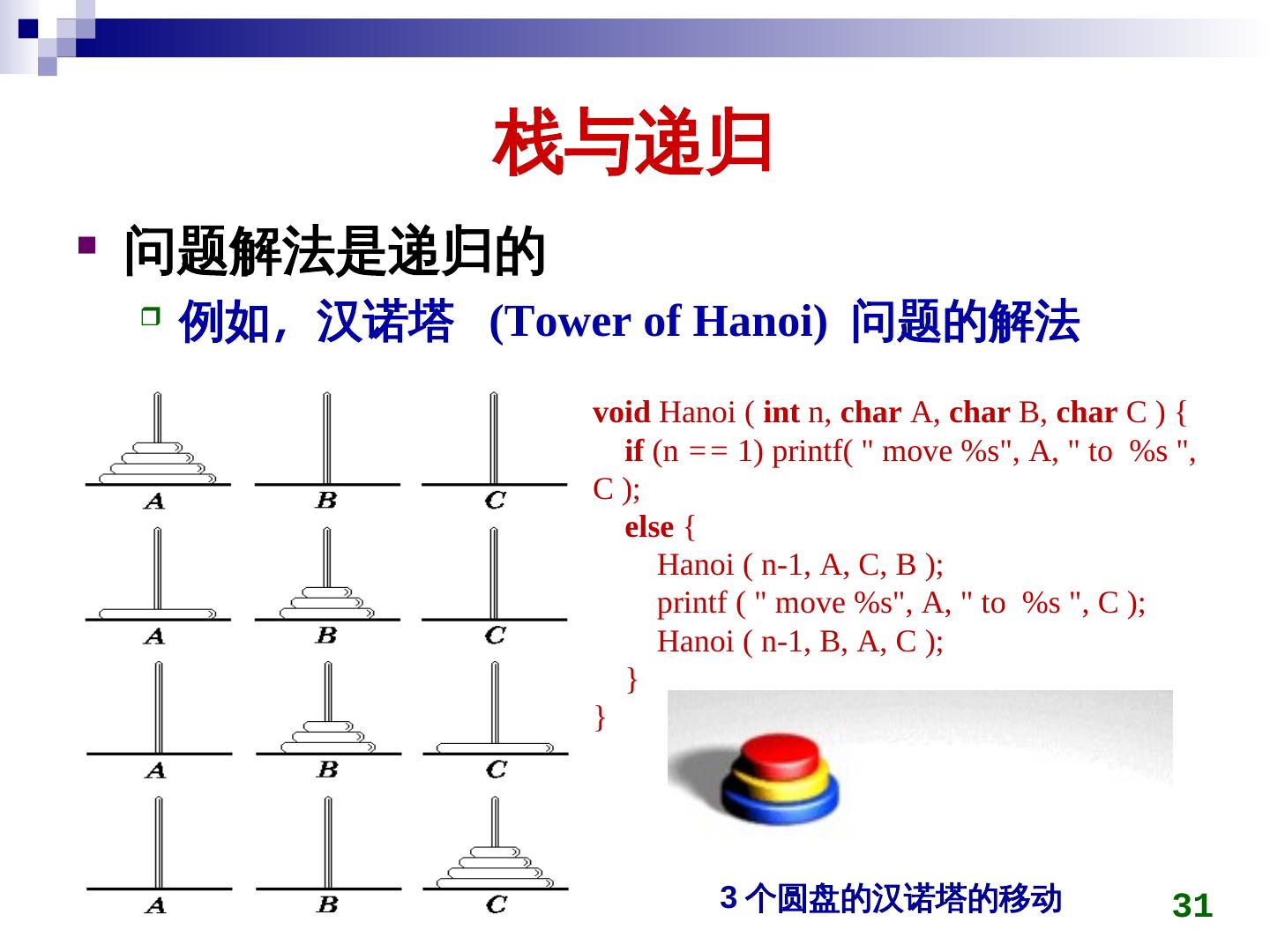
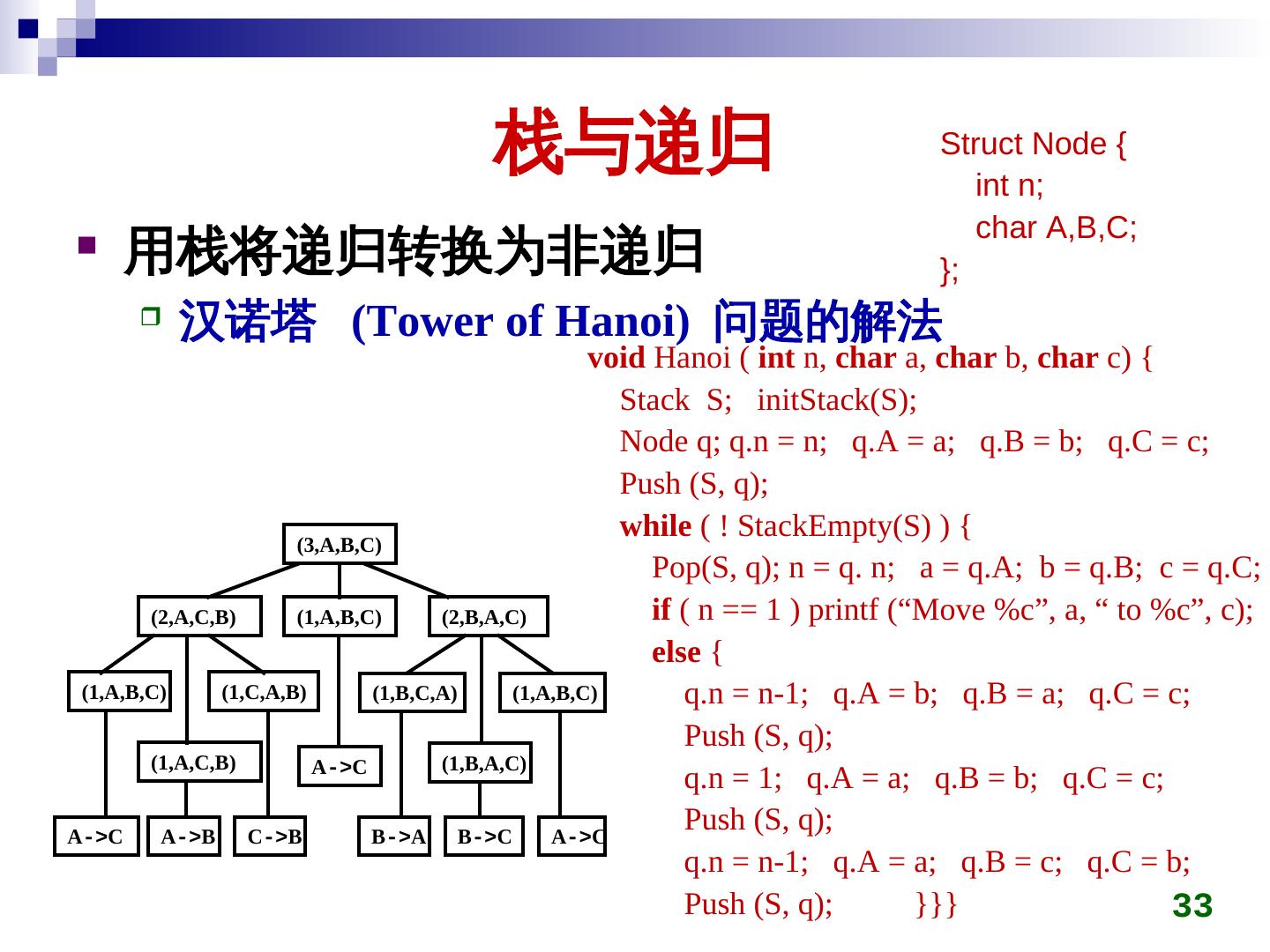
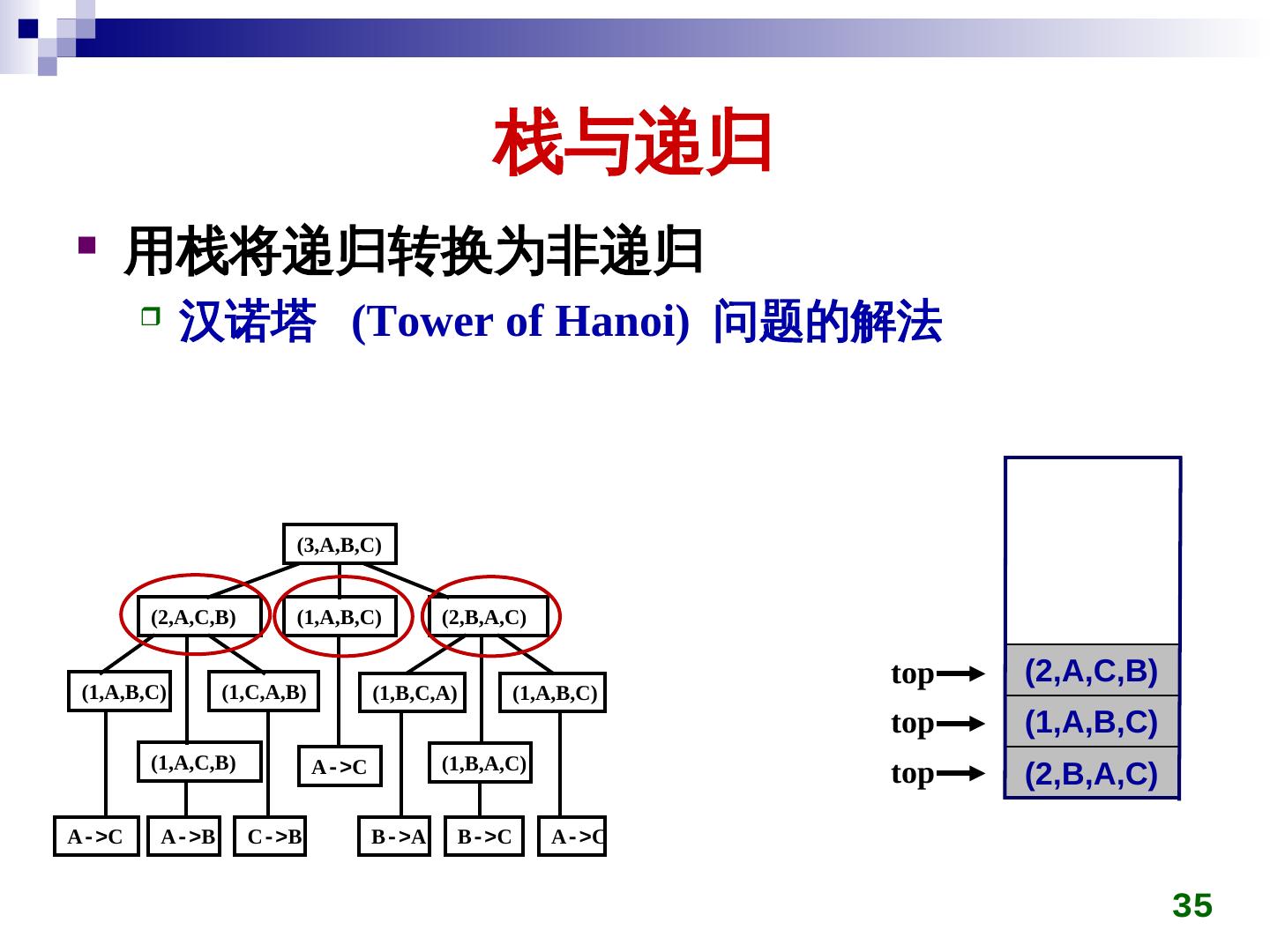
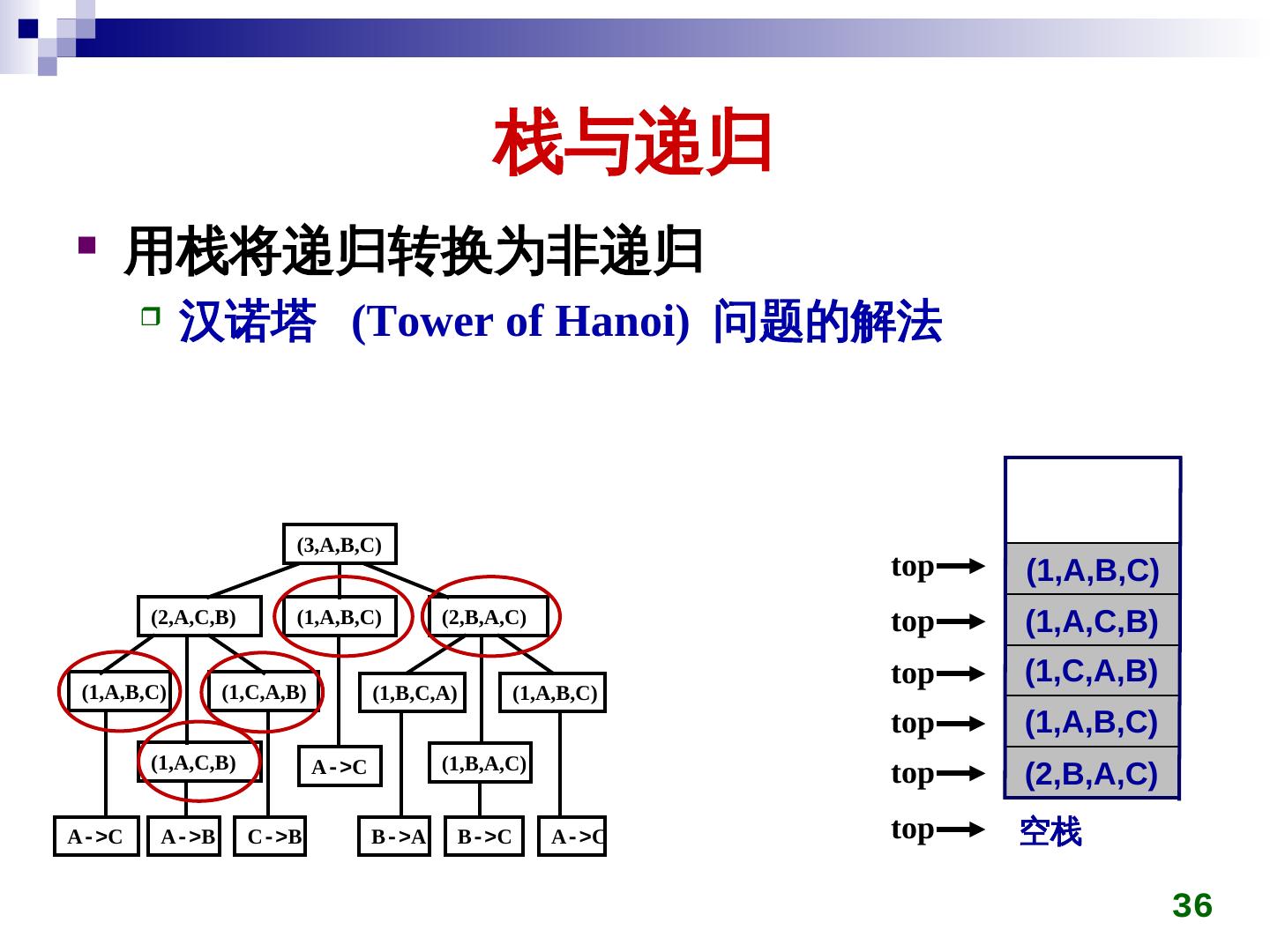
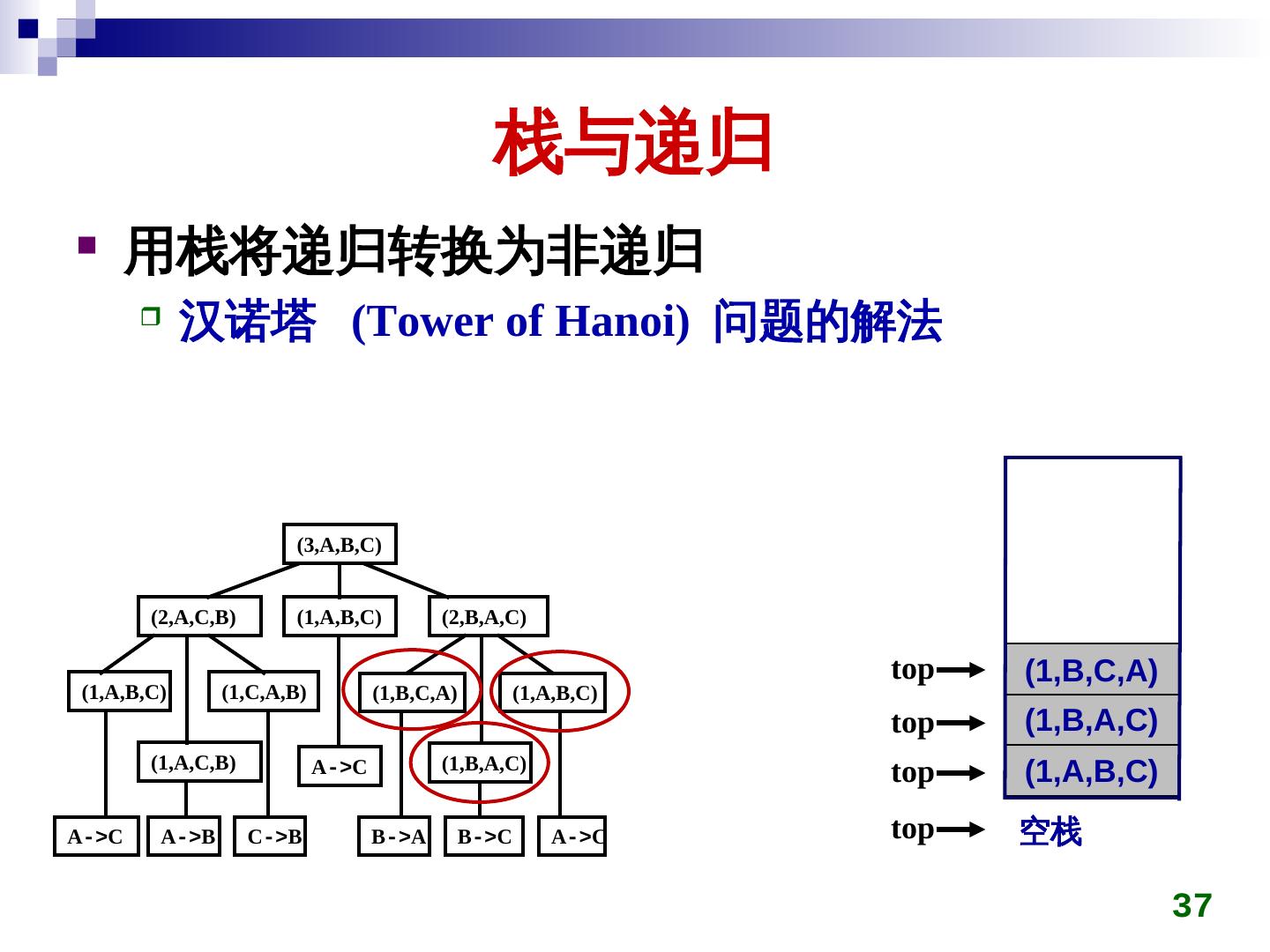
26 . 栈与递归  递归的定义  若一个对象部分地包含它自己，或用它自己给自己 定义，则称这个对象是递归的；若一个过程直接地 或间接地调用自己，则称这个过程是递归的过程。  以下三种情况常常用到递归方法。  定义是递归的  数据结构是递归的  问题的解法是递归的 26 

27 . 栈与递归  定义是递归的  例如，阶乘函数 (Factorial))  1, 当 n 0 时 n!    n  ( n  1)! , 当 n 1 时  求解阶乘函数的递归算法 l)ong Factorial ( l)ong n ) { if (n == 0) return 1; el)se return n*Factorial(n-1); } 27 

28 . 栈与递归  定义是递归的  例如，阶乘函数 (Factorial)) 主程序 main : fact(4) 参数 4 计算 4*fact(3) 返 递 参 回 24 结 回 归 数 参数 3 计算 3*fact(2) 返 果 归 调 传 回 6 返 求 参数 2 计算 2*fact(1) 返 用 递 回 值 回 2 参数 1 计算 1*fact(0) 返 回 1 参数 0 直接定值 = 1 返 回 1 28 

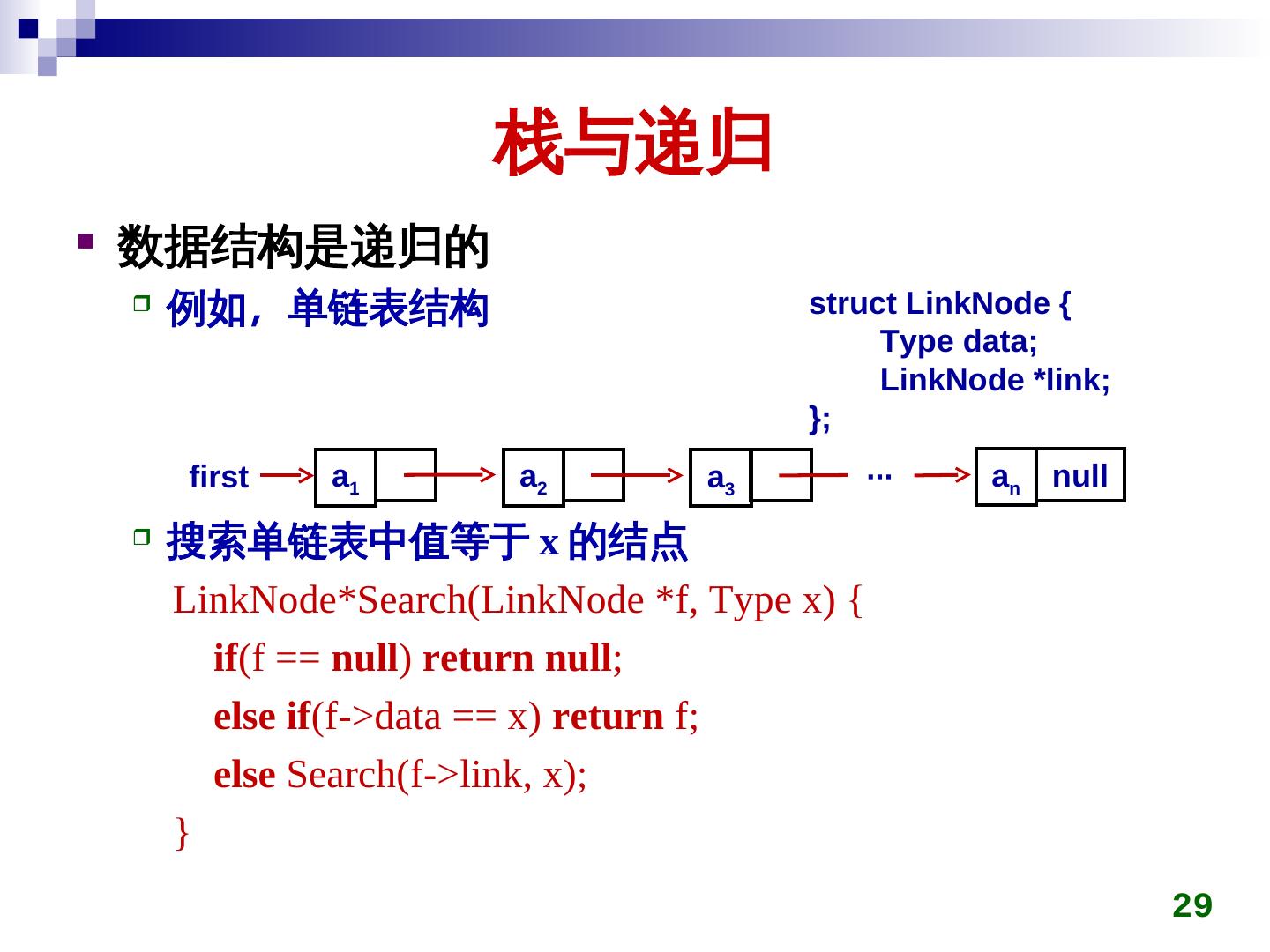
29 . 栈与递归  数据结构是递归的  例如，单链表结构 struct LinkNode { Type data; LinkNode *link; }; first a1 a2 a3 ∙∙∙ an null  搜索单链表中值等于 x 的结点 LinkNode*Search(LinkNode *f, Type x) { if(f == nul)l)) return nul)l); el)se if(f->data == x) return f; el)se Search(f->link, x); } 29