- 快召唤伙伴们来围观吧
- 微博 QQ QQ空间 贴吧
- 文档嵌入链接
- 复制
- 微信扫一扫分享
- 已成功复制到剪贴板
02数据结构---线性表
展开查看详情
1 . 第二章 线性表 东南大学计算机学院 方效林 方效林 本课件借鉴了清华大学殷人昆老师 和哈尔滨工业大学张岩老师的课件
2 . 本章主要内容 线性表 顺序表 单链表 线性表的变形 双向链表 循环链表 多项式及其运算 2
3 . 线性表 定义: n 个数据元素的有限序列,记为 (aa1,a2, …,an) ai 是线性表中的数据元素 n 是线性表的长度 a1 an 线性表的性质 除第一个元素外,其他每一个元素有一个且仅有一 个直接前驱。 除最后一个元素外,其他每一个元素有一个且仅有 一个直接后继。 3
4 . 线性表 线性表的一些基本操作 查找 插入 删除 ∙∙∙∙∙∙ 线性表的存储方式 基于数组 (a 顺序表 ) 基于链表 (a 链表 ) 基于散列 (a 散列表 ) …… 4
5 . 顺序表 顺序表是线性表基于数组的存储表示 存储空间 a1 a2 ∙∙∙ ai ai+1 ∙∙∙ an ∙∙∙ 下标 0 1 i-1 i n-1 SIZE-1 5
6 . 顺序表 顺序表的查找操作 25 34 57 16 48 09 63 ∙∙∙ 0 1 2 3 4 5 6 查找 16 平均比较次数 n -1 Search(aType x) { ACN = p c i 0 i i for(ai=0; i<n; i++) if(aa[i] == x) return i+1; 假设每个值查找概率相同 return 0; 1 n -1 1 } ACN = (i 1) (1 2 n) n i 0 n 1 (1 n) n 1 n n 2 2 6
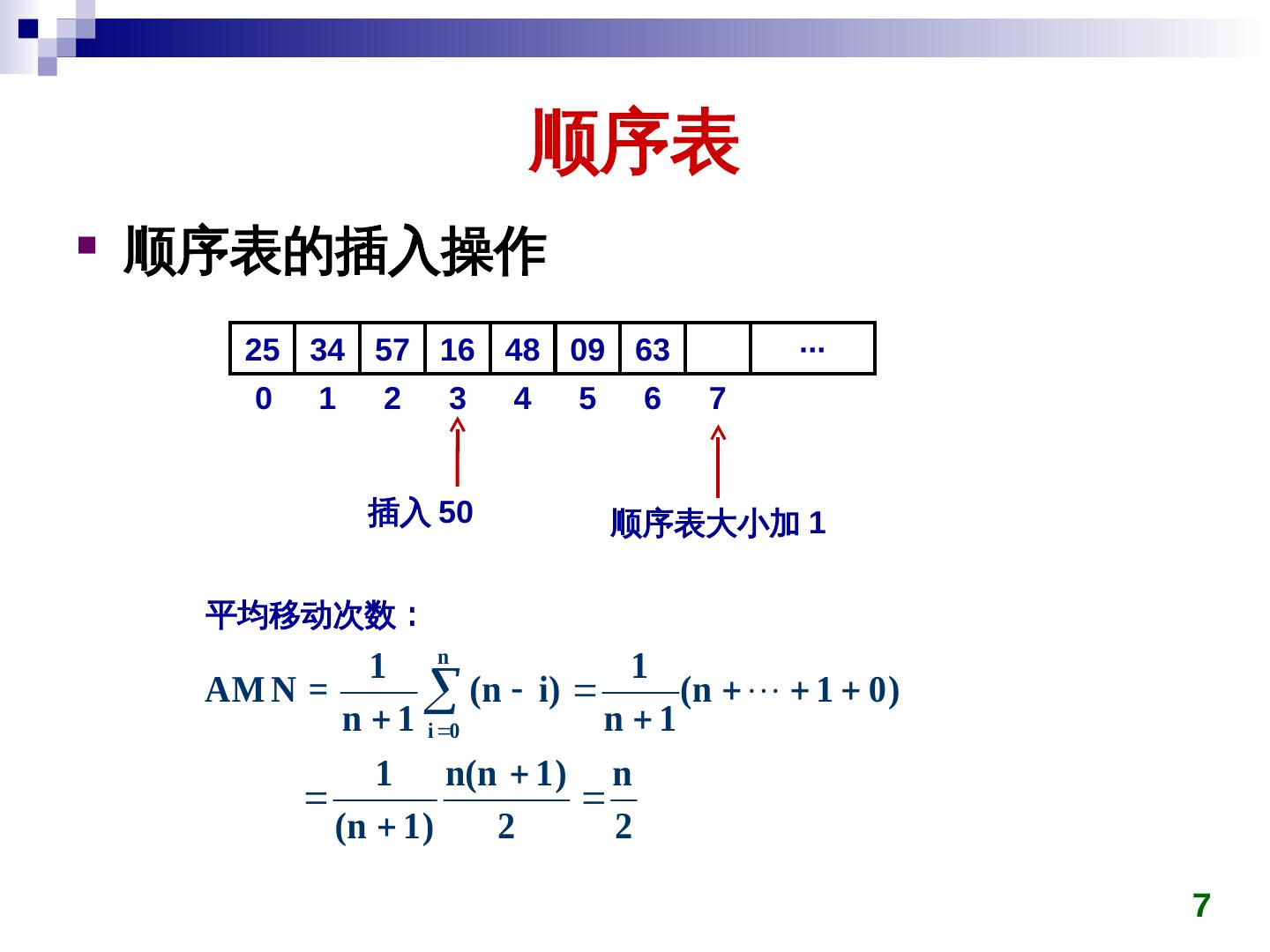
7 . 顺序表 顺序表的插入操作 25 34 57 16 48 09 63 ∙∙∙ 0 1 2 3 4 5 6 7 插入 50 顺序表大小加 1 平均移动次数: 1 n 1 AM N = n 1 i 0 (n i) n 1 (n 1 0) 1 n(n 1) n (n 1) 2 2 7
8 . 顺序表 顺序表的删除操作 25 34 57 16 48 09 63 ∙∙∙ 0 1 2 3 4 5 6 删除 16顺序表大小减 1 平均移动次数: 1 n -1 1 (n 1 )n n 1 AM N = n i 0 (n i 1 ) n 2 2 8
9 . 顺序表 顺序表的优点 无需保存与逻辑关系相关的信息 给定下标时,存取速度快 顺序表的缺点 插入删除操作移动开销大 需要固定的存储空间 9
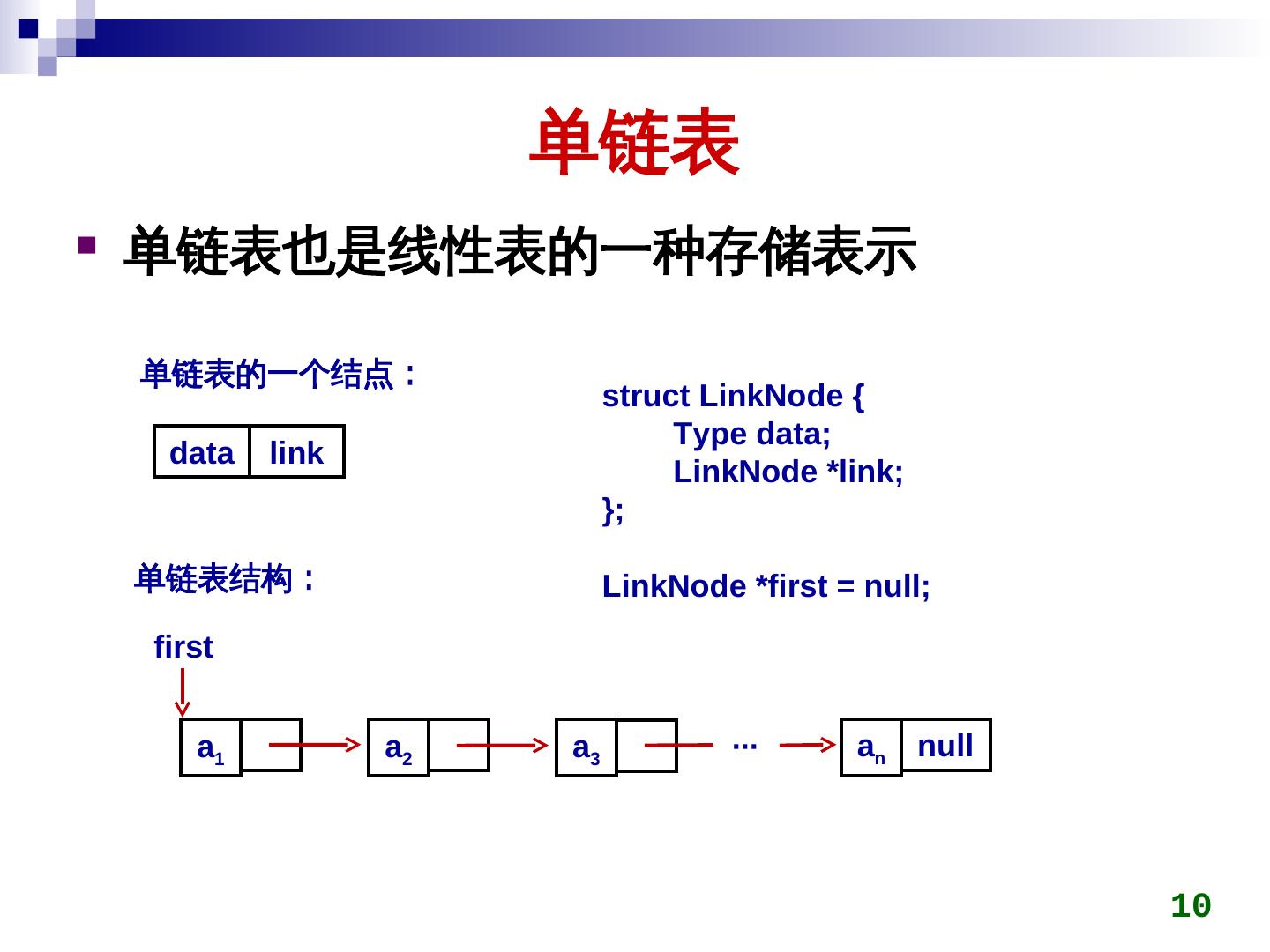
10 . 单链表 单链表也是线性表的一种存储表示 单链表的一个结点: struct LinkNode { Type data; data link LinkNode *link; }; 单链表结构: LinkNode *first = null; first a1 a2 a3 ∙∙∙ an null 10
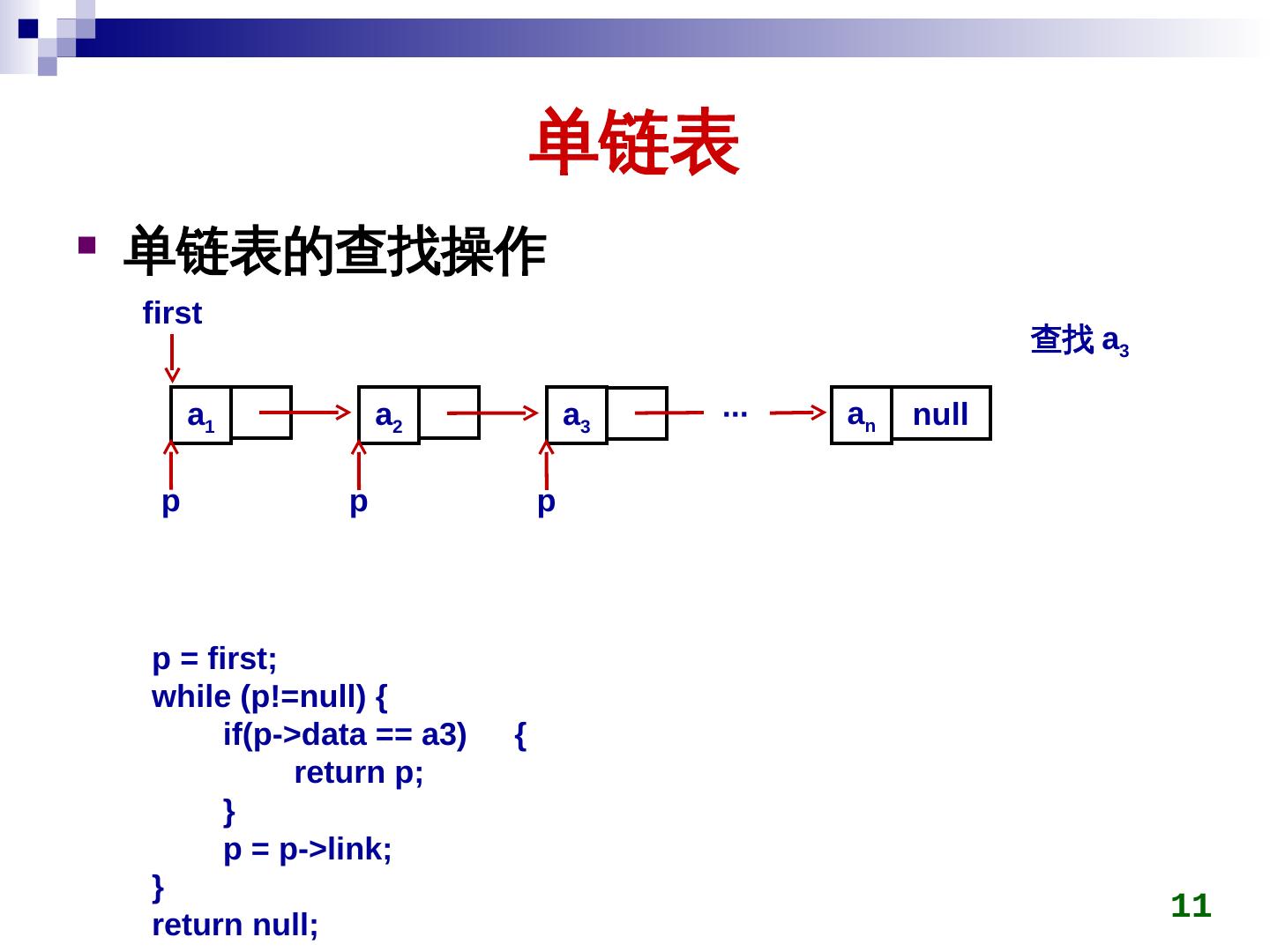
11 . 单链表 单链表的查找操作 first 查找 a3 a1 a2 a3 ∙∙∙ an null p p p p = first; while (ap!=null) { if(ap->data == a3) { return p; } p = p->link; } 11 return null;
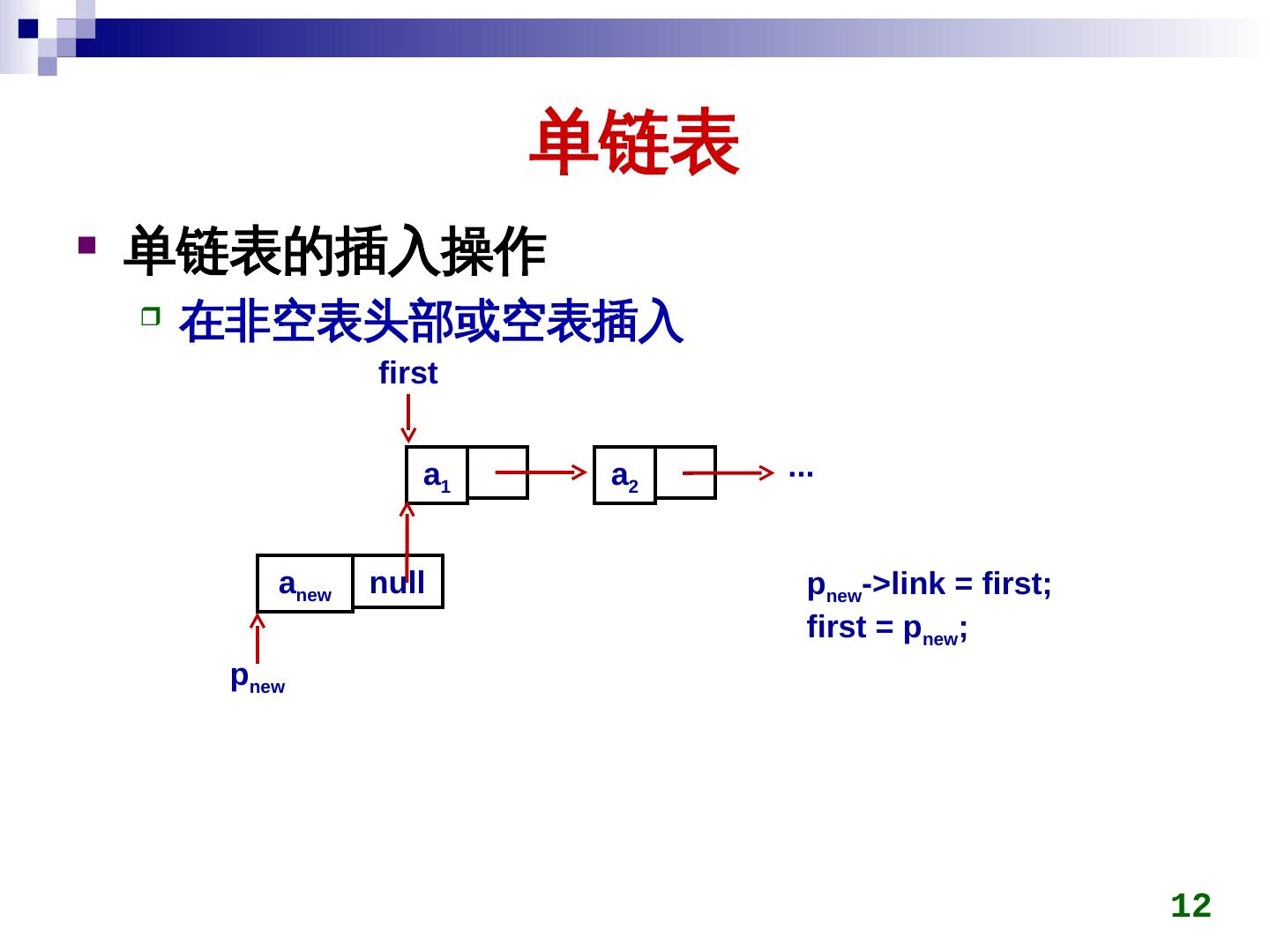
12 . 单链表 单链表的插入操作 在非空表头部或空表插入 first a1 a2 ∙∙∙ anew null pnew->link = first; first = pnew; pnew 12
13 . 单链表 单链表的插入操作 在非空表头部或空表插入 在非空表中部或尾部插入 p ∙∙∙ ai ai+1 ∙∙∙ pnew->link = p->link; anew null p->link = pnew; pnew 13
14 . 单链表 单链表的删除操作 在单链表头部删除 first a1 a2 ∙∙∙ p p = first; first = first->link; delete p; 14
15 . 单链表 单链表的删除操作 在单链表头部删除 在单链表中部或尾部删除 p ∙∙∙ ai ai+1 ai+2 ∙∙∙ temp temp = p->link; p->link = temp->link; delete temp; 15
16 . 单链表 单链表的删除操作 在单链表头部删除 在单链表中部或尾部删除 空链表删除:无结点删除 16
17 . 带附加头结点的单链表 struct LinkNode { 附加头结点 Type data; LinkNode *link; 不带附加头结点单链表结构: }; first 不带附加头结点头指针初始化: LinkNode *first = null; a1 a2 a3 ∙∙∙ an null 带附加头结点单链表结构: first 带附加头结点时头指针初始化: LinkNode *first = new LinkNode; first->link = null; a1 a2 a3 ∙∙∙ an null 17
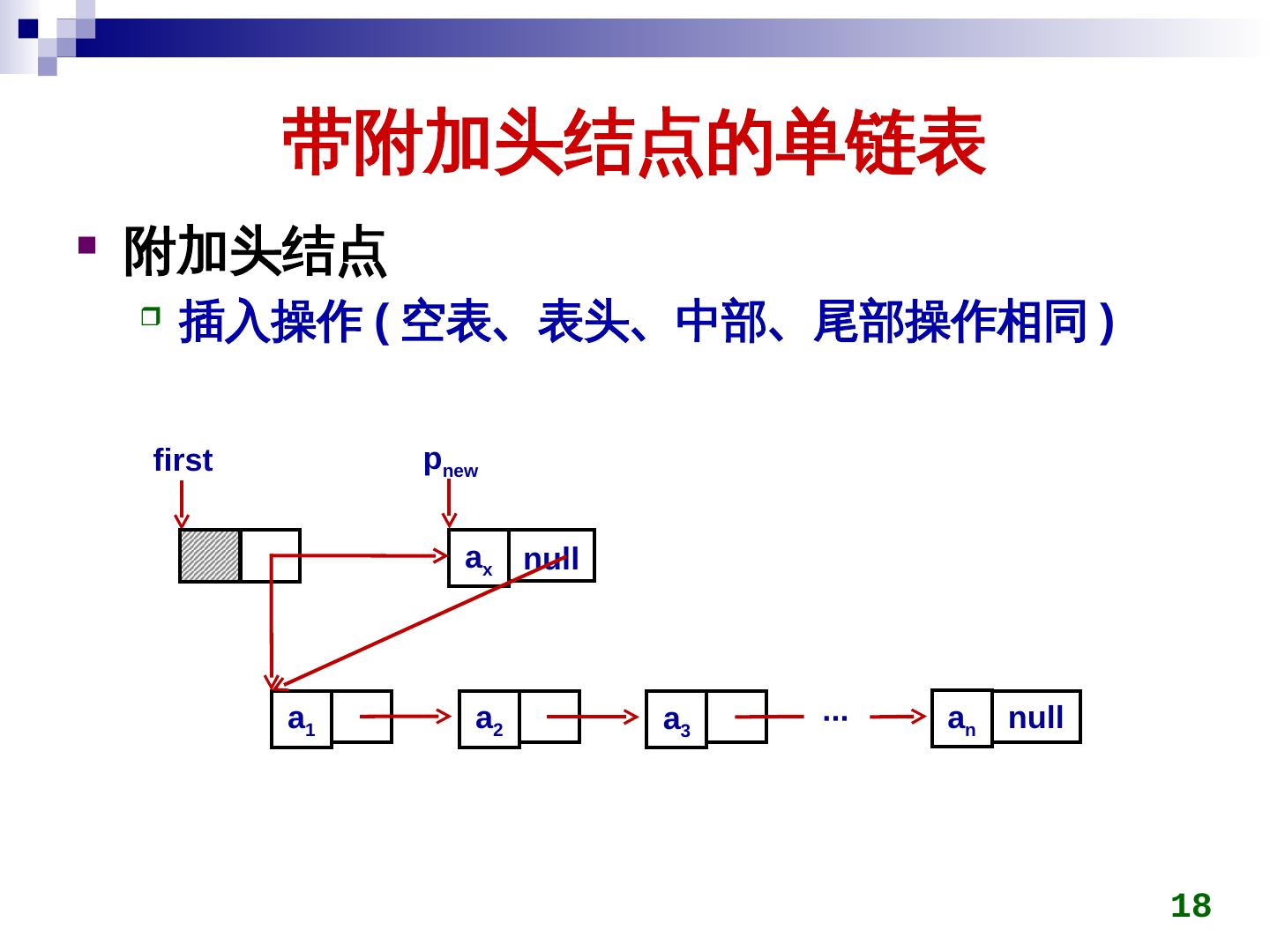
18 . 带附加头结点的单链表 附加头结点 插入操作 (a 空表、表头、中部、尾部操作相同 ) first pnew ax null a1 a2 a3 ∙∙∙ an null 18
19 . 带附加头结点的单链表 附加头结点 插入操作 (a 空表、表头、中部、尾部操作相同 ) 删除操作 (a 表头、中部、尾部操作相同 ) first temp = p->link; p->link = temp->link; Delete temp; a1 a2 a3 ∙∙∙ an null 删除 a1 temp 19
20 . 带附加头结点的单链表 附加头结点优点 空表和非空表的表示统一 在任意位置插入删除代码统一 附加头结点缺点 浪费了一个节点的空间 作业: 1.顺序表和链表存储表示的优缺点 2.若表的长度经常动态变化,应使用什么存储表示?为什么? 3.若表很少进行插入删除操作,应使用什么存储表示?为什么? 4.针对不带附加头结点的单链表,找到值为 x 的结点 (a 假设只有一个结点的值为 x) ,并删除该结点,函数名 FindAndDelete(aLinkNode *first, Type x) 20
21 . 单链表的应用:多项式运算 多项式 n P ( x ) a 0 a1 x a 2 x 2 a n x n i 0 ai x i 21
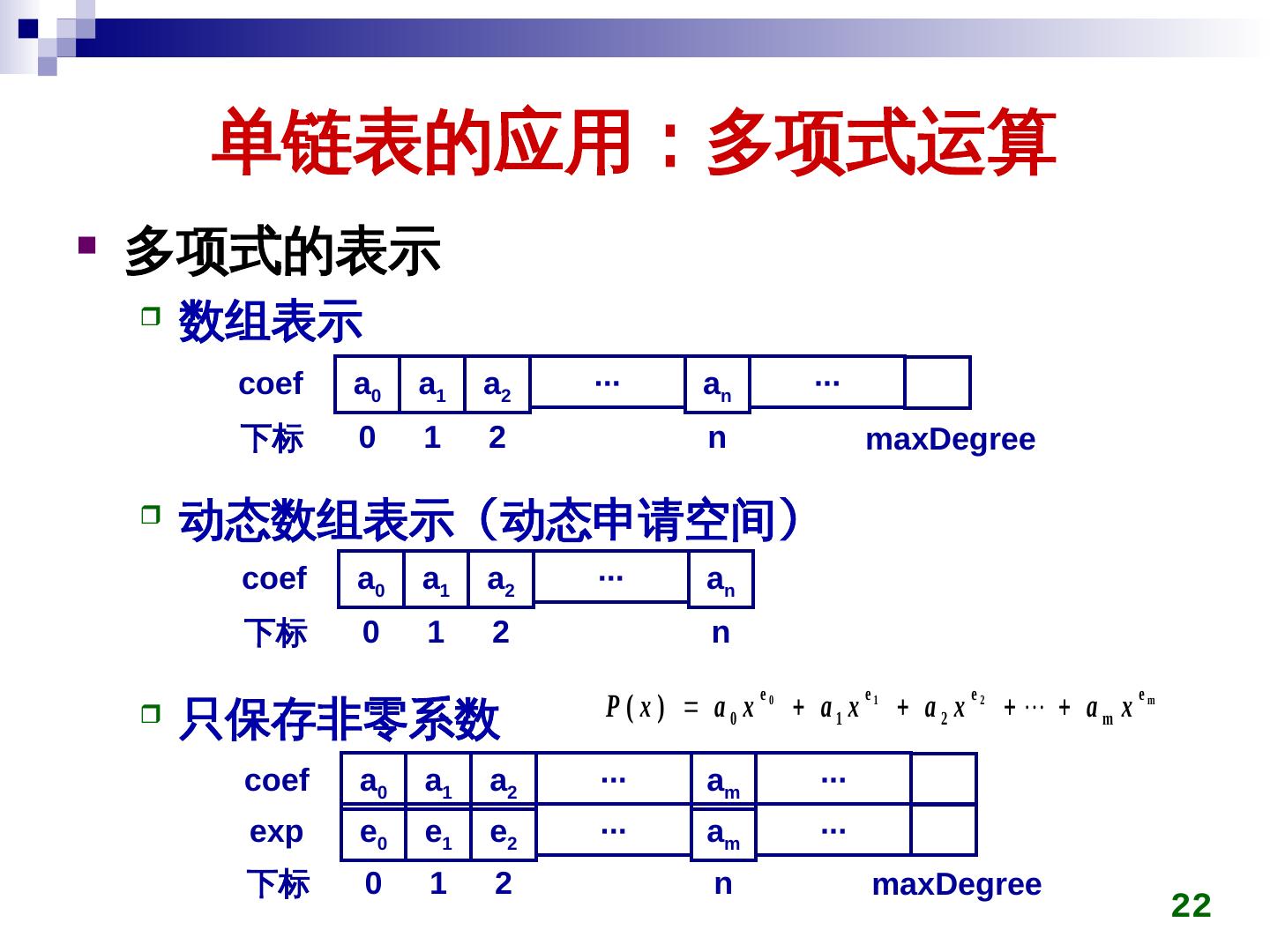
22 . 单链表的应用:多项式运算 多项式的表示 数组表示 coef a0 a1 a2 ∙∙∙ an ∙∙∙ 下标 0 1 2 n maxDegree 动态数组表示(动态申请空间) coef a0 a1 a2 ∙∙∙ an 下标 0 1 2 n e0 e1 e2 em P ( x) a0 x a1 x a2x am x 只保存非零系数 coef a0 a1 a2 ∙∙∙ am ∙∙∙ exp e0 e1 e2 ∙∙∙ am ∙∙∙ 下标 0 1 2 n maxDegree 22
23 . 单链表的应用:多项式运算 多项式的表示 单链表 PA(ax) = 3 + 7x11 - 9x51 firstA 3 0 7 11 -9 51 null 23
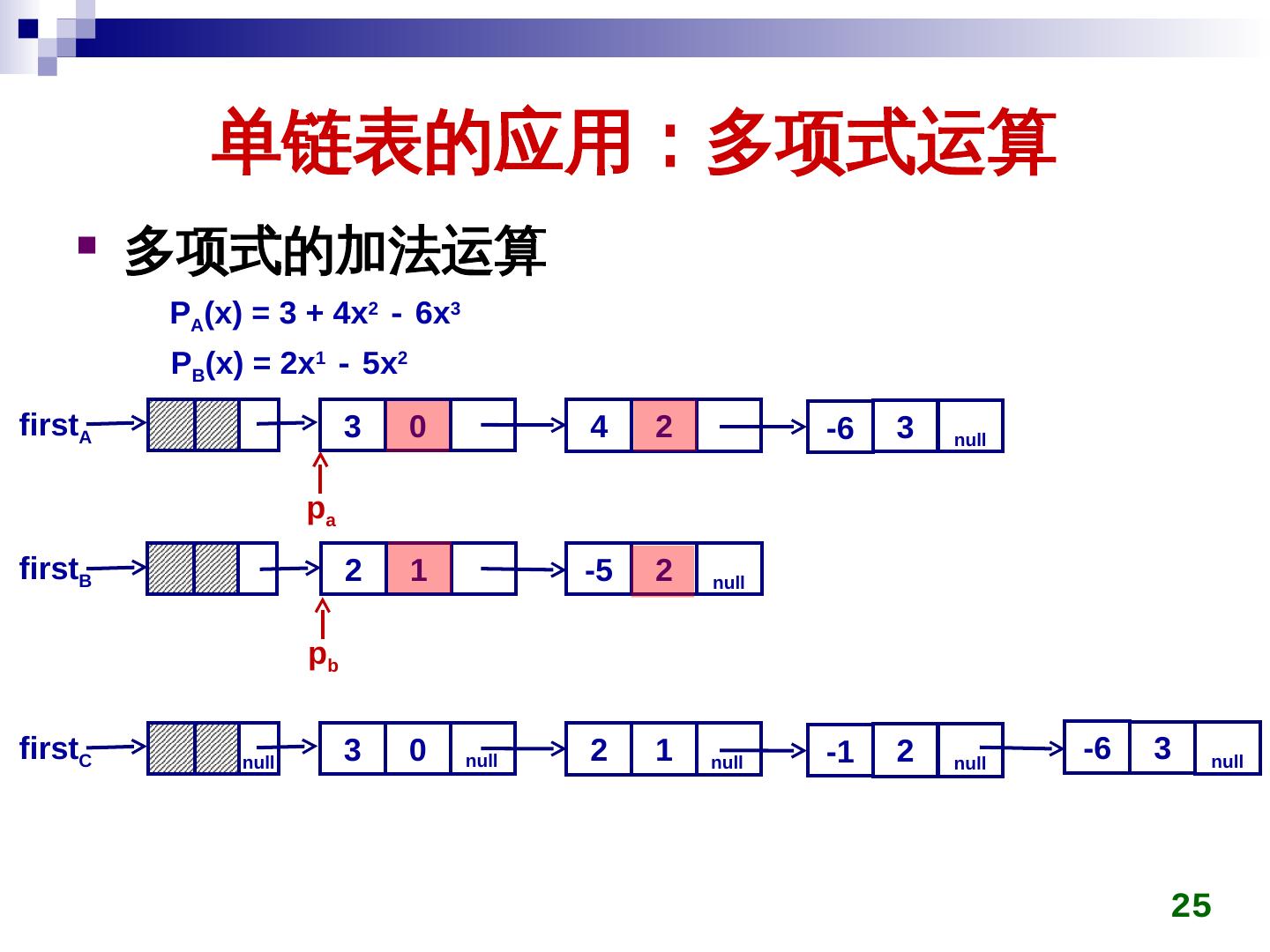
24 . 单链表的应用:多项式运算 多项式的加法运算 PA(ax) = 3 + 4x2 - 6x3 PB(ax) = 2x1 - 5x2 firstA 3 0 4 2 -6 3 null pa firstB 2 1 -5 2 null pb firstC null 3 0 null 2 1 null -1 2 null -6 3 null 25
25 . 单链表的应用:多项式运算 多项式的乘法运算 PA(ax) = 3 + 4x2 - 6x3 PB(ax) = 2x1 - 5x2 firstA 3 0 4 2 -6 3 null pa firstB 2 1 -5 2 null pb coef 0 1 2 3 4 5 0 0 0 0 0 0 3*2 3*-5 4*2 4*-5 -6*-5 + -6*2 0 6 -15 8 -32 30 Pc=6x-15x2+8x3-32x4+30x5 26
26 . 作业:使用无附加头结点单链表,实现多项式 加法和乘法运算 27
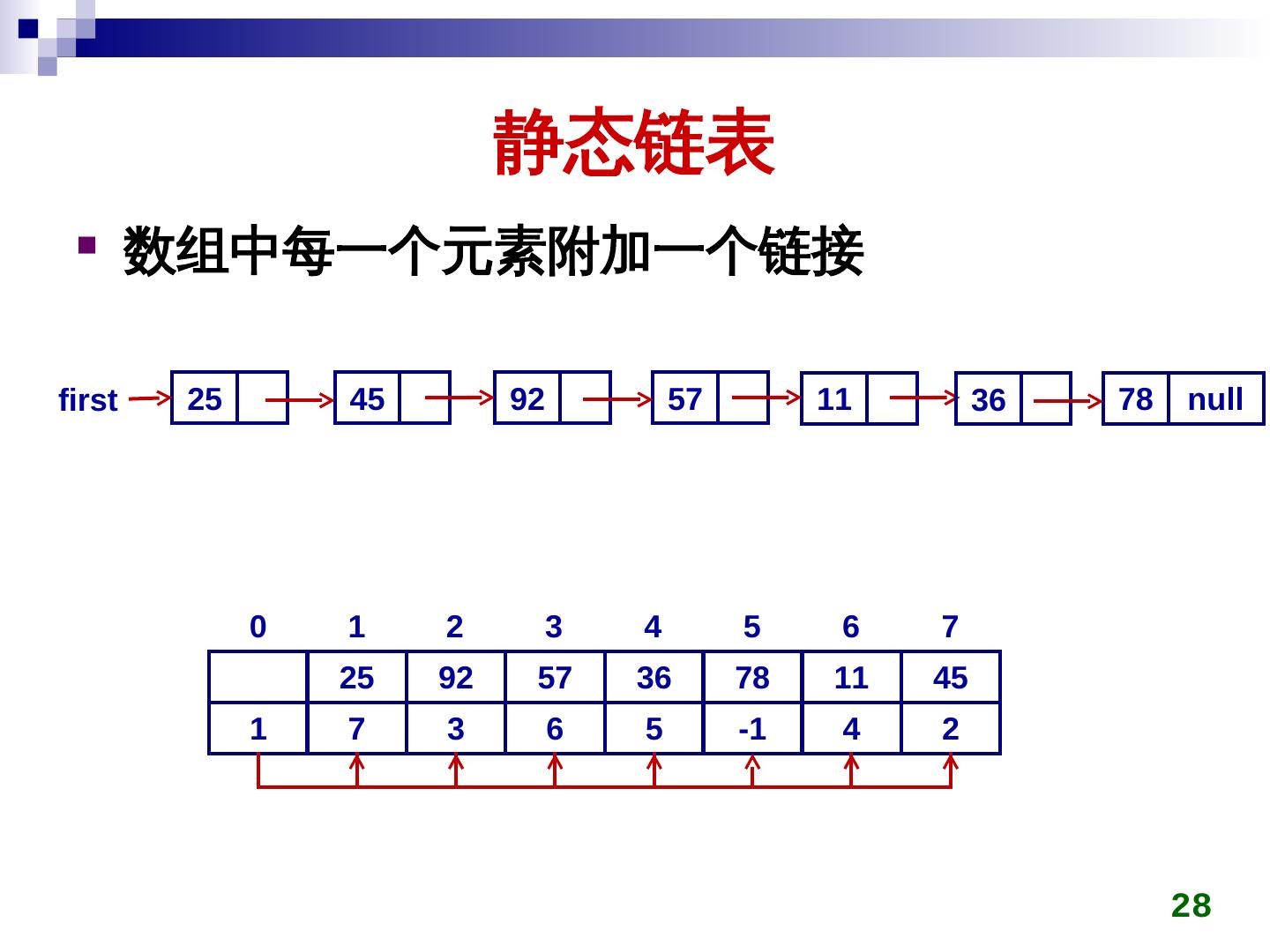
27 . 静态链表 数组中每一个元素附加一个链接 first 25 45 92 57 11 36 78 null 0 1 2 3 4 5 6 7 25 92 57 36 78 11 45 1 7 3 6 5 -1 4 2 28