lecture-26Logistic Regression

1 . Logistic Regression and Newton’s Method 36-350, Data Mining 18 November 2009 Readings in textbook: Sections 10.7 (logistic regression), sections 8.1 and 8.3 (optimization), and 11.3 (generalized linear models). Contents 1 Logistic Regression 1 1.1 Likelihood Function for Logistic Regression . . . . . . . . . . . . 4 1.2 Logistic Regression with More Than Two Classes . . . . . . . . . 5 2 Newton’s Method for Numerical Optimization 5 2.1 Newton’s Method in More than One Dimension . . . . . . . . . . 7 3 Generalized Linear Models and Generalized Additive Models 8 3.1 Generalized Additive Models . . . . . . . . . . . . . . . . . . . . 9 3.2 An Example (Including Model Checking) . . . . . . . . . . . . . 9 Last time, we looked at the situation where we have a vector of input fea- tures1 X, and we want to predict a binary class Y . In that lecture, the two classes were Y = +1 and Y = −1; in this one, it will simplify the book-keeping to make the classes Y = 1 and Y = 0. 1 Logistic Regression A linear classifier, as such, doesn’t give us probabilities for the classes in any par- ticular case. But we’ve seen that we often want such probabilities — to handle different error costs between classes, or to give us some indication of confidence for bet-hedging, or (perhaps most important) when perfect classification isn’t possible. People sometimes try to get conditional probabilities for classes by learning a linear classifier, and then saying the class probabilities at a point depend on its margin from the boundary, but this is a dubious hack, and should be avoided unless you want to descend to the level of (bad) psychologists and economists. If you want to estimate probabilities, fit a stochastic model. 1 If we have some discrete features, we can handle them through indicator variables, as in linear regression. 1 

2 . Several steps above that level, one can think like an old-school statistician, and ask “how can I use linear regression on this problem?” 1. The most obvious idea is to let Pr Y = 1|X = x — for short, p(x) — be a linear function of x. Every increment of a component of x would add or subtract so much to the probability. The conceptual problem here is that p must be between 0 and 1, and linear functions are unbounded. 2. The next most obvious idea is to let log p(x) be a linear function of x, so that changing an input variable multiplies the probability by a fixed amount. The problem is that logarithms are unbounded in only one di- rection, and linear functions are not. 3. Finally, the easiest modification of log p which has an unbounded range p is the logistic (or logit) transformation, log 1−p . We can make this a linear function of x without fear of nonsensical results. (Of course the results could still happen to be wrong, but they’re not guaranteed to be wrong.) This last alternative is logistic regression. Formally, the model logistic regression model is that p(x) log =b+x·w (1) 1 − p(x) Solving for p, this gives eb+x·w 1 p= b+x·w = −(b+x·w) (2) 1+e 1+e Notice that the over-all specification is a lot easier to grasp in terms of the transformed probability that in terms of the untransformed probability.2 Recall that to minimize the mis-classification rate, we should predict Y = 1 when p ≥ 0.5 and Y = 0 when p < 0.5. This means guessing 1 whenever b + x · w is non-negative, and 0 otherwise. So logistic regression gives us a linear classifier, like we saw last time. Recall further that the distance from the decision boundary is b/ w + x · w/ w . So logistic regression not only says where the boundary between the classes is, but also says (via Eq. 2) that the class probabilities depend on distance from the boundary, in a particular way, and that they go towards the extremes (0 and 1) more rapidly when w is larger. It’s these statements about proba- bilities which make logistic regression more than just a linear classifier. It makes stronger, more detailed predictions, and can be fit in a different way; but those strong predictions could be wrong. Using logistic regression to predict class probabilities is a modeling choice, just like it’s a modeling choice to predict quantitative variables with linear 2 Unless you’ve taken statistical mechanics, in which case you recognize that this is the Boltzmann distribution for a system with two states, which differ in energy by b + x · w. 2 

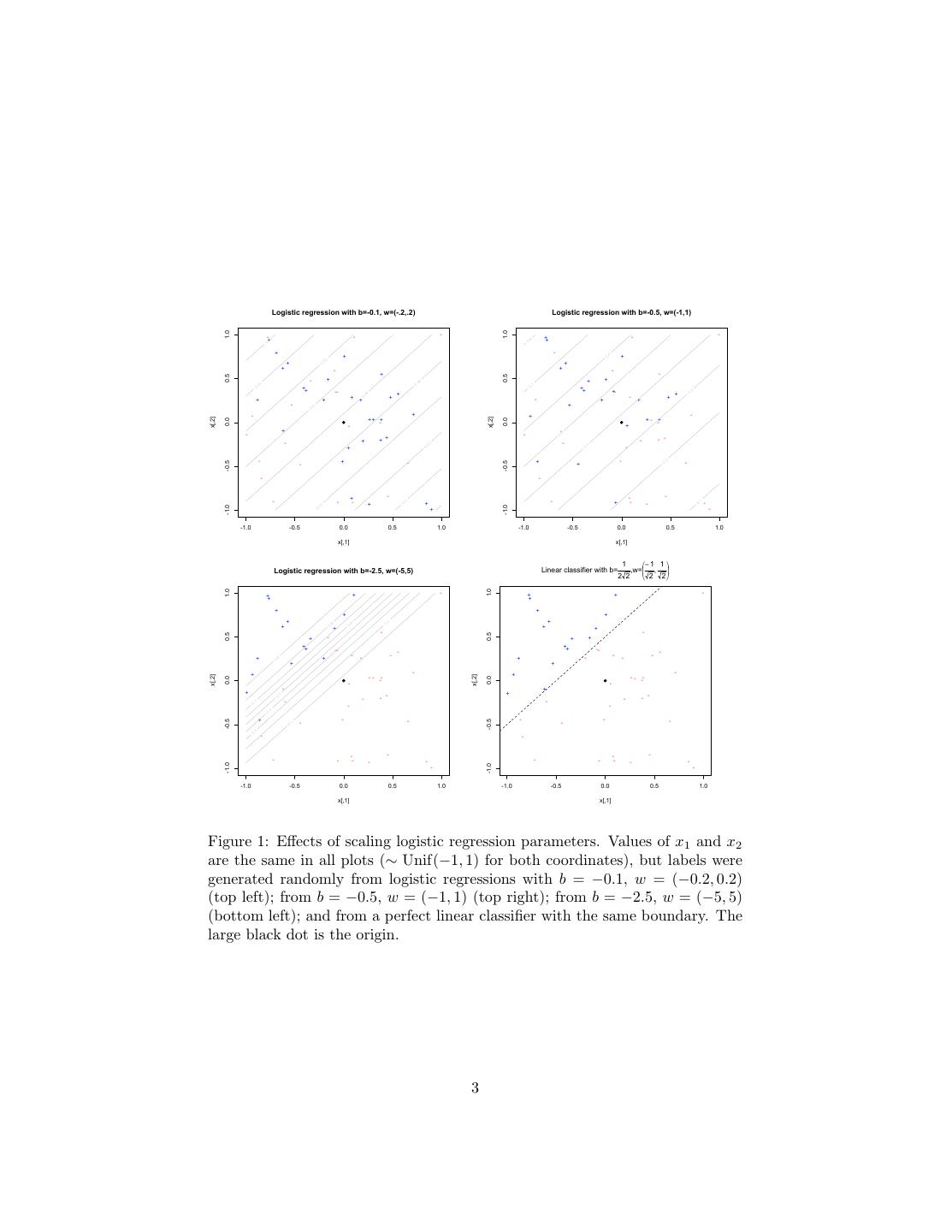
3 . Logistic regression with b=-0.1, w=(-.2,.2) Logistic regression with b=-0.5, w=(-1,1) 1.0 1.0 - - - - - + ++ + - + + + + + - + - + - 0.5 0.5 - + + + ++ -- ++ + +- + + + - + + + + - + + - + - + + - + + -+ + - -+ x[,2] x[,2] 0.0 0.0 - + + - - - - + + + - - - - + - - - + - + - - -0.5 -0.5 + - - + - - - - - - + - + - - - + -1.0 -1.0 + - -1.0 -0.5 0.0 0.5 1.0 -1.0 -0.5 0.0 0.5 1.0 x[,1] x[,1] 1 − 1 1  Logistic regression with b=-2.5, w=(-5,5) Linear classifier with b= ,w= ,  2 2  2 2 1.0 1.0 - + - ++ + ++ + + + + + + + + + + - - 0.5 0.5 + - + + ++ ++ -- -- - - - - - - - + + - + - + + + - + - - - -- - - -- x[,2] x[,2] 0.0 0.0 - - - + + + - - - - - - - - - - + - - - - - - -0.5 - -0.5 - - - - - - - - - - - - - - - - -1.0 -1.0 - - -1.0 -0.5 0.0 0.5 1.0 -1.0 -0.5 0.0 0.5 1.0 x[,1] x[,1] Figure 1: Effects of scaling logistic regression parameters. Values of x1 and x2 are the same in all plots (∼ Unif(−1, 1) for both coordinates), but labels were generated randomly from logistic regressions with b = −0.1, w = (−0.2, 0.2) (top left); from b = −0.5, w = (−1, 1) (top right); from b = −2.5, w = (−5, 5) (bottom left); and from a perfect linear classifier with the same boundary. The large black dot is the origin. 3 

4 .regression. In neither case is the appropriateness of the model guaranteed by the gods, nature, mathematical necessity, etc. We begin by positing the model, to get something to work with, and we end (if we know what we’re doing) by checking whether it really does match the data, or whether it has systematic flaws. Logistic regression is one of the most commonly used tools for applied statis- tics and data mining. There are basically four reasons for this. 1. Tradition. 2. In addition to the heuristic approach above, the quantity log p/(1 − p) plays an important role in the analysis of contingency tables (the “log odds”). Classification is a bit like having a contingency table with two columns (classes) and infinitely many rows (values of x). With a finite contingency table, we can estimate the log-odds for each row empirically, by just taking counts in the table. With infinitely many rows, we need some sort of interpolation scheme; logistic regression is linear interpolation for the log-odds. 3. It’s closely related to “exponential family” distributions, where the prob- m ability of some vector v is proportional to exp w0 + j=1 fj (v)wj . If one of the components of v is binary, and the functions fj are all the identity function, then we get a logistic regression. Exponential families arise in many contexts in statistical theory (and in physics!), so there are lots of problems which can be turned into logistic regression. 4. It often works surprisingly well as a classifier. But, many simple techniques often work surprisingly well as classifiers, and this doesn’t really testify to logistic regression getting the probabilities right. 1.1 Likelihood Function for Logistic Regression Because logistic regression predicts probabilities, rather than just classes, we can fit it using likelihood. For each training data-point, we have a vector of features, xi , and an observed class, yi . The probability of that class was either p, if yi = 1, or 1 − p, if yi = 0. The likelihood is then n 1−yi L(w, b) = p(xi )yi (1 − p(xi ) (3) i=1 (I could substitute in the actual equation for p, but things will be clearer in a moment if I don’t.) The log-likelihood turns products into sums: n (w, b) = yi log p(xi ) + (1 − yi ) log 1 − p(xi ) (4) i=1 n n p(xi ) = log 1 − p(xi ) + yi log (5) i=1 i=1 1 − p(xi ) 4 

5 . n n = log 1 − p(xi ) + yi (b + xi · w) (6) i=1 i=1 n n = − log 1 + eb+xi ·w + yi (b + xi · w) (7) i=1 i=1 where in the next-to-last step we finally use equation 1. Typically, to find the maximum likelihood estimates we’d differentiate the log likelihood with respect to the parameters, set the derivatives equal to zero, and solve. To start that, take the derivative with respect to one component of w, say wj . n n ∂ 1 = − eb+xi ·w xij + yi xij (8) ∂wj i=1 1 + eb+xi ·w i=1 n = (yi − p(xi ; b, w))xij (9) i=1 We are not going to be able to set this to zero and solve exactly. (It’s a tran- scendental equation!) We can however approximately solve it numerically. 1.2 Logistic Regression with More Than Two Classes If Y can take on more than two values, we can still use logistic regression. Instead of having one set of parameters b, w, each class c will have its own offset bc and vector wc , and the predicted conditional probabilities will be ebc +x·wc Pr Y = c|X = x = bc +x·wc (10) ce It can be shown that when there are only two classes (say, 0 and 1), equation 10 reduces to equation 2, with b = b1 − b0 and w = w1 − w0 . (Exercise: Show this.) In fact, one can pick one of the classes, say c = 0, and fix b0 = 0, w0 = 0, without any loss of generality. Calculation of the likelihood now proceeds as before (only with more book- keeping), and so does maximum likelihood estimation. 2 Newton’s Method for Numerical Optimization There are a huge number of methods for numerical optimization; we can’t cover all bases, and there is no magical method which will always work better than anything else. However, there are some methods which work very well on an awful lot of the problems which keep coming up, and it’s worth spending a moment to sketch how they work. One of the most ancient yet important of them is Newton’s method (alias “Newton-Raphson”). Let’s start with the simplest case of minimizing a function of one scalar variable, say f (w). We want to find the location of the global minimum, w∗ . 5 

6 .We suppose that f is smooth, and that w∗ is an interior minimum, meaning that the derivative at w∗ is zero and the second derivative is positive. Near the minimum we could make a Taylor expansion: 2 1 2 d f f (w) ≈ f (w∗ ) + (w − w∗ ) (11) 2 dw2 w=w∗ (We can see here that the second derivative has to be positive to ensure that f (w) > f (w∗ ).) In words, f (w) is close to quadratic near the minimum. Newton’s method uses this fact, and minimizes a quadratic approximation to the function we are really interested in. (In other words, Newton’s method is to replace the problem we want to solve with a problem we can solve.) Guess an initial point w0 . If this is close to the minimum, we can take a second order Taylor expansion around w0 and it will still be accurate: 2 df 1 2 d f f (w) ≈ f (w0 ) + (w − w0 ) + (w − w0 ) (12) dw w=w0 2 dw2 w=w0 Now it’s easy to minimize the right-hand side of equation 12. Let’s abbreviate df the derivatives, because they get tiresome to keep writing out: dw = w=w0 d2 f f (w0 ), dw2 = f (w0 ). We just take the derivative with respect to w, and w=w0 set it equal to zero at a point we’ll call w1 : 1 0 = f (w0 ) + f (w0 )2(w1 − w0 ) (13) 2 f (w0 ) w1 = w0 − (14) f (w0 ) The value w1 should be a better guess at the minimum w∗ than the initial one w0 was. So if we use it to make a quadratic approximation to f , we’ll get a better approximation, and so we can iterate this procedure, minimizing one approximation and then using that to get a new approximation: f (wn ) wn+1 = wn − (15) f (wn ) Notice that the true minimum w∗ is a fixed point of equation 15: if we happen to land on it, we’ll stay there (since f (w∗ ) = 0). We won’t show it, but it can be proved that if w0 is close enough to w∗ , then wn → w∗ , and that in general |wn − w∗ | = O(n−2 ), a very rapid rate of convergence. (Doubling the number of iterations we use doesn’t reduce the error by a factor of two, but by a factor of four.) 6 

7 . Let’s put this together in an algorithm. my.newton = function(f,f.prime,f.prime2,w0,tolerance=1e-3,max.iter=50) { w = w0 old.f = f(w) iterations = 0 made.changes = TRUE while(made.changes & (iterations < max.iter)) { iterations <- iterations +1 made.changes <- FALSE new.w = w - f.prime(w)/f.prime2(w) new.f = f(new.w) relative.change = abs(new.f - old.f)/old.f -1 made.changes = (relative.changes > tolerance) w = new.w old.f = new.f } if (made.changes) { warning("Newton’s method terminated before convergence") } return(list(minimum=w,value=f(w),deriv=f.prime(w),deriv2=f.prime2(w), iterations=iterations,converged=!made.changes)) } The first three arguments here have to all be functions. The fourth argument is our initial guess for the minimum, w0 . The last arguments keep Newton’s method from cycling forever: tolerance tells it to stop when the function stops changing very much (the relative difference between f (wn ) and f (wn−1 ) is small), and max.iter tells it to never do more than a certain number of steps no matter what. The return value includes the estmated minimum, the value of the function there, and some diagnostics — the derivative should be very small, the second derivative should be positive, etc. You may have noticed some potential problems — what if we land on a point where f is zero? What if f (wn+1 ) > f (wn )? Etc. There are ways of handling these issues, and more, which are incorporated into real optimization algorithms from numerical analysis — such as the optim function in R; I strongly recommend you use that, or something like that, rather than trying to roll your own optimization code.3 2.1 Newton’s Method in More than One Dimension Suppose that the objective f is a function of multiple arguments, f (w1 , w2 , . . . wp ). Let’s bundle the parameters into a single vector, w. Then the Newton update is wn+1 = wn − H −1 (wn )∇f (wn ) (16) 3 optim actually is a wrapper for several different optimization methods; method=BFGS selects a Newtonian method; BFGS is an acronym for the names of the algorithm’s inventors. 7 

8 .where ∇f is the gradient of f , its vector of partial derivatives [∂f /∂w1 , ∂f /∂w2 , . . . ∂f /∂wp ], and H is the Hessian of f , its matrix of second partial derivatives, Hij = ∂ 2 f /∂wi ∂wj . Calculating H and ∇f isn’t usually very time-consuming, but taking the inverse of H is, unless it happens to be a diagonal matrix. This leads to various quasi-Newton methods, which either approximate H by a diagonal matrix, or take a proper inverse of H only rarely (maybe just once), and then try to update an estimate of H −1 (wn ) as wn changes. (See section 8.3 in the textbook for more.) 3 Generalized Linear Models and Generalized Additive Models We went into the discussion of Newton’s method because we wanted to maximize the likelihood for logistic regression. We could actually trace this through, but instead I’ll just point you to section 11.3 of the textbook.4 Logistic regression is part of a broader family of generalized linear mod- els (GLMs), where the conditional distribution of the response falls in some parametric family, and the parameters are set by the linear predictor. Ordi- nary, least-squares regression is the case where response is Gaussian, with mean equal to the linear predictor, and constant variance. Logistic regression is the case where the response is binomial, with n equal to the number of data-points with the given x (often but not always 1), and p is given by Equation 2. Chang- ing the relationship between the parameters and the linear predictor is called changing the link function. For computational reasons, the link function is actually the function you apply to the mean response to get back the linear pre- dictor, rather than the other way around — (1) rather than (2). There are thus other forms of binomial regression besides logistic regression.5 There is also Poisson regression (appropriate when the data are counts without any upper limit), gamma regression, etc. In R, any standard GLM can be fit using the (base) glm function, whose syntax is very similar to that of lm. The major wrinkle is that, of course, you need to specify the family of probability distributions to use, by the family option — family=binomial defaults to logistic regression. (See help(glm) for the gory details on how to do, say, probit regression.) All of these are fit by the same sort of numerical likelihood maximization. One caution about using maximum likelihood to fit logistic regression is that it can seem to work badly when the training data can be linearly separated. The reason is that, to make the likelihood large, p(xi ) should be large when yi = 1, and p should be small when yi = 0. If b, w is a set of parameters which perfectly classifies the training data, then bc, cw is too, for any c > 1, 4 Faraway (2006), while somewhat light on theory, is good on the practicalities of using GLMs, especially (as the title suggests) the R practicalities. 5 My experience is that these tend to give similar error rates as classifiers, but have rather different guesses about the underlying probabilities. 8 

9 .but in a logistic regression the second set of parameters will have more extreme probabilities, and so a higher likelihood. For linearly separable data, then, there is no parameter vector which maximizes the likelihood, since L can always be increased by making the vector larger but keeping it pointed in the same direction. You should, of course, be so lucky as to have this problem. 3.1 Generalized Additive Models A natural step beyond generalized linear models is generalized additive mod- els (GAMs), where instead of making the transformed mean response a linear function of the inputs, we make it an additive function of the inputs. This means combining a function for fitting additive models with likelihood maximization. The R function here is gam, from the CRAN package of the same name. (Alter- nately, use the function gam in the package mgcv, which is part of the default R installation.) GAMs can be used to check GLMs in much the same way that smoothers can be used to check parametric regressions: fit a GAM and a GLM to the same data, then simulate from the GLM, and re-fit both models to the simulated data. Repeated many times, this gives a distribution for how much better the GAM will seem to fit than the GLM does, even when the GLM is true. You can then read a p-value off of this distribution. 3.2 An Example (Including Model Checking) Here’s a worked R example, using the data from the upper right panel of Fig- ure 1. The 50 × 2 matrix x holds the input variables (the coordinates are independently and uniformly distributed on [−1, 1]), and y.1 the correspond- ing class labels, themselves generated from a logistic regression with b = −0.5, w = (−1, 1). > logr = glm(y.1 ~ x[,1] + x[,2], family=binomial) > logr Call: glm(formula = y.1 ~ x[, 1] + x[, 2], family = binomial) Coefficients: (Intercept) x[, 1] x[, 2] -0.410 -1.050 1.366 Degrees of Freedom: 49 Total (i.e. Null); 47 Residual Null Deviance: 68.59 Residual Deviance: 58.81 AIC: 64.81 > sum(ifelse(logr$fitted.values<0.5,0,1) != y.1)/length(y.1) [1] 0.32 9 

10 . The deviance of a model fitted by maximum likelihood is (twice) the differ- ence between its log likelihood and the maximum log likelihood for a saturated model, i.e., a model with one parameter per observation. Hopefully, the sat- urated model can give a perfect fit.6 Here the saturated model would assign probability 1 to the observed outcomes7 , and the logarithm of 1 is zero, so D = 2 (b, w). The null deviance is what’s achievable by using just a constant bias b and setting w = 0. The fitted model definitely improves on that.8 The fitted values of the logistic regression are the class probabilities; this shows that the error rate of the logistic regression, if you force it to predict actual classes, is 32%. This sounds bad, but notice from the contour lines in the figure that lots of the probabilities are near 0.5, meaning that the classes are just genuinely hard to predict. To see how well the logistic regression assumption holds up, let’s compare this to a GAM. > gam.1 = gam(y.1~lo(x[,1])+lo(x[,2]),family="binomial") > gam.1 Call: gam(formula = y.1 ~ lo(x[, 1]) + lo(x[, 2]), family = "binomial") Degrees of Freedom: 49 total; 41.39957 Residual Residual Deviance: 49.17522 This fits a GAM to the same data, using lowess smoothing of both input vari- ables. Notice that the residual deviance is lower. That is, the GAM fits better. We expect this; the question is whether the difference is significant, or within the range of what we should expect when logistic regression is valid. To test this, we need to simulate from the logistic regression model. simulate.from.logr = function(x, coefs) { require(faraway) # For accessible logit and inverse-logit functions n = nrow(x) linear.part = coefs[1] + x %*% coefs[-1] probs = ilogit(linear.part) # Inverse logit y = rbinom(n,size=1,prob=probs) return(y) } 6 The factor of two is so that the deviance will have a χ2 distribution. Specifically, if the model with p parameters is right, the deviance will have a χ2 distribution with n − p degrees of freedom. 7 This is not possible when there are multiple observations with the same input features, but different classes. 8 AIC is of course the Akaike information criterion, −2 + 2q, with q being the number of parameters (here, q = 3). AIC has some truly devoted adherents, especially among non- statisticians, but I have been deliberately ignoring it and will continue to do so. Claeskens and Hjort (2008) is a thorough, modern treatment of AIC and related model-selection criteria from a statistical viewpoint. 10 

11 . Now we simulate from our fitted model, and re-fit both the logistic regression and the GAM. delta.deviance.sim = function (x,logistic.model) { y.new = simulate.from.logr(x,logistic.model$coefficients) GLM.dev = glm(y.new ~ x[,1] + x[,2], family="binomial")$deviance GAM.dev = gam(y.new ~ lo(x[,1]) + lo(x[,2]), family="binomial")$deviance return(GLM.dev - GAM.dev) } Notice that in this simulation we are not generating new X values. The logistic regression and the GAM are both models for the response conditional on the inputs, and are agnostic about how the inputs are distributed, or even whether it’s meaningful to talk about their distribution. Finally, we repeat the simulation a bunch of times, and see where the ob- served difference in deviances falls in the sampling distribution. > delta.dev = replicate(1000,delta.deviance.sim(x,logr)) > delta.dev.observed = logr$deviance - gam.1$deviance # 9.64 > sum(delta.dev.observed > delta.dev)/1000 [1] 0.685 In other words, the amount by which a GAM fits the data better than logistic regression is pretty near the middle of the null distribution. This is typical, in quite compatible with logistic regression being true. Since the example data really did come from a logistic regression, this is a relief. References Claeskens, Gerda and Nils Lid Hjort (2008). Model Selection and Model Aver- aging. Cambridge, England: Cambridge University Press. Faraway, Julian J. (2006). Extending the Linear Model with R: Generalized Linear, Mixed Effects and Nonparametric Regression Models. Boca Raton, Florida: Chapman and Hall/CRC. 11 

12 . Amount by which GAM fits better than logistic regression 0.10 0.08 Density 0.06 0.04 0.02 0.00 0 10 20 30 N = 1000 Bandwidth = 0.8386 Sampling distribution under logistic regression Figure 2: Sampling distribution for the difference in deviance between a GAM and a logistic regression, on data generated from a logistic regression. The observed difference in deviances is shown by the dashed horizontal line. 12