Tuning to the Underlying Hardware

1 . Main-Memory Hash Joins on Multi-Core CPUs: Tuning to the Underlying Hardware ¨ Cagri Balkesen #1 , Jens Teubner #2 , Gustavo Alonso #3 , M. Tamer Ozsu ∗4 # Systems Group, Department of Computer Science, ETH Zurich, Switzerland 1, 2, 3 {name.surname}@inf.ethz.ch ∗ University of Waterloo, Canada 4 tamer.ozsu@uwaterloo.ca Abstract—The architectural changes introduced with multi- hides the performance loss inherent in multi-layer memory core CPUs have triggered a redesign of main-memory join hierarchy. In addition, so the argument goes, fine tuning of algorithms. In the last few years, two diverging views have the algorithms to specific hardware makes them less portable appeared. One approach advocates careful tailoring of the algorithm to the architectural parameters (cache sizes, TLB, and and less robust to, e.g., data skew. memory bandwidth). The other approach argues that modern A third line of thought claims that sort-merge join is already hardware is good enough at hiding cache and TLB miss latencies better than hash join and can be efficiently implemented and, consequently, the careful tailoring can be omitted without without using SIMD [3]. These results contradict the claims of sacrificing performance. both Blanas et al. [2] because they are based on careful tuning In this paper we demonstrate through experimental analysis of different algorithms and architectures that hardware still to the hardware (in this case to its non-uniform memory access matters. Join algorithms that are hardware conscious perform characteristics) as well as the claims of Kim et al. [1] regarding better than hardware-oblivious approaches. The analysis and the behavior of sort-merge vs. hashing when using SIMD. comparisons in the paper show that many of the claims regarding For reasons of space, in this paper we focus on the question the behavior of join algorithms that have appeared in literature of whether it is important to tune the main-memory hash join are due to selection effects (relative table sizes, tuple sizes, the underlying architecture, using sorted data, etc.) and are to the underlying hardware as claimed explicitly by [1] and not supported by experiments run under different parameters implicitly by [3]. We also focus on radix join algorithms and settings. Through the analysis, we shed light on how modern leave the comparison with sort-merge joins for future work. hardware affects the implementation of data operators and Answering the question of whether hardware still matters is provide the fastest implementation of radix join to date, reaching a complex task because of the intricacies of modern hardware close to 200 million tuples per second. and the many possibilities available when implementing and tuning main-memory joins. To make matters worse, there are I. I NTRODUCTION many parameters that affect the behavior of join operators: Modern processors provide parallelism at various levels: relative table sizes, use of SIMD, page sizes, TLB sizes, instruction parallelism via super scalar execution; data-level structure of the tables and organization, hardware architecture, parallelism by extended support for single instruction over tuning of the implementation, etc. Existing studies share very multiple data (SIMD; i.e., SSE, 128-bits; AVX, 256-bits); and few points in common in terms of the space explored, making thread-level parallelism through multiple cores and simulta- it difficult to compare their claims. As shown in the paper, neous multi-threading (SMT). Such changes are triggering a many of these claims are specific to the choice of certain profound redesign of main-memory join algorithms. However, parameters and architectures and cannot be generalized. the landscape that has emerged so far is rather inconclusive. The first contribution of the paper is algorithmic. We One line of argument maintains that main-memory parallel analyze the algorithms proposed in the literature and propose joins should be hardware-conscious: the best performance can several important optimizations leading to new algorithms that only be achieved by fine tuning the algorithm to the underlying are more efficient and robust to parameter changes. In doing architecture [1]. These results also show that SIMD is still not so, we provide important insights on the effects of multi-core good enough to tip the decision on join algorithm towards hardware on algorithm design. sort-merge join instead of the more commonly used hash join. The second contribution is to put existing claims into con- In the future, however, as SIMD becomes wider, sort-merge text, showing what choice of parameters or hardware features join is likely to perform better. cause the observed behaviors. These results shed light on Another line of argument suggests that join algorithms what parameters play a role in multi-core systems, thereby can be made efficient while remaining hardware-oblivious establishing the basis for the choices a query optimizer for [2]. That is, there is no need for tuning—particularly of the multi-core will need to make. The third and final contribution partition phase of a join where data is carefully arranged to is to settle the issue of whether tuning to the underlying fit into the corresponding caches—because modern hardware hardware plays a role. The answer is a definitive yes, as it 

2 . shared one hash table hash table hash table per partition S b1 S R b1 R S b2 h R r1 h2 .. h2 s1 b2 h . .. .. .. .. h ... .. h r2 s2 scan scan .. . .. . . .. . scan scan . . . h1 .. . .. h1 h r3 . . s3 h bk bk r4 .. s4 h2 h2 . 1 build 2 probe 1 build 2 probe 1 part. 2 build 3 probe 1 part. Fig. 1. Hash join. Fig. 2. No partitioning join. Fig. 3. Partitioned hash join (following Shatdal et al. [7]). is only on a narrow combination of parameters and certain architectures where hardware-oblivious approaches have an is that the partitioning phase requires multiple passes over advantage. the data and can be omitted by relying on modern processor features such as simultaneous multi-threading (SMT) to hide II. BACKGROUND : I N -M EMORY H ASH J OINS cache latencies. Existing algorithms can be classified into two camps. Both input relations are divided into equi-sized portions that Hardware-oblivious hash join variants, represented here by are assigned to a number of worker threads. As shown in no partitioning join (Section II-B), do not depend on any Figure 2, in the build phase, all worker threads populate a hardware-specific parameters. Rather, they consider qualitative shared hash table that all worker threads can access. characteristics of modern hardware and are expected to achieve After synchronization via a barrier, all worker threads enter good performance on any technologically similar hardware. the probe phase and concurrently find matching join partners Hardware-conscious implementations, such as (parallel) radix for their assigned S portions. join (Sections II-C and II-D), aim to maximally exploit a given An important characteristic of no partitioning is that the piece of hardware by tuning algorithm parameters (e.g., hash hash table is shared among all participating threads. This table sizes) to its particular features. The goal of our work is to means that concurrent insertions into the hash table must be compare two alternatives. One is to assume hardware has now synchronized. To this end, each bucket is protected via a latch become good enough at hiding its own limitations—through that a thread must obtain before it can insert a tuple. The automatic hardware prefetching or out-of-order execution—to potential latch contention is expected to remain low, because make hardware-oblivious algorithms competitive. The other the number of hash buckets is typically large (in the millions). is to assume that explicit parameter tuning1 yields enough The probe phase accesses the hash table in read-only mode. performance advantages to warrant the effort required. Thus, no latches have to be acquired in that second phase. On a system with p cores, the expected complexity of this A. Canonical Hash Join Algorithm parallel version of hash join is O (1/p(|R| + |S|)). The basis behind any modern hash join implementation is C. Radix Join the canonical hash join algorithm [5], [6], which operates in Hardware-conscious, main-memory hash join implementa- two phases as shown in Figure 1. In the first build phase, the tions build upon the findings of Shatdal et al. [7] and Manegold smaller of the two input relations, R, is scanned to populate a et al. [4], [8]. While the principle of hashing—direct positional hash table with all R tuples. The probe phase then scans the access based on a key’s hash value—is appealing, the resulting second input relation, S, and probes the hash table for each S random access to memory can lead to cache misses. Thus, tuple to find matching R tuples. the main focus is on tuning main-memory access by using Both input relations are scanned once and, with an assumed caches more efficiently, which has been shown to impact query constant-time cost for hash table accesses, the expected com- performance [9]. Shatdal et al. [7] identify that when the hash plexity for the canonical hash join algorithm is O(|R| + |S|). table is larger than the cache size, almost every access to the B. No Partitioning Join hash table results in a cache miss. Consequently, partitioning the hash table into cache-sized chunks reduces cache misses To benefit from modern parallel hardware, Blanas et al. [2] and improves performance. Manegold et al. [4] refined this proposed a variant of the canonical algorithm that they termed idea by considering as well the effects of translation look- no partitioning join, essentially a direct parallel version of aside buffers (TLBs) during the partitioning phase. This led the canonical hash join. It does not depend on any hardware- to multi-pass partitioning, now a standard component of the specific parameters and—unlike alternatives that we will dis- radix join algorithm. cuss shortly—does not physically partition data. The argument Partitioned Hash Join. The partitioning idea is illustrated 1 usually by means of automated tools, such as Calibrator [4] in Figure 3. In the first phase of the algorithm the two 

3 . one hash table again is the smaller input relation. Thus, we expect a runtime per partition complexity of O ((|R| + |S|) log |R|) for radix join. S R r1 h2 .. h2 s1 Hardware Parameters. Radix join needs to be tuned to a h1,2 . . .. h1,2 r2 .. particular piece of hardware essentially via two parameters: .. . s2 scan scan h1,1 . . .. h1,1 (i) the maximum fanout per radix pass is primarily limited by r3 .. . s3 h the number of TLB entries of the hardware; (ii) the resulting h1,2 1,2 r4 h2 .. h2 s4 partition size should roughly be the size of the system’s . CPU cache. Both parameters can be obtained in a rather pass 1 pass 2 pass 2 pass 1 straightforward way, e.g., with help of benchmark tools, such as Calibrator [4]. As we shall see later, radix join is not overly 1 partition 2 build 3 probe 1 partition sensitive to a potential mis-configuration of either parameter. Fig. 4. Radix join (as proposed by Manegold et al. [4]). D. Parallel Radix Join Radix join can be parallelized by subdividing both input input relations R and S are divided into partitions ri and s j , relations into sub-relations that are assigned to individual respectively. During the build phase, a separate hash table is threads [1]. During the first pass, all threads create a shared set created for each ri partition (assuming R is the smaller input of partitions. As before, the number of partitions in this set relation). Each of these hash tables now fits into the CPU is limited by hardware parameters and typically small (few cache. During the final probe phase, s j partitions are scanned tens of partitions). They are accessed by potentially many and the respective hash table is probed for matching tuples. execution threads, creating a contention problem (the low- During the partitioning phase, input tuples are divided up contention assumption of Section II-B no longer applies). using hash partitioning (via hash function h1 in Figure 3) on To avoid this contention, for each thread a dedicated range their key values (thus, ri s j = ∅ for i = j) and another hash is reserved within each output partition. To this end, both input function h2 is used to populate the hash tables. relations are scanned twice. The first scan computes a set of histograms over the input data, so the exact output size is While avoiding cache misses during the build and probe known for each thread and each partition. Next, a contiguous phases, partitioning the input data may cause a different memory space is allocated for the output and, by computing a type of cache problem. The partitions will typically reside prefix-sum over the histogram, each thread pre-computes the on different memory pages with a separate entry for virtual exclusive location where it writes its output. Finally, all threads memory mapping required for each partition. This mapping is perform their partitioning without any need to synchronize. cached by TLBs in modern processors. As Manegold et al. [4] After the first partitioning pass, there is typically enough point out, the partitioning phase may cause TLB misses if the independent work in the system (cf. Figure 4) that workers can number of created partitions is too large. perform work on their own. Load distribution among worker Essentially, the number of available TLB entries defines an threads is typically implemented via task queueing (cf. [1]). upper bound on the number of partitions that can be created or accessed efficiently at the same time. III. E XPERIMENTAL S ETUP Radix Partitioning. Excessive TLB misses can be avoided by In this section we describe the experimental setup used for partitioning the input data in multiple passes. In each pass j, the evaluation of the algorithms. all partitions produced by the preceding pass j − 1 are refined, A. Workload such that the partitioning fan-out never exceeds the hardware limit given by the number of TLB entries. In practice, each For the comparison, we use machine and workload configu- pass looks at a different set of bits from the hash function h1 , rations that mimic scenarios where in-memory join processing which is why this is called radix partitioning. For typical in- is most relevant. In particular, all systems where the compo- memory data sizes, two or three passes are sufficient to create nent truly matters assume a column-oriented storage model. cache-sized partitions, without suffering from TLB capacity We thus deliberately choose very narrow key, payload tuple limitations. configurations, where key and payload are four or eight bytes wide. As a side effect, narrow tuples better pronounce the Radix Join. The complete radix join is illustrated in Figure 4. effects that we are interested in, since they put more pressure 1 Both inputs are partitioned using two-pass radix partition- on the system’s caching system.2 ing (two TLB entries would be sufficient to support this toy We adopted the particular configuration of our workloads example). 2 Hash tables are then built over each ri partition from existing work, which also eases the comparison of our of input table R. 3 Finally, all si partitions are scanned and results with those published in the past. the respective ri partitions probed for join matches. As illustrated in Table I, we adopted workloads from Blanas In radix join, multiple passes have to be done over both et al. [2] and Kim et al. [1] and refer to them as A and B here, input relations. Since the maximum “fanout” per pass is fixed by hardware parameters, log |R| passes are necessary, where R 2 The effect of tuple widths was studied, e.g., by Manegold et al. [10]. 

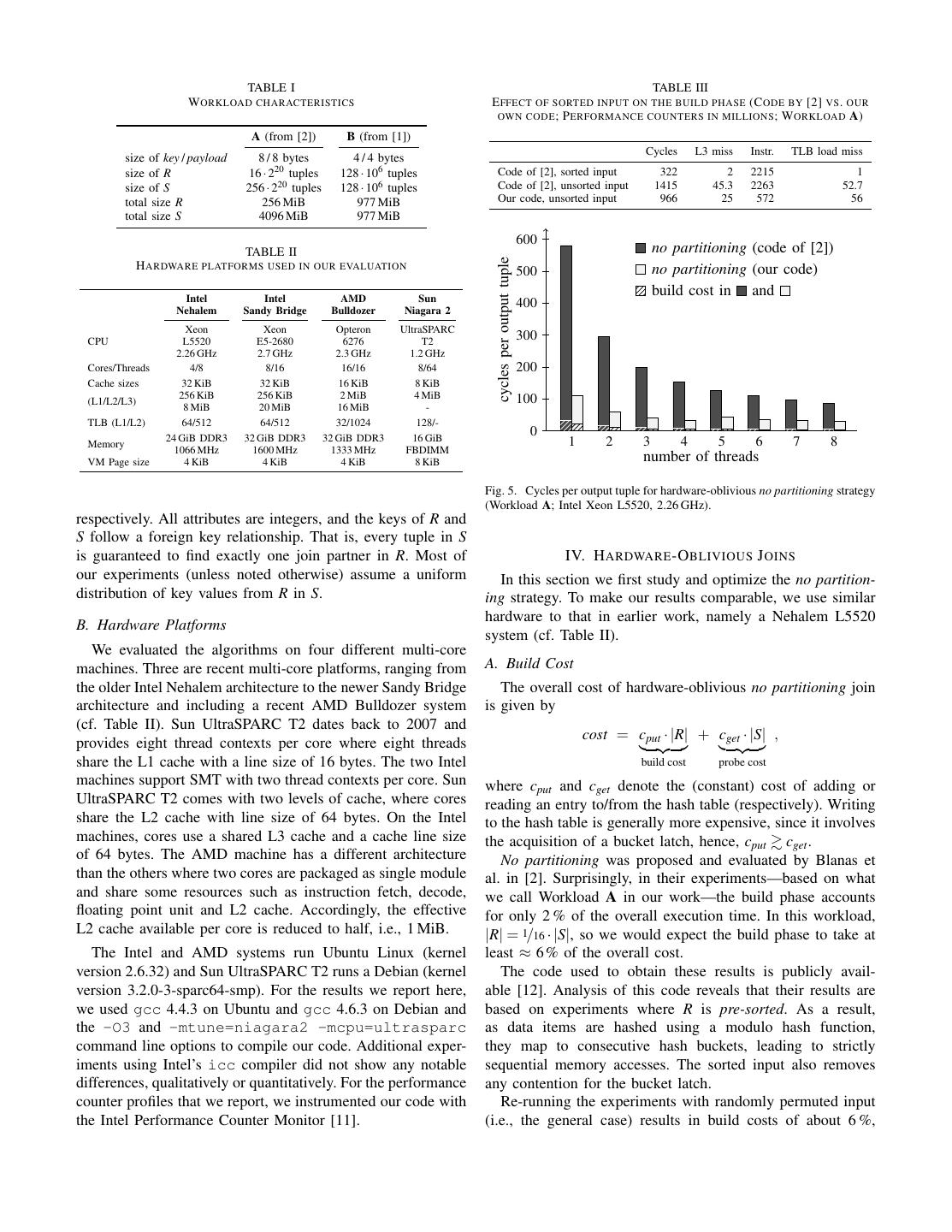
4 . TABLE I TABLE III W ORKLOAD CHARACTERISTICS E FFECT OF SORTED INPUT ON THE BUILD PHASE (C ODE BY [2] VS . OUR OWN CODE ; P ERFORMANCE COUNTERS IN MILLIONS ; W ORKLOAD A) A (from [2]) B (from [1]) Cycles L3 miss Instr. TLB load miss size of key / payload 8 / 8 bytes 4 / 4 bytes size of R 16 · 220 tuples 128 · 106 tuples Code of [2], sorted input 322 2 2215 1 size of S 256 · 220 tuples 128 · 106 tuples Code of [2], unsorted input 1415 45.3 2263 52.7 total size R 256 MiB 977 MiB Our code, unsorted input 966 25 572 56 total size S 4096 MiB 977 MiB 600 TABLE II no partitioning (code of [2]) cycles per output tuple H ARDWARE PLATFORMS USED IN OUR EVALUATION 500 no partitioning (our code) Intel Intel AMD Sun build cost in and Nehalem Sandy Bridge Bulldozer Niagara 2 400 Xeon Xeon Opteron UltraSPARC CPU L5520 E5-2680 6276 T2 300 2.26 GHz 2.7 GHz 2.3 GHz 1.2 GHz Cores/Threads 4/8 8/16 16/16 8/64 200 Cache sizes 32 KiB 32 KiB 16 KiB 8 KiB 256 KiB 256 KiB 2 MiB 4 MiB 100 (L1/L2/L3) 8 MiB 20 MiB 16 MiB - TLB (L1/L2) 64/512 64/512 32/1024 128/- 24 GiB DDR3 32 GiB DDR3 32 GiB DDR3 16 GiB 0 Memory 1 2 3 4 5 6 7 8 1066 MHz 1600 MHz 1333 MHz FBDIMM VM Page size 4 KiB 4 KiB 4 KiB 8 KiB number of threads Fig. 5. Cycles per output tuple for hardware-oblivious no partitioning strategy (Workload A; Intel Xeon L5520, 2.26 GHz). respectively. All attributes are integers, and the keys of R and S follow a foreign key relationship. That is, every tuple in S is guaranteed to find exactly one join partner in R. Most of IV. H ARDWARE -O BLIVIOUS J OINS our experiments (unless noted otherwise) assume a uniform In this section we first study and optimize the no partition- distribution of key values from R in S. ing strategy. To make our results comparable, we use similar hardware to that in earlier work, namely a Nehalem L5520 B. Hardware Platforms system (cf. Table II). We evaluated the algorithms on four different multi-core machines. Three are recent multi-core platforms, ranging from A. Build Cost the older Intel Nehalem architecture to the newer Sandy Bridge The overall cost of hardware-oblivious no partitioning join architecture and including a recent AMD Bulldozer system is given by (cf. Table II). Sun UltraSPARC T2 dates back to 2007 and cost = cput · |R| + cget · |S| , provides eight thread contexts per core where eight threads share the L1 cache with a line size of 16 bytes. The two Intel build cost probe cost machines support SMT with two thread contexts per core. Sun where cput and cget denote the (constant) cost of adding or UltraSPARC T2 comes with two levels of cache, where cores reading an entry to/from the hash table (respectively). Writing share the L2 cache with line size of 64 bytes. On the Intel to the hash table is generally more expensive, since it involves machines, cores use a shared L3 cache and a cache line size the acquisition of a bucket latch, hence, cput cget . of 64 bytes. The AMD machine has a different architecture No partitioning was proposed and evaluated by Blanas et than the others where two cores are packaged as single module al. in [2]. Surprisingly, in their experiments—based on what and share some resources such as instruction fetch, decode, we call Workload A in our work—the build phase accounts floating point unit and L2 cache. Accordingly, the effective for only 2 % of the overall execution time. In this workload, L2 cache available per core is reduced to half, i.e., 1 MiB. |R| = 1/16 · |S|, so we would expect the build phase to take at The Intel and AMD systems run Ubuntu Linux (kernel least ≈ 6 % of the overall cost. version 2.6.32) and Sun UltraSPARC T2 runs a Debian (kernel The code used to obtain these results is publicly avail- version 3.2.0-3-sparc64-smp). For the results we report here, able [12]. Analysis of this code reveals that their results are we used gcc 4.4.3 on Ubuntu and gcc 4.6.3 on Debian and based on experiments where R is pre-sorted. As a result, the -O3 and -mtune=niagara2 -mcpu=ultrasparc as data items are hashed using a modulo hash function, command line options to compile our code. Additional exper- they map to consecutive hash buckets, leading to strictly iments using Intel’s icc compiler did not show any notable sequential memory accesses. The sorted input also removes differences, qualitatively or quantitatively. For the performance any contention for the bucket latch. counter profiles that we report, we instrumented our code with Re-running the experiments with randomly permuted input the Intel Performance Counter Monitor [11]. (i.e., the general case) results in build costs of about 6 %, 

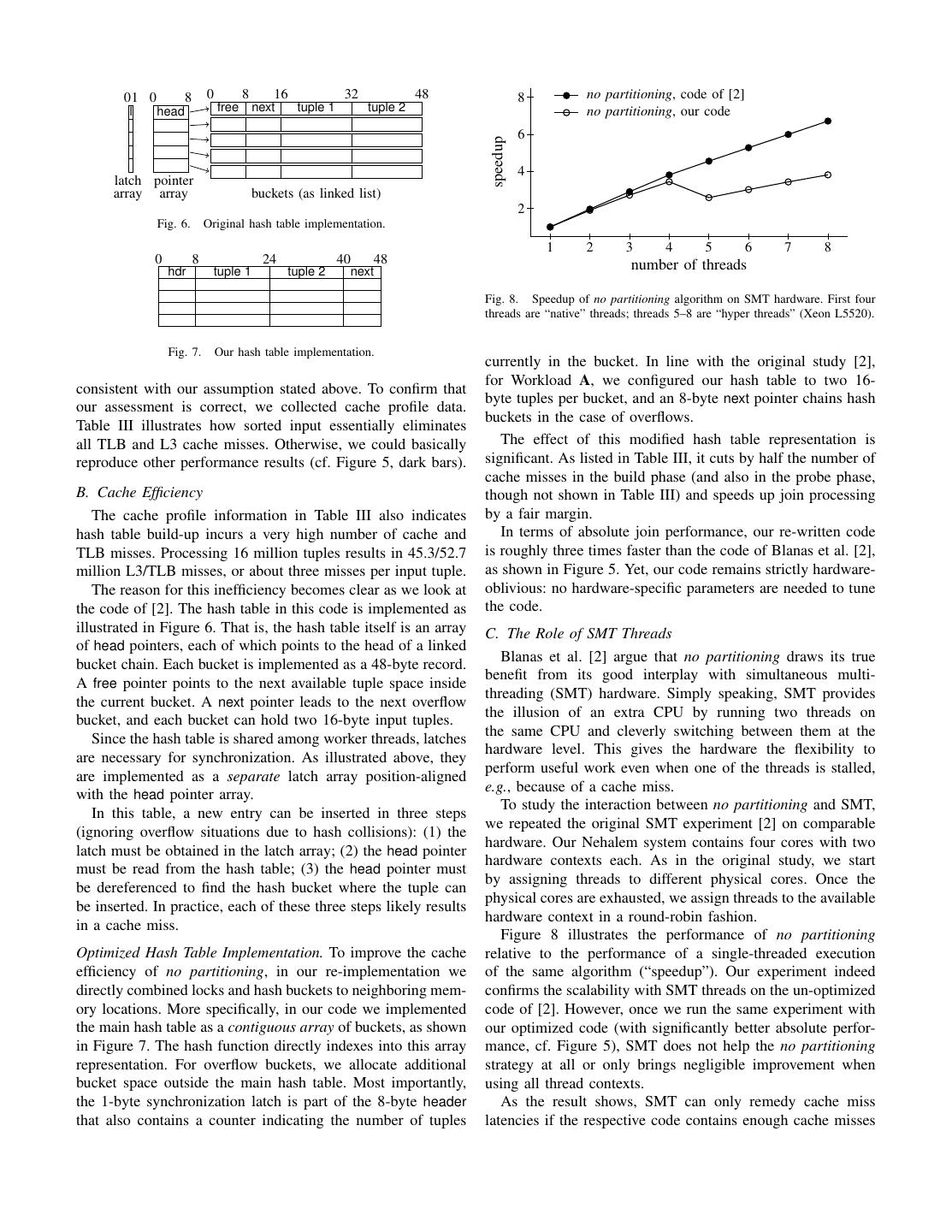
5 . 01 0 8 0 8 16 32 48 8 no partitioning, code of [2] l head free next tuple 1 tuple 2 no partitioning, our code 6 speedup 4 latch pointer array array buckets (as linked list) 2 Fig. 6. Original hash table implementation. 1 2 3 4 5 6 7 8 0 8 24 40 48 number of threads hdr tuple 1 tuple 2 next Fig. 8. Speedup of no partitioning algorithm on SMT hardware. First four threads are “native” threads; threads 5–8 are “hyper threads” (Xeon L5520). Fig. 7. Our hash table implementation. currently in the bucket. In line with the original study [2], for Workload A, we configured our hash table to two 16- consistent with our assumption stated above. To confirm that byte tuples per bucket, and an 8-byte next pointer chains hash our assessment is correct, we collected cache profile data. buckets in the case of overflows. Table III illustrates how sorted input essentially eliminates all TLB and L3 cache misses. Otherwise, we could basically The effect of this modified hash table representation is reproduce other performance results (cf. Figure 5, dark bars). significant. As listed in Table III, it cuts by half the number of cache misses in the build phase (and also in the probe phase, B. Cache Efficiency though not shown in Table III) and speeds up join processing The cache profile information in Table III also indicates by a fair margin. hash table build-up incurs a very high number of cache and In terms of absolute join performance, our re-written code TLB misses. Processing 16 million tuples results in 45.3/52.7 is roughly three times faster than the code of Blanas et al. [2], million L3/TLB misses, or about three misses per input tuple. as shown in Figure 5. Yet, our code remains strictly hardware- The reason for this inefficiency becomes clear as we look at oblivious: no hardware-specific parameters are needed to tune the code of [2]. The hash table in this code is implemented as the code. illustrated in Figure 6. That is, the hash table itself is an array C. The Role of SMT Threads of head pointers, each of which points to the head of a linked Blanas et al. [2] argue that no partitioning draws its true bucket chain. Each bucket is implemented as a 48-byte record. benefit from its good interplay with simultaneous multi- A free pointer points to the next available tuple space inside threading (SMT) hardware. Simply speaking, SMT provides the current bucket. A next pointer leads to the next overflow the illusion of an extra CPU by running two threads on bucket, and each bucket can hold two 16-byte input tuples. the same CPU and cleverly switching between them at the Since the hash table is shared among worker threads, latches hardware level. This gives the hardware the flexibility to are necessary for synchronization. As illustrated above, they perform useful work even when one of the threads is stalled, are implemented as a separate latch array position-aligned e.g., because of a cache miss. with the head pointer array. To study the interaction between no partitioning and SMT, In this table, a new entry can be inserted in three steps we repeated the original SMT experiment [2] on comparable (ignoring overflow situations due to hash collisions): (1) the hardware. Our Nehalem system contains four cores with two latch must be obtained in the latch array; (2) the head pointer hardware contexts each. As in the original study, we start must be read from the hash table; (3) the head pointer must by assigning threads to different physical cores. Once the be dereferenced to find the hash bucket where the tuple can physical cores are exhausted, we assign threads to the available be inserted. In practice, each of these three steps likely results hardware context in a round-robin fashion. in a cache miss. Figure 8 illustrates the performance of no partitioning Optimized Hash Table Implementation. To improve the cache relative to the performance of a single-threaded execution efficiency of no partitioning, in our re-implementation we of the same algorithm (“speedup”). Our experiment indeed directly combined locks and hash buckets to neighboring mem- confirms the scalability with SMT threads on the un-optimized ory locations. More specifically, in our code we implemented code of [2]. However, once we run the same experiment with the main hash table as a contiguous array of buckets, as shown our optimized code (with significantly better absolute perfor- in Figure 7. The hash function directly indexes into this array mance, cf. Figure 5), SMT does not help the no partitioning representation. For overflow buckets, we allocate additional strategy at all or only brings negligible improvement when bucket space outside the main hash table. Most importantly, using all thread contexts. the 1-byte synchronization latch is part of the 8-byte header As the result shows, SMT can only remedy cache miss that also contains a counter indicating the number of tuples latencies if the respective code contains enough cache misses 

6 . R re-ordered R R 0 join cost partitioning cost a ··· a ··· cycles per output tuple 35 b ··· Hist Psum a ··· 30 Nehalem AMD a · · · hist. a 3 prefix a 0 build a ··· 3 a ··· b 2 b 3 b ··· 25 c ··· c 2 sum c 5 b ··· 5 20 b ··· c ··· c ··· c ··· 15 10 used as hash table 5 0 Fig. 10. Relation re-ordering and histogram-based hash table design. 12 13 14 15 16 17 9 10 11 12 13 14 number of radix bits (log2 (number of partitions)) bucket chaining as in [4] Fig. 9. Cost vs. radix bits (Workload B; Nehalem: 2-passes; AMD: 1-pass). 16 histogram mechan. of [1] cycles per output tuple 14 [1] without SIMD 12 and enough additional work for the second thread while the 10 first one is waiting. For code with less redundancy, SMT brings only negligible benefit. These results raise questions about a 8 key hypothesis behind the hardware-oblivious no partitioning 6 strategy. 4 2 V. H ARDWARE -C ONSCIOUS J OINS 0 We perform a similar analysis for the parallel radix join. 12 13 14 15 16 Blanas et al. [2] also provide an implementation for this number of radix bits (log2 (number of partitions)) hardware-conscious join execution strategy. Fig. 11. Cost of join phase in radix join for three different hash table A. Configuration Parameters implementation techniques (Workload B; Intel Xeon L5520, 2.26 GHz; Using 8 threads and 2 pass partitioning). The key configuration parameter of radix join is the number of radix bits for the partitioning phase (2 # radix bits partitions are created during that phase). Figure 9 illustrates the effect that this parameter has on the runtime of radix join. tuples with the same hash value appear contiguously in R . The figure confirms the expected behavior that partitioning The prefix sum table and the re-ordered relation now together cost increases with the partition count, whereas the join phase serve as a hash table as shown in Figure 10. becomes faster as partitions become smaller. Configurations The advantage of this strategy is that contiguous tuples with 14 and 11 radix bits are the best trade-offs between these can now be compared using SIMD instructions. In addition, opposing effects for the Nehalem and AMD architectures, software prefetching mechanisms can be applied to bring respectively. But even more interestingly, the figure shows potential matches to the L1 cache before comparisons. that radix join is fairly robust against a parameter mis- configuration: within a range of configurations, the perfor- Evaluation. We evaluated the impact of different hash table mance of radix join degrades only marginally. implementation strategies on the join phase of radix join. Figure 11 shows the join phase cost in cycles per output tuple B. Hash Tables and Cache Efficiency for three different strategies. Following the partitioning of the input tables, hash tables As can be seen, the Manegold et al. implementation [4] are very small and always fully cache resident. Thus, our still has an edge over the more recent one by Kim et al. [1], assessment about cache misses for hash table accesses in the in spite of the potential for SIMD optimization in the latter previous section no longer holds for the hardware-conscious implementation. The graph also confirms that the join cost join execution strategy. generally decreases as the input data is partitioned in a more Various implementations have been proposed for radix join. fine-granular way. In practice, there is a sweet spot, because Manegold et al. [4] use a rather classical bucket chaining the partitioning cost (which has to be invested before joining) mechanism, where individual tuples are chained to form a increases with the number of partitions (cf. Figure 9). bucket. Following good design principles for efficient in- Since the Manegold et al. approach comes out best in this memory algorithms, all pointers are implemented as array comparison, we will use it for all following experiments. We position indexes (as opposed to actual memory pointers). note that the choice we are making here does not depend on Kim et al. [1] build their hash table analogously to the hardware parameters (this is a hardware-oblivious optimiza- parallel partitioning stage. The input relation is first scanned tion). As we shall see in a moment, the impact of our choice to obtain a histogram over hash values. Then, a prefix sum is limited, however, since the cost of partitioning adds to either is used to help re-order relation R (to obtain R ), such that of those implementation techniques. 

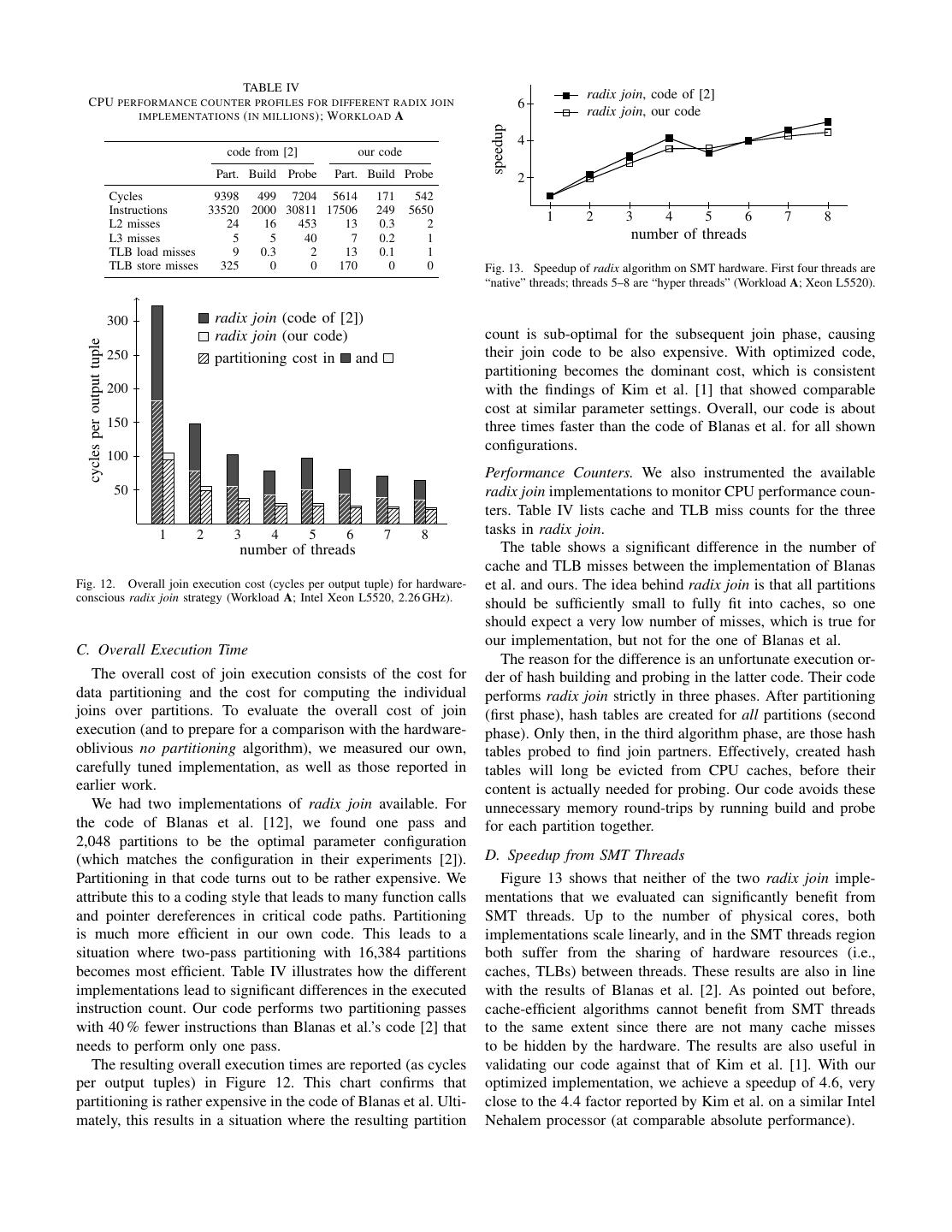
7 . TABLE IV radix join, code of [2] CPU PERFORMANCE COUNTER PROFILES FOR DIFFERENT RADIX JOIN 6 IMPLEMENTATIONS ( IN MILLIONS ); W ORKLOAD A radix join, our code speedup 4 code from [2] our code Part. Build Probe Part. Build Probe 2 Cycles 9398 499 7204 5614 171 542 Instructions 33520 2000 30811 17506 249 5650 1 2 3 4 5 6 7 8 L2 misses 24 16 453 13 0.3 2 L3 misses 5 5 40 7 0.2 1 number of threads TLB load misses 9 0.3 2 13 0.1 1 TLB store misses 325 0 0 170 0 0 Fig. 13. Speedup of radix algorithm on SMT hardware. First four threads are “native” threads; threads 5–8 are “hyper threads” (Workload A; Xeon L5520). 300 radix join (code of [2]) radix join (our code) count is sub-optimal for the subsequent join phase, causing cycles per output tuple 250 partitioning cost in and their join code to be also expensive. With optimized code, partitioning becomes the dominant cost, which is consistent 200 with the findings of Kim et al. [1] that showed comparable cost at similar parameter settings. Overall, our code is about 150 three times faster than the code of Blanas et al. for all shown configurations. 100 Performance Counters. We also instrumented the available 50 radix join implementations to monitor CPU performance coun- ters. Table IV lists cache and TLB miss counts for the three 1 2 3 4 5 6 7 8 tasks in radix join. number of threads The table shows a significant difference in the number of cache and TLB misses between the implementation of Blanas Fig. 12. Overall join execution cost (cycles per output tuple) for hardware- et al. and ours. The idea behind radix join is that all partitions conscious radix join strategy (Workload A; Intel Xeon L5520, 2.26 GHz). should be sufficiently small to fully fit into caches, so one should expect a very low number of misses, which is true for our implementation, but not for the one of Blanas et al. C. Overall Execution Time The reason for the difference is an unfortunate execution or- The overall cost of join execution consists of the cost for der of hash building and probing in the latter code. Their code data partitioning and the cost for computing the individual performs radix join strictly in three phases. After partitioning joins over partitions. To evaluate the overall cost of join (first phase), hash tables are created for all partitions (second execution (and to prepare for a comparison with the hardware- phase). Only then, in the third algorithm phase, are those hash oblivious no partitioning algorithm), we measured our own, tables probed to find join partners. Effectively, created hash carefully tuned implementation, as well as those reported in tables will long be evicted from CPU caches, before their earlier work. content is actually needed for probing. Our code avoids these We had two implementations of radix join available. For unnecessary memory round-trips by running build and probe the code of Blanas et al. [12], we found one pass and for each partition together. 2,048 partitions to be the optimal parameter configuration (which matches the configuration in their experiments [2]). D. Speedup from SMT Threads Partitioning in that code turns out to be rather expensive. We Figure 13 shows that neither of the two radix join imple- attribute this to a coding style that leads to many function calls mentations that we evaluated can significantly benefit from and pointer dereferences in critical code paths. Partitioning SMT threads. Up to the number of physical cores, both is much more efficient in our own code. This leads to a implementations scale linearly, and in the SMT threads region situation where two-pass partitioning with 16,384 partitions both suffer from the sharing of hardware resources (i.e., becomes most efficient. Table IV illustrates how the different caches, TLBs) between threads. These results are also in line implementations lead to significant differences in the executed with the results of Blanas et al. [2]. As pointed out before, instruction count. Our code performs two partitioning passes cache-efficient algorithms cannot benefit from SMT threads with 40 % fewer instructions than Blanas et al.’s code [2] that to the same extent since there are not many cache misses needs to perform only one pass. to be hidden by the hardware. The results are also useful in The resulting overall execution times are reported (as cycles validating our code against that of Kim et al. [1]. With our per output tuples) in Figure 12. This chart confirms that optimized implementation, we achieve a speedup of 4.6, very partitioning is rather expensive in the code of Blanas et al. Ulti- close to the 4.4 factor reported by Kim et al. on a similar Intel mately, this results in a situation where the resulting partition Nehalem processor (at comparable absolute performance). 

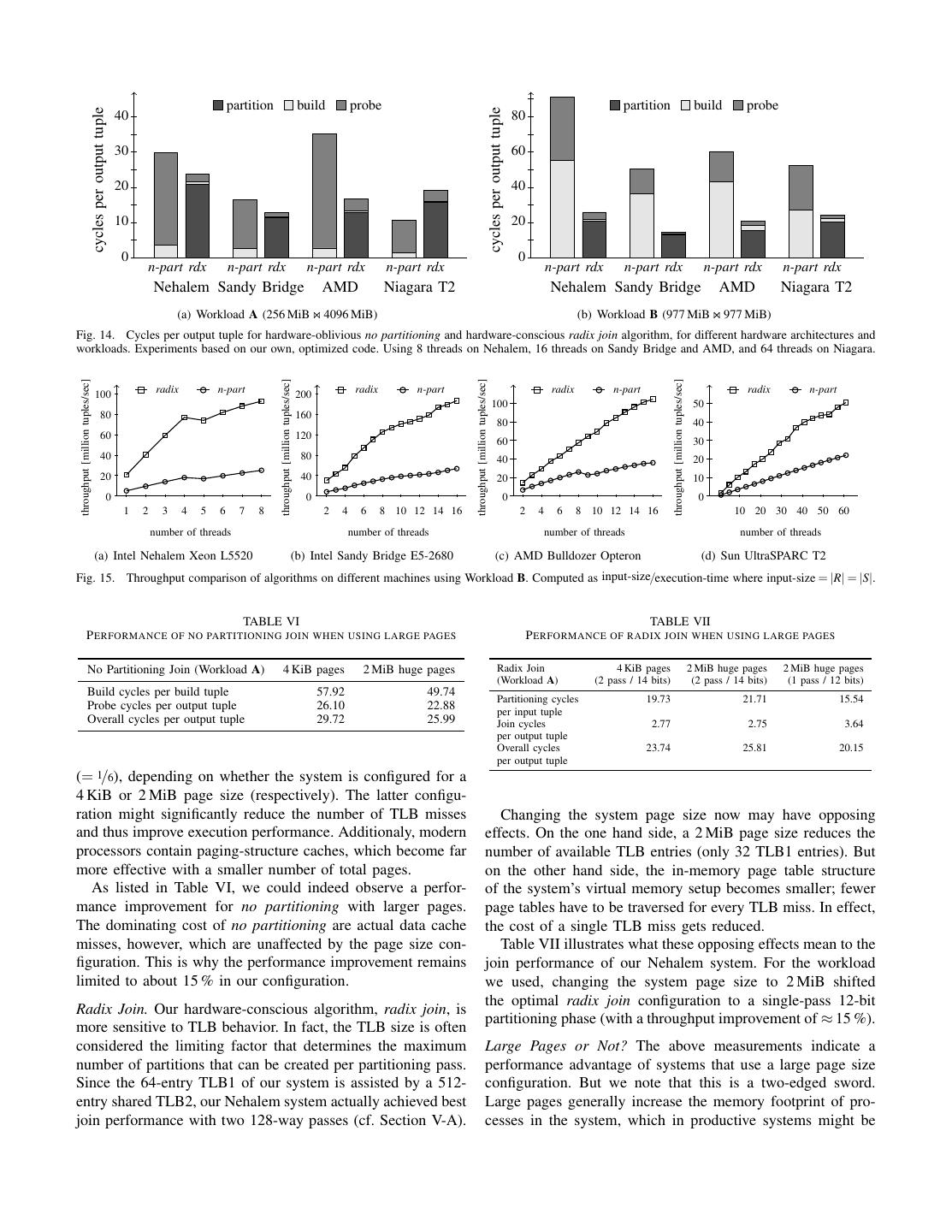
8 . TABLE V VI. H ARDWARE -C ONSCIOUS OR N OT ? L ATCH COST PER BUILD TUPLE IN DIFFERENT MACHINES In this section we compare the algorithms above under a Nehalem Sandy Bridge Bulldozer Niagara 2 wide range of parameters and hardware platforms. Used instruction xchgb xchgb xchgb ldstub A. Effect of Workloads Reported instruction latency in [14], [15] ∼20 cycles ∼25 cycles ∼50 cycles 3 cycles The results of extended experiments over all workloads and Measured impact per build tuple 7-9 cycles 6-9 cycles 30-34 cycles 1-1.5 cycles hardware platforms are summarized in Figure 14. Figure 14(a) shows the performance of our own implementation using Workload A on several hardware platforms (this workload is the one used by Blanas et al. [2]). C. Sun UltraSPARC T2 “Niagara” While Blanas et al. [2] reported only a marginal perfor- On the Sun UltraSPARC T2, a totally different architecture mance difference between no partitioning and radix join on than the x86 platforms, we see a similar result with Work- x86 architectures, in our results the hardware-conscious radix load B. Hardware-conscious radix join achieves a throughput join is appreciably faster when both implementations are of 50 million tuples per second (cf. Figure 15(d)), whereas no equally optimized. Only on the Sun Niagara the situation looks partitioning achieves only 22 million tuples per second. different. We look into this architecture in the next sub-section. However, when looking to Workload A, no partitioning be- The results in Figure 14(a) may still be seen as a good ar- comes faster than radix join on the Niagara 2 (shown in Figure gument for the hardware-oblivious approach. An approximate 14(a)). One could attribute this effect to the highly effective on 25 % performance advantage, e.g., on the two Intel platforms chip multi-threading functionality of the Niagara 2. However, might not justify the effort needed for parameter tuning in there is more than that. First, the virtual memory page size radix join. on UltraSPARC T2 is 8 KiB and the TLB is fully associative, Running the same experiments with our second workload, which are significant differences from other architectures. Workload B (Figure 14(b)), however, radically changes the Second, the Niagara 2 architecture turns out to have ex- picture. Radix join is approximately 3.5 times faster than no tremely efficient thread synchronization mechanisms. To il- partitioning on Intel machines and 2.5 times faster on AMD lustrate that, we deliberately disabled the latch code in the no and Sun machines. That is, no partitioning only has compara- partitioning join. We found out that the ldstub instruction ble performance to radix join when the relative relation sizes which is used to implement the latch on UltraSPARC T2 is are very different. This is because in such a situation, the very efficient compared to other architectures as shown in cost of the build phase is minimized. As soon as table sizes Table V. These special characteristics of Sun UltraSPARC T2 grow and become similar, the overhead of not being hardware- also show the importance of architecture-sensitive decisions in conscious becomes clearly visible (see the differences in the algorithm implementations. build phases for no partitioning). D. TLB and Virtual Memory Page Sizes B. Scalability In-memory hash joins are known to be sensitive to the vir- To study the scalability of our two join variants, we re-ran tual memory subsystem of the underlying system, in particular our experiments with a varying number of threads, up to the to the caching of address translations via translation look-aside maximum number of hardware contexts available on each of buffers (TLBs). The virtual memory setup of modern systems our architectures. Figure 15 illustrates the results. is, to a small extent, configurable. By changing a system’s Besides the SMT issues that we already discussed in Sec- page size, every address mapping (potentially cached in the tions IV-C and V-D, all platforms and both join implemen- TLB) covers a different amount of main memory, and with a tations show good scalability. Thanks to this scalability, our large page size, fewer TLB entries might be needed for the radix join implementation reaches a throughput of 196 million operations on a given memory region. tuples per second. As far as we are aware, this is the highest Intel Nehalem hardware can essentially be operated in either throughput reached for in-memory hash joins so far. of two modes with the support of the OS [16]: (i) with a page On the AMD machine, no partitioning shows a clear bump size of 4 KiB (the default), the level 1 data TLB can hold up to around 8–10 threads. This is an artifact of the particular AMD 64 memory mappings; (ii) alternatively, when the page size is architecture. Though the Opteron is marketed as a 16-core set to 2 MiB, only 32 mappings can be cached in TLB1. Here processor, the chip internally consists of two interconnected we study the effect of these two options on join performance. CPU dies [13]. It is likely that such an architecture requires a tailored design for the algorithms to perform well, removing an No Partitioning Joins. During the hash table build and probe argument in favor of hardware-conscious algorithms as, even if phases, the hardware-oblivious no partitioning join algorithm it is parameter-free, some multi-core architectures may require randomly accesses an element in the hash table that is created specialized designs anyway. NUMA would create significant for the smaller join relation R. For our workload configuration problems for the shared hash table used in no partitioning A, this hash table is 384 MiB in size (tuples plus latches and (let alone future designs where memory may not be coherent bucket structure). Consequently, the chance to hit a memory across the machine). page that is cached in TLB1 is 64/ 98304 (= 1/1536) or 32/ 192 

9 . cycles per output tuple partition build probe partition build probe cycles per output tuple 40 80 30 60 20 40 10 20 0 0 n-part rdx n-part rdx n-part rdx n-part rdx n-part rdx n-part rdx n-part rdx n-part rdx Nehalem Sandy Bridge AMD Niagara T2 Nehalem Sandy Bridge AMD Niagara T2 (a) Workload A (256 MiB 4096 MiB) (b) Workload B (977 MiB 977 MiB) Fig. 14. Cycles per output tuple for hardware-oblivious no partitioning and hardware-conscious radix join algorithm, for different hardware architectures and workloads. Experiments based on our own, optimized code. Using 8 threads on Nehalem, 16 threads on Sandy Bridge and AMD, and 64 threads on Niagara. throughput [million tuples/sec] throughput [million tuples/sec] throughput [million tuples/sec] throughput [million tuples/sec] radix n-part radix n-part radix n-part radix n-part 100 200 100 50 80 160 80 40 60 120 60 30 40 80 40 20 20 40 20 10 0 0 0 0 1 2 3 4 5 6 7 8 2 4 6 8 10 12 14 16 2 4 6 8 10 12 14 16 10 20 30 40 50 60 number of threads number of threads number of threads number of threads (a) Intel Nehalem Xeon L5520 (b) Intel Sandy Bridge E5-2680 (c) AMD Bulldozer Opteron (d) Sun UltraSPARC T2 Fig. 15. Throughput comparison of algorithms on different machines using Workload B. Computed as input-size/execution-time where input-size = |R| = |S|. TABLE VI TABLE VII P ERFORMANCE OF NO PARTITIONING JOIN WHEN USING LARGE PAGES P ERFORMANCE OF RADIX JOIN WHEN USING LARGE PAGES No Partitioning Join (Workload A) 4 KiB pages 2 MiB huge pages Radix Join 4 KiB pages 2 MiB huge pages 2 MiB huge pages (Workload A) (2 pass / 14 bits) (2 pass / 14 bits) (1 pass / 12 bits) Build cycles per build tuple 57.92 49.74 Partitioning cycles 19.73 21.71 15.54 Probe cycles per output tuple 26.10 22.88 per input tuple Overall cycles per output tuple 29.72 25.99 Join cycles 2.77 2.75 3.64 per output tuple Overall cycles 23.74 25.81 20.15 per output tuple (= 1/6), depending on whether the system is configured for a 4 KiB or 2 MiB page size (respectively). The latter configu- ration might significantly reduce the number of TLB misses Changing the system page size now may have opposing and thus improve execution performance. Additionaly, modern effects. On the one hand side, a 2 MiB page size reduces the processors contain paging-structure caches, which become far number of available TLB entries (only 32 TLB1 entries). But more effective with a smaller number of total pages. on the other hand side, the in-memory page table structure As listed in Table VI, we could indeed observe a perfor- of the system’s virtual memory setup becomes smaller; fewer mance improvement for no partitioning with larger pages. page tables have to be traversed for every TLB miss. In effect, The dominating cost of no partitioning are actual data cache the cost of a single TLB miss gets reduced. misses, however, which are unaffected by the page size con- Table VII illustrates what these opposing effects mean to the figuration. This is why the performance improvement remains join performance of our Nehalem system. For the workload limited to about 15 % in our configuration. we used, changing the system page size to 2 MiB shifted the optimal radix join configuration to a single-pass 12-bit Radix Join. Our hardware-conscious algorithm, radix join, is partitioning phase (with a throughput improvement of ≈ 15 %). more sensitive to TLB behavior. In fact, the TLB size is often considered the limiting factor that determines the maximum Large Pages or Not? The above measurements indicate a number of partitions that can be created per partitioning pass. performance advantage of systems that use a large page size Since the 64-entry TLB1 of our system is assisted by a 512- configuration. But we note that this is a two-edged sword. entry shared TLB2, our Nehalem system actually achieved best Large pages generally increase the memory footprint of pro- join performance with two 128-way passes (cf. Section V-A). cesses in the system, which in productive systems might be 

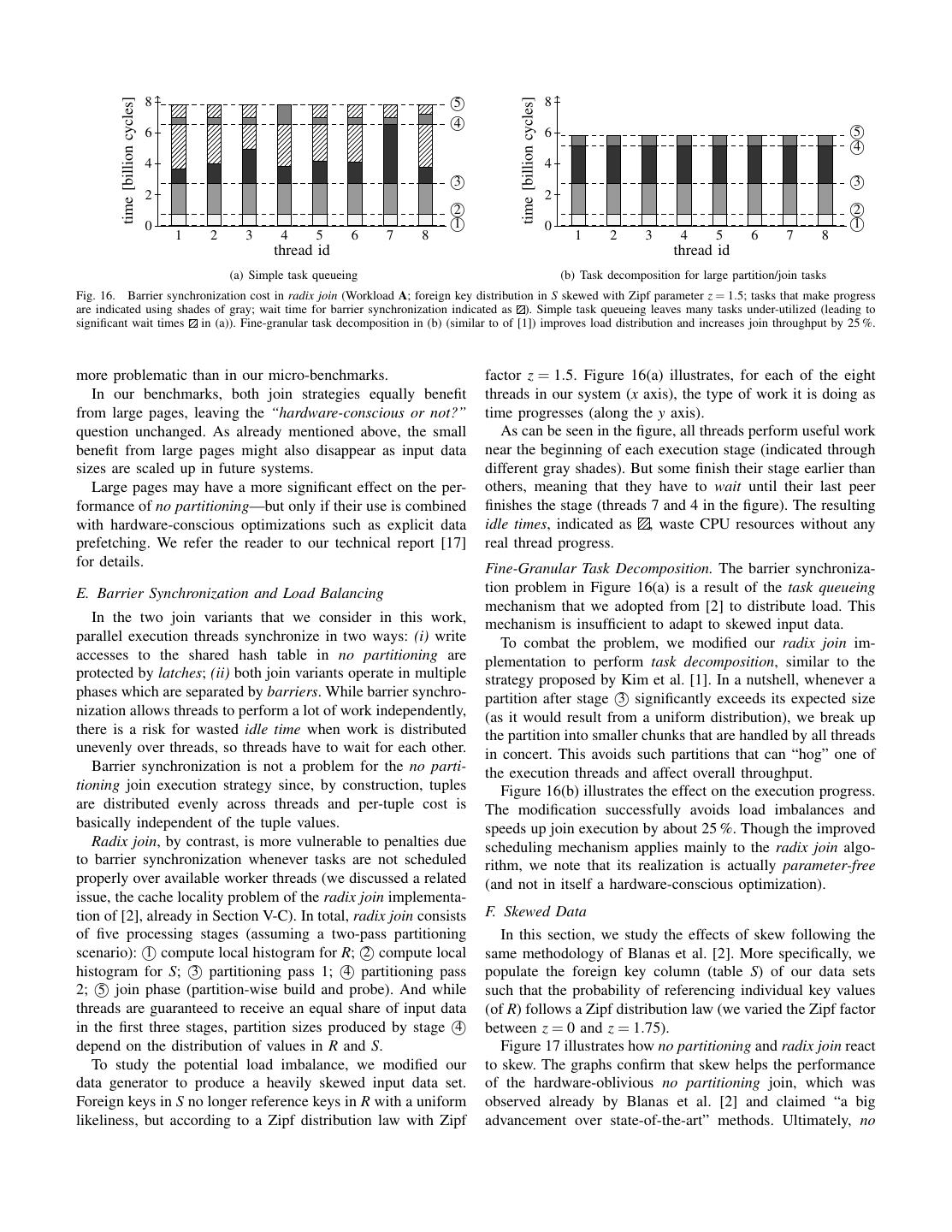
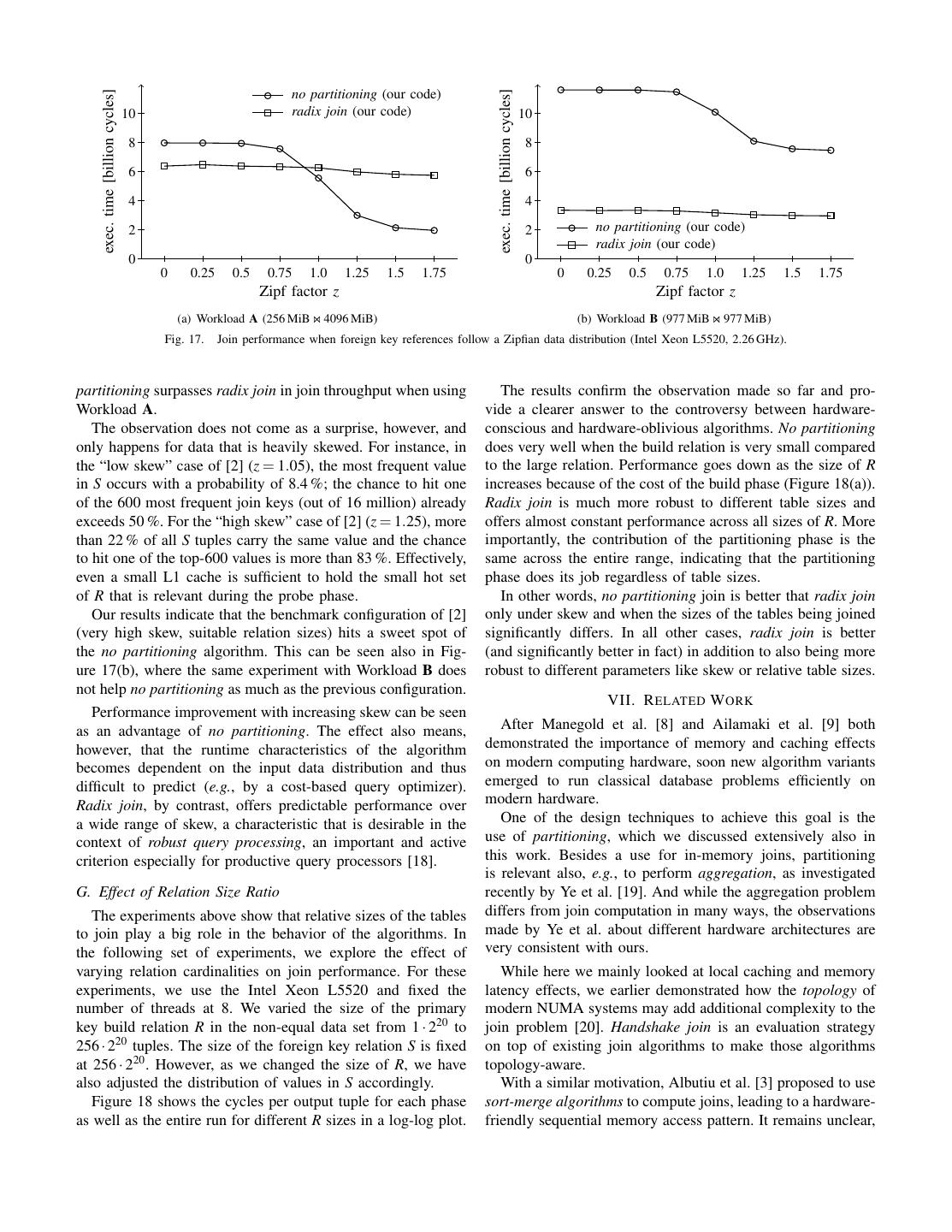
10 . time [billion cycles] time [billion cycles] 8 5 8 4 6 6 5 4 4 4 3 3 2 2 2 2 0 1 0 1 1 2 3 4 5 6 7 8 1 2 3 4 5 6 7 8 thread id thread id (a) Simple task queueing (b) Task decomposition for large partition/join tasks Fig. 16. Barrier synchronization cost in radix join (Workload A; foreign key distribution in S skewed with Zipf parameter z = 1.5; tasks that make progress are indicated using shades of gray; wait time for barrier synchronization indicated as ). Simple task queueing leaves many tasks under-utilized (leading to significant wait times in (a)). Fine-granular task decomposition in (b) (similar to of [1]) improves load distribution and increases join throughput by 25 %. more problematic than in our micro-benchmarks. factor z = 1.5. Figure 16(a) illustrates, for each of the eight In our benchmarks, both join strategies equally benefit threads in our system (x axis), the type of work it is doing as from large pages, leaving the “hardware-conscious or not?” time progresses (along the y axis). question unchanged. As already mentioned above, the small As can be seen in the figure, all threads perform useful work benefit from large pages might also disappear as input data near the beginning of each execution stage (indicated through sizes are scaled up in future systems. different gray shades). But some finish their stage earlier than Large pages may have a more significant effect on the per- others, meaning that they have to wait until their last peer formance of no partitioning—but only if their use is combined finishes the stage (threads 7 and 4 in the figure). The resulting with hardware-conscious optimizations such as explicit data idle times, indicated as , waste CPU resources without any prefetching. We refer the reader to our technical report [17] real thread progress. for details. Fine-Granular Task Decomposition. The barrier synchroniza- E. Barrier Synchronization and Load Balancing tion problem in Figure 16(a) is a result of the task queueing mechanism that we adopted from [2] to distribute load. This In the two join variants that we consider in this work, mechanism is insufficient to adapt to skewed input data. parallel execution threads synchronize in two ways: (i) write To combat the problem, we modified our radix join im- accesses to the shared hash table in no partitioning are plementation to perform task decomposition, similar to the protected by latches; (ii) both join variants operate in multiple strategy proposed by Kim et al. [1]. In a nutshell, whenever a phases which are separated by barriers. While barrier synchro- partition after stage 3 significantly exceeds its expected size nization allows threads to perform a lot of work independently, (as it would result from a uniform distribution), we break up there is a risk for wasted idle time when work is distributed the partition into smaller chunks that are handled by all threads unevenly over threads, so threads have to wait for each other. in concert. This avoids such partitions that can “hog” one of Barrier synchronization is not a problem for the no parti- the execution threads and affect overall throughput. tioning join execution strategy since, by construction, tuples Figure 16(b) illustrates the effect on the execution progress. are distributed evenly across threads and per-tuple cost is The modification successfully avoids load imbalances and basically independent of the tuple values. speeds up join execution by about 25 %. Though the improved Radix join, by contrast, is more vulnerable to penalties due scheduling mechanism applies mainly to the radix join algo- to barrier synchronization whenever tasks are not scheduled rithm, we note that its realization is actually parameter-free properly over available worker threads (we discussed a related (and not in itself a hardware-conscious optimization). issue, the cache locality problem of the radix join implementa- tion of [2], already in Section V-C). In total, radix join consists F. Skewed Data of five processing stages (assuming a two-pass partitioning In this section, we study the effects of skew following the scenario): 1 compute local histogram for R; 2 compute local same methodology of Blanas et al. [2]. More specifically, we histogram for S; 3 partitioning pass 1; 4 partitioning pass populate the foreign key column (table S) of our data sets 2; 5 join phase (partition-wise build and probe). And while such that the probability of referencing individual key values threads are guaranteed to receive an equal share of input data (of R) follows a Zipf distribution law (we varied the Zipf factor in the first three stages, partition sizes produced by stage 4 between z = 0 and z = 1.75). depend on the distribution of values in R and S. Figure 17 illustrates how no partitioning and radix join react To study the potential load imbalance, we modified our to skew. The graphs confirm that skew helps the performance data generator to produce a heavily skewed input data set. of the hardware-oblivious no partitioning join, which was Foreign keys in S no longer reference keys in R with a uniform observed already by Blanas et al. [2] and claimed “a big likeliness, but according to a Zipf distribution law with Zipf advancement over state-of-the-art” methods. Ultimately, no 

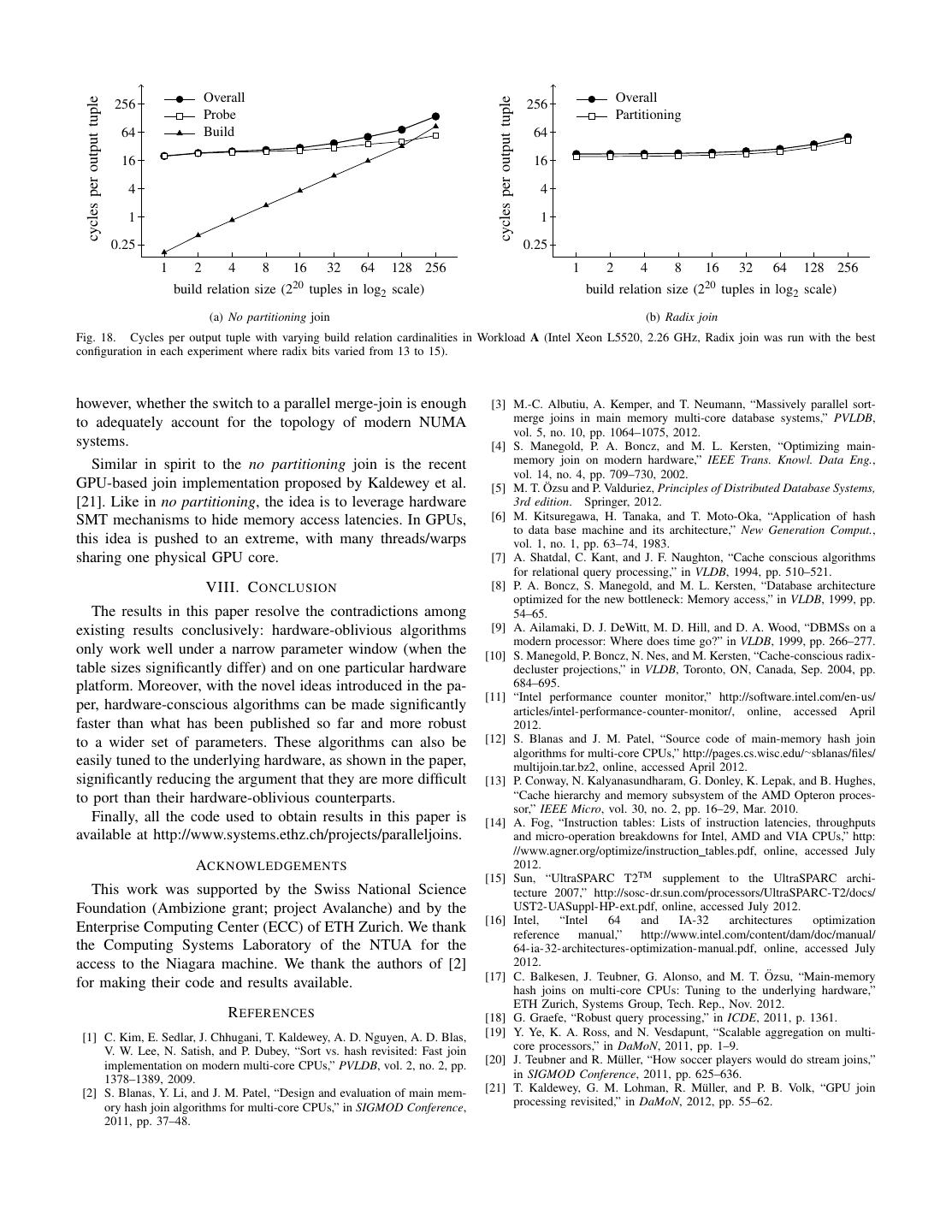
11 . exec. time [billion cycles] exec. time [billion cycles] no partitioning (our code) 10 radix join (our code) 10 8 8 6 6 4 4 2 2 no partitioning (our code) radix join (our code) 0 0 0 0.25 0.5 0.75 1.0 1.25 1.5 1.75 0 0.25 0.5 0.75 1.0 1.25 1.5 1.75 Zipf factor z Zipf factor z (a) Workload A (256 MiB 4096 MiB) (b) Workload B (977 MiB 977 MiB) Fig. 17. Join performance when foreign key references follow a Zipfian data distribution (Intel Xeon L5520, 2.26 GHz). partitioning surpasses radix join in join throughput when using The results confirm the observation made so far and pro- Workload A. vide a clearer answer to the controversy between hardware- The observation does not come as a surprise, however, and conscious and hardware-oblivious algorithms. No partitioning only happens for data that is heavily skewed. For instance, in does very well when the build relation is very small compared the “low skew” case of [2] (z = 1.05), the most frequent value to the large relation. Performance goes down as the size of R in S occurs with a probability of 8.4 %; the chance to hit one increases because of the cost of the build phase (Figure 18(a)). of the 600 most frequent join keys (out of 16 million) already Radix join is much more robust to different table sizes and exceeds 50 %. For the “high skew” case of [2] (z = 1.25), more offers almost constant performance across all sizes of R. More than 22 % of all S tuples carry the same value and the chance importantly, the contribution of the partitioning phase is the to hit one of the top-600 values is more than 83 %. Effectively, same across the entire range, indicating that the partitioning even a small L1 cache is sufficient to hold the small hot set phase does its job regardless of table sizes. of R that is relevant during the probe phase. In other words, no partitioning join is better that radix join Our results indicate that the benchmark configuration of [2] only under skew and when the sizes of the tables being joined (very high skew, suitable relation sizes) hits a sweet spot of significantly differs. In all other cases, radix join is better the no partitioning algorithm. This can be seen also in Fig- (and significantly better in fact) in addition to also being more ure 17(b), where the same experiment with Workload B does robust to different parameters like skew or relative table sizes. not help no partitioning as much as the previous configuration. VII. R ELATED W ORK Performance improvement with increasing skew can be seen as an advantage of no partitioning. The effect also means, After Manegold et al. [8] and Ailamaki et al. [9] both however, that the runtime characteristics of the algorithm demonstrated the importance of memory and caching effects becomes dependent on the input data distribution and thus on modern computing hardware, soon new algorithm variants difficult to predict (e.g., by a cost-based query optimizer). emerged to run classical database problems efficiently on Radix join, by contrast, offers predictable performance over modern hardware. a wide range of skew, a characteristic that is desirable in the One of the design techniques to achieve this goal is the context of robust query processing, an important and active use of partitioning, which we discussed extensively also in criterion especially for productive query processors [18]. this work. Besides a use for in-memory joins, partitioning is relevant also, e.g., to perform aggregation, as investigated G. Effect of Relation Size Ratio recently by Ye et al. [19]. And while the aggregation problem The experiments above show that relative sizes of the tables differs from join computation in many ways, the observations to join play a big role in the behavior of the algorithms. In made by Ye et al. about different hardware architectures are the following set of experiments, we explore the effect of very consistent with ours. varying relation cardinalities on join performance. For these While here we mainly looked at local caching and memory experiments, we use the Intel Xeon L5520 and fixed the latency effects, we earlier demonstrated how the topology of number of threads at 8. We varied the size of the primary modern NUMA systems may add additional complexity to the key build relation R in the non-equal data set from 1 · 220 to join problem [20]. Handshake join is an evaluation strategy 256 · 220 tuples. The size of the foreign key relation S is fixed on top of existing join algorithms to make those algorithms at 256 · 220 . However, as we changed the size of R, we have topology-aware. also adjusted the distribution of values in S accordingly. With a similar motivation, Albutiu et al. [3] proposed to use Figure 18 shows the cycles per output tuple for each phase sort-merge algorithms to compute joins, leading to a hardware- as well as the entire run for different R sizes in a log-log plot. friendly sequential memory access pattern. It remains unclear, 

12 . cycles per output tuple Overall Overall cycles per output tuple 256 256 Probe Partitioning 64 Build 64 16 16 4 4 1 1 0.25 0.25 1 2 4 8 16 32 64 128 256 1 2 4 8 16 32 64 128 256 build relation size (220 tuples in log2 scale) build relation size (220 tuples in log2 scale) (a) No partitioning join (b) Radix join Fig. 18. Cycles per output tuple with varying build relation cardinalities in Workload A (Intel Xeon L5520, 2.26 GHz, Radix join was run with the best configuration in each experiment where radix bits varied from 13 to 15). however, whether the switch to a parallel merge-join is enough [3] M.-C. Albutiu, A. Kemper, and T. Neumann, “Massively parallel sort- to adequately account for the topology of modern NUMA merge joins in main memory multi-core database systems,” PVLDB, vol. 5, no. 10, pp. 1064–1075, 2012. systems. [4] S. Manegold, P. A. Boncz, and M. L. Kersten, “Optimizing main- Similar in spirit to the no partitioning join is the recent memory join on modern hardware,” IEEE Trans. Knowl. Data Eng., vol. 14, no. 4, pp. 709–730, 2002. GPU-based join implementation proposed by Kaldewey et al. ¨ [5] M. T. Ozsu and P. Valduriez, Principles of Distributed Database Systems, [21]. Like in no partitioning, the idea is to leverage hardware 3rd edition. Springer, 2012. SMT mechanisms to hide memory access latencies. In GPUs, [6] M. Kitsuregawa, H. Tanaka, and T. Moto-Oka, “Application of hash to data base machine and its architecture,” New Generation Comput., this idea is pushed to an extreme, with many threads/warps vol. 1, no. 1, pp. 63–74, 1983. sharing one physical GPU core. [7] A. Shatdal, C. Kant, and J. F. Naughton, “Cache conscious algorithms for relational query processing,” in VLDB, 1994, pp. 510–521. VIII. C ONCLUSION [8] P. A. Boncz, S. Manegold, and M. L. Kersten, “Database architecture optimized for the new bottleneck: Memory access,” in VLDB, 1999, pp. The results in this paper resolve the contradictions among 54–65. existing results conclusively: hardware-oblivious algorithms [9] A. Ailamaki, D. J. DeWitt, M. D. Hill, and D. A. Wood, “DBMSs on a modern processor: Where does time go?” in VLDB, 1999, pp. 266–277. only work well under a narrow parameter window (when the [10] S. Manegold, P. Boncz, N. Nes, and M. Kersten, “Cache-conscious radix- table sizes significantly differ) and on one particular hardware decluster projections,” in VLDB, Toronto, ON, Canada, Sep. 2004, pp. platform. Moreover, with the novel ideas introduced in the pa- 684–695. [11] “Intel performance counter monitor,” http://software.intel.com/en-us/ per, hardware-conscious algorithms can be made significantly articles/intel-performance-counter-monitor/, online, accessed April faster than what has been published so far and more robust 2012. to a wider set of parameters. These algorithms can also be [12] S. Blanas and J. M. Patel, “Source code of main-memory hash join algorithms for multi-core CPUs,” http://pages.cs.wisc.edu/∼sblanas/files/ easily tuned to the underlying hardware, as shown in the paper, multijoin.tar.bz2, online, accessed April 2012. significantly reducing the argument that they are more difficult [13] P. Conway, N. Kalyanasundharam, G. Donley, K. Lepak, and B. Hughes, to port than their hardware-oblivious counterparts. “Cache hierarchy and memory subsystem of the AMD Opteron proces- sor,” IEEE Micro, vol. 30, no. 2, pp. 16–29, Mar. 2010. Finally, all the code used to obtain results in this paper is [14] A. Fog, “Instruction tables: Lists of instruction latencies, throughputs available at http://www.systems.ethz.ch/projects/paralleljoins. and micro-operation breakdowns for Intel, AMD and VIA CPUs,” http: //www.agner.org/optimize/instruction tables.pdf, online, accessed July ACKNOWLEDGEMENTS 2012. [15] Sun, “UltraSPARC T2TM supplement to the UltraSPARC archi- This work was supported by the Swiss National Science tecture 2007,” http://sosc-dr.sun.com/processors/UltraSPARC-T2/docs/ Foundation (Ambizione grant; project Avalanche) and by the UST2-UASuppl-HP-ext.pdf, online, accessed July 2012. [16] Intel, “Intel 64 and IA-32 architectures optimization Enterprise Computing Center (ECC) of ETH Zurich. We thank reference manual,” http://www.intel.com/content/dam/doc/manual/ the Computing Systems Laboratory of the NTUA for the 64-ia-32-architectures-optimization-manual.pdf, online, accessed July access to the Niagara machine. We thank the authors of [2] 2012. [17] C. Balkesen, J. Teubner, G. Alonso, and M. T. Ozsu, ¨ “Main-memory for making their code and results available. hash joins on multi-core CPUs: Tuning to the underlying hardware,” ETH Zurich, Systems Group, Tech. Rep., Nov. 2012. R EFERENCES [18] G. Graefe, “Robust query processing,” in ICDE, 2011, p. 1361. [1] C. Kim, E. Sedlar, J. Chhugani, T. Kaldewey, A. D. Nguyen, A. D. Blas, [19] Y. Ye, K. A. Ross, and N. Vesdapunt, “Scalable aggregation on multi- V. W. Lee, N. Satish, and P. Dubey, “Sort vs. hash revisited: Fast join core processors,” in DaMoN, 2011, pp. 1–9. implementation on modern multi-core CPUs,” PVLDB, vol. 2, no. 2, pp. [20] J. Teubner and R. M¨uller, “How soccer players would do stream joins,” 1378–1389, 2009. in SIGMOD Conference, 2011, pp. 625–636. [2] S. Blanas, Y. Li, and J. M. Patel, “Design and evaluation of main mem- [21] T. Kaldewey, G. M. Lohman, R. M¨uller, and P. B. Volk, “GPU join ory hash join algorithms for multi-core CPUs,” in SIGMOD Conference, processing revisited,” in DaMoN, 2012, pp. 55–62. 2011, pp. 37–48.