线性子空间中数据

1 . Principal Components: Mathematics, Example, Interpretation 36-350: Data Mining 18 September 2009 Reading: Section 3.6 in the textbook. Contents 1 Mathematics of Principal Components 1 1.1 Minimizing Projection Residuals . . . . . . . . . . . . . . . . . . 2 1.2 Maximizing Variance . . . . . . . . . . . . . . . . . . . . . . . . . 3 1.3 More Geometry; Back to the Residuals . . . . . . . . . . . . . . . 5 2 Example: Cars 6 2.1 A Recipe . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 8 3 PCA Cautions 10 At the end of the last lecture, I set as our goal to find ways of reducing the dimensionality of our data by means of linear projections, and of choosing pro- jections which in some sense respect the structure of the data. I further asserted that there was one way of doing this which was far more useful and important than others, called principal components analysis, where “respecting struc- ture” means “preserving variance”. This lecture will explain that, explain how to do PCA, show an example, and describe some of the issues that come up in interpreting the results. PCA has been rediscovered many times in many fields, so it is also known as the Karhunen-Lo`eve transformation, the Hotelling transformation, the method of empirical orthogonal functions, and singular value decomposition1 . We will call it PCA. 1 Mathematics of Principal Components We start with p-dimensional feature vectors, and want to summarize them by projecting down into a q-dimensional subspace. Our summary will be the pro- 1 Strictly speaking, singular value decomposition is a matrix algebra trick which is used in the most common algorithm for PCA. 1 

2 .jection of the original vectors on to q directions, the principal components, which span the sub-space. There are several equivalent ways of deriving the principal components math- ematically. The simplest one is by finding the projections which maximize the variance. The first principal component is the direction in feature space along which projections have the largest variance. The second principal component is the direction which maximizes variance among all directions orthogonal to the first. The k th component is the variance-maximizing direction orthogonal to the previous k − 1 components. There are p principal components in all. Rather than maximizing variance, it might sound more plausible to look for the projection with the smallest average (mean-squared) distance between the original vectors and their projections on to the principal components; this turns out to be equivalent to maximizing the variance. Throughout, assume that the data have been “centered”, so that every fea- ture has mean 0. If we write the centered data in a matrix X, where rows are objects and columns are features, then XT X = nV, where V is the covariance matrix of the data. (You should check that last statement!) 1.1 Minimizing Projection Residuals We’ll start by looking for a one-dimensional projection. That is, we have p- dimensional feature vectors, and we want to project them on to a line through the origin. We can specify the line by a unit vector along it, w, and then the projection of a data vector xi on to the line is xi · w, which is a scalar. (Sanity check: this gives us the right answer when we project on to one of the coordinate axes.) This is the distance of the projection from the origin; the actual coordinate in p-dimensional space is (xi · w)w. The mean of the projections will be zero, because the mean of the vectors xi is zero: n n 1 1 (xi · w)w = xi ·w w (1) n i=1 n i=1 If we try to use our projected or image vectors instead of our original vectors, there will be some error, because (in general) the images do not coincide with the original vectors. (When do they coincide?) The difference is the error or residual of the projection. How big is it? For any one vector, say xi , it’s 2 2 2 xi − (w · xi )w = xi − 2(w · xi )(w · xi ) + w (2) 2 2 = xi − 2(w · xi ) + 1 (3) (This is the same trick used to compute distance matrices in the solution to the first homework; it’s really just the Pythagorean theorem.) Add those residuals up across all the vectors: n 2 2 RSS(w) = xi − 2(w · xi ) + 1 (4) i=1 2 

3 . n n 2 2 = n+ xi −2 (w · xi ) (5) i=1 i=1 The term in the big parenthesis doesn’t depend on w, so it doesn’t matter for trying to minimize the residual sum-of-squares. To make RSS small, what we must do is make the second sum big, i.e., we want to maximize n 2 (w · xi ) (6) i=1 Equivalently, since n doesn’t depend on w, we want to maximize n 1 2 (w · xi ) (7) n i=1 2 which we can see is the sample mean of (w · xi ) . The mean of a square is always equal to the square of the mean plus the variance: n n 2 1 2 1 (w · xi ) = xi · w + Var [w · xi ] (8) n i=1 n i=1 Since we’ve just seen that the mean of the projections is zero, minimizing the residual sum of squares turns out to be equivalent to maximizing the variance of the projections. (Of course in general we don’t want to project on to just one vector, but on to multiple principal components. If those components are orthogonal and have the unit vectors w1 , w2 , . . . wk , then the image of xi is its projection into the space spanned by these vectors, k (xi · wj )wj (9) j=1 The mean of the projection on to each component is still zero. If we go through the same algebra for the residual sum of squares, it turns out that the cross- terms between different components all cancel out, and we are left with trying to maximize the sum of the variances of the projections on to the components. Exercise: Do this algebra.) 1.2 Maximizing Variance Accordingly, let’s maximize the variance! Writing out all the summations grows tedious, so let’s do our algebra in matrix form. If we stack our n data vectors into an n × p matrix, X, then the projections are given by Xw, which is an n × 1 matrix. The variance is 2 1 2 σw = (xi · w) (10) n i 3 

4 . 1 T = (Xw) (Xw) (11) n 1 T T = w X Xw (12) n XT X = wT w (13) n = wT Vw (14) 2 We want to chose a unit vector w so as to maximize σw . To do this, we need to make sure that we only look at unit vectors — we need to constrain the maximization. The constraint is that w · w = 1, or wT w = 1. This needs a brief excursion into constrained optimization. We start with a function f (w) that we want to maximize. (Here, that function is wT V w.) We also have an equality constraint, g(w) = c. (Here, g(w) = wT w and c = 1.) We re-arrange the constraint equation so its right- hand side is zero, g(w) − c = 0. We now add an extra variable to the problem, the Lagrange multiplier λ, and consider u(w, λ) = f (w)−λ(g(w)−c). This is our new objective function, so we differentiate with respect to both arguments and set the derivatives equal to zero: ∂u ∂f ∂g =0= −λ (15) ∂w ∂w ∂w ∂u = 0 = −(g(w) − c) (16) ∂λ That is, maximizing with respect to λ gives us back our constraint equation, g(w) = c. At the same time, when we have the constraint satisfied, our new ob- jective function is the same as the old one. (If we had more than one constraint, we would just need more Lagrange multipliers.)23 For our projection problem, u = wT Vw − λ(wT w − 1) (17) ∂u = 2Vw − 2λw = 0 (18) ∂w Vw = λw (19) Thus, desired vector w is an eigenvector of the covariance matrix V, and the maximizing vector will be the one associated with the largest eigenvalue λ. This is good news, because finding eigenvectors is something which can be done comparatively rapidly (see Principles of Data Mining p. 81), and because eigen- vectors have many nice mathematical properties, which we can use as follows. We know that V is a p × p matrix, so it will have p different eigenvectors.4 We know that V is a covariance matrix, so it is symmetric, and then linear 2 To learn more about Lagrange multipliers, read Boas (1983) or (more compactly) Klein (2001). 3 Thanks to Ramana Vinjamuri for pointing out a sign error in an earlier version of this paragraph. 4 Exception: if n < p, there are only n distinct eigenvectors and eigenvalues. 4 

5 .algebra tells us that the eigenvectors must be orthogonal to one another. Again because V is a covariance matrix, it is a positive matrix, in the sense that x · Vx ≥ 0 for any x. This tells us that the eigenvalues of V must all be ≥ 0. The eigenvectors of V are the principal components of the data. We know that they are all orthogonal top each other from the previous paragraph, so together they span the whole p-dimensional feature space. The first principal component, i.e. the eigenvector which goes the largest value of λ, is the direction along which the data have the most variance. The second principal component, i.e. the second eigenvector, is the direction orthogonal to the first component with the most variance. Because it is orthogonal to the first eigenvector, their projections will be uncorrelated. In fact, projections on to all the principal components are uncorrelated with each other. If we use q principal components, our weight matrix w will be a p×q matrix, where each column will be a different eigenvector of the covariance matrix V. The eigenvalues will give the total variance described by each component. The variance of the projections on to q the first q principal components is then i=1 λi . 1.3 More Geometry; Back to the Residuals Suppose that the data really are q-dimensional. Then V will have only q positive eigenvalues, and p − q zero eigenvalues. If the data fall near a q-dimensional subspace, then p − q of the eigenvalues will be nearly zero. If we pick the top q components, we can define a projection operator Pq . The images of the data are then XPq . The projection residuals are X − XPq or X(1 − Pq ). (Notice that the residuals here are vectors, not just magnitudes.) If the data really are q-dimensional, then the residuals will be zero. If the data are approximately q-dimensional, then the residuals will be small. In any case, we can define the R2 of the projection as the fraction of the original variance kept by the image vectors, q λi R2 ≡ pi=1 (20) j=1 λj just as the R2 of a linear regression is the fraction of the original variance of the dependent variable retained by the fitted values. The q = 1 case is especially instructive. We know, from the discussion of projections in the last lecture, that the residual vectors are all orthogonal to the projections. Suppose we ask for the first principal component of the residuals. This will be the direction of largest variance which is perpendicular to the first principal component. In other words, it will be the second principal component of the data. This suggests a recursive algorithm for finding all the principal components: the k th principal component is the leading component of the residuals after subtracting off the first k − 1 components. In practice, it is faster to use eigenvector-solvers to get all the components at once from V, but we will see versions of this idea later. This is a good place to remark that if the data really fall in a q-dimensional subspace, then V will have only q positive eigenvalues, because after subtracting 5 

6 . Variable Meaning Sports Binary indicator for being a sports car SUV Indicator for sports utility vehicle Wagon Indicator Minivan Indicator Pickup Indicator AWD Indicator for all-wheel drive RWD Indicator for rear-wheel drive Retail Suggested retail price (US$) Dealer Price to dealer (US$) Engine Engine size (liters) Cylinders Number of engine cylinders Horsepower Engine horsepower CityMPG City gas mileage HighwayMPG Highway gas mileage Weight Weight (pounds) Wheelbase Wheelbase (inches) Length Length (inches) Width Width (inches) Table 1: Features for the 2004 cars data. off those components there will be no residuals. The other p − q eigenvectors will all have eigenvalue 0. If the data cluster around a q-dimensional subspace, then p − q of the eigenvalues will be very small, though how small they need to be before we can neglect them is a tricky question.5 2 Example: Cars Today’s dataset is 388 cars from the 2004 model year, with 18 features (from http://www.amstat.org/publications/jse/datasets/04cars.txt, with in- complete records removed). Eight features are binary indicators; the other 11 features are numerical (Table 1). All of the features except Type are numeri- cal. Table 2 shows the first few lines from the data set. PCA only works with numerical features, so we have ten of them to play with. There are two R functions for doing PCA, princomp and prcomp, which differ in how they do the actual calculation.6 The latter is generally more robust, so 5 One tricky case where this can occur is if n < p. Any two points define a line, and three points define a plane, etc., so if there are fewer data points than features, it is necessarily true that the fall on a low-dimensional subspace. If we look at the bags-of-words for the Times stories, for instance, we have p ≈ 4400 but n ≈ 102. Finding that only 102 principal components account for all the variance is not an empirical discovery but a mathematical artifact. 6 princomp actually calculates the covariance matrix and takes its eigenvalues. prcomp uses a different technique called “singular value decomposition”. 6 

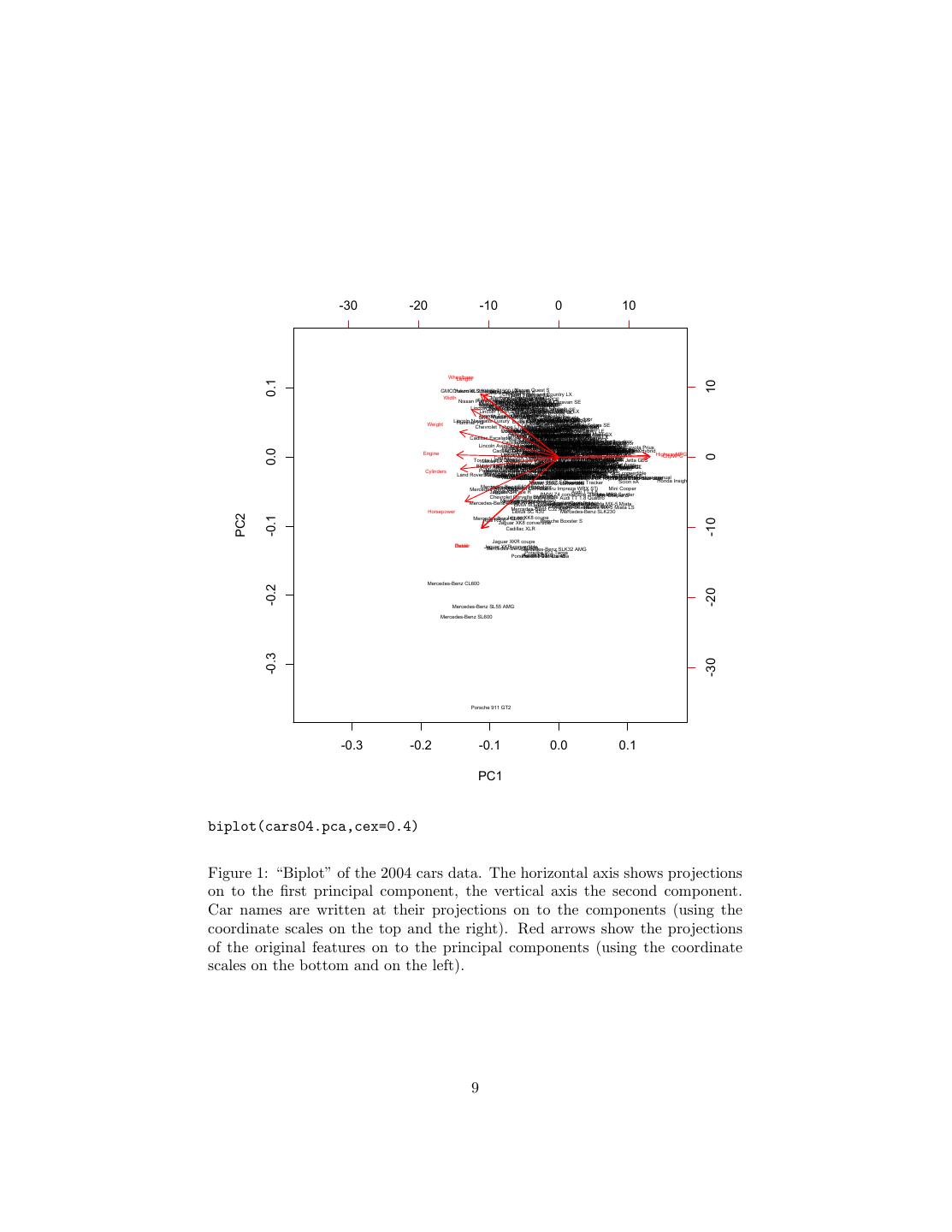
7 .Sports, SUV, Wagon, Minivan, Pickup, AWD, RWD, Retail,Dealer,Engine,Cylinders,Horsepower,Cit Acura 3.5 RL,0,0,0,0,0,0,0,43755,39014,3.5,6,225,18,24,3880,115,197,72 Acura MDX,0,1,0,0,0,1,0,36945,33337,3.5,6,265,17,23,4451,106,189,77 Acura NSX S,1,0,0,0,0,0,1,89765,79978,3.2,6,290,17,24,3153,100,174,71 Table 2: The first few lines of the 2004 cars data set. we’ll just use it. cars04 = read.csv("cars-fixed04.dat") cars04.pca = prcomp(cars04[,8:18], scale.=TRUE) The second argument to prcomp tells it to first scale all the variables to have variance 1, i.e., to standardize them. You should experiment with what happens with this data when we don’t standardize. We can now extract the loadings or weight matrix from the cars04.pca object. For comprehensibility I’ll just show the first two components. > round(cars04.pca$rotation[,1:2],2) PC1 PC2 Retail -0.26 -0.47 Dealer -0.26 -0.47 Engine -0.35 0.02 Cylinders -0.33 -0.08 Horsepower -0.32 -0.29 CityMPG 0.31 0.00 HighwayMPG 0.31 0.01 Weight -0.34 0.17 Wheelbase -0.27 0.42 Length -0.26 0.41 Width -0.30 0.31 This says that all the variables except the gas-mileages have a negative projection on to the first component. This means that there is a negative correlation between mileage and everything else. The first principal component tells us about whether we are getting a big, expensive gas-guzzling car with a powerful engine, or whether we are getting a small, cheap, fuel-efficient car with a wimpy engine. The second component is a little more interesting. Engine size and gas mileage hardly project on to it at all. Instead we have a contrast between the physical size of the car (positive projection) and the price and horsepower. Basi- cally, this axis separates mini-vans, trucks and SUVs (big, not so expensive, not so much horse-power) from sports-cars (small, expensive, lots of horse-power). To check this interpretation, we can use a useful tool called a biplot, which plots the data, along with the projections of the original features, on to the first two components (Figure 1). Notice that the car with the lowest value of the 7 

8 .second component is a Porsche 911, with pick-up trucks and mini-vans at the other end of the scale. Similarly, the highest values of the first component all belong to hybrids. 2.1 A Recipe There is a more-or-less standard recipe for interpreting PCA plots, which goes as follows. To begin with, find the first two principal components of your data. (I say “two” only because that’s what you can plot; see below.) It’s generally a good idea to standardized all the features first, but not strictly necessary. Coordinates Using the arrows, summarize what each component means. For the cars, the first component is something like size vs. fuel economy, and the second is something like sporty vs. boxy. Correlations For many datasets, the arrows cluster into groups of highly cor- related attributes. Describe these attributes. Also determine the overall level of correlation (given by the R2 value). Here we get groups of arrows like the two MPGs (unsurprising), retail and dealer price (ditto) and the physical dimensions of the car (maybe a bit more interesting). Clusters Clusters indicate a preference for particular combinations of attribute values. Summarize each cluster by its prototypical member. For the cars data, we see a cluster of very similar values for sports-cars, for instance, slightly below the main blob of data. Funnels Funnels are wide at one end and narrow at the other. They happen when one dimension affects the variance of another, orthogonal dimension. Thus, even though the components are uncorrelated (because they are perpendicular) they still affect each other. (They are uncorrelated but not independent.) The cars data has a funnel, showing that small cars are similar in sportiness, while large cars are more varied. Voids Voids are areas inside the range of the data which are unusually unpop- ulated. A permutation plot is a good way to spot voids. (Randomly permute the data in each column, and see if any new areas become occu- pied.) For the cars data, there is a void of sporty cars which are very small or very large. This suggests that such cars are undesirable or difficult to make. Projections on to the first two or three principal components can be visu- alized; however they may not be enough to really give a good summary of the data. Usually, to get an R2 of 1, you need to use all p principal components.7 7 The exceptions are when some of your features are linear combinations of the others, so that you don’t really have p different features, or when n < p. 8 

9 . -30 -20 -10 0 10 Wheelbase Length 0.1 10 GMCChevrolet Yukon XLSuburban 2500 1500 SLTEnvoy Isuzu Nissan LT Ascender S Quest S GMC XUVTown Chrysler SLE andSE Country LX Width Mercury Ford Ford Grand Crown Freestar Marquis Victoria GSCE Ford Expedition Nissan PathfinderFord Dodge Nissan Crown Armada 4.6SE Grand Quest Toyota XLT Victoria Caravan SE Sienna LX SXT Mercury Monterey Dodge Caravan SE Mercury Mercury Ford Grand Marquis Honda GrandHonda Crown Marquis Toyota Victoria LSLuxury LS Odyssey Kia Odyssey Sedona Sienna Premium LXLX Ultimate XLE Toyota Lincoln TownSequoia Dodge ChryslerCar SR5 Ultimate Chrysler Durango Town and LLX Pacifica SLT Country Sport EX Dodge Limited Intrepid Lincoln Town Pontiac Car Montana Signature Chrysler Oldsmobile EWB SE Concorde LX Lincoln Town1500 Mercury Chevrolet GMC Car Ultimate MarauderDodge AstroSLE ES GL Silhouette SafariIntrepid GMC Yukon Chrysler SLE Mercury Pontiac Concorde Chevrolet Sable Ford Grand LXi Impala GS Taurus Prix four-door LX LS GT1 Lincoln Navigator Hummer H2 Luxury Buick Chevrolet Buick Pontiac Park LeSabre Avenue Mercury Ford Monte Custom Grand Sable TaurusPrix Carlo SEGS four-door GT2 Weight Chevrolet Impala LS Chevrolet Tahoe LT Chevrolet Mercury Ford Buick BuickMonte Taurus Century Sable RendezvousToyota LSCarlo Dodge SES Dodge Kia SS Custom Camry Optima Premium Stratus Chrysler Duratec CX Stratus Solara LX SE SXT Sebring Buick Ford Volkswagen Buick Park Explorer Chevrolet Mercury Chevrolet LeSabre Buick Avenue Pontiac Chrysler Touareg TrailBlazer Mitsubishi Honda XLT Montero Pilot 300M MountaineerV6 Limited Regal Ultra V6 Impala Suzuki LT Pontiac LX Nissan MontanaSSLS Altima Verona Toyota Aztekt LXSSE LE Camry Chrysler Toyota Lincoln 300M Kia 4Runner LS Hyundai Chevrolet V6 Kia Special Hyundai Sorento Chevrolet Hyundai SR5 Luxury XG350 Venture XG350 Chevrolet Oldsmobile LLS Saturn Optima Edition LX Sonata Malibu V6 LX VUE V6 GLS Maxx Malibu Alero GX Cadillac Escaladet Buick Toyota Mitsubishi Rainier Mazda Buick Camry Hyundai Endeavor ChryslerMPV Regal Solara GSESSonata SebringHonda SE LXV6L300 Accord Touring Saturn LX LincolnNissan LS Nissan Infiniti Murano Suzuki V6Maxima Toyota Mitsubishi FX35 XL-7 Premium Honda SE Avalon Galant EX Chevrolet XL Accord Mazda6 i EXIon1 Saturn Cavalier two-door CadillacToyota Camry Deville Nissan BMW Honda Jeep Solara Accord Saturn Chevrolet Maxima Nissan 525i Ford Altima Liberty SLE Camry SL four-door LX SE Mustang V6 LE V6 Saturn L300-2 Sport two-door V6 Chevrolet Chevrolet Malibu Saturn LS Ion2 Ion3 quad coupe Cavalier Cavalier quad LS four-door coupe Lincoln Aviator Ultimate Volvo Acura Cadillac Acura XC90 3.5Pontiac Oldsmobile Toyota Toyota MDX T6 RL CTS Hyundai VVTGrand Camry Avalon Chevrolet Subaru Santa Pontiac Alero XLE XLS Am Fe Malibu GLS V6GT Legacy Suzuki GLS Sunfire Saturn Saturn LT 1SA Ion2 LSpectra Forenza Ion3 Shatch Acura Infiniti FX45 Toyota 3.5 RL Mitsubishi Volkswagen Highlander Navigation Isuzu Volvo Volvo Subaru Diamante Mazda Rodeo V6 Volkswagen S80 Honda XC702.5TS Passat LSOutback Hyundai Pontiac Tribute CR-V Hyundai Kia Hyundai GLS Kia DX Passat four-door Elantra Sunfire2.0 GLS Spectra LX Elantra Dodge 1SC GS GT Elantra Neon GLS GT SE Toyota Prius Jeep Lincoln LSGrand V8 Sport Cherokee Mitsubishi Chrysler Laredo Kia Suzuki Sebring Spectra Outlander Forenza Dodge Honda Honda GSX Neon convertible Civic EX Civic SXT DX LX 0.0 Engine Cadillac Deville Cadillac DTS Jaguar Seville Nissan Chrysler Nissan S-Type Volvo Lexus S80 Pathfinder Subaru Sebring Xterra Subaru 3.0 ES 2.9 XE 330Audi SE Outback Limited Legacy Limited Toyota GT Toyota Toyota Pontiac Toyota Nissan convertibleSedanHonda Honda Matrix Civic Corolla Corolla Vibe Corolla Sentra 1.8 SHXHybrid HighwayMPG Civic CE LE LincolnGX Lexus LS Infiniti BMW V8 470 Audi BMW G35 530i Audi Ultimate A6 Sport Jaguar 3.0 X3 Coupe Honda four-door A6 Infiniti Infiniti Honda G353.0 I35 Accord X-Type Quattro 3.0i EX 2.5 Ford Element V6 A4 Focus LX Honda Nissan Ford 1.8T ZTW Civic Sentra Focus EX 1.8 LX S CityMPG 0 Cadillac Audi SRX V8A6 Lexus 3.0 Infiniti Avant G35 RXVolvo 330 Quattro AWD Saab S60 9-52.5 Acura Mercedes-Benz Arc TSX Ford Volkswagen C230 Focus Jetta ZX3 GL Jetta GLS SportZX5 VolkswagenLexus Acura GS TLV6 Chrysler 300 Ford Ford Focus Focus Toyota Land Lexus LX Cruiser 470 Audi A6 2.7 Passat Land Turbo Jaguar GLX Rover Ford Subaru Audi Quattro X-Type Hyundai BMW Saab A4 BMW 4MOTION Nissan Freelander Escape Subaru Outback 1.8T 3.0 XLS H6 325i four-door Tiburon 325xi 9-3 Arc Suzuki SE Impreza Volkswagen PTfour-door Sentra convertible GT Suzuki Sport Cruiser V6 SE-R Aeno 2.5 AerioRS SSE Aveo LX Chevrolet BMW Land Audi745Li A8 Jaguar Rover L four-door Jaguar Quattro Ford XJ8 Discovery Subaru Mercedes-Benz Mercedes-Benz Mercedes-Benz S-Type Mustang SaabSE 4.2 Volvo Outback E320 BMW9-5 Mercedes-Benz Saab C70 BMW C320 S60 325xi Aero 9-5 E320 Mercedes-Benz GT Premium LPT 325Ci H-6 Sport four-door ChryslerT5 Subaru Aero VDC SportPT four-door C240C240 two-door Cruiser Forester Volkswagen RWD Limited Golf Hyundai Accent Lexus Infiniti Q45 Ford LS 430 LuxuryVolvo Thunderbird S80 T6 Mercedes-Benz Deluxe Audi MitsubishiSaab A4 9-3Volvo Ford C240 3.0 Aero Volvo Eclipse AWD SuzukiGTSV40 Focus S40 Kia Hyundai SVT Aerio Kia Rio SX Rio manual Accent auto Cinco GT GL Cylinders Mercedes-Benz Porsche Cayenne Mercedes-Benz S Infiniti S430 Audi ML500Audi M45 A4 3.0 A4 IS3.0 Mitsubishi BMW Quattro 325Ci Mitsubishi Volvo Quattro C70 Eclipsemanual Toyota auto Toyota Honda Volkswagen Spyder convertible Lancer HPT EvolutionRAV4 GTCelica Civic Si convertible GTI Land Rover BMW Range 745i Rover BMW Jaguar four-door X5 Mercedes-Benz HSE 4.4i Vanden Plas Lexus LexusLexus Volvo Nissan IS 300 S60 BMW IS C320 300 300 Subaru R 350Z manual SportCross Volkswagen auto Sport 330i New Acura Beetle RSX four-door Impreza WRX GLS Scion xB BMW 545iA AudiVolkswagen A6 Volkswagen Lexus four-door 4.2 Quattro Audi GS BMW BMW Mercedes-Benz Passat 430 A4 SaabW8 3.0 Saab Volkswagen 4MOTION Chrysler 9-3 Aero 9-3 Volkswagen 330xi 330Ci SuzukiC320 convertible Arc Jetta PTVitara Cruiser convertible GLI New Beetle Chevrolet GT Toyota LX Toyota GLS Aveo Echo 1.8T LS two-door manual Audi A4 3.0 Quattro Mercedes-Benz Passat W8 convertible CLK320 Toyota EchoEcho four-door two-door auto Nissan BMW 330Ci Chevrolet Tracker 350Z Enthusiast convertible Scion xA Honda Insight Mercedes-Benz Mercedes-Benz E500E500 Chevrolet four-door CorvetteSubaru Impreza WRX STi Mini Cooper Mercedes-Benz S500 Audi TT 1.8 JaguarXJR Jaguar S-Type R BMW Z4 convertible 2.5i two-door Chevrolet Corvette BMW convertible M3 Audi TT 1.8 Quattro Toyota Mini MR2 Spyder Cooper S Mercedes-Benz Audi Audi S4 Quattro S4 Avant QuattroCLK500 Mercedes-Benz G500 BMW M3BMW Chrysler Jeep Audi convertible Wrangler TT Crossfire Honda 3.2SaharaS2000 Mazda MX-5 Miata Mercedes-Benz Z4 C32 convertible Porsche AMG Boxster 3.0i two-door Mazda MX-5 Miata LS Horsepower Lexus SC 430 Mercedes-Benz SLK230 PC2 Jaguar XK8 coupe -0.1 Mercedes-Benz Audi RS 6 CL500 -10 Jaguar XK8 convertible Porsche Boxster S Cadillac XLR Jaguar XKR coupe Retail Dealer Jaguar XKR convertible Mercedes-Benz SL500 Mercedes-Benz SLK32 AMG Porsche Acura 911 Targa Porsche 911NSX Porsche 911SCarrera Carrera 4S Mercedes-Benz CL600 -0.2 -20 Mercedes-Benz SL55 AMG Mercedes-Benz SL600 -0.3 Porsche 911 GT2 -30 -0.3 -0.2 -0.1 0.0 0.1 PC1 biplot(cars04.pca,cex=0.4) Figure 1: “Biplot” of the 2004 cars data. The horizontal axis shows projections on to the first principal component, the vertical axis the second component. Car names are written at their projections on to the components (using the coordinate scales on the top and the right). Red arrows show the projections of the original features on to the principal components (using the coordinate scales on the bottom and on the left). 9 

10 .How many principal components you should use depends on your data, and how big an R2 you need. In some fields, you can get better than 80% of the variance described with just two or three components. A sometimes-useful device is to plot 1 − R2 versus the number of components, and keep extending the curve it until it flattens out. 3 PCA Cautions Trying to guess at what the components might mean is a good idea, but like many god ideas it’s easy to go overboard. Specifically, once you attach an idea in your mind to a component, and especially once you attach a name to it, it’s very easy to forget that those are names and ideas you made up; to reify them, as you might reify clusters. Sometimes the components actually do measure real variables, but sometimes they just reflect patterns of covariance which have many different causes. If I did a PCA of the same features but for, say, 2007 cars, I might well get a similar first component, but the second component would probably be rather different, since SUVs are now common but don’t really fit along the sports car/mini-van axis. A more important example comes from population genetics. Starting in the late 1960s, L. L. Cavalli-Sforza and collaborators began a huge project of map- ping human genetic variation — of determining the frequencies of different genes in different populations throughout the world. (Cavalli-Sforza et al. (1994) is the main summary; Cavalli-Sforza has also written several excellent popular- izations.) For each point in space, there are a very large number of features, which are the frequencies of the various genes among the people living there. Plotted over space, this gives a map of that gene’s frequency. What they noticed (unsurprisingly) is that many genes had similar, but not identical, maps. This led them to use PCA, reducing the huge number of features (genes) to a few components. Results look like Figure 2. They interpreted these components, very reasonably, as signs of large population movements. The first principal component for Europe and the Near East, for example, was supposed to show the expansion of agriculture out of the Fertile Crescent. The third, centered in steppes just north of the Caucasus, was supposed to reflect the expansion of Indo-European speakers towards the end of the Bronze Age. Similar stories were told of other components elsewhere. Unfortunately, as Novembre and Stephens (2008) showed, spatial patterns like this are what one should expect to get when doing PCA of any kind of spatial data with local correlations, because that essentially amounts to taking a Fourier transform, and picking out the low-frequency components.8 They simulated genetic diffusion processes, without any migration or population expansion, and 8 Remember that PCA re-writes the original vectors as a weighted sum of new, orthogonal vectors, just as Fourier transforms do. When there is a lot of spatial correlation, values at nearby points are similar, so the low-frequency modes will have a lot of amplitude, i.e., carry a lot of the variance. So first principal components will tend to be similar to the low-frequency Fourier modes. 10 

11 .got results that looked very like the real maps (Figure 3). This doesn’t mean that the stories of the maps must be wrong, but it does undercut the principal components as evidence for those stories. References Boas, Mary L. (1983). Mathematical Methods in the Physical Sciences. New York: Wiley, 2nd edn. Cavalli-Sforza, L. L., P. Menozzi and A. Piazza (1994). The History and Geog- raphy of Human Genes. Princeton: Princeton University Press. Klein, Dan (2001). “Lagrange Multipliers without Permanent Scar- ring.” Online tutorial. URL http://dbpubs.stanford.edu:8091/~klein/ lagrange-multipliers.pdf. Novembre, John and Matthew Stephens (2008). “Interpreting principal compo- nent analyses of spatial population genetic variation.” Nature Genetics, 40: 646–649. doi:10.1038/ng.139. 11 

12 .Figure 2: Principal components of genetic variation in the old world, according to Cavalli-Sforza et al. (1994), as re-drawn by Novembre and Stephens (2008). 12 

13 .Figure 3: How the PCA patterns can arise as numerical artifacts (far left col- umn) or through simple genetic diffusion (next column). From Novembre and Stephens (2008). 13