Integrating Compression and Execution

1 . Integrating Compression and Execution in Column-Oriented Database Systems Daniel J. Abadi Samuel R. Madden Miguel C. Ferreira MIT MIT MIT dna@csail.mit.edu madden@csail.mit.edu mferreira@alum.mit.edu ABSTRACT commercial arena [21, 1, 19], we believe the time is right to Column-oriented database system architectures invite a re- systematically revisit the topic of compression in the context evaluation of how and when data in databases is compressed. of these systems, particularly given that one of the oft-cited Storing data in a column-oriented fashion greatly increases advantages of column-stores is their compressibility. the similarity of adjacent records on disk and thus opportuni- Storing data in columns presents a number of opportuni- ties for compression. The ability to compress many adjacent ties for improved performance from compression algorithms tuples at once lowers the per-tuple cost of compression, both when compared to row-oriented architectures. In a column- in terms of CPU and space overheads. oriented database, compression schemes that encode multi- In this paper, we discuss how we extended C-Store (a ple values at once are natural. In a row-oriented database, column-oriented DBMS) with a compression sub-system. We such schemes do not work as well because an attribute is show how compression schemes not traditionally used in row- stored as a part of an entire tuple, so combining the same oriented DBMSs can be applied to column-oriented systems. attribute from different tuples together into one value would We then evaluate a set of compression schemes and show that require some way to “mix” tuples. the best scheme depends not only on the properties of the Compression techniques for row-stores often employ dic- data but also on the nature of the query workload. tionary schemes where a dictionary is used to code wide val- ues in the attribute domain into smaller codes. For example, a simple dictionary for a string-typed column of colors might 1. INTRODUCTION map “blue” to 0, “yellow” to 1, “green” to 2, and so on [13, Compression in traditional database systems is known to 26, 11, 37]. Sometimes these schemes employ prefix-coding improve performance significantly [13, 16, 25, 14, 17, 37]: it based on symbol frequencies (e.g., Huffman encoding [15]) reduces the size of the data and improves I/O performance or express values as small differences from some frame of ref- by reducing seek times (the data are stored nearer to each erence and remove leading nulls from them (e.g., [29, 14, 26, other), reducing transfer times (there is less data to trans- 37]). In addition to these traditional techniques, column- fer), and increasing buffer hit rate (a larger fraction of the stores are also well-suited to compression schemes that com- DBMS fits in buffer pool). For queries that are I/O limited, press values from more than one row at a time. This al- the CPU overhead of decompression is often compensated lows for a larger variety of viable compression algorithms. for by the I/O improvements. For example, run-length encoding (RLE), where repeats of In this paper, we revisit this literature on compression the same element are expressed as (value, run-length) pairs, in the context of column-oriented database systems [28, 9, is an attractive approach for compressing sorted data in a 10, 18, 21, 1, 19]. A column-oriented database system (or column-store. Similarly, improvements to traditional com- “column-store”) is one in which each attribute is stored in pression algorithms that allow basic symbols to span more a separate column, such that successive values of that at- than one column entry are also possible in a column-store. tribute are stored consecutively on disk. This is in contrast Compression ratios are also generally higher in column- to most common database systems (e.g. Oracle, IBM DB2, stores because consecutive entries in a column are often quite Microsoft SQL Server) that store relations in rows (“row- similar to each other, whereas adjacent attributes in a tu- stores”) where values of different attributes from the same ple are not [21]. Further, the CPU overhead of iterating tuple are stored consecutively. Since there has been signif- through a page of column values tends to be less than that icant recent interest in column-oriented databases in both of iterating through a page of tuples (especially when all the research community [28, 9, 10, 18, 24, 34] and in the values in a column are the same size), allowing for increased decompression speed by using vectorized code that takes ad- vantage of the super-scalar properties of modern CPUs [10, 37]. Finally, column-stores can store different columns in Permission to make digital or hard copies of all or part of this work for different sort-orders [28], further increasing the potential for personal or classroom use is granted without fee provided that copies are compression, since sorted data is usually quite compressible. not made or distributed for profit or commercial advantage and that copies Column-oriented compression schemes also improve CPU bear this notice and the full citation on the first page. To copy otherwise, to performance by allowing database operators to operate di- republish, to post on servers or to redistribute to lists, requires prior specific rectly on compressed data. This is particularly true for com- permission and/or a fee. pression schemes like run length encoding that refer to mul- SIGMOD 2006, June 27–29, 2006, Chicago, Illinois, USA. Copyright 2006 ACM 1-59593-256-9/06/0006 ...$5.00. tiple entries with the same value in a single record. For ex- 

2 .ample, if a run-length encoded column says the value “42” compression but that have low CPU overhead so that per- appears 1000 times consecutively in a particular column for formance is improved when taking into consideration all rel- which we are computing a SUM aggregate, the operator can evant costs. simply take the product of the value and run-length as the One way that the CPU overhead of compression has been SUM, without having to decompress. reduced over the years is by integrating knowledge about In this paper we study a number of alternative compres- compression into the query executor and allowing some amount sion schemes that are especially well-suited to column stores, of operation directly on compressed data. In early databases, and show how these schemes can easily be integrated into C- data would be compressed on disk and then eagerly decom- Store, an open-source column-oriented database [3, 28]. pressed upon being read into memory. This had the dis- In summary, in this paper we demonstrate several fun- advantage that everything read into memory had to be de- damental results related to compression in column-oriented compressed whether or not it was actually used. Graefe and database systems: Shapiro [13] (and later Goldstein et. al. [14], and Westmann et. al [29], and in the context of column-oriented DBMSs, • We overview commonly used DBMS compression algo- MonetDB/X100 [37]) cite the virtues of lazy decompression, rithms and show how they can be applied in column- where data is compressed on the attribute level and held store systems. We compare this traditional set of algo- compressed in memory, and data is decompressed only if rithms with compression algorithms especially suited needed to be operated on. This has the advantage that some for column-store systems. operations such as a hybrid hash join see improved perfor- mance by being able to keep a higher percentage of the ta- • Through experiments, we explore the trade-offs be- ble in memory, reducing the number of spills to disk. Chen tween these algorithms, varying the characteristics of et. al. [11] note that some operators can decompress tran- the data set and the query workload. We use results siently, decompressing to perform operations such as apply- from these experiments to create a decision tree to aid ing a predicate, but keeping a copy of the compressed data the database designer to decide how to compress a par- and returning the compressed data if the predicate succeeds. ticular column. The idea of decreasing CPU costs by operating directly on compressed data was introduced by Graefe and Shapiro • We introduce an architecture for a query executor that [13]. They pointed out that exact-match comparisons and allows for direct operation on compressed data while natural joins can be performed directly on compressed data minimizing the complexity of adding new compression if the constant portion of the predicate is compressed in the algorithms. We experimentally show the benefits of same way as the data. Also exact-match index lookups are operating directly on compressed data. possible on compressed data if an order-preserving (consis- • We illustrate the importance of introducing as much tent) compression scheme is used. Further, projection and order as possible into columns and demonstrate the duplicate elimination can be performed on compressed data. value of having secondary and tertiary sort orders. However, this is the extent of research on direct operation on compressed data. In particular, to the best of our knowledge, As a caveat, we note that the purpose of this paper is not there has been no attempt to take advantage of some com- to propose fundamental new compression schemes. Many of pression algorithms’ ability to represent multiple values in the approaches we employ have been investigated in isolation a single field to simultaneously apply an operation on these in the context of row-oriented databases, and all are known many values at once. In essence, previous work has viewed in the data compression literature (we only propose slight each tuple as compressed or uncompressed, and when oper- variations to these schemes). Our purpose is to explore the ations cannot simply compare compressed values, they must performance and architectural implications of integrating a be performed on decompressed tuples. Our work shows that wide range of compression schemes into a column-oriented column-oriented compression schemes provide further oppor- database. Our focus in this paper is in using compression to tunity for direct operation on compressed data. maximize query performance, not to minimize storage sizes. Our work also introduces a novel architecture for passing compressed data between operators that minimizes operator code complexity while maximizing opportunities for direct 2. RELATED WORK operation on compressed data. Previous work [14, 29, 11] While research in database compression has been around also stresses the importance of insulating the higher levels nearly as long as there has been research in databases [20, of the DBMS code from the details of the compression tech- 27, 12], compression methods were not commonly used in nique. In general, this is accomplished by decompressing DBMSs until the 1990s. This is perhaps because much of the the data before it reaches the operators (unless dictionary early work concentrated on reducing the size of the stored compression is used and the data can be processed directly). data, and it was not until the 90s when researchers began However, in some cases increased performance can be ob- to concentrate on how compression affects database perfor- tained in query processing if operators can operate directly mance [13, 16, 25, 14, 17]. This research observed that while on compressed data (beyond simple dictionary schemes) and compression does reduce I/O, if the CPU cost of compress- our work is the first to propose a solution to profit from these ing/decompressing the data outweighs this savings, then the potential optimizations while keeping the higher levels of the overall performance of the database is reduced. As improve- DBMS as insulated as possible. ments in CPU speed continue to outpace improvements in In summary, in this paper we revisit much of this re- memory and disk access [8], this trade-off becomes more fa- lated work on compression in the context of column-oriented vorable for compression. In order to keep CPU costs down, database systems and we differ from other work on com- most papers focus on light-weight techniques (in the sense pression in column-oriented DBMSs (Zukowski et. al [37] on that they are not CPU-intensive) that result in sub-optimal 

3 .MonetDB/X100) in that we focus on column-oriented com- • Projection is free since it requires no changes to the pression algorithms and direct operation on compressed data data, and two projections in the same order can be (whereas [37] focuses on improving CPU/cache performance concatenated for free as well. of standard row-based light-weight techniques). • Joins produce positions rather than values. A complete discussion of this distinction is given in Section 5.2 3. C-STORE ARCHITECTURE For this study on compression in column-oriented DBMSs, we chose to extend the C-Store system [28] since the C-Store 4. COMPRESSION SCHEMES architecture is designed to maximize the ability to achieve In this section we briefly describe the compression schemes good compression ratios. We now present a brief overview that we implemented and experimented with in our column- of the salient parts of the C-Store architecture. oriented DBMS. For each scheme, we first give a brief de- C-Store provides a relational interface on top of a column- scription of the traditional version of the scheme as previ- store. Logically, users interact with tables in SQL. Each ta- ously used in row store systems (due to lack of space we do ble is physically represented as a collection of projections. not give complete descriptions, but cite papers that provide Each projection consists of a set of columns, each stored more detail when possible). We then describe how the algo- column-wise, along with a common sort order for those columns. rithm is used in the context of column-oriented databases. Every column of each table is represented in at least one pro- jection, and columns are allowed to be stored in multiple pro- 4.1 Null Suppression jections – this allows the query optimizer to choose from one There are many variations on the null compression tech- of several available sort orders for a given column. Columns nique (see [26, 29] for some examples), but the fundamen- within a projection can be secondarily or tertiarily sorted; tal idea is that consecutive zeros or blanks in the data are e.g. an example C-Store projection with four columns taken deleted and replaced with a description of how many there from TPC-H could be: were and where they existed. Generally, this technique per- forms well on data sets where zeros or blanks appear fre- (shipdate, quantity, retflag, suppkey | shipdate, quently. We chose to implement a column-oriented version quantity, retflag) of the scheme described in [29]. Specifically, we allow field sizes to be variable and encode the number of bytes needed indicating that the projection is sorted by shipdate, secon- to store each field in a field prefix. This allows us to omit darily sorted by quantity, and tertiarily sorted by return flag leading nulls needed to pad the data to a fixed size. For in the example above. These secondary levels of sorting in- example, for integer types, rather than using the full 4 bytes crease the locality of the data, improving the performance to store the integer, we encoded the exact number of bytes of most of the compression algorithms (for example, RLE needed using two bits (1, 2, 3, or 4 bytes) and placed these compression can now be used on quantity and return flag). two bits before the integer. To stay byte-aligned (see Sec- Projections in C-Store typically have few columns and mul- tion 4.2 for a discussion on why we do this), we combined tiple secondary sort orders, which allows most columns to these bits with the bits for three other integers (to make a compress quite well. Thus, with a given space budget, it is full byte’s worth of length information) and used a table to often possible to store the same column in multiple projec- decode this length quickly as in [29]. tions, each with a different sort order. Projections in C-Store are related to each other via join 4.2 Dictionary Encoding indices [28], which are simply permutations that map tuples Dictionary compression schemes are perhaps the most preva- in one projection to the corresponding tuples in another pro- lent compression schemes found in databases today. These jection from the same source relation. schemes replace frequent patterns with smaller codes for We extended C-Store such that each column is compressed them. One example of such a scheme is the color-mapping using one of the methods described in Section 4. As the re- given in the introduction. Other examples can be found in sults in Section 6 show, different types of data are best rep- [13, 26, 11, 37]. resented with different compressions schemes. For example, We implemented a column-optimized version of dictionary a column of sorted numerical data is likely best compressed encoding. All of the row-oriented dictionary schemes cited with RLE compression, whereas a column of unsorted data above have the limitation that they can only map attribute from a smaller domain is likely best compressed using our values from a single tuple to dictionary entries. This is be- dictionary compression method. An interesting direction for cause row-stores fundamentally are incapable of mixing at- future research could be to use these results to develop a tributes from more than one tuple in a single entry if other set of tools that automatically select the best partitions and attributes of the tuples are not also included in the same compression schemes for a given logical table. entry (by definition of “row-store” – this statement does not C-Store includes column-oriented versions of most of the hold for PAX-like [4] techniques that columnize blocks). familiar relational operators. The major differences between Our dictionary encoding algorithm first calculates the num- C-Store operators and relational operators are: ber of bits, X, needed to encode a single attribute of the • Selection operators produce bit-columns that can be column (which can be calculated directly from the number efficiently combined. A special “mask” operator is used of unique values of the attribute). It then calculates how to materialize a subset of values from a column and a many of these X-bit encoded values can fit in 1, 2, 3, or 4 bitmap. bytes. For example, if an attribute has 32 values, it can be encoded in 5 bits, so 1 of these values can fit in 1 byte, 3 • A special permute operator is used to reorder a column in 2 bytes, 4 in 3 bytes, or 6 in 4 bytes. We choose one of using a join index. these four options using the algorithm described in Section 

4 .4.2.1. Suppose that the 3-value/2-byte option was chosen. characters. But RLE can be much more widely used in In that case, a mapping is created between every possible column-oriented systems where attributes are stored consec- set of 3 5-bit values and the original 3 values. For example, utively and runs of the same value are common (especially if the value 1 is encoded by the 5 bits: 00000; the value 25 is in columns that have few distinct values). As described in encoded by the 5 bits: 00001; and the value 31 is encoded by Section 3, the C-Store architecture results in a high percent- the 5 bits 00010; then the dictionary would have the entry age of columns being sorted (or secondarily sorted) and thus (read entries right-to-left) provides many opportunities for RLE-type encoding. X000000000100010 -> 31 25 1 4.4 Bit-Vector Encoding where the X indicates an unused “wasted” bit. The decoding Bit-vector encoding is most useful when columns have a algorithm for this example is then straight-forward: read in limited number of possible data values (such as states in the 2-bytes and lookup entry in dictionary to get 3 values back US, or flag columns). In this type of encoding, a bit-string at once. Our decision to keep data byte-aligned might be is associated with each value with a ’1’ in the corresponding considered surprising in light of recent work that has shown position if that value appeared at that position and a ’0’ that bit-shifting in the processor is relatively cheap. However otherwise. For example, the following data: our experiments show that column stores are so I/O efficient that even a small amount of compression is enough to make 1132231 queries on that column become CPU-limited (Zukowski et. al observe a similar result [37]) so the I/O savings one obtains would be represented as three bit-strings: by not wasting the extra space are not important. Thus, we have found that it is worth byte-aligning dictionary entries bit-string for value 1: 1100001 to obtain even modest CPU savings. bit-string for value 2: 0001100 bit-string for value 3: 0010010 4.2.1 Cache-Conscious Optimization The decision as to whether values should be packed into Since an extended version of this scheme can be used to 1, 2, 3, or 4 bytes is decided by requiring the dictionary to index row-stores (so-called bit-map indices [23]), there has fit in the L2 cache. In the above example, we fit each entry been much work on further compressing these bit-maps and into 2 bytes and the number of dictionary entries is 323 = the implications of this further compression on query per- 32768. Therefore the size of the dictionary is 524288 bytes formance [22, 5, 17, 31, 30, 32, 6]; however, the most recent which is half of the L2 cache on our machine (1MB). Note work in this area [31, 32] indicates that one needs the bit- that for cache sizes on current architectures, the 1 or 2 byte maps to be fairly sparse (on the order of 1 bit in 1000) in options will be used exclusively. order for query performance to not be hindered by this fur- ther compression, and since we only use this scheme when 4.2.2 Parsing Into Single Values the column cardinality is low, our bit-maps are relatively Another convenient feature of this scheme is that it de- dense and we choose not to perform further compression. grades gracefully into a single-entry per attribute scheme which is useful for operating directly on compressed data. 4.5 Heavyweight Compression Schemes For example, instead of decoding a 16-bit entry in the above Lempel-Ziv Encoding. Lempel-Ziv ([35, 36]) compres- example into the 3 original values, one could instead apply 3 sion is the most widely used technique for lossless file com- masks (and corresponding bit-shifts) to get the three single pression. This is the algorithm upon which the UNIX com- attribute dictionary values. For example: mand gzip is based. Lempel-Ziv takes variable sized pat- terns and replaces them with fixed length codes. This is (X000000000100010 & 0000000000011111) >> 0 = 00010 in contrast to Huffman encoding which produces variable (X000000000100010 & 0000001111100000) >> 5 = 00001 sized codes. Lempel-Ziv encoding does not require knowl- (X000000000100010 & 0111110000000000) >> 10 = 00000 edge about pattern frequencies in advance; it builds the pat- tern table dynamically as it encodes the data. The basic idea These dictionary values in many cases can be operated on is to parse the input sequence into non-overlapping blocks directly (as described in Section 5) and lazily decompressed of different lengths while constructing a dictionary of blocks at the top of the query-plan tree. seen thus far. Subsequent appearances of these blocks are We chose not to use an order preserving dictionary encod- replaced by a pointer to an earlier occurrence of the same ing scheme such as ALM [7] or ZIL [33] since these schemes block. We refer the reader to [35, 36] for more details. typically have variable-length dictionary entries and we pre- For our experiments, we used a freely available version of fer the performance advantages of having fixed length dic- the Lempel-Ziv algorithm [2] that is optimized for decom- tionary entries. pression performance (we found it to be much faster than 4.3 Run-length Encoding UNIX gzip). We experimented with several other heavyweight compres- Run-length encoding compresses runs of the same value sion schemes, including Huffman and Arithmetic encoding, in a column to a compact singular representation. Thus, but found that their decompression costs were prohibitively it is well-suited for columns that are sorted or that have expensive for use inside of a database system. reasonable-sized runs of the same value. These runs are re- placed with triples: (value, start position, run length) where each element of the triple is given a fixed number of bits. 5. COMPRESSED QUERY EXECUTION When used in row-oriented systems, RLE is only used for In this section we describe how we integrate the compres- large string attributes that have many blanks or repeated sion schemes discussed above into the C-Store query execu- 

5 . Properties Iterator Access Block Information Selection predicates from the query can be pushed down isOneValue() getNext() getSize() into DataSources. For example, if an equality predicate is isValueSorted() asArray() getStartValue() pushed down into a DataSource operator sitting on top of isPosContig() getEndPosition() bit-vector encoded data, the operator performs a projection, returning only the bit-vector for the requested value. The Table 1: Compressed Block API selection thus becomes trivial. For an equality predicate on a dictionary encoded column, the DataSource converts the tor in a way that allows for direct operation on compressed predicate value to its dictionary entry and does a direct com- data while minimizing the complexity of adding new com- parison on dictionary data (without having to perform de- pression algorithms to the system. compression). In other cases, selection simply evaluates the predicate as data is read from disk (avoiding decompression whenever possible). 5.1 Query Executor Architecture We extended C-Store to handle a variety of column com- pression techniques by adding two classes to the source code 5.2 Compression-Aware Optimizations for each new compression technique. The first class encap- We will show in Section 6 that there are clear performance sulates an intermediate representation for compressed data advantages to operating directly on compressed data, but called a compression block. A compression block contains a these advantages come at a cost: query executor complex- buffer of the column data in compressed format and provides ity. Every time a new compression scheme is added to the an API that allows the buffer to be accessed in several ways. system, all operators that operate directly on this type of Table 1 lists the salient methods of the compression block data have to be supplemented to handle the new scheme. API. Without careful engineering, there would end up being n The methods listed in the properties column of Table 1 versions of each operator – one for each type of compression will be discussed in Section 5.2 and are a way for operators scheme that can be input to the operator. Operators that to facilitate operating directly on compressed data instead of take two inputs (like joins) would need n2 versions. This having to decompress and iterate through it. For the cases clearly causes the code to become very complex very quickly. where decompression cannot be avoided, there are two ways To illustrate this, we study a nested loops join opera- to iterate through block data. First is through repeated use tor. We note that joins in column-oriented DBMSs can of the getNext() method which will progress through the look different from joins in row-oriented DBMSs. In C- compressed buffer, transiently decompressing the next value Store, if columns have already been stitched together into and returning that value along with the position (a position row-store tuples, joins work identically as in row-store sys- is the ordinal offset of a value in a column) that the value tems. However, joins can alternatively receive as input only was located at in the original column. Second is through the the columns needed to evaluate the join predicate. The out- asArray() method which decompresses the entire buffer and put of the join is then set of pairs of positions in the input returns a pointer to an array of data in the uncompressed columns for which the predicate succeeded. For example, column type. the figure below shows the results of a join of a column of The block information methods (see Table 1) return data size 5 with a column of size 3. The positions that are output that can be extracted from the compressed block without de- can then be sent to other columns from the input relations compressing it. For example, for RLE, a block consists of a (since only the columns in the join predicate were sent to single RLE triple of the form (value, start pos, run length). the join) to extract the values at these positions. getSize() returns run length, getStartValue() returns value, 42 and getEndPosition() returns (start pos + run length − 1). 36 38 1 2 A more complex example is for bit-vector encoding: a block 42 ✶ 42 = 3 2 is a subset of the bit-vector associated with a single value. 44 46 5 1 Thus, we call a bit-vector block a non position-contiguous 38 block, since it contains a compressed representation of a An outline for the code for this operator is shown Figure set of (usually non-consecutive) positions for a single value. 1 (assume that the join predicate is an equality predicate on Here, getSize() returns the number of on bits in the bitstring, one attribute from each relation). getStartValue() returns the value with which the bit-string The pseudocode shows the join operator making some op- is associated, and getEndPosition() returns the position of timizations if the input columns are compressed. If one of the last on bit in the bitstring. the input columns is RLE and the other is uncompressed, The other class that we added to the source code for the resulting position columns of the join can be expressed each new compression technique is a DataSource operator. directly in RLE. This reduces the number of necessary op- A DataSource operator serves as the interface between the erations by a factor of k, where k is the run-length of the query plan and the storage manager and has compression RLE triple whose value matches a value from the uncom- specific knowledge about how pages for that compression pressed column. If one of the input columns is bit-vector technique are stored on disk and what indexes are available encoded, then the resulting column of positions for the un- on that column. It thus is able to serve as a scan oper- encoded column can be represented using RLE encoding and ator, reading in compressed pages from disk and convert- the resulting column of positions for the bit-vector column ing them into the compressed blocks described above. For can be copied from the appropriate bit-vector for the value some heavy-weight compression schemes (e.g., LZ), the cor- that matched the predicate. Again, this reduces the number responding DataSource operator may simply decompress the of necessary operations by a large factor. data as it is read from disk, presenting uncompressed blocks So while many optimizations are possible if operators are to parent operators. allowed to work directly on compressed data, the example 

6 .NLJoin(Predicate q, Column c1, Column c2) compression scheme is agnostic to the property and the value if c1 is not compressed and c2 is not compressed is determined by the data. for each value valc1 with position i in c1 do for each value valc2 with position j in c2 do Encoding Type Sorted? 1 value? Pos. contig.? if q(valc1,valc2) then output-left: (i), output-right: (j) end RLE yes yes yes end Bit-string yes yes no if c1 is not compressed and c2 is RLE compressed Null Supp. no/yes no yes for each value valc1 with position i in c1 do Lempel-Ziv no/yes no yes for each triple t with val v,startpos j and runlen k in c2 if q(valc1,v) then: Dictionary no/yes no yes output-left: t, Uncompressed no/yes no no/yes output-right: (j ... j+k-1) end When an operator cannot operate on compressed data (if, end if c1 is not compressed and c2 is bit-vector compressed for example, it cannot make any optimizations based on the for each value valc1 with position i in c1 do block properties), it repeatedly accesses the block through for each value valc2 with bitstring b in c2 do an iterator, as described in Section 5.1. If, however, the //assume that there are num ’1’s in b operator can operate on compressed data, it can use the if q(valc1,valc2) then output block information methods described in Section 5.1 to take output-left: new RLE triple (N U LL,i,num), output-right: b shortcuts in operation. For example, the pseudocode for a end Count aggregator is shown in Figure 2. Here, the passed end in column is used for grouping (e.g., in a query of the form etc. etc. for every possible combination of encoding types SELECT c1, COUNT(*) FROM t GROUP BY c1). (Note: this code is simplified from the actual aggregation code for ease Figure 1: Pseudocode for NLJoin of exposition). shows that the code becomes complex fairly quickly, since an if statement and an appropriate block of code is needed Count(Column c1) for each possible combination of compression types. b = get next compressed block from c1 while b is not null We alleviate this complexity by abstracting away the prop- if b.isOneValue() erties of compressed data that allow the operators to perform x = fetch current count for b.getStartVal() optimizations when processing. In the example above, the x = x + b.getSize() operator was able to optimize processing because the com- else a = b.asArray() pression schemes encoded multiple positions for the same for each element i in a value (e.g., RLE indicated multiple consecutive positions for x = fetch current count for i the same value and bit-vector encoding indicated multiple x=x+1 non-consecutive positions for the same value). This knowl- b = get next compressed block from c1 edge allowed the operator to directly output the join result for multiple tuples without having to actually perform the Figure 2: Pseudocode for Simple Count Aggregation execution more than once. The operator simply forwarded Note that despite RLE and bit-vector encoding being very on the positions for each copy of the joining values rather different compression techniques, the pseudocode in Figure 2 than dealing with each record independently. need not distinguish between them, pushing the complexity Hence, we enhanced each compression block with meth- of calculating the block size into the compressed block code. ods that make it possible for operators to determine the In both cases, the size of the block can be calculated without properties of each block of data. The properties we have block decompression. added thus far are shown in the Properties column of Table Figure 3 gives some more examples of how join and gener- 1. isOneValue() returns whether or not the block contains alized aggregation operators can take advantage of operating just one value (and many positions for that value). isValue- on compressed data given block properties. Sorted() returns whether or not the block’s values are sorted In summary, by using compressed blocks as an intermedi- (blocks with one value are trivially sorted). isPosContig() ate representation of data, operators can operate directly returns whether the block contains a consecutive subset of on compressed data whenever possible, and can degener- a column (i.e. for a given position range within a column, ate to a lazy decompression scheme when this is impossible the block contains all values located in that range). Proper- (by iterating through block values). Further, by abstracting ties are usually fixed for each compression scheme but could general properties about compression techniques and hav- in principle be set on a per-block basis by the DataSource ing operators check these properties rather than hardcoding operator. knowledge of a specific compression algorithm, operators are The table below gives the value of these properties for var- shielded from needing knowledge about the way data is en- ious encoding schemes. Note that there are many variations coded. They simply have to condition for these basic prop- of each scheme. For example, we experimented with three erties of the blocks of data they receive as input. We have versions of dictionary encoding before settling on the one found that this architecture significantly reduces the query described in this paper; in one version there was a single executor complexity while still allowing direct operation on dictionary entry per row value – i.e., a standard row-based compressed data whenever possible. dictionary scheme; another version was a pure column-based scheme that did not gracefully degenerate into single values as in the current scheme. In most cases, each variation of 6. EXPERIMENTAL RESULTS the same scheme will have the same block properties in the We ran experiments on our extended version of the C- table below. A no/yes entry in the table indicates that the Store system with two primary goals. First, we wanted to 

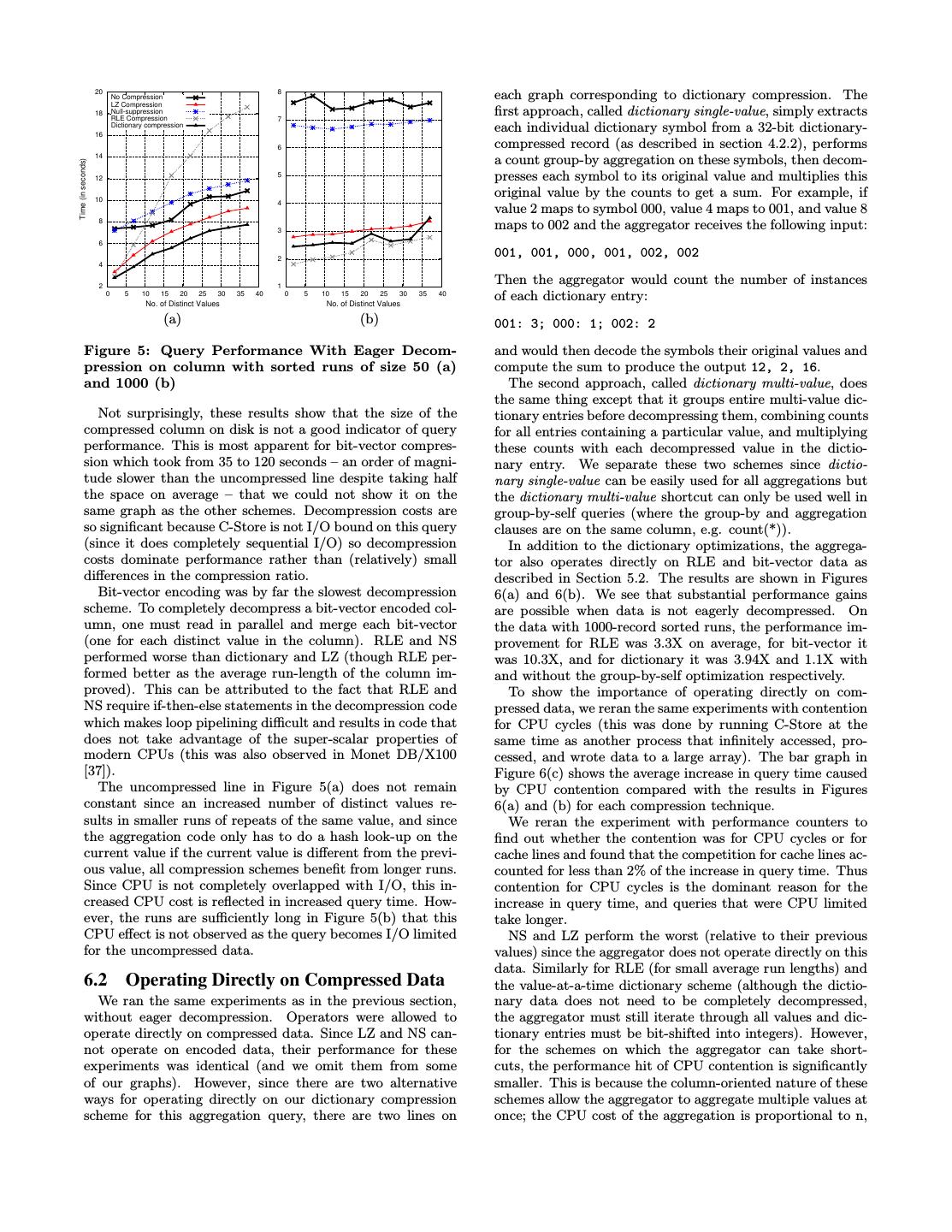
7 . Property Optimization tertiarily sorted and the first column in the projection has One value, Aggregation: If both the group-by and aggre- 500 unique values and the second column in the projection Contiguous gate input blocks are of this type, then the ag- Positions gregate input block can be aggregated with one has 1000 unique values then C will have average sorted runs operation (e.g. if size was 8 and aggregation was of size 100000000/(500*1000)=200. If C itself has 10 unique sum, result is 8*value) values, then within each of these sorted runs, each value Join: Perform optimization shown in the second would appear 20 times. Since bit-vector compression is only if statement in Figure 1 (works in general, not designed to be able to run on columns with few distinct just for RLE). values, in our first set of experiments, we allowed the number One value, Join: Perform optimization shown in the third if of distinct values in C to vary between 2 and 40 (so that Pos. Non- statement in Figure 1 (works in general, not just contiguous for bit-vector compression). we could directly compare all the introduced compression One value Aggregation Group-By clause: The position techniques). Also, in most data-warehousing environments, list of the value can be used to probe the data there are a large number of columns with few distinct values; source for the aggregate column so that only val- for example, in the TPC-H lineitem fact table, 25% of the ues relevant to the group by clause are read in columns have fewer than 50 distinct values. We experiment Sorted Max or Min Aggregation: Finding the max- with columns with a higher number of distinct values in imum or minimum value in a sorted block is a single operation Section 6.3. Join Finding a value within a block can be done We experimented with 4 sorted run lengths in C: 50, 100, via binary search. 500, and 1000. We compressed the data in each of the fol- lowing six ways: Null suppression, Lempel-Ziv, RLE, bit- Figure 3: Optimizations on Compressed Data vector, dictionary, and no compression. The sizes of the compressed columns are shown in Figures 4(a) and 4(b) for identify situations in which the encoding types described in different cardinalities of C (here, we use cardinality to mean Section 4 perform well. Second we wanted to demonstrate the number of distinct values). We omit the plots for the the benefits of operating directly on compressed data. 100 and 500 sorted runs cases as they follow the trends ob- Our benchmarking system is a 3.0 GHz Pentium IV, run- served in Figure 4. In these experiments, dictionary and LZ ning RedHat Linux, with 2 Gbytes of memory, 1MB L2 compression consistently get the highest compression ratios, cache, and 750 Gbytes of disk. The disk can read cold data at with RLE also performing well for low-cardinalities (this is 50-60MB/sec. We used a combination of synthetically gen- because RLE performs better with large runs of repeated erated and TPC-H data. For the experiments where we used values and the average run-length of a point on these graphs TPC-H data, we used columns from the lineitem fact table can be calculated directly by dividing the sorted run-length at scale 10 which consists of just under 60,000,000 lineitems. by the number of unique values). Interestingly, dictionary We begin by presenting results from a simple aggregation does a slightly better job compressing the data than the query on a single column of data encoded with each of the heavy-weight LZ scheme at low column cardinalities. The six encoding schemes described in Section 4. We used gen- compression ratio for bit-vector is linear in the number of erated data so that we could carefully vary the data charac- unique values in the column. Since we do not further com- teristics. We ran three variations of this experiment. In the press the bit-vectors, as soon as the column cardinality is first variation, we required the column to be decompressed more than 32, type-2 compression is no longer more com- as it was brought off disk. In the second variation, we lazily pressed than the original 32-bit data. decompressed the data and allowed operators to apply opti- The performance of the aggregation query on these same mizations to compressed data. In the third variation, queries compressed columns is shown in Figures 5(a) and 5(b) (again ran with competition for CPU cycles. In these experiments, we do not show the plots for sorted runs of 100 and 500 since we observe that the number of distinct values and sorted run we have limited space and they follow the trends between lengths are the primary determinant of query performance; these two graphs). we use these metrics to predict performance on TPC-H data. We also present results from more complicated queries 600 500 to further illustrate the benefits of different compression No Compression LZ Compression Null-suppression 450 schemes and the interaction of these schemes with each other 500 RLE Compression Dictionary compression in multi-column queries. Section 7 summarizes our results. Bit-vector compression 400 350 400 6.1 Eager Decompression Column size in MB 300 In this experiment, we ran a simple aggregation on a sin- 300 250 gle column of data encoded with each of the six encoding 200 schemes described in Section 4. We ran on generated data 200 150 and required that the column be decompressed as it was brought off disk. The query that we ran was simply: 100 100 50 SELECT SUM(C) 0 0 FROM TABLE 0 5 10 15 20 25 30 35 40 0 5 10 15 20 25 30 35 40 No. of Distinct Values No. of Distinct Values GROUP BY C (a) (b) The column that we are aggregating has 100 million 32-bit integer values. Since most columns in C-Store projections Figure 4: Compressed column sizes for varied com- have some kind of order (see section 3), we assume sorted pression schemes on column with sorted runs of size runs of size X (we vary X). For example, if column C is 50 (a) and 1000 (b) 

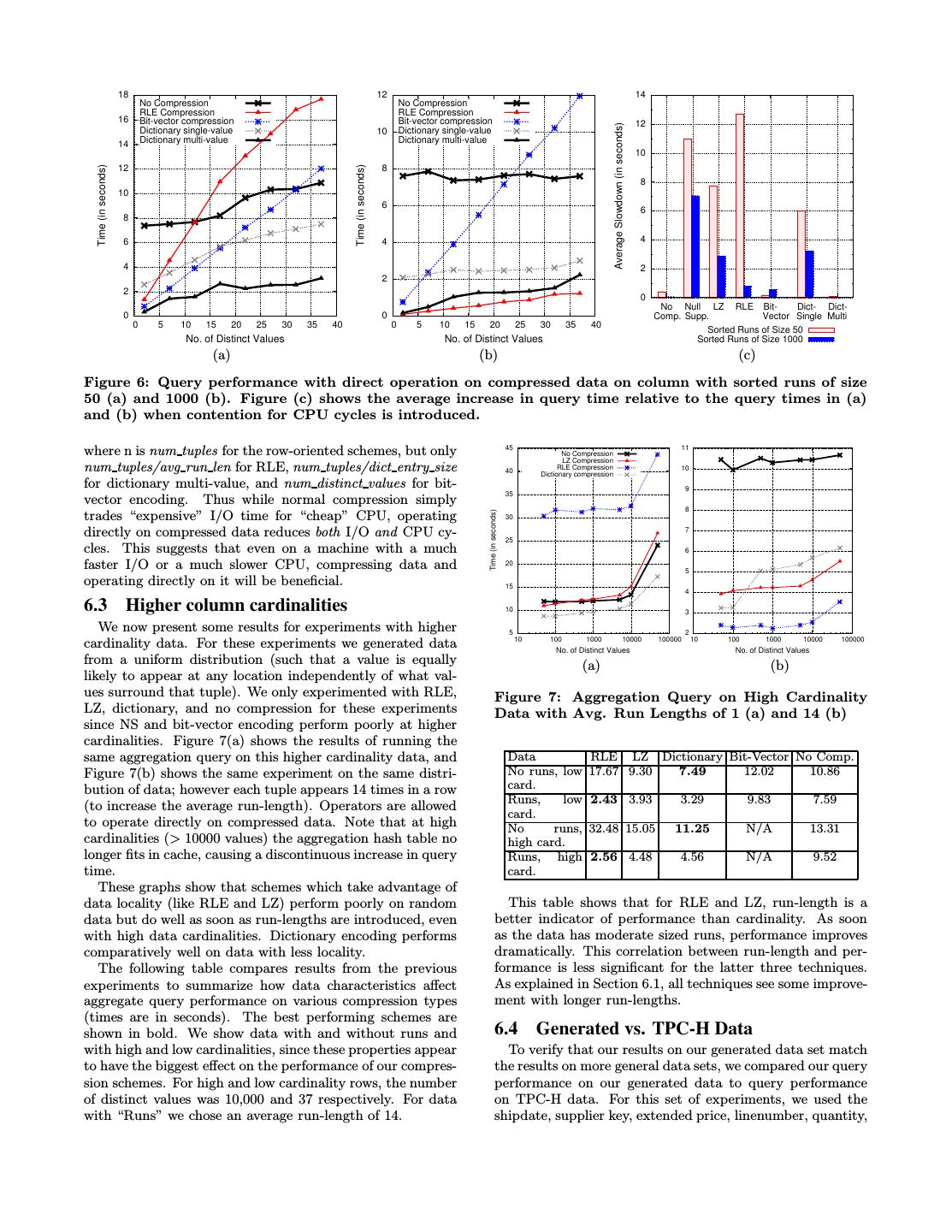
8 . 20 No Compression 8 each graph corresponding to dictionary compression. The LZ Compression 18 Null-suppression RLE Compression 7 first approach, called dictionary single-value, simply extracts 16 Dictionary compression each individual dictionary symbol from a 32-bit dictionary- 6 compressed record (as described in section 4.2.2), performs 14 a count group-by aggregation on these symbols, then decom- Time (in seconds) 12 5 presses each symbol to its original value and multiplies this 10 original value by the counts to get a sum. For example, if 4 value 2 maps to symbol 000, value 4 maps to 001, and value 8 8 3 maps to 002 and the aggregator receives the following input: 6 2 001, 001, 000, 001, 002, 002 4 2 1 Then the aggregator would count the number of instances 0 5 10 15 20 25 30 No. of Distinct Values 35 40 0 5 10 15 20 25 30 No. of Distinct Values 35 40 of each dictionary entry: (a) (b) 001: 3; 000: 1; 002: 2 Figure 5: Query Performance With Eager Decom- and would then decode the symbols their original values and pression on column with sorted runs of size 50 (a) compute the sum to produce the output 12, 2, 16. and 1000 (b) The second approach, called dictionary multi-value, does the same thing except that it groups entire multi-value dic- Not surprisingly, these results show that the size of the tionary entries before decompressing them, combining counts compressed column on disk is not a good indicator of query for all entries containing a particular value, and multiplying performance. This is most apparent for bit-vector compres- these counts with each decompressed value in the dictio- sion which took from 35 to 120 seconds – an order of magni- nary entry. We separate these two schemes since dictio- tude slower than the uncompressed line despite taking half nary single-value can be easily used for all aggregations but the space on average – that we could not show it on the the dictionary multi-value shortcut can only be used well in same graph as the other schemes. Decompression costs are group-by-self queries (where the group-by and aggregation so significant because C-Store is not I/O bound on this query clauses are on the same column, e.g. count(*)). (since it does completely sequential I/O) so decompression In addition to the dictionary optimizations, the aggrega- costs dominate performance rather than (relatively) small tor also operates directly on RLE and bit-vector data as differences in the compression ratio. described in Section 5.2. The results are shown in Figures Bit-vector encoding was by far the slowest decompression 6(a) and 6(b). We see that substantial performance gains scheme. To completely decompress a bit-vector encoded col- are possible when data is not eagerly decompressed. On umn, one must read in parallel and merge each bit-vector the data with 1000-record sorted runs, the performance im- (one for each distinct value in the column). RLE and NS provement for RLE was 3.3X on average, for bit-vector it performed worse than dictionary and LZ (though RLE per- was 10.3X, and for dictionary it was 3.94X and 1.1X with formed better as the average run-length of the column im- and without the group-by-self optimization respectively. proved). This can be attributed to the fact that RLE and To show the importance of operating directly on com- NS require if-then-else statements in the decompression code pressed data, we reran the same experiments with contention which makes loop pipelining difficult and results in code that for CPU cycles (this was done by running C-Store at the does not take advantage of the super-scalar properties of same time as another process that infinitely accessed, pro- modern CPUs (this was also observed in Monet DB/X100 cessed, and wrote data to a large array). The bar graph in [37]). Figure 6(c) shows the average increase in query time caused The uncompressed line in Figure 5(a) does not remain by CPU contention compared with the results in Figures constant since an increased number of distinct values re- 6(a) and (b) for each compression technique. sults in smaller runs of repeats of the same value, and since We reran the experiment with performance counters to the aggregation code only has to do a hash look-up on the find out whether the contention was for CPU cycles or for current value if the current value is different from the previ- cache lines and found that the competition for cache lines ac- ous value, all compression schemes benefit from longer runs. counted for less than 2% of the increase in query time. Thus Since CPU is not completely overlapped with I/O, this in- contention for CPU cycles is the dominant reason for the creased CPU cost is reflected in increased query time. How- increase in query time, and queries that were CPU limited ever, the runs are sufficiently long in Figure 5(b) that this take longer. CPU effect is not observed as the query becomes I/O limited NS and LZ perform the worst (relative to their previous for the uncompressed data. values) since the aggregator does not operate directly on this data. Similarly for RLE (for small average run lengths) and 6.2 Operating Directly on Compressed Data the value-at-a-time dictionary scheme (although the dictio- We ran the same experiments as in the previous section, nary data does not need to be completely decompressed, without eager decompression. Operators were allowed to the aggregator must still iterate through all values and dic- operate directly on compressed data. Since LZ and NS can- tionary entries must be bit-shifted into integers). However, not operate on encoded data, their performance for these for the schemes on which the aggregator can take short- experiments was identical (and we omit them from some cuts, the performance hit of CPU contention is significantly of our graphs). However, since there are two alternative smaller. This is because the column-oriented nature of these ways for operating directly on our dictionary compression schemes allow the aggregator to aggregate multiple values at scheme for this aggregation query, there are two lines on once; the CPU cost of the aggregation is proportional to n, 

9 . 18 12 14 No Compression No Compression RLE Compression RLE Compression 16 Bit-vector compression Bit-vector compression 12 Average Slowdown (in seconds) Dictionary single-value 10 Dictionary single-value 14 Dictionary multi-value Dictionary multi-value 10 Time (in seconds) Time (in seconds) 12 8 8 10 6 6 8 6 4 4 4 2 2 2 0 No Null LZ RLE Bit- Dict- Dict- 0 0 Comp. Supp. Vector Single Multi 0 5 10 15 20 25 30 35 40 0 5 10 15 20 25 30 35 40 Sorted Runs of Size 50 No. of Distinct Values No. of Distinct Values Sorted Runs of Size 1000 (a) (b) (c) Figure 6: Query performance with direct operation on compressed data on column with sorted runs of size 50 (a) and 1000 (b). Figure (c) shows the average increase in query time relative to the query times in (a) and (b) when contention for CPU cycles is introduced. where n is num tuples for the row-oriented schemes, but only 45 No Compression 11 LZ Compression num tuples/avg run len for RLE, num tuples/dict entry size 40 RLE Compression Dictionary compression 10 for dictionary multi-value, and num distinct values for bit- 9 35 vector encoding. Thus while normal compression simply 8 Time (in seconds) trades “expensive” I/O time for “cheap” CPU, operating 30 directly on compressed data reduces both I/O and CPU cy- 25 7 cles. This suggests that even on a machine with a much 6 faster I/O or a much slower CPU, compressing data and 20 5 operating directly on it will be beneficial. 15 4 6.3 Higher column cardinalities 10 3 We now present some results for experiments with higher 5 2 10 100 1000 10000 100000 10 100 1000 10000 100000 cardinality data. For these experiments we generated data No. of Distinct Values No. of Distinct Values from a uniform distribution (such that a value is equally (a) (b) likely to appear at any location independently of what val- ues surround that tuple). We only experimented with RLE, Figure 7: Aggregation Query on High Cardinality LZ, dictionary, and no compression for these experiments Data with Avg. Run Lengths of 1 (a) and 14 (b) since NS and bit-vector encoding perform poorly at higher cardinalities. Figure 7(a) shows the results of running the same aggregation query on this higher cardinality data, and Data RLE LZ Dictionary Bit-Vector No Comp. Figure 7(b) shows the same experiment on the same distri- No runs, low 17.67 9.30 7.49 12.02 10.86 bution of data; however each tuple appears 14 times in a row card. Runs, low 2.43 3.93 3.29 9.83 7.59 (to increase the average run-length). Operators are allowed card. to operate directly on compressed data. Note that at high No runs, 32.48 15.05 11.25 N/A 13.31 cardinalities (> 10000 values) the aggregation hash table no high card. longer fits in cache, causing a discontinuous increase in query Runs, high 2.56 4.48 4.56 N/A 9.52 time. card. These graphs show that schemes which take advantage of data locality (like RLE and LZ) perform poorly on random This table shows that for RLE and LZ, run-length is a data but do well as soon as run-lengths are introduced, even better indicator of performance than cardinality. As soon with high data cardinalities. Dictionary encoding performs as the data has moderate sized runs, performance improves comparatively well on data with less locality. dramatically. This correlation between run-length and per- The following table compares results from the previous formance is less significant for the latter three techniques. experiments to summarize how data characteristics affect As explained in Section 6.1, all techniques see some improve- aggregate query performance on various compression types ment with longer run-lengths. (times are in seconds). The best performing schemes are shown in bold. We show data with and without runs and 6.4 Generated vs. TPC-H Data with high and low cardinalities, since these properties appear To verify that our results on our generated data set match to have the biggest effect on the performance of our compres- the results on more general data sets, we compared our query sion schemes. For high and low cardinality rows, the number performance on our generated data to query performance of distinct values was 10,000 and 37 respectively. For data on TPC-H data. For this set of experiments, we used the with “Runs” we chose an average run-length of 14. shipdate, supplier key, extended price, linenumber, quantity, 

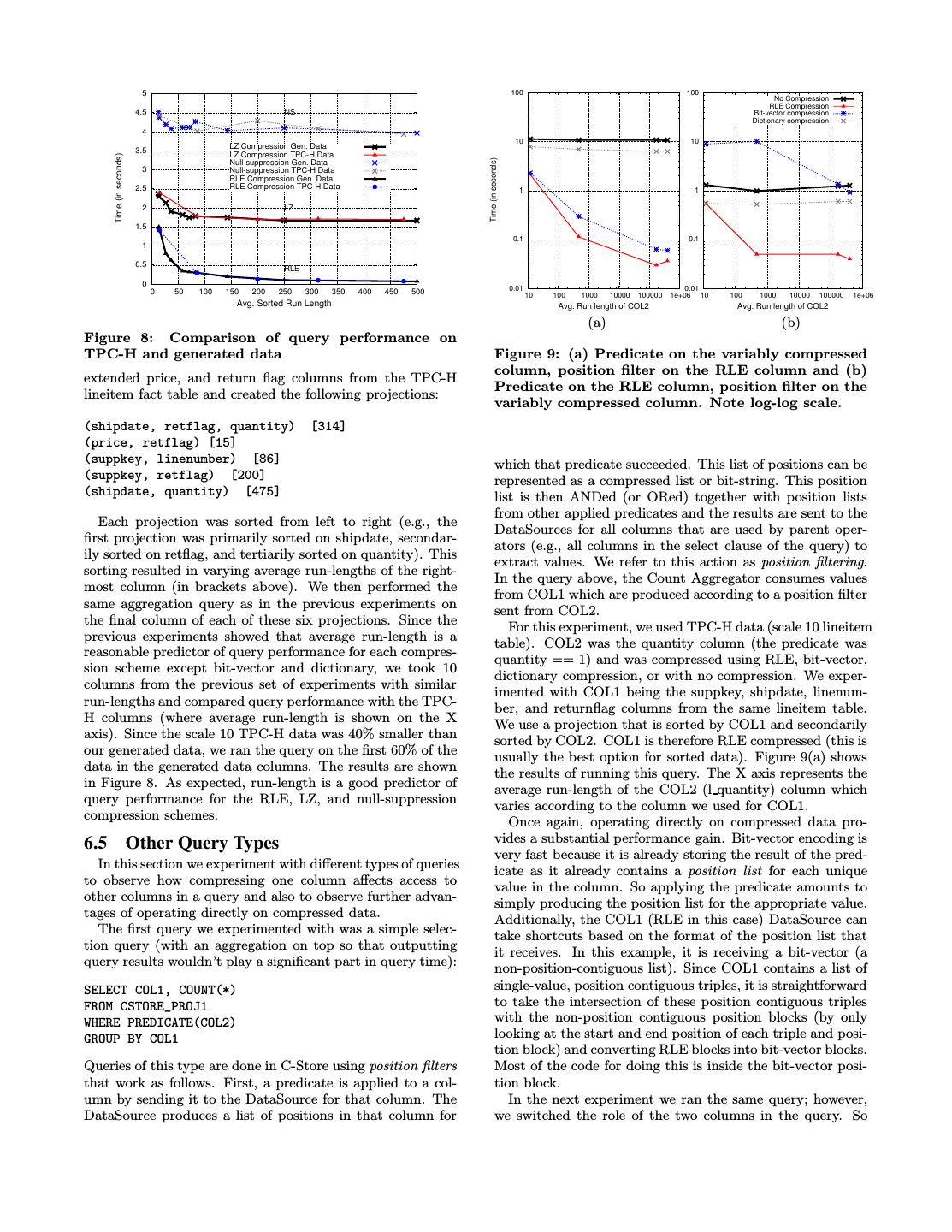
10 . 5 100 100 No Compression RLE Compression 4.5 NS Bit-vector compression Dictionary compression 4 10 10 3.5 LZ Compression Gen. Data LZ Compression TPC-H Data Time (in seconds) Time (in seconds) Null-suppression Gen. Data 3 Null-suppression TPC-H Data RLE Compression Gen. Data 2.5 RLE Compression TPC-H Data 1 1 2 LZ 1.5 0.1 0.1 1 0.5 RLE 0 0.01 0.01 0 50 100 150 200 250 300 350 400 450 500 10 100 1000 10000 100000 1e+06 10 100 1000 10000 100000 1e+06 Avg. Sorted Run Length Avg. Run length of COL2 Avg. Run length of COL2 (a) (b) Figure 8: Comparison of query performance on TPC-H and generated data Figure 9: (a) Predicate on the variably compressed column, position filter on the RLE column and (b) extended price, and return flag columns from the TPC-H Predicate on the RLE column, position filter on the lineitem fact table and created the following projections: variably compressed column. Note log-log scale. (shipdate, retflag, quantity) [314] (price, retflag) [15] (suppkey, linenumber) [86] which that predicate succeeded. This list of positions can be (suppkey, retflag) [200] represented as a compressed list or bit-string. This position (shipdate, quantity) [475] list is then ANDed (or ORed) together with position lists from other applied predicates and the results are sent to the Each projection was sorted from left to right (e.g., the DataSources for all columns that are used by parent oper- first projection was primarily sorted on shipdate, secondar- ators (e.g., all columns in the select clause of the query) to ily sorted on retflag, and tertiarily sorted on quantity). This extract values. We refer to this action as position filtering. sorting resulted in varying average run-lengths of the right- In the query above, the Count Aggregator consumes values most column (in brackets above). We then performed the from COL1 which are produced according to a position filter same aggregation query as in the previous experiments on sent from COL2. the final column of each of these six projections. Since the For this experiment, we used TPC-H data (scale 10 lineitem previous experiments showed that average run-length is a table). COL2 was the quantity column (the predicate was reasonable predictor of query performance for each compres- quantity == 1) and was compressed using RLE, bit-vector, sion scheme except bit-vector and dictionary, we took 10 dictionary compression, or with no compression. We exper- columns from the previous set of experiments with similar imented with COL1 being the suppkey, shipdate, linenum- run-lengths and compared query performance with the TPC- ber, and returnflag columns from the same lineitem table. H columns (where average run-length is shown on the X We use a projection that is sorted by COL1 and secondarily axis). Since the scale 10 TPC-H data was 40% smaller than sorted by COL2. COL1 is therefore RLE compressed (this is our generated data, we ran the query on the first 60% of the usually the best option for sorted data). Figure 9(a) shows data in the generated data columns. The results are shown the results of running this query. The X axis represents the in Figure 8. As expected, run-length is a good predictor of average run-length of the COL2 (l quantity) column which query performance for the RLE, LZ, and null-suppression varies according to the column we used for COL1. compression schemes. Once again, operating directly on compressed data pro- 6.5 Other Query Types vides a substantial performance gain. Bit-vector encoding is very fast because it is already storing the result of the pred- In this section we experiment with different types of queries icate as it already contains a position list for each unique to observe how compressing one column affects access to value in the column. So applying the predicate amounts to other columns in a query and also to observe further advan- simply producing the position list for the appropriate value. tages of operating directly on compressed data. Additionally, the COL1 (RLE in this case) DataSource can The first query we experimented with was a simple selec- take shortcuts based on the format of the position list that tion query (with an aggregation on top so that outputting it receives. In this example, it is receiving a bit-vector (a query results wouldn’t play a significant part in query time): non-position-contiguous list). Since COL1 contains a list of SELECT COL1, COUNT(*) single-value, position contiguous triples, it is straightforward FROM CSTORE_PROJ1 to take the intersection of these position contiguous triples WHERE PREDICATE(COL2) with the non-position contiguous position blocks (by only GROUP BY COL1 looking at the start and end position of each triple and posi- tion block) and converting RLE blocks into bit-vector blocks. Queries of this type are done in C-Store using position filters Most of the code for doing this is inside the bit-vector posi- that work as follows. First, a predicate is applied to a col- tion block. umn by sending it to the DataSource for that column. The In the next experiment we ran the same query; however, DataSource produces a list of positions in that column for we switched the role of the two columns in the query. So 

11 .now the predicate is on COL1 and we position filter COL2 (which is again encoded using the same four compression techniques as in the previous query). The results of this experiment are shown in Figure 9(b). Bit-vector performs much more poorly (note the log scale). This is because the query requires the values of the bit-vector column in position order which forces decompression which has already been shown to be slow (at very high run-lengths bit-vector en- coding starts to see entire pages of ’1’s and ’0’s which causes it to optimize its operation, which is why it starts to perform well in the final two points in the graph). This difference in performance between Figures 9(a) and 9(b) illustrates that the proper choice of encoding type for a column depends not just on data characteristics, but also on the expected query workload. This observation supports a major future research Figure 10: Decision tree summarizing our results re- goal of exploring the interaction between physical database garding the proper selection of compression scheme. design, optimization, and compression. It also indicates that redundantly storing the same column in the same sort order using different compression schemes might be a good idea. 7. CONCLUSION The next query that we experimented with was a join The decision tree in Figure 10 summarizes our results and query (again with an aggregation): provides a heuristic for deciding which encoding scheme to use for a column. SELECT S.COL3, COUNT(*) In this tree, “exhibits good locality” means that the col- FROM CSTORE_P1 AS L, CSTORE_P2 AS S umn is either one of the sort columns in the projection, is WHERE PREDICATE(S.COL2) AND PREDICATE(L.COL1) correlated with one of the sort columns in the projection, or AND L.COL2=S.COL1 otherwise contains repeated patterns of data. “Likely to be GROUP BY S.COL3 used in a position contiguous manner” means that that the The algorithm for performing joins in C-Store was described column needs to be read in parallel with another column, in Section 5.1. Assume for this query that so the column is not accessed out of order. For example, if CSTORE P1 is a projection from the fact table and that the column is in the WHERE clause, accessing it in position CSTORE P2 is a projection from a dimension table that contiguous fashion is not required, but if it is in the SELECT contains its primary key (which is the common join case clause it is likely to be accessed via a sorted position list in in star schema queries). Hence, L.COL2 is a foreign key a position contiguous manner. into CSTORE P2 (S.COL1 is the key). This query applies In addition to the observations regarding when to use each a predicate to each table before the join, does a foreign- of the various compression schemes, our results also illustrate primary key join, and then uses the position list result from the following important points: the join to filter and aggregate a column from CSTORE P2. Again, we started with CSTORE P1 being the lineitem • Physical database design should be aware of the com- fact table from TPC-H. The join attribute is the supplier for- pression subsystem. Performance is improved by com- eign key. We assume the projections are sorted on S.COL2 pression schemes that take advantage of data locality. and L.COL1 (this is the common case since the C-Store op- Queries on columns in projections with secondary and timizer will have a choice as to what projections to use for a tertiary sort orders perform well, and it is generally query and will choose projections that are sorted by predi- beneficial to have low cardinality columns serve as the cated columns) and are therefore RLE encoded. We allowed leftmost sort orders in the projection (to increase the L.COL2 (suppkey) to be secondarily sorted and encoded it average run-lengths of columns to the right). The more with the same four coding algorithms as the previous (select) order and locality in a column, the better. queries. In order to show results for the bit-vector case, we reduced the number of unique supplier keys in the fact table • It is a good idea to operate directly on compressed to just 50 values in one of our experiments (we allowed 50000 data. Sacrificing the compression ratio of heavy-weight values in the other experiment). The results of performing schemes for the efficiency light-weight schemes in oper- this join are shown in the table below (times are in seconds). ating on compressed data is a good trade-off to make. Encoding Type 50 keys 50000 keys • The optimizer needs to be aware of the performance RLE 0.06 0.07 implications of operating directly on compressed data Bit-vector 0.97 N/A in its cost models. Further, cost models that only take Dictionary 3.15 3.86 into account I/O costs will likely perform poorly in the No Compression 4.08 4.3 context of column-oriented systems since CPU cost is often the dominant factor. The techniques for operating directly on RLE and bit- vector data have been discussed previously, for the join part In summary, this paper shows that significant database of this query in Section 5.1 and for the resulting position performance gains can be had by implementing light-weight filtering in the previous query in this section. To operate compression schemes and operators that work directly on directly on dictionary data, the dimension table join column compressed data. By classifying compression schemes ac- had to be recoded using the fact table’s dictionary at the cording to a set of basic properties, we were able to extend beginning of the query (this is included in the query time.) C-Store to perform this direct operation without requiring 

12 .new operator code for each compression scheme. Further- [19] Kx Sytems, Inc. Faster database platforms for the more, our focus on column-oriented compression allowed us real-time enterprise: How to get the speed you need to to demonstrate that the performance benefits of operating break through business intelligence bottlenecks in directly on compressed data in column-oriented schemes is financial institutions. much greater than the benefit in operating directly on row- http://library.theserverside.com/ oriented schemes. Hence, we see this work as an important data/document.do?res id=1072792428 967, 2003. step in understanding the substantial performance benefits [20] C. A. Lynch and E. B. Brownrigg. Application of data of column-oriented database designs. compression to a large bibliographic data base. In VLDB ’81, Cannes, France, pages 435–447, 1981. 8. ACKNOWLEDEMENTS & REFERENCES [21] R. MacNicol and B. French. Sybase IQ multiplex - We would like to thank Michael Stonebraker, David De- designed for analytics. In VLDB, pages 1227–1230, Witt, Pat O’Neil, Stavros Harizopoulos, and Alex Rasin for 2004. their helpful feedback and ideas. [22] A. Moffat and J. Zobel. Compression and fast indexing This work was supported by the National Science Founda- for multi-gigabyte text databases. Australian tion under NSF Grant number IIS-0325525 and by an NSF Computer Journal, 26(1):1–9, 1994. Graduate Research Fellowship. [23] P. O’Neil and D. Quass. Improved query performance with variant indexes. In SIGMOD, pages 38–49, 1997. [1] http://www.addamark.com/products/sls.htm. [24] R. Ramamurthy, D. Dewitt, and Q. Su. A case for [2] http://www.lzop.org. fractured mirrors. In VLDB, pages 89 – 101, 2002. [3] C-Store code release under bsd license. [25] G. Ray, J. R. Haritsa, and S. Seshadri. Database http://db.csail.mit.edu/projects/cstore/, 2005. compression: A performance enhancement tool. In [4] A. Ailamaki, D. J. DeWitt, M. D. Hill, and COMAD, 1995. M. Skounakis. Weaving relations for cache [26] M. A. Roth and S. J. V. Horn. Database compression. performance. In VLDB, pages 169–180, 2001. SIGMOD Rec., 22(3):31–39, 1993. [5] S. Amer-Yahia and T. Johnson. Optimizing queries on [27] D. G. Severance. A practitioner’s guide to data base compressed bitmaps. In VLDB, pages 329–338, 2000. compression - tutorial. Inf. Syst., 8(1):51–62, 1983. [6] G. Antoshenkov. Byte-aligned data compression. U.S. [28] M. Stonebraker, D. J. Abadi, A. Batkin, X. Chen, Patent Number 5,363,098. M. Cherniack, M. Ferreira, E. Lau, A. Lin, S. Madden, [7] G. Antoshenkov, D. B. Lomet, and J. Murray. Order E. J. O’Neil, P. E. O’Neil, A. Rasin, N. Tran, and preserving compression. In ICDE ’96, pages 655–663. S. B. Zdonik. C-Store: A column-oriented DBMS. In IEEE Computer Society, 1996. VLDB, pages 553–564, 2005. [8] P. Boncz, S. Manegold, and M. Kersten. Database [29] T. Westmann, D. Kossmann, S. Helmer, and architecture optimized for the new bottleneck: G. Moerkotte. The implementation and performance Memory access. In VLDB, pages 54–65, 1999. of compressed databases. SIGMOD Rec., 29(3):55–67, [9] P. A. Boncz and M. L. Kersten. MIL primitives for 2000. querying a fragmented world. VLDB Journal: Very [30] K. Wu, E. Otoo, and A. Shoshani. Compressed bitmap Large Data Bases, 8(2):101–119, 1999. indices for efficient query processing. Technical Report [10] P. A. Boncz, M. Zukowski, and N. Nes. LBNL-47807, 2001. Monetdb/x100: Hyper-pipelining query execution. In [31] K. Wu, E. Otoo, and A. Shoshani. Compressing CIDR, pages 225–237, 2005. bitmap indexes for faster search operations. In [11] Z. Chen, J. Gehrke, and F. Korn. Query optimization SSDBM’02, pages 99–108, 2002. LBNL-49627., 2002. in compressed database systems. In SIGMOD ’01, [32] K. Wu, E. Otoo, A. Shoshani, and H. Nordberg. Notes pages 271–282, 2001. on design and implementation of compressed bit [12] G. V. Cormack. Data compression on a database vectors. Technical Report LBNL/PUB-3161, 2001. system. Commun. ACM, 28(12):1336–1342, 1985. [33] A. Zandi, B. R. Iyer, and G. G. Langdon Jr. Sort order [13] G.Graefe and L.Shapiro. Data compression and preserving data compression for extended alphabets. database performance. In ACM/IEEE-CS Symp. On In Data Compression Conference, pages 330–339, 1993. Applied Computing pages 22 -27, April 1991. [34] J. Zhou and K. Ross. A multi-resolution block storage [14] J. Goldstein, R. Ramakrishnan, and U. Shaft. model for database design. In Proceedings of the 2003 Compressing relations and indexes. In ICDE ’98, IDEAS Conference, pages 22–33, 2003. pages 370–379, 1998. [35] J. Ziv and A. Lempel. A universal algorithm for [15] D. Huffman. A method for the construction of sequential data compression. IEEE Transactions on minimum-redundancy codes. Proc. IRE, Information Theory, 23(3):337–343, 1977. 40(9):1098-1101, September 1952. [36] J. Ziv and A. Lempel. Compression of individual [16] B. R. Iyer and D. Wilhite. Data compression support sequences via variable-rate coding. IEEE Transactions in databases. In VLDB ’94, pages 695–704, 1994. on Information Theory, 24(5):530–536, 1978. [17] T. Johnson. Performance measurements of compressed [37] M. Zukowski, S. Heman, N. Nes, and P. Boncz. bitmap indices. In VLDB, pages 278–289, 1999. Super-scalar ram-cpu cache compression. In ICDE, [18] S. Khoshafian, G. P. Copeland, T. Jagodis, H. Boral, 2006. and P. Valduriez. A query processing strategy for the decomposed storage model. In ICDE, pages 636–643. IEEE Computer Society, 1987.