Fast Checkpoint Recovery Algorithms

1 . Fast Checkpoint Recovery Algorithms for Frequently Consistent Applications Tuan Cao, Marcos Vaz Salles, Benjamin Sowell, Yao Yue, Alan Demers, Johannes Gehrke, Walker White Cornell University Ithaca, NY 14853, USA {tuancao,vmarcos,sowell,yaoyue,ademers,johannes,wmwhite}@cs.cornell.edu ABSTRACT tions and execute them sequentially [36, 28] or develop application- Advances in hardware have enabled many long-running applica- specific ways to avoid locking and prevent costly conflicts and roll- tions to execute entirely in main memory. As a result, these appli- backs [34, 35, 29]. These approaches lead to applications with cations have increasingly turned to database techniques to ensure frequent points of consistency, which we call frequently consistent durability in the event of a crash. However, many of these ap- or FC applications. Unlike traditional database applications, which plications, such as massively multiplayer online games and main- may never reach a point of consistency without quiescing the sys- memory OLTP systems, must sustain extremely high update rates – tem, FC applications reach natural points of consistency very fre- often hundreds of thousands of updates per second. Providing dura- quently (typically at least once a second) during normal operation. bility for these applications without introducing excessive overhead Since FC applications store data in main memory, durability is or latency spikes remains a challenge for application developers. an important and challenging property to ensure, particularly given In this paper, we take advantage of frequent points of consistency the strict performance requirements of many FC applications. In in many of these applications to develop novel checkpoint recovery this paper we leverage frequent points of consistency to develop algorithms that trade additional space in main memory for signif- checkpoint recovery algorithms with extremely low overhead. We icantly lower overhead and latency. Compared to previous work, start by describing several important use cases. our new algorithms do not require any locking or bulk copies of MMOs are an important class of FC applications that have the application state. Our experimental evaluation shows that one recently received attention in the database community [27, 11]. of our new algorithms attains nearly constant latency and reduces MMOs are large persistent games that allow users to socialize and overhead by more than an order of magnitude for low to medium compete in a virtual world. Most MMOs use a time-stepped pro- update rates. Additionally, in a heavily loaded main-memory trans- cessing model where character behavior is divided into atomic time action processing system, it still reduces overhead by more than a steps or ticks that are executed many times per second and update factor of two. the entire state of the game [35]. The game state is guaranteed to be consistent at tick boundaries. Behavioral and agent-based simula- Categories and Subject Descriptors tions, which are often used by scientists to model phenomena such as traffic congestion and animal motion, also use a time-stepped H.2.2 [Information Systems]: Database Management—Recovery model and have similar points of consistency [34]. and restart Though we use MMOs as a running example throughout this General Terms paper, our techniques can be applied to any application with fre- quent points of consistency. For example, certain classes of main- Algorithms, Performance, Reliability memory OLTP systems also have frequent points of consistency. Traditional OLTP systems are heavily mutli-threaded to mask 1. INTRODUCTION the huge differences between access times to main memory and An increasing number of data-intensive applications are be- disk, but the tradeoffs change when all data is stored in memory. ing executed entirely in main memory and eschewing traditional New OLTP systems like H-Store [28] (and its commercial version database concurrency control mechanisms in order to achieve high VoltDB [33]) serialize all transactions so that each machine can ex- throughput. Examples include applications as diverse as mas- ecute them using a single thread in order to avoid the overhead of sively multiplayer online games (MMOs) and scientific simula- concurrency control and increase throughput. In these applications tions, as well as certain classes of main-memory OLTP systems the end of each transaction marks a point of consistency [32]. Other and search engines. Many of these systems either serialize opera- examples of FC applications include new data-parallel systems to program the cloud, such as BOOM [2], deterministic transaction processing systems [30, 36], and in-memory search engines [29]. Many frequently consistent applications must handle very high Permission to make digital or hard copies of all or part of this work for update rates, which can complicate recovery. For example, popular personal or classroom use is granted without fee provided that copies are MMO servers may have to process hundreds of thousands of up- not made or distributed for profit or commercial advantage and that copies bear this notice and the full citation on the first page. To copy otherwise, to dates per second, including behaviors such as character movement. republish, to post on servers or to redistribute to lists, requires prior specific Many traditional database recovery algorithms that rely on physi- permission and/or a fee. cal logging simply cannot sustain this update rate without resorting SIGMOD’11, June 12–16, 2011, Athens, Greece. to expensive special-purpose hardware [20, 24]. Another common Copyright 2011 ACM 978-1-4503-0661-4/11/06 ...$10.00. 265 

2 .recovery approach, used by some OLTP systems such as H-Store, 2. BACKGROUND is to replicate state on several machines and apply updates to all A frequently consistent (FC) application is a distributed applica- replicas [28]. While this provides high availability, replication is tion in which the state of each node frequently reaches a point of usually still combined with additional mechanisms such as regular consistency. A point of consistency is simply a time at which the checkpointing to protect against large scale failures such as power state of the node is valid according to the semantics of the applica- outages. Checkpointing can also be used to transfer state between tion. The definition of frequently depends on the application, but nodes during recovery or when a new replica is added to the system. we expect it to be less than a second. For example, MMO servers We can take advantage of frequent points of consistency to take execute approximately 10 ticks/sec, while modern OLTP systems periodic consistent checkpoints of the entire application state and may be able to execute a small transaction in tens of microsec- use logical logging to provide durability between checkpoints. onds [28, 17]. Since we have frequent points of consistency, there is no need to Throughout the paper, we use application state to refer to the quiesce the system in order to take a checkpoint, and we benefit dynamic, memory-resident state of an FC application. FC applica- from not having to maintain a costly physical log. Furthermore, tions may have additional read-only or read-mostly state that can we can avoid the primary disadvantage of logical logging, namely simply be written to stable storage when it is created. For exam- the cost of replaying the log during recovery. Since there are many ple, in an MMO, each character will have some attributes such as points of consistency, we can take checkpoints very frequently (ev- position, health, or experience that are frequently updated and thus ery few seconds), so the log can be replayed very fast. part of the dynamic state, but it will also have other attributes such Of course, taking very frequent checkpoints can increase the as name, race, or class (the type or job of the character) that are overhead associated with providing durability. To make this fea- unlikely to change. Additionally, some applications include sec- sible, we need high performance checkpointing algorithms. In par- ondary data structures such as indices that can be rebuilt during re- ticular, we have identified several important requirements. First, covery. We will focus exclusively on making the primary dynamic the algorithm should have low overhead during normal operation. state durable. Ideally, taking a checkpoint should have very little impact on the In this paper, we use coordinated checkpointing to provide dura- throughput of the system. Second, the algorithm should distribute bility for distributed FC applications at low cost [6]. Many appli- its overhead uniformly and not introduce performance spikes or cations already use replication to increase availability and provide highly variable response times. This is particularly important in some fault tolerance [28], but checkpointing can still be used to applications such as MMOs where high latency may create “hic- copy state during recovery and provide durability to protect against cups” in the immersive virtual experience. Finally, it should be power outages and other widespread failures. possible to take checkpoints very frequently so that the logical log Furthermore, we will focus exclusively on developing robust can be replayed quickly in the event of a failure. In a recent ex- single-node checkpointing algorithms, as these form the core of perimental study, Vaz Salles et al. evaluated existing main-memory most distributed checkpointing schemes. There is a large dis- checkpointing algorithms for use in MMOs [27], however these tributed systems literature that explores how to generalize efficient algorithms either use locks or large synchronous copy operations, single-node checkpointing algorithms to multiple nodes. Tightly which hurt throughput and latency, respectively. synchronized FC applications that reach global points of consis- In this paper we propose and evaluate two new checkpointing al- tency during normal operation are particularly easy to checkpoint, gorithms, called Wait-Free Zigzag and Wait-Free Ping-Pong, which as they can reuse their existing synchronization mechanisms to de- avoid the use of locks and are designed to distribute overhead cide on a global point of consistency at which each node can take a smoothly. Wait-Free Ping-Pong also makes use of additional main local checkpoint. More general distributed applications may need memory to further reduce overhead. We evaluate these algorithms to use techniques such as message logging to create a consistent using a high-performance implementation of TPC-C running in the checkpoint. These distributed approaches are discussed at length cloud as well a synthetic workload with a wide variety of update in a recent survey by Elnozahy et al [9]. rates. Our experiments show that both algorithms are successful in In the remainder of this section we discuss requirements for greatly reducing the latency spikes associated with checkpointing checkpoint-recovery algorithms targeted at FC applications (Sec- and that Wait-Free Ping-Pong also has considerably lower over- tion 2.1) and we present existing checkpoint-recovery methods for head: up to an order of magnitude less for low to medium update these applications (Sections 2.2 and 2.3). rates and more than a factor of two in our TPC-C experiments. In Section 2 of this paper, we review several existing checkpoint- 2.1 Requirements for Checkpoint Recovery ing algorithms [27]. We then make the following contributions: Algorithms 1. We analyze the performance bottlenecks in prior work, and We can summarize the requirements for a checkpointing algo- propose two new algorithms to address them (Section 3). rithm for FC applications as follows: 2. We explore the impact of data layout in main memory on 1. The method must have low overhead. During normal oper- cache performance and do a careful cache-aware implemen- ation, FC applications must process very high update rates, tation of all of our algorithms, as well as the best previous and the cost of checkpointing state for recovery should not algorithms [27]. We find that our algorithms are particularly greatly reduce the throughput. amenable to these low level optimizations (Section 4). 2. The method should distribute overhead uniformly, so that 3. We perform a thorough evaluation of our new algorithms and application performance is consistent. Even when the total compare them to existing methods. We find that Wait-Free overhead is low, many applications depend on predictable Ping-Pong exhibits lower overhead than all other algorithms performance. For example, fluctuations in overhead affect by up to an of magnitude over a wide range of update rates. MMOs by interfering with time-synchronized subsystems It also completely eliminates the latency spikes that plagued like the physics engine [16]. This problem is made even previous consistent checkpointing algorithms (Section 5). worse when the checkpointing algorithm must pause the sys- We review related work in Section 6 and conclude in Section 7. tem in order to perform a synchronous operation like a bulk 266 

3 . Interface 1: Algorithmic Framework The final thread, the Asynchronous Writer, writes some or all of the main-memory state to disk. Note that this thread can be Mutator::PrepareForNextCheckpoint() run in the background while the Mutator concurrently updates the Mutator::PointOfConsistency() state. Since the performance of the Asynchronous Writer thread Mutator::HandleRead(index) is primarily determined by disk bandwidth, we will focus on the Mutator::HandleWrite(index, update) synchronous overhead introduced in the Mutator thread. However, AsynchronousWriter::WriteToStableStorage() it is important to note that some existing checkpointing algorithms require that the Asynchronous Writer acquire locks on portions of copy. Such latency spikes can also be a problem for dis- the application state, which can impact the performance of all of tributed applications. If a node sending a message experi- the threads [27]. ences a latency spike, the receiver may block, spreading the The Mutator thread makes function calls before starting a new effect of the latency spike throughout the system and reduc- checkpoint (PrepareForNextCheckpoint), when a point of con- ing overall throughput. sistency is reached (PointOfConsistency), and during each read and write of the application state (HandleRead and HandleWrite). 3. The method should have fast recovery in the event of failure. The PointOfConsistency method must be executed at a point of Ideally, the recovery time should be on the order of a few consistency, but it need not be executed at every point of consis- seconds to avoid significant disruption. We will accomplish tency. If points of consistency are very frequent (e.g., every few this primarily by increasing the frequency of checkpoints. microseconds), we can wait for several of them to pass before call- Traditional approaches to database recovery such as ARIES- ing the method. style physiological logging [21] and fuzzy checkpointing [12, 26], Different algorithms will implement these methods differently which uses physical logging, cannot keep up with the extremely depending on how they manage the application state. Most algo- high update rates of FC applications without resorting to ex- rithms will maintain one or more shadow copies of the state in main tremely expensive special-purpose hardware such as battery backed memory. The Mutator may use this shadow state during the check- RAM [10, 20, 24]. As the dollar cost per gigabyte of battery-backed point before it is written to stable storage by the Asynchronous RAM exceeds the cost of traditional RAM by over an order of mag- Writer. In the rest of the paper, we will refer to the time between nitude, it is unlikely that cloud infrastructures or large enterprise successive calls to PrepareForNextCheckpoint as a checkpoint clusters will package this technology for use by FC applications. period. Note that this must be long enough for the Asynchronous In the following subsections, we review the framework we previ- Writer to finish creating a checkpoint on disk. These checkpoints ously proposed for checkpointing MMOs on commodity hardware may be organized on disk in several different ways. In our im- and discuss how it can be extended to support FC applications [27]. plementation, we use a double-backup organization for all of the algorithms, as it was reported in previous work to consistently out- 2.2 Algorithmic Framework perform a log-based implementation [27]. The recovery procedure is the same for all algorithms that imple- In this section we discuss the basic algorithmic framework we ment this framework. First, the most recent consistent checkpoint is use for checkpointing. During normal operation, the application read from disk and materialized as the new application state. Then, takes periodic checkpoints of its entire dynamic state and maintains the logical log is replayed from the time of the last checkpoint until a logical log of all actions. For example, in an MMO we would log the state is up-to-date. Since we take checkpoints very frequently, all user actions sent to the server; in a system like H-Store, we the time to replay the logical log is quite small. would log all stored procedure calls. Because each logical update may translate into many physical updates, we expect the overhead of maintaining this log to be quite small, and we will focus pri- 2.3 Existing Algorithms marily on the overhead associated with checkpointing. In order to Based on their experimental evaluation for MMOs, Vaz Salles compare with existing algorithms for games, we will use the same et al. concluded that there was no single checkpointing algorithm algorithmic framework for checkpointing originally introduced by that outperformed all the others over the entire range of update Vaz Salles et al. [27]. Interface 1 lists the key methods in this API. rates [27]. Their evaluation included a number of synthetic exper- We model main-memory checkpointing algorithms using a sin- iments, and we believe they provide a reasonable model for many gle Mutator thread that executes the application logic and syn- FC applications. They concluded that two algorithms, Copy-on- chronously updates the application state. Our techniques can be Update and Naive-Snapshot, performed best for low and high up- naturally extended to support applications with multithreaded mu- date rates, respectively. tators as long as we include enough information in the logical log Naive-Snapshot synchronously copies the entire state of the ap- to enable deterministic replay. For OLTP applications, for instance, plication to the shadow copy at a point of consistency and then this might include transaction commit order so that transactions can writes it out asynchronously to disk. Naive-Snapshot is among be serialized during replay. This may lengthen the recovery time the best algorithms when the update rate is very high since it does somewhat, but in practice we have observed that many FC applica- not perform any checkpoint-specific work in the HandleRead or tions are already deterministic or can be made deterministic using HandleWrite functions. existing methods [30]. Copy-on-Update groups application objects into blocks and In addition to the Mutator, we use two threads to write data to copies each block to the shadow state the first time it is updated dur- disk. The Logical Logger thread synchronously flushes logical log ing a checkpoint period. During a checkpoint, the Asynchronous entries to disk. This could be done directly in the Mutator thread, writer either reads state from the application state or the shadow but we implement it as a separate thread so that we can overlap copy based on whether the corresponding block has been updated. computation and process additional actions while we are waiting Since the Mutator is concurrently updating the application state, it for the disk write to complete. Note that we must wait for all disk must acquire locks on the blocks it references. This may introduce writes to finish before proceeding to the next point of consistency considerable overhead. By varying the memory block size, Copy- (e.g. reporting a transaction as committed). on-Update can trade off between copying and locking overhead. 267 

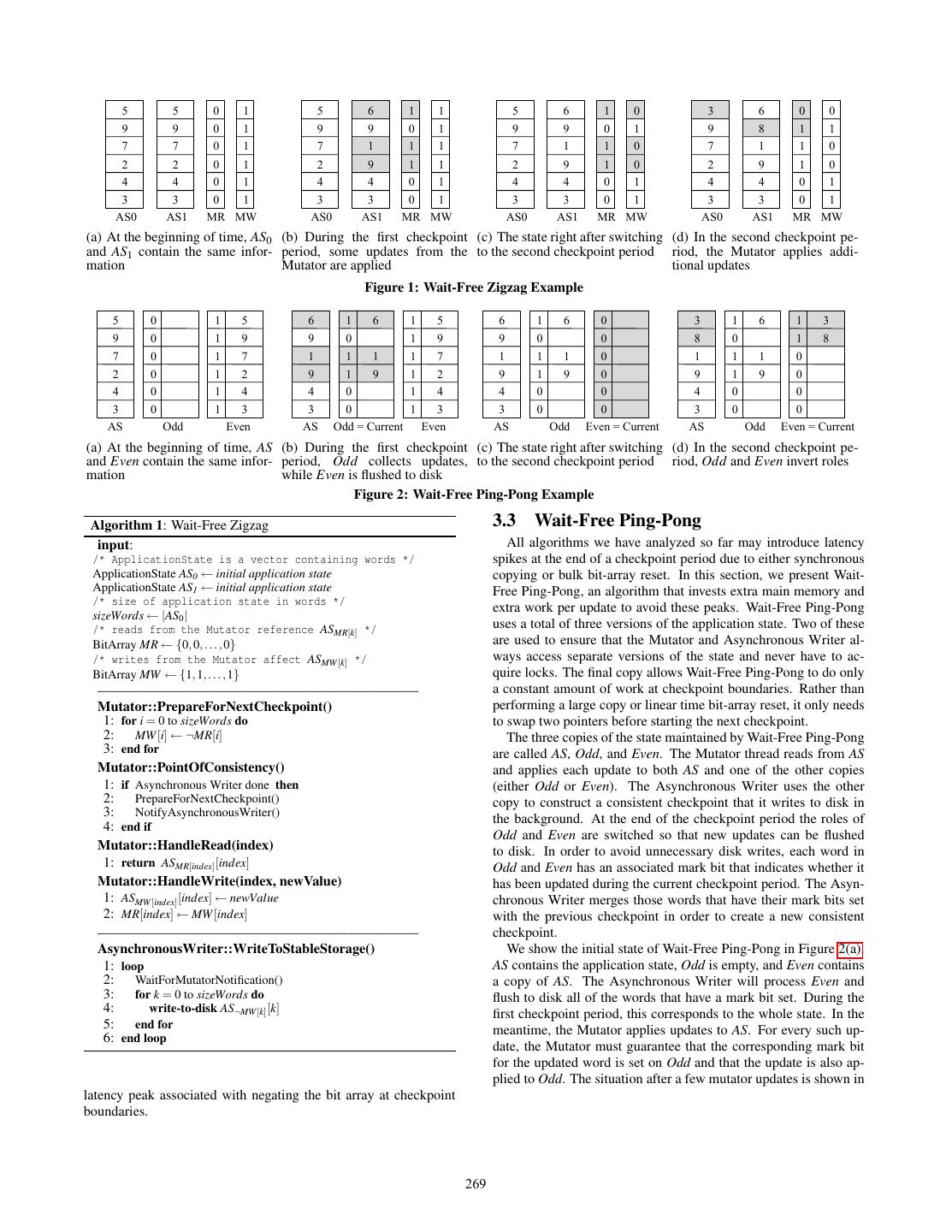
4 . Overhead Factor Zigzag, like Naive-Snapshot and Copy-On-Update, uses additional Method Bulk Bulk Memory Locking Bit-Array main memory on the order of the size of the application state. Wait- Copying Reset Usage Free Ping-Pong, however, requires twice that amount. We believe Naive-Snapshot Yes No No ×2 that this is a reasonable tradeoff for most MMOs and OLTP appli- Copy-on-Update No Yes Yes ×2 cations, as the size of the dynamically updated state is generally Wait-Free Zigzag No No Yes ×2 quite small – usually only a small fraction of the whole state. Wait-Free Ping-Pong No No No ×3 Table 1: Overhead factors of checkpoint-recovery algorithms. 3.2 Wait-Free Zigzag The main intuition behind Wait-Free Zigzag is to maintain an un- 3. NEW ALGORITHMS touched copy of every word in the application state for the duration In this section, we present two novel checkpoint recovery algo- of a checkpoint period. These copies form the consistent image rithms for FC applications. We first discuss important design trade- that is written to disk by the Asynchronous Writer. As these copies offs that differentiate our algorithms from state-of-the-art meth- are never changed during the checkpoint period, the Asynchronous ods (Section 3.1) and then introduce each algorithm in turn (Sec- Writer is free to read them without acquiring locks. tions 3.2 and 3.3). The algorithm starts with two identical copies of the application state: AS0 and AS1 (Figure 1(a)). For each word i in the application 3.1 Design Overview state, we maintain two bits: MR[i] and MW [i]. The first bit, MR[i], We have identified four primary factors that affect the perfor- indicates which application state should be used for Mutator reads mance of checkpoint recovery algorithms: from word i, while the second bit, MW [i], indicates which should be used for Mutator writes. The bit array MR is initialized with 1. Bulk State Copying: The method may need to pause the zeros and MW with ones. application to take a snapshot of the whole application state, The bits in MW are never updated during a checkpoint period. as in Naive-Snapshot. This ensures that for every word i, AS¬MW [i] [i] is also never updated 2. Locking: The method may need to use locking to isolate by the Mutator during a checkpoint period. The Asynchronous the Mutator from the Asynchronous Writer, if they work on Writer flushes exactly these words to disk in order to take a check- shared regions of the application state. point. To avoid blocking the Mutator, however, we must also apply 3. Bulk Bit-Array Reset: If the method uses metadata bits to updates to the application state. Whenever a new update comes to flag dirty portions of the state, it may need to pause the ap- word i, we write that update to position ASMW [i] [i] and set MR[i] to plication and perform a bulk clean-up of this metadata before MW [i]. Before any read of a word i, the Mutator inspects MR[i] and the start of a new checkpoint period. directs the read to the most recently updated word ASMR[i] [i]. Fig- ure 1(b) shows the situation after updates are applied to the shaded 4. Memory Usage: In order to avoid synchronous writes to words. For example, the value written for the third word by the disk, the method may need to allocate additional main mem- Asynchronous Writer resides in AS0 and remains unchanged dur- ory to hold copies of the application state. ing the first checkpoint. Any reads by the Mutator after the first Table 1 shows how the factors above apply to both Naive- update return the value in AS1 . Snapshot and Copy-on-Update. Naive-Snapshot eliminates all At the end of the checkpoint period, the Mutator assigns the locking and bulk bit-array resetting overhead, but must perform negation of MR to MW , i.e., ∀i, MW [i] := ¬MR[i]. This is done so a bulk copy of the whole application state. This introduces a la- that the current state of the application is not updated by the Mu- tency spike in the application since it must block during the copy. tator during the next checkpoint period and can be written to disk Copy-on-Update avoids this problem since it does not perform syn- by the Asynchronous Writer. Figure 1(c) shows the state right after chronous bulk copies, but incurs both locking and bulk bit-array re- the Mutator performs this assignment in our example. Again, up- setting overhead. This extra overhead is small for moderate update dates during the next checkpoint period follow the same procedure rates, but is significant for higher update rates [27]. Both methods outlined above. Figure 1(d) shows the application state after two require additional main memory of roughly the size of the entire ap- updates during the second checkpoint period. Note that the current plication state. So the memory usage for the dynamic application application state, as well as the state being checkpointed to disk, is state increases to about twice its original size. now distributed between AS0 and AS1 . Our new algorithms, Wait-Free Zigzag and Wait-Free Ping- Algorithm 1 summarizes Wait-Free Zigzag. While most of this Pong, are designed to eliminate all overhead associated with bulk algorithm is a straightforward translation of the explanation above, state copying and locking. Unlike Naive-Snapshot, they spread one further observation applies to the PointOfConsistency pro- their overhead over time instead of concentrating it at a single point cedure. This Mutator procedure checks whether the Asynchronous of consistency. Unlike Copy-on-Update, they only require synchro- Writer has finished writing the current checkpoint to disk. Though nization between the Mutator and Asynchronous Writer at the end the threads communicate, this does not violate the wait-free prop- of a checkpoint period. This eliminates all locking overhead during erty of the algorithm, as it can be implemented using store and load state updates. Additionally, the Mutator and Asynchronous Writer barriers instead of locks. Heavier synchronization methods are only are each guaranteed to make progress even if the other is preempted necessary at the end of every checkpoint period. within a checkpoint period. As a consequence, both algorithms are Wait-Free Zigzag does not require any lock synchronization dur- wait-free within a checkpoint period [13]. Table 1 also summarizes ing a checkpoint period. In addition, there is no need to copy the overhead factors our algorithms incur. memory blocks in response to an update from the Mutator. This To eliminate overhead factors, both of our new algorithms eliminates some of the largest overheads of Copy-on-Update. In strictly separate the state being updated by the Mutator from the addition, Wait-Free Zigzag distributes its overhead smoothly and state being read by the Asynchronous Writer. In addition, both avoids the latency spikes of Naive-Snapshot. On the other hand, track updates at very fine, word-level granularity. However, the Wait-Free Zigzag adds bit checking and setting overhead to both algorithms use different amounts of main memory. Wait-Free reads and writes issued by the Mutator. It also exhibits a small 268 

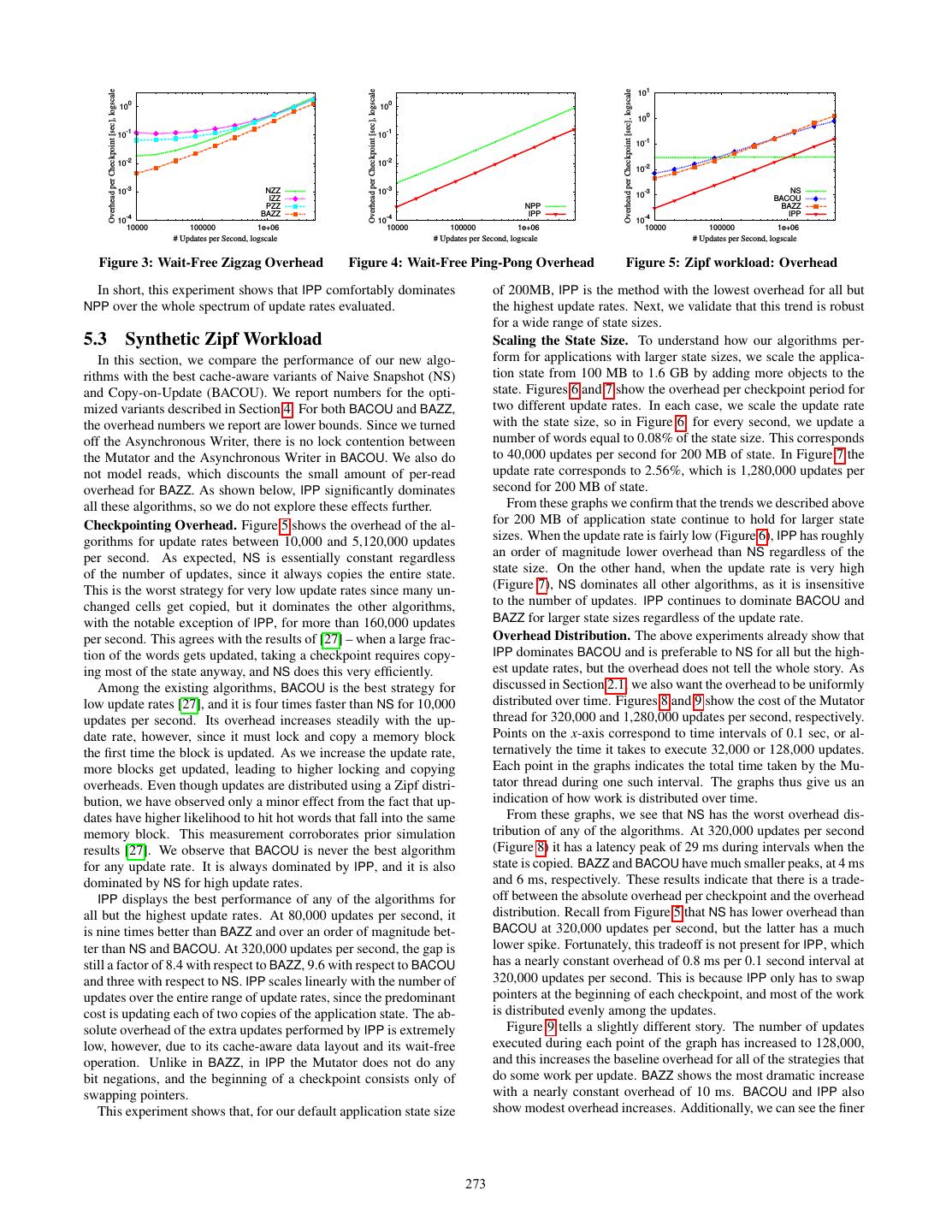
5 . 5 5 0 1 5 6 1 1 5 6 1 0 3 6 0 0 9 9 0 1 9 9 0 1 9 9 0 1 9 8 1 1 7 7 0 1 7 1 1 1 7 1 1 0 7 1 1 0 2 2 0 1 2 9 1 1 2 9 1 0 2 9 1 0 4 4 0 1 4 4 0 1 4 4 0 1 4 4 0 1 3 3 0 1 3 3 0 1 3 3 0 1 3 3 0 1 AS0 AS1 MR MW AS0 AS1 MR MW AS0 AS1 MR MW AS0 AS1 MR MW (a) At the beginning of time, AS0 (b) During the first checkpoint (c) The state right after switching (d) In the second checkpoint pe- and AS1 contain the same infor- period, some updates from the to the second checkpoint period riod, the Mutator applies addi- mation Mutator are applied tional updates Figure 1: Wait-Free Zigzag Example 5 0 1 5 6 1 6 1 5 6 1 6 0 3 1 6 1 3 9 0 1 9 9 0 1 9 9 0 0 8 0 1 8 7 0 1 7 1 1 1 1 7 1 1 1 0 1 1 1 0 2 0 1 2 9 1 9 1 2 9 1 9 0 9 1 9 0 4 0 1 4 4 0 1 4 4 0 0 4 0 0 3 0 1 3 3 0 1 3 3 0 0 3 0 0 AS Odd Even AS Odd = Current Even AS Odd Even = Current AS Odd Even = Current (a) At the beginning of time, AS (b) During the first checkpoint (c) The state right after switching (d) In the second checkpoint pe- and Even contain the same infor- period, Odd collects updates, to the second checkpoint period riod, Odd and Even invert roles mation while Even is flushed to disk Figure 2: Wait-Free Ping-Pong Example Algorithm 1: Wait-Free Zigzag 3.3 Wait-Free Ping-Pong input: All algorithms we have analyzed so far may introduce latency /* ApplicationState is a vector containing words */ spikes at the end of a checkpoint period due to either synchronous ApplicationState AS0 ← initial application state copying or bulk bit-array reset. In this section, we present Wait- ApplicationState AS1 ← initial application state Free Ping-Pong, an algorithm that invests extra main memory and /* size of application state in words */ extra work per update to avoid these peaks. Wait-Free Ping-Pong sizeWords ← |AS0 | /* reads from the Mutator reference ASMR[k] */ uses a total of three versions of the application state. Two of these BitArray MR ← {0, 0, . . . , 0} are used to ensure that the Mutator and Asynchronous Writer al- /* writes from the Mutator affect ASMW [k] */ ways access separate versions of the state and never have to ac- BitArray MW ← {1, 1, . . . , 1} quire locks. The final copy allows Wait-Free Ping-Pong to do only ——————————————————————— a constant amount of work at checkpoint boundaries. Rather than Mutator::PrepareForNextCheckpoint() performing a large copy or linear time bit-array reset, it only needs 1: for i = 0 to sizeWords do to swap two pointers before starting the next checkpoint. 2: MW [i] ← ¬MR[i] The three copies of the state maintained by Wait-Free Ping-Pong 3: end for are called AS, Odd, and Even. The Mutator thread reads from AS Mutator::PointOfConsistency() and applies each update to both AS and one of the other copies 1: if Asynchronous Writer done then (either Odd or Even). The Asynchronous Writer uses the other 2: PrepareForNextCheckpoint() copy to construct a consistent checkpoint that it writes to disk in 3: NotifyAsynchronousWriter() the background. At the end of the checkpoint period the roles of 4: end if Odd and Even are switched so that new updates can be flushed Mutator::HandleRead(index) to disk. In order to avoid unnecessary disk writes, each word in 1: return ASMR[index] [index] Odd and Even has an associated mark bit that indicates whether it Mutator::HandleWrite(index, newValue) has been updated during the current checkpoint period. The Asyn- 1: ASMW [index] [index] ← newValue chronous Writer merges those words that have their mark bits set 2: MR[index] ← MW [index] with the previous checkpoint in order to create a new consistent ——————————————————————— checkpoint. AsynchronousWriter::WriteToStableStorage() We show the initial state of Wait-Free Ping-Pong in Figure 2(a). 1: loop AS contains the application state, Odd is empty, and Even contains 2: WaitForMutatorNotification() a copy of AS. The Asynchronous Writer will process Even and 3: for k = 0 to sizeWords do flush to disk all of the words that have a mark bit set. During the 4: write-to-disk AS¬MW [k] [k] first checkpoint period, this corresponds to the whole state. In the 5: end for meantime, the Mutator applies updates to AS. For every such up- 6: end loop date, the Mutator must guarantee that the corresponding mark bit for the updated word is set on Odd and that the update is also ap- plied to Odd. The situation after a few mutator updates is shown in latency peak associated with negating the bit array at checkpoint boundaries. 269 

6 . Algorithm 2: Wait-Free Ping-Pong checkpoint in order to construct a new consistent checkpoint that input: can be written to disk (lines 5 and 9). This merge can be done /* ApplicationState is vector containing words */ in one of two ways. In the first method, which we call Copy, the ApplicationState AS ← initial application state Asynchronous Writer maintains an extra copy of the application ApplicationState currentAS state which it “rolls forward” by applying the new updates before ApplicationState previousAS ← initial application state flushing the full checkpoint to disk. In the second method, called /* size of application state in words */ Merge, the Asynchronous Writer reads the most recent checkpoint sizeWords ← |AS| /* dirty words in the current checkpoint */ from disk and applies the new updates before streaming the new BitArray currentBA ← {0, 0, . . . , 0} checkpoint to disk. Note that the updates can be applied as the /* dirty words from the last checkpoint */ checkpoint is read, so it is not necessary to maintain an additional BitArray previousBA ← {1, 1, . . . , 1} copy of the state in main memory. We compare these alternatives ——————————————————————— in Section 5.5 Mutator::PrepareForNextCheckpoint() Wait-Free Ping-Pong introduces negligible overhead to the Mu- 1: /* pointer swapping */ tator at the end of a checkpoint period; only simple pointer swaps swap (previousAS, currentAS) are needed. Thus, there is no single point in time at which the algo- swap (previousBA, currentBA) rithm introduces a latency peak. On the other hand, this algorithm Mutator::PointOfConsistency() doubles the number of updates, as each update is applied both to 1: if Asynchronous Writer done then the application state and to a copy. 2: PrepareForNextCheckpoint() 3: NotifyAsynchronousWriter() 4: end if Mutator::HandleWrite(index, newValue) 4. IMPLEMENTATION 1: AS[index] ← newValue Since all of the algorithms we evaluate make frequent access to 2: currentAS[index] ← newValue multiple copies of the application state in main memory, cache and 3: currenBA[index] ← 1 TLB performance are important considerations to reduce overhead. ——————————————————————— In this section, we describe the important features of our cache- AsynchronousWriter::WriteToStableStorage() optimized implementations. 1: loop 2: WaitForMutatorNotification() 3: for k = 0 to sizeWords do 4.1 Existing Algorithms 4: if previousBA[k] then We start by describing our implementations of the two existing 5: write-to-disk previousAS[k] 6: previousBA[k] ← 0 algorithms: Naive-Snapshot and Copy-on-Update. 7: previousAS[k] ← empty Naive Snapshot (NS). As this algorithm is relatively straightfor- 8: else ward, we focused on making the memory copy at the beginning of 9: write-to-disk word k from previous checkpoint a new checkpoint period as efficient as possible. With microbench- 10: end if marks, we observed that a memcpy of a memory-aligned application 11: end for 12: end loop state was better than our attempts to manually unroll the copy loop. Bit-Array Packed Copy-on-Update (BACOU). The main data structures used by Copy-on-Update include the primary and Figure 2(b). Updated words are shaded in the figure – their most shadow states maintained by the algorithm, bit arrays with meta- recent values are present in both AS and Odd. data on dirty memory blocks, and lock information for these blocks. At the end of the first checkpoint period, the Asynchronous In order to minimize the overhead of bulk bit-array resetting, we Writer will have written all of the marked words in Even out to packed the bits into (64 byte) cache lines and used long word in- disk. In addition, it will have reset their mark bits. For clarity of structions for all operations. Furthermore, we interleaved blocks presentation, we assume that not only the mark bits but also the of the primary and shadow copies of the application state into one contents of those words are reset by the Asynchronous Writer. In cache line, so that they will be fetched together. This optimized an implementation, however, this latter action may be skipped for implementation gave us a factor of five improvement over a naive performance. Note that the Mutator is still applying updates to Odd implementation of the algorithm. up to this point. Now, the Asynchronous Writer is done with this checkpoint period. The next checkpoint period proceeds similarly with the roles of Odd and Even inverted. This is shown in Fig- 4.2 Wait-Free Zigzag ure 2(c). During the next checkpoint period, the algorithm applies The Wait-Free Zigzag algorithm has two major sources updates to Even and the words marked in Odd are flushed to disk by of overhead: the bit array lookups in the handleRead the Asynchronous Writer. Figure 2(d) displays the situation after a and handleWrite routines, and the bulk negation in the few updates from the Mutator in the second checkpoint period. prepareForNextCheckpoint routine. To address these sources Algorithm 2 presents the logic of Wait-Free Ping-Pong. Note of overhead, we devised the following data layout variations. that currentAS and currentBA point to the copy of the applica- Naive Wait-Free Zigzag (NZZ). This is the naive translation of the tion state collecting updates for the current checkpoint period (ei- algorithm presented in Section 3.2. We represented each of AS0 , ther Odd or Even). From a high-level perspective, currentAS and AS1 , MR, and MW as a separate array in main memory and encoded currentBA may be seen as an in-memory, compressed implementa- each bit of MR and MW as one byte for efficient access. tion of a log of updates for this checkpoint period. Interleaved Wait-Free Zigzag (IZZ). In this variant, we inter- Note that as part of the WriteToStableStorage method, the leaved the main-memory layout of AS0 , AS1 , MR, and MW . Each Asynchronous Writer must merge the words updated during the cache line holds a fixed number of interleaved records, containing most recent checkpoint (previousAS[k]) with the last consistent a word from each data structure, stored in order. Placing all of the 270 

7 .words necessary for handleRead and handleWrite in the same fects. Updates are applied as fast as possible by our benchmark, cache line reduces memory stalls on read and write instructions. but to normalize results for presentation, we group updates into Packed Wait-Free Zigzag (PZZ). This variant is similar to IZZ, intervals that correspond to 0.1 seconds of simulated application but organizes data inside of a cache line differently. Instead of logic. In addition, to meaningfully compare the overhead of check- laying out interleaved records row-at-a-time, we laid them out pointing algorithms, we ensure that the checkpointing interval is column-at-a-time, in a style reminiscent of PAX [1]. This maintains the same for all algorithms. the benefits for handleRead and handleWrite, while allowing In the first workload, we model the application state as a set of prepareForNextCheckpoint to be implemented more efficiently 8 KB objects. Different FC applications may have different data with long word negation instructions. models or schemas, but this is a reasonable general model that al- Bit-Array Packed Wait-Free Zigzag (BAZZ). We observed ex- lows us to vary the state size by changing the number of objects. We perimentally that negating the MR bits at the end of each check- use 25,000 rows as a default, which yields approximately 200 MB point period was the major source of overhead in Wait-Free Zigzag of dynamic state. In this workload, we distribute updates by select- (Section 5.2). As with BACOU, we optimized this bulk negation ing an object and then selecting one of the 2,000 four-byte words by combining the representation of MR and MW into a single bit- of the object using identical Zipf-distributions with parameter α. packed array. We divided each cache line in the array in half, and Using this skewed distribution allows us to model applications in used the first half for the bits of MR and the second half for bits which part of the state is “hot” and is frequently updated. We have of MW . In a system with a cache line size of 64 bytes, each cache found that our results remain consistent across a range of α values, line encodes 256 bits from each array. We negated the bits of MR so for space reasons we present all results with α = 0.5. efficiently with long word instructions. We also experimented with a synthetic MMO workload. Accu- rately modeling an MMO is challenging as games vary widely, but 4.3 Wait-Free Ping-Pong we have attempted to capture the salient features using a Markov Unlike Wait-Free Zigzag, Wait-Free Ping-Pong has a very inex- model. Each agent in the game is represented as an object and pensive prepareForNextCheckpoint routine. On the other hand, modeled with a set of five semi-independent probabilistic state ma- it must write to two copies of the application state during each up- chines associated with common gameplay behaviors. We tuned the date. With this in mind, we investigate the following two variants transition probabilities for each state machine by looking at up- of Wait-Free Ping-Pong. date rates produced for each type of action. We then adjusted the state-transition probabilities until these update rates corresponded Naive Wait-Free Ping-Pong (NPP). In this variant, we allocated to those we have observed in specific MMOs. For our experiments, AS, Odd, Even, and their respective bit arrays as independent arrays we used 2,000 players and a total of 531,530 updates per second. in main memory. Additionally, we also represented each bit using Each player object contains roughly 100 KB of state corresponding one byte in order to avoid bit encoding overhead on writes. to a wide variety of character attributes. Interleaved Wait-Free Ping-Pong (IPP). As in the correspond- We ran all synthetic experiments on a local Intel Xeon 5500 ing variant for Wait-Free Zigzag, we interleaved the memory lay- 2.66 GHz with 12 GB RAM and four cores running CentOS. Its out of AS, Odd, Even, and their respective bit arrays. Each cache Nehalem-based CPU has 32 KB L1 cache, 256 KB L2 cache for line contains a set of interleaved records with one word from each each core and a shared L3 cache of 8 MB. We measured disk band- data structure in sequence. In this way, the additional writes of width in this server to be roughly 60 MB/s. For the experiments handleWrite fall on the same cache line as the original write to the with synthetic workloads, we first ensured that the checkpoint inter- application state. We thus expect to eliminate any DTLB or cache val was large enough for any of the algorithms to finish writing the miss overheads associated with the additional writes of Wait-Free entire checkpoint to disk. Then, we normalized checkpoint interval Ping-Pong using this organization. at roughly 4 seconds, so as to provide for short estimated recov- We also applied a number of other optimizations, including us- ery time. Once we established this, we turned off both the Asyn- ing different page sizes, eliminating conditionals, and aggressively chronous Writer and logical logging. These mechanisms perform inlining code. Using large pages resulted in a considerable perfor- the same amount of work independently of checkpointing method, mance improvement, which we report in Section 5.6. and disabling them enabled us to measure the synchronous over- head introduced by different algorithms more accurately. 5. EXPERIMENTS TPC-C Application. We implemented a single-threaded transac- In this section we compare the performance of Wait-Free Zigzag tion processing system in main memory. Following the method- and Wait-Free Ping-Pong with existing algorithms. We consider ology from [28], we implemented the TPC-C workload by writ- several metrics in our evaluation. First, we look at the synchronous ing stored procedures in C++. We drive this application with a overhead per checkpoint. This added overhead indicates the to- memory-resident trace containing transaction procedure calls re- tal amount of work done by the checkpointing algorithm during specting the transaction mix dictated by the TPC-C specification. a checkpoint period. We also measure how the overhead is dis- As in [28], we do not model think times in order to stress our im- tributed over time in order to see whether the checkpointing algo- plementation. As usual, we report the number of new order trans- rithms introduce any unacceptable latency peaks. actions per second. Unlike in the synthetic benchmark experiments, we checkpoint 5.1 Setup and Datasets as frequently as possible in order to understand the maximum im- We compare Wait-Free Zigzag and Wait-Free Ping-Pong with pact of our algorithms in a realistic application. This yields the Naive-Snapshot and Copy-on-Update using two different synthetic minimum possible recovery time, as the length of the log since workloads and a main-memory TPC-C application. the last checkpoint is minimized. We ran our TPC-C application Synthetic Workloads. For the synthetic workloads, we produced on an Amazon Cluster Compute Quadruple Extra Large instance trace files containing the sequence of physical updates to apply to with 23 GB RAM, and computing power equivalent to two In- the application. We make these traces sufficiently large to avoid tel Xeon X5570 quad-core Nehalem-based processors. We write transient effects and keep them in main memory to avoid I/O ef- checkpoints and the log to two separate RAID-0 devices, which 271 

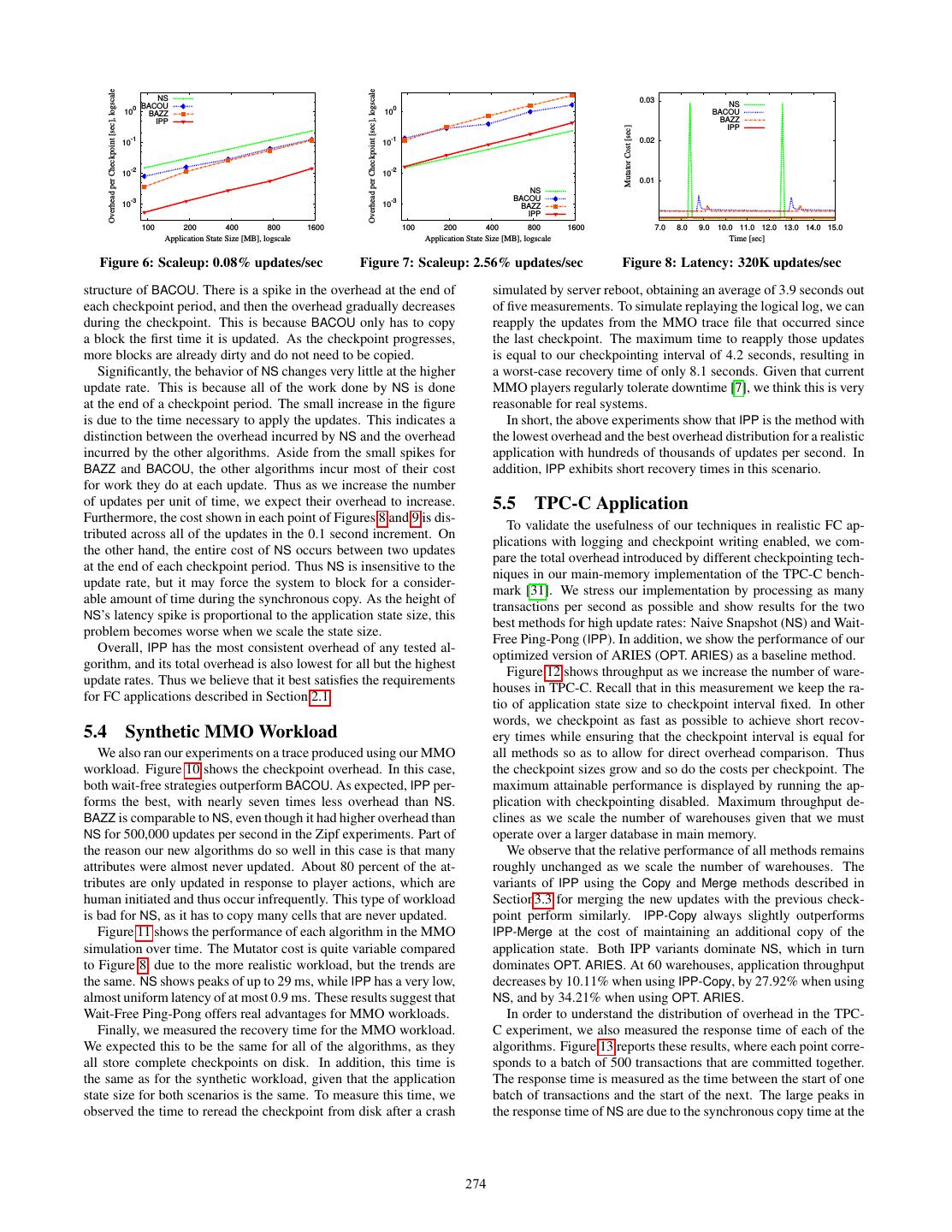
8 . L1D L1D L2 DTLB # Page we configured with ten Amazon Elastic Block Storage (Amazon Algorithma CPI Misses / Miss Miss Miss % Walks / EBS) volumes. We observed that the aggregate bandwidth of these Update Rate Rate (STORE) Update RAID-0 devices depended on the size of the I/O request, ranging NS 1.79 2.1 6.6% 10.8% 7.1% 0.50 from under 10 MB/s for small requests to over 150 MB/s for large COU 2.91 1.2 8.5% 9.2% 23.5% 0.53 requests exceeding 1 GB. In order to completely utilize disk band- BACOU 2.51 1.1 4.5% 4.5% 6.5% 0.41 width, we scale the checkpoint interval with the size of the dynamic NZZ-UP 13.6 0.8 22.3% 24.6% 95.2% 0.78 application state, so that the Asynchronous Writer always writes NZZ-NE 0.7 0.2 3.1% 3.1% 0.8% - IZZ-UP 11.1 0.2 7.7% 7.2% 49.2% 0.29 data to disk as fast as possible. This differs from our synthetic IZZ-NE 0.7 1.0 3.0% 3.4% 1.6% 0.02 experiments where we set the checkpoint interval to a constant for PZZ-UP 7.1 0.3 5.0% 5.2% 48.7% 0.37 all measurements. Nevertheless, to fairly compare the overhead of PZZ-NE 5.0 0.8 22.8% 25.4% 3.3% 0.02 different algorithms, we set the length of the checkpoint interval to BAZZ-UP 1.5 0.04 6.9% 7.2% 0.03% - be the same for all methods at each database size. BAZZ-NE 1.6 0.03 6.9% 8.0% - - Since each EC2 instance communicates with EBS over the net- NPP 7.1 1.9 23.6% 24.0% 97.4% 0.96 IPP 2.5 1.7 7.4% 7.8% 98.3% .85 work, there is a CPU cost to writing out state in the Asynchronous Raw Mutator 2.4 2.0 9.4% 8.0% 96.0% 1.00 Writer. To limit this effect, we set the thread affinity so that the a -UP: update handling phase; -NE: bulk negation phase Asynchronous Writer always runs on a separate core from the Mu- tator thread. As the number of cores per machine continues to in- Table 2: Profiling on synthetic workload, 320K updates/sec crease, we believe that it will become increasingly feasible to de- vote a core to durability in this way. A thorough evaluation of these methods on a single core remains future work. except for extremely high update rates. With NZZ and PZZ, the In addition to turning on the Asynchronous Writer, we also en- use of long word instructions during negation brings benefits over able logging for these experiments. To minimize synchronous I/O IZZ, which negates single bytes at a time. However, the benefits effects, we configured the Logger thread to perform group commit are much smaller for PZZ, given that it still interleaves state infor- in batches of 500 transactions. We also overlap computation with mation between small bit blocks. BAZZ, a variant that focuses on IO operations so that when the Logger is writing the actions of one optimizing bulk bit-array negation, dominates all other variants. batch of transactions, the Mutator is processing the next batch. In general, there is a tension between accelerating bulk bit-array In standard OLTP systems, it is common to use the ARIES re- negation and reducing per-update overhead. Table 2 shows pro- covery algorithm [21]. As a baseline for our TPC-C experiments, filing results for 320,000 updates per second. NZZ’s update han- we have implemented an optimized version of ARIES for main- dling phase has an L1D cache miss rate of 22.3% and an L2 cache memory databases. As FC applications do not have transactions miss rate of 24.6%. In addition, every update incurs 0.78 page in flight at points of consistency, checkpointing does not need to walks on average, given NZZ’s independent allocation of data struc- be aware of transaction aborts. This eliminates the need to main- tures. Bulk negation, on the other hand, benefits from prefetching tain undo information. In addition, since the database is entirely on these data structures. The cache miss rate is about 3% for both resident in main memory, there is no need to keep a dirty page ta- the L1D and the L2 cache; the DTLB miss rate is also low. IZZ ble. So in our scenario, ARIES reduces to physical redo logging trades bulk negation performance for better update performance. with periodic fuzzy checkpoints. To optimize it as much as possi- Its DTLB miss rate is much lower than that of NZZ. The ratio of ble, we compressed the format of physical log records by exploit- cache misses to updates for IZZ is much higher during the bulk ing schema information instead of recording explicit offsets and negation phase, however. PZZ pays more on cache misses and lengths whenever profitable. page walks at the update phase, but less during the bulk negation In the remainder of this section, we first compare the different phase. Meanwhile, BAZZ focuses solely on making negation more implementation options from Section 4 for our algorithms (Sec- compact, and dramatically improves performance despite a higher tion 5.2). After selecting the alternatives with the best performance, cache miss rate. As Figure 3 shows, this is an important effect at we observe how our new algorithms compare to existing methods most update rates. using both the Zipf and MMO workloads (Sections 5.3 and 5.4). Overall, we have observed that negation is the most significant Then, we report on how our methods affect application throughput source of overhead for Wait-Free Zigzag unless the update rate is in our TPC-C application (Section 5.5). Finally, we investigate the extremely high. Thus, BAZZ is the best variant for this algorithm impact of a further optimization, using large pages, on the relative under typical workloads. For example, at 320,000 updates per sec- performance of all algorithms (Section 5.6). ond, BAZZ exhibits about half as much overhead as NZZ and one third the overhead of IZZ. 5.2 Comparison of Implementation Variants In this section we compare the performance of the different im- 5.2.2 Wait-Free Ping-Pong plementations of our algorithms on the Zipf workload. To get a Figure 4 shows the overhead of the two variants of Wait-Free deeper understanding of the runtime characteristics, we profiled our Ping-Pong. NPP’s overhead is roughly six times higher than IPP’s implementation with the Intel VTune Performance Analyzer [15]. over all update rates. Like NZZ, NPP runs into similar problems Table 2 shows a subset of the statistics we collected from VTune. with DTLB and cache performance. Table 2 shows observation. It includes cycles per instruction (CPI) as well as various measures that NPP’s cycle-per-instruction ratio (CPI) is 2.8 times higher. to characterize the behavior of cache, DTLB, and page walks. For IPP, on the other hand, potentially incurs a cache miss on the reference, we display these statistics not only for all algorithms, but write to the application state, but then is guaranteed to find the other also for the raw Mutator program without checkpointing. words to be written on the same cache line. This has a positive effect in the L1D LOAD hit rate and eliminates most of the stalls 5.2.1 Wait-Free Zigzag on LOAD. IPP pays only a 43% performance overhead on top of Figure 3 shows the average overhead per checkpoint period of the raw Mutator, a great improvement compared to the 258% of the different variants. Both IZZ and PZZ are less efficient than NZZ, NPP. These numbers are very consistent across update rates. 272 

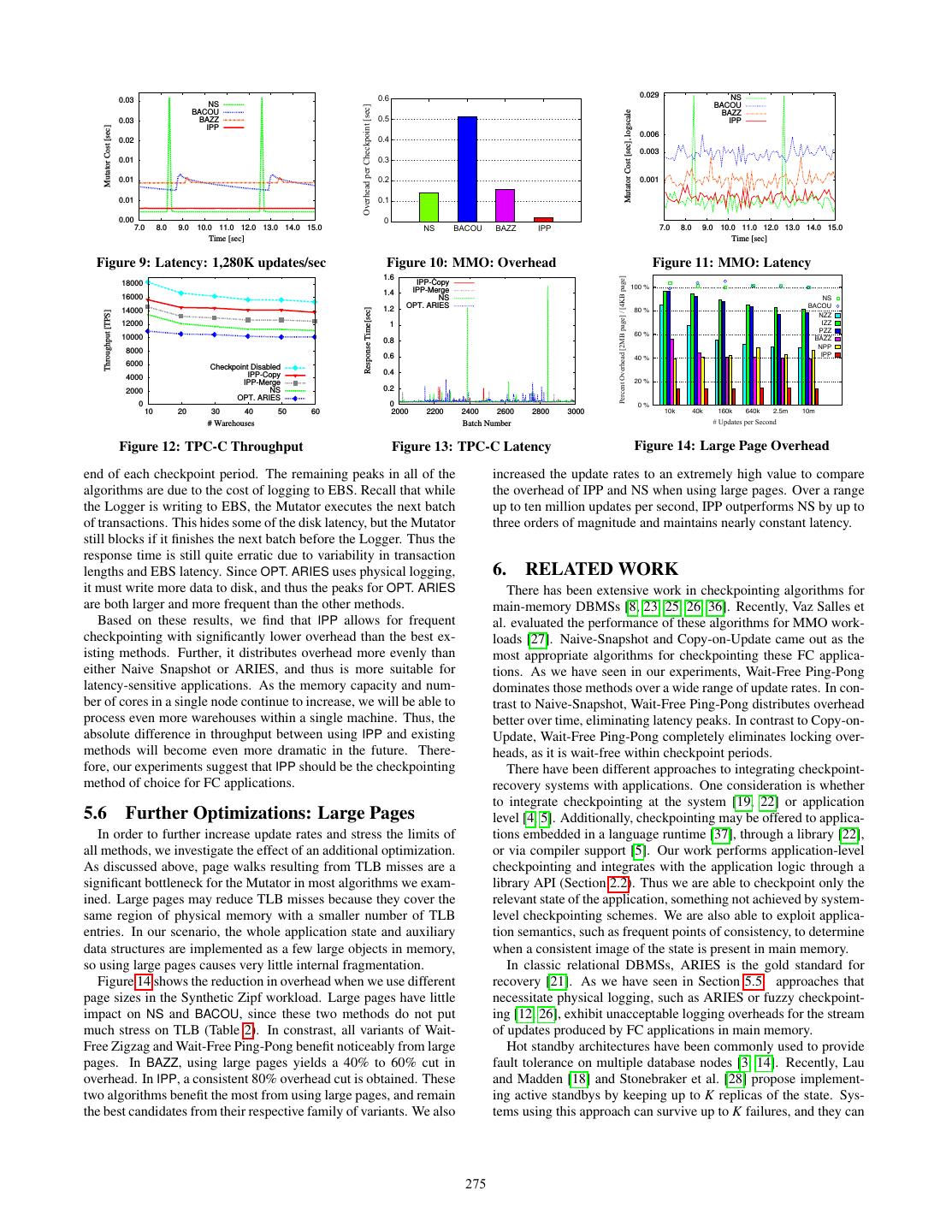
9 . 101 Overhead per Checkpoint [sec], logscale Overhead per Checkpoint [sec], logscale Overhead per Checkpoint [sec], logscale 0 0 10 10 100 -1 -1 10 10 10-1 10-2 10-2 -2 10 -3 NZZ -3 NS 10 10 10-3 IZZ BACOU PZZ NPP BAZZ -4 BAZZ -4 IPP -4 IPP 10 10 10 10000 100000 1e+06 10000 100000 1e+06 10000 100000 1e+06 # Updates per Second, logscale # Updates per Second, logscale # Updates per Second, logscale Figure 3: Wait-Free Zigzag Overhead Figure 4: Wait-Free Ping-Pong Overhead Figure 5: Zipf workload: Overhead In short, this experiment shows that IPP comfortably dominates of 200MB, IPP is the method with the lowest overhead for all but NPP over the whole spectrum of update rates evaluated. the highest update rates. Next, we validate that this trend is robust for a wide range of state sizes. 5.3 Synthetic Zipf Workload Scaling the State Size. To understand how our algorithms per- In this section, we compare the performance of our new algo- form for applications with larger state sizes, we scale the applica- rithms with the best cache-aware variants of Naive Snapshot (NS) tion state from 100 MB to 1.6 GB by adding more objects to the and Copy-on-Update (BACOU). We report numbers for the opti- state. Figures 6 and 7 show the overhead per checkpoint period for mized variants described in Section 4. For both BACOU and BAZZ, two different update rates. In each case, we scale the update rate the overhead numbers we report are lower bounds. Since we turned with the state size, so in Figure 6, for every second, we update a off the Asynchronous Writer, there is no lock contention between number of words equal to 0.08% of the state size. This corresponds the Mutator and the Asynchronous Writer in BACOU. We also do to 40,000 updates per second for 200 MB of state. In Figure 7 the not model reads, which discounts the small amount of per-read update rate corresponds to 2.56%, which is 1,280,000 updates per overhead for BAZZ. As shown below, IPP significantly dominates second for 200 MB of state. all these algorithms, so we do not explore these effects further. From these graphs we confirm that the trends we described above Checkpointing Overhead. Figure 5 shows the overhead of the al- for 200 MB of application state continue to hold for larger state gorithms for update rates between 10,000 and 5,120,000 updates sizes. When the update rate is fairly low (Figure 6), IPP has roughly per second. As expected, NS is essentially constant regardless an order of magnitude lower overhead than NS regardless of the of the number of updates, since it always copies the entire state. state size. On the other hand, when the update rate is very high This is the worst strategy for very low update rates since many un- (Figure 7), NS dominates all other algorithms, as it is insensitive changed cells get copied, but it dominates the other algorithms, to the number of updates. IPP continues to dominate BACOU and with the notable exception of IPP, for more than 160,000 updates BAZZ for larger state sizes regardless of the update rate. per second. This agrees with the results of [27] – when a large frac- Overhead Distribution. The above experiments already show that tion of the words gets updated, taking a checkpoint requires copy- IPP dominates BACOU and is preferable to NS for all but the high- ing most of the state anyway, and NS does this very efficiently. est update rates, but the overhead does not tell the whole story. As Among the existing algorithms, BACOU is the best strategy for discussed in Section 2.1, we also want the overhead to be uniformly low update rates [27], and it is four times faster than NS for 10,000 distributed over time. Figures 8 and 9 show the cost of the Mutator updates per second. Its overhead increases steadily with the up- thread for 320,000 and 1,280,000 updates per second, respectively. date rate, however, since it must lock and copy a memory block Points on the x-axis correspond to time intervals of 0.1 sec, or al- the first time the block is updated. As we increase the update rate, ternatively the time it takes to execute 32,000 or 128,000 updates. more blocks get updated, leading to higher locking and copying Each point in the graphs indicates the total time taken by the Mu- overheads. Even though updates are distributed using a Zipf distri- tator thread during one such interval. The graphs thus give us an bution, we have observed only a minor effect from the fact that up- indication of how work is distributed over time. dates have higher likelihood to hit hot words that fall into the same From these graphs, we see that NS has the worst overhead dis- memory block. This measurement corroborates prior simulation tribution of any of the algorithms. At 320,000 updates per second results [27]. We observe that BACOU is never the best algorithm (Figure 8) it has a latency peak of 29 ms during intervals when the for any update rate. It is always dominated by IPP, and it is also state is copied. BAZZ and BACOU have much smaller peaks, at 4 ms dominated by NS for high update rates. and 6 ms, respectively. These results indicate that there is a trade- IPP displays the best performance of any of the algorithms for off between the absolute overhead per checkpoint and the overhead all but the highest update rates. At 80,000 updates per second, it distribution. Recall from Figure 5 that NS has lower overhead than is nine times better than BAZZ and over an order of magnitude bet- BACOU at 320,000 updates per second, but the latter has a much ter than NS and BACOU. At 320,000 updates per second, the gap is lower spike. Fortunately, this tradeoff is not present for IPP, which still a factor of 8.4 with respect to BAZZ, 9.6 with respect to BACOU has a nearly constant overhead of 0.8 ms per 0.1 second interval at and three with respect to NS. IPP scales linearly with the number of 320,000 updates per second. This is because IPP only has to swap updates over the entire range of update rates, since the predominant pointers at the beginning of each checkpoint, and most of the work cost is updating each of two copies of the application state. The ab- is distributed evenly among the updates. solute overhead of the extra updates performed by IPP is extremely Figure 9 tells a slightly different story. The number of updates low, however, due to its cache-aware data layout and its wait-free executed during each point of the graph has increased to 128,000, operation. Unlike in BAZZ, in IPP the Mutator does not do any and this increases the baseline overhead for all of the strategies that bit negations, and the beginning of a checkpoint consists only of do some work per update. BAZZ shows the most dramatic increase swapping pointers. with a nearly constant overhead of 10 ms. BACOU and IPP also This experiment shows that, for our default application state size show modest overhead increases. Additionally, we can see the finer 273 

10 . Overhead per Checkpoint [sec], logscale Overhead per Checkpoint [sec], logscale NS 0.03 BACOU NS 100 BAZZ 100 BACOU IPP BAZZ IPP Mutator Cost [sec] -1 -1 0.02 10 10 10-2 10-2 0.01 NS -3 -3 BACOU 10 10 BAZZ IPP 100 200 400 800 1600 100 200 400 800 1600 7.0 8.0 9.0 10.0 11.0 12.0 13.0 14.0 15.0 Application State Size [MB], logscale Application State Size [MB], logscale Time [sec] Figure 6: Scaleup: 0.08% updates/sec Figure 7: Scaleup: 2.56% updates/sec Figure 8: Latency: 320K updates/sec structure of BACOU. There is a spike in the overhead at the end of simulated by server reboot, obtaining an average of 3.9 seconds out each checkpoint period, and then the overhead gradually decreases of five measurements. To simulate replaying the logical log, we can during the checkpoint. This is because BACOU only has to copy reapply the updates from the MMO trace file that occurred since a block the first time it is updated. As the checkpoint progresses, the last checkpoint. The maximum time to reapply those updates more blocks are already dirty and do not need to be copied. is equal to our checkpointing interval of 4.2 seconds, resulting in Significantly, the behavior of NS changes very little at the higher a worst-case recovery time of only 8.1 seconds. Given that current update rate. This is because all of the work done by NS is done MMO players regularly tolerate downtime [7], we think this is very at the end of a checkpoint period. The small increase in the figure reasonable for real systems. is due to the time necessary to apply the updates. This indicates a In short, the above experiments show that IPP is the method with distinction between the overhead incurred by NS and the overhead the lowest overhead and the best overhead distribution for a realistic incurred by the other algorithms. Aside from the small spikes for application with hundreds of thousands of updates per second. In BAZZ and BACOU, the other algorithms incur most of their cost addition, IPP exhibits short recovery times in this scenario. for work they do at each update. Thus as we increase the number of updates per unit of time, we expect their overhead to increase. 5.5 TPC-C Application Furthermore, the cost shown in each point of Figures 8 and 9 is dis- To validate the usefulness of our techniques in realistic FC ap- tributed across all of the updates in the 0.1 second increment. On plications with logging and checkpoint writing enabled, we com- the other hand, the entire cost of NS occurs between two updates pare the total overhead introduced by different checkpointing tech- at the end of each checkpoint period. Thus NS is insensitive to the niques in our main-memory implementation of the TPC-C bench- update rate, but it may force the system to block for a consider- mark [31]. We stress our implementation by processing as many able amount of time during the synchronous copy. As the height of transactions per second as possible and show results for the two NS’s latency spike is proportional to the application state size, this best methods for high update rates: Naive Snapshot (NS) and Wait- problem becomes worse when we scale the state size. Free Ping-Pong (IPP). In addition, we show the performance of our Overall, IPP has the most consistent overhead of any tested al- optimized version of ARIES (OPT. ARIES) as a baseline method. gorithm, and its total overhead is also lowest for all but the highest Figure 12 shows throughput as we increase the number of ware- update rates. Thus we believe that it best satisfies the requirements houses in TPC-C. Recall that in this measurement we keep the ra- for FC applications described in Section 2.1. tio of application state size to checkpoint interval fixed. In other words, we checkpoint as fast as possible to achieve short recov- 5.4 Synthetic MMO Workload ery times while ensuring that the checkpoint interval is equal for We also ran our experiments on a trace produced using our MMO all methods so as to allow for direct overhead comparison. Thus workload. Figure 10 shows the checkpoint overhead. In this case, the checkpoint sizes grow and so do the costs per checkpoint. The both wait-free strategies outperform BACOU. As expected, IPP per- maximum attainable performance is displayed by running the ap- forms the best, with nearly seven times less overhead than NS. plication with checkpointing disabled. Maximum throughput de- BAZZ is comparable to NS, even though it had higher overhead than clines as we scale the number of warehouses given that we must NS for 500,000 updates per second in the Zipf experiments. Part of operate over a larger database in main memory. the reason our new algorithms do so well in this case is that many We observe that the relative performance of all methods remains attributes were almost never updated. About 80 percent of the at- roughly unchanged as we scale the number of warehouses. The tributes are only updated in response to player actions, which are variants of IPP using the Copy and Merge methods described in human initiated and thus occur infrequently. This type of workload Section3.3 for merging the new updates with the previous check- is bad for NS, as it has to copy many cells that are never updated. point perform similarly. IPP-Copy always slightly outperforms Figure 11 shows the performance of each algorithm in the MMO IPP-Merge at the cost of maintaining an additional copy of the simulation over time. The Mutator cost is quite variable compared application state. Both IPP variants dominate NS, which in turn to Figure 8, due to the more realistic workload, but the trends are dominates OPT. ARIES. At 60 warehouses, application throughput the same. NS shows peaks of up to 29 ms, while IPP has a very low, decreases by 10.11% when using IPP-Copy, by 27.92% when using almost uniform latency of at most 0.9 ms. These results suggest that NS, and by 34.21% when using OPT. ARIES. Wait-Free Ping-Pong offers real advantages for MMO workloads. In order to understand the distribution of overhead in the TPC- Finally, we measured the recovery time for the MMO workload. C experiment, we also measured the response time of each of the We expected this to be the same for all of the algorithms, as they algorithms. Figure 13 reports these results, where each point corre- all store complete checkpoints on disk. In addition, this time is sponds to a batch of 500 transactions that are committed together. the same as for the synthetic workload, given that the application The response time is measured as the time between the start of one state size for both scenarios is the same. To measure this time, we batch of transactions and the start of the next. The large peaks in observed the time to reread the checkpoint from disk after a crash the response time of NS are due to the synchronous copy time at the 274 

11 . 0.6 0.029 NS 0.03 NS BACOU Overhead per Checkpoint [sec] BACOU Mutator Cost [sec], logscale BAZZ 0.03 BAZZ 0.5 IPP IPP Mutator Cost [sec] 0.006 0.02 0.4 0.003 0.01 0.3 0.01 0.2 0.001 0.01 0.1 0.00 0 7.0 8.0 9.0 10.0 11.0 12.0 13.0 14.0 15.0 NS BACOU BAZZ IPP 7.0 8.0 9.0 10.0 11.0 12.0 13.0 14.0 15.0 Time [sec] Time [sec] Figure 9: Latency: 1,280K updates/sec Figure 10: MMO: Overhead Figure 11: MMO: Latency 1.6 !"#$%#&'!()#$*#+,!-./0!1+2#3!4!-560!1+2#3 18000 IPP-Copy 100 % 1.4 IPP-Merge 16000 NS NS 1.2 OPT. ARIES BACOU Response Time[sec] 14000 80 % Throughput [TPS] NZZ 12000 1 IZZ 60 % PZZ 10000 0.8 BAZZ NPP 8000 IPP 0.6 40 % 6000 Checkpoint Disabled IPP-Copy 0.4 4000 20 % IPP-Merge 2000 NS 0.2 OPT. ARIES 0 0 0% 10 20 30 40 50 60 2000 2200 2400 2600 2800 3000 10k 40k 160k 640k 2.5m 10m # Warehouses Batch Number 7!81,+'#9!1#$!:#%;&, Figure 12: TPC-C Throughput Figure 13: TPC-C Latency Figure 14: Large Page Overhead end of each checkpoint period. The remaining peaks in all of the increased the update rates to an extremely high value to compare algorithms are due to the cost of logging to EBS. Recall that while the overhead of IPP and NS when using large pages. Over a range the Logger is writing to EBS, the Mutator executes the next batch up to ten million updates per second, IPP outperforms NS by up to of transactions. This hides some of the disk latency, but the Mutator three orders of magnitude and maintains nearly constant latency. still blocks if it finishes the next batch before the Logger. Thus the response time is still quite erratic due to variability in transaction lengths and EBS latency. Since OPT. ARIES uses physical logging, 6. RELATED WORK it must write more data to disk, and thus the peaks for OPT. ARIES There has been extensive work in checkpointing algorithms for are both larger and more frequent than the other methods. main-memory DBMSs [8, 23, 25, 26, 36]. Recently, Vaz Salles et Based on these results, we find that IPP allows for frequent al. evaluated the performance of these algorithms for MMO work- checkpointing with significantly lower overhead than the best ex- loads [27]. Naive-Snapshot and Copy-on-Update came out as the isting methods. Further, it distributes overhead more evenly than most appropriate algorithms for checkpointing these FC applica- either Naive Snapshot or ARIES, and thus is more suitable for tions. As we have seen in our experiments, Wait-Free Ping-Pong latency-sensitive applications. As the memory capacity and num- dominates those methods over a wide range of update rates. In con- ber of cores in a single node continue to increase, we will be able to trast to Naive-Snapshot, Wait-Free Ping-Pong distributes overhead process even more warehouses within a single machine. Thus, the better over time, eliminating latency peaks. In contrast to Copy-on- absolute difference in throughput between using IPP and existing Update, Wait-Free Ping-Pong completely eliminates locking over- methods will become even more dramatic in the future. There- heads, as it is wait-free within checkpoint periods. fore, our experiments suggest that IPP should be the checkpointing There have been different approaches to integrating checkpoint- method of choice for FC applications. recovery systems with applications. One consideration is whether to integrate checkpointing at the system [19, 22] or application 5.6 Further Optimizations: Large Pages level [4, 5]. Additionally, checkpointing may be offered to applica- In order to further increase update rates and stress the limits of tions embedded in a language runtime [37], through a library [22], all methods, we investigate the effect of an additional optimization. or via compiler support [5]. Our work performs application-level As discussed above, page walks resulting from TLB misses are a checkpointing and integrates with the application logic through a significant bottleneck for the Mutator in most algorithms we exam- library API (Section 2.2). Thus we are able to checkpoint only the ined. Large pages may reduce TLB misses because they cover the relevant state of the application, something not achieved by system- same region of physical memory with a smaller number of TLB level checkpointing schemes. We are also able to exploit applica- entries. In our scenario, the whole application state and auxiliary tion semantics, such as frequent points of consistency, to determine data structures are implemented as a few large objects in memory, when a consistent image of the state is present in main memory. so using large pages causes very little internal fragmentation. In classic relational DBMSs, ARIES is the gold standard for Figure 14 shows the reduction in overhead when we use different recovery [21]. As we have seen in Section 5.5, approaches that page sizes in the Synthetic Zipf workload. Large pages have little necessitate physical logging, such as ARIES or fuzzy checkpoint- impact on NS and BACOU, since these two methods do not put ing [12, 26], exhibit unacceptable logging overheads for the stream much stress on TLB (Table 2). In constrast, all variants of Wait- of updates produced by FC applications in main memory. Free Zigzag and Wait-Free Ping-Pong benefit noticeably from large Hot standby architectures have been commonly used to provide pages. In BAZZ, using large pages yields a 40% to 60% cut in fault tolerance on multiple database nodes [3, 14]. Recently, Lau overhead. In IPP, a consistent 80% overhead cut is obtained. These and Madden [18] and Stonebraker et al. [28] propose implement- two algorithms benefit the most from using large pages, and remain ing active standbys by keeping up to K replicas of the state. Sys- the best candidates from their respective family of variants. We also tems using this approach can survive up to K failures, and they can 275 

12 .also use those replicas to speed up query processing. Our check- [11] N. Gupta, A. J. Demers, J. Gehrke, P. Unterbrunner, and W. M. pointing algorithms can be used in tandem with these approaches to White. Scalability for virtual worlds. In ICDE, 2009. bulk-copy state during recovery or when the set of replicas changes. [12] R. Hagmann. A Crash Recovery Scheme for a Memory-Resident Many replicated systems (such as VoltDB [33]) also include check- Database System. IEEE Transactions on Computers, 35(9):839–843, 1986. pointing in order to ensure durability in the event that all replicas [13] M. Herlihy. Wait-free Synchronization. ACM TOPLAS, fail (e.g., due to a power outage). 13(1):124–149, 1991. [14] S.-O. Hvasshovd, O. Torbjornsen, S. Bratsberg, and P. Holager. The 7. CONCLUSIONS ClustRa Telecom Database: High Availability, High Throughput, and Real-Time Response. In Proc. VLDB, 1995. In this paper, we have proposed two novel checkpoint recovery [15] Intel VTune Performance Analyzer. algorithms optimized for frequently-consistent applications. Both http://software.intel.com/en-us/intel-vtune. methods implement highly granular tracking of updates to elimi- [16] Jason Gregory. Game Engine Architecture (Section 7.5). A K Peters, nate latency spikes due to bulk state copying. Moreover, the wait- 2009. free properties of our methods within a checkpoint period allow [17] E. P. C. Jones, D. J. Abadi, and S. Madden. Low overhead them to benefit significantly from cache-aware data layout opti- concurrency control for partitioned main memory databases. In Proc. mizations, dramatically reducing overhead. Wait-Free Zigzag elim- SIGMOD, 2010. inates locking overhead by keeping an untouched copy of the state [18] E. Lau and S. Madden. An Integrated Approach to Recovery and High Availability in an Updatable, Distributed Data Warehouse. In during a checkpoint period. Wait-Free Ping-Pong improves both Proc. VLDB, 2006. overhead and latency even more by using additional main memory [19] M. Litzkow, T. Tannenbaum, J. Basney, and M. Livny. Checkpoint space. Our thorough experimental evaluation shows that Wait-Free and Migration of Unix Processes in the Condor Distributed Ping-Pong outperforms the state of the art in terms of overhead Processing System. Technical Report 1346, University of as well as maximum latency by over an order of magnitude. In Winsconsin-Madison, 1997. fact, given that Wait-Free Ping-Pong dominates Copy-on-Update [20] T. MacDonald. Solid-state Storage Not Just a Flash in the Pan. and may have significantly lower overhead than Naive-Snapshot Storage Magazine, 2007. http://searchStorage.techtarget.com/ over a wide range of update rates, our new algorithm should be magazineFeature/0,296894,sid5_gci1276095,00.html . [21] C. Mohan, D. Haderle, B. Lindsay, H. Pirahesh, and P. Schwarz. considered as an alternative wherever copy on write methods have ARIES: A Transaction Recovery Method Supporting been used in the past. Fine-Granularity Locking and Partial Rollbacks Using Write-Ahead Acknowledgments. We would like to thank our shepherd, Logging. ACM TODS, 17(1):94–162, 1992. Daniel Abadi, for his detailed and insightful comments as well [22] J. S. Plank, M. Beck, G. Kingsley, and K. Li. Libckpt: Transparent as the anonymous reviewers for their feedback. This material is Checkpointing under UNIX. In Proc. USENIX Winter Technical based upon work supported by the New York State Foundation for Conference, 1995. Science, Technology, and Innovation under Agreement C050061, [23] C. Pu. On-the-Fly, Incremental, Consistent Reading of Entire by the National Science Foundation under Grants 0725260 and Databases. Algorithmica, 1:271–287, 1986. [24] RamSan-400 Specifications. 0534404, by the iAd Project funded by the Research Council of http://www.ramsan.com/products/ramsan-400.htm . Norway, by the AFOSR under Award FA9550-10-1-0202, and by [25] D. Rosenkrantz. Dynamic Database Dumping. In Proc. SIGMOD, Microsoft. Any opinions, findings and conclusions or recommen- 1978. dations expressed in this material are those of the authors and do [26] K. Salem and H. Garcia-Molina. Checkpointing Memory-Resident not necessarily reflect the views of the funding agencies. Databases. In Proc. ICDE, 1989. [27] M. V. Salles, T. Cao, B. Sowell, A. Demers, J. Gehrke, C. Koch, and 8. REFERENCES W. White. An evaluation of checkpoint recovery for massively [1] A. Ailamaki, D. DeWitt, M. Hill, and M. Skounakis. Weaving multiplayer online games. In Proc. VLDB, 2009. Relations for Cache Performance. In Proc. VLDB, 2001. [28] M. Stonebraker, S. Madden, D. Abadi, S. Harizopoulos, N. Hachem, [2] P. Alvaro, T. Condie, N. Conway, K. Elmeleegy, J. M. Hellerstein, and P. Helland. The End of an Architectural Era (It‘s Time for a and R. C. Sears. BOOM: Data-centric programming in the Complete Rewrite). In Proc. VLDB, 2007. datacenter. Technical Report UCB/EECS-2009-113, EECS [29] T. Strohman and W. B. Croft. Efficient Document Retrieval in Main Department, University of California, Berkeley, 2009. Memory. In Proc. SIGIR, 2007. [3] J. Bartlett, J. Gray, and B. Horst. Fault tolerance in tandem computer [30] A. Thomson and D. Abadi. The case for determinism in database systems. Technical Report 86.2, PN87616, Tandem Computers, 1986. systems. In Proc. VLDB, 2010. [4] A. Beguelin, E. Seligman, and P. Stephan. Application Level Fault [31] Transaction Processing Council. TPC Benchmark(TM) C, 2010. Tolerance in Heterogeneous Networks of Workstations. Journal of http://www.tpc.org/tpcc/spec/tpcc_current.pdf. Parallel and Distributed Computing, 43(2):147–155, 1997. [32] P. Unterbrunner, G. Giannikis, G. Alonso, D. Fauser, and [5] G. Bronevetsky, M. Schulz, P. Szwed, D. Marques, and K. Pingali. D. Kossmann. Predictable performance for unpredictable workloads. Application-level Checkpointing for Shared Memory Programs. In PVLDB, 2(1):706–717, 2009. Proc. ASPLOS, 2004. [33] VoltDB. http://voltdb.com/product. [6] K. M. Chandy and L. Lamport. Distributed Snapshots: Determining [34] G. Wang, M. V. Salles, B. Sowell, X. Wang, T. Cao, A. Demers, Global States of Distributed Systems. ACM TOCS, 3(1):63–75, 1985. J. Gehrke, and W. White. Behavioral simulations in mapreduce. In [7] R. Cortez. World Class Networking Infrastructure. In Proc. Austin Proc. VLDB, 2010. GDC, 2007. [35] W. White, A. Demers, C. Koch, J. Gehrke, and R. Rajagopalan. [8] D. J. DeWitt, R. Katz, F. Olken, L. Shapiro, M. Stonebraker, and Scaling Games to Epic Proportions. In Proc. SIGMOD, 2007. D. Wood. Implementation Techniques for Main Memory Database [36] A. Whitney, D. Shasha, and S. Apter. High Volume Transaction Systems. In Proc. SIGMOD, 1984. Processing Without Concurrency Control, Two Phase Commit, SQL, [9] M. Elnozahy, L. Alvisi, Y.-M. Wang, and D. B. Johnson. A Survey of or C++. In Proc. HPTS, 1997. Rollback-Recovery Protocols in Message-Passing Systems. ACM [37] G. Zheng, L. Shi, and L. V. Kale. FTC-Charm++: an In-Memory Computing Surveys, 34(3):375–408, 2002. Checkpoint-Based Fault Tolerant Runtime for Charm++ and MPI. In [10] H. F. Guðjónsson. The Server Technology of EVE Online: How to Proc. CLUSTER, 2004. Cope With 300,000 Players on One Server. In Proc. Austin GDC, 2008. 276