Eddies: Continuously Adaptive Query Processing

1 . Eddies: Continuously Adaptive Query Processing Ron Avnur Joseph M. Hellerstein University of California, Berkeley avnur@cohera.com, jmh@cs.berkeley.edu  ✂✁☎✄✝✆✟✞✡✠☎☛☞✆ In large federated and shared-nothing databases, resources can exhibit widely fluctuating characteristics. Assumptions made at the time a query is submitted will rarely hold throughout the duration of query processing. As a result, traditional static query optimization and execution techniques are ineffective in these environments. In this paper we introduce a query processing mechanism called an eddy, which continuously reorders operators in a query plan as it runs. We characterize the moments of sym- metry during which pipelined joins can be easily reordered, and the synchronization barriers that require inputs from dif- ferent sources to be coordinated. By combining eddies with appropriate join algorithms, we merge the optimization and execution phases of query processing, allowing each tuple to have a flexible ordering of the query operators. This flexibility is controlled by a combination of fluid dynamics and a simple learning algorithm. Our initial implementation demonstrates Figure 1: An eddy in a pipeline. Data flows into the eddy from promising results, with eddies performing nearly as well as input relations ✚✜✛✝✢ and ✣ . The eddy routes tuples to opera- a static optimizer/executor in static scenarios, and providing tors; the operators run as independent threads, returning tuples dramatic improvements in dynamic execution environments. to the eddy. The eddy sends a tuple to the output only when ✌✎✍✑✏ ✆✟✞✓✒✕✔✕✖✗☛✘✆✝✙ ✒ ✏ it has been handled by all the operators. The eddy adaptively chooses an order to route each tuple through the operators. There is increasing interest in query engines that run at un- precedented scale, both for widely-distributed information re- meric data sets is fairly well understood, and there has been sources, and for massively parallel database systems. We are initial work on estimating statistical properties of static sets of building a system called Telegraph, which is intended to run data with complex types [Aok99] and methods [BO99]. But queries over all the data available on line. A key requirement federated data often comes without any statistical summaries, of a large-scale system like Telegraph is that it function ro- and complex non-alphanumeric data types are now widely in bustly in an unpredictable and constantly fluctuating environ- use both in object-relational databases and on the web. In these ment. This unpredictability is endemic in large-scale systems, scenarios – and even in traditional static relational databases – because of increased complexity in a number of dimensions: selectivity estimates are often quite inaccurate. Hardware and Workload Complexity: In wide-area envi- User Interface Complexity: In large-scale systems, many ronments, variabilities are commonly observable in the bursty queries can run for a very long time. As a result, there is in- performance of servers and networks [UFA98]. These systems terest in Online Aggregation and other techniques that allow users to “Control” properties of queries while they execute, based on refining approximate results [HAC ✤ 99]. often serve large communities of users whose aggregate be- havior can be hard to predict, and the hardware mix in the wide area is quite heterogeneous. Large clusters of computers can For all of these reasons, we expect query processing param- exhibit similar performance variations, due to a mix of user eters to change significantly over time in Telegraph, typically requests and heterogeneous hardware evolution. Even in to- many times during a single query. As a result, it is not appro- tally homogeneous environments, hardware performance can priate to use the traditional architecture of optimizing a query be unpredictable: for example, the outer tracks of a disk can and then executing a static query plan: this approach does exhibit almost twice the bandwidth of inner tracks [Met97]. not adapt to intra-query fluctuations. Instead, for these en- Data Complexity: Selectivity estimation for static alphanu- vironments we want query execution plans to be reoptimized regularly during the course of query processing, allowing the system to adapt dynamically to fluctuations in computing re- Permission to make digital or hard copies of part or all of this sources, data characteristics, and user preferences. work or personal or classroom use is granted without fee In this paper we present a query processing operator called provided that copies are not made or distributed for profit or an eddy, which continuously reorders the application of pipe- commercial advantage and that copies bear this notice and the full citation on the first page. To copy otherwise, to republish, to post on servers, or to redistribute to lists, requires prior specific permission and/or a fee. MOD 2000, Dallas, T X USA © ACM 2000 1-58113-218-2/00/05 . . .$5.00 261 

2 .lined operators in a query plan, on a tuple-by-tuple basis. An this paper we narrow our focus somewhat to concentrate on eddy is an ✥ -ary tuple router interposed between ✥ data sources the initial, already difficult problem of run-time operator re- and a set of query processing operators; the eddy encapsulates ordering in a single-site query executor; that is, changing the the ordering of the operators by routing tuples through them effective order or “shape” of a pipelined query plan tree in the dynamically (Figure 1). Because the eddy observes tuples en- face of changes in performance. tering and exiting the pipelined operators, it can adaptively In our discussion we will assume that some initial query change its routing to effect different operator orderings. In this plan tree will be constructed during parsing by a naive pre- paper we present initial experimental results demonstrating the optimizer. This optimizer need not exercise much judgement viability of eddies: they can indeed reorder effectively in the since we will be reordering the plan tree on the fly. However face of changing selectivities and costs, and provide benefits by constructing a query plan it must choose a spanning tree of in the case of delayed data sources as well. the query graph (i.e. a set of table-pairs to join) [KBZ86], and Reoptimizing a query execution pipeline on the fly requires algorithms for each of the joins. We will return to the choice of significant care in maintaining query execution state. We high- join algorithms in Section 2, and defer to Section 6 the discus- light query processing stages called moments of symmetry, dur- sion of changing the spanning tree and join algorithms during ing which operators can be easily reordered. We also describe processing. synchronization barriers in certain join algorithms that can re- We study a standard single-node object-relational query pro- strict performance to the rate of the slower input. Join algo- cessing system, with the added capability of opening scans and rithms with frequent moments of symmetry and adaptive or indexes from external data sets. This is becoming a very com- non-existent barriers are thus especially attractive in the Tele- mon base architecture, available in many of the commercial graph environment. We observe that the Ripple Join family object-relational systems (e.g., IBM DB2 UDB [RPK ✤ 99], [HH99] provides efficiency, frequent moments of symmetry, Informix Dynamic Server UDO [SBH98]) and in federated and adaptive or nonexistent barriers for equijoins and non- database systems (e.g., Cohera [HSC99]). We will refer to equijoins alike. these non-resident tables as external tables. We make no as- The eddy architecture is quite simple, obviating the need for sumptions limiting the scale of external sources, which may be traditional cost and selectivity estimation, and simplifying the arbitrarily large. External tables present many of the dynamic logic of plan enumeration. Eddies represent our first step in a challenges described above: they can reside over a wide-area larger attempt to do away with traditional optimizers entirely, network, face bursty utilization, and offer very minimal infor- in the hope of providing both run-time adaptivity and a reduc- mation on costs and statistical properties. tion in code complexity. In this paper we focus on continuous ✌✗✦✮❂✩❃❅❄ ✯❁✞ ❄ ✙ ✯✵❆ operator reordering in a single-site query processor; we leave other optimization issues to our discussion of future work. Before introducing eddies, in Section 2 we discuss the prop- ✌✗✦✧✌✩★ ✖ ✏☎✪✬✫ ✙✮✭✰✯✲✱✴✳ ✖✗☛☞✆✟✖☎✠✵✆✝✙ ✒ ✏ ✄ erties of query processing algorithms that allow (or disallow) them to be frequently reordered. We then present the eddy ar- Three properties can vary during query processing: the costs chitecture, and describe how it allows for extreme flexibility of operators, their selectivities, and the rates at which tuples in operator ordering (Section 3). Section 4 discusses policies arrive from the inputs. The first and third issues commonly for controlling tuple flow in an eddy. A variety of experiments occur in wide area environments, as discussed in the literature in Section 4 illustrate the robustness of eddies in both static [AFTU96, UFA98, IFF ✤ 99]. These issues may become more and dynamic environments, and raise some questions for fu- common in cluster (shared-nothing) systems as they “scale ture work. We survey related work in Section 5, and in Sec- out” to thousands of nodes or more [Bar99]. tion 6 lay out a research program to carry this work forward. Run-time variations in selectivity have not been widely dis- ✶ ★ ✯✵✒✗✞✓✔✺✯❁✞✓✠✗✁✗✙✮✳ ✙ ✆❈❇❉✒☎❊●❋❍✳ ✠ ✏ ✄ cussed before, but occur quite naturally. They commonly arise due to correlations between predicates and the order of tuple A basic challenge of run-time reoptimization is to reorder pipe- delivery. For example, consider an employee table clustered lined query processing operators while they are in flight. To by ascending age, and a selection salary > 100000; age change a query plan on the fly, a great deal of state in the var- and salary are often strongly correlated. Initially the selection ious operators has to be considered, and arbitrary changes can will filter out most tuples delivered, but that selectivity rate require significant processing and code complexity to guaran- will change as ever-older employees are scanned. Selectivity tee correct results. For example, the state maintained by an over time can also depend on performance fluctuations: e.g., in operator like hybrid hash join [DKO ✤ 84] can grow as large as a parallel DBMS clustered relations are often horizontally par- the size of an input relation, and require modification or re- titioned across disks, and the rate of production from various computation if the plan is reordered while the state is being partitions may change over time depending on performance constructed. characteristics and utilization of the different disks. Finally, By constraining the scenarios in which we reorder opera- Online Aggregation systems explicitly allow users to control tors, we can keep this work to a minimum. Before describing the order in which tuples are delivered based on data prefer- eddies, we study the state management of various join algo- ences [RRH99], resulting in similar effects. ✌✗✦✮✶  ✂✞✷☛✹✸✺✙ ✆✻✯✵☛☞✆✟✖✺✞✓✠☎✳✼ ✽✄✝✄✾✖✴✭❀✿❁✆✝✙ ✒ ✏ ✄ rithms; this discussion motivates the eddy design, and forms the basis of our approach for reoptimizing cheaply and con- tinuously. As a philosophy, we favor adaptivity over best-case Telegraph is intended to efficiently and flexibly provide both performance. In a highly variable environment, the best-case distributed query processing across sites in the wide area, and scenario rarely exists for a significant length of time. So we parallel query processing in a large shared-nothing cluster. In 262 

3 .will sacrifice marginal improvements in idealized query pro- cessing algorithms when they prevent frequent, efficient reop- timization. ✶■✦✧✌❑❏ ❇ ✏ ☛✵✸✺✞✓✒ ✏ ✙ ▲☞✠✵✆✝✙ ✒ ✏◆▼ ✠✵✞✬✞✷✙ ✯☎✞✓✄ Binary operators like joins often capture significant state. A particular form of state used in such operators relates to the interleaving of requests for tuples from different inputs. As an example, consider the case of a merge join on two sorted, duplicate-free inputs. During processing, the next tu- ple is always consumed from the relation whose last tuple had the lower value. This significantly constrains the order in which tuples can be consumed: as an extreme example, con- Figure 2: Tuples generated by a nested-loops join, reordered at sider the case of a slowly-delivered external relation slowlow two moments of symmetry. Each axis represents the tuples of with many low values in its join column, and a high-bandwidth the corresponding relation, in the order they are delivered by but large local relation fasthi with only high values in its join an access method. The dots represent tuples generated by the join, some of which may be eliminated by the join predicate. The numbers correspond to the barriers reached, in order. ◗✘❘ column – the processing of fasthi is postponed for a long time and ◗✘❙ are the cursor positions maintained by the correspond- while consuming many tuples from slowlow. Using terminol- ogy from parallel programming, we describe this phenomenon as a synchronization barrier: one table-scan waits until the ing inputs at the time of the reorderings. other table-scan produces a value larger than any seen before. In general, barriers limit concurrency – and hence perfor- the iterator producing ✚ notes its current cursor position ◗❚❘ . mance – when two tasks take different amounts of time to com- In that case, the new “outer” loop on ✢ begins rescanning by plete (i.e., to “arrive” at the barrier). Recall that concurrency fetching the first tuple of ✢ , and ✚ is scanned from ◗❚❘ to the arises even in single-site query engines, which can simultane- end. This can be repeated indefinitely, joining ✢ tuples with ously carry out network I/O, disk I/O, and computation. Thus all tuples in ✚ from position ◗❚❘ to the end. Alternatively, at it is desirable to minimize the overhead of synchronization the end of some loop over ✚ (i.e. at a moment of symmetry), barriers in a dynamic (or even static but heterogeneous) per- the order of inputs can be swapped again by remembering the formance environment. Two issues affect the overhead of bar- current position of ✢ , and repeatedly joining the next tuple in riers in a plan: the frequency of barriers, and the gap between ✚ (starting at ◗ ❘ ) with tuples from ✢ between ◗ ❙ and the end. arrival times of the two inputs at the barrier. We will see in up- Figure 2 depicts this scenario, with two changes of ordering. coming discussion that barriers can often be avoided or tuned Some operators like the pipelined hash join of [WA91] have no by using appropriate join algorithms. barriers whatsoever. These operators are in constant symme- ✶■✦✮✶ ❖ ✒✴✭✰✯ ✏ ✆✻✄●✒☎❊ ❏ ❇✵✭❀✭✰✯✹✆✟✞✓❇ try, since the processing of the two inputs is totally decoupled. Moments of symmetry allow reordering of the inputs to a Note that the synchronization barrier in merge join is stated single binary operator. But we can generalize this, by noting in an order-independent manner: it does not distinguish be- that since joins commute, a tree of ✥❱❯❳❲ binary joins can be tween the inputs based on any property other than the data viewed as a single ✥ -ary join. One could easily implement a they deliver. Thus merge join is often described as a symmet- doubly-nested-loops join operator over relations ✚ , ✢ and ✣ , ric operator, since its two inputs are treated uniformly1 . This is and it would have moments of complete symmetry at the end not the case for many other join algorithms. Consider the tra- of each loop of ✢ . At that point, all three inputs could be re- ditional nested-loops join, for example. The “outer” relation ordered (say to ✣ then ✚ then ✢ ) with a straightforward exten- in a nested-loops join is synchronized with the “inner” rela- sion to the discussion above: a cursor would be recorded for tion, but not vice versa: after each tuple (or block of tuples) each input, and each loop would go from the recorded cursor is consumed from the outer relation, a barrier is set until a full position to the end of the input. scan of the inner is completed. For asymmetric operators like The same effect can be obtained in a binary implementa- nested-loops join, performance benefits can often be obtained tion with two operators, by swapping the positions of binary by reordering the inputs. operators: effectively the plan tree transformation would go When a join algorithm reaches a barrier, it has declared the in steps, from ❨✡✚❬❩❪❭✴❫❴✢❛❵❜❩❪❭☎❝❴✣ to ❨✡✚❞❩❪❭❁❝❴✣❡❵❀❩❪❭✴❫❢✢ and end of a scheduling dependency between its two input rela- then to ❨❣✣❤❩❪❭☎❝❱✚✐❵✜❩❪❭✺❫❥✢ . This approach treats an operator tions. In such cases, the order of the inputs to the join can of- and its right-hand input as a unit (e.g., the unit ❦ ❩❪❭ ❝ ✣♠❧ ), and ten be changed without modifying any state in the join; when swaps units; the idea has been used previously in static query this is true, we refer to the barrier as a moment of symmetry. optimization schemes [IK84, KBZ86, Hel98]. Viewing the sit- Let us return to the example of a nested-loops join, with outer uation in this manner, we can naturally consider reordering relation ✚ and inner relation ✢ . At a barrier, the join has com- multiple joins and their inputs, even if the join algorithms are pleted a full inner loop, having joined each tuple in a subset different. In our query ❨✡✚❳❩❪❭ ❫ ✢♥❵❛❩❪❭ ❝ ✣ , we need ❦ ❩❪❭ ❫ ✢♦❧ and of ✚ with every tuple in ✢ . Reordering the inputs at this point ❦ ❩❪❭☎❝✐✣♠❧ to be mutually commutative, but do not require them can be done without affecting the join algorithm, as long as to be the same join algorithm. We discuss the commutativity € If there are duplicates in a merge join, the duplicates are handled by an of join algorithms further in Section 2.2.2. Note that the combination of commutativity and moments asymmetric but usually small nested loop. For purposes of exposition, we can ignore this detail here. of symmetry allows for very aggressive reordering of a plan 263 

4 .tree. A single ✥ -ary operator representing a reorderable plan have infrequent moments of symmetry and imbalanced barri- tree is therefore an attractive abstraction, since it encapsulates ers, making them undesirable as well. any ordering that may be subject to change. We will exploit The other algorithms we consider are based on frequent- this abstraction directly, by interposing an ✥ -ary tuple router ly-symmetric versions of traditional iteration, hashing and in- (an “eddy”) between the input tables and the join operators. dexing schemes, i.e., the Ripple Joins [HH99]. Note that the ✶■✦✮✶■✦✧✌q♣ ✒✺✙ ✏ ✄●✠ ✏ ✔ ✍✑✏ ✔✗✯✵rs✯✵✄ original pipelined hash join of [WA91] is a constrained ver- sion of the hash ripple join. The external hashing extensions Nested-loops joins can take advantage of indexes on the in- of [UF99, IFF ✤ 99] are directly applicable to the hash rip- ner relation, resulting in a fairly efficient pipelining join algo- ple join, and [HH99] treats index joins as a special case as rithm. An index nested-loops join (henceforth an “index join”) well. For non-equijoins, the block ripple join algorithm is ef- is inherently asymmetric, since one input relation has been fective, having frequent moments of symmetry, particularly pre-indexed. Even when indexes exist on both inputs, chang- at the beginning of processing [HH99]. Figure 3 illustrates ing the choice of inner and outer relation “on the fly” is prob- block, index and hash ripple joins; the reader is referred to lematic2 . Hence for the purposes of reordering, it is simpler [HH99, IFF ✤ 99, UF99] for detailed discussions of these al- to think of an index join as a kind of unary selection operator gorithms and their variants. These algorithms are adaptive on the unindexed input (as in the join of ✢ and t in Figure 1). without sacrificing much performance: [UF99] and [IFF ✤ 99] The only distinction between an index join and a selection is demonstrate scalable versions of hash ripple join that perform that – with respect to the unindexed relation – the selectivity competitively with hybrid hash join in the static case; [HH99] of the join node may be greater than 1. Although one cannot shows that while block ripple join can be less efficient than swap the inputs to a single index join, one can reorder an index nested-loops join, it arrives at moments of symmetry much join and its indexed relation as a unit among other operators in more frequently than nested-loops joins, especially in early a plan tree. Note that the logic for indexes can be applied to stages of processing. In [AH99] we discuss the memory over- external tables that require bindings to be passed; such tables heads of these adaptive algorithms, which can be larger than may be gateways to, e.g., web pages with forms, GIS index standard join algorithms. systems, LDAP servers and so on [HKWY97, FMLS99]. Ripple joins have moments of symmetry at each “corner” ✶■✦✮✶■✦✮✶ ❋✉✸☎❇✹✄✟✙ ☛☞✠✗✳✴❋❍✞✓✒✴✿✴✯☎✞❪✆✝✙ ✯✵✄☞✈✼❋✉✞✡✯❁✔✺✙ ☛☞✠✵✆✻✯✵✄☞✈✴✇❛✒✴✭❀✭❀✖❁✆✻✠✵✆✝✙ ❄ ✙ ✆❈❇ of a rectangular ripple in Figure 3, i.e., whenever a prefix of the input stream ✚ has been joined with all tuples in a prefix Clearly, a pre-optimizer’s choice of an index join algorithm of input stream ✢ and vice versa. For hash ripple joins and in- constrains the possible join orderings. In the ✥ -ary join view, dex joins, this scenario occurs between each consecutive tuple an ordering constraint must be imposed so that the unindexed consumed from a scanned input. Thus ripple joins offer very join input is ordered before (but not necessarily directly be- frequent moments of symmetry. fore) the indexed input. This constraint arises because of a Ripple joins are attractive with respect to barriers as well. physical property of an input relation: indexes can be probed Ripple joins were designed to allow changing rates for each but not scanned, and hence cannot appear before their cor- input; this was originally used to proactively expend more pro- responding probing tables. Similar but more complex con- cessing on the input relation with more statistical influence on straints can arise in preserving the ordered inputs to a merge intermediate results. However, the same mechanism allows re- join (i.e., preserving “interesting orders”). active adaptivity in the wide-area scenario: a barrier is reached The applicability of certain join algorithms raises additional at each corner, and the next corner can adaptively reflect the constraints. Many join algorithms work only for equijoins, and relative rates of the two inputs. For the block ripple join, the will not work on other joins like Cartesian products. Such al- next corner is chosen upon reaching the previous corner; this gorithms constrain reorderings on the plan tree as well, since can be done adaptively to reflect the relative rates of the two they always require all relations mentioned in their equijoin inputs over time. predicates to be handled before them. In this paper, we con- The ripple join family offers attractive adaptivity features sider ordering constraints to be an inviolable aspect of a plan at a modest overhead in performance and memory footprint. tree, and we ensure that they always hold. In Section 6 we Hence they fit well with our philosophy of sacrificing marginal sketch initial ideas on relaxing this requirement, by consider- speed for adaptability, and we focus on these algorithms in ing multiple join algorithms and query graph spanning trees. ✶■✦✮✶■✦✮❂①♣ ✒✺✙ ✏  ✂✳ ②✗✒✗✞✓✙ ✆✟✸✺✭✰✄●✠ ✏ ✔ ★ ✯✹✒✗✞✷✔✗✯☎✞✓✙ ✏ ② Telegraph. ❂ ★ ✙ ❄ ✯☎✞✓✄❡✠ ✏ ✔◆⑧■✔✺✔✴✙ ✯✹✄ In order for an eddy to be most effective, we favor join algo- rithms with frequent moments of symmetry, adaptive or non- The above discussion allows us to consider easily reordering existent barriers, and minimal ordering constraints: these al- query plans at moments of symmetry. In this section we pro- gorithms offer the most opportunities for reoptimization. In ceed to describe the eddy mechanism for implementing re- [AH99] we summarize the salient properties of a variety of ordering in a natural manner during query processing. The join algorithms. Our desire to avoid blocking rules out the use techniques we describe can be used with any operators, but al- of hybrid hash join, and our desire to minimize ordering con- gorithms with frequent moments of symmetry allow for more straints and barriers excludes merge joins. Nested loops joins frequent reoptimization. Before discussing eddies, we first in- ③ troduce our basic query processing environment. In unclustered indexes, the index ordering is not the same as the scan order- ing. Thus after a reordering of the inputs it is difficult to ensure that – using the ❂■✦✧✌✩★ ✙ ❄ ✯☎✞ ④ ⑤⑦⑥ ④ terminology of Section 2.2 – lookups on the index of the new “inner” relation produce only tuples between and the end of . We implemented eddies in the context of River [AAT ✤ 99], a shared-nothing parallel query processing framework that dy- 264 

5 .Figure 3: Tuples generated by block, index, and hash ripple join. In block ripple, all tuples are generated by the join, but some may be eliminated by the join predicate. The arrows for index and hash ripple join represent the logical portion of the cross-product space checked so far; these joins only expend work on tuples satisfying the join predicate (black dots). In the hash ripple diagram, one relation arrives 3 ⑨ faster than the other. namically adapts to fluctuations in performance and workload. that they are relatively low selectivity), followed by as many River has been used to robustly produce near-record perfor- arbitrary non-equijoin edges as required to complete a span- mance on I/O-intensive benchmarks like parallel sorting and ning tree. hash joins, despite heterogeneities and dynamic variability in Given a spanning tree of the query graph, the pre-optimizer hardware and workloads across machines in a cluster. For needs to choose join algorithms for each edge. Along each more details on River’s adaptivity and parallelism features, the equijoin edge it can use either an index join if an index is avail- interested reader is referred to the original paper on the topic able, or a hash ripple join. Along each non-equijoin edge it can [AAT ✤ 99]. In Telegraph, we intend to leverage the adaptabil- use a block ripple join. ity of River to allow for dynamic shifting of load (both query These are simple heuristics that we use to allow us to focus processing and data delivery) in a shared-nothing parallel en- on our initial eddy design; in Section 6 we present initial ideas vironment. But in this paper we restrict ourselves to basic on making spanning tree and algorithm decisions adaptively. (single-site) features of eddies; discussions of eddies in par- ❂■✦✮✶   ✏ ⑧■✔✺✔✺❇❜✙ ✏ ✆✟✸✗✯ ★ ✙ ❄ ✯❁✞ allel rivers are deferred to Section 6. Since we do not discuss parallelism here, a very simple An eddy is implemented via a module in a river containing overview of the River framework suffices. River is a dataflow an arbitrary number of input relations, a number of partici- query engine, analogous in many ways to Gamma [DGS ✤ 90], pating unary and binary modules, and a single output relation Volcano [Gra90] and commercial parallel database engines, (Figure 1)3 . An eddy encapsulates the scheduling of its par- in which “iterator”-style modules (query operators) commu- ticipating operators; tuples entering the eddy can flow through nicate via a fixed dataflow graph (a query plan). Each mod- its operators in a variety of orders. ule runs as an independent thread, and the edges in the graph In essence, an eddy explicitly merges multiple unary and correspond to finite message queues. When a producer and binary operators into a single ✥ -ary operator within a query consumer run at differing rates, the faster thread may block plan, based on the intuition from Section 2.2 that symmetries on the queue waiting for the slower thread to catch up. As can be easily captured in an ✥ -ary operator. An eddy module in [UFA98], River is multi-threaded and can exploit barrier- maintains a fixed-sized buffer of tuples that are to be processed free algorithms by reading from various inputs at indepen- by one or more operators. Each operator participating in the dent rates. The River implementation we used derives from eddy has one or two inputs that are fed tuples by the eddy, and the work on Now-Sort [AAC ✤ 97], and features efficient I/O an output stream that returns tuples to the eddy. Eddies are so mechanisms including pre-fetching scans, avoidance of oper- named because of this circular data flow within a river. ating system buffering, and high-performance user-level net- A tuple entering an eddy is associated with a tuple descrip- working. tor containing a vector of Ready bits and Done bits, which ❂■✦✧✌✗✦✧✌ ❋✉✞✡✯ ✪❈❃ ✿☎✆✝✙ ✭❉✙ ▲☞✠✵✆✝✙ ✒ ✏ indicate respectively those operators that are elgibile to pro- cess the tuple, and those that have already processed the tuple. Although we will use eddies to reorder tables among joins, The eddy module ships a tuple only to operators for which the a heuristic pre-optimizer must choose how to initially pair off corresponding Ready bit turned on. After processing the tuple, relations into joins, with the constraint that each relation par- the operator returns it to the eddy, and the corresponding Done ticipates in only one join. This corresponds to choosing a span- bit is turned on. If all the Done bits are on, the tuple is sent ning tree of a query graph, in which nodes represent relations to the eddy’s output; otherwise it is sent to another eligible and edges represent binary joins [KBZ86]. One reasonable operator for continued processing. heuristic for picking a spanning tree forms a chain of cartesian ⑩ Nothing prevents the use of ❶ -ary operators with ❶❢❷❹❸ in an eddy, but products across any tables known to be very small (to handle since implementations of these are atypical in database query processing we do “star schemas” when base-table cardinality statistics are avail- not discuss them here. able); it then picks arbitrary equijoin edges (on the assumption 265 

6 . When an eddy receives a tuple from one of its inputs, it ze- Table Cardinality values in column ❻ roes the Done bits, and sets the Ready bits appropriately. In R 10,000 500 - 5500 the simple case, the eddy sets all Ready bits on, signifying S 80,000 0 - 5000 that any ordering of the operators is acceptable. When there T 10,000 N/A are ordering constraints on the operators, the eddy turns on U 50,000 N/A only the Ready bits corresponding to operators that can be ex- ecuted initially. When an operator returns a tuple to the eddy, Table 1: Cardinalities of tables; values are uniformly dis- the eddy turns on the Ready bit of any operator eligible to pro- tributed. cess the tuple. Binary operators generate output tuples that 250 correspond to combinations of input tuples; in these cases, the Done bits and Ready bits of the two input tuples are ORed. In this manner an eddy preserves the ordering constraints while maximizing opportunities for tuples to follow different possi- 200 completion time (secs) ble orderings of the operators. Two properties of eddies merit comment. First, note that ed- ➂ s1 before s2 s2 before s1 dies represent the full class of bushy trees corresponding to the 150 Naive set of join nodes – it is possible, for instance, that two pairs of Lottery tuples are combined independently by two different join mod- ules, and then routed to a third join to perform the 4-way con- 100 catenation of the two binary records. Second, note that eddies do not constrain reordering to moments of symmetry across the eddy as a whole. A given operator must carefully refrain from fetching tuples from certain inputs until its next moment 50 ❼ ❽ ❾ ❿ ➀ ➁ 0 2 4 6 8 10 cost of s1. of symmetry – e.g., a nested-loops join would not fetch a new tuple from the current outer relation until it finished rescan- Figure 4: Performance of two 50% selections, ➃☞➄ has cost 5, ning the inner. But there is no requirement that all operators in the eddy be at a moment of symmetry when this occurs; just ➃✵❲ varies across runs. the operator that is fetching a new tuple. Thus eddies are quite as spin loops corresponding to their relative costs, followed flexible both in the shapes of trees they can generate, and in by a randomized selection decision with the appropriate selec- the scenarios in which they can logically reorder operators. ❺ ★ ✒✴✖☎✆✝✙ ✏ ② ✫ ✖✴✿✺✳ ✯✵✄●✙ ✏ ⑧■✔✺✔✺✙ ✯✵✄ tivity. We describe the relative costs of selections in terms of abstract “delay units”; for studying optimization, the absolute number of cycles through a spin loop are irrelevant. We imple- An eddy module directs the flow of tuples from the inputs mented the simplest version of hash ripple join, identical to the through the various operators to the output, providing the flex- original pipelining hash join [WA91]; our implementation here ibility to allow each tuple to be routed individually through does not exert any statistically-motivated control over disk re- the operators. The routing policy used in the eddy determines source consumption (as in [HH99]). We simulated index joins the efficiency of the system. In this section we study some by doing random I/Os within a file, returning on average the promising initial policies; we believe that this is a rich area for number of matches corresponding to a pre-programmed selec- future work. We outline some of the remaining questions in tivity. The filesystem cache was allowed to absorb some of the Section 6. index I/Os after warming up. In order to fairly compare eddies An eddy’s tuple buffer is implemented as a priority queue to static plans, we simulate static plans via eddies that enforce with a flexible prioritization scheme. An operator is always a static ordering on tuples (setting Ready bits in the correct given the highest-priority tuple in the buffer that has the corre- order). sponding Ready bit set. For simplicity, we start by considering ❺ ✦✮✶ ➅ ✠☎✙ ❄ ✯✲⑧■✔✺✔✺❇✗➆✐✱✴✳ ✖✗✙ ✔❴➇✽❇ ✏ ✠✗✭❉✙ ☛☞✄❡✠ ✏ ✔ ❃ ✿✴✯☎✞✡✠✵✆✻✒✗✞➈✇✉✒✗✄✝✆✻✄ a very simple priority scheme: tuples enter the eddy with low priority, and when they are returned to the eddy from an oper- To illustrate how an eddy works, we consider a very simple ator they are given high priority. This simple priority scheme single-table query with two expensive selection predicates, un- ensures that tuples flow completely through the eddy before der the traditional assumption that no performance or selec- new tuples are consumed from the inputs, ensuring that the tivity properties change during execution. Our SQL query is eddy does not become “clogged” with new tuples. simply the following: ❺ ✦✧✌ ⑧✕r✵✿✴✯☎✞✓✙✮✭✰✯ ✏ ✆✻✠✗✳ ❏ ✯s✆✟✖✴✿ SELECT * FROM U In order to illustrate how eddies work, we present some initial WHERE ➃✵❲❁❨✓❵ AND ➃☞➄✗❨✓❵ ; experiments in this section; we pause briefly here to describe In our first experiment, we wish to see how well a “naive” eddy our experimental setup. All our experiments were run on a can account for differences in costs among operators. We run single-processor Sun Ultra-1 workstation running Solaris 2.6, the query multiple times, always setting the cost of ➃☞➄ to 5 with 160 MB of RAM. We used the Euphrates implementation delay units, and the selectivities of both selections to 50%. In of River [AAT ✤ 99]. We synthetically generated relations as in each run we use a different cost for ➃✵❲ , varying it between Table 1, with 100 byte tuples in each relation. 1 and 9 delay units across runs. We compare a naive eddy To allow us to experiment with costs and selectivities of se- of the two selections against both possible static orderings of lections, our selection modules are (artificially) implemented 266 

7 . 60 100 cumulative % of tuples routed to s1 first 80 completion time (secs) 50 ➋➌ s1 before s2 s2 before s1 ➐ 60 ➑➒ Naive Naive Lottery Lottery 40 40 20 30 ➉ ➉ ➉ ➉ ➉ ➉ 0 ➎ ➎ ➎ ➎ ➎ ➎ ➊ ➏ 0.0 0.2 0.4 0.6 0.8 1.0 0.0 0.2 0.4 0.6 0.8 1.0 selectivity of s1 Selectivity of s1 Figure 5: Performance of two selections of cost 5, ➃☞➄ has 50% Figure 6: Tuple flow with lottery scheme for the variable- selectivity, ➃✵❲ varies across runs. selectivity experiment(Figure 5). the two selections (and against a “lottery”-based eddy, about does not capture differing selectivities. which we will say more in Section 4.3.) One might imagine To track both consumption and production over time, we that the flexible routing in the naive eddy would deliver tuples enhance our priority scheme with a simple learning algorithm to the two selections equally: half the tuples would flow to implemented via Lottery Scheduling [WW94]. Each time the ➃✵❲ before ➃s➄ , and half to ➃☞➄ before ➃✵❲ , resulting in middling eddy gives a tuple to an operator, it credits the operator one performance over all. Figure 4 shows that this is not the case: “ticket”. Each time the operator returns a tuple to the eddy, the naive eddy nearly matches the better of the two orderings in one ticket is debited from the eddy’s running count for that op- all cases, without any explicit information about the operators’ erator. When an eddy is ready to send a tuple to be processed, relative costs. it “holds a lottery” among the operators eligible for receiving The naive eddy’s effectiveness in this scenario is due to the tuple. (The interested reader is referred to [WW94] for simple fluid dynamics, arising from the different rates of con- a simple and efficient implementation of lottery scheduling.) sumption by ➃✵❲ and ➃☞➄ . Recall that edges in a River dataflow An operator’s chance of “winning the lottery” and receiving graph correspond to fixed-size queues. This limitation has the the tuple corresponds to the count of tickets for that operator, same effect as back-pressure in a fluid flow: production along which in turn tracks the relative efficiency of the operator at the input to any edge is limited by the rate of consumption at draining tuples from the system. By routing tuples using this the output. The lower-cost selection (e.g., ➃❁❲ at the left of Fig- lottery scheme, the eddy tracks (“learns”) an ordering of the ure 4) can consume tuples more quickly, since it spends less operators that gives good overall efficiency. time per tuple; as a result the lower-cost operator exerts less The “lottery” curve in Figures 4 and 5 show the more in- back-pressure on the input table. At the same time, the high- telligent lottery-based routing scheme compared to the naive cost operator produces tuples relatively slowly, so the low-cost back-pressure scheme and the two static orderings. The lottery operator will rarely be required to consume a high-priority, scheme handles both scenarios effectively, slightly improv- previously-seen tuple. Thus most tuples are routed to the low- ing the eddy in the changing-cost experiment, and performing cost operator first, even though the costs are not explicitly ex- much better than naive in the changing-selectivity experiment. posed or tracked in any way. To explain this a bit further, in Figure 6 we display the per- ❺ ✦✮❂ ✱❁✠❁✄✻✆✰⑧✕✔✴✔✗❇✺➆●➍✵✯✵✠✵✞ ✏ ✙ ✏ ② ❏ ✯☎✳ ✯✵☛☞✆✝✙ ❄ ✙ ✆✝✙ ✯✵✄ cent of tuples that followed the order ➃✵❲✹✛✝➃☞➄ (as opposed to ➃☞➄✗✛✝➃✵❲ ) in the two eddy schemes; this roughly represents the The naive eddy works well for handling operators with differ- average ratio of lottery tickets possessed by ➃✵❲ and ➃☞➄ over ent costs but equal selectivity. But we have not yet considered time. Note that the naive back-pressure policy is barely sen- differences in selectivity. In our second experiment we keep sitive to changes in selectivity, and in fact drifts slightly in the costs of the operators constant and equal (5 units), keep the wrong direction as the selectivity of ➃✵❲ is increased. By the selectivity of ➃☞➄ fixed at 50%, and vary the selectivity of contrast, the lottery-based scheme adapts quite nicely as the ➃✵❲ across runs. The results in Figure 5 are less encouraging, selectivity is varied. showing the naive eddy performing as we originally expected, In both graphs one can see that when the costs and selec- about half-way between the best and worst plans. Clearly our tivities are close to equal ( ➃✵❲➔➓→➃☞➄➣➓↕↔s➙❁➛ ), the percent- naive priority scheme and the resulting back-pressure are in- age of tuples following the cheaper order is close to 50%. sufficient to capture differences in selectivity. This observation is intuitive, but quite significant. The lottery- To resolve this dilemma, we would like our priority scheme based eddy approaches the cost of an optimal ordering, but to favor operators based on both their consumption and pro- does not concern itself about strictly observing the optimal or- duction rate. Note that the consumption (input) rate of an oper- dering. Contrast this to earlier work on runtime reoptimiza- ator is determined by cost alone, while the production (output) tion [KD98, UFA98, IFF ✤ 99], where a traditional query op- rate is determined by a product of cost and selectivity. Since timizer runs during processing to determine the optimal plan an operator’s back-pressure on its input depends largely on its remnant. By focusing on overall cost rather than on finding consumption rate, it is not surprising that our naive scheme 267 

8 . 200 the optimal plan, the lottery scheme probabilistically provides nearly optimal performance with much less effort, allowing re-optimization to be done with an extremely lightweight tech- execution time of plan (secs) nique that can be executed multiple times for every tuple. 150 A related observation is that the lottery algorithm gets closer to perfect routing (➜➝➓➞➙ %) on the right of Figure 6 than it ➾Hash First does (➜❉➓➟❲❚➙✵➙ %) on the left. Yet in the corresponding perfor- ➽ ➚Lottery ➪Naive ➶Index First 100 mance graph (Figure 5), the differences between the lottery- based eddy and the optimal static ordering do not change much in the two settings. This phenomenon is explained by exam- ining the “jeopardy” of making ordering errors in either case. 50 Consider the left side of the graph, where the selectivity of ➃✵❲ is 10%, ➃☞➄ is 50%, and the costs of each are ◗✂➓➠↔ delay units. Let ➡ be the rate at which tuples are routed erroneously (to ➃☞➄ before ➃✵❲ in this case). Then the expected cost of the query 0 is ❨❈❲✐❯❹➡✹❵✽➢✕❲✹➤➥❲❚◗❅➦➧➡➨➢✕❲✹➤ ↔☞◗✲➓❞➤ ➩✵➡☞◗♠➦➫❲✵➤➥❲✾◗ . By contrast, in Figure 7: Performance of two joins: a selective Index Join and the second case where the selectivity of ➃✵❲ is changed to 90%, a Hash Join the expected cost is ❨❈❲❡❯➭➡s❵♥➢✗❲✹➤ ↔☞◗➈➦❹➡❡➢✗❲✹➤ ➯s◗✜➓❤➤ ➩✵➡☞◗✽➦➧❲✵➤ ↔☞◗ . Since the jeopardy is higher at 90% selectivity than at 10%, the 150 lottery more aggressively favors the optimal ordering at 90% selectivity than at 10%. ❺ ✦❺ ♣ ✒✺✙ ✏ ✄ execution time of plan (secs) 100 ➘20%, ST before SR We have discussed selections up to this point for ease of ex- ➘20%, Eddy position, but of course joins are the more common expensive ➹ ➘20%, SR before ST operator in query processing. In this section we study how 180%, ST before SR eddies interact with the pipelining ripple join algorithms. For 180%, Eddy 180%, SR before ST the moment, we continue to study a static performance envi- 50 ronment, validating the ability of eddies to do well even in scenarios where static techniques are most effective. We begin with a simple 3-table query: SELECT * FROM ✚✜✛✝✢❍✛❈✣ 0 WHERE ✚✜➤ ❻✰➓➧✢❍➤ ❻ AND ✢❍➤ ➲♠➓❹✣✂➤ ➲ Figure 8: Performance of hash joins ✚➴❩❪❭❳✢ and ✢❤❩❪❭❹✣ . ✚➣❩❪❭➺✢ has selectivity 100% w.r.t. ✢ , the selectivity of ✢❴❩❪❭✐✣ w.r.t. ✢ varies between 20% and 180% in the two runs. In our experiment, we constructed a preoptimized plan with a hash ripple join between ✚ and ✢ , and an index join between ✢ and ✣ . Since our data is uniformly distributed, Table 1 in- dicates that the selectivity of the ✚✐✢ join is ❲✵➤ ➳❱⑨➝❲✘➙✺➵■➸ ; its quite close in the case of the experiment where the hash join selectivity with respect to ✢ is 180% – i.e., each ✢ tuple enter- should precede the index join. In this case, the relative cost ing the join finds 1.8 matching ✚ tuples on average [Hel98]. of index join is so high that the jeopardy of choosing it first We artificially set the selectivity of the index join w.r.t. ✢ to be drives the hash join to nearly always win the lottery. ❲✘➙✵➛ (overall selectivity ❲♦⑨➺❲❚➙ ➵➼➻ ). Figure 7 shows the relative ❺ ✦✮➷ ★ ✯✵✄✾✿✴✒ ✏ ✔✴✙ ✏ ②❥✆✻✒◆➇✽❇ ✏ ✠✗✭❉✙ ☛❱✱✕✳ ✖✺☛✘✆✟✖✗✠✹✆✝✙ ✒ ✏ ✄ performance of our two eddy schemes and the two static join orderings. The results echo our results for selections, show- Eddies should adaptively react over time to the changes in ing the lottery-based eddy performing nearly optimally, and performance and data characteristics described in Section 1.1. the naive eddy performing in between the best and worst static The routing schemes described up to this point have not con- plans. sidered how to achieve this. In particular, our lottery scheme As noted in Section 2.2.1, index joins are very analogous to weighs all experiences equally: observations from the distant selections. Hash joins have more complicated and symmetric past affect the lottery as much as recent observations. As a re- behavior, and hence merit additional study. Figure 8 presents sult, an operator that earns many tickets early in a query may performance of two hash-ripple-only versions of this query. become so wealthy that it will take a great deal of time for it Our in-memory pipelined hash joins all have the same cost. to lose ground to the top achievers in recent history. We change the data in ✚✜✛✝✢ and ✣ so that the selectivity of the To avoid this, we need to modify our point scheme to for- ✢♦✣ join w.r.t. ✢ is 20% in one version, and 180% in the other. get history to some extent. One simple way to do this is to In all runs, the selectivity of the ✚✐✢ join predicate w.r.t. ✢ is use a window scheme, in which time is partitioned into win- fixed at 100%. As the figure shows, the lottery-based eddy dows, and the eddy keeps track of two counts for each op- continues to perform nearly optimally. erator: a number of banked tickets, and a number of escrow Figure 9 shows the percent of tuples in the eddy that follow tickets. Banked tickets are used when running a lottery. Es- one order or the other in all four join experiments. While the crow tickets are used to measure efficiency during the win- eddy is not strict about following the optimal ordering, it is dow. At the beginning of the window, the value of the es- 268 

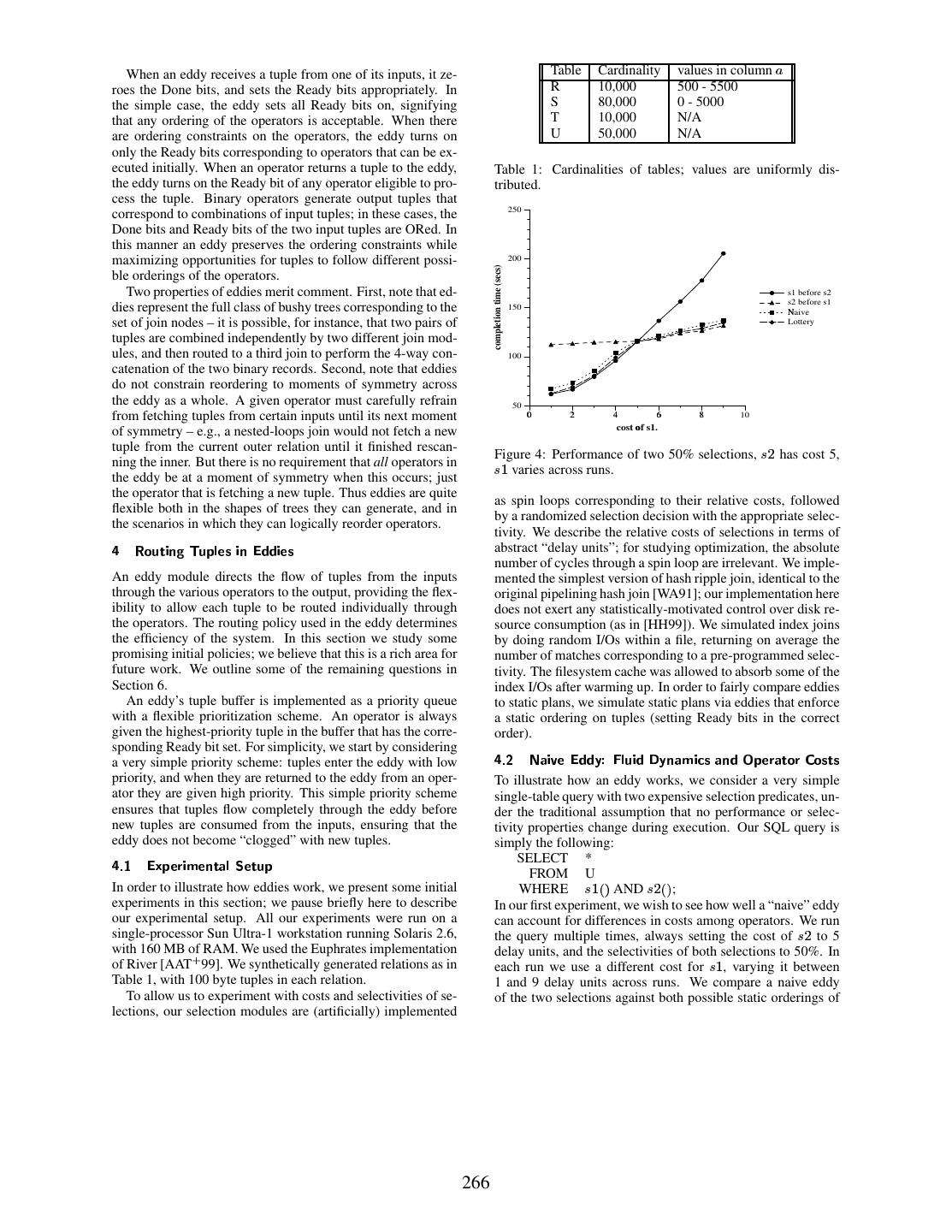
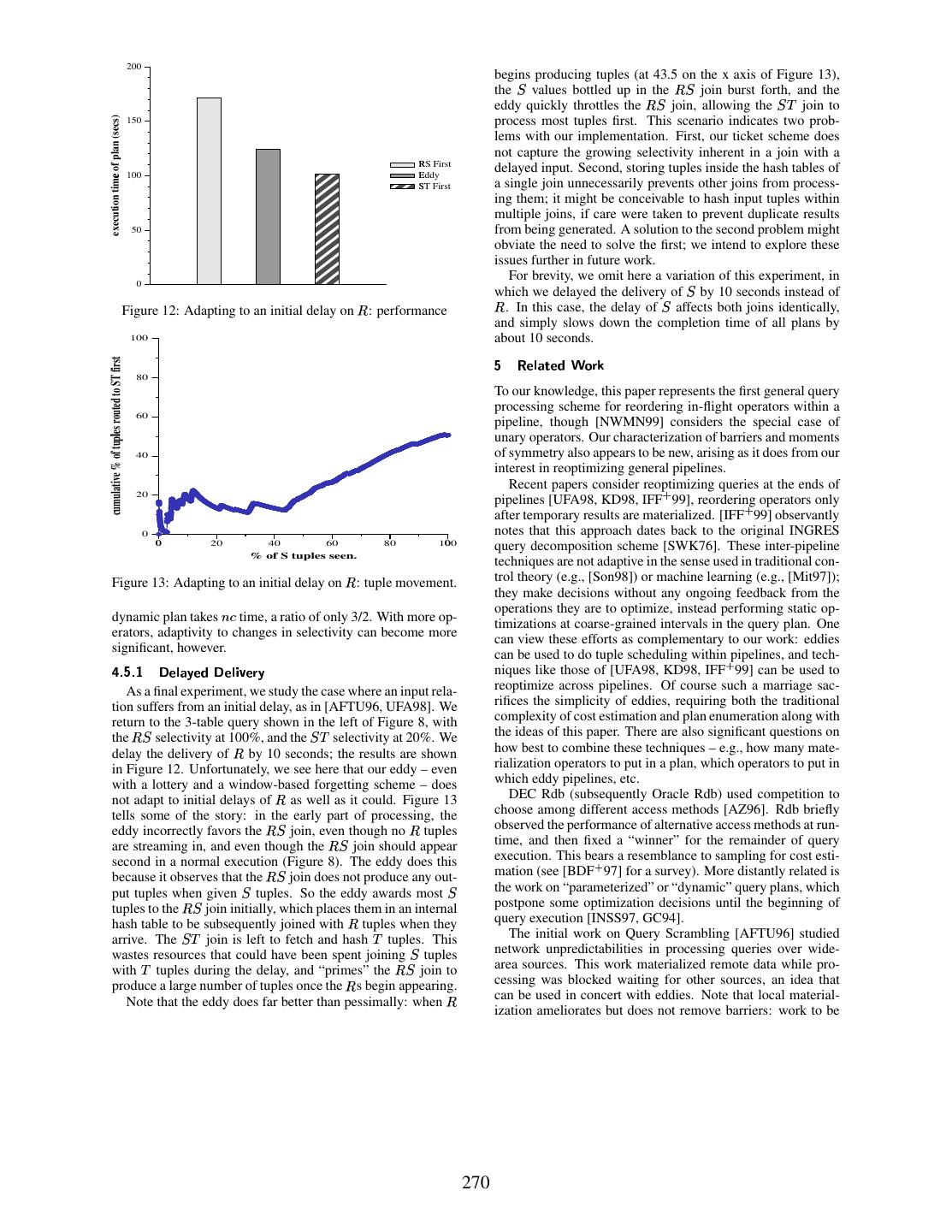
9 . 100 cumulative % of tuples routed to Index #1 first. cumulative % of tuples routed to the correct join first 100 80 80 60 ➬ 60 index beats hash hash beats index hash/hash 20% hash/hash 180% 40 40 20 20 0 0 ❮ ❮ ❰ 0 20 40 60 80 100 % of tuples seen. Figure 9: Percent of tuples routed in the optimal order in all of Figure 11: Adapting to changing join costs: tuple movement. the join experiments. plan (✃☞❐✘❒ before ✃✘❒❈❐ ), the initial join begins fast, processing 5000 about 29,000 tuples, and passing about 290 of those to the sec- ond (slower) join. After 30 seconds, the second join becomes fast and handles the remainder of the 290 tuples quickly, while execution time of plan (secs) 4000 the first join slowly processes the remaining 1,000 tuples at 5 seconds per tuple. The eddy outdoes both static plans: in the 3000 first phase it behaves identically to the second static plan, con- ➮ I_sf first suming 29,000 tuples and queueing 290 for the eddy to pass to ✃ ❒❈❐ . Just after phase 2 begins, the eddy adapts its ordering Eddy and passes tuples to ✃✘❒❈❐ – the new fast join – first. As a result, I_fs first 2000 the eddy spends 30 seconds in phase one, and in phase two it has less then 290 tuples queued at ✃✘❒⑦❐ (now fast), and only 1000 1,000 tuples to process, only about 10 of which are passed to ✃ ❐✘❒ (now slow). A similar, more controlled experiment illustrates the eddy’s 0 adaptability more clearly. Again, we run a three-table join, Figure 10: Adapting to changing join costs: performance. with two external indexes that return a match 10% of the time. We read 4,000 tuples from the scanned table, and toggle costs between 1 and 100 cost units every 1000 tuples – i.e., three crow account replaces the value of the banked account (i.e., times during the experiment. Figure 11 shows that the eddy banked = escrow), and the escrow account is reset (es- adapts correctly, switching orders when the operator costs crow = 0). This scheme ensures that operators “re-prove switch. Since the cost differential is less dramatic here, the themselves” each window. jeopardy is lower and the eddy takes a bit longer to adapt. De- We consider a scenario of a 3-table equijoin query, where spite the learning time, the trends are clear – the eddy sends two of the tables are external and used as “inner” relations most of the first 1000 tuples to index #1 first, which starts off by index joins. Our third relation has 30,000 tuples. Since cheap. It sends most of the second 1000 tuples to index #2 we assume that the index servers are remote, we implement first, causing the overall percentage of tuples to reach about the “cost” in our index module as a time delay (i.e., while (gettimeofday() ➱ x) ;) rather than a spin loop; this 50%, as reflected by the near-linear drift toward 50% in the second quarter of the graph. This pattern repeats in the third better models the behavior of waiting on an external event like and fourth quarters, with the eddy eventually displaying an a network response. We have two phases in the experiment: initially, one index (call it ✃☞❐✘❒ ) is fast (no time delay) and the even use of the two orderings over time – always favoring the other (✃ ❒⑦❐ ) is slow (5 seconds per lookup). After 30 seconds best ordering. For brevity, we omit here a similar experiment in which we begin the second phase, in which the two indexes swap speeds: the ✃☞❐✘❒ index becomes slow, and ✃✘❒⑦❐ becomes fast. we fixed costs and modified selectivity over time. The re- sults were similar, except that changing only the selectivity of Both indexes return a single matching tuple 1% of the time. two operators results in less dramatic benefits for an adaptive Figure 10 shows the performance of both possible static scheme. This can be seen analytically, for two operators of cost ◗ whose selectivites are swapped from low to hi in a man- plans, compared with an eddy using a lottery with a window scheme. As we would hope, the eddy is much faster than ei- ther static plan. In the first static plan (✃✘❒⑦❐ before ✃☞❐✘❒ ), the ner analogous to our previous experiment. To lower-bound the performance of either static ordering, selectivities should be initial index join in the plan is slow in the first phase, process- toggled to their extremes (100% and 0%) for equal amounts of time – so that half the ✥ tuples go through both operators. Ei- ing only 6 tuples and discarding all of them. In the remainder ther static plan thus takes ✥✼◗✹➦❜❲✘Ï✵➄s✥✼◗ time, whereas an optimal of the run, the plan quickly discards 99% of the tuples, passing 300 to the (now) expensive second join. In the second static 269 

10 . 200 begins producing tuples (at 43.5 on the x axis of Figure 13), the ✢ values bottled up in the ✚✐✢ join burst forth, and the eddy quickly throttles the ✚✐✢ join, allowing the ✢♦✣ join to execution time of plan (secs) 150 process most tuples first. This scenario indicates two prob- lems with our implementation. First, our ticket scheme does ÑRS First not capture the growing selectivity inherent in a join with a Ð ÒEddy delayed input. Second, storing tuples inside the hash tables of 100 ÓST First a single join unnecessarily prevents other joins from process- ing them; it might be conceivable to hash input tuples within multiple joins, if care were taken to prevent duplicate results 50 from being generated. A solution to the second problem might obviate the need to solve the first; we intend to explore these issues further in future work. For brevity, we omit here a variation of this experiment, in which we delayed the delivery of ✢ by 10 seconds instead of 0 Figure 12: Adapting to an initial delay on ✚ : performance ✚ . In this case, the delay of ✢ affects both joins identically, and simply slows down the completion time of all plans by 100 about 10 seconds. ➷ ★ ✯☎✳ ✠✹✆✻✯❁✔❱×Ø✒✗✞❈Ù cumulative % of tuples routed to ST first 80 To our knowledge, this paper represents the first general query processing scheme for reordering in-flight operators within a 60 Õ pipeline, though [NWMN99] considers the special case of unary operators. Our characterization of barriers and moments 40 of symmetry also appears to be new, arising as it does from our interest in reoptimizing general pipelines. Recent papers consider reoptimizing queries at the ends of 20 pipelines [UFA98, KD98, IFF ✤ 99], reordering operators only after temporary results are materialized. [IFF ✤ 99] observantly notes that this approach dates back to the original INGRES 0 Ô 0 20 40 60 80 100Ô query decomposition scheme [SWK76]. These inter-pipeline % of S tuples seen. techniques are not adaptive in the sense used in traditional con- Figure 13: Adapting to an initial delay on ✚ : tuple movement. trol theory (e.g., [Son98]) or machine learning (e.g., [Mit97]); they make decisions without any ongoing feedback from the dynamic plan takes ✥✼◗ time, a ratio of only 3/2. With more op- operations they are to optimize, instead performing static op- timizations at coarse-grained intervals in the query plan. One erators, adaptivity to changes in selectivity can become more can view these efforts as complementary to our work: eddies significant, however. ❺ ✦✮➷■✦✧✌ ➇✽✯☎✳ ✠✹❇✘✯✵✔Ö➇✽✯☎✳ ✙ ❄ ✯❁✞✓❇ can be used to do tuple scheduling within pipelines, and tech- niques like those of [UFA98, KD98, IFF ✤ 99] can be used to As a final experiment, we study the case where an input rela- reoptimize across pipelines. Of course such a marriage sac- tion suffers from an initial delay, as in [AFTU96, UFA98]. We rifices the simplicity of eddies, requiring both the traditional return to the 3-table query shown in the left of Figure 8, with complexity of cost estimation and plan enumeration along with the ✚✐✢ selectivity at 100%, and the ✢❍✣ selectivity at 20%. We the ideas of this paper. There are also significant questions on delay the delivery of ✚ by 10 seconds; the results are shown how best to combine these techniques – e.g., how many mate- in Figure 12. Unfortunately, we see here that our eddy – even rialization operators to put in a plan, which operators to put in with a lottery and a window-based forgetting scheme – does which eddy pipelines, etc. not adapt to initial delays of ✚ as well as it could. Figure 13 DEC Rdb (subsequently Oracle Rdb) used competition to tells some of the story: in the early part of processing, the choose among different access methods [AZ96]. Rdb briefly eddy incorrectly favors the ✚✐✢ join, even though no ✚ tuples observed the performance of alternative access methods at run- are streaming in, and even though the ✚✐✢ join should appear time, and then fixed a “winner” for the remainder of query execution. This bears a resemblance to sampling for cost esti- mation (see [BDF ✤ 97] for a survey). More distantly related is second in a normal execution (Figure 8). The eddy does this because it observes that the ✚✐✢ join does not produce any out- put tuples when given ✢ tuples. So the eddy awards most ✢ the work on “parameterized” or “dynamic” query plans, which tuples to the ✚✐✢ join initially, which places them in an internal postpone some optimization decisions until the beginning of hash table to be subsequently joined with ✚ tuples when they query execution [INSS97, GC94]. arrive. The ✢♦✣ join is left to fetch and hash ✣ tuples. This The initial work on Query Scrambling [AFTU96] studied wastes resources that could have been spent joining ✢ tuples network unpredictabilities in processing queries over wide- with ✣ tuples during the delay, and “primes” the ✚●✢ join to area sources. This work materialized remote data while pro- produce a large number of tuples once the ✚ s begin appearing. cessing was blocked waiting for other sources, an idea that Note that the eddy does far better than pessimally: when ✚ can be used in concert with eddies. Note that local material- ization ameliorates but does not remove barriers: work to be 270 

11 .done locally after a barrier can still be quite significant. Later of output from a plan, and the rate of refinement for online ag- work focused on rescheduling runnable sub-plans during ini- gregation estimators. We have also begun studying schemes to tial delays in delivery [UFA98], but did not attempt to reorder allow eddies to effectively order dependent predicates, based in-flight operators as we do here. on reinforcement learning [SB98]. In a related vein, we would Two out-of-core versions of the pipelined hash join have like to automatically tune the aggressiveness with which we been proposed recently [IFF ✤ 99, UF99]. The X-Join [UF99] forget past observations, so that we avoid introducing a tun- enhances the pipelined hash join not only by handling the out- ing knob to adjust window-length or some analogous constant of-core case, but also by exploiting delay time to aggressively (e.g., a hysteresis factor). match previously-received (and spilled) tuples. We intend to Another main goal is to attack the remaining static aspects experiment with X-Joins and eddies in future work. of our scheme: the “pre-optimization” choices of spanning The Control project [HAC ✤ 99] studies interactive analysis tree, join algorithms, and access methods. Following [AZ96], of massive data sets, using techniques like online aggregation, we believe that competition is key here: one can run multi- online reordering and ripple joins. There is a natural syn- ple redundant joins, join algorithms, and access methods, and ergy between interactive and adaptive query processing; online track their behavior in an eddy, adaptively choosing among techniques to pipeline best-effort answers are naturally adap- them over time. The implementation challenge in that sce- tive to changing performance scenarios. The need for opti- nario relates to preventing duplicates from being generated, mizing pipelines in the Control project initially motivated our while the efficiency challenge comes in not wasting too many work on eddies. The Control project [HAC ✤ 99] is not ex- computing resources on unpromising alternatives. plicitly related to the field of control theory [Son98], though A third major challenge is to harness the parallelism and eddies appears to link the two in some regards. adaptivity available to us in rivers. Massively parallel systems The River project [AAT ✤ 99] was another main inspiration are reaching their limit of manageability, even as data sizes of this work. River allows modules to work as fast as they continue to grow very quickly. Adaptive techniques like ed- can, naturally balancing flow to whichever modules are faster. dies and rivers can significantly aid in the manageability of a We carried the River philosophy into the intial back-pressure new generation of massively parallel query processors. Rivers design of eddies, and intend to return to the parallel load- have been shown to adapt gracefully to performance changes balancing aspects of the optimization problem in future work. in large clusters, spreading query processing load across nodes In addition to commercial projects like those in Section 1.2, and spreading data delivery across data sources. Eddies face there have been numerous research systems for heterogeneous additional challenges to meet the promise of rivers: in particu- data integration, e.g. [GMPQ ✤ 97, HKWY97, IFF ✤ 99], etc. lar, reoptimizing queries with intra-operator parallelism entails Ú ✇✉✒ ✏ ☛✹✳ ✖☎✄✾✙ ✒ ✏ ✄❡✠ ✏ ✔Û✱✗✖❁✆✟✖✺✞✓✯❀×Ø✒✗✞❈Ù repartitioning data, which adds an expense to reordering that was not present in our single-site eddies. An additional com- Query optimization has traditionally been viewed as a coarse- plication arises when trying to adaptively adjust the degree of grained, static problem. Eddies are a query processing mech- partitioning for each operator in a plan. On a similar note, we anism that allow fine-grained, adaptive, online optimization. would like to explore enhancing eddies and rivers to tolerate Eddies are particularly beneficial in the unpredictable query failures of sources or of participants in parallel execution. processing environments prevalent in massive-scale systems, Finally, we are exploring the application of eddies and rivers and in interactive online query processing. They fit naturally to the generic space of dataflow programming, including appli- with algorithms from the Ripple Join family, which have fre- cations such as multimedia analysis and transcoding, and the quent moments of symmetry and adaptive or non-existent syn- composition of scalable, reliable internet services [GWBC99]. chronization barriers. Eddies can be used as the sole optimiza- Our intent is for rivers to serve as a generic parallel dataflow tion mechanism in a query processing system, obviating the engine, and for eddies to be the main scheduling mechanism need for much of the complex code required in a traditional in that environment. query optimizer. Alternatively, eddies can be used in con-  ➈☛✵Ù ✏ ✒❁❆❅✳ ✯✵✔✺②✴✭✰✯ ✏ ✆✻✄ cert with traditional optimizers to improve adaptability within pipelines. Our initial results indicate that eddies perform well Vijayshankar Raman provided much assistance in the course under a variety of circumstances, though some questions re- of this work. Remzi Arpaci-Dusseau, Eric Anderson and Noah main in improving reaction time and in adaptively choosing Treuhaft implemented Euphrates, and helped implement ed- join orders with delayed sources. We are sufficiently encour- dies. Mike Franklin asked hard questions and suggested direc- aged by these early results that we are using eddies and rivers tions for future work. Stuart Russell, Christos Papadimitriou, as the basis for query processing in the Telegraph system. Alistair Sinclair, Kris Hildrum and Lakshminarayanan Subra- In order to focus our energies in this initial work, we have manian all helped us focus on formal issues. Thanks to Navin explicitly postponed a number of questions in understanding, Kabra and Mitch Cherniack for initial discussions on run-time tuning, and extending these results. One main challenge is reoptimization, and to the database group at Berkeley for feed- to develop eddy “ticket” policies that can be formally proved back. Stuart Russell suggested the term “eddy”. to converge quickly to a near-optimal execution in static sce- This work was done while both authors were at UC Berke- narios, and that adaptively converge when conditions change. ley, supported by a grant from IBM Corporation, NSF grant This challenge is complicated by considering both selections IIS-9802051, and a Sloan Foundation Fellowship. Computing and joins, including hash joins that “absorb” tuples into their and network resources for this research were provided through hash tables as in Section 4.5.1. We intend to focus on multiple NSF RI grant CDA-9401156. performance metrics, including time to completion, the rate 271 

12 .★ ✯s❊✡✯☎✞✡✯ ✏ ☛s✯✹✄ [HH99] P. J. Haas and J. M. Hellerstein. Ripple Joins for Online Ag- [AAC Ü 97] gregation. In Proc. ACM-SIGMOD International Conference on A. C. Arpaci-Dusseau, R. H. Arpaci-Dusseau, D. E. Culler, J. M. Management of Data, pages 287–298, Philadelphia, 1999. Hellerstein, and D. A. Patterson. High-Performance Sorting on Networks of Workstations. In Proc. ACM-SIGMOD Interna- [HKWY97] L. Haas, D. Kossmann, E. Wimmers, and J. Yang. Optimizing tional Conference on Management of Data, Tucson, May 1997. Queries Across Diverse Data Sources. In Proc. 23rd Interna- [AAT 99] Ü R. H. Arpaci-Dusseau, E. Anderson, N. Treuhaft, D. E. Culler, tional Conference on Very Large Data Bases (VLDB), Athens, 1997. J. M. Hellerstein, D. A. Patterson, and K. Yelick. Cluster I/O with River: Making the Fast Case Common. In Sixth Workshop [HSC99] J. M. Hellerstein, M. Stonebraker, and R. Caccia. Open, Inde- on I/O in Parallel and Distributed Systems (IOPADS ’99), pages pendent Enterprise Data Integration. IEEE Data Engineering 10–22, Atlanta, May 1999. Bulletin, 22(1), March 1999. http://www.cohera.com. [AFTU96] L. Amsaleg, M. J. Franklin, A. Tomasic, and T. Urhan. Scram- Ü [IFF 99] Z. G. Ives, D. Florescu, M. Friedman, A. Levy, and D. S. Weld. bling Query Plans to Cope With Unexpected Delays. In 4th In- An Adaptive Query Execution System for Data Integration. In ternational Conference on Parallel and Distributed Information Proc. ACM-SIGMOD International Conference on Management Systems (PDIS), Miami Beach, December 1996. of Data, Philadelphia, 1999. [IK84] T. Ibaraki and T. Kameda. Optimal Nesting for Computing [AH99] R. Avnur and J. M. Hellerstein. Continuous query optimization. N-relational Joins. ACM Transactions on Database Systems, Technical Report CSD-99-1078, University of California, Berke- 9(3):482–502, October 1984. ley, November 1999. [INSS97] Y. E. Ioannidis, R. T. Ng, K. Shim, and T. K. Sellis. Parametric [Aok99] P. M. Aoki. How to Avoid Building DataBlades That Know the Query Optimization. VLDB Journal, 6(2):132–151, 1997. Value of Everything and the Cost of Nothing. In 11th Interna- tional Conference on Scientific and Statistical Database Man- [KBZ86] R. Krishnamurthy, H. Boral, and C. Zaniolo. Optimization of agement, Cleveland, July 1999. Nonrecursive Queries. In Proc. 12th International Conference on Very Large Databases (VLDB), pages 128–137, August 1986. [AZ96] G. Antoshenkov and M. Ziauddin. Query Processing and Opti- mization in Oracle Rdb. VLDB Journal, 5(4):229–237, 1996. [KD98] N. Kabra and D. J. DeWitt. Efficient Mid-Query Reoptimization of Sub-Optimal Query Execution Plans. In Proc. ACM-SIGMOD [Bar99] R. Barnes. Scale Out. In High Performance Transaction Pro- International Conference on Management of Data, pages 106– cessing Workshop (HPTS ’99), Asilomar, September 1999. 117, Seattle, 1998. Ü [BDF 97] D. Barbara, W. DuMouchel, C. Faloutsos, P. J. Haas, J. M. [Met97] R. Van Meter. Observing the Effects of Multi-Zone Disks. In Hellerstein, Y. E. Ioannidis, H. V. Jagadish, T. Johnson, R. T. Proceedings of the Usenix 1997 Technical Conference, Anaheim, Ng, V. Poosala, K. A. Ross, and K. C. Sevcik. The New Jersey January 1997. Data Reduction Report. IEEE Data Engineering Bulletin, 20(4), [Mit97] T. Mitchell. Machine Learning. McGraw Hill, 1997. December 1997. [NWMN99] K. W. Ng, Z. Wang, R. R. Muntz, and S. Nittel. Dynamic Query [BO99] J. Boulos and K. Ono. Cost Estimation of User-Defined Meth- Re-Optimization. In 11th International Conference on Scientific ods in Object-Relational Database Systems. SIGMOD Record, and Statistical Database Management, Cleveland, July 1999. Ü 28(3):22–28, September 1999. [DGS 90] Ü D. J. DeWitt, S. Ghandeharizadeh, D. Schneider, A. Bricker, [RPK 99] B. Reinwald, H. Pirahesh, G. Krishnamoorthy, G. Lapis, B. Tran, and S. Vora. Heterogeneous Query Processing Through SQL Ta- H.-I Hsiao, and R. Rasmussen. The Gamma database machine ble Functions. In 15th International Conference on Data Engi- project. IEEE Transactions on Knowledge and Data Engineer- neering, pages 366–373, Sydney, March 1999. ing, 2(1):44–62, Mar 1990. [DKO 84] Ü D. J. DeWitt, R. H. Katz, F. Olken, L. D. Shapiro, M. R. Stone- [RRH99] V. Raman, B. Raman, and J. M. Hellerstein. Online Dynamic Reordering for Interactive Data Processing. In Proc. 25th Inter- braker, and D. Wood. Implementation Techniques for Main national Conference on Very Large Data Bases (VLDB), pages Memory Database Systems. In Proc. ACM-SIGMOD Interna- 709–720, Edinburgh, 1999. tional Conference on Management of Data, pages 1–8, Boston, June 1984. [SB98] R. S. Sutton and A. G. Bartow. Reinforcement Learning. MIT Press, Cambridge, MA, 1998. [FMLS99] D. Florescu, I. Manolescu, A. Levy, and D. Suciu. Query Optimization in the Presence of Limited Access Patterns. In [SBH98] M. Stonebraker, P. Brown, and M. Herbach. Interoperability, Proc. ACM-SIGMOD International Conference on Management Distributed Applications, and Distributed Databases: The Virtual of Data, Phildelphia, June 1999. Table Interface. IEEE Data Engineering Bulletin, 21(3):25–34, September 1998. [GC94] G. Graefe and R. Cole. Optimization of Dynamic Query Evalua- [Son98] E. D. Sontag. Mathematical Control Theory: Deterministic tion Plans. In Proc. ACM-SIGMOD International Conference on Finite-Dimensional Systems, Second Edition. Number 6 in Texts Management of Data, Minneapolis, 1994. in Applied Mathematics. Springer-Verlag, New York, 1998. Ü [GMPQ 97] H. Garcia-Molina, Y. Papakonstantinou, D. Quass, A Rajaraman, [SWK76] M. R. Stonebraker, E. Wong, and P. Kreps. The Design and Im- Y. Sagiv, J. Ullman, and J. Widom. The TSIMMIS Project: Inte- plementation of INGRES. ACM Transactions on Database Sys- gration of Heterogeneous Information Sources. Journal of Intel- tems, 1(3):189–222, September 1976. ligent Information Systems, 8(2):117–132, March 1997. [UF99] T. Urhan and M. Franklin. XJoin: Getting Fast Answers From [Gra90] G. Graefe. Encapsulation of Parallelism in the Volcano Query Slow and Bursty Networks. Technical Report CS-TR-3994, Uni- Processing System. In Proc. ACM-SIGMOD International Con- versity of Maryland, February 1999. ference on Management of Data, pages 102–111, Atlantic City, May 1990. [UFA98] T. Urhan, M. Franklin, and L. Amsaleg. Cost-Based Query Scrambling for Initial Delays. In Proc. ACM-SIGMOD Interna- [GWBC99] S. D. Gribble, M. Welsh, E. A. Brewer, and D. Culler. The Multi- tional Conference on Management of Data, Seattle, June 1998. Space: an Evolutionary Platform for Infrastructural Services. In Proceedings of the 1999 Usenix Annual Technical Conference, [WA91] A. N. Wilschut and P. M. G. Apers. Dataflow Query Execution Monterey, June 1999. in a Parallel Main-Memory Environment. In Proc. First Interna- Ü tional Conference on Parallel and Distributed Info. Sys. (PDIS), [HAC 99] J. M. Hellerstein, R. Avnur, A. Chou, C. Hidber, C. Olston, pages 68–77, 1991. V. Raman, T. Roth, and P. J. Haas. Interactive Data Analysis: The [WW94] C. A. Waldspurger and W. E. Weihl. Lottery scheduling: Flex- Control Project. IEEE Computer, 32(8):51–59, August 1999. ible proportional-share resource management. In Proc. of the [Hel98] J. M. Hellerstein. Optimization Techniques for Queries with First Symposium on Operating Systems Design and Implemen- Expensive Methods. ACM Transactions on Database Systems, tation (OSDI ’94), pages 1–11, Monterey, CA, November 1994. 23(2):113–157, 1998. USENIX Assoc. 272